| Главная > Учебные материалы > Математика: Функция | ||||
1.Понятие функции. 2.Свойства функций. 3.Основные элементарные функции.
|
||||
| 1 2 3 4 5 6 7 8 9 | ||||
1. Понятие функции Понятие «функция» является одним из основных понятий в математике. Под функцией понимают некий закон, по которому одна переменная величина зависит от другой. Согласно определению, если каждому значению переменной х множества Х ставится в соответствие одно определенное значение переменной у множества Y, то такое соответствие называется функцией. Исходя из этого, можно дать другую формулировку: однозначное соответствие двух переменных величин на множестве действительных чисел R называется функцией.
|
||||
2. Cвойства функций1.Четность и нечетность. Функция f(x) называется четной, если ее значения симметричны относительно оси OY, т.е. f(-x) = f(x). Функция f(x) называется нечетной, если ее значение изменяется на противоположное при изменении переменной х на -х , т.е. f(-x) = -f(x). В противном случае функция называется функцией общего вида. 2.Монотонность. 3.Периодичность. Если значение функции f(x) повторяется через определенный период Т, то функция называется периодической с периодом Т ≠ 0 , т.е. f(x + T) = f(x). В противном случае непериодической. 4. Ограниченность. Функция f (x) называется ограниченной на промежутке Х, если существует такое положительное число М > 0 , что для любого x, принадлежащего промежутку Х, | f (x) | < M. В противном случае функция называется неограниченной.
|
||||
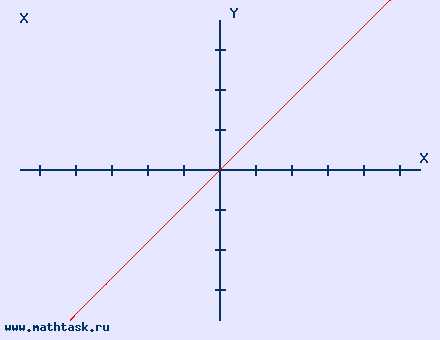
3. Основные элементарные функцииСтепенная функция у = х |
|
|||
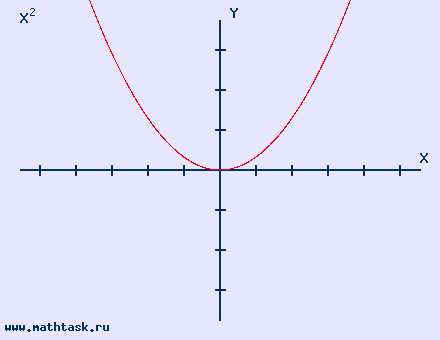
| у = х² область определения (-∞,∞) |
|
|||
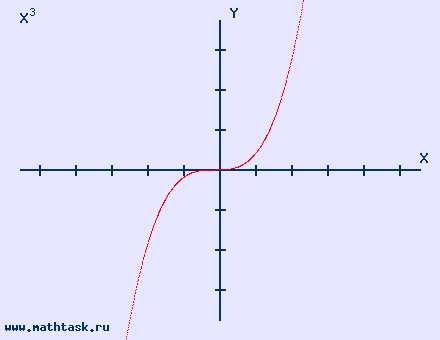
| у = х³ область определения (-∞,∞) нечетная возрастает на (-∞,∞) непериодическая |
|
|||
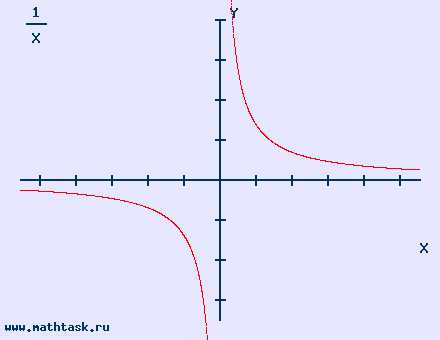
| у = 1/х область определения (-∞,0)U(0,∞) |
|
|||
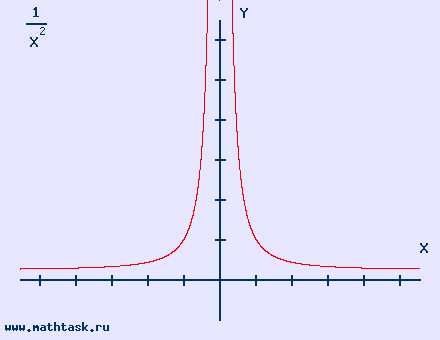
| у = 1/х² область определения (-∞,0)U(0,∞) |
|
|||
|
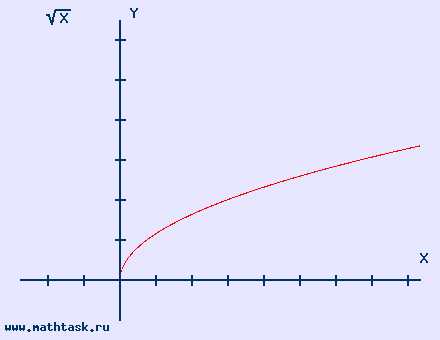
область определения [0,∞) |
|
|||
|
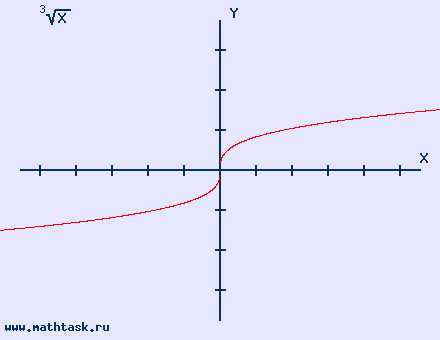
область определения (-∞,∞) |
|
|||
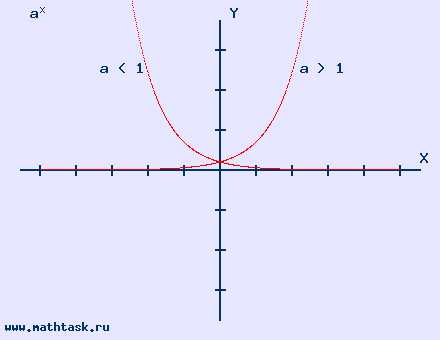
Показательная функция у = а ͯ (a>0 a≠1) область определения (-∞,∞) |
|
|||
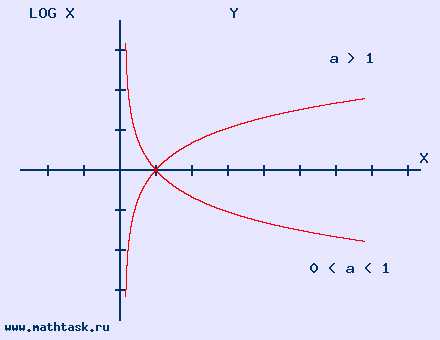
Логарифмическая функция у = log ₐ x (a>0 a≠1) область определения (0,∞) |
|
|||
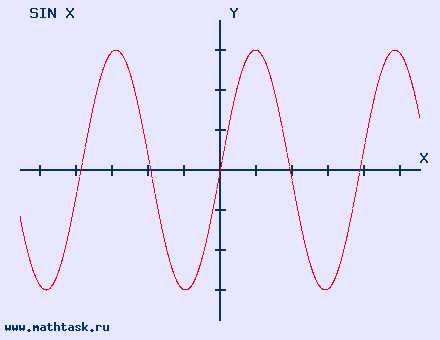
Тригонометрические функции y = sin x область определения (-∞; ∞) |
|
|||
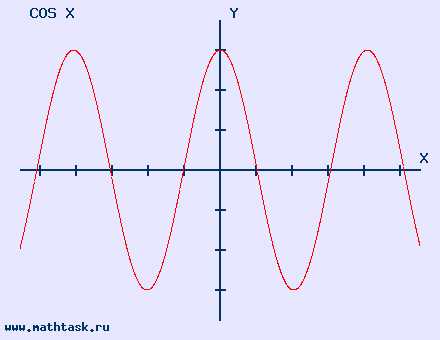
y = cos x область определения (-∞; ∞) |
|
|||
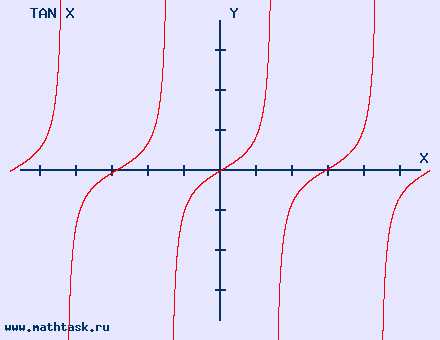
y = tg x область определения |
|
|||
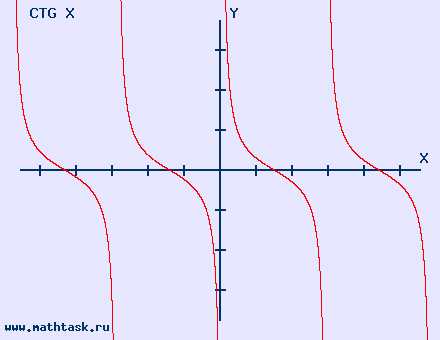
y = ctg x область определения |
|
|||
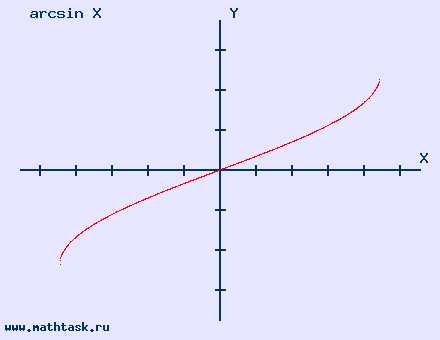
y = arcsin x область определения [-1; 1] |
|
|||
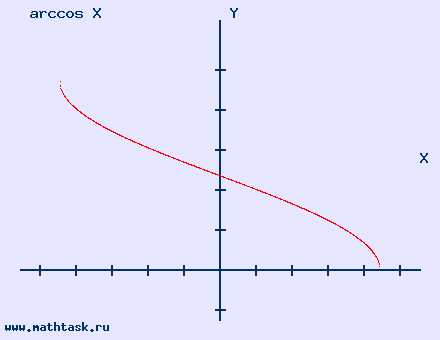
y = arccos x область определения [-1; 1] |
|
|||
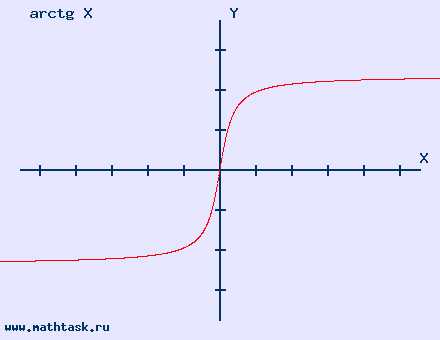
y = arctg x область определения (-∞; ∞) |
|
|||
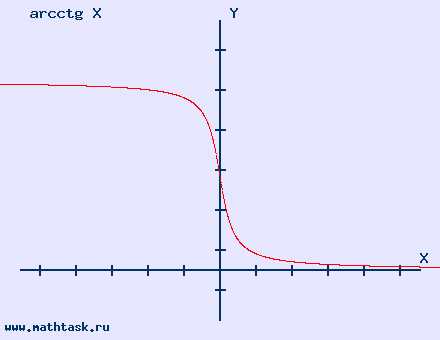
y = arcctg x область определения (-∞; ∞) |
 |
|||
 |
||||
Пример 1.Найти область определения функции.
|
||||
Пример 2Выяснить четность или нечетность функции.
|
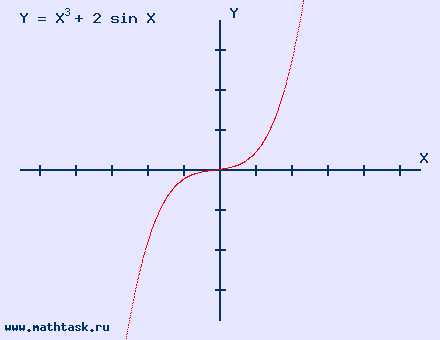
График функции y=x³+2sin x |
|||
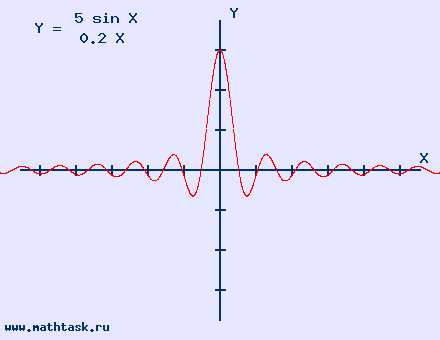
Пример 3 |
||||
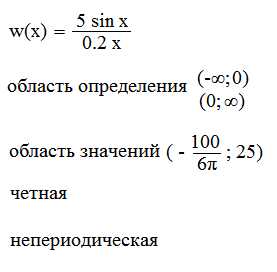 |
 |
|||
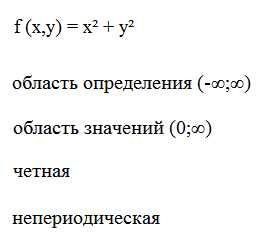 |
 |
|||
| 1 2 3 4 5 6 7 8 9 | ||||
www.mathtask.ru
Значение функции это x или y — Функция это x или y ? — 22 ответа
X это
В разделе Естественные науки на вопрос Функция это x или y ? заданный автором Павел Барамыков лучший ответ это пример:
y=5х+(3-1,6х)
здесь y — функция. .
х — это переменная, от которой и зависит значание самой функции
Привет! Вот подборка тем с ответами на Ваш вопрос: Функция это x или y ?
Ответ от Невропатолог[новичек]
это у
Ответ от АЛЬБЕРТ МАМОНТОВ[мастер]
Конечно y.
Как ты так учишься что даже не знаешь что такое y и x?
Ответ от Допроситься[новичек]
пример:
y=5х+(3-1,6х)
здесь y — функция. .
х — это переменная, от которой и зависит значание самой функции
Ответ от Присосок[новичек]
Y — функция
X — аргумент
Ответ от Ѝкстраполятор[гуру]
Функция — это зависимость одной величины от другой, необязательно в виде математической формулы. (График, таблицы значений) .
Для конкретности обычно обозначают У величину, которую определяют (и называют функцией) , а Х — величина (называемая аргументом) , от которой каким-то образом зависит У.
Точно так же можно сказать, например, по закону Ома: I = U/R. Как видно из формулы, функция — I, а вот аргумент может быть один (U или R). а могут быть одновременно и оба.
В таком случае уже будет функция двух аргументов.
Ответ от Максим Вирус[эксперт]
Функция — это f, g,h… в зависимости кто ее задал.
А точнее это отображение множества х в у, или наоборот у в х, и обозначением того самого отображения и есть f,g,h…
*при условии что функция от одной переменной
Ответ от Elena lusuca[гуру]
допустим икс равно функция от игрек
Ответ от Nick Storozhev[гуру]
у, х — аргумент
Ответ от Kaletta[гуру]
То, от чего зависит, это аргумент, а то, что зависит — функция. Какими буквами это назвать не имеет значения, хоть А и В, хоть альфа и бета.
Ответ от Вот так.[гуру]
это и то и то
Ответ от An V[гуру]
Функция это y
Ответ от 2 ответа[гуру]
Привет! Вот еще темы с нужными ответами:
X на Википедии
Посмотрите статью на википедии про X
Функция математика на Википедии
Посмотрите статью на википедии про Функция математика
Ответить на вопрос:
22oa.ru
Функция sgn(x) — это… Что такое Функция sgn(x)?
График функции y = sgn xФункция (другое обозначение: ), читается «сигнум» (от лат. signum — знак) — кусочно-постоянная функция, определённая следующим образом:
Функция не является элементарной.
Часто используется представление
При этом производная модуля в нуле, которая, строго говоря, не определена, доопределяется средним арифметическим соответствующих производных слева и справа.
Функция применяется в теории обработки сигналов, в математической статистике и других разделах математики, где требуется компактная запись для индикации знака числа.
История
Функцию sgn(x) ввёл Леопольд Кронекер в 1878 г., сначала он обозначал её иначе: [x]. В 1884 г. Кронекеру понадобилось в одной статье использовать, наряду с sgn, функцию «целая часть», которая также обозначалась квадратными скобками. Во избежание путаницы Кронекер ввёл обозначение , которое (за вычетом точки перед аргументом) и закрепилось в науке.
Свойства функции
См. также
Источники
- Бронштейн И. Н., Семендяев К. А. Справочник по математике. — М.: Наука, 1964. — 608 с.
- Воднев В. Т., Наумович А. Ф., Наумович Н. Ф. Основные математические формулы. Справочник. — Минск: Вышэйшая школа, 1988. — 269 с.
dic.academic.ru
Функция sign(x) — это… Что такое Функция sign(x)?
функция mod_osso — Новое функциональное средство, введенное в Oracle9iAS Release 2. Оно является расширением Oracle HTTP Server, которое позволяет HTTP серверу стать партнерским приложением (см. Partner Applications) для SSO (см. Single Sign On, SSO). Приложения,… … Справочник технического переводчика
Функция ошибок — График функции ошибок В математике функция ошибок (функция Лапласа) это неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных ур … Википедия
Функция Лапласа — График функции ошибок В математике функция ошибок это неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных. Она определяется как . Дополнительная функция ошибок,… … Википедия
Функция Ляпунова — Стиль этой статьи неэнциклопедичен или нарушает нормы русского языка. Статью следует исправить согласно стилистическим правилам Википедии. В теории обыкновенных дифференциальных уравнений, функция Ляпунова является скалярной функцией, которая… … Википедия
Функция sgn(x) — График функции y = sgn x Функция (другое обозначение: ), читается «сигнум» (от лат. signum знак) кусочно постоянная функция, определённа … Википедия
Sign функция — График функции y = sgn(x) Функция (другое обозначение: , читается: «сигнум», от лат. signum знак) определяется следующим образом … Википедия
Функция Радемахера — Графики функций Радемахера с Функция Радемахера кусочно постоянная периодическая функция, принимающая только два значения 1 и −1 на всей обл … Википедия
Функция знака — График функции y = sgn(x) Функция (другое обозначение: , читается: «сигнум», от лат. signum знак) определяется следующим образом … Википедия
R-функция — (функция В. Л. Рвачёва) числовая функция действительных переменных, знак которой вполне определяется знаками ее аргументов при соответствующем разбиении числовой оси на интервалы и . Впервые R функции были введены в работах… … Википедия
Однородная функция — степени числовая функция такая, что для любого и выполняется равенство: причём называют порядком однородности. Различают также положительно однородные функции, для которых равенство … Википедия
dic.academic.ru
Функция sgn(x) — это… Что такое Функция sgn(x)?
График функции y = sgn xФункция (другое обозначение: ), читается «сигнум» (от лат. signum — знак) — кусочно-постоянная функция, определённая следующим образом:
Функция не является элементарной.
Часто используется представление
При этом производная модуля в нуле, которая, строго говоря, не определена, доопределяется средним арифметическим соответствующих производных слева и справа.
Функция применяется в теории обработки сигналов, в математической статистике и других разделах математики, где требуется компактная запись для индикации знака числа.
История
Функцию sgn(x) ввёл Леопольд Кронекер в 1878 г., сначала он обозначал её иначе: [x]. В 1884 г. Кронекеру понадобилось в одной статье использовать, наряду с sgn, функцию «целая часть», которая также обозначалась квадратными скобками. Во избежание путаницы Кронекер ввёл обозначение , которое (за вычетом точки перед аргументом) и закрепилось в науке.
Свойства функции
См. также
Источники
- Бронштейн И. Н., Семендяев К. А. Справочник по математике. — М.: Наука, 1964. — 608 с.
- Воднев В. Т., Наумович А. Ф., Наумович Н. Ф. Основные математические формулы. Справочник. — Минск: Вышэйшая школа, 1988. — 269 с.
dvc.academic.ru
Обратная функция | Алгебра
Что такое обратная функция? Как найти функцию, обратную данной?
Определение.
Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо:
1) В формулу функции вместо y подставить x, вместо x — y:
x=f(y).
2) Из полученного равенства выразить y через x:
y=g(x).
Пример.
Найти функцию, обратную функции y=2x-6.
1) x=2y-6
2) -2y=-x-6
y=0,5x+3.
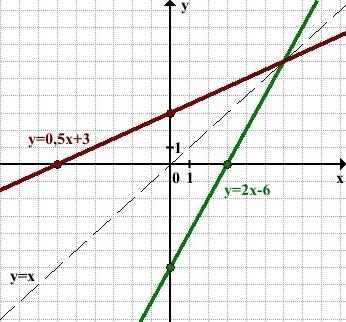
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.
Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).
y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая. Для построения прямой берём две точки.
 Однозначно выразить y через x можно в том случае, когда уравнение x=f(y) имеет единственное решение. Это можно сделать в том случае, если каждое своё значение функция y=f(x) принимает в единственной точке её области определения (такая функция называется обратимой).
Однозначно выразить y через x можно в том случае, когда уравнение x=f(y) имеет единственное решение. Это можно сделать в том случае, если каждое своё значение функция y=f(x) принимает в единственной точке её области определения (такая функция называется обратимой).
Теорема (необходимое и достаточное условие обратимости функции)
Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.
Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.
Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.
Классический пример — функция y=x². На промежутке [0;∞) функция возрастает. Условие обратимости выполнено, следовательно, можем искать обратную функцию.
Так как область определения функции y=x² — промежуток [0;∞), область значений на этом промежутке — также [0;∞), то область определения и область значений обратной функции — также [0;∞).
1) x=y².
2)
Так как y≥0, то
то есть на промежутке [0;∞) y=√x — функция, обратная к функции y=x². Их графики симметричны относительно биссектрисы I и III координатных четвертей:
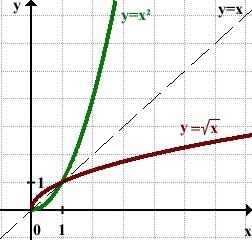
В алгебре наиболее известными примерами взаимно обратных функций являются показательная и логарифмическая функция, а также тригонометрические и обратные тригонометрические функции.
www.algebraclass.ru
линейная функция, квадратичная, кубическая и y=1/x
Степенной называется функция вида y=xn (читается как y равно х в степени n), где n – некоторое заданное число. Частными случаями степенных функций является функции вида y=x, y=x2, y=x3, y=1/x и многие другие. Расскажем подробнее о каждой из них.
Линейная функция y=x1 (y=x)
График прямая линия, проходящая через точку (0;0) под углом 45 градусов к положительному направлению оси Ох.
График представлен ниже.
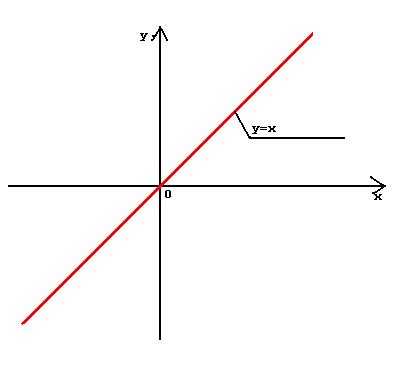
Основные свойства линейной функции:
- Функция возрастающая и определена на всей числовой оси.
- Не имеет максимального и минимального значений.
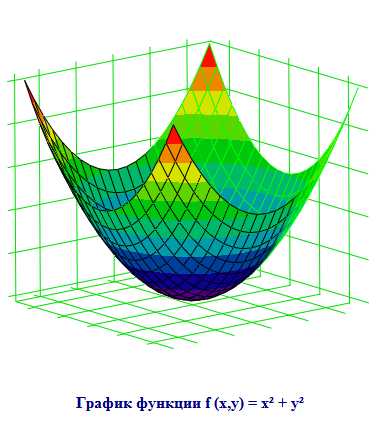
Квадратичная функция y=x2
Графиком квадратичной функции является парабола.
Общий вид параболы представлен на рисунке ниже.
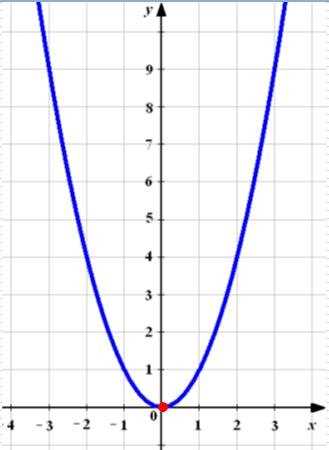
Основные свойства квадратичной функции:
- 1. При х =0, у=0, и у>0 при х0
- 2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
- 3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке [0;+∞).
- 4. Противоположным значениям х соответствует одинаковые значения y.
Кубическая функция y=x3
Графиком кубической функции называется кубическая парабола.
Общий вид параболы представлен на рисунке ниже.
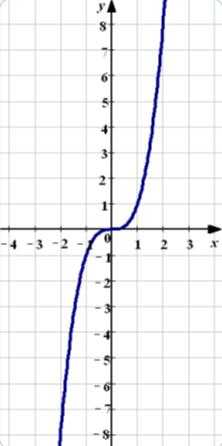
Основные свойства кубической функции:
- 1. При х =0, у=0. у>0 при х>0 и y
- 2. У кубической функции не существует не максимального ни минимального значения.
- 3. Кубическая функция возрастает на всей числовой оси (-∞;+∞).
- 4. Противоположным значениям х, соответствуют противоположные значения y.
Функция вида y=x-1 (y=1/x)
Графиком функции y=1/x называется гипербола.
Общий вид гиперболы представлен на рисунке ниже.
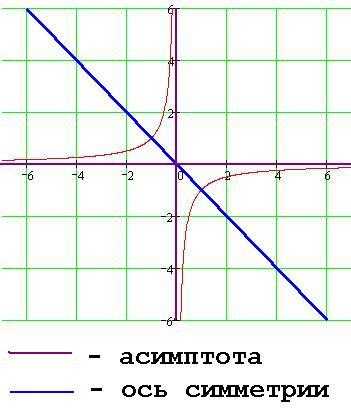
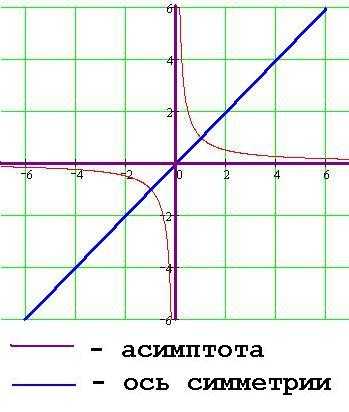
Основные свойства функции y = 1/x:
- 1. Точка (0;0) центр симметрии гиперболы.
- 2. Оси координат – асимптоты гиперболы.
- 3. Прямая y=x ось симметрии гиперболы.
- 4. Область определения функции все х, кроме х=0.
- 5. y>0 при x>0; y
- 6. Функция убывает как на промежутке (-∞;0), так и на промежутке (0;+∞).
- 7. Функция не ограничена ни снизу, ни сверху.
- 8. У функции нет ни наибольшего, ни наименьшего значений.
- 9. Функция непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
- 10. Область значений функции два открытых промежутка (-∞;0) и (0;+∞).
Нужна помощь в учебе?
Предыдущая тема: Четные и нечетные функции: графики и свойства
Следующая тема:   Определение корня n-ой степени: извлечение корня
Все неприличные комментарии будут удаляться.
www.nado5.ru