Законы пространственной геометрии — Графическая магия Инессы Горт
В этом рисунке показана вся пространственная геометрия и ее основополагающие законы.
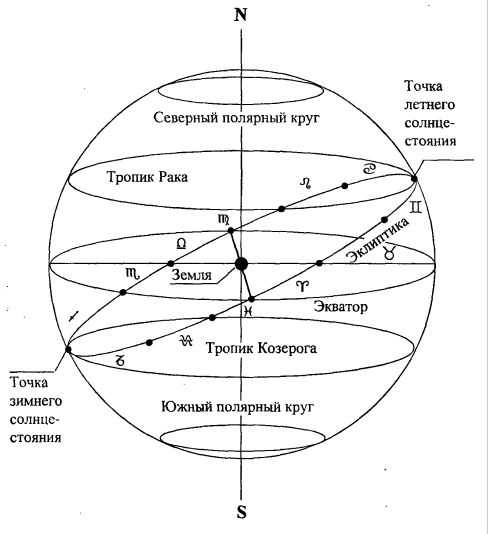
Пространственная геометрия гениальная по простоте и краткости, парадоксальная наука. Она возникла в древности и позволила понять, осознать, выстроить в систему и начертить на бумаге то, чего нет. Все линии, круги и плоскости пространственной геометрии воображаемые. Их нет, они не имеют материальности, но они работают, вот в чем заключен парадокс пространственной геометрии.
Некоторые ученые считают пространственную геометрию лженаукой. Они не могут понять гармонию тонкой материи. Пространственная геометрия входит в состав науки астрономии специальным разделом. Это астрономия Земли, астрономия ближайшего космоса. Почему эта наука так называется? Кто-то считает, что геометрия напрямую связана с земной твердью и изучает вопросы ее обмера. А «пространственного» землемерия быть не может. Гео-метрия — с греч. землемерие; наука, изучающая законы и правила точного обмера земли.
Пространственная геометрия измеряет пространство, а значит она пространственная. А геометрия она потому, что меряет пространство исключительно вокруг планеты Земля (Геи), опоясывая ее воображаемыми кругами. Эти круги и плоскости рождаются от Земли, ее особенностей и физических характеристик. Они — продолжение земной тверди, в се отношениях с Солнцем и Луной.
Следствия глобальных законов пространственной геометрии, запечатленных на рисунке, могут проявляться в виде аксиом и теорем более мелкого масштаба. Они входят в науки геометрию и математику. Все эти законы тесно связаны между собой и переплетаются в астрологии, астрономии, математике и физике.
Кто-то может размышлять над пространственной геометрией на небольших фрагментах пространства, подтверждая сложные законы, аксиомы, и доказывая оригинальные теоремы ученых древности и средневековья. Но не стоит забывать, основные постулаты пространственной геометрии произошли именно от особенностей циклов Земли, Солнца и Луны.
Это связано с древним принципом Гермеса Трисмегиста: «внизу то же, что и вверху». Полагаясь на космос, его законы, мы решаем свои практические задачи, связанные с преломлением законов просгранственной геометрии в области частной жизни человека. Особенности орбит Земли и Луны в их отношении к Солнцу родили науку о числах — математику (геометрию) и важные принципы философии (время и просгранство, развитие по спирали). Многие науки древние греки знали в целостности. Это было их мировоззрением. Они оставили свои знания нам не всегда в явном виде. Не все потомки смогли вместить в себя целостные знания и разбили их на разные отрасли. Пространственная геометрия в ее глобальном околоземном проявлении ближе к астрологии. Она не связана с планетами, но связана с Зодиаком, на который они и проецируются. Это наука трех небесных тел — Земли, Солнца и Луны. Она изучает земные-солнечноые-лунные взаимодействия. Основа этих взаимодействий уже давно ясна. Лишь веяния цивилизации и перемены в жизни людей могут дать ей новое наполнение, в основном в различии свойств разных знаков Зодиака, в их новой интерпретации.
Геометрия Евклида была важна в практических целях для справедливого и точного дележа земной тверди. Она позволяла обрести свой участок каждому человеку или крестьянину для выращивания зерна, плодов, фруктов или постройки жилья, а также продавать и покупать по справедливой цене. Этот вопрос родил множество абстрактных аксиом и теорем, которые на первый взгляд мало относились к самим участкам земли. Они мерили не только землю, но и другие вещи (их объем, количество). Геометрия в широком смысле — это наука о мере.
Но выяснилось, помимо почвы можно померить и воздушное или космическое пространство. Тонкое пространство — тоже материально и живет по своим законам. Мы живем на Земле и воспринимаем влияние космоса лично. Мы не можем воспринимать космос через третьи элементы, находящиеся вне нас. Даже если мы запустили на орбиту Земли мощный телескоп на спутнике, и мы видим космос и далекие пространства вселенной через него, но все равно мы видим их лично. Пусть мы используем для этого различные инструменты, подобные телескопам, органу зрения. Мы все чувствуем внутри себя.
Надо налагать любые влияния планет на нас. Если Земля двигается по кругу, надо рисовать круг. Однако по кругу в гороскопе двигается Солнце, а не Земля, — это очень важно и правильно, хотя и неточно. Мы хоть и воспринимаем все лично, но у нас есть разные периоды, разнос время. Это обуславливается орбитой Земли — эклиптикой. Раз есть круг, круг жизни, и важные планеты проецируются на него, есть время и пространство.
Если бы мы жили на Солнце и учитывали, как важные планеты солнечной системы двигаются, мы бы жили вне времени и пространства. Вот где время остановилось, вот где нет пространства. Как бы планеты не вращались, они всегда смотрят на Солнце. На Земле люди зависят от Солнца. А на Солнце существа не зависят ни от чего. Солнце их греет, кормит и обогревает. У солнечных обитателей нет источника жизни, находящегося вне их места существования и жизни.
Чтобы было время и пространство — эти категории, давно подмеченные ищущими умами, нужно собственное вращение вокруг судьбоносного центра, каким для Земли является Солнце. И тогда планеты и Солнце будут как бы разными. Появляется время, появляется пространство.
Луна имеет одинаковый цикл обращения вокруг Земли и вокруг своей оси. В связи с этим она всегда к нам повернута одной стороной. На Луне время как бы остановилось. Но это ловушка.
Времена года связаны с конкретными территориями земли. На территориях близких к полюсам день длится полгода и эквивалентен лету. Ночь также длиться полгода. Она эквивалентна зиме. На экваторе почти нет времен года — там всегда тепло. Обычные день и ночь. Это сохраняется до тропиков. Близ экватора нет знаков долгого и короткого восхождения. Все знаки восходят с одинаковой скоростью: 4 минуты градус. За тропиками половина знаков восходит быстрее, чем другая половина.
В северном полушарии знаками короткого восхождения является знаки восточной полусферы Зодиака: Козерог, Водолей, Рыбы, Овен, Телец, Близнецы. Знаки короткого восхождения восходят 3 или менее минут — градус. Другие знаки — долгого восхождения, и восходят градус более 4 или 5 минут. В южном полушарии Земли за южным тропиком Козерога — наоборот.
На средних широтах длина дня и ночи совпадает только в весеннее и осеннее равноденствия. В другие времена года день длиннее (летом) или короче (зимой) ночи. Осевое движение Земли — суточный цикл. С ним связан экватор. Это та плоскость, в которой Земля вращается вокруг своей оси. С этим циклом связаны дома гороскопа.
Обращение Земли вокруг Солнца — годовой цикл. С годовым циклом связаны знаки Зодиака. Годовой цикл — главный.
Плоскость орбиты Земли отличается от экваториальной плоскости Земли. Земля находится немного на боку в своем движении вокруг Солнца. Плоскость обращения Земли вокруг Солнца в проекции на Землю называется эклиптикой. Это видимый солнечный путь по небу. Эклиптика находится под углом 23 градуса 26 минут к экватору. Солнце дальше всего заходит в северное полушарие Земли Солнце дальше всего заходит в северное полушарие Земли летом (в южном полушарии в это время зима). Эта точка называется тропиком Рака. Противоположная точка в южном полушарии называется тропиком Козерога.
Вращение Земли вокруг своей оси относительно звездного неба меньше на 4 минуты в сравнении с суточным оборотом Земли относительно Солнца. За сутки Земля успевает немного сдвинуться по своей околосолнечной орбите вперед, а далекие звезды остаются практически на своих местах за это малое по космическим меркам время.
Существует два варианта суток — звездные и солнечные. Если разбить солнечные сутки на 24 часа, то звездные сутки равны 23 часам 56 минутам. Используют средние солнечные сутки, называемые гражданскими.
Если в жизни полагаться на звездные сутки, то полдень, с которым все ассоциируют середину дня, может периодически приходиться на темную ночь.
Земля обращается вокруг Солнца не по кругу, а по эллипсу. Она бывает то ближе к Солнцу (зимой), то дальше от Солнца (летом) — для северного полушария. Согласно второму закону Кеплера, в перигелии Земля быстрее движется, чем в афелии. Скорость вращения Земли вокруг своей оси практически равномерна. Реальные солнечные сутки имеют разную временную продолжительность в году.
Принято использовать средние сутки, которые одинаковы весь год. Это гражданские сутки, равные 24 часам. Они равны истинным солнечным суткам всего несколько раз в году. Истинные солнечные сутки в году то чуть больше гражданских суток, то чуть меньше.
Если есть 12 знаков Зодиака в большом цикле жизни Земли (в году), то очень удобно суточный цикл Земли разделить по аналогии. Дома гороскопа явились продолжением знаков Зодиака. Это оказалось удачным решением в астрологическом методе.
Меридианы — это параллельные линии, по окружности соединяющие полюса Земли и перпендикулярные экватору и широтам. В Гринвиче (пригород Лондона, Великобритания) проходит нулевой меридиан. Этот меридиан был назван нулевым по соглашению всех стран. Он называется полуденным и обозначается, как GMT (Greenwich middle time).
Меридианы в системе географических координат включают, как и любой круг, 360 градусов. Гринвичский меридиан делит земной шар на восточное и западное полушария. Счет градусов по географическим меридианам идет к востоку от Гринвича. Меридиан, противостоящий гринвичскому, связан со 180-м градусом. Он проходит в Тихом океане от полюса к полюсу. С этим меридианом связана линия смены дат. Здесь сутки разделяются между собой, закапчиваются старые и начинаются новые.
На разных меридианах Земли свои местные части суток. И если у нас день, то в противоположной части Земли в этот момент — ночь. Чем восточнее Гринвича находится местность, тем раньше там наступает полдень. Чем западнее Гринвича находится местность, тем позже там наступает полдень.
Раньше время в каждом городе было своим. Позднее страны договорились делить территории на часовые пояса, чтобы рядом расположенные населенные пункты, входящие в полосу одного часового пояса, жили по общему для их часового пояса времени. Неудобно, когда в населенном пункте, находящемся немного восточнее или западнее нашего, время немного отличалось. Это важная веха развития цивилизации и коммуникаций.
В странах, находящихся в умеренных широтах, экономически выгодно вводить летнее время. Солнце летом всходит раньше времени, когда людям необходимо идти на работу.
Календарь с его праздниками и буднями выражает потребности людей, их чаяния. Если астрологический подход к годовому циклу, оформленному в Зодиак, сокровенен, то календарь отражает жизнь всего общества, как его понимает большинство. Зодиак и астрология — это тайные знания.
Люди специально сделали новый год зимой в месяц Козерога, что бы развеять это темное и депрессивное время. Многие праздники, особенно зимние — это возможность обойти тягостное время зимы и наполнить его праздником, весельем, которых так нс хватает. Они работают как компенсация негативного времени.
В социальном понимании годового цикла время зимы — это время нелегкой работы, накопления материальных ценностей, денег. Лето *- это время отдохновения, отпусков, поездок в южные страны на отдых. Рабочая жизнь многих начинается в сентябре, а прекращается в начале лета.
Мы можем обладать каким-то уникальными и точными данными, но это не обязательно принесет нам признание. Важно мнение каждого человека, как он воспринимает нас. Любой человек -потенциальный творец, и если ему не понравится что-то гениальное, то это сработает. Мало создать что-то совершенное, надо чтобы это еще признали.
Месяц и знак Зодиака — эквивалентные категории. Из-за нестыковок гражданские месяцы перестали совпадать с астрологическими — знаками Зодиака. Современные месяцы, как календарные, так и зодиакальные стали только символичны истинным синодическим месяцам Луны. И этот символизм лучше стали отражать только знаки Зодиака.
В разных странах существуют разные календари, но везде годовой цикл делится на месяцы. Современный григорианский календарь — по-своему астрологическая система. Это астрология, как се способны воспринять большинство обычных людей, живущих своими насущными нуждами и не вникающих глубоко в вопросы изучения законов мира и космоса.
Круг — это эквивалент околосолнечной орбиты Земли. Геометрия, которой учат в школах, усеченный вариант древних знаний. Геометрия и астрология имеют общие корни. Астрология возникла на базе законов пространственной геометрии. Древние греки обнаружили возможность опоясать Землю различными воображаемыми кругами. Раньше Земля считалась плоской, но астрологи знали, что Земля — шарообразная.
Крест — хранитель земных сезонов, времен года. В эту систему и в сезоны чудесным образом вписываются синодические лунные месяцы. Налицо гармония. Один сезон содержит три лунных месяца, а значит и три знака Зодиака, так как знаки Зодиака — суть символические синодические лунные месяцы.
Знак Зодиака имеет протяженность тридцать градусов и длится тридцать суток, а реальный синодический лунный месяц длится всего примерно 29,5 су ток. Тридцать суток и тридцать градусов чуть больше чем реальный лунный цикл, их образовавший. Как всегда мы вынуждены упрощать и сквозь пальцы смотреть на погрешности. Это лишние 5,25 суток года, и половинка суток от синодического лунного месяца. Они рождают неполный тринадцатый лунный месяц в году. Отсюда возникают идеи астрологов о тринадцатом знаке Зодиака.
Нелогично делить сутки на половину и начинать новый знак посредине тридцатого градуса. Знак Зодиака должен включать в себя целое число суток — ровно тридцать. Последние полградуса знака будут особыми — это зона перехода. Счет суток, градусов и знаков Зодиака надо вести от первого восхода Солнца после точки весеннего равноденствия. Небольшая дуга эклиптики между весенним равноденствием и первым восходом Солнца выделяется, как пробная жертва в году. Последние пять градусов Зодиака относятся к тринадцатому знаку Зодиака.
Знаки Зодиака непосредственно связаны с пространственной геометрией. Они возникли с зарождением жизни и отражают реакцию человека на времена года в его широтной полосе. Так получилось, что первыми, кто изучил это, были вавилоняне. Они, естественно, сделали это только для своих географических широт. Вавилоняне были великими исследователями мира и космоса, настоящими пионерами в астрологии. Другие народы, жившие в других широтных полосах Земли, этим, видимо, не интересовались.
Течение года было разбито на 12 знаков Зодиака по числу полных оборотов Луны вокруг Земли за 1 год. Нужно было еще определить, что существует год и годы повторяются.
Газы Солнечной системы сгущались, и, по сути, из ничего появилось Солнце и другие планеты, а потом возникла жизнь — как мы ее понимаем. И особенности солнечного освещения для тех или иных мест на Земле породили Зодиак, а потом и гражданский календарь, который, по сути, — упрощенная форма зодиакальной астрологии, или социальный Зодиак — та астрологическая основа, которая понятна большинству непосвященных.
Естественно, что точка начала гражданского календаря — Новый год — была взята практически наугад и соответствует социальным тенденциям, зародившимся в Риме — империи, ставшей основой современной цивилизации. Возможно, в будущем гражданский календарь станет конкурентом астрологической зодиакальной системе. Календарь ведь тоже форма существования жизни людей в течение года, с его буднями и праздниками.
Зодиак позволяет понять, как проявляются основные факторы астрологии — планеты и звезды — в жизни людей. Каждый знак Зодиака несет в себе повторяющийся архетип, опыт и реакцию человека на этот период во времени и пространстве. Зодиакальная астрология, как и социальная астрология — гражданский календарь, — возникли вместе с человечеством и зависят от него. Если бы на Земле была другая форма жизни, которая бы реагировала по-другому на степень солнечного освещения для тех или иных географических широт Земли, то знаки Зодиака имели бы другие качества. Знаки Зодиака напрямую формируются человеческой природой. На животных это срабатывает схожим образом, ибо они имеют тот же набор генов, пусть и в другой вариации. Они также едят, пьют воду и дышат воздухом.
Сложившаяся зодиакальная система мира, в принципе, является субъективным моментом. Солнце всегда светит приблизительно ровным светом. Но особенности положения Земли и Луны относительно Солнца рождают особое солнечное освещение в течение года. При этом на разных широтах Земли это освещение, а значит, и количество солнечного тепла в течение года различно. Это рождает разность зодиакальных архетипов в разных географических широтах. В этом и заключается основополагающее открытие автора, реформирующее общепринятый тропический Зодиак.
Астрология зародилась в Вавилоне. Древние астрологи-халдеи были первооткрывателями. Им трудно было представить, что свойства знаков Зодиака зависят от солнечного света, а не от далеких звезд. Тот астролог, который понял это, вспомнит о том, что на разных географических широтах Земли в течение года количество солнечного света различно.
Земной шар делится на несколько широтных поясов. Границы этим полосам дали земные-солнечные отношения — положение Земли относительно Солнца. Центральную широтную полосу прямо по центру делит экватор, ограничивают ее с двух сторон плоскости северного и южного тропиков. В видимости, в связи с особенностями положения земного шара, Солнце не проецируется севернее тропика Рака в Северном полушарии и южнее тропика Козерога в Южном полушарии. Это связано с тем, что планета Земля — шар. Полюса связаны с особым солнечным освещением.
Таким образом, вычленяют три широтные полосы Земли, для которых работает разное наполнение знаков Зодиака. Причем две полосы (кроме экваториальной) имеют место быть в двух полушариях по одной в Северном и Южном полушарии. Это широтная полоса умеренных широт — от тропика до полярного круга и приполярная широтная полоса. Они есть и в Северном, и в Южном полушарии. Третья широтная полоса существует в единственном экземпляре и находится рядом с экватором — между тропиками. Широтные границы земного шара не взяты с потолка. Они напрямую связаны с солнечным освещением в течение года. Это открытие влияет только на знаки Зодиака, на их свойства для разных широт Земли.
Поделиться ссылкой:
Понравилось это:
Нравится Загрузка…
graficheskayamagiya.wordpress.com
Геометрии пространства
показали, что их возраст около 2,5 млн. лет. Возраст определен по соотношению изотопов аргона в исследованных образцах.
Точно таким же способом оценено время существования Солнечной системы – по измерению содержания радиоактивных элементов в метеоритах. Оказалось, что все метеориты имеют примерно одинаковый возраст – 4-5млрд. лет.
Одна из последних оценок возраста Вселенной – 16±2 млрд. лет. Метод нуклеокосмохронологии показал, что возраст одной из самых старых звезд CS22892-052составляет от 13 до 21 млрд. лет.
Но насколько можно верить этой оценке, если она сделана по спектру одной всего звезды по одиночной линии излучения тория?
Таким образом, в самой природе, существуют физические явления и процессы, определяющие направление течения времени. В отличии от пространства, в каждую точку которого можно снова и снова возвращаться (и в этом отношении оно является как бы обратимым), время –необратимо иодномерно. Оно течет из прошлого через настоящее к будущему. Нельзя возвращаться назад вкакую-либоточку времени, но нельзя и перескочить черезкакой-либовременной промежуток в будущее. Необратимые процессы лежат в основе многих процессов, с особой отчетливостью они появляются на биологическом уровне. В30-хгг. XX в. английский астрофизик А.С. Эддингтон (1882 – 1944) ввел понятие «стрелы времени».
Приведем примеры процессов, характеризующих направление времени, воплощающих необратимость времени.
Излучение — волны всегда испускаются источником и являются расходящимися, затухающими по прошествии времени (т.е. уходящими в будущее). Но не обнаружены волны, сходящиеся к источнику из прошлого (хотя теоретических можно решить уравнения, рассматривающие эту возможность).
Термодинамика – второе начало устанавливает закон возрастания энтропиив системе,
не обменивающейся с внешним миром ни энергией, ни веществом, выражает увеличение молекулярного хаоса до тех пор, пока система не достигнет термодинамического равновесия.
Эволюция – для незамкнутых систем свойственна динамическая самоорганизации материи. Она наблюдается в биологической эволюции, эволюция общества и эволюции Вселенной в целом. Эволюция, другими словами, это возрастание порядка в системе, следовательно она противоречит второму началу термодинамики – закону возрастания энтропии.
Радиоактивный распад – происходит необратимое преобразование одних атомов в другие, обратного процесса не наблюдается. Например, конечным продуктом распада урана является свинец.
Уже в античном мире мыслители задумывались над природой и сущностью пространства и времени. Знаменитый врач и философ из города Акраганта Эмпедокл считал «пустого пространства не существует». Демокрит утверждал, что пустота существует, как материи и атомы, и необходима для их перемещений и соединений.
И только в «Началах» древнегреческого математика Евклида пространственные характеристики объектов обрели строгую математическую форму. В это время
studfiles.net
Пространство геометрическое
Геометрическая ось главного вала наклонена под небольшим углом е = 2° (угол нутации) к вертикальной оси дробилки, поэтому при вращении эксцентрикового стакана ось вала 5 описывает в пространстве коническую поверхность. В результате сидящий на валу дробящий конус 4 совершает круговые колебательные движения по типу конического маятника (прецессионное движение) поверхность его постепенно приближается, а затем удаляется от поверхности неподвижного конуса 3.[ …]
Геометрическое и логарифмически нормальное распределения могут на самом деле отражать крайности в величине выборки. Например, если объединить все данные по биомассе калифорнийских злаковых лугов, то получится логарифмически нормальное распределение. Если же постепенно выделять данные по отдельным травостоям, то распределение все больше и больше отклоняется от логарифмически нормального, приближаясь к геометрическому [6]. Подобным же образом в двух-выборках, взятых дночерпателем из соседних участков морского бентосного сообщества, обычно наблюдается совершенно различная картина доминирования, но если объединить пять или более выборок, то получится логарифмически нормальное распределение [257]. В небольших масштабах характер распределения сильнее зависит от биологических факторов, таких как хищничество, конкуренция, пополнение, дифференциальная смертность и т. п., поэтому, возможно, что геометрическое распределение описывает разделение пространства реализованных ииш между сосуществующими популяциями или в пределах отдельных гильдий. А логарифмически нормальное распределение, вероятно, описывает разделение пространства реализованных ниш между разными гильдиями или даже сообществами.[ …]
Об этих пространствах с рассеянными атомами и молекулами правильнее мыслить не как о материальной пустоте «вакуума», но как о концентрации своеобразной энергии, в рассеянном виде содержащей колоссальные запасы материн и энергии. Если это так, то едва ли правильно думать, что температура этих пространств будет близка к абсолютному нулю; она будет очень разнообразна . Ближайшим аналогом этого явления будут для нас верхние геологические оболочки нашей планеты, которые, по-видимому, геометрически неотделимы от этих космических пространств. Это — тоже мощное поле сил.[ …]
Понятие «пространства», без сомнения, одно из самых древних в математике. Оно является до такой степени основополагающим для нашего «геометрического» понимания мира, что принималось на веру, практически не требуя описаний, в течение более чем двух тысяч лет. И лишь в прошлом веке понятие это постепенно освободилось из-под тирании непосредственного восприятия (как единственно пространства, нас окружающего) и связанных с ним традиционных (евклидовых) теоретических разработок, чтобы обрести теперь уже свои собственные динамику и независимость. В наши дни оно входит в число понятий, наиболее часто и повсеместно используемых в математике, безусловно известных всем математикам без исключения. Понятие, впрочем, изменчивое, не поспоришь; у него сотни, тысячи обликов, в зависимости от того, какую структуру ему придать. Есть из них богатейшие (как почтенные «евклидовы» структуры, или «аффинные», или «проективные», или еще «алгебраические» структуры одноименных «многообразий»; эти обобщают все предыдущие, придавая им гибкость), есть аскетически строгие. Последние таковы, что всякий элемент информации «качественной» из них словно бы исчез безвозвратно, и присутствует лишь намек на количественную сущность понятия близости, или предела46, и наличествует лишь вернее всего ускользающая от интуиции («топологическая») версия понятия формы. Наиболее безыскусное среди всех, топологическое пространство в течение истекшей половины столетия играло роль своего рода широкого лона общих концепций, охватывающих все прочие структуры. Изучением таких пространств занимается одна из самых увлекательных, самых животрепещущих ветвей геометрии: топология.[ …]
Боскет — четкое геометрическое пространство в саду или парке, ритмично обсаженное деревьями, кроны которых регулярно подстригаются.[ …]
Неоднородное земное пространство геометрически отвечает точке в Эвклидовом пространстве Ньютона и в пространстве—времени Эйнштейна. Планетные состояния пространства. Симметрия как состояние пространства земных природных тел и явлений. Сложность планетного физико-химического пространства. Связь его с состоянием вещества. Пространство-время реально проявляется и живом веществе (§ 121).[ …]
С другой стороны, Эйнштейново пространство—время, принятое физиками в XX в. по логическим предпосылкам, в него вложенным, едва ли может приниматься в конкретных фактах на нашей планете в геологических явлениях, так как наша планета проявляется в нем в качестве геометрической точки, в которой плотность ее, в отличие от других точек, равна 5,52 (отнесенная к воде при 0° и 760 мм давления: среди планет плотность Земли самая большая).[ …]
В результате новых представлений пространство в аспекте реальности отходит на второй план по сравнению с прежними научными представлениями. Пространство—время Эйнштейна не есть пространство геометра, к которому мы привыкли. Когда говорят о том, что пространство Эйнштейна является римановским пространством четырех измерений — это только приближенная попытка выразить пространство—время Эйнштейна. В теории относительности приходится образно принимать во внимание замкнутое геометрическое сферическое пространство, имеющее свою иную, чем эвклидова, геометрическую структуру, но не охватывающее целиком пространство — время Эйнштейна, а только приближающееся к нему с достаточной для теории относительности точностью, но, возможно, сильно от реальности отличающееся. Когда говорят, что пространство Эйнштейна есть не эвклидово, а римановское пространство 4 измерений, это лишь приближенно отвечает действительности, нельзя оба эти явления (ньютоново, эвклидово пространство и часть пространство—времени Эйнштейна — римановское) так в научной работе сравнивать.[ …]
Симметрия в системе наук как учение о геометрических свойствах состояний земных, т. е. геологических пространств, их сложности и неоднородности (§ 125). Логика естествознания. История симметрии: бытовое понимание и развитие его в науке. Разная симметрия живых веществ и природных косных тел (§ 126). Кристаллические пространства и федоровские группы (§ 127). Реальный и идеальный монокристалл. Проявления времени. Идеальные и реальные кристаллические пространства (§ 128). Диссимметрия Кюри и Пастера и состояния пространства (§ 129).[ …]
Организмы конкурируют в занимаемом ими пространстве прежде всего за ресурсы. Пространство может стать и лимитирующим ресурсом, если при избытке пищи оно не сможет вместить в свои геометрические размеры все организмы, которые могли бы успешно жить в этом пространстве за счет избытка его ресурсов. Например, скальная поверхность может быть настолько плотно заселена мидиями, что другим моллюскам, потенциально способным еще прокормиться на этой площади, места уже не осталось. Ряд животных стремится к «захвату» определенной территории, где они смогут обеспечить себя пищей. Кроме того, потенциальными ресурсами для животных являются гнездовые участки и убежища.[ …]
В науках о природе симметрия есть выражение геометрических пространственных правильностей, эмпирически наблюдаемых в природных телах (и явлениях). Она, следовательно, проявляется, очевидно, не только в пространстве, во и на плоскости, и на линии. Эти правильности более глубоки, чем физические и химические явления, в которых они нам проявляются и которые они охватывают. Законы симметрии — это геометрические законы природных тел, т. е. физико-химических пространств нашей планеты, как я теперь бы их определил. В нашем современном представлении — это геометрическая основа всех природных физико-химических пространств (§ 119), в том числе и кристаллических. Физические и химические явления подчинены симметрии, так как симметрия определяет расположение атомов в пространстве, как это проявляется в законах кристаллографии и стереохимии и может быть проверено наблюдениями в рентгеновском и электронном свете.[ …]
Для Земли — точки — выявлением ее планетного пространства являются пространственные проявления ее земных естественных тел и явлений. Они определяются симметрией. Я рассматриваю симметрию, согласно Кюри, как состояние физико-химического пространства. Она отвечает природной геометрии. Только научным изучением симметрии можно выяснить, какие геометрические пространственные состояния могут на Земле встречаться. Земное пространство есть всегда физико-химическое пространство. Очевидно, оно многообразно. Многообразие это может выясниться только научным наблюдением и возможно, что мы можем выйти здесь за пределы эвклидовой геометрии, ибо все геометрии одинаково правильны и какие из них проявляются в окружающей нас среде, мы не знаем. Это нельзя решить a priori. Но можно решить только из научного изучения симметрии. Если они реально существуют, то они в ней выявятся 86.[ …]
Он имеет дело с Землей, с маленькой планетой, т. е. с геометрической точкой в том мировом пространстве—времени Эйнштейна, с которым, думает, что имеет дело физик, и с которым должен считаться на каждом шагу в своей эмпирической работе астрофизик. Геолог с этим пространством—временем физика и астрофизика, может быть, и не связан, как это и было до сих пор в истории геологии. Я буду исходить из логически другой постановки вопроса, буду исходить из наблюдения и изучения естественных — больших и малых — земных и космических природных тел и явлений пространственно или простран-ственно-временно ограниченных. Так строится все естествознание, все научное представление о реальности.[ …]
Я также прошу моих читателей иметь в виду, что понятие пространства не имеет ничего общего с восприятием. Геометрическое пространство — это чистая абстракция, Открытое пространство можно мысленно представить себе, но его невозможно увидеть. Признаки глубины имеют отношение только к живописи. Третье визуальное измерение — это неправильное использование идеи Декарта о координатных осях.[ …]
Мы заключаем, что: 1) общее представление — разграничение пространства ресурсов (и ниши) сопровождается ослаблением конкуренции между видами — может лежать в основе существования различных по форме кривых значимости видов, но 2) разнообразие форм этих кривых, ранжированных от геометрической через логнормальную к кривой случайных границ, проявляется лишь тогда, когда значимость анализируется у разных групп организмов и разных сообществ; в этих случаях 3) учеты, если они включают ограниченное число видов, связанных друг с другом конкуренцией в пределах одного и того же сообщества, могут соответствовать кривой случайных границ ниш или геометрической форме, тогда как 4) для учетов, которые включают большое число видов, независимо от того, являются ли они конкурентами или нет и получены ли они из одного или нескольких сообществ, соответствующей будет логнормальная форма.[ …]
Переменные хи х2,…, хк называются факторами; координатное пространство с координатами хи х2,…, хк — факторным пространством, а геометрический образ, соответствующий функции отклика, — поверхностью отклика у. Критериями оптимальности планирования эксперимента [3, 4] являются ортогональность и ротатабельность плана эксперимента (методической сетки опытов).[ …]
Необходимо уяснить, по крайней мере следующее: «линии» на рисунке и геометрические «линии» — это» со-вершенно разные вещи. Изображение поверхности- не нужно путать с идеальными сущностями абстрактной геометрии. На уроках геометрии нас учили, что линия состоит из точек, плоскость — из линий, а пространство — из плоскостей. Мы прочно усвоили декартову геометрию с ее тремя координатными осями и понятие пространства в виде ящика — вместилища для точек ои-ний, объединение которых образует плоскости и трехмерные тела. В результате современные художники вынуждены соглашаться с тем, что утверждал Пауль Клее, а именно что графические элементы, которыми они, «художники, располагают,— это «точки, линии, плоскости и объемы». В процессе работы, конечной целью которой являете извлечение и запечатление инвариантов, единственное, что может сказать художник о том, чем он -при этом занят,— что он изображает «пространство». Но-это утверждение ошибочно.[ …]
Во-первых, новое понятие не чересчур широко, в том смысле, что на новые «пространства» (лучше называть их топосами, чтобы не задеть чуткого уха)54 самые важные интуитивные представления и геометрические конструкции55, знакомые по старым добрым пространствам прежних времен, переносятся более или менее очевидным образом. Иначе говоря, для новых объектов имеется в распоряжении вся богатая гамма мысленных образов и ассоциаций, понятий и определенных технических средств, какие прежде не выходили за границы области объектов старинного толка.[ …]
В этом вопросе возможны и существовали две принципиально разные точки зрения. Во-первых, точка зрения о геометрической сложности окружающей нас реальности и, во-вторых, о господстве единой геометрии в окружающем нас Космосе. То представление о космическом пространстве как об одной из форм римановской геометрии (Эйнштейн) как будто бы приводит к представлению о геометрическом единообразии окружающего нас мира. Но, с другой стороны, эмпирическая неизбежность признания планетного пространства, отличного от пространства Космоса (§ 121) и входящего в рамки эвклидова, а может быть, и римановского пространства, заставляет натуралиста-эмпири-ка считать геометрическую структуру материальных и энергетических природных проявлений сложной.[ …]
Под этим термином я подразумеваю не геометрическую точку в абстрактном пространстве, а местоположение в экологическом прост ранстве, то есть в среде, а не в пустоте. Это место, где наблюдатель мог бы находиться и с которого он мог бы осуществить адст наблюдения, В то время как абстрактное пространство состоит из точек, экологическое пространство состоит из мест — позиций или местоположений.[ …]
Нет никаких оснований сомневаться, что и для всех других косных природных тел: жидкостей, газов, мезоморфных и аморфных состояний пространства мы из приближения к идеальным геометрическим пространствам Эвклидовой геометрии не выйдем. Мы не встретились до сих пор ни с какими указаниями, что в явлениях симметрии были какие бы то ни было для этого данные.[ …]
Модель разломанного стержня (иногда называемая гипотезой случайной границы ниши) была предложена Макартуром в 1975 г. Он сравнил разделение пространства нишн в пределах сообщества со случайным и одновременным разламыванием стержня на S кусков. В противоположность логнормальной модели Сугихары модель разломанного стержня рассматривает только один ресурс. Она отражает гораздо более равномерное его разделение, чех описываемое лог-нормальной моделью, логарифмическим и геометрическим рядами. Это — реалистичное с биологической точки зрения выражение однородного распределения. Главная критика модели состоит в том, что ее можно вывести из нескольких разных гипотез (Pielou, 1975), и, поскольку она характеризуется только одним параметром S (числом видов), наблюдается сильная зависимость от объема выборки (Cohen, 1968; Poole, 1974). Тем не менее распределение по типу «разломанного стержня» соответствует случаю более или менее равномерного распределения между видами какого-то важного экологического фактора (May, 1974). А то, что данная модель выводится на основе нескольких гипотез, характерно и для других моделей распределения обилий видов.[ …]
Таким образом, расстояние не является линией, упирающейся одним своим концом в глаз, как думал епископ Беркли. Думать так — значит путать абстрактное геометрическое пространство с жизненным пространством окружающего мира. Это значит подменять осью Z в декартовой системе координат число шагов, которое нужно пройти по земле до фиксированного объекта.[ …]
Так как в живом веществе могут быть правые и левые молекулы (§ 140— 142), и в то же время молекулы основных первичных соединений всегда стери-чески левые, то должна быть в геометрическом строении пространства какая-то разница для основных соединений, определяющих протоплазму, которая определяет их устойчивость для левых атомных спиралей и неустойчивость для правых. К сожалению, геометрическое значение правизны и левизны до сих пор геометрами не разработано.[ …]
Эти состояния более или менее обособлены, иногда вполне замкнуты, могут принадлежать к разным геометриям, учитывая возможность в ближайшем будущем единой геометрии. Физическое пространство может быть не материальным, а энергетическим, например пространство, заполненное только световыми лучами. Но такого мы в окружающей нас земной природе не видим. Химическое пространство всегда материально, состоит ли оно из атомов или из электронов. Земные пространства отвечают всегда состояниям физико-химического пространства, всегда материального или энергетически-материального. Оми геометрически определяются симметрией (§ 121).[ …]
Эксперименты по комплексной очистке локальных сточных вод проводились на лабораторной установке только в узловых точках границы области исследования, которые наглядно видно после построения геометрического образа, соответствующего функции отклика — поверхности отклика на факторное пространство (рисунок 97). Анализ технологического процесса дал нам только перечень воздействующих параметров, которые, по нашему мнению, наиболее значительно влияют на степень очистки сточных вод. Это недостаточно, чтобы управлять разработанной схемой, но достаточно, чтобы начать переход к конкретным параметрам процесса, которые войдут в »математическую модель разрабатываемого программного обеспечения — конечную цель данной главы, необходимую ступень на пути к АСУ ТП.[ …]
Если рассмотрение начинать с наиболее общего случая, когда точка наблюдения движется, то становится более понятным и случай с неподвижной точкой наблюдения. Она выступает теперь не как единичная геометрическая точка в пространстве, а как пауза в локомоции, как временно зафиксированное положение в окружающем мире. Соответственно, остановленная перспективная структура в объемлющем строе задает для наблюдателя это фиксированное положение, то есть покой, а текучая перспективная структура задает нефиксированное положение, то есть локомоцию. Следовательно, существует оптическая информация, позволяющая отличить локомоцию от неподвижности, и это в высшей степени значимо для всех наблюдателей — людей и животных. В физике движение наблюдателя в пространстве «относительно», поскольку то, что мы называем движением в одной выбранной системе отсчета, может не быть движением в другой системе отсчета. В экологии такого быть не может, и локомоция наблюдателя в окружающем мире абсолютна. Окружающий мир — это просто то, относительно чего осуществляется либо локомоция, либо состояние покоя, и проблема относительности не возникает.[ …]
Катализаторы готовят осаждением или соосаждением компонентов из растворов, их смешиванием. Полученную массу сушат, прокаливают. В результате образуется структура из слипшихся, спекшихся мелких частиц. Пространство между ними — поры, по которым диффундируют реагенты. Это — осажденные или смесные катализаторы. Таким же образом готовят инертный пористый материал — носитель. На него наносят активные компоненты, например пропиткой из раствора, из которого на внутреннюю поверхность носителя осаждаются каталитически активные компоненты (нанесенные катализаторы). Другие методы приготовления также приводят к образованию сети капилляров сложной формы. Заметим, что такие же методы используют в приготовлении твердых сорбентов — адсорбентов. Полученный пористый материал формуют в виде элементов цилиндрической, кольцеобразной или иной формы, в том числе геометрически неправильной. Размер элементов, или, как их называют, зерен промышленного катализатора, составляет несколько миллиметров (3-6 мм — наиболее распространенный). Таким образом, катализатор представляет собой пористые зерна с развитой внутренней поверхностью.[ …]
Вследствие этого мы не всегда можем быть уверены в реальности всех тех возможностей, которые математики логически правильно выводят. У нас нет никакого другого пути для проверки, как путь обращения к научно точно установленным фактам и к таким же эмпирическим обобщениям. С одним из таких выводов мне пришлось иметь дело, с вопросом о существовании разных геометрических пространств, разных геометрий в окружающей природе и разных пространств—времен (§ 128).[ …]
Построение физической модели к(г) является самостоятельной весьма сложной задачей, решение которой должно основываться на фундаментальных уравнениях облакообразования. В настоящее время эта задача полностью не решена, поэтому исследователи вынуждены использовать некоторые математические модели к(г). Естественными представляются модели в виде совокупности стохастически распределенных в пространстве отдельных облаков той или иной геометрической формы. В таких моделях одним из основных является вопрос о законе распределения облаков в пространстве, который мы коротко обсудим.[ …]
Разлад возник в конце прошлого столетия, с появлением и развитием того, что иногда называют «абстрактной (алгебраической) геометрией». В общих чертах она состояла в введении для каждого простого числа р геометрии (алгебраической) «в характеристике р», скопированной с непрерывной модели геометрии (алгебраической), унаследованной от предыдущих столетий, но все же в контексте, который выступал непримиримо «разрывным», «дискретным». Эти новые геометрические объекты приобрели все возрастающее значение в начале века, и особенно ввиду тесной их связи с арифметикой, наукой в полном смысле этого слова дискретной структуры. Похоже, одна из ведущих идей труда Андрэ Вейля39 , даже может быть, главная движущая сила (которая, как водится, осталась более или менее невысказанной в его записанных работах), состоит в том, что «собственно» геометрия (алгебраическая), и в особенности «дискретные» геометрии, соответствующие различным простым числам, предоставляют ключ к широчайшему обновлению арифметики. Именно этим духом пронизаны прогремевшие в 1949 г. знаменитые гипотезы Вейля. Гипотезы совершенно потрясающие, по правде сказать, позволившие предвидеть для этих новых «многообразий» (или «пространств») дискретной природы возможность определенных типов конструкций и рассуждений40, казавшихся до тех пор немыслимыми вне рамок тех «пространств», которые одни только почитались аналитиками достойными этого имени — именно, пространства, называемые «топологическими» (для которых применимо понятие непрерывного изменения).[ …]
Противоречие в положении геологических и гуманитарных наук в человеческих представлениях и н реальности (§ 113). Планетное значение жизни. Жизнь геологически, вечна на нашей планете. Длительность криптозоя. Скачок эволюционного процесса в нижнем кембрии. Господство членистоногих и позвоночных (таблица 19, § 114, 115). Биосфера и живое вещество геологически вечны. Эволюционный процесс живого вещества в ходе времени и его выявление в земных глубинах 116). Существование биосферы на Венере и Марсе. Основное значение для планетной астрономии эмпирических выводов геологии (§ 117). Ошибочность поисков начала жизни на планетах. Материально-энергетические предпосылки ее в них нахождения. Идея Пьера Кюри о состояниях пространства (§ 118). Значение для понимания пространственных отношений в новой физике понятия о естественных телах. Естественные тела, нам. доступные в космическом масштабе. Ньютон и миропредставление, им данное, к началу XX в. Эйнштейн и новые идеи в физике XX в. Поправка Эддингтона (§ 119, 120). Неоднородное земное пространство геометрически отвечает точке в Эвклидовом пространстве Ньютона и в пространстве—времени Эйнштейна. Планетные состояния пространства. Симметрия как состояние пространства земных природных тел и явлений. Сложность планетного физико-химического пространства. Связь его с состоянием вещества. Пространство — время реально проявляется в живом веществе (§ 121).[ …]
В современной литературе техногенное воздействие часто отождествляется с источниками деятельности или даже их последствиями, что приводит к несогласованности в итоговых документах и проведению исследований, не отвечающих целевому назначению. Многие классификации не учитывают правило деления объема понятия и лишены элементарной логики построения. Признаки изменчивости антропогенеза должны отражать основные черты техногенных воздействий на ГС, поэтому в таксономическом ряду воздействий целесообразно выделить класс, подкласс, тип, вид и разновидность воздействия. При этом класс выделяется по природе (механизму) воздействия; тип — по характеру воздействия с учетом “прямого” и “обратного” действия безотносительно к источнику воздействия; вид — по конкретному техногенному влиянию, которое оказывает тот или иной источник, что раскрывает его индивидуальность; разновидность воздействия — по дополнительным частным признакам (временный характер действия, геометрические размеры, положение в пространстве и др.).[ …]
ru-ecology.info
Геометрия в пространстве

Введение.
В своей деятельности человеку повсюду приходится сталкиваться с необходимостью изучать форму, размеры, взаимное расположение пространственных фигур. Подобные задачи решают и астрономы, имеющие дело с самыми большими масштабами, и физики, исследующие структуру атомов и молекул. Раздел геометрии, в котором изучаются такие задачи, называется стереометрией (от греческого «стереос»- объемный, пространственный).
Может показаться парадоксальным, но фактически понятие «плоскость» в планиметрии- геометрии на плоскости — не нужно. Ведь если мы, например, говорим, что в плоскости многоугольника дана точка, мы тем самым подразумеваем, что такие точки существуют и вне этой плоскости. В планиметрии такое предположение излишние: все происходит в одной и той же единственной плоскости. В стереометрии нам приходится иметь дело уже с несколькими плоскостями. В каждой из них сохраняют свою силу все известные из планиметрии определения и теоремы, относящиеся к точкам, прямым, расстояниям и т.д., но свойства самих плоскостей необходимо описывать отдельно.План.
I. Основные аксиомы стереометрии————— 4 II . Прямые, плоскости, параллельность———— 6
III . Изображение пространственных фигур—— 7 IV . Перпендикулярность. Углы. Расстояния—— 12 V . Несколько задач на построение, воображение, изображение и соображение———————— 17I.Основные аксиомы стереометрии
Итак, в стереометрии к основным понятиям планиметрии добавляется еще одно — плоскость, а вместе с ним — аксиомы, регулирующие «взаимоотношения» плоскостей с другими объектами геометрии. Таких аксиом три.
Первая- аксиома выхода в пространство — придает «театру геометрических действий» новое, третье измерение:
· Имеется четыре точки, не лежащие в одной плоскости (рис. 1)
mirznanii.com
13.6. Вспомогательная геометрия и пространственные кривые
366 |
| Глава 13 | |
|
|
|
|
|
|
| Таблица 13.3 (окончание) |
|
|
|
|
| Объект | Визуализация | Комментарий |
|
|
|
|
| Дуга окружности |
| Степени свободы центра, ра- |
|
|
| диуса и концов дуги |
|
|
|
|
| Эллипс |
| Степени свободы центра, по- |
|
|
| луосей и степень свободы |
|
|
| поворота вокруг центра |
|
|
|
|
| Дуга эллипса |
| Степени свободы центра, кон- |
|
|
| цов и степень свободы пово- |
|
|
| рота вокруг центра |
|
|
|
|
| NURBS |
| Степени свободы концов и |
|
|
| опорных точек |
|
|
|
|
Операции над эскизом, созданным в параметрическом режиме, позволяют построить параметрическую модель — устойчивый комплекс объектов, элементы которого находятся в параметрической связи. Такая модель может динамично менять свою форму без нарушения связей между элементами.
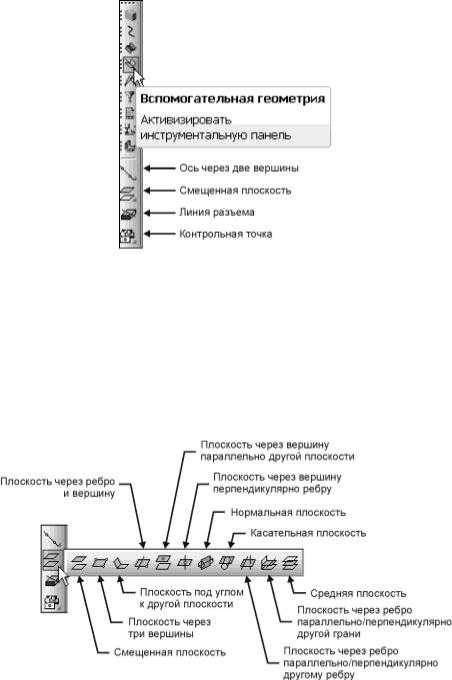
Применение вспомогательных конструктивных элементов значительно расширяет возможности трехмерного моделирования. Инструментальная панель вспомогательных построений открывается нажатием на кнопку Вспомогательная геометрия на панели переключения (рис. 13.28).
На инструментальной панели находятся четыре кнопки:
панель расширенных команд построения вспомогательных осей;
панель расширенных команд построения вспомогательных плоскостей;
кнопка Линия разъема для разбиения грани детали на несколько граней;
панель расширенных команд построения контрольных и присоединительных точек.
Введение в трехмерное моделирование | 367 |
|
|
Рис. 13.28. Инструментальная панель Вспомогательная геометрия
Часто эскизы требуется размещать не в основных плоскостях проекций, а в некоторых вспомогательных плоскостях, занимающих определенное положение по отношению к имеющимся плоскостям проекций или каким-либоконструктивным элементам модели. На панели расширенных команд построения вспомогательных плоскостей можно задать плоскости 11 видов
(рис. 13.29).
Рис. 13.29. Панель расширенных команд построения вспомогательных плоскостей

Созданные при помощи этих команд плоскости отображаются в окне детали в виде прямоугольников, а в дереве модели — в виде специальной пиктограммы. Если перед вызовом команды были выделены какие-либообъекты (например, плоскость или грань), то они будут восприняты в качестве опорных при создании новой плоскости.
Для создания сложных пространственных форм служат команды инструментальной панели Пространственные кривые. В системеКОМПАС-3Dвозможно построение пространственных кривых следующих типов
(рис. 13.30):
Цилиндрическая спираль;
Коническая спираль;
Ломаная;
Сплайн.
Рис. 13.30. Инструментальная панель Пространственные кривые
На инструментальной панели Пространственные кривые находится также командаТочка, позволяющая создать точку в пространстве. Расположение точки может быть задано введением значений координатX,Y иZ на панели свойств или простым щелчком мыши в окне документа.
Введение в трехмерное моделирование | 369 |
|
|
13.7. Выбор объектов
Для выполнения многих команд трехмерного моделирования надо указывать уже созданные объекты — вершины, ребра, грани, оси и плоскости. Это легко сделать прямо на изображении модели в окне документа. При прохождении курсора над объектом, который может быть выбран, этот объект подсвечивается, а сам курсор меняет внешний вид (табл. 13.4).
Таблица 13.4. Вид курсора при выборе объектов в окне документа
Вид курсора | Выбор объекта |
|
|
| Точка или вершина |
|
|
| Ребро |
|
|
| Ось |
|
|
| Поверхность или грань |
|
|
| Плоскость |
|
|
| Пространственная кривая или эскиз |
|
|
| Условное изображение резьбы |
|
|
Для выделения объекта убедитесь, что курсор принял соответствующий вид, и щелкните левой кнопкой мыши. Если цвет объекта изменится, то объект будет выделен. Цвет выделенного объекта установлен в настройках системы. Чтобы снять выделение объекта, щелкните левой кнопкой мыши в любом месте окна документа.
Чтобы выделить в окне документа одновременно несколько объектов, следует выбирать их, удерживая нажатой клавишу <Ctrl>. Щелчок мыши на модели с нажатой клавишей <Shift> позволяет выделить всю деталь.
После того как объект выделен, соответствующая ему пиктограмма в дереве модели поменяет цвет с синего на зеленый. Например, при выделении плоскости цвет изменяет пиктограмма этой плоскости, а при выделении ребра — пиктограмма операции, образовавшей это ребро.
Иногда в «ловушку» курсора попадает сразу несколько объектов (например, грань и ее ребро), причем подсвечивается не тот объект, который вам необходимо выделить. Для облегчения выделения объекта, скрытого другими объектами, можно выбрать тип отображения модели Каркас илиНевиди-
мые линии тонкие.

Если объект по-прежнемуне доступен для выделения, то упростить выбор нужного объекта позволяют две дополнительные возможности, предусмотренные системойКОМПАС-3D:
последовательно перебирать близко расположенные (в том числе наложенные друг на друга) объекты;
»фильтровать» объекты, т. е. выделять объекты определенного типа.
Режим перебора графических объектов доступен, если в ловушку курсора попадает более одного объекта. Поместите курсор на объект и правой кнопкой мыши вызовите контекстное меню (рис. 13.31).
Рис. 13.31. Контекстное меню окна документа
Рис. 13.32. Инструментальная панельФильтры
studfiles.net
Аналитическая геометрия в пространстве
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}$
НАПРАВЛЯЮЩИЙ КОСИНУС ЛИНИИ, СОЕДИНЯЮЩЕЯ ТОЧКИ $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$
$l=\cos\alpha=\frac{(x_2-x_1)}{d}$, $m=\cos\beta=\frac{y_2-y_1}{d}$, $n=\cos\gamma=\frac{z_2-z_1}{d}$
где $\alpha,\beta,\gamma$ углы, которые линия $P_1P_2$ образовывает с положительными осями $x,y,z$ соответственно, а $d$ определено на рисунке вверху.
ОТНОШЕНИЕ МЕЖДУ НАПРЯВЛЯЮЩИМИ КОСИНУСАМИ
$\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1$ или $l^2+m^2+n^2=1$
НАПРАВЛЯЮЩИЕ ЧИСЛА
Числа $L,M,N$, которые есть пропорциональны к направляющим косинусам $l, m, n$ называются направляющими числами. Отношение между ними
$l=\frac{L}{\sqrt{L^2+M^2+N^2}}$, $m=\frac{M}{\sqrt{L^2+M^2+N^2}}$, $n=\frac{N}{\sqrt{L^2+M^2+N^2}}$
УРАВНЕНИЯ ЛИНИИ, СОЕДИНЯЮЩЕЙ $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$ В СТАНДАРТНОЙ ФОРМЕ
$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$ или $\frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n}$
Это также действительно, если $l, m, n$ заменяются на $L, M, N$ соответственно.
УРАВНЕНИЯ ЛИНИИ, СОЕДИНЯЮЩЕЙ $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ
$x=x_1+lt$, $y=y_1+mt$, $z=z_1+nt$
Это также действительно если $l, m, n$ заменяются на $L, M, N$ соответственно.
УГОЛ $\phi$ МЕЖДУ ДВУМЯ ЛИНЯМИ С НАПРАВЛЯЮЩИМИ КОСИНУСАМИ $l_1, m_1, n_1$ И $l_2, m_2, n_2$
$\cos\phi=l_1l_2+m_1m_2+n_1n_2$
ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ
$Ax + By + Cz + D = 0$ [$A, B, C, D$ — константы]
УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ТОЧКИ $(x_1,y_1,z_1),(x_2,y_2,z_2),(x_3,y_3,z_3)$
$\begin{vmatrix}x-x_1 & y-y_1 & z-z_1\\ x_2-x_1 & y_2-y_1 & z_2-z_1\\ x_3-x_1 & y_3-y_1 & z_3-z_1\end{vmatrix}=0$
или
$\begin{vmatrix} y_2-y_1 & z_2-z_1\\ y_3-y_1 & z_3-z_1\end{vmatrix}(x-x_1)$ $+\begin{vmatrix} z_2-z_1 & x_2-x_1\\ z_3-z_1 & x_3-x_1\end{vmatrix}(y-y_1)$ $+\begin{vmatrix} x_2-x_1 & y_2-y_1\\ x_3-x_1 & y_3-y_1\end{vmatrix}(z-z_1)=0$
УРАВНЕНИЕ ПЛОСКОСТИ В ФОРМЕ ПЕРЕСЕЧЕНИЯ
$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$
где $a, b, c$ есть пересечения на осях $x, y, z$ соответственно.
УРАВНЕНИЕ ЛИНИИ ЧЕРЕЗ $(x_0,y_0,z_0)$ И ПЕРПЕНДИКУЛЯРНОЙ К ПЛОСКОСТИ $Ax + By + Cz + D = 0$
$\frac{x-x_0}{A}=\frac{y-y_0}{B}=\frac{z-z_0}{C}$ или $x=x_0+At, y=y_0+Bt, z=z_0+Ct$
Обратите внимание, что направляющие числа для линии, перпендикулярной к плоскости $Ax + By + Cz + D = 0$ есть $A, B, C$.
РАССТОЯНИЕ ОТ ТОЧКИ $(x_0,y_0,z_0)$ К ПЛОСКОСТИ $Ax+By+Cz+D=0$.
$\frac{Ax_0+By_0+Cz_0+D}{\pm\sqrt{A^2+B^2+C^2}}$
где знак выбирается так, что расстояние не является отрицательным.
НОРМАЛЬНОЕ УРАВНЕНИЯ ПЛОСКОСТИ
$x\cos\alpha+y\cos\beta+z\cos\gamma=p$
где $p$ = перпендикулярному расстоянию от $O$ к плоскости в $P$ и $\alpha, \beta, \gamma$ есть углами между $OP$ и положительными осями $x, y, z$.
ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПЕРЕМЕЩЕНИИ
$\left\{\begin{array}{lr}x=x’+x_0\\ y=y’+y_0\\ z=z’+z_0\end{array}\right.$
$\left\{\begin{array}{lr}x’=x-x_0\\ y’=y-y_0\\ z’=z-z_0\end{array}\right.$
где $(x, y, z)$ — старые координаты [т.e. координаты относительно системы xyz], $(x’, y’, z’)$ — новые координаты [относительно системы $x’y’z’$] и $(x_0,y_0,z_0)$ координаты нового центра $O’$ относительно старой координатной системы $xyz$.
ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ВРАЩЕНИИ
$\left\{\begin{array}{lr}x=l_1x’+l_2y’+l_3z’\\ y=m_1x’+m_2y’+m_3z’\\ z=n_1x’+n_2y’+n_3z’\end{array}\right.$
или
$\left\{\begin{array}{lr}x’=l_1x+m_1y+n_1z\\ y’=l_2x+m_2y+n_2z\\ z’=l_3x+m_3y+n_3z\end{array}\right.$
где центры систем $xyz$ и $x’y’z’$ находятся в одной точке и $l_1,m_1,n_1; l_2,m_2,n_2; l_3,m_3,n_3$ направляющие косинусы осей $x’, y’, z’$ относительно осей $x, y, z$ соответственно.
ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПЕРЕМЕЩЕНИИ И ВРАЩЕНИИ
$\left\{\begin{array}{lr}x=l_1x’+l_2y’+l_3z’+x_0\\ y=m_1x’+m_2y’+m_3z’+y_0\\ z=n_1x’+n_2y’+n_3z’+z_0\end{array}\right.$
или
$\left\{\begin{array}{lr}x’=l_1(x-x_0)+m_1(y-y_0)+n_1(z-z_0)\\ y’=l_2(x-x_0)+m_2(y-y_0)+n_2(z-z_0)\\ z’=l_3(x-x_0)+m_3(y-y_0)+n_3(z-z_0)\end{array}\right.$
где $O’$ системы $x’y’z’$ имеет координаты $(x_0,y_0,z_0)$ относительно системы $xyz$ и $l_1,m_1,n_1; l_2,m_2,n_2; l_3,m_3,n_3$ направляющие косинусы осей $x’, y’, z’$ относительно осей $x, y, z$ соответственно.
ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ $(r, \theta, z)$
Точка $P$ может быть определена как цилиндрическими координатами $(r, \theta, z)$,
так и прямоугольными координатами $(x, y, z)$.
Преобразование между этими двумя координатами есть
$\left\{\begin{array}{lr}x=r\cos\theta\\ y=r\sin\theta\\ z=z\end{array}\right.$ или $\left\{\begin{array}{lr}r=\sqrt{x^2+y^2}\\ \theta=\tan^{-1}\frac{y}{x}\\ z=z\end{array}\right.$
СФЕРИЧЕСКИЕ КООРДИНАТЫ $(r, \theta, \phi)$
Точка $P$ может быть определена как сферическими координатами $(r, \theta, \phi)$ так и прямоугольными координатами $(x, y, z)$.
Преобразование между этими двумя кординатами есть
$\left\{\begin{array}{lr}x=r\sin\theta\cos\phi\\ y=r\sin\theta\sin\phi\\
www.math10.com
ОБЪЕКТИВНАЯ ГЕОМЕТРИЯ АРХИТЕКТУРНОГО ПРОСТРАНСТВА | Опубликовать статью РИНЦ
Горшкова Г.Ф.
Доктор архитектуры, профессор, Нижегородский архитектурно-строительный университет
ОБЪЕКТИВНАЯ ГЕОМЕТРИЯ АРХИТЕКТУРНОГО ПРОСТРАНСТВА
Аннотация
На примере чертежных проекций раскрывается формальная взаимосвязанность контурных очертаний архитектурных объектов и геометрии архитектурного пространства. Графический метод позволяет увидеть закономерности в построении формы любого из материальных объектов на Земле.
Ключевые слова: архитектура, объективная форма, геометрия пространства
Gorshkova G.F.
The doctor of architecture, the professor, Nizhniy Novgorod architectural-building university
OBJECTIVE GEOMETRY OF ARCHITECTURAL SPACE
Abstract
By the example of drawing projections the formal coherence of planimetric outlines of architectural objects and geometry of architectural space is opened. The graphic method allows to see laws in construction of the form of any of material objects on the Earth.
Key words: architecture, the objective form, geometry of space
Пространство расценивается как «центральная проблема архитектуры, которая не поддается измерениям и оценкам для всех искусств, так как в нем происходят движение человека и его деятельность» [1, с.336]. Архитектурное пространство напрямую связано с законами построения и проявления жизненного пространства человека, одновременно воздействуя на него как субъективного потребителя, так и объективного организатора. Поэтому архитектура часто воспринимается и оценивается как каменная летопись исторического развития человеческой цивилизации.
Современное ощущение жизненного пространства дает представление о том, что окружающий «материальный мир – это проявленный мир, видимый его существами мир. Духовный же мир – не проявленный, не видимый для его материальных существ и его они могут фиксировать опосредовано, по некоторым физическим нюансам, которые наблюдаются только тогда, когда известно о возможности их проявления. Или окажутся обнаруженными (наличествуют) некоторые искусственные сооружения в комплексе с природными объектами, которая не могла возвести ни одна человеческая цивилизация» [2, с.45]. То есть, в архитектуре, как в совокупности искусственно создаваемых объектов, фиксируются и отражаются свойства не только актуального мира на физическом и оптическом уровне, но также в построении формы проявляются невидимые глазу скрытые закономерности некого идеального, изначально заданного мира. Через геометрию считываются невидимые линейные взаимосвязи пространственного формообразования. В архитектуре геометрия – это средство, форма и инструмент планиметрического моделирования земных объектов и одновременно качественного проявления духовной сферы пространственной ауры в сознании человека.
Чувствование и осознание человеком пространства возникли и развивались на длительном историческом пути развития земной цивилизации. Архитектурные объекты, создаваемые человеком, – это своеобразный мост между разномасштабными бытийными мирами единого земного пространства. Объективное формообразование, в котором участвует человек, происходит в световом проекционном пространстве, которое проявляет себя «следами» линейных очертаний на земную поверхность.
Изучение геометрических особенностей земного пространства, проведенное на основе схемы известной пирамиды Хеопса в Гизе позволило выявить закономерную проекционную структуру, в которой существует объективный пространственный мир [3]. Очертание равнобедренного треугольника в сечении пирамиды проявило множество отношений между его элементами: высотами, медианами и биссектрисами. Так, например, только при угле у основания, близком к 52˚ точки касания боковых сторон для вписанных в треугольник фигур квадрата и окружности совпадают. При этом отношение высоты к основанию треугольника округленно равно 0,64, что позволяет это число математически сравнивать с величиной радиуса планеты Земля, исчисляемой как 0,64*107м. При этом сторона вписанного квадрата в этой схеме условно равна 1.
Схематично проекционную модель архитектурного пространства можно изобразить как линейное взаимодействие главных его составляющих частей: квадрата, круга и треугольника (рис. 1).
Точки и линии пересечения этих трех фигур и их основных элементов определяют все важнейшие и второстепенные геометрические отношения еще на виртуальном (информационном) плане, а затем фиксируются в линейных очертаниях архитектурных объектов, проявленных уже на стадии их проекций: планов, разрезов, фасадов.
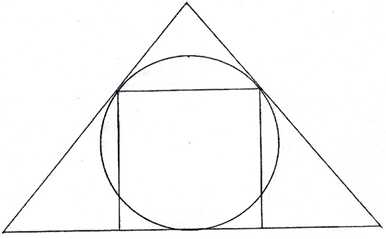
Рис. 1 – Геометрические элементы объективного пространства: квадрат (куб) – структурный модуль пространства; круг (сфера) – волновая проекция света; треугольник (пирамида) a=52˚ – границы видимого света
С точки зрения математического и философского представлений, отношения круга и квадрата являются прообразом полной определенности, достигаемой с помощью конечного набора характеристик, окончательно и полно определенных понятий, точного измерения. Но и здесь существует согласие с мыслью, что «круг олицетворяет то же самое, что и в Великой пирамиде, да и во всей символике вообще : нечто кроющееся за рамками любых определимых понятий, древний Мир Небесный, сферу непостижимого» [4, с.146].
На протяжении большей части 5-тысяч лет архитектурной эволюции сознание человека осуществляло последовательный переход со ступени созерцания на ступень образных представлений о мироустройстве. Сначала «созерцательное знание о мире получало форму произведений искусства. На ступени представления – форму религиозной картины мира. На ступени мышления – форму научной картины мира» [5, с.601]. Поэтому изобразительные и пластические искусства, в том числе архитектура, являлись и до сих пор являются самым значительными и емкими носителями концентрированного знания о пространстве и проявителями его сущностного содержания.
В архитектуре этот путь от природного созерцания через творческое освоение к рациональному пониманию объективной формы можно проследить на примерах сооружений, символизирующих построение человеком сакрального пространства: от поверхностных лабиринтов до купольных построек.
С незапамятных времен круглая форма пространства фиксировалась в каменных построениях, встречающихся в самых разнообразных землях в наземном или подземном уровнях и называемых лабиринтами. Как говорится в специальной литературе об этих символических формообразованиях, «некоторые спиральные и эллипсовидные изображения лабиринта, в особенности наиболее древние, следует рассматривать как первые простейшие диаграммы неба» [6, с.289] (Рис.2).
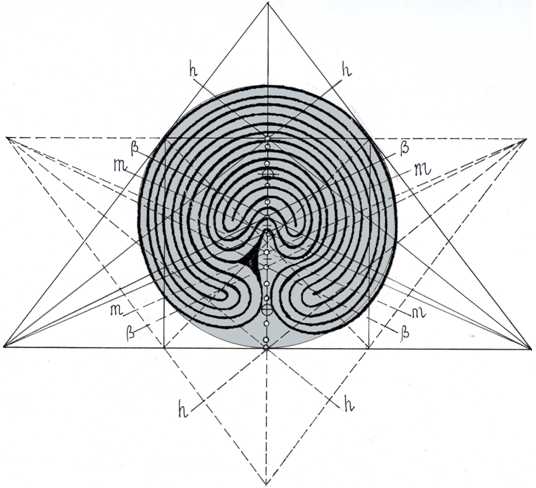
Рис. 2 – Очертания лабиринта, как проекция «Неба» на земную поверхность
В архитектурных исследованиях [7] установлено, что по мере перехода человека к оседлому образу жизни центром обитаемой местности, центром пространства жизнедеятельности становился алтарь, а позднее – святилище и храм. По закону обязательной фиксации такого центра мы, хотя и неосознанно, все еще продолжаем жить и сейчас. Центральная точка любого пространства всегда предназначена для фиксации проекции небесных (духовных) сил или как стартовая опора для подъема земных энергий на недостижимую духовную высоту. Архитектурная история человечества представляет целую галерею храмовых сооружений, сопровождавших человека и общество на протяжении тысячелетий, служивших задаче развития их сознания и духовному постижению законов миропорядка и мироустройства на земле и в космосе и дошедших до наших дней в материальной или виртуальной форме.

Рис.3 – Вертикальный разрез храмового здания (Римский Пантеон) как проекция Вселенной на Землю
Большое число разнообразных по времени, месту и смысловому содержанию архитектурных памятников храмового зодчества указывают на единообразие пространственного построения зданий и сооружений всех культов и религий. В самых разнообразных формальных очертаниях осуществляется единая последовательность развёртывания: развёртывание алтарного камня, столпа, простейшей постройки (сени) в конструкцию, представляющую мироздание. Изначальный смысл, заложенный в природный объект (камень) или в простейшее укрытие (сень), трансформирует строение храма в очевидно выраженную пространственную систему. После утверждения принципиальной формы мироздания её развёртывание идет по двум направлениям: по горизонтали и вертикали.
Представление о такой принципиальной форме мироздания возникает, когда совмещаются проекционные контуры идеального человеческого тела, образцового храмового здания (в профильном разрезе) и проекционной схемы земного пространства (рис.3). Возникает картина единства всех уровней пространственных отношений и взаимосвязей не только в пределах треугольника, то есть земного 3-мерного пространства, но простирающихся за его пределы.
Исходя из современных представлений о пространственном формотворчестве в архитектуре, важно отметить следующие профессиональные и интуитивные оценки объективных качеств известных исторических образцов храмового зодчества [8].
- «Линии в данном пространстве не должны только служить для обозначения контуров тел, а приобрести непосредственную самодостаточность, графическое качество, одновременно ясное в своей простоте и иррациональное» [8, с.288].
- «Форма, легшая в план творимой вещи, является смыслоопределяющей в символике данной вещи. Существуют лишь три формы, с которыми возможно оперировать – это круг, квадрат и треугольник (все разнообразие деформаций плоскостных форм сводимо к этим трем) и которые означают следующее : круг – природу внешних вещей, а от того публичное пространство; квадрат – природу внутренних вещей, а от того частное пространство; треугольник – природу переменных, неустойчивых вещей, а от того промежуточное пространство» [8, с.289].
- «Архитектура есть процесс овеществления, через индивидуальную сопричастность творящего творящему, одного и того же плана (ведь план — это свернутое пространство в плоскость идеи-знака), всегда приводящего к различным результатам, т.е. это есть процесс овеществления единичной идеи Единого во множество образов Множественного» [8, с.290].
Архитектурная традиция, по словам классика итальянского Возрождения Альберти, еще со времени Витрувия понимала, что «никакой храм без соразмерности и пропорции не может иметь правильной композиции, если в нем не будет такого же точного членения, как у хорошо сложенного человека. Как в живом существе (in animate) одни члены должны находиться в соответствии с другими» [9, с.67], так и отдельные части храмового сооружения во внешней и внутренней пространственной организации связаны между собой по определенным законам, отношениям, правилам.
Универсальная проекционная модель объективного пространства, выстроенная на основе представленных выше геометрических фигур, показывает, как через геометрию демонстрируются, раскрываются и подтверждаются все возможные процессы архитектурного формообразования. Зарождаясь и протекая в виртуальных сферах пространства «высших миров», жизнетворные процессы реализуются в 3-х-мерном физическом пространстве, пронизывая все уровни его иерархической системы и находя формальное выражение в конкретном пространстве-времени конкретной 3-х-мерной реальности.
В проявленной физической форме любого архитектурного объекта содержится все формальное многообразие пространственного Абсолюта. На этой основе строится эволюционное развитие архитектуры как объективной человеческой деятельности в пространственной среде. Архитектурное творчество человека через здания, сооружения и генеральные планы территории отражает архетипические образы природы и одновременно способствует проникновению в ещё неизведанные возможности объективного пространства. На этом основывается не только историческая картина архитектурного развития искусственной пространственной среды человечества, но также предопределяется вектор возможного его развития в будущем. Проникая глубже в виртуальную структуру феномена пространства, человечество расширяет свое пространственное сознание, гармонизируя тем самым свои рациональные и интуитивные сущности.
Литература
- Новикова, Е. Б. Интерьер общественных зданий: Художественные проблемы / Е. Б. Новикова. – М.: Стройиздат, 1991. – 368 с.: ил.
- Черняев, А. Ф. Духовные основы науки / А. Ф. Черняев. – М.: Принтер, 2003. – 107 с.: ил.
- Горшкова, Г.Ф. Геометрическая система архитектурного пространства: монография / Г.Ф. Горшкова. – Н. Новгород, ННГАСУ, 2007. – 243 с.: ил.
- Мерелл-Вольф, Ф. Математика, философия и йога / Ф. Мерелл-Вольф; пер. с англ. К. Семенова; ред. В. Трилис. – К.: София, 1999. – 160 с.
- Труфанов, С.Н. Грамматика разума. – Самара, Гегель-фонд, 2003. – 624 с.
- Турскова, Т.А. Новый справочник символов и знаков / Т.А. Турскова. – М.: РИПОЛ КЛАССИК, 2003. – 800с.
- Павлов, Н.Л. Алтарь. Ступа. Храм. Архаическое мироздание в архитектуре индоевропейцев / Н.Л. Павлов. – М.: ОЛМА-ПРЕСС, 2001. -368 с.: ил.
- Колосов, А.Б. Утверждения о началах ментального мира и природе иного / А.Б. Колосов. – М: АЛЬЯНС, АГРАФ, 2001. – 432 с., рис., табл.
- Альберти. Л.Б. – М: Наука, 1977. – 191 с.
References
- Novikova, E. B. Inter’er obshhestvennyh zdanij: Hudozhestvennye problemy / E. B. Novikova. – M.: Strojizdat, 1991. – 368 s.
- Chernjaev, A. F. Duhovnye osnovy nauki / A. F. Chernjaev. – M.: Printer, 2003. – 107 s.
- Gorshkova, G.F. Geometricheskaja sistema arhitekturnogo prostranstva: monografija / G.F. Gorshkova. – N. Novgorod, NNGASU, 2007. – 243 s.
- Merell-Vol’f, F. Matematika, filosofija i joga / F. Merell-Vol’f; per. s angl. K. Semenova; red. V. Trilis. – K.: Sofija, 1999. – 160 s.
- Trufanov, S.N. Grammatika razuma. – Samara, Gegel’-fond, 2003. – 624 s.
- Turskova, T.A. Novyj spravochnik simvolov i znakov / T.A. Turskova. – M.: RIPOL KLASSIK, 2003. – 800s.
- Pavlov, N.L. Altar’. Stupa. Hram. Arhaicheskoe mirozdanie v arhitekture indoevropejcev / N.L. Pavlov. – M.: OLMA-PRESS, 2001. -368 s.
- Kolosov, A.B. Utverzhdenija o nachalah mental’nogo mira i prirode inogo / A.B. Kolosov. – M: AL”JaNS, AGRAF, 2001. – 432 s.
- Al’berti. L.B. – M: Nauka, 1977. – 191 s.
research-journal.org

 С третьей аксиомой мы сталкиваемся, когда складываем фигурки из бумаги: все знают, что, образующиеся при этом линии сгиба — прямые. Аксиома пересечения плоскостей звучит так:
С третьей аксиомой мы сталкиваемся, когда складываем фигурки из бумаги: все знают, что, образующиеся при этом линии сгиба — прямые. Аксиома пересечения плоскостей звучит так:
 На рис. 4 изображён куб; прямые АВ и ВС пересекаются, АВ и CD — параллельны, а АВ и В¹С¹ — скрещиваются. В дальнейшем мы часто будем прибегать к помощи куба, чтобы иллюстрировать понятия и факты стереометрии. Наш куб склеен из шести граней-квадратов. Исходя из этого, мы будем выводить и другие его свойства. Например, можно утверждать, что прямая АВ параллельна C¹D¹, потому что обе они параллельны общей стороне CD содержащих их квадратов.
На рис. 4 изображён куб; прямые АВ и ВС пересекаются, АВ и CD — параллельны, а АВ и В¹С¹ — скрещиваются. В дальнейшем мы часто будем прибегать к помощи куба, чтобы иллюстрировать понятия и факты стереометрии. Наш куб склеен из шести граней-квадратов. Исходя из этого, мы будем выводить и другие его свойства. Например, можно утверждать, что прямая АВ параллельна C¹D¹, потому что обе они параллельны общей стороне CD содержащих их квадратов.