Постройте график функции y = x^3 – x^2
Задание.
Постройте график функции y = x^3 — x^2.
Решение.
- Функция степенная без каких-либо ограничений, поэтому область определения будет вся числовая прямая. Значения функции — вся числовая прямая.
- Четная или нечетная функция.
Подставим вместо переменной х значение —х и по результату сделаем вывод:
В результате получили, что функция не является ни четной, ни нечетной.
- Функция должна пересекаться с координатными осями. Вычислим точки пересечения функции с ними.
Для вычисления точек пересечения с осью Ох, подставим в функцию вместо переменной х число 0:
Функция пересекается с осью Ох в точке с координатами (0; 0).
Вычислим точку пересечения с осью Оу. Для этого подставим вместо переменной у значение 0 и решим полученное уравнение:
или
или
Функция пересекается с осью Оу в двух точках, первая— это пересечение с осью Ох, так как это начало координат — (0; 0). У второй точки координаты (1; 0).
- Поскольку функция степенная, то должна иметь экстремумы. Вычислим их, рассчитав производную:
Запишем производную, как равную нулю, и вычислим корни уравнения:
или
или
Проверим полученные точки на экстремум. Для этого возьмем какую-нибудь точку из каждого полученного промежутка между найденными точками и найдем знак производной на всех полученных промежутках.
Первый промежуток от минус бесконечности до 0. Возьмем точку —1 и рассчитаем для нее производную:
— функция возрастает.
Второй промежуток от 0 до 2/3. Выберем точку 0,5 и вычислим от нее производную:
— функция убывает.
Третий промежуток от 2/3 до + бесконечности. Возьмем точку 1 и вычислим от нее производную:
— функция возрастает на этом промежутке.
Когда функция переходит через точку с абсциссой 0, она изменяет знак производной с + на —. Значит, это точка максимума, а при переходе через точку 2/3 знак производной меняется с — на +, значит, это точка минимума.
Максимум — точка (0; 0)
Минимум — точка .
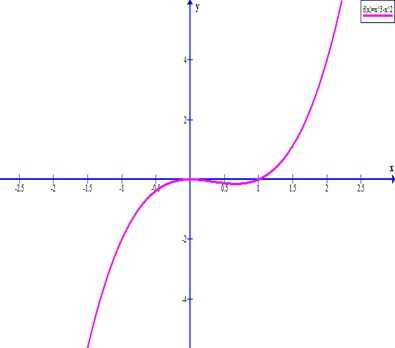
ru.solverbook.com
их графики, функции и свойства
Функция y=x^2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
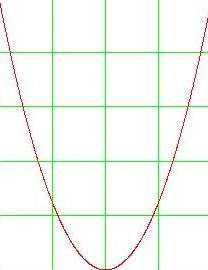
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке [0;+∞).
4. Противоположным значениям х соответствует одинаковые значения y.
Кубическая функция
Функция y=x^3 называется кубической функцией. Графиком кубической функции называется кубическая парабола. Общий вид параболы представлен на рисунке ниже.
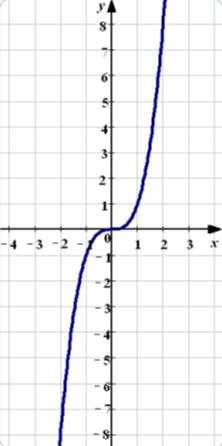
Если график квадратичной функции был симметричен оси Оу, то график кубической параболы симметричен относительно начала координат, то есть точки (0;0).
Свойства кубической функции
Перечислим основные свойства кубической функции
- При х =0, у=0. у>0 при х>0 и y
- У кубической функции не существует не максимального ни минимального значения.
- Кубическая функция возрастает на всей числовой оси (-∞;+∞).
- Противоположным значениям х, соответствуют противоположные значения y.
Нужна помощь в учебе?
Предыдущая тема: Умножение одночленов и возведение одночлена в степень + примеры
Следующая тема:   Абсолютная погрешность: понятие, как вычислить + примеры
Все неприличные комментарии будут удаляться.
www.nado5.ru
Постройте график функции y = |x| (x + 2) – 3x
Задание.
Построить график функции y = |x| (x + 2) — 3x.
Решение.
Рассмотрим уравнение функции. Оно содержит модуль от переменной х. Это значит, что переменная х может быть как отрицательным, так и положительным числом. Из этого можно сделать вывод, что график функции будет состоять из двух парабол, ветви у которых направлены в разные стороны.
Допустим, переменная х будет положительным числом. Запишем вид функции после раскрытия модуля:
сли х будет отрицательным числом, то функция будет выглядеть следующим образом:
Построение сводится к тому, для положительных значений х (промежуток от 0 до + бесконечности) нужно построить первую параболу, а для отрицательных значений х (промежуток от — бесконечности до 0) — ворую параболу. Получается, что обе параболы будет отделять ось Оу.
Вычислим вершину первой параболы:
Вершина первой параболы — точка (0,5; —0,25).
Вычислим вершину второй параболы:
Вершина первой параболы — точка (2,5; —18,75).
Далее найдем точки пересечения парабол с осями координат.
Первая парабола :
Ось Оу: х = 0
Ось Ох: у = 0
или
Первая парабола пересекается с координатными осями в двух точках — (0; 0) и (1; 0).
Вторая парабола :
Ось Оу: х = 0
Ось Ох: у = 0
или
Вторая парабола пересекается с координатными осями в двух точках — (0; 0) и (—5; 0).
Нанесем все точки на график и соединим их кривой.

ru.solverbook.com
Постройте график функции y = (x^3+x^2)/(x+1)
Задание.
Построить график функции y = (x^3 + x^2) / (х+1).
Решение.
Запишем функцию:
Проанализируем ее. В числителе в обоих слагаемых есть общий множитель, который можно вынести за скобку:
Теперь очевидно, что можно сократить и числитель, и знаменатель на х + 1. Получим:
Это парабола, направленная ветвями вверх.
Но при этом нужно учесть, что знаменатель не должен быть равным нулю. Поэтому:
Для построения графика параболы необходимо рассчитать координаты ее вершины. Для этого воспользуемся формулой:
Получили вершину параболы в точке (0; 0), то есть в начале координат.
Найдем точки пересечения параболы с осями координат.
Начнем с оси Оу. Для этой оси х = 0. Подставим данное значение в функцию:
Найдем пересечение с осью Ох. Для этой оси у = 0. Подставим в функцию и решим простое уравнение:
Получили одну точку пересечения с осью Оу с координатами (0: 0).
Найдем дополнительные точки, необходимые для построения. Для этого вместо переменной х подставим значения 1 и —1, а также 2 и —2:
Отметим полученные точки на координатной плоскости и соединим их плавной кривой, поскольку данная функция является параболой.
ru.solverbook.com
Функции $y=x^2$ и $y=x^3$ и их графики
Функция $f\left(x\right)=x^2$ является частным случаем квадратичной функции, когда $a=1,\ b,c=0$. Графиком такой функции называется парабола.
Исследуем и построим график функции $f\left(x\right)=x^2$
- Область определения — все числа.
- Так как квадрат любого числа всегда больше или равен нулю, то область значения $[0,\infty )$
- $f\left(-x\right)={(-x)}^2=x^2=f(x)$. Значит функция четна.
- При $x=0,\ y=0$ -0 функция проходит через начало координат.
- $f’\left(x\right)={\left(x^2\right)}’=2x$ \[2x=0,\] \[x=0\]
- $f^{»}\left(x\right)={\left(2x\right)}^{»}=2>0$.
- Для построения графика функции составим таблицу её значений:
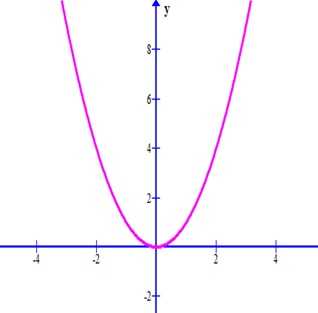
- График функции — парабола (рис. 1)
Методом интервалов, получим:
Функция возрастает при $x\in (0,+\infty )$
Функция убывает при $x\in (-\infty ,0)$
Следовательно, функция выпукла на всей области определения.
\[{\mathop{lim}_{x\to -\infty } x^2\ }=+\infty \] \[{\mathop{lim}_{x\to +\infty } x^2\ }=+\infty \]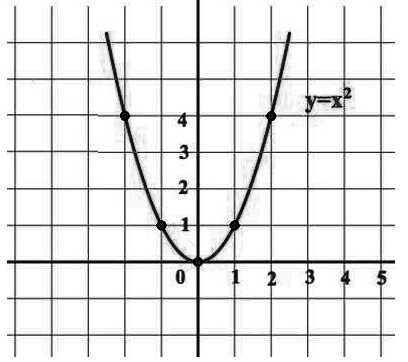
Рис. 1. Парабола $f\left(x\right)=x^2$.
Функция $f(x)=x^3$
Для начала вспомним определение кубической функции.
Функция $f\left(x\right)=x^3$ является частным случаем кубической функции, когда $a=1,\ b,c=0$. Графиком такой функции называется кубическая парабола.
Исследуем и построим график функции $f\left(x\right)=x^3$
- Область определения — все числа.
- Область значения — все числа
- $f\left(-x\right)={(-x)}^3=-x^3=-f(x)$. Значит функция нечетна.
- При $x=0,\ y=0$ -0 функция проходит через начало координат.
- $f’\left(x\right)={\left(x^3\right)}’=3x^2$ \[3x^2=0,\] \[x=0\]
- $f^{»}\left(x\right)={\left(3x^2\right)}^{»}=6x$. \[6x=0\] \[x=0\]
- Для построения графика функции составим таблицу её значений:
- График функции — кубическая парабола (рис. 2)
Так как квадрат любого числа всегда больше или равен нулю, то функция убывает на всей области определения.
Методом интервалов, получим:
Функция выпукла при $x\in (0,+\infty )$
Функция вогнута при $x\in (-\infty ,0)$
\[{\mathop{lim}_{x\to -\infty } x^2\ }=-\infty \] \[{\mathop{lim}_{x\to +\infty } x^2\ }=+\infty \]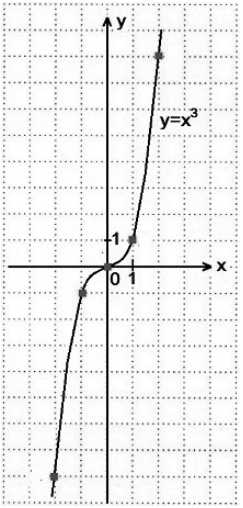
Рис. 2. Кубическая парабола $f\left(x\right)=x^3$.
spravochnick.ru
