Имеется плоский воздушный конденсатор площадь каждой обкладки которого s – Задача по физике — 7440

Задача по физике — 7440

2018-05-14   
Имеется плоский воздушный конденсатор, площадь каждой обкладки которого равна $S$. Какую работу необходимо совершить, чтобы медленно увеличить расстояние между обкладками от $x_{1}$ до $x_{2}$, если при этом поддерживать неизменным:
а) заряд конденсатора, равный $q$;
б) напряжение на конденсаторе, равное $U$?

Решение:

(а) Произведенная работа эквивалентна работе, выполненной против электрического поля, созданного одной пластиной, находящийся в покое и работе по перемещению другой пластины. Поэтому требуемая работа,

$A_{внеш} = qE (x_{2} — x_{1})$

где $E = \frac{ \sigma }{2 \epsilon_{0} }$ — напряженность поля, создаваемого одной пластиной в месте расположения другой.

Так, $A_{внеш} = q \frac{ \sigma}{2 \epsilon_{0} }(x_{2} — x_{1} ) = \frac{q^{2} }{2 \epsilon_{0} S } (x_{2} — x_{1} )$

Альтернативный вариант: $A_{внеш} = \Delta U$ (поскольку поле является потенциальным)

$= \frac{q^{2} }{2 \epsilon_{0}S } x_{2} — \frac{q^{2} }{2 \epsilon_{0}S } x = \frac{q^{2} }{2 \epsilon_{0}S } (x_{2} — x_{1})$

(б) Когда напряжение поддерживается постоянным, сила действующая на каждую пластину конденсатора будет зависеть от расстояния между пластинами.
Итак, элементарная работа, выполняемая внешним полем, при смещении на расстояние $dx$, одной пластины относительно другой,

$dA = — F_{x}dx$

Но, $F_{x} = — \left ( \frac{ \sigma (x) }{2 \epsilon_{0} } \right ) S \sigma (x)$ и $\sigma(x) = \frac{ \epsilon_{0}V}{x}$

Следовательно, $A = \int dA = \int_{x_{1} }^{x_{2} } \frac{1}{2} \epsilon_{0} \frac{SV^{2} }{x^{2} } dx = \frac{ \epsilon_{0} SV^{2} }{2} \left [ \frac{1}{x_{1} } — \frac{1}{x_{2} } \right ]$

Альтернативный способ: из закона сохранения энергии,

$U_{кон} — U_{нач} = A_{ист} + A_{внеш}$

или $\frac{1}{2} \frac{ \epsilon_{0}S }{x_{2} } V^{2} — \frac{1}{2} \frac{ \epsilon_{0}S }{x_{1} } V^{2} = \left [ \frac{ \epsilon_{0}S }{x_{2} } — \frac{ \epsilon_{0}S }{x_{1} } \right ] V^{2} + A_{внеш}$

(при $A_{ист} = (q_{кон} — q_{нач}) V = (C_{кон} — C_{нач}) V^{2}$

тогда $A_{внеш} = \frac{ \epsilon SV^{2} }{2} \left [ \frac{1}{x_{1} } — \frac{1}{x_{2} } \right ]$

earthz.ru

Физика. Иродов Е.А. Задача № 3.141

1. Физика. Иродов Е.А.
2. Электродинамика
3. Электроемкость. Энергия электрического поля
4. 3.141

Условие задачи 3.141:

Имеется плоский воздушный конденсатор, площадь каждой обкладки которого равна S. Какую работу необходимо совершить, чтобы медленно увеличить расстояние между обкладками от x₁ до x₂, если при этом поддерживать неизменным:
а) заряд конденсатора, равный q;

б) напряжение на конденсаторе, равное U?

Решение задачи:

СДЕЛАЙТЕ РЕПОСТ

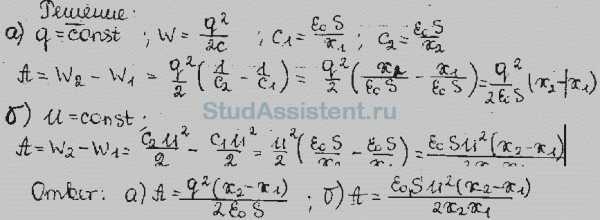
Решение задачи 3.141

С другими задачами из решебника по физике Иродова вы можете ознакомиться в соответствующем разделе решебника Физика. Иродов Е.А.

Материалы:

studassistent.ru

Задача Плоский конденсатор, площадь каждой обкладки которого см2, а расстояние

Задача. Плоский конденсатор, площадь каждой обкладки которого

см², а расстояние между ними мм, заполнен трансформаторным маслом, диэлектрическая проницаемость которого . Определите энергию и модуль напряжённости электростатического поля конденсатора, если напряжение на нём В.

Решение

Думаем: энергию плоского конденсатора можно найти различными способами, попробуем выбрать наиболее быстрый. У нас в дано присутствует напряжение (

), о геометрические параметры конденсатора могут дать электроёмкость системы (1). (1)

Тогда энергию конденсатора проще найти через:

(2)

Напряжённость поля внутри конденсатора можно найти через:

(3)

Заряд конденсатора можно найти через напряжение и электроёмкость:

(4)

Решаем: подставим (1) в (2).

(5)

Для решения вопроса о напряжённости, подставим (4) в (3), а затем в получившееся уравнение в (1):

(6)

Соотношение (6) получилось достаточно логичным и его можно было сразу найти через определение напряжённости.

Считаем: вспоминаем необходимые константы 

Ф/м. И не забываем перевести все параметры в единицы СИ. Дж Н/м

Ответ: 

мкДж;  Н/м.

Ещё задачи на тему «Плоский конденсатор. Электроёмкость»

Плоский конденсатор, площадь каждой обкладки которого обновлено: Март 4, 2018 автором: Иван Иванович

Поделиться ссылкой:

www.abitur.by

Физика — Страница 100

Раздел: Иродов, Решения задач, Физика

Иродов 3.141. Имеется плоский воздушный конденсатор, площадь каждой обкладки которого равна S. Какую работу необходимо совершить, чтобы медленно увеличить расстояние между обкладками от x1 до x2, если при этом поддерживать неизменным: а) заряд конденсатора, равный q; б) напряжение на конденсаторе, равное U? Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.139. Сферическая оболочка заряжена равномерно с поверхностной плотностью σ. Воспользовавшись законом сохранения энергии, найти модуль вектора электрической силы, которая действует на единицу поверхности оболочки. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.138. Имеется сферическая оболочка, равномерно заряженная зарядом q, в центре которой расположен точечный заряд q0. Найти работу, совершенную электрическими силами при расширении оболочки — увеличении ее радиуса от R1 до R2. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.137. Сферическую оболочку радиуса R1, равномерно заряженную зарядом q, расширили до радиуса R2. Найти работу, совершенную при этом электрическими силами. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.136. Точечный заряд q = 3,0 мкКл находится в центре шарового слоя из однородного изотропного диэлектрика с проницаемостью ε = 3,0. Внутренний радиус слоя a = 250 мм, внешний b = 500 мм. Найти электростатическую энергию, заключенную в диэлектрическом слое. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.135. Заряд q распределен равномерно по объему шара радиуса R. Полагая диэлектрическую проницаемость равной единице, найти: а) собственную электростатическую энергию шара; б) отношение энергии W1, запасенной внутри шара, к энергии W2, заключенной в окружающем пространстве. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.134. Система состоит из двух концентрических тонких металлических оболочек радиусами R1 и R2 с соответствующими зарядами q1 и q2. Найти значения собственной энергии каждой оболочки W1 и W2, энергии взаимодействия оболочек W12 и полную электрическую энергию W системы. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.132. Какое количество тепла выделится в цепи (рис. 3.30) после переключения ключа К из положения 1 в положение 2? Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.131. Конденсатор емкости C1 = 1,0 мкФ, предварительно заряженный до напряжения U = 300 В, подключили параллельно к незаряженному конденсатору емкости C2 = 2,0 мкФ. Найти приращение электрической энергии этой системы к моменту установления равновесия. Объяснить полученный результат. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.129. Точечный заряд q находится на расстоянии l от безграничной проводящей плоскости. Найти энергию взаимодействия этого заряда с зарядами, индуцированными на плоскости. Скачать решение: Скачать решение задачи

Смотреть материал

reshal.ru

Решения задач — Страница 101

Главная / Материалы раздела: Решения задач (Page 101) Раздел: Иродов, Решения задач, Физика

Иродов 3.141. Имеется плоский воздушный конденсатор, площадь каждой обкладки которого равна S. Какую работу необходимо совершить, чтобы медленно увеличить расстояние между обкладками от x1 до x2, если при этом поддерживать неизменным: а) заряд конденсатора, равный q; б) напряжение на конденсаторе, равное U? Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.139. Сферическая оболочка заряжена равномерно с поверхностной плотностью σ. Воспользовавшись законом сохранения энергии, найти модуль вектора электрической силы, которая действует на единицу поверхности оболочки. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.138. Имеется сферическая оболочка, равномерно заряженная зарядом q, в центре которой расположен точечный заряд q0. Найти работу, совершенную электрическими силами при расширении оболочки — увеличении ее радиуса от R1 до R2. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.137. Сферическую оболочку радиуса R1, равномерно заряженную зарядом q, расширили до радиуса R2. Найти работу, совершенную при этом электрическими силами. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.136. Точечный заряд q = 3,0 мкКл находится в центре шарового слоя из однородного изотропного диэлектрика с проницаемостью ε = 3,0. Внутренний радиус слоя a = 250 мм, внешний b = 500 мм. Найти электростатическую энергию, заключенную в диэлектрическом слое. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.135. Заряд q распределен равномерно по объему шара радиуса R. Полагая диэлектрическую проницаемость равной единице, найти: а) собственную электростатическую энергию шара; б) отношение энергии W1, запасенной внутри шара, к энергии W2, заключенной в окружающем пространстве. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.134. Система состоит из двух концентрических тонких металлических оболочек радиусами R1 и R2 с соответствующими зарядами q1 и q2. Найти значения собственной энергии каждой оболочки W1 и W2, энергии взаимодействия оболочек W12 и полную электрическую энергию W системы. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.132. Какое количество тепла выделится в цепи (рис. 3.30) после переключения ключа К из положения 1 в положение 2? Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.131. Конденсатор емкости C1 = 1,0 мкФ, предварительно заряженный до напряжения U = 300 В, подключили параллельно к незаряженному конденсатору емкости C2 = 2,0 мкФ. Найти приращение электрической энергии этой системы к моменту установления равновесия. Объяснить полученный результат. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.129. Точечный заряд q находится на расстоянии l от безграничной проводящей плоскости. Найти энергию взаимодействия этого заряда с зарядами, индуцированными на плоскости. Скачать решение: Скачать решение задачи

Смотреть материал

reshal.ru

Иродов — Страница 45

Раздел: Иродов, Решения задач, Физика

Иродов 3.151. При каком значении сопротивления Rx в цепочке (рис. 3.36) сопротивление между точками A и B не будет зависеть от числа ячеек? Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.150. Найти сопротивление проволочного каркаса, имеющего форму куба (рис. 3.35), при включении его в цепь между точками: а) 1 — 7; б) 1 — 2; в) 1—3. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.148. Воздушный цилиндрический конденсатор, подключенный к источнику постоянного напряжения U = 200 В, погружают в вертикальном положении в сосуд с дистиллированной водой со скоростью v = 5,0 мм/с. Зазор между обкладками конденсатора d = 2,0 мм, средний радиус кривизны обкладок r = 50 мм. Имея в виду, что d << r, найти ток, текущий […]

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.147. Длинный равномерно заряженный по поверхности цилиндр радиусом сечения a = 1,0 см движется с постоянной скоростью v = 10 м/с вдоль своей оси. Напряженность электрического поля непосредственно у поверхности цилиндра Е = 0,9 кВ/см. Чему равен соответствующий конвекционный ток, т.е. ток, обусловленный механическим переносом заряда? Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.143. Плоский конденсатор опустили в горизонтальном положении в воду, которая заполнила зазор между пластинами шириной d = 1,0 мм. Затем конденсатор подключили к постоянному напряжению U = 500 В. Найти приращение давления воды в зазоре. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.142. Внутри плоского конденсатора находится параллельная обкладкам пластинка, толщина которой составляет η = 0,60 части зазора между обкладками. Емкость конденсатора в отсутствие пластинки C = 20 нФ. Конденсатор сначала подключили параллельно к источнику постоянного напряжения U = 200 В, затем отключили и после этого медленно извлекли пластинку из зазора. Найти работу, затраченную на извлечение […]

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.141. Имеется плоский воздушный конденсатор, площадь каждой обкладки которого равна S. Какую работу необходимо совершить, чтобы медленно увеличить расстояние между обкладками от x1 до x2, если при этом поддерживать неизменным: а) заряд конденсатора, равный q; б) напряжение на конденсаторе, равное U? Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.139. Сферическая оболочка заряжена равномерно с поверхностной плотностью σ. Воспользовавшись законом сохранения энергии, найти модуль вектора электрической силы, которая действует на единицу поверхности оболочки. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.138. Имеется сферическая оболочка, равномерно заряженная зарядом q, в центре которой расположен точечный заряд q0. Найти работу, совершенную электрическими силами при расширении оболочки — увеличении ее радиуса от R1 до R2. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.137. Сферическую оболочку радиуса R1, равномерно заряженную зарядом q, расширили до радиуса R2. Найти работу, совершенную при этом электрическими силами. Скачать решение: Скачать решение задачи

Смотреть материал

reshal.ru

Плоский воздушный конденсатор емкостью с квадратными обкладками, сторона каждой из которых равна , подключен к источнику с ЭДС . В конденсатор вставляют пластинку с диэлектрической проницаемостью , занимающую все пространство между обкладками, а затем выдвигают ее из конденсатора на небольшое расстояние, как показано на рисунке. Какую силу нужно приложить к пластинке, чтобы удерживать ее в таком положении?  

Решение

Обозначим через расстояние, на которое диэлектрическая пластинка выдвинута из конденсатора. Емкость конденсатора с частично выдвинутой пластинкой равна

При выдвигании пластинки заряд на конденсаторе изменится на величину: . Поскольку заряд на конденсаторе уменьшается, работа источника отрицательна: . Энергия конденсатора при выдвигании пластинки также уменьшится: . Изменение энергии конденсатора равно сумме работы силы и работы источника : , откуда . Поскольку , ответ имеет вид: .  

Ответ

.

gitun.com