Графический способ решения систем уравнений
Графиками таких уравнений могут являться различные линии.
Решить систему — значит найти все её решения или доказать, что их нет.
Определение:
Решением системы называется пара значений переменных, обращающая каждое уравнение системы уравнений с двумя переменными в верное равенство.
Пример.
Нужно проверить, обращают ли пара значений уравнения системы в верные равенства.
1. Первая пара (-2, 1). Подставим их в систему:
Первое уравнение обратилось в верное равенство, а второе — нет. Значит, пара чисел (-2;1) не является решением данной системы.
2. Вторая пара (1;-2). Поставим эти значения в систему:
Получаем два верных равенства. Значит, пара чисел (1;-2) является решением данной системы.
Пример.
Решить систему двух уравнений:
Изобразим график системы:
Видим, что графики пересеклись в двух точках. Их координаты и являются решением системы. Данная система имеет два решения: (0;3) и (3;0).
Проверим, действительно ли они являются решениями. Подставим эти значения в систему:
Проверка необходима потому, что графический метод позволяет получить приближённые значения. Иногда их сложно указать точно.
Получили две пары значений: (0;3) и (3;0).
Пример.
Решить систему уравнений:
Изобразим график системы:
Точку пересечения этих графиков имеет координаты (0;1). Подставим значения в систему:
Получили верные равенства. Значит, решением данной системы является пара чисел (0;1).
Пример.
Решить систему двух уравнений:
Изобразим график системы:
Видим две точки пересечения. Их координаты трудно указать точно. Поэтому прежде чем записать ответ, полученные значения нужно подставить в систему:
Решением системы будут две пары чисел(2,5;2,5) и (6,5;6,5).
videouroki.net
Решение системы уравнений графическим методом средствами MS Excel
Разделы: Математика, Информатика
Цели и задачи.
- Развитие приемов умственной деятельности, формирование и развитие функционального мышления учащихся, развитие познавательных потребностей учащихся, создание условий для приобретения опыта работы учащихся в среде ИКТ.
- Достижение сознательного усвоения учебного материала учащимися, работа над повышением грамотности устной речи, правильного использования компьютерных терминов.
- Научить применять возможности MS Excel в повседневной жизни, в познавательной деятельности.
- Закрепить навыки создания таблиц и диаграмм.
- Научить решать систему уравнений графическим методом, исследовать график функции.
Оборудование урока: компьютеры, мультимедиа проектор.
Программное обеспечение: Windows XP, пакет программ MS Office 2003.
Содержание урока
Организационный момент.
Здравствуйте.
Тема нашего урока тесно связана с математикой разделы “Графики функций” и “Решение систем уравнений”. Поэтому нам понадобятся ранее полученные навыки. Но мы постараемся упростить нашу задачу с помощью применения современных вычислительных средств.
Запишите в тетради тему урока и укажите дату.
Назовите мне кого из класса сегодня нет.
Актуализация знаний.
Давайте вспомним, что такое уравнение, и как его можно решить графически.
Назовите, пожалуйста, что в математике называют уравнением, решением уравнения и системой уравнений.
(Учащиеся приводят определения)
Уравнение – это математическое выражение, содержащее неизвестную величину (переменную) и 0 с правой стороны от знака =.
Система уравнений – несколько связанных уравнений, имеющих одинаковые обозначения неизвестных величин (переменных).
Решением уравнения – называют такое значение неизвестной величины, при подстановке которого левая часть выражения принимает значение 0. И мы получаем верное равенство.
Но, с другой стороны, подобное выражение можно представить как функцию с зависимой и независимой величинами. Если мы слева от знака = поставим Y, а справа заданное выражение. Y – зависимая величина, Х – независимая величина. В этом случае Решением уравнения является точка пересечения графика функции с осью ОХ.
Постановка проблемы.
Для решения уравнения графическим методом необходимо рассчитать значения функции в ключевых точках с координатой Х (Х меняется в диапазоне допустимых значений), нанести эти точки на систему координат, построить график функции и определить координаты точки пересечения графика с осью ОХ.
Это достаточно сложная задача. Нужно достаточно много вычислений и аккуратное построение графика функции. Также мы заранее не можем сказать, из какого диапазона чисел необходимо брать значения Х.
Но эту задачу может взять на себя ЭВМ.
Мы воспользуемся возможностями программы MS Excel.
Основная часть
Давайте разобьемся на 2 группы. Сильные ученики, которые уже хорошо владеют средствами MS Excel, попытаются самостоятельно разработать таблицу. А остальные ребята будут вместе со мной последовательно выполнять действия.
Сильные ученики пересаживаются за дальние компьютеры и самостоятельно разрабатывают таблицу для решения системы уравнений. Они должны получить примерно такую картинку на экране.
С остальными мы работаем в режиме “Делай как Я”. Я демонстрирую действия на экране проектора и комментирую, вы стараетесь выполнять эти действия у себя на ЭВМ.
И так. Мы запустили программу MS Excel.
Y = x ^ 2 + 2
Y = 2 * x + 3
Нам необходимо задать диапазон изменения величины Х и рассчитать соответствующее значение Y.
Сформируем начальные данные.
В ячейку A1 запишем – нач Х =. В ячейку D1 запишем – шаг Х =. В ячейках B1, E1 их соответствующие значения – (-2,5) и 0,15.
В ячейках C4, F4 запишем общий вид наших уравнений. В строке 5 сформируем заголовки будущих таблиц значений заданных функций.
Теперь в столбиках B, E мы должны сформировать значения для величины Х. А в столбиках C, E значения величин Y. У нас должна получиться вот такая картинка. Столбики со значением величины X мы должны сформировать так, чтобы было удобно менять начальное его значение и шаг X, которые мы создали в заголовке.
Приложение 1
Приложение 2
Формулы, которые нам нужно ввести приведены на рисунке.
Заметьте, что большинство формул повторяются, и их можно ввести методом копирования.
Заполните, пожалуйста, в каждой таблице 20-25 строчек.
Символ $ в формуле обозначает, что данный адрес ячейки является абсолютным и он не будет изменяться при копировании формулы.
Проверьте, чтобы ваши расчётные данные совпадали с рисунком 2.
Нам осталось красиво оформить таблицы. Для этого нужно указать, какие границы отображать в ячейках расположения расчётных таблиц. Выделите их указателем мышки и задайте режим “Все границы”.
Теперь нам необходимо построить графики заданных функций. Для этого воспользуемся инструментом “Диаграммы”.
Выберем тип диаграммы Точечная-Сглаженная и на следующем экране укажем необходимые нам диапазоны данных, как указано на рисунке. Незабудем указать название для каждого графика. Легенду расположим снизу. А саму диаграмму “На текущем листе”, поместив её справа от расчётных таблиц.
Если вы всё сделали правильно, то у вас на экране должна получиться вот такая картинка.
У кого не получилось, давайте вместе разберёмся в ошибках и добъёмся требуемого результата.
Теперь изменяя значения в ячейках B1, D1 можно смещать графики функций вдоль оси ОХ и изменять их масштаб.
Мы видим, что одно из решений нашей системы уравнений равно -1,5.
Задание 1.
Изменяя начальное значение Х, найдите на графике второе решение системы уравнений.
Сколько у вас получилось?
Великолепно. У нас получилось. Мы легко решили такую сложную систему уравнений.
Но можно немного изменить нашу таблицу и усовершенствовать для решения множества подобных систем уравнений или для исследования графиков заданных функций.
Приложение 1
Приложение 2
Для этого нужно внести изменения в таблицу и расчётные формулы.
Можно сделать следующим образом, как показано на рисунке. Формулы в ячейках показаны на следующем рисунке.
Задание 2.
Самостоятельно внесите все необходимые изменения.
Задание 3.
Попробуйте изменять коофициенты A, B, C, D и посмотрите, как меняется форма и положение графиков соответствующих формул.
Заключительный этап урока
Ребята, как вы думаете, что удобней самостоятельно строить график функции на бумаге или поручить эту задачу ЭВМ?
А что легче для вас?
Конечно же, на данном этапе вам удобней самостоятельно на бумаге построить график функции. Но в конце урока мы получили универсальную таблицу, которая позволяет решать множество подобных заданий.
Мы ещё раз убедились, что компьютер это мощный инструмент, который позволяет не только приятно проводить время за играми, но и решать серьёзные задачи.
Надеюсь, что вам понравилось сегодняшняя работа. И вы Довольны достигнутыми результатами.
Спасибо за урок.
20.06.2012
urok.1sept.ru
Графический способ решения систем уравнений: алгоритм и пример решения
Рассмотрим следующие уравнения:
1. 2*x + 3*y = 15;
2. x2 + y2 = 4;
3. x*y = -1;
4. 5*x3 + y2 = 8.
Каждое из представленных выше уравнений является уравнением с двумя переменными. Множество точек координатной плоскости, координаты которых обращают уравнение в верное числовое равенство, называется графиком уравнения с двумя неизвестными.
График уравнения с двумя переменными
Уравнения с двумя переменными имеют большое многообразие графиков. Например, для уравнения 2*x + 3*y = 15 графиком будет прямая линия, для уравнения x2 + y2 = 4 графиком будет являться окружность с радиусом 2, графиком уравнения y*x = 1 будет являться гипербола и т.д.
У целых уравнений с двумя переменными тоже существует такое понятие, как степень. Определяется эта степень, так же как для целого уравнения с одной переменной. Для этого приводят уравнение к виду, когда левая часть есть многочлен стандартного вида, а правая – нуль. Это осуществляется путем равносильных преобразований.
Графический способ решения систем уравнения
Разберемся, как решать системы уравнений, которые будут состоять из двух уравнений с двумя переменными. Рассмотрим графический способ решения таких систем.
Пример 1. Решить систему уравнений:
{ x2 + y2 = 25
{y = -x2 + 2*x + 5.
Построим графики первого и второго уравнений в одной системе координат. Графиком первого уравнения будет окружность с центром в начале координат и радиусом 5. Графиком второго уравнения будет являться парабола с ветвями, опущенными вниз.
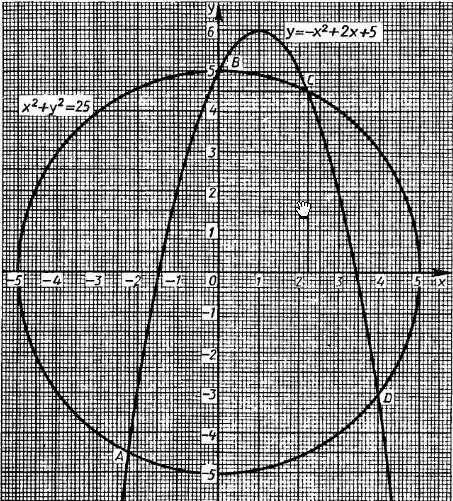
Все точки графиков будут удовлетворять каждый своему уравнению. Нам же необходимо найти такие точки, которые будут удовлетворять как первому, так и второму уравнению. Очевидно, что это будут точки, в которых эти два графика пересекаются.
Используя наш рисунок находим приблизительные значения координат, в которых эти точки пересекаются. Получаем следующие результаты:
A(-2,2;-4,5), B(0;5), C(2,2;4,5), D(4,-3).
Значит, наша система уравнений имеет четыре решения.
x1 ≈ -2,2; y1 ≈ -4,5;
x2 ≈ 0; y2 ≈ 5;
x3 ≈ 2,2; y3 ≈ 4,5;
x4 ≈ 4,y4 ≈ -3.
Если подставить данные значения в уравнения нашей системы, то можно увидеть, что первое и третье решение являются приближенными, а второе и четвертое – точными. Графический метод часто используется, чтобы оценить количество корней и примерные их границы. Решения получаются чаще приближенными, чем точными.
Нужна помощь в учебе?
Предыдущая тема: Уравнения, приводимые к квадратным: биквадратные и рациональные
Следующая тема:   Последовательности: виды числовых последовательностей и примеры
Все неприличные комментарии будут удаляться.
www.nado5.ru
Графический способ решения систем уравнений
Разделы: Математика, Информатика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (1,6 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
- Обобщить графический способ решения систем уравнений;
- Сформировать умения графически решать системы уравнений второй степени, привлекая известные учащимся графики;
- Дать наглядные представления, что система двух уравнений с двумя переменными второй степени может иметь от одного до четырех решений, или не иметь решений.
Структура урока:
- Орг. момент
- Актуализация знаний учащихся.
- Объяснение нового материала.
- Закрепление изученного материала. Работа в табличном процессоре Excel с последующей проверкой..
- Домашнее задание.
Ход урока
1. Организационный момент
Объявляется тема, цель, ход урока.
2. Актуализация знаний.
1) Повторить элементарные функции и их графики.
Учитель математики задает вопрос об изученных ранее элементарных функциях и их графиках и через проектор обобщает ответы учащихся.
2) Устная работа.
Учитель проводит устную работу с использованием проектора с целью подготовки учащихся к восприятию новой темы.
3. Объяснение нового материала.
1) Объяснение нового материала через проектор и разбор решения стандартной математической задачи.
2) Учитель информатики и ИКТ через проектор напоминает учащимся алгоритм решения системы уравнений графическим способом в табличном процессоре Excel.
4. Закрепление изученного материала. Работа в табличном процессоре Excel с последующей проверкой.
1) Учитель предлагает учащимся пересесть за компьютеры и выполнить задания в табличном процессоре Excel.
2) Решение каждой системы уравнений проверяется через проектор.
5. Домашнее задание.
Список используемой литературы:
- Учебник для 9 класса общеобразовательных учреждений «Алгебра», авторы Ю.Н. Макарычев Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, «Просвещение», ОАО «Московские учебники», Москва, 2008 г.
- Поурочное планирование по алгебре к учебнику Ю.Н.Макарычева и др. «Алгебра. 9 класс», «Экзамен», Москва, 2008 г.
- Алгебра. 9 класс. Поурочные планы к учебнику Ю.Н.Макарычева и др., автор-составитель С.П.Ковалева, Волгоград, 2007 г.
- Тетрадь-конспект по алгебре, авторы Ершова А.П., Голобородько В.В., Крижановский А.Ф., ИЛЕКСА, Москва, 2006 г.
- Учебник Информатика. Базовый курс. 9 класс, автор Угринович Н.Д., БИНОМ. Лаборатория знаний, 2010 г.
- Современные открытые уроки информатики 8-11 классы, авторы В.А. Молодцов, Н.Б. Рыжикова, Феникс, 2006 г.
24.03.2011
Поделиться страницей:urok.1sept.ru
Графическое решение систем уравнений
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (290,8 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
Обучающие:
- Обеспечить в ходе урока закрепление основных понятий темы «Решение систем уравнений графически»
- Провести актуализацию опорных знаний по следующим вопросам:
- Свойства элементарных функций;
- Виды преобразований графиков функций;
- Поиск различных способов и методов решения систем уравнений.
- Обобщить и систематизировать знания учащихся по данной теме, обучить работе со справочной и дополнительной литературой.
- Сформировать навыки планирования ответа.
Развивающие:
- Расширить кругозор учащихся, способствовать развитию познавательного интереса.
- Развить математическое мышление, взаимовыручку, взаимопомощь.
- Стимулировать творческое мышление нестандартными методами.
Воспитательные:
- Воспитать чувство ответственности;
- Сформировать графическую культуру.
Этапы урока:
- Постановка цели урока.
- Подготовка к восприятию новых знаний.
- Закрепление знаний.
- Работа в группах практикум по решению систем уравнений.
- Решение систем уравнений с параметром.
- Подведение итогов урока.
Ход урока
1. Вступительное слово учителя: «Мы знаем, что одним из способов решения систем уравнений с двумя переменными является графический способ. К тому же существует достаточно много задач, в которых важен поиск не самого решения систем уравнений, а только определение количества решений или доказательство, что их нет. Работать мы сегодня будем по следующей схеме. Мы покажем связь тем изученных на предыдущих уроках, «преобразование графиков функций», «графики функций», «свойства функции», «способы решение систем уравнений».
Эпиграф: «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи – решайте их» (Д. Пойа «Математическое открытие»)
2. Подготовка к восприятию новых знаний
Задачи этапа: Актуализация опорных знаний и умений по данной теме, повторение свойств функций, преобразование графиков функций.
Учитель: «Сейчас мы вспомним свойства некоторых функций, а также виды преобразования графика»
Рисунок 1
Рисунок 2
Рисунок 3
3. Закрепление знаний
Задачи этапа: Вспомнить графический способ решения систем уравнений, определение количества решений, повторить схематичное построение графиков.
Учитель: «Объясните, что значит решить систему уравнений? Что значит решить систему графически?»
Задание: «Укажите, сколько решений имеет система уравнений, построив схематично на графики функций»
Рисунок 4
Рисунок 5
4. Работа в группах, практикум по решению систем уравнений
Задачи этапа: Рассмотреть различные способы решения систем уравнений, найти правильное решение системы, научиться работать в группах.
Учитель: «Мы рассмотрели одну из задач: нахождение количества решений системы, а сейчас постараемся найти решение системы, но разными способами. Работаем группами. Первая группа будет решать систему аналитически. Вторая группа на координатной плоскости построит два графика и найдет общее решение системы. Группа имеет право совещаться, через 10 мин проводится подведение итогов, группы представляют результаты работы»
Задания группам:
Рисунок 6
Рисунок 7
5. Решение систем уравнений с параметром
Задачи этапа: Показать применение графического способа решения систем уравнений к нестандартным задачам, задачам повышенной сложности, встречающимся во второй части ГИА, получение новых знаний.
Учитель: «Сейчас мы попробуем решить графически еще один вид задач на решение системы уравнений. Такая система называется системой уравнений с параметром. Укажите кол-во решений системы уравнений. Как называется функция во втором уравнении, как проходит ее график? Рассмотрим поведение функции и число решений системы»
Рисунок 8
Рисунок 9
6. Подведение итогов урока, выставление отметок
Задачи этапа: Подвести итоги; определить: что получилось, что нет; оценить учащихся; дать анализ успешности овладения знаниями.
Учитель: «Давайте еще раз посмотрим на тему урока и цели урока. Ответьте, пожалуйста, на мои вопросы.
- Что мы сегодня учились делать на уроке?
- Для решения каких задач мы строили графики?
- Что значит решить систему уравнений графически?»
10.03.2011
Поделиться страницей:urok.1sept.ru
