Как производится сложение двух или нескольких векторов – Сложение и вычитание векторов

Содержание

Операции над векторами и их свойства.

Навигация по странице.

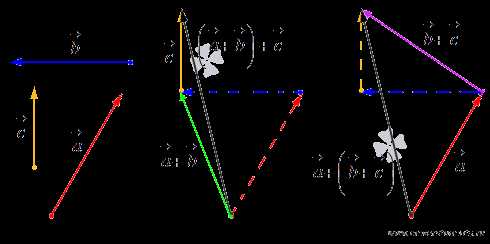
Операция сложения двух векторов — правило треугольника.

Покажем как происходит сложение двух векторов.

Проиллюстрируем сложение не коллинеарных векторов на плоскости по правилу треугольника.

А на чертеже ниже показано сложение сонаправленных и противоположно направленных векторов.

Сложение нескольких векторов — правило многоугольника.

Основываясь на рассмотренной операции сложения двух векторов, мы можем сложить три вектора и более. В этом случае складываются первые два вектора, к полученному результату прибавляется третий вектор, к получившемуся прибавляется четвертый и так далее.

Сложение нескольких векторов выполняется следующим построением. От произвольной точкиА плоскости или пространства откладывается вектор, равный первому слагаемому, от его конца откладывается вектор, равный второму слагаемому, от его конца откладывается третье слагаемое, и так далее. Пусть точка B — это конец последнего отложенного вектора. Суммой всех этих векторов будет вектор .

Сложение нескольких векторов на плоскости таким способом называется правилом многоугольника. Приведем иллюстрацию правила многоугольника.

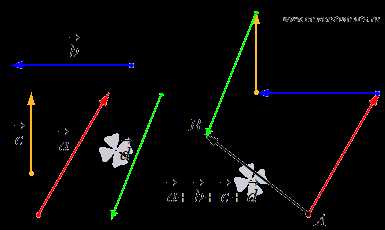
Абсолютно аналогично производится сложение нескольких векторов в пространстве.

Операция умножения вектора на число.

Сейчас разберемся как происходит умножение вектора на число.

Умножение вектора на число k соответствует растяжению вектора в k раз при k > 1 или сжатию в раз при 0 < k < 1, при k = 1 вектор остается прежним (для отрицательных k еще изменяется направление на противоположное). Если произвольный вектор умножить на ноль, то получим нулевой вектор. Произведение нулевого вектора и произвольного числа есть нулевой вектор. К примеру, при умножении вектора на число
2 нам следует вдвое увеличить его длину и сохранить направление, а при умножении вектора на минус одну треть следует уменьшить его длину втрое и изменить направление на противоположное. Приведем для наглядности иллюстрацию этого случая.

Свойства операций над векторами.

Итак, мы определили операцию сложения векторов и операцию умножения вектора на число. При этом для любых векторов и произвольных действительных чисел можно при помощи геометрических построений обосновать следующие свойства операций над векторами. Некоторые из них очевидны.

Свойство коммутативности .
Свойство ассоциативности сложения .
Существует нейтральный элемент по сложению, которым является нулевой вектор , и . Это свойство очевидно.
Для любого ненулевого вектора существует противоположный вектор и верно равенство . Это свойство очевидно без иллюстрации.

Сочетательное свойство умножения . К примеру, растяжение вектора в 6 раз можно произвести, если сначала его растянуть вдвое и полученный вектор растянуть еще втрое. Аналогичного результата можно добиться, например, сжав вектор вдвое, а полученный вектор растянуть в 12 раз.
Первое распределительное свойство . Это свойство достаточно очевидно.
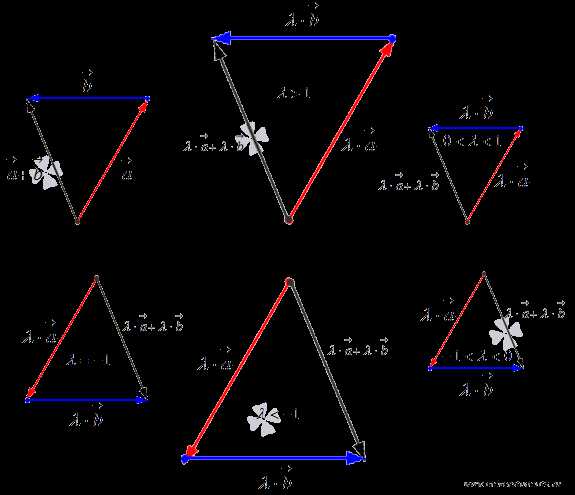
Второе распределительное свойство . Это свойство справедливо в силу подобия треугольников, изображенных ниже.
Нейтральным числом по умножению является единица, то есть, . При умножении вектора на единицу с ним не производится никаких геометрических преобразований.

Рассмотренные свойства дают нам возможность преобразовывать векторные выражения.

Свойства коммутативности и ассоциативности операции сложения векторов позволяют складывать векторы в произвольном порядке.

Операции вычитания векторов как таковой нет, так как разность векторов и есть сумма векторов и .

Учитывая рассмотренные свойства операций над векторами, мы можем в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования так же как и в числовых выражениях.

Разберем на примере.

Упростите выражение, содержащее векторы . .

matematika-2014elena-viktorovna.blogspot.com

Сумма нескольких векторов

Вам уже известны правила сложения двух векторов.

Cегодня мы будем учиться складывать несколько векторов.

Построим вектор суммы векторов , , . От некоторой точки А отложим вектор
. Далее от точки B отложим вектор . А от точки C отложим вектор
.

Будем последовательно складывать наши векторы, пользуясь

правилом треугольника.

Сумма векторов , равна вектору .

Теперь к вектору добавим вектор . В результате мы получаем вектор .

Тогда можем сказать, что сумма .

Так, последовательно складывая первый вектор со вторым, затем их сумму с третьим и так далее, можно найти суммы четырёх, пяти и большего числа векторов.

Такое правило построения суммы векторов называют правилом многоугольника.

Сформулируем его в общем виде.

Если А₁, А₂, …, A_n — произвольные точки плоскости, то сумма векторов

Это равенство справедливо для любых точек А₁, А₂, …, A_n. И, в частности, для случая, когда некоторые из них совпадают.

Например, если начало первого вектора совпадает с концом последнего, то сумма данных векторов равна нулевому вектору.

Задача. Построить вектор суммы попарно неколлинеарных векторов , , , и .

Построение

Задача. В соответствии с правилом многоугольника составить равенство,выражающее сумму нескольких векторов.

Посмотрим на первый рисунок. Мы видим, что последовательно складывают векторы . Но, так как начало вектора совпадает с концом вектора , то сумма данных векторов равна нулевому вектору .

Перейдём к следующему случаю.

Видим, что сумма состоит из векторов . А вот вектор , как раз таки, и равен ей.

На рисунке в последовательно, друг за другом, отложены векторы Ну, а вектор равен их сумме.

На последнем рисунке последовательно, друг за другом, отложены векторы . При этом Начало вектора К совпадает с концом вектора С. Поэтому сумма данных векторов равна нулевому вектору .

Задача. равнобокая трапеция. и — её основания, боковая сторона равна . Построить вектор и найти его длину.

Построение

Решение.

Ответ:

А теперь подведём итоги нашего урока.

Сегодня мы познакомились с правилом многоугольника, которое позволяет строить вектор суммы нескольких векторов.

Его суть заключается в том, что векторы-слагаемые последовательно откладывают друг от друга, суммой является вектор, начало которого совпадает с началом первого вектора-слагаемого, а конец совпадает с концом последнего вектора-слагаемого.

Если эти точки совпадают, то сумма данных векторов равна нулевому вектору.

videouroki.net

Правила сложения векторов

Для того чтобы совершить операцию сложения векторов, существует несколько способов, которые, в зависимости от ситуации и типа рассматриваемых векторов, могут быть более удобны в применении. Давайте рассмотрим правила сложения векторов:

Правило треугольника

Правило треугольника заключается в следующем: для того чтобы сложить два вектора х, y нужно построить вектор х так, чтобы его начало совпадало с концом вектора у. Тогда их суммой будет являться значение вектора z, при этом начало вектора z будет совпадать с началом вектора х, а конец — с концом вектора у.

Правило треугольника помогает, в случае если количество векторов, которые необходимо просуммировать, не более двух.

Правило многоугольника

Правило многоугольника наиболее простое и удобно для сложения любого количества векторов на плоскости или в пространстве. Суть правила заключается в следующем: при сложении векторов нужно последовательно пристраивать их один за другим, так чтобы начало последующего вектора совпадало с концом предыдущего, при этом вектор, который замыкает образовавшуюся кривую, является суммой слагаемых векторов. Наглядно это отображает равенство w= x + y + z, где вектор w является суммой указанных векторов. Кроме того, необходимо отметить, что от перемены мест слагаемых векторов сумма не меняется, то есть (x +y) + z = x + (y +z).

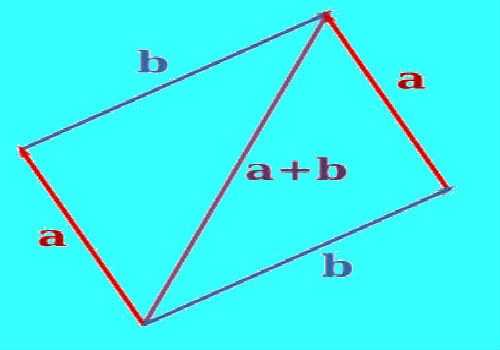
Правило параллелограмма

Правило параллелограмма используется для сложения векторов, которые исходят из одной точки. В этом правиле говорится о том, что суммой векторов x и y, имеющих начало в одной точке, будет являться третий вектор z, исходящий также из этой точки и при этом векторы x и y являются сторонами параллелограмма, а вектор z — его диагональю. В этом случае также не имеет значения, в каком порядке будут складываться векторы.

Таким образом, правило многоугольника, правило треугольника и правило параллелограмма помогают решать задачи сложения векторов абсолютно любой с

elhow.ru

сложение векторов — это… Что такое сложение векторов?

сложение векторов: мат. composition of vectors

сложение без переноса
сложение вычитанием

Смотреть что такое «сложение векторов» в других словарях:

сложение векторов — vektorių sudėtis statusas T sritis fizika atitikmenys: angl. composition of vectors; vector addition vok. Zusammensetzung von Vektoren, f rus. сложение векторов, n pranc. addition des vecteurs, f; addition vectorielle, f … Fizikos terminų žodynas
Сложение векторов: — 1) скоростей и ускорений, 2) сил, 3) моментов сил и количества движения. С. скоростей и ускорений. При разложении движения точки или твердого тела на составляющие движения и при соединении нескольких движений (см. Соединение движений) является… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Сложение векторов — 1) скоростей и ускорений, 2) сил, 3) моментов сил и количества движения. С. скоростей и ускорений. При разложении движения точки или твердого тела на составляющие движения и при соединении нескольких движений (см. Соединение движений) является… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
СЛОЖЕНИЕ СИЛ — операция определения векторной величины R, равной геом. сумме векторов, изображающих силы данной системы и наз. главным вектором этой системы сил. С. с. производится по правилу сложения векторов, в частности построением параллелограмма сил или… … Физическая энциклопедия
СЛОЖЕНИЕ — арифметическое Действие. Обозначается знаком + (плюс). В области целых положительных чисел (натуральных чисел) в результате сложения по данным числам (слагаемым) находится новое число (сумма), содержащее столько единиц, сколько их содержится во… … Большой Энциклопедический словарь
сложение — я; ср. 1. к Сложить (2, 5, 9 зн.). С. чисел. С. депутатских полномочий. С. стихов. 2. Обратное вычитанию математическое действие, посредством которого из двух или нескольких чисел (или величин) получают новое, содержащее столько единиц (или… … Энциклопедический словарь
Сложение сил — операция определения векторной величины R, равной геометрической сумме векторов, изображающих силы данной системы и называется главным вектором этой системы сил. С. с. производится по правилу сложения векторов, в частности построением… … Большая советская энциклопедия
Сложение — арифметическое действие. Результатом С. чисел а и b является число, называемое суммой чисел а и b (слагаемых) и обозначаемое а + b. При С. выполняются переместительный (коммутативный) закон: а + b = b + а и сочетательный (ассоциативный)… … Большая советская энциклопедия
СЛОЖЕНИЕ — арифметич. действие. Обозначается знаком + (плюс). В области целых положит. чисел (натуральных чисел) в результате С. по данным числам (слагаемым) находится новое число (сумма), содержащее столько единиц, сколько их содержится во всех слагаемых.… … Естествознание. Энциклопедический словарь
Позиционные коды векторов — Содержание 1 Специальная алгебра многомерных векторов[1] 1.1 Специальное умножение … Википедия
Геометрические сложения и вычитания векторов — встречаются весьма часто в физике и механике; таковы, например, сложения сил, приложенных к одной точке, сложения скоростей, ускорений и проч. Геометрическое сложение двух векторов АА1 и BB1 имеет целью построение третьего вектора СС1, такого,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

dic.academic.ru

Вектор. Сложение векторов

Изучение математики приводит к постоянному обогащению и увеличению многообразия средств моделирования объектов и явлений окружающей среды. Так, расширение понятия числа позволяет представить количественную характеристику объектов окружающей среды, с помощью новых классов геометрических фигур получается описывать разнообразие их форм. Но развитие естественных наук и запросы самой математики требуют введения и изучения новых и новых средств моделирования. В частности, большое количество физических величин невозможно охарактеризовать только числами, потому что важно и направление их действия. А благодаря тому, что направленные отрезки характеризуют и направления, числовые значения, то на этой основе и получилось новое понятие математики – понятие вектора.

Выполнение основных математических действий над ними тоже определилось по физическим соображениям, и это в конце концов привело к основанию векторной алгебры, которая сейчас выполняет огромную роль при формировании физических теорий. Одновременно с этим, в математике, такой вид алгебры и ее обобщения стали очень удобным языком, а также средством получения и определения новых результатов.

Что же такое вектор?

Вектором называют совокупность всех направленных отрезков, имеющих одинаковую длину и заданное направление. Каждый из отрезков этой совокупности называют изображением вектора.

Понятно, что вектор обозначается своим изображением. Все направленные отрезки, которые изображают вектор а, имеют одинаковую длину и направление, которые называются, соответственно, длиной (модулем, абсолютным значением) и направлением вектора. Его длина обозначается IaI. Два вектора называют равными, если у них одинаковое направление и одинаковая длина.

Направленный отрезок, началом которого является точка А, а концом – точка В, однозначно характеризуется упорядоченной парой точек (А; В). Рассмотрим также множество пар (А; А), (В; В)… . Это множество обозначает вектор, который называется нулевым и обозначается 0. Изображением нулевого вектора является любая точка. Модуль нулевого вектора считается равным нулю. Понятие направления нулевого вектора не определено.

Для любого ненулевого вектора определяют вектор, противоположный заданному, то есть такой, который имеет такую же длину, но противоположное направление. Векторы, имеющие одинаковое либо противоположные направления, называются коллинеарными.

Возможности применения векторов связаны с введением действий над векторами и созданием векторной алгебры, которая имеет много общих свойств с обычной «числовой» алгеброй (хотя, конечно, есть и существенные отличия).

Сложение двух векторов (неколлинеарных) выполняется по правилу треугольника (поместим начало вектора b в конец вектора a, тогда вектор a +b соединяет начало вектора a с концом вектора b) или параллелограмма (поместим начала векторов a и b в одну точку, тогда вектор a + b, имея начало в той же точке, является диагональю параллелограмма, который построен на векторах a и b). Сложение векторов (нескольких) можно выполнить, воспользовавшись правилом многоугольника. Если слагаемые коллинеарны, то соответствующие геометрические конструкции сокращаются.

Операции с векторами, которые заданы координатами, сводятся к операциям с числами: сложение векторов – сложение соответствующих координат, например, если а = (х1; у1), а b = (х2; у2), то a + b = ( x1 + x2; y1 + y2).

Правило сложения векторов обладает всеми алгебраическими свойствами, которые присущи сложению чисел:

От перестановки слагаемых сумма не меняется:
a +b = b + a
Сложение векторов с помощью этого свойства следует из правила параллелограмма. Действительно, какая разница, в каком порядке суммировать векторы a и b, если диагональ параллелограмма всё равно одна и та же?
Свойство ассоциативности:
(a +b) + c = a + (b + c).
Прибавление к вектору нулевого вектора ничего не меняет:
a +0 = a
Это совершенно очевидно, если представить себе такое сложение с точки зрения правила треугольника.
У каждого вектора a есть противоположный вектор, обозначаемый — a; сложение векторов, положительных и отрицательных, будет равняться нулю: a + (- a) = 0.

fb.ru

Как сложить два вектора 🚩 как складывать векторы 🚩 Математика

13 января 2012

Автор КакПросто!

Вектор представляет собой направленный отрезок. Сложение двух векторов производится как с помощью геометрического или аналитического метода. В первом случае результат сложения измеряется после построения, во втором – рассчитывается. Результатом сложения двух векторов является новый вектор.

Статьи по теме:

Вам понадобится

— линейка;
— калькулятор.

Инструкция

Чтобы построить сумму двух векторов, при помощи параллельного переноса совместите их так, чтобы они исходили из одной точки. Через конец одного из векторов проведите прямую, параллельную второму вектору. Через конец второго вектора проведите прямую, параллельную первому вектору. Построенные прямые пересекутся в некоторой точке. При правильном построении, вектора и отрезки прямых между концами векторов и точкой пересечения дадут параллелограмм. Постройте вектор, начало которого будет в точке совмещения векторов, а конец в точке пересечения построенных прямых. Это будет сумма двух данных векторов. Измерьте длину полученного вектора линейкой.

Если вектора параллельны и направлены в одну сторону, то измерьте их длины. Отложите параллельный им отрезок, длина которого равна сумме длин данных векторов. Направьте его в ту же сторону, что и исходные вектора. Это и будет их сумма. Если вектора направлены в противоположные стороны, отнимите их длины. Постройте отрезок, параллельно векторам, направьте его в сторону большего вектора. Это будет сумма противоположно направленных параллельных векторов.

Если известны длины двух векторов и угол между ними, найдите модуль (абсолютную величину) их суммы не производя построения. Подсчитайте сумму квадратов длин векторов a и b, и прибавьте к ней их удвоенное произведение, умноженное на косинус угла α между ними. Из полученного числа извлеките корень квадратный c=√(a²+b²+a∙b∙cos(α)). Это будет длина вектора, равного сумме векторов a и b.

Если вектора заданы координатами, найдите их сумму, сложив соответствующие координаты. Например, если вектор a имеет координаты (x1; y1; z1), вектор b (x2; y2; z2), то сложив почленно координаты, получите вектор c, координаты которого (x1+x2; y1+y2; z1+z2). Этот вектор и будет суммой векторов a и b. В случае когда вектора находятся на плоскости, координату z не учитывайте.

Источники:

длина суммы векторов

Совет полезен?