Как решать уравнение с параметрами – .

Уравнения с параметром, формулы и примеры

Определение и формулы уравнений с параметром

ОПРЕДЕЛЕНИЕ Уравнением вида с неизвестными и параметрами называется уравнением с параметрами.

Например.

ОПРЕДЕЛЕНИЕ

Решить уравнение, содержащее параметры, это значит, для каждой допустимой системы значений этих параметров найти множество всех решений заданного уравнения.

Два уравнения с параметрами называются эквивалентными, если при всякой допустимой системе значений параметров имеют одно и то же множество решений.

Для уравнения с параметром особым или контрольным значением параметра называется такое значение, при котором обращается в нуль коэффициент при неизвестном.

При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него.

Линейное уравнение

   

записанное в общем виде, можно рассматривать как уравнение с параметрами, где является неизвестной величиной, а — параметры.

Для линейного уравнения (1) особым значением параметра есть значение .

Рассмотрим два случая значения указанного параметра (параметр равен своему особому значению и отличен от него).

Случай 1а. Если , то при любой паре параметров и уравнение (1) имеет единственное решение

   

Случай 2а. Если , то уравнение (1) принимает вид:

   

А тогда значение является особым значением параметра . Поэтому рассмотрим далее два случая этого параметра:

Случай 1b. При уравнение решений не имеет: .

Случай 2b. При уравнение принимает вид

   

Решением последнего является любое действительное число, то есть .

Примеры решения задач

ПРИМЕР 1

Задание	Решить уравнение
Решение	Определим контрольные значения параметра, то есть такие значения, при которых коэффициент при неизвестной величине обращается в нуль, то есть необходимо найти решение уравнения . Его решениями являются значения и . При полученных значениях параметра деление обеих частей уравнения на коэффициент при неизвестной невозможно. Но если , , то деление возможно. Для нахождения решения заданного уравнения разобьем множество всех допустимых значений параметра на следующие случаи: 1) ; 2) ; 3) , . 1) При заданное уравнение принимает вид     Полученное уравнение решений не имеет (см. случай 1b), поскольку умножение любого числа на нуль в результате дает нуль. Итак, имеем, что . 2) При решаемое уравнение записывается в виде     Его решением является любое действительное число (случай 2b): . 3) При , левую и правую часть исходного уравнения можно поделить на коэффициент при неизвестной . В итоге получаем     Откуда, после сокращения числителя и знаменателя на , находим корень
Ответ	Если ,то уравнение решений не имеет; если , то ; если , , то

ПРИМЕР 2

Задание	Решить иррациональное уравнение
Решение	Для нахождения корней заданного уравнения возведем обе его части в квадрат, а в конце выполним проверку полученных решений, для предотвращения появления сторонних решений. Исходное уравнение запишем в виде:     Решаем полученное квадратное уравнение. Его дискриминант:     В зависимости от знака дискриминанта, полученное квадратное уравнение может иметь два различных действительных корня, кратный корень или вовсе действительных корней не иметь: 1) :     2) :     3) . Сделаем проверку: 1) подставляем в полученное уравнение значения . Для имеем:                 Рассмотрим возможные случаи знака подмодульного выражения: — если . В пересечении с неравенством , для которого получен корень, имеем, что . В этом случае     а равенство принимает вид:     Таким образом, является корнем исходного уравнения для . — если . В пересечении с имеем, что . В этом случае модуль раскрывается со знаком «минус»:     равенство записывается в виде:     То есть для решений нет. Для будем иметь:                         Левая часть последнего равенства принимает неположительные значения (то есть ), а правая строго положительна: . Поэтому равенство не может быть верным, а, значит, значение не является корнем заданного уравнения. 2) :     Получили неверное равенство, значит, значение не является решением исходного уравнения.
Ответ

ru.solverbook.com

Линейные уравнения с параметром

К задачам с параметром можно отнести, например, поиск решения линейных и квадратных уравнений в общем виде, исследование уравнения на количество имеющихся корней в зависимости от значения параметра.

Не приводя подробных определений, в качестве примеров рассмотрим следующие уравнения:

у = kx, где x, y – переменные, k – параметр;

у = kx + b, где x, y – переменные, k и b – параметр;

аx² + bх + с = 0, где x – переменные, а, b и с – параметр.

Решить уравнение (неравенство, систему) с параметром это значит, как правило, решить бесконечное множество уравнений (неравенств, систем).

Задачи с параметром можно условно разделить на два типа:

а) в условии сказано: решить уравнение (неравенство, систему) – это значит, для всех значений параметра найти все решения. Если хотя бы один случай остался неисследованным, признать такое решение удовлетворительным нельзя.

б) требуется указать возможные значения параметра, при которых уравнение (неравенство, система) обладает определенными свойствами. Например, имеет одно решение, не имеет решений, имеет решения, принадлежащие промежутку и т. д. В таких заданиях необходимо четко указать, при каком значении параметра требуемое условие выполняется.

Параметр, являясь неизвестным фиксированным числом, имеет как бы особую двойственность. В первую очередь, необходимо учитывать, что предполагаемая известность говорит о том, что параметр необходимо воспринимать как число. Во вторую очередь, свобода обращения с параметром ограничивается его неизвестностью. Так, например, операции деления на выражение, в котором присутствует параметр или извлечения корня четной степени из подобного выражения требуют предварительных исследований. Поэтому необходима аккуратность в обращении с параметром.

Например, чтобы сравнить два числа -6а и 3а, необходимо рассмотреть три случая:

1) -6a будет больше 3a, если а отрицательное число;

2) -6а = 3а в случае, когда а = 0;

3) -6а будет меньше, чем 3а, если а – число положительное 0.

Решение и будет являться ответом.

Линейные уравнения с параметром

Пусть дано уравнение kx = b. Это уравнение – краткая запись бесконечного множества уравнений с одной переменной.

При решении таких уравнений могут быть случаи:

1. Пусть k – любое действительное число не равное нулю и b – любое число изR, тогда x = b/k.

2. Пусть k = 0 и b ≠ 0, исходное уравнение примет вид  0 · x = b. Очевидно, что у такого уравнения решений нет.

3. Пусть k и b числа, равные нулю, тогда имеем равенство 0 · x = 0. Его решение  – любое действительное число.

Алгоритм решения такого типа уравнений:

1. Определить «контрольные» значения параметра.

2. Решить исходное уравнение относительно х при тех значениях параметра, которые были определены в первом пункте.

3. Решить исходное уравнение относительно х при значениях параметра, отличающихся от выбранных в первом пункте.

4. Записать ответ можно в следующем виде:

Ответ:

1) при … (значения параметра), уравнение имеет корни …;

2) при … (значения параметра), в уравнении корней нет.

Пример 1.

Решить уравнение с параметром |6 – x| = a.

Решение.

Легко видеть, что здесь a ≥ 0.

По правилу модуля 6 – x = ±a, выразим х:

x = 6 ± a.

Ответ: х = 6 ± a, где a ≥ 0.

Пример 2.

Решить уравнение a(х – 1) + 2(х – 1) = 0 относительно переменной х.

Решение.

Раскроем скобки: aх – а + 2х – 2 = 0

Запишем уравнение в стандартном виде: х(а + 2) = а + 2.

В случае, если выражение а + 2 не нуль , т. е. если а ≠ -2, имеем решение х = (а + 2) / (а + 2), т.е. х = 1.

В случае, если а + 2 равно нулю, т.е. а = -2, то имеем верное равенство 0 · x = 0, поэтому х – любое действительное число.

Ответ: х = 1 при а ≠ -2 и х € R при а = -2.

Пример 3.

Решить уравнение x/a + 1 = а + х относительно переменной х.

Решение.

Если а = 0, то преобразуем уравнение к виду а + х = а² + ах или (а – 1)х = -а(а – 1). Последнее уравнение при а = 1 имеет вид 0 · x = 0, следовательно, х – любое число.

Если а ≠ 1, то последнее уравнение примет вид х = -а.

Данное решение можно проиллюстрировать на координатной прямой (рис. 1)

Ответ: нет решений при а = 0; х – любое число при а = 1; х = -а при а ≠ 0 и а ≠ 1.

Графический метод

Рассмотрим еще один способ решения уравнений с параметром – графический. Этот метод применяется достаточно часто.

Пример 4.

Сколько корней в зависимости от параметра a имеет уравнение ||x| – 2| = a?

Решение.

Для решения графическим методом строим графики функций y = ||x| – 2| и y = a

(рис. 2).

На чертеже наглядно видны возможные случаи расположения прямой y = a и количество корней в каждом из них.

Ответ: корней у уравнения не будет, если а < 0; два корня будет в случае, если a > 2 и а = 0; три корня уравнение будет иметь в случае а = 2; четыре корня – при 0 < a < 2.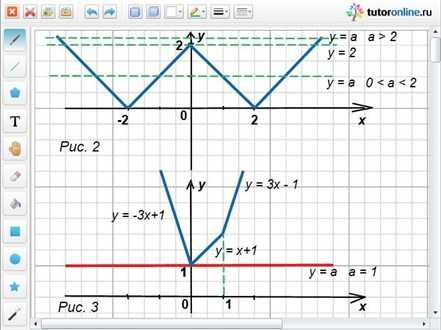

Пример 5.

При каком а уравнение 2|x| + |x – 1| = a имеет единственный корень?

Решение.

Изобразим графики функций  y = 2|x| + |x – 1| и y = a. Для  y = 2|x| + |x – 1|, раскрыв модули методом промежутков, получим:

      {-3x + 1, при x < 0,

y = {x + 1, при  0 ≤ x ≤ 1,

      {3x – 1, при x > 1.

На рисунке 3 хорошо видно, что единственный корень уравнение будет иметь только при а = 1.

Ответ: а = 1.

Пример 6.

Определить число решений уравнения |x + 1| + |x + 2| = a в зависимости от параметра а?

Решение.

График функции  y = |x + 1| + |x + 2| будет представлять собой ломаную. Ее вершины будут располагаться в точках (-2; 1) и (-1; 1) (рисунок 4).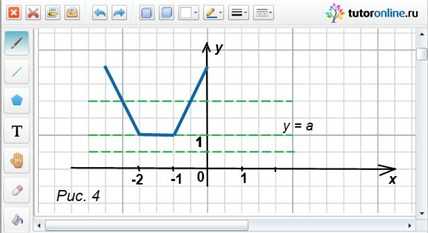

Ответ: если параметр a будет меньше единицы, то корней у уравнения не будет; если а = 1, то решение уравнения является бесконечное множество чисел из отрезка [-2; -1]; если значения параметра а будут больше одного, то уравнение будет иметь два корня.

 Остались вопросы? Не знаете, как решать уравнения с параметром?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Уравнения и неравенства с параметром, простейшие примеры

В данном уроке мы рассмотрим такие уравнения и неравенства, в которых присутствует параметр, приведем простые примеры.

Тема: Уравнения и неравенства. Системы уравнений и неравенств

Урок: Уравнения и неравенства с параметром, простейшие примеры

Напомним смысл выражения «решить с параметром» – можно решать уравнения, неравенства, системы с параметром.

Решить задачу, например уравнение  или неравенство  с параметром а – означает «перебрать» все значения параметра и для каждого из них указать ответ.

Поясним на простейших примерах.

Пример 1 – решить уравнение с параметром:

Задача состоит в том, чтобы для каждого значения параметра  решить уравнение относительно .

Пусть , тогда имеем простейшее линейное уравнение:

В общем случае в данном уравнении возможны два варианта решения – когда можно делить на коэффициент а и когда нельзя, необходимо перебрать все допустимые значения параметра а ()

Рассмотрим два случая. При  мы не имеем права разделить единицу на коэффициент а, поэтому подставляем значение ноль в заданное уравнение и изучаем его. При любых других значениях а имеем право выполнить деление:

Ответ: при  решений нет, при

Рассмотрим решение простейшего неравенства с параметром.

Рассмотрим решение простейшего неравенства с параметром.

Пример 2 – решить неравенство с параметром:

Если а – конкретное число, мы можем легко решить заданное неравенство, например:

у нас же есть коэффициент а в общем виде. Рассмотрим три случая:

Ответ: при  решений нет; при

interneturok.ru

Уравнения с параметром | LAMPA

Исследование квадратного трёхчлена

Часто уравнение с параметром удаётся привести к квадратному. В таких задачах нужно найти значения параметра, при которых корни лежат на некотором промежутке. Для решения подобных примеров необходимо произвести анализ расположения корней. Чтобы определить взаимное расположение границ промежутка и корней уравнения, следует воспользоваться следующими утверждениями:

• Чтобы число ppp находилось между корнями квадратичной функции f(x)=ax2+bx+cf(x)=ax^2+bx+cf(x)=ax2+bx+c, необходимо и достаточно, чтобы выполнялось условие a⋅f(p)<0a\cdot f(p)\lt 0a⋅f(p)<0;
• Чтобы число ppp было меньше корней квадратичной функции f(x)=ax2+bx+cf(x)=ax^2+bx+cf(x)=ax2+bx+c, необходимо и достаточно, чтобы {D≥0,a⋅f(p)>0,p<−b2a;\begin{cases} D\ge 0{,}\\ a\cdot f(p)\gt 0{,}\\ p\lt -\frac{b}{2a}{;}\end{cases}⎩⎪⎨⎪⎧​D≥0,a⋅f(p)>0,p<−2ab​;​
• Чтобы число ppp было больше корней квадратичной функции f(x)=ax2+bx+cf(x)=ax^2+bx+cf(x)=ax2+bx+c, необходимо и достаточно, чтобы {D≥0,a⋅f(p)>0,p>−b2a.\begin{cases} D\ge 0{,}\\ a\cdot f(p)\gt 0{,}\\ p\gt -\frac{b}{2a}{.}\end{cases}⎩⎪⎨⎪⎧​D≥0,a⋅f(p)>0,p>−2ab​.​

Для использования приведённых выше утверждений не нужно непосредственно вычислять корни уравнения.

При каких значениях параметра aaa оба корня уравнения x2+ax−1=0x^2+ax-1=0x2+ax−1=0 меньше 3?

Воспользуемся утверждением, приведённым выше, для f(x)=x2+ax−1f(x)=x^2+ax-1f(x)=x2+ax−1. Система примет вид: {D>0,1⋅f(3)>0,3>−a2⋅1.\begin{cases} D\gt 0{,}\\ 1\cdot f(3)\gt 0{,}\\ 3\gt -\frac{a}{2\cdot 1}{.}\end{cases}⎩⎪⎨⎪⎧​D>0,1⋅f(3)>0,3>−2⋅1a​.​D=a2+4>0,D=a^2+4\gt 0,D=a2+4>0,Первое условие выполняется автоматически. Запишем два других условия:1⋅f(3)>0⇔32+a⋅3−1=3a+8>0⇔a>−83,1\cdot f(3)\gt 0 \,\,\,\,\Leftrightarrow \,\,\,\, 3^2+a\cdot 3-1=3a+8\gt 0\,\,\,\,\Leftrightarrow \,\,\,\,a\gt -\frac{8}{3},1⋅f(3)>0⇔32+a⋅3−1=3a+8>0⇔a>−38​,3>−a2⇔a>−6.3\gt -\frac{a}{2}\,\,\,\,\Leftrightarrow \,\,\,\,a\gt -6.3>−2a​⇔a>−6.
Взяв наиболее сильное из этих условий, получим a>−83a\gt -\frac{8}{3}a>−38​.

Ответ: (−83;+∞)(-\frac{8}{3}; +\infty )(−38​;+∞).

Параметр как равноправная переменная

Несмотря на то, что выше параметр рассматривался как фиксированное, но неизвестное число, можно считать его равноправной переменной.

При каких aaa уравнение a+a+sinx=sinx\sqrt{a+\sqrt{a+\sin x}}=\sin xa+a+sinx​​=sinx имеет решения?

Обозначим sinx=t\sin x = tsinx=t. Исходное уравнение примет вид a+a+t=t\sqrt{a+\sqrt{a+t}}=ta+a+t​​=t. С учётом ∣t∣≤1|t|\le 1∣t∣≤1 это уравнение равносильно системе: {a+t=(t2−a)2,1≥t≥0,t2≥a.\begin{cases} a+t=(t^2-a)^2{,}\\ 1\ge t\ge 0{,}\\ t^2\ge a{.}\end{cases}⎩⎪⎨⎪⎧​a+t=(t2−a)2,1≥t≥0,t2≥a.​
Уравнение удобно представить как квадратное относительно aaa. Получим a2−a(2t2+1)+t4−t=0⇔(a−t2−t−1)(a−t2+t)=0⇔a^2-a(2t^2+1)+t^4-t=0\,\,\Leftrightarrow \,\,(a-t^2-t-1)(a-t^2+t)=0\,\,\Leftrightarrowa2−a(2t2+1)+t4−t=0⇔(a−t2−t−1)(a−t2+t)=0⇔⇔[a=t2+t+1,a=t2−t.\Leftrightarrow \,\,\left[\begin{array}{l} a=t^2+t+1{,}\\ a=t^2-t{.}\end{array}\right.⇔[a=t2+t+1,a=t2−t.​
Так как t2≥at^2\ge at2≥a и 1≥t≥01\ge t\ge 01≥t≥0, то t2−a+t+1>0t^2-a+t+1\gt 0t2−a+t+1>0. Поэтому первое равенство совокупности не может выполняться. Тогда выполняется второе, и исходная система равносильна такой: {a=t2−t,1≥t≥0,t2≥a.⇔{a=t2−t,1≥t≥0.\begin{cases} a=t^2-t{,}\\ 1\ge t\ge 0{,}\\ t^2\ge a{.}\end{cases}\,\,\,\,\Leftrightarrow \,\,\,\,\begin{cases} a=t^2-t{,}\\ 1\ge t\ge 0{.}\end{cases}⎩⎪⎨⎪⎧​a=t2−t,1≥t≥0,t2≥a.​⇔{a=t2−t,1≥t≥0.​
Условие t2≥at^2\ge at2≥a выполняется автоматически при a=t2−ta=t^2-ta=t2−t и t≥0t\ge 0t≥0.

lampa.io

Линейные уравнения с параметром

Рассмотрим линейные уравнения с параметром вида: $$p(a)x-q(a)=0,$$ где \(p(a)\) и \(q(a)\)- выражения, которые зависят от параметра. Для того, чтобы решить такое уравнение, нужно найти все \(x\) при всех значениях параметра \(a\). Приведем наше уравнение к виду: $$p(a)x=q(a),$$ Отсюда единственное решение:

\(x=\frac{q(a)}{p(a)}\) при \(p(a)≠0.\) Если же \(p(a)=0\) и \(q(a)=0\), то решением данного уравнения является любое число. И последний случай, когда \(p(a)=0\),а \(q(a)≠0\), то уравнение не имеет решений. Замечу, что по некоторым уравнениям сразу невозможно определить, являются ли они линейными. Выполнив некоторые преобразования, вдруг обнаружим, что в уравнении отсутствуют члены с \(x\) в степени большей, чем 1. Если изначально у нас и были старшие степени, то теперь они сократились. Мы провели анализ линейного уравнения в общем виде, теперь разберем несколько примеров:

Пример 1

Решить уравнение \(ax-5a=7x-3\) при всех возможных \(a\).

Перенесем все одночлены с \(x\) влево, а оставшиеся члены – вправо. И вынесем \(x\) за скобку, как общий множитель: $$x(a-7)=5a-3;$$ Первый случай, когда \((a-7)≠0\). Тогда мы можем поделить все уравнение на \(a-7\) и выразить: $$x=\frac{5a-3}{a-7}.$$ Второй случай, когда \((a-7)=0\), получим уравнение $$x*0=32,$$ которое не имеет решений. Таким образом, мы нашли решения уравнения для всех значений параметра \(а\). Например, \(x=\frac{2}{7}\) при \(a=0,\) \(x=\frac{-1}{3}\) при \(a=1\) и т.д.
Ответ: При \(a=7\) \(x∈∅;\)
при \(a≠7\) \(x=\frac{5a-3}{a-7}.\)

Пример 2

Найдите все \(a\), при которых корнем уравнения $$ax+5a-2(3x+2)=-5x+a^2$$ будет любое число.

Раскроем скобки и перенесем все члены, содержащие \(x\), влево, а остальные – вправо. $$ax-6x+5x=-5a+4+a^2$$ Приведем подобные: $$ax-x=a^2-5a+4$$ И вынесем за скобку \(x\) и разложим квадратный многочлен на множители: $$x(a-1)=a^2-5a+4$$ $$x(a-1)=(a-1)(a-4)$$ Первый случай: \((a-1)=0\),т.е. \(a=1\) $$x*0=(a-1)(a-4)$$ $$x*0=0.$$ Решением уравнения будет любое число.
Второй случай: \((a-1)≠0\), т.е. \(a≠1\) $$x=\frac{(a-1)(a-4)}{a-1}=a-4.$$ Решением данного уравнения будет одно число \(x=a-4\).
Ответ: \(a=1.\)

Пример 3

Решите уравнение \(\frac{x}{5a+x}-\frac{5a+x}{x-5a}=\frac{100a^2}{25a^2-x^2}.\)

Из ОДЗ видно, что \(5a+x≠0\) и \(x-5a≠0,\) таким образом, \(x≠±5a.\) Приведем уравнение к общему знаменателю \(x^2-25a^2\) и умножим на него все уравнение: $$x^2-5ax-x^2-10ax-25a^2=-100a^2$$ $$-15ax=-75a^2$$ $$ax=5a^2.$$

После преобразований получили линейное уравнение.

Первый случай: \(a=0.\) Получаем уравнение \(0*x=0.\) Решениями этого уравнения будет любое число, кроме \(x=0\) (ОДЗ \(x≠±5a\)).

Второй случай: \(a≠0.\) Выражаем \(x=\frac{5a^2}{a}=5a.\) Этот корень не будет удовлетворять ОДЗ.

Ответ: При \(a=0\) решениями уравнения будут все действительные числа, кроме \(x=0.\) Если \(a≠0,\) то решений нет.

sigma-center.ru

Системы уравнений с параметром

1. Системы линейных уравнений с параметром

Системы линейных уравнений с параметром решаются теми же основными методами, что и обычные системы уравнений: метод подстановки, метод сложения уравнений и графический метод. Знание графической интерпретации линейных систем позволяет легко ответить на вопрос о количестве корней и их существовании.

Пример 1.

Найти все значения для параметра а, при которых система уравнений не имеет решений.

{х + (а² – 3)у = а,
{х + у = 2.

Решение.

Рассмотрим несколько способов решения данного задания.

1 способ. Используем свойство: система не имеет решений, если отношение коэффициентов перед х равно отношению коэффициентов перед у, но не равно отношению свободных членов (а/а₁ = b/b₁ ≠ c/c₁). Тогда имеем:

1/1 = (а² – 3)/1 ≠ а/2 или систему

{а² – 3 = 1,
{а ≠ 2.

Из первого уравнения а² = 4, поэтому с учетом условия, что а ≠ 2, получаем ответ.

Ответ: а = -2.

2 способ. Решаем методом подстановки.

{2 – у + (а² – 3)у = а,
{х = 2 – у,

или

{(а² – 3)у – у = а – 2,
{х = 2 – у.

После вынесения в первом уравнении общего множителя у за скобки, получим:

{(а² – 4)у = а – 2,
{х = 2 – у.

Система не имеет решений, если первое уравнение не будет иметь решений, то есть

{а² – 4 = 0,
{а – 2 ≠ 0.

Очевидно, что а = ±2, но с учетом второго условия в ответ идет только ответ с минусом.

Ответ: а = -2.

Пример 2.

Найти все значения для параметра а, при которых система уравнений имеет бесконечное множество решений.

{8х + ау = 2,
{ах + 2у = 1.

Решение.

По свойству, если отношение коэффициентов при х и у одинаковое, и равно отношению свободных членов системы, то она имеет бесконечное множество решений (т. е. а/а₁ = b/b₁ = c/c₁). Следовательно 8/а = а/2 = 2/1. Решая каждое из полученных уравнений находим, что а = 4 – ответ в данном примере.

Ответ: а = 4.

2. Системы рациональных уравнений с параметром

Пример 3.

Найти все значения параметра а, при которых система уравнений имеет единственное решение.

{3|х| + у = 2,
{|х| + 2у = a.

Решение.

Умножим первое уравнение системы на 2:

{6|х| + 2у = 4,
{|х| + 2у = a.

Вычтем из первого второе уравнение, получим 5|х| = 4 – а. Это уравнение будет иметь единственное решение при а = 4. В других случаях это уравнение будет иметь два решения (при а < 4) или ни одного (при а > 4).

Ответ: а = 4.

Пример 4.

Найти все значения параметра а, при которых система уравнений имеет единственное решение.

{х + у = а,
{у – х² = 1.

Решение.

Данную систему решим с использованием графического метода. Так, графиком второго уравнения системы является парабола, поднятая по оси Оу вверх на один единичный отрезок. Первое уравнение задает множество прямых, параллельных прямой y = -x (рисунок 1). Из рисунка хорошо видно, что система имеет решение, если прямая у = -х + а является касательной к параболе в точке с координатами (-0,5; 1,25). Подставив в уравнение прямой вместо х и у эти координаты, находим значение параметра а: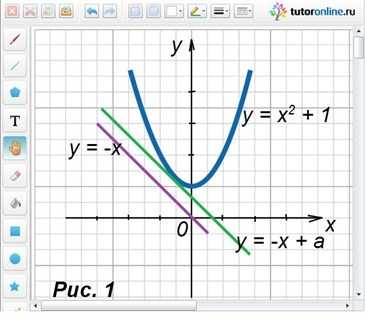

1,25 = 0,5 + а;

а = 0,75.

Ответ: а = 0,75.

Пример 5.

Используя метод подстановки, выясните, при каком значении параметра а, система имеет единственное решение.

{ах – у = а + 1,
{ах + (а + 2)у = 2.

Решение.

Из первого уравнения выразим у и подставим во второе:

{у = ах – а – 1,
{ах + (а + 2)(ах – а – 1) = 2.

Приведем второе уравнение к виду kx = b, которое будет иметь единственное решение при k ≠ 0. Имеем:

ах + а²х – а² – а + 2ах – 2а – 2 = 2;

а²х + 3ах = 2 + а² + 3а + 2.

Квадратный трехчлен а² + 3а + 2 представим в виде произведения скобок

(а + 2)(а + 1), а слева вынесем х за скобки:

(а² + 3а)х = 2 + (а + 2)(а + 1).

Очевидно, что а² + 3а не должно быть равным нулю, поэтому,

а² + 3а ≠ 0, а(а + 3) ≠ 0, а значит а ≠ 0 и ≠ -3.

Ответ: а ≠ 0; ≠ -3.

Пример 6.

Используя графический метод решения, определите, при каком значении параметра а, система имеет единственное решение.

{х² + у² = 9,
{у – |х| = а.

Решение.

Исходя из условия, строим окружность с центром в начале координат и радиусом 3 единичных отрезка, именно ее задает первое уравнение системы

х² + у² = 9. Второе уравнение системы (у = |х| + а) – ломаная. С помощью рисунка 2 рассматриваем все возможные случаи ее расположения относительно окружности. Легко видеть, что а = 3.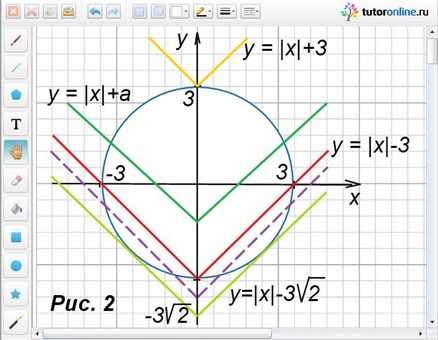

Ответ: а = 3.

 Остались вопросы? Не знаете, как решать системы уравнений?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Задачи с параметрами из ЕГЭ

Автор Сергей Валерьевич

Воскресенье, Март 11, 2012

Решение задач с параметрами требует наличия определенной математической культуры. С реше-нием задач с параметрами приходится сталкиваться не только в математике. Очень многие законы и закономерности из физики, эконо-мики и других областей описываются уравнениями и неравенствами с параметрами. Фактически, решая задачи по физике, химии, экономике и некоторым другим школьным дисциплинам, ученик имеет дело с параметрами. Решению задач с параметрами посвящено большое количество учебно-методической литературы. В данной статей приводятся лишь некоторые представления о том, как рассуждают при решении подобных заданий. С этой целью рассмотрены несколько примеров, большая часть которых взята из вариантов ЕГЭ по математике прошлых лет (задача C5).

Решение «типичных» задач с параметрами

Пример 1. При каких значениях корни уравнения положительны?

Решение.

1) Начнем с рассмотрения случая, когда . Тогда уравнение принимает вид , откуда получаем, что — положительный корень. Значит данное значение нам подходит. Запомнили.

2) Теперь рассматриваем случай, когда . Разделим обе части уравнения на . В результате получаем следующее квадратное уравнение:

   

Так как ветви соответствующей параболы направлены вверх, данное уравнение имеет два положительных корня в том случае, если эта парабола пересекает ось OY в точке, находящейся выше нуля (то есть значение соответствующей квадратичной функции при положительно), абсцисса вершины параболы положительна, а дискриминант квадратного уравнения неотрицателен. То есть имеет место следующая система:

   

Решая данную систему н

yourtutor.info