Как решать задачи?
Хороший вопрос, верно?
Очень хочется знать ответ … Должна же быть какая-то тайна, недостающее звено, утерянное школьным образованием, из-за отсутствия которого распадается на куски полотно понимания! И не только математики, но и понимания вообще. И главная болезнь школьного образования — «наличие этого отсутствия».
… В статье я покажу на простом примере :
Совсем.
Да, метод решения задач существует. Но в школе он
не применяется. Фактически он под запретом. Большинство школьников потеряли способность разбираться с решением задач настолько, что не улавливают правильное направление, даже когда его показываешь.
Как я решаю школьные задачи (пример)
И как я решал их, когда был школьником. Это было давно, но я все помню … Видимо, потому, что учился решать задачи, а не запоминать «типовые решения определенного класса задач».
Вот задача:
«Одну сторону прямоугольника увеличили на 25%. Как нужно изменить другую сторону, чтобы площадь осталась прежней?»
Откуда эта задача я забыл. Но помню, что сын, решая ее в третьем классе, неожиданно «притормозил».
… Чтобы уловить причину затруднения при решении такой простой задачи нужно уметь решать самому, а не просто «знать ход решения». Это намек на учителей. Большинство из них не понимают, где здесь можно запутаться и сразу начинают орать: «Такие задачи мы уже решали» и «Ты должен знать» и прочую хрень. Потому, что никогда в своей жизни задач по математике не решали. Только «проходили решение задач этого типа».
Поскольку я не учитель, то увидеть «ровное место», на котором споткнулся сын, мне было нетрудно.
Вот реконструкция мыслей думающего человека при решении подобных задач.
Почему сложно решать текстовые задачи
«Если бы мне дали час на решение задачи, то 55 минут я думал бы над условием, а 5 над решением»
А.Эйнштейн
«Понять условие – значит решить задачу». Известная мудрость.
Где в условии задачи подвох?
«У прямоугольника 2 стороны: большая и меньшая. Площадь прямоугольника равна произведению … и т.п.». Так «решают» задачи учителя.
Но третьекласснику показалось, что сторон у четырехугольника больше двух. Аж четыре!.. Поэтому представив условие он «притормозил»: «Какую именно другую сторону следует уменьшить?..»
Взрослому трудно понять такого рода трудности. Большинство «знает», что у прямоугольника две стороны: А и В. Поэтому большинство взрослых не способно к творчеству.
И большинство взрослых не умеют учить.
А дети пока умеют: и учиться и творить…
Решение задачи школьным методом
Решение несложное. Нужно знать, как вычислить площадь прямоугольника.
А х В = S.
Если один из сомножителей умножить на 1,25 (то есть увеличить на 25%), то для сохранения произведения нужно другой сомножитель разделить на 1,25.
(А х 1,25) х (В : 1,25) = S
Несложно.
Хотя я рекомендовал бы расписать все на бумажке.
Зачем? Давайте смотреть дальше…
Обязательно ли четырехугольник после увеличения «одной из сторон» останется прямоугольным?
И если нет, то:
«Узри, чтобы понять!»,
— воскликнул арабский, кажется, математик, обнаружив еще одно доказательство теоремы Пифагора. Не «Посчитай» …
Я простой смертный и могу ошибаться. Мое отличие от большинства других смертных в том, что зная это, я не полагаюсь на «абстрактный» ум, забитый «типовыми решениями».
… Давайте изобразим частный случай трансформации прямоугольника после увеличения «одной из сторон» на 25%.
Менее очевидное, но не менее шаблонное решение
Пользователь оставил комментарий к моему видео «Как понимать математику (абстрактное и конкретное мышление)».
«Задача, как ее понял ваш сын, также решается просто: другую сторону прямоугольника нужно уменьшить на 25%».
Я ответил:
«Неверно. Площадь произвольного четырехугольника не будет равна площади исходного прямоугольника. И видео это не о том, как считать, а о том, как понять, что именно нужно считать».
Честно говоря, я попался ….
… Но знание того, что люди склонны ошибаться, а я — человек, помогает выбираться из ловушек очевидности. Даже если в них попадаешься …
Может ли быть более одного правильного решения задачи?
Почувствовав неладное, я нарисовал картинку:
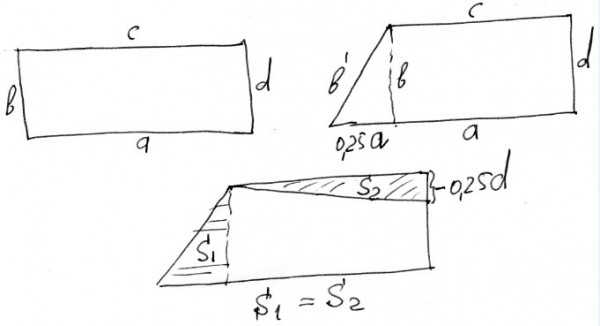
И … понял, что комментатор прав.
Можно алгебраически показать, что площади двух заштрихованных треугольников равны. Следовательно, площадь получившегося четырехугольника также равна площади исходного прямоугольника …
Здесь «Правое» встречается с «Левым». (Декарт, кажется, впервые ввел в алгебру геометрию, придумав систему координат.)
Эта задачка — пример, в котором весьма затруднительно доказать равенство чисто геометрически. Алгебраически же … А что именно тогда считать, не изобразив условие?..)
Чувство правильного решения
Некоторое чувство, инстинкт понимания, которые развиваются в процессе решения задач, шептали мне: что-то здесь не сходится …
… Наш мозг так устроен, что экономит энергию буквально на всем. А очевидное — это привычное, шаблонное, легкое. Поэтому мозг всегда толкает нас в сторону известного и привычного …
Комментатор (нужно отдать ему должное) внимательно смотрел видео и решил задачу менее стандартно. Но … действовал по той же схеме «энергосбережения».
Шаблоны бывают разного уровня, но шаблон есть шаблон. Всегда найдется задача, на которой он не сработает и привычное решение окажется неверным …
(На это, замечу и рассчитана ловушка ЕГЭ: учить запоминать, а потом давать задачи на понимание).
Еще менее очевидное решение задачи …
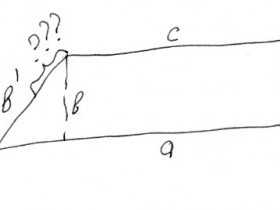
«У прямоугольника 4 стороны. И если одну из них увеличили на 25%, то почему он взял именно эту, «удобную» сторону?»,- подумал я. Как, видимо, подумал и мой сын, который не смог оформить эту мысль, поэтому просто «притормозил».
Почему не взять другую сторону b? Ту, что изменилась при увеличении стороны a? Ведь говорится просто о «другой» стороне?
Да потому, что ум нашептывает: этот вариант посчитать будет труднее!
В предыдущих двух примерах решение получалось:
В третьем же случае …
… Изобразим условие задачи и узрим ответ.
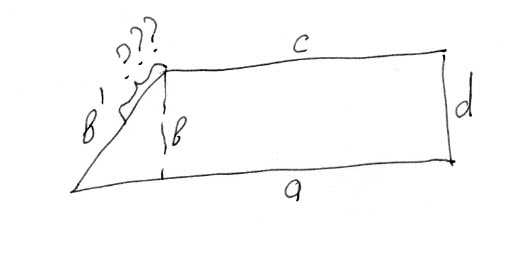
Что получится, если после увеличения на 25% стороны a уменьшить на 25% сторону b, а не удобную для решения сторону d? Что будет, если мы уменьшим на 25% сторону, только что ставшую функцией изменения другой стороны?
… Сравнить площади возникшего неправильного и исходного правильного четырехугольников с использованием только Пифагоровой теоремы не получится.
И совсем не очевидно, что
равны …
А что есть математика, если не приведение условия задачи к очевидному (аксиоматическому) виду?
В науке утверждение считается верным после того, как оно будет до казано через:
Если бы мы не изобразили задачу, не поигрались с рисунком, то не подобрались бы к более глубокому пониманию … Не решили бы задачу.
И вот правильное направление в обучении.
Равно, как и школьных учителей, абсолютное большинство которых думать и решать задачи не умеет. И не может этому научить.
…Откуда возникает чувство, которое подсказывает: что-то здесь не складывается … Давай взглянем еще раз…
Решение задач, имеющих практический смысл (источник понимания)
Поскольку мне пришлось довольно плотно заниматься финансовыми инструментами, то я вынужден был научиться чувствовать
Просто взглянув на задачу о прямоугольнике, можно почувствовать: что-то здесь не так.
Попробуйте доказать (или опровергнуть) утверждение:
при уменьшении на 25% любой другой стороны получившегося неправильного четырехугольника его площадь окажется равной исходному прямоугольнику.
И если вы это сделаете, то поймете:
И еще вы заметите, что на «простой» задаче можно научить ребенка думать и решать очень широкий класс задач … Если учить именно решать и думать, а не умножать «ширину на высоту».
Да, иногда чувства обманывают.
Но иногда они же подсказывают направление, в котором есть смысл двигаться и, возможно, что-то найти. В этом мире нет точных шаблонов на все случаи, но есть направления, двигаясь по которым чаще находишь что-то полезное. И становишься умнее, способнее, успешнее. Иногда даже счастливее …На закуску еще одна
действительно простая задачка.
Решите ее быстро, как это требуют в школе.
Величину А увеличили на 100%. На сколько процентов нужно уменьшить результат, чтобы вернуться в «исходное состояние»?
По опыту: менее одного человека из ста правильно решают подобные задачи. А ведь стоит нарисовать это, как получить неправильный ответ становится сложно!
Вот и думайте:
P.S.
Меня уже успели спросить: а при чем тут проценты и эта задача?
Это третья модель решения
По условию одну сторону (допустим ширину) увеличили на четверть. Получился прямоугольник, площадь которого увеличилась на четверть.
На сколько нужно изменить «другую сторону» …
Ваше решение?
Запись только для зарегистрированных
butorov.ru
Как научить ребенка решать задачи на движение
В четвертом классе многих детей и родителей пугают задачи на движение. Сегодня мы поделимся, как одно небольшое изменение подачи формулы, может научить ребенка щелкать подобные задачи, словно орешки.
Пример задач на движение:
Лыжник шел со скоростью 18 км/ч и был в пути 3 часа. Сколько времени потребуется пешеходу, чтобы пройти такое же расстояние, если его скорость 9 км час
Расстояние между селами 48 км. Через сколько часов встретятся два пешехода, которые вышли одновременны навстречу друг другу, если скорость одного 3 км/ч, а другого 5 км/ч?
В этой статье вы узнаете простую технику, которая позволяет детям легко применять практически первую в их жизни серьезную математическую формулу (до этого дети применяли формулу вычисления площади и периметра)
В школе, по традиционной программе, детей знакомят с формулой в линейной структуре, записывая ее на доске и поясняя S=v*t
Опытный учитель не только расскажет, что S — расстояние v — скорость t — время, а обязательно объяснит, почему обозначение происходит именно такими буквами.
Дальше ребенку последовательно предлагается блок задач, сначала на применение прямой формулы S=v*t
Потом обратной. V=S:t t=S:v
Конечно ребенку нужно будет выучить правило нахождения расстояния, времени или скорости. Правила с одной стороны, очень понятны взрослым, с другой очень трудны для детей.
Потому что читая задачу, маленький ученик, который только учится решать задачи, в голове прокручивает алгоритм:
1. Известно, что …
2. Надо узнать…
3. Чтобы ответить на вопрос, надо … (тут происходит процесс определения нужной формулы, обычно это самая трудная часть)
4. Можем сразу ответить на вопрос? Нет. Сразу мы не можем ответить на вопрос задачи, так как не знаем…
5. Поэтому в первом действии мы узнаем …
6. Во втором действии мы ответим на вопрос задачи. Для этого …
Сложный алгоритм, но именно так решают задачи младшие школьники! Некоторые делают это очень быстро, а некоторые продумывают каждый шаг.
Упростите ребенку решение задач. Станьте для него магом и лучшим проводником по школе.
Нарисуйте вместе с ним треугольник. И впишите в него формулу следующим образом:
Закройте карточкой или рукой то, что нужно найти (например, время) Тогда сразу найдется «нужная формула»
Горизонтальная черта в треугольнике обозначает деление. Вертикальная — умножение. Ребенку можно поставить точку (знак умножения), что будет для него подсказкой.
Так подбор правильной формулы для решения задачи на движение становится не только простым, но и интересным ребенку.
У меня дети просили все больше и больше задач, закрывали разные части формулы, и тем самым, запоминали ее.
Если речь идет о двух, трех движущихся объектах, то треугольник с формулой применяется для каждого в отдельности. Хотя об этом обычно догадываются сами дети.
Взаимодействие и обмен полезными техниками между родителями и учениками может помочь ребенку как добиться хороших результатов в учебе, так и улучшить свою самооценку.
Используйте техники эффективного обучения, помогайте детям учиться.
Ведь очень часто одно простое действие может убрать непонимание, слезы, истерики, нежелание ребенка учиться, замотивировать его на учебу и показать ему простые и легкие способы решения сложных для него задач.
- Можно стирать белье руками, а можно в стиральной машинке
- Можно идти пешком, а можно доехать на автомобиле
- Можно делать дырку в стене ручной дрелью, а можно перфоратором
- Можно решеть задачи по-старинке, а можно дать ребенку техники эффективного решения задач.
Результат одинаков — усилие разное
Именно для этих целей, создана Школа умных детей.
В каждом классе по курсу «Математика», в уроках школы по блоку «решение задач» Вы узнаете:
- Как научить ребенка понимать текст задачи
- Как научить ребенка оформлять краткую запись
- Как научить ребенка определить, как решать задачу
- Сможете объяснить разницу между 2*9 и 9*2 в задаче
- Получите простой Алгоритм-инструкцию «Как решать задачи»
- Узнаете типы задач 1 класса и способы простого объяснения
- Узнаете типы задач 2 класса и способы простого объяснения
- Узнаете типы задач 3 класса и способы простого объяснения
- Узнаете типы задач 4 класса и способы простого объяснения
- Узнаете Формулу «треугольник» для решения задач на движение, цену, количество и стоимость и все тонкости ее применения
Присоединяйтесь прямо сейчас, пока действует специальная цена на участие
Хочу учить ребенка эффективно>>
Вам понравилась статья? Сохраните себе на стену, чтобы не потерять
Похожее
gladtolearn.ru
Как решать задачи правильно и с чего начать решение задачи
В этой статье Вы узнаете как решать задачи по математике, если не знаете с чего начать.
 Часто при решении задач школьники «входят в ступор» — в голове туман, мысли куда-то разбежались, и кажется, что собрать их уже не возможно.
Часто при решении задач школьники «входят в ступор» — в голове туман, мысли куда-то разбежались, и кажется, что собрать их уже не возможно.
Я хочу на примере решения задачи из Открытого банка заданий показать, какие простые действия нужно сделать, чтобы собраться с мыслями и как решать задачи правильно.
Как решать задачи. Задание B13 (№ 26582)
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
1. Внимательно читаем задачу. Возможно, несколько раз.
2. Определяем, о каком процессе идет речь в задаче, и какие формулы описывают этот процесс. Выписываем эти формулы. В данном случае это задача на движение, и формула, которая описывает этот процесс S=vt.
3. Выписываем размерность каждой переменной, которая входит в состав уравнения:
- S — расстояние — км
- v — скорость — км/ч
- t — время — ч
Знание размерности поможет нам при проверке получившихся формул.
4. Выписываем все числа, которые встречаются в условии задачи, пишем, что они обозначают и их размерность:
98 км — расстояние между городами,
7 км/ч — на столько скорость велосипедиста на обратном пути больше, чем скорость на пути из города А в город В,
7 часов — время остановки велосипедиста (это время он не ехал)
5. Ещё раз читаем вопрос задачи.
6. Решаем, какую величину мы примем за неизвестное. Удобно принимать за неизвестное ту величину, которую надо узнать в задаче. В данном случае это скорость велосипедиста на пути из А в В.
Итак: пусть скорость велосипедиста на пути из А в В равна х. Тогда, поскольку скорость велосипедиста на обратном пути на 7 км/ч больше, чем скорость на пути из города А в город В, то она равна x+7.
7. Составляем уравнение. Для этого выразим третью величину уравнения движения (время) через первые две. Тогда:
- время, которое затратил велосипедист на дорогу из А в В равно 98/x,
- а на дорогу из В в А — 98/(x+7)+7 — вспомним, что на пути обратно велосипедист сделал остановку на 7 часов, то есть его время в пути складывается из времени движение и времени стоянки.
Уравнение составляем для времени. Ещё раз читаем в условии задачи, что в нем говорится о времени: В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. То есть время «туда » равно времени «обратно». Приравниваем время «туда» и время «обратно» Получим уравнение:
98/x=98/(x+7)+7.
Ещё раза проверяем размерность величин, которые входят в уравнение — нужно следить за тем, чтобы, например, не прибавлять к километрам часы.
8. Решаем уравнение. Теперь нужно сосредоточиться на решении уравнения. Для этого определим, какого типа это уравнение. Поскольку неизвестное находится в знаменателе дробей, это рациональное уравнение. Чтобы его решить, нужно перенести все слагаемые влево и привести дроби к общему знаменателю. Заметим, что числа 98 и 7 кратны 7.
Чтобы упростить решение, разделим обе части уравнения на 7. Получим уравнение: 14/x=14/(x+7)+1
После этого переносим все слагаемые влево, приводим к общему знаменателю, и приравниваем числитель к нулю.
Получаем в числителе: 14(x+7)-14x-x(x+7)=0 Раскроем скобки, приведем подобные слагаемые и решим квадратное уравнение.
Его корни: -14 и 7.
Число -14 не подходит по условию задачи: скорость должна быть положительной.
Ещё раз читаем вопрос задачи и соотносим его с величиной, которую мы нашли: за неизвестное мы приняли скорость велосипедиста на пути из А в В, и эту же величину требуется найти.
Ответ: 7 км/ч.
Как решать задачи. Итог
Заметим, что весь путь решения задачи мы разбили на маленькие кусочки, и на каждом участке сосредотачивались именно на обдумывании конкретного действия. И только после того, как это действие выполнялось, делали следующий шаг.
Когда не ясно что делать, нужно решить, какой маленький шаг можно сделать прямо сейчас, сделать его, а потом уже думать о следующем.
ege-ok.ru
Как решать задачи на движение?
Задачи на движение не любят многие, так как зачастую недопонимают, как их решать. Но, как известно, нет ничего невозможного, и поэтому можно научиться тому, как решать задачи на движение, было бы желание.
Как решать задачи на движение: теория
Все задачи, связанные с движением решаются по одной формуле, которую вы должны знать наизусть. Вот она: S=Vt. S – это расстояние, V- скорость движения, и t – это время.
Эта формула — ключ к решению всех этих задач, а все остальное написано в тексте задачи, главное, задачу внимательно прочесть и понять.
Второй важный момент, это приведение всех данных в задаче величин к единым единицам измерения. То есть, если время дается в часах, то расстояние должно измеряться в километрах, если в секундах, то расстояние в метрах соответственно.
Решение задач
Итак, рассмотрим три основных примера на решение задач на движение.
Два объекта выехали друг за другом.
Предположим, что вам дана такая задача: из города выехал первый автомобиль со скоростью 60 км/ч, через полчаса выехал второй автомобиль со скоростью 90 км/ч. Через сколько километров, второй автомобиль догонит первый?Для решения такой задачи у нас имеется формула: t = S /(v1 — v2).Так как время нам известно, а расстояние нет, то мы ее трансформируем S= t(v1 — v2).Подставляем цифры: S=0,5(90-60), S=15 км.То есть оба автомобиля встретятся через 15 км.
Два объекта выехали в противоположенном направлении
Если вам дана задача, в которой два объекта выехали навстречу друг другу, и нужно узнать, когда они встретятся, то нужно применять следующую формулу:t = S /(v1 + v2).Например, из пункта А и Б, между которыми 43 км, ехал автомобиль со скоростью 80 км/ч, а из пункта Б в А ехал автобус со скоростью 60 км/ч. Через сколько времени они встретятся?Решение: 43/(80+60)=0,30 часа.
Два объекта выехали одновременно в одном направлении
Дана задача: из пункта А в пункт Б вышел пешеход, двигающийся со скоростью 5 км/ч , а также выехал велосипедист со скоростью 15 км/ч. Во сколько раз велосипедист быстрее доберется из пункта А в пункт Б, если известно, что расстояние между этими пунктами 10 км.Сначала нужно найти время, за которое пешеход пройдет это расстояние. Переделываем формулу S=Vt, получаем t =S/V. Подставляем числа 10/5=2. то есть пешеход потратит на дорогу 2 часа.
Теперь высчитываем время для велосипедиста. t =S/V или 10/15=0,7 часа.Третье действие совсем уж простое, мы должны найти разность времени пешехода и человека на велосипеде. 2/0,7=2,8. Ответ таков: велосипедист доберется до пункта Б быстрее пешехода в 2,8 раза.
Таким образом, применяя эти нехитрые формулы, вы всегда будет знать, как решаются задачи на движение. Нужно только очень внимательно прочитать задачу, принять во внимание все данные, прив
elhow.ru
