Как выразить в часовой мере градусы – .

Содержание

Перевод мер угла в градусной часовой системе

Перевод мер угла в градусной системе

Классическая запись меры угла в градусной системе выглядит следующим образом:

Эта запись обозначает, что мера угла содержит А градусов, В минут и С секунд.

Но иногда необходимо выразить меру угла только в секундах или только в градусах. Возможна и другая ситуация, когда мера угла задано либо в градусах, либо в секундах, а нам необходимо записать эту меру в классической форме. Далее мы покажем, как это делается.

Перевод меры угла из классического вида в секунды

Для того, чтобы перевести меру угла, записанного в классическом виде, в секундный необходимо:

· Количество градусов А умножить на 3600,

· Количество минут В’ умножить на 60,

· К количеству секунд С» прибавить ранее вычисленные значения.

В общем виде наши операции запишутся как:

Перевод меры угла из секундного вида в классический вид

Для перевода меры угла из секунд в классический вид, потребуется более сложный метод. Алгоритм (правила) перевода следующий:

Заданное число секунд S» делится на 3600 до целого числа. Этим самым мы вычисляем число градусов в мере угла S» / 3600 = A (до целого)

2. Умножаем полученное число градусов А на 3600 А1 = А * 3600

3. Из числа секунд S» вычитаем полученный результат умножения А1

S1″ = S» — A1

4. Полученную разность S1″ делим на 60 до целого, тем самым получаем число минут B’ в мере угла B’ = S1″ / 60 (до целого).

5. Умножаем полученное число минут В’ на 60 В1″ = В’ * 60

6. Вычитаем из числа S1″ число B1″ , и тем самым получаем число секунд С» в мере угла C» = S1″ — B1″

7. Записываем меру угла в классическом виде

ПРИМЕР:

Задана мера угла, равная 19936. Привести ее к классическому виду.

РЕШЕНИЕ:

ОТВЕТ:

В классическом виде мера угла запишется как :

Перевод меры угла из классического вида в десятичный

Для перевода меры угла из классического вида в десятичный, проделаем следующие операции. Следует, однако, помнить, что при переводе меры угла в десятичный вид точность вычислений должна быть равна

1. Отделим градусную часть меры угла (А) от минутной (B’) и секундной (C»).

2. Преобразуем минутную часть меры угла (B’) в секунды, для чего умножим ее на 60.

3. Сложим секундную часть меры угла (C») с полученным произведением.

4. Разделим полученную сумму на 3600, тем самым получаем десятичную часть меры угла.

5. Объединяем градусную часть меры угла и десятичную, отделив их запятой.

ПРИМЕР:

Мера угла представлена в классическом виде как

. Представить ее в десятичном виде.

РЕШЕНИЕ:

1. Отделим градусную часть меры угла А = 5;

4 Преобразуем минутную часть меры угла в секунды S1 = (B’) * 60 = 32 * 60 = 1920

3. Сложим полученный результат с секундной частью S2 = (C») + S1 = 16 + 1920 = 1932.

4. Разделим полученный результат на 3600 D = S2 / 3600 = 1932 / 3600 = 0,53666667

5. Объединим между собой градусную часть меры угла и частное от деления.

Перевод меры угла из десятичного вида в классический вид

В десятичном виде меру угла можно записать следующим образом:

A , aaaaaaaa Где

А – целая часть меры угла

аааааааа – дробная часть меры угла.

Для перевода меры угла из десятичного представления в классическое представление мы поступаем следующим образом:

1. Отделяем целую и дробную части меры угла. После этого у нас получится два числа:

А – количество градусов в мере угла;

0,аааааааа – дробная часть числа.

2. Умножим получившуюся дробную часть на 60

· Из получившегося числа отделим друг от друга целую и дробную части. После этого у нас получится два числа:

В (целая часть числа) представляет собой количество минут в мере угла

0, bbbbb – дробная часть числа

3. Умножим получившуюся дробную часть на 60

Получившееся число представляет собой количество секунд в мере угла

4 Объединив градусную, минутную и секундную части, мы получим классический вид записи меры угла.

ПРИМЕР:

Мера угла представлена в десятичном виде как

. Представить ее в классическом виде.

РЕШЕНИЕ:

1. Число градусов

равно целой части меры угла, то есть

2. Составим дробь следующего вида

3. Умножим эту дробь на 60

4. Число минут в мере угла

равно целой части получившегося числа, то есть:

5. Составим дробь следующего вида

6. Умножив эту дробь на 60, получим число секунд

в мере угла

7. Объединив градусную, минутную и секундную части, мы получим классический вид записи меры угла.

ОТВЕТ:

Перевод мер угла в часовой системе

Классическая запись меры угла в часовой системе выглядит следующим образом:

Эта запись обозначает, что мера угла содержит А часов, В минут и С секунд.

Но иногда необходимо выразить меру угла только в секундах или только в часах. Возможна и другая ситуация, когда мера угла задано либо в часах, либо в секундах, а нам необходимо записать эту меру в классической форме. Далее мы покажем, как это делается.

Перевод меры угла из классического вида в секунды

Для того, чтобы перевести меру угла, записанного в классическом виде, в секундный необходимо:

· Количество часов А(h) умножить на 3600,

· Количество минут В(m) умножить на 60,

· К количеству секунд С(s) прибавить ранее вычисленные значения.

В общем виде наши операции запишутся как:

Перевод меры угла из секундного вида в классический вид

Заданное число секунд S делится на 3600 до целого числа. Этим самым мы вычисляем количество часов в мере угла S / 3600 = A(h) (до целого)

2. Умножаем полученное число часов А(h) на 3600 А1 = А(h) * 3600

3. Из числа секунд S вычитаем полученный результат умножения А1 S1 = S — A1

4. Полученную разность S1 делим на 60 до целого, тем самым получаем число минут B(m) в мере угла B(m) = S1 / 60 (до целого).

5. Умножаем полученное число минут В(m) на 60 В1 = В(m) * 60

6. Вычитаем из числа S1 число B1 , и тем самым получаем число секунд С(s) в мере угла C(s) = S1 — B1

8. Записываем меру угла в классическом виде

ПРИМЕР:

Задана мера угла, равная 19936. Привести ее к классическому виду.

РЕШЕНИЕ:

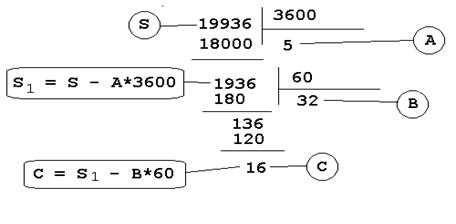
ОТВЕТ:

В классическом виде мера угла запишется как :

Перевод меры угла из классического вида в десятичный

6. Отделим часовую часть меры угла (А(h)) от минутной (B(m)) и секундной (C(s)).

7. Преобразуем минутную часть меры угла (B(m)) в секунды, для чего умножим ее на 60.

8. Сложим секундную часть меры угла (C(s)) с полученным произведением.

9. Разделим полученную сумму на 3600, тем самым получаем десятичную часть меры угла.

10. Объединяем часовую часть меры угла и десятичную, отделив их запятой.

ПРИМЕР:

Мера угла представлена в классическом виде как

. Представить ее в десятичном виде.

РЕШЕНИЕ:

2. Отделим часовую часть меры угла А(h) = 5;

mirznanii.com

Переход из часовой меры в градусную — Мегаобучалка

Один полный оборот Земли за 1 звездные сутки соответствует 360°.

Средние звездные сутки — 23^h56^m04^s = 23,93445^h = 1436,067 мин.

Следовательно, 1 час = 1^h соответствует 15,041068°.

1 мин = 1^m соответствует 0,2506845°.

Поэтому, например, 2,9268125^h

2) Составим матрицу :

3) Составим матрицу движения полюсов:

4) Вычислим матрицу :

5) Определяем гринвичские координаты ИСЗ X, Y, Z:

Если полагать матрицу движения полюсов единичной, то гринвичские координаты в данном примере будут следующими: то есть погрешности, обусловленные движением полюса, составят по модулю ΔX = 1,2 м; ΔY = 4,7 м; ΔZ = 0,3 м. Эти значения невелики. Следовательно, при первичном расчёте

матрицу движения полюсов можно считать единичной (т.е. пренебречь движением полюсов).

6) Поскольку информация об ориентации системы координат эллипсоида МАС относительно гринвичской системы отсутствует, то полагаем, что X = X_Г, Y = Y_Г, Z = Z_Г.

7) Находим по формуле Боуринга геодезическую широту B:

Сначала вычисляем вспомогательный угол j:

где Î_Å — эксцентриситет земного эллипсоида; Î²_Å= 0,006694385.

j = 38,509734°;

Затем широту B определяют (уточняют) по формуле:

где параметры эллипсоида км; км.

8) Определяем геодезическую долготу L:

9) Рассчитываем N — нормаль к поверхности эллипсоида:

где a_e – большая полуось земного эллипсоида;

a_e = 6378,140 км.

N = 6386,463 км.

10) Находим высоту H, отсчитанную по нормали к земному эллипсоиду:

11) Находим высоту H, отсчитанную по нормали к земному эллипсоиду. Высоту рассчитываем по трём следующим формулам:

Если результаты по всем формулам совпадают, то расчёт выполнен правильно

Построение трассы спутника в координатах долгота-широта

Трасса полета спутника – проекция орбиты на поверхность вращающейся Земли.

Рассчитывается широта В и долгота L (географические) для ряда точек по формулам:

;

где J— наклонение орбиты; W — начальное значение долготы восходящего узла; S⁽⁰⁾ — звездное время в момент наблюдения спутника, выраженное в градусах, то есть S⁽⁰⁾ = 15,0411 S⁽

h); w_Å = 0,2506845 град·мин^–1 — угловая скорость вращения Земли; t — текущее время полета; T — период обращения спутника, мин.

DW — прецессия узла орбиты за один оборот, вычисляется по формуле:

где A = 2,378·10⁷ град×км²; p — фокальный параметр орбиты, км.

sin J = ; cos J =

t, мин
B, °		37,0	73,0	66,6	30,1
L, °	-245	-242	-224	-271	-260

t, мин
B, °	-6,93	-43,9	-78,8	-59,9	-23,2	13,8
L, °	-257	-253	-220	-279	-272	–269,

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Сформулируйте и напишите математические выражения законов Кеплера (формулы и формулировки).

2. Сформулируйте и напишите закон всемирного тяготения (формула и формулировка). Какова область применения этого закона?

3. Какие законы используют, чтобы получить уравнения движения ИСЗ? Запишите эти уравнения для невозмущенного движения ИСЗ.

4. Какие системы отсчета называют инерциальными? Как строится инерциальная геоцентрическая система координат?

5. Как строится гринвичская система координат? Как осуществляется переход от инерциальной геоцентрической системы к гринвичской?

6. Чем отличаются геодезические координаты от гринвичских? Как осуществляется переход от последних к первым?

7. Поясните понятия «радиус-вектор», «восхождение», «склонение», «прецессия», «нутация».

8. Напишите уравнение эллиптической орбиты ИСЗ в полярных координатах. Каковы основные параметры этой орбиты?

9. Назовите основные факторы, возмущающие движение ИСЗ.

10. Напишите формулу силового потенциала гравитационного поля земного эллипсоида.

11. Поясните понятия «пертурбационная функция» и «зональные гармоники».

12. Дайте определения эйлеровых углов (J, W, w).

13. Какие требования предъявляются к орбитам ИСЗ для дистанционного зондирования?

14. Поясните понятия геосинхронная, гелиосинхронная (солнечно-синхронная), геостационарная орбита.

Варианты исходных данных к заданиям

Таблица А.1 – Параметры орбит

Вариант	Долгота восходящего узла W, градусы	Наклонение орбиты J, градусы	Аргумент перицентра w, градусы	Высота
апогей H_А	перигей H_П
	33,75	51,62	32,05
	41,05	51,85	53,20
	44,67	28,56	43,31
	48,89	49,55	61,57
	23,35	57,07	31,35
	31,87	82,32	57,04
	62,27	82,51	47,46
	70,13	99,86	08,30
	15,62	82,54	89,22
	63,01	45,01	04,00
	41,53	82,37	27,83
	98,49	98,04	66,75
	25,45	99,15	11,26
	99,26	82,33	67,26
	33,61	44,72	55,90
	10,37	57,18	51,27
	94,01	40,64	54,58
	24,61	43,20	94,66
	93,13	51,79	82,33
	30,10	42,42	98,04
	35,85	59,50	99,10
	84,62	04,56	82,62
	06,72	51,73	65,04
	49,95	67,51	63,11
	06,55	52,53	71,86
	39,61	62,43	82,46
	49,11	72,64	44,73
	50,14	12,76	98,48
	10,02	02,47	98,85
	11,26	63,45	88,72

Таблица А.2 – Астрономические параметры съемки

Вариант	Средняя аномалия в начальную эпоху М₀, градусы	Начальная эпоха (UT1), t₀	Время съемки (UT1), t₁	Истинное звездное время S₀ в гринвичскую полночь даты съемки
h час	m мин	s сек	h час	m мин	s сек
				44,50		45,51	1,923296^h
				29,46		35,21	5,657456
				14,89		24,90	2,126467
				57,79		02,55	3,537030
				29,25		31,04	6,768968
				37,28		37,30	4,457141
				27,23		46,64	15,860497
				45,64		24,70	9,114838
				10,50		15,03	14,773100
				56,09		40,02	10,723409
				44,30		00,11	11,355181
				18,87		45,15	12,748380
				39,96		19,90	8,400612
				15,74		42,21	7,882355
				36,24		48,24	13,603643
				55,25		23,51	3,337132
				40,31		57,04	2,551813
				05,14		12,21	0,143740
				57,18		01,15	12,905013
				49,01		31,82	2,126467
				45,08		37,53	3,537030
				14,06		07,85	6,330099
				57,18		56,61	12,748380
				09,40		42,11	6,067252
				40,54		31,88	12,304310
				54,58		22,19	4,242396
				14,32		15,04	1,871970
				50,93		00,37	2,626307
				10,95		40,56	0,400186
				42,42		32,13	3,243295

Литература

1. Трофимова Т.И. Курс физики [Текст]: учеб. пособие для вузов / Т.И. Трофимова. – М.: Издат. центр «Академия» – 2007. – 560 с.

2. Безруков Л.В. Физика [Текст]: в 3 ч. Ч.2: Электричество. Атомная и ядерная физика: Курс лекций для студ. землеустроительных спец./ Л.В. Безруков.– Новочерк. гос. мелиор. акад. – Новочеркасск, 2003. – 162 с.

3. Безруков Л.В. Физика. Сборник задач для студ. инж.-техн. спец. спец. [Текст]: в 2 ч. Ч.2: Электричество и магнетизм. Колебания и волны. Оптика и атомная физика. / Л.В. Безруков. – Новочерк. гос. мелиор. акад. – Новочеркасск, 2008. – 235 с.

4. Чертов А.Г. Задачник по физике [Текст]: учеб. пособие для втузов / А.Г. Чертов, А.А. Воробьев. – М.: Изд. физ.-мат. лит., 2005. – 640 с.

5. Безруков Л.В. Физические основы и методы дистанционного зондирования. — Новочеркасск, НГМА, 1998. — 246 с.

Учебное — методическое издание

Безруков Леонид Владимирович

ФИЗИКА. Расчет координат и скорости ИСЗ в момент съёмки

Методические указания к выполнению расчетно-графической работы

Подписано к печати		Формат 60х84 ¹/₁₆
Объем	Тираж	Заказ
Отдел оперативной полиграфии ФГБОУ ВПО НГМА, 346428, г. Новочеркасск, ул. Пушкинская, 111

Рекомендуемые страницы:

Как перевести долготу во время? Академия фэншуй

0 00

0 04

0 08

0 12

0 16

0 20

0 24

0 28

0 32

0 36

0 40

0 44

0 48

0 52

0 56

1 00

1 04

1 08

1 12

1 16

1 20

1 24

1 28

1 32

1 36

1 40

1 44

1 48

1 52

1 56

2 00

2 04

2 08

2 12

2 16

2 20

2 24

2 28

2 32

2 36

2 40

2 44

2 48

2 52

2 56

3 00

3 04

3 08

3 12

3 16

3 20

3 24

3 28

3 32

3 36

3 40

3 44

3 48

3 52

3 56

4 00

4 04

4 08

4 12

4 16

4 20

4 24

4 28

4 32

4 36

4 40

4 44

4 48

4 52

4 56

5 00

5 04

5 08

5 12

5 16

5 20

5 24

5 28

5 32

5 36

5 40

5 44

5 48

5 52

5 56

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

6 00

6 04

6 08

6 12

6 16

6 20

6 24

6 28

6 32

6 36

6 40

6 44

6 48

6 52

6 56

7 00

7 04

7 08

7 12

7 16

7 20

7 24

7 28

7 32

7 36

7 40

7 44

7 48

7 52

7 56

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

8 00

8 04

8 08

8 12

8 16

8 20

8 24

8 28

8 32

8 36

8 40

8 44

8 48

8 52

8 56

9 00

9 04

9 08

9 12

9 16

9 20

9 24

9 28

9 32

9 36

9 40

9 44

9 48

9 52

9 56

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

10 00

10 04

10 08

10 12

10 16

10 20

10 24

10 28

10 32

10 36

10 40

10 44

10 48

10 52

10 56

11 00

11 04

11 08

11 12

11 16

11 20

11 24

11 28

11 32

11 36

11 40

11 44

11 48

11 52

11 56

academia-fengshui.ru

*часы минуты секунды в градусы? формула перевода?

часы в градусы? ? ?время в углы? вы не скажете, сколько сейчас времени в радианах?

Эм, ну ваши «часы» они и есть градусы, а минуты они и есть минуты, в одном градусе 60 минут. А в одной минуте 60 секунд.

В общем я понимаю что нужно вот что: a°b’c»=(a+b/60+c/3600)° Угадал?

24 часа = 360 угловых градусов (т. е. длина окружности полностью) . Тогда 1 час = 15 угловых градусов. 4 минуты (=1/15 часа) = 1 угловой градус. А 1 минута, соответственно = 15 угловых минут. С секундами точно также: 4 секунды времени = 1 угловая минута. 1 секунда времени = 15 угловых секунд.

Готовлюсь к ЗНО по географии, освежаю знания. Спасибо, а то забыл ))) 4 года прошло когда учили это.

touch.otvet.mail.ru

Перевод мер угла в градусной часовой системе

Классическая запись меры угла в градусной системе выглядит следующим образом: ,

Эта запись обозначает, что мера угла содержит А градусов, В минут и С секунд.

Перевод меры угла из классического вида в секунды

Возможно вы искали — Реферат: Передаточная функция дискретной системы

Для того, чтобы перевести меру угла, записанного в классическом виде, в секундный необходимо:

· Количество градусов А умножить на 3600,

· Количество минут В’ умножить на 60,

· К количеству секунд С» прибавить ранее вычисленные значения.

В общем виде наши операции запишутся как:

Похожий материал — Реферат: Переключательные функции одного и двух аргументов

Перевод меры угла из секундного вида в классический вид

2. Умножаем полученное число градусов А на 3600 А1 = А * 3600

Очень интересно — Реферат: Пересечение кривых поверхностей

3. Из числа секунд S» вычитаем полученный результат умножения А1

S1″ = S» — A1

5. Умножаем полученное число минут В’ на 60 В1″ = В’ * 60

6. Вычитаем из числа S1″ число B1″ , и тем самым получаем число секунд С» в мере угла C» = S1″ — B1″

Вам будет интересно — Курсовая работа: Перетворення Фур’є. Спектри неперіодичних функцій

7. Записываем меру угла в классическом виде

ПРИМЕР:

Задана мера угла, равная 19936. Привести ее к классическому виду.

РЕШЕНИЕ:

Похожий материал — Реферат: Перпендикулярность геометрических элементов

ОТВЕТ:

В классическом виде мера угла запишется как :

Перевод меры угла из классического вида в десятичный

К-во Просмотров: 136

Бесплатно скачать Контрольная работа: Перевод мер угла в градусной часовой системе

cwetochki.ru

как определить градусную меру угла между часовой и минутной стрелкой . Время 17:00

(360/12)*5=150 градусов

150 градусов отметка каждого часа на часах это 30 градусов 360 делим на 12 и умножаем на 5

градусная мера между 6 и 12 часами равна 180 градусов, угол между 5 и 6 часами равен180/6=30 значит угол между минутной и часовой стрелкой в 5 часов равен 180-30=160 градусов

от 12 часов до 18часов — 180 градусов. шесть делений. по 30 градусов. 17 часов это пятое деление. 5 умножить на 30 =150

циферблат=360гр. делим на12 умножаем на 5 или на 7 получаем 150гр. (между минутной и часовой) или210гр. (между часовой и минутной)

touch.otvet.mail.ru

Перевод мер угла в градусной часовой системе

Перевод мер угла в градусной системе

Классическая запись меры угла в градусной системе выглядит следующим образом: ,

Эта запись обозначает, что мера угла содержит А градусов, В минут и С секунд.

Перевод меры угла из классического вида в секунды

Для того, чтобы перевести меру угла, записанного в классическом виде, в секундный необходимо:

· Количество градусов А умножить на 3600,

· Количество минут В’ умножить на 60,

· К количеству секунд С» прибавить ранее вычисленные значения.

В общем виде наши операции запишутся как:

Перевод меры угла из секундного вида в классический вид

2. Умножаем полученное число градусов А на 3600 А1 = А * 3600

3. Из числа секунд S» вычитаем полученный результат умножения А1

S1″ = S» — A1

5. Умножаем полученное число минут В’ на 60 В1″ = В’ * 60

6. Вычитаем из числа S1″ число B1″ , и тем самым получаем число секунд С» в мере угла C» = S1″ — B1″

7. Записываем меру угла в классическом виде

ПРИМЕР:

Задана мера угла, равная 19936. Привести ее к классическому виду.

РЕШЕНИЕ:

ОТВЕТ:

В классическом виде мера угла запишется как :

Перевод меры угла из классического вида в десятичный

1. Отделим градусную часть меры угла (А) от минутной (B’) и секундной (C»).

2. Преобразуем минутную часть меры угла (B’) в секунды, для чего умножим ее на 60.

3. Сложим секундную часть меры угла (C») с полученным произведением.

4. Разделим полученную сумму на 3600, тем самым получаем десятичную часть меры угла.

5. Объединяем градусную часть меры угла и десятичную, отделив их запятой.

ПРИМЕР:

Мера угла представлена в классическом виде как . Представить ее в десятичном виде.

РЕШЕНИЕ:

1. Отделим градусную часть меры угла А = 5;

4 Преобразуем минутную часть меры угла в секунды S1 = (B’) * 60 = 32 * 60 = 1920

3. Сложим полученный результат с секундной частью S2 = (C») + S1 = 16 + 1920 = 1932.

4. Разделим полученный результат на 3600 D = S2 / 3600 = 1932 / 3600 = 0,53666667

5. Объединим между собой градусную часть меры угла и частное от деления.

Перевод меры угла из десятичного вида в классический вид

В десятичном виде меру угла можно записать следующим образом:

A , aaaaaaaa Где

А – целая часть меры угла

аааааааа – дробная часть меры угла.

1. Отделяем целую и дробную части меры угла. После этого у нас получится два числа:

А – количество градусов в мере угла;

0,аааааааа – дробная часть числа.

2. Умножим получившуюся дробную часть на 60

· Из получившегося числа отделим друг от друга целую и дробную части. После этого у нас получится два числа:

В (целая часть числа) представляет собой количество минут в мере угла 0, bbbbb – дробная часть числа

3. Умножим получившуюся дробную часть на 60

Получившееся число представляет собой количество секунд в мере угла

4 Объединив градусную, минутную и секундную части, мы получим классический вид записи меры угла.

ПРИМЕР:

Мера угла представлена в десятичном виде как . Представить ее в классическом виде.

РЕШЕНИЕ:

1. Число градусов равно целой части меры угла, то есть

2. Составим дробь следующего вида

3. Умножим эту дробь на 60

4. Число минут в мере угла равно целой части получившегося числа, то есть:

5. Составим дробь следующего вида

6. Умножив эту дробь на 60, получим число секунд в мере угла

7. Объединив градусную, минутную и секундную части, мы получим классический вид записи меры угла.

ОТВЕТ:

Перевод мер угла в часовой системе

Классическая запись меры угла в часовой системе выглядит следующим образом:,

Эта запись обозначает, что мера угла содержит А часов, В минут и С секунд.

Перевод меры угла из классического вида в секунды

Для того, чтобы перевести меру угла, записанного в классическом виде, в секундный необходимо:

· Количество часов А(h) умножить на 3600,

· Количество минут В(m) умножить на 60,

· К количеству секунд С(s) прибавить ранее вычисленные значения.

В общем виде наши операции запишутся как:

Перевод меры угла из секундного вида в классический вид

2. Умножаем полученное число часов А(h) на 3600 А1 = А(h) * 3600

3. Из числа секунд S вычитаем полученный результат умножения А1 S1 = S — A1

4. Полученную разность S1 делим на 60 до целого, тем самым получаем число минут B(m) в мере угла B(m) = S1 / 60 (до целого).

5. Умножаем полученное число минут В(m) на 60 В1 = В(m) * 60

6. Вычитаем из числа S1 число B1 , и тем самым получаем число секунд С(s) в мере угла C(s) = S1 — B1

8. Записываем меру угла в классическом виде

ПРИМЕР:

Задана мера угла, равная 19936. Привести ее к классическому виду.

РЕШЕНИЕ:

ОТВЕТ:

В классическом виде мера угла запишется как :

Перевод меры угла из классического вида в десятичный

6. Отделим часовую часть меры угла (А(h)) от минутной (B(m)) и секундной (C(s)).

7. Преобразуем минутную часть меры угла (B(m)) в секунды, для чего умножим ее на 60.

8. Сложим секундную часть меры угла (C(s)) с полученным произведением.

9. Разделим полученную сумму на 3600, тем самым получаем десятичную часть меры угла.

10. Объединяем часовую часть меры угла и десятичную, отделив их запятой.

ПРИМЕР:

Мера угла представлена в классическом виде как . Представить ее в десятичном виде.

РЕШЕНИЕ:

2. Отделим часовую часть меры угла А(h) = 5;

4 Преобразуем минутную часть меры угла в секунды S1 = (B(m)) * 60 = 32 * 60 = 1920

4. Сложим полученный результат с секундной частью S2 = (C(s)) + S1 = 16 + 1920 = 1932.

5. Разделим полученный результат на 3600 D = S2 / 3600 = 1932 / 3600 = 0,53666667

6. Объединим между собой градусную часть меры угла и частное от деления.

Перевод меры угла из десятичного вида в классический вид

В десятичном виде меру угла можно записать следующим образом:

A , aaaaaaaa Где

А – целая часть меры угла

аааааааа – дробная часть меры угла.

4. Отделяем целую и дробную части меры угла. После этого у нас получится два числа:

А – количество часов в мере угла;

0,аааааааа – дробная часть числа.

5. Умножим получившуюся дробную часть на 60

· Из получившегося числа отделим друг от друга целую и дробную части. После этого у нас получится два числа:

В (целая часть числа) представляет собой количество минут в мере угла 0, bbbbb – дробная часть числа

6. Умножим получившуюся дробную часть на 60

Получившееся число представляет собой количество секунд в мере угла

4 Объединив часовую, минутную и секундную части, мы получим классический вид записи меры угла.

ПРИМЕР:

Мера угла представлена в десятичном виде как . Представить ее в классическом виде.

РЕШЕНИЕ:

8. Число градусов равно целой части меры угла, то есть

9. Составим дробь следующего вида

10. Умножим эту дробь на 60

11. Число минут в мере угла равно целой части получившегося числа, то есть:

12. Составим дробь следующего вида

13. Умножив эту дробь на 60, получим число секунд в мере угла

14. Объединив градусную, минутную и секундную части, мы получим классический вид записи меры угла.

ОТВЕТ:

Соотношения между градусной и часовой системами счисления

Как мы договорились, за единицу измерения меры угла мы выбрали угол, величина которого равняется одному обороту () Но мы знаем, что угол, равный одному обороту , содержит 360 градусной системы счисления или 24(h) часовой системы счисления. Таким образом, мы можем записать следующее соотношение: Из этого соотношения легко вывести и соотношение между единицами мер угла разных систем счисления. Полученные результаты занесем в таблицы.

Таблица соотношений между единицами мер угла.

Градусная система Часовая система

1 градус 4m (минуты)

1 минута (1′) 4s (секунды)

1 секунда (1″) 1/15 s (секунды)

Часовая система Градусная система

1 час (1h) 15 градусов

1 минута (1m) 15 минут (15′)

1 секунда (1s) 15 секунд (15″)

botanim.ru

Перевод мер угла в градусной часовой системе

Переход из часовой меры в градусную — Мегаобучалка

Как перевести долготу во время? Академия фэншуй

*часы **минуты **секунды в градусы? формула перевода?

Перевод мер угла в градусной часовой системе

как определить градусную меру угла между часовой и минутной стрелкой . Время 17:00

Перевод мер угла в градусной часовой системе

Добавить комментарий Отменить ответ

*часы минуты секунды в градусы? формула перевода?