Калькулятор матриц методом гаусса с решением – Метод Гаусса онлайн

Решение системы линейных уравнений методом Гаусса с нахождением общего решения

Вообще говоря, на сайте уже есть один калькулятор, решающий СЛАУ методом Гаусса — Решение системы линейных алгебраических уравнений методом Гаусса. Он даже расписывает решение пошагово.

Однако, у него есть некоторые недостатки, которые будет решать новый калькулятор из этой статьи:

Во-первых, предыдущий калькулятор выдает решение в формате с плавающей запятой, тогда как во многих задачниках ответ обычно дается в виде дроби.

Во-вторых, предыдущий калькулятор только определяет факт наличия бесконечного множества решений (неопределенная система), но не выдает решение в общем виде.

В-третьих, предыдущий калькулятор работает только в случае когда число уравнений совпадает с числом неизвестных, и таким образом, не может решать недоопределенных (число неизвестных больше числа уравнений) и переопределенных систем (число неизвестных меньше числа уравнений).

Что касается, второго и третьего пунктов, то универсальность метода Гаусса состоит в том, что на самом деле он годится для систем линейных уравнений с любым числом уравнений и неизвестных, просто это не было использовано.

Описание самого метода Гаусса можно посмотреть по ссылке выше, а под калькулятором подробнее рассмотрены разные случаи (виды систем).

Сам калькулятор, помимо нахождения единственного решения, может находить и общее решение в случае неопределенной системы уравнений.
Матрица уравнений из случая 2 ниже (совместная неопределенная система линейных уравнений) использована в нем в качестве входных данных по умолчанию:

1 2 -3 5 1 1 3 -13 22 -1 3 5 1 -2 5 2 3 4 -7 4СЛАУ в матричном виде

Количество решений

 

Коэффициенты решения

 

Сохранить share extension

1. Совместная определенная система линейных уравнений (имеющая одно решение)

Пример: пусть дана система линейных уравнений

После приведения матрицы к трапециевидной форме методом Гаусса получим:

Откуда обратным ходом находим единственное решение:

Система совместна и определена.

2. Совместная неопределенная система линейных уравнений (имеющая бесконечное множество решений)

Пример: пусть дана система линейных уравнений:

После приведения матрицы к трапециевидной форме методом Гаусса получим:

В результате приходим к системе:

Последние два уравнения верны при любых значениях переменных:

поэтому их можно отбросить.

Чтобы найти решения оставшихся двух уравнений, x1 и x2 можно выразить через x3 и x4.

При этом сами x3 и x4 могут принимать любые значения

Полученная эквивалентная система совместна, но неопределена. Формулы:
;
при произвольных x3 и x4 описывают бесконечное множество решений заданной системы.

3. Несовместная система линейных уравнений (не имеющая решений)

Пример: пусть дана система линейных уравнений:

После приведения матрицы к трапециевидной форме методом Гаусса получим:

Полученная эквивалентная система несовместна, так как последнее уравнение:

не может быть удовлетворено никакими значениями неизвестных.
Эта система несовместна, т. е. не имеет решения.

4. Переопределенная система линейных уравнений (число неизвестных меньше числа уравнений)

Пример: пусть дана система линейных уравнений

После приведения матрицы к трапециевидной форме методом Гаусса получим

Как видим, в данном случае «лишнее» уравнение можно просто отбросить. Также в результате преобразований можно получить одинаковые строки, «лишние» из которых тоже можно отбросить — после чего задача сводится к случаям 1 или 2.

5. Недоопределенная система линейных уравнений (число неизвестных больше числа уравнений)

Пример: пусть дана система линейных уравнений:

После приведения матрицы к трапециевидной форме методом Гаусса получим:

Полученная эквивалентная система имеет вид:

Как видно, в ней отсутствуют уравнения, дающие однозначные значения для x3 и x4, что равносильно появлению уравнений вида:

которые можно отбросить.

Таким образом этот случай сводится к случаю 2 с бесконечным множеством решений, которые описываются следующими формулами:

skokaskoka.ru

Ранг матрицы методом Гаусса | Мозган калькулятор онлайн

Для того что бы вычислить ранг матрицы можно применить метод окаймляющих миноров или метод Гаусса. Рассмотрим метод Гаусса или метод элементарных преобразований.

Рангом матрицы называют максимальный порядок её миноров, среди которых есть хотя бы один, не равный нулю.

Рангом системы строк (столбцов) называется максимальное количество линейно независимых строк (столбцов) этой системы.

Метод Гаусса использует элементарные преобразования, которые не изменяют ее ранг:

1. Транспонирование.
   

   ---

2. Перестановка местами строк или столбцов.
   

   ---

3. Прибавление одной строки/столбца к другой строке/столбцу умноженного на ненулевое число.
   

   ---

4. Умножение строки или столбца на ненулевое число.
   

   ---

С помощью данного метода нужно привести матрицу к ступенчатому виду и посчитать количество строк, в которых есть хоть один не нулевой элемент.

Пример

Рассмотрим данный метод на примере. Дана матрицы:

Для облегчения дальнейших расчетов поменяем местами строку №1 со строкой №2.

Сделаем элемент a_3,1 равный нулю.

Из строки №3 вычтем строку №1, умноженную на 3/2.

Сделаем элемент a_4,1 равный нулю.

Из строки №4 вычитаем строку №1, умноженную на 2.

Сделаем элемент a_3,2 равный нулю.

Из строки №3 вычтем строку №2, умноженную на -1/4. Мы его получили разделив элимент a

3,2 = -0.5 на элимент a_2,2 = 2.

Сделаем элемент a_4,2 равный нулю.

Из строки №4 вычтем строку №2, умноженную на -1/2.

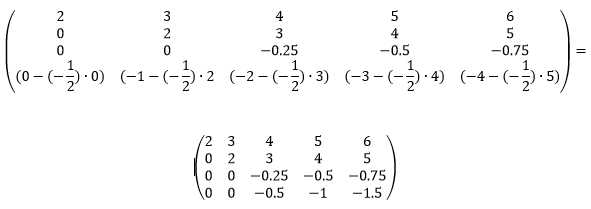
Сделаем элемент a_4,3 равный нулю.

Из строки №4 вычитаем строку №3, умноженную на 2.

В получившейся матрице одна строка содержит нулевые элементы, а три строки имеют не нулевые элементы. Ответ: Ранг=3.

www.mozgan.ru

Решение системы линейных алгебраических уравнений методом Гаусса

Система линейных уравнений вида:

может быть решена методом Гаусса при помощи нашего калькулятора.

Система уравнений задается в виде расширенной матрицы, т. е. матрицы коэффициентов и свободных членов размерности [n : n+1] вида:

Описание метода Гаусса следует сразу за калькулятором.

8 3 4 5 31 14 4 33 23 17 15 4 23 7 22 4 11 17 1 51СЛАУ в матричном видеТочность вычисления

Знаков после запятой: 2

Количество решений

 

Вектор решения системы уравнений

 

Сохранить share extension

Метод Гаусса

Метод был назван в честь гениального немецкого математика XIX века Карла Фридриха Гаусса. Сам Гаусс не был первооткрывателем метода (метод был известен и ранее (еще в I-II веке до н. э. метод упоминался в китайском труде «Математика в девяти книгах»).

Приведение матрицы к ступенчатому виду

На первом шаге решения системы уравнений методом Гаусса матрица коэффициентов и свободных членов приводится к ступенчатому виду:

Матрица превращается в ступенчатую форму путем элементарных преобразований — перемена строк местами, умножение строки на коэффициент, сложение строк.
В нашем калькуляторе для перехода к ступенчатому виду осуществляется последовательное вычитание из нижних строк матрицы, помноженных на , верхних строк , помноженных на коэффициент , где i — индекс текущей строки (индекс строки, которую вычитают из нижних строк).

При осуществлении этой операции требуется, чтобы коэффициент главной переменной был не нулевым. В случае нулевого коэффициента, строка меняется местами с любой другой нижней строкой, в которой в текущем столбце значение отлично от нуля.

Выражение базисных переменных

Получив ступенчатую матрицу, мы переходим к выражению базисных переменных, для этого сначала выполняется деление текущей строки на коэффициент , затем производится обратное вычитание из верхних строк , этой строки , помноженных на коэффициент , где j — индекс текущей строки (индекс строки, которую вычитают из верхних строк). Операция повторяется с каждой строкой, начиная от n-й до 1-й.
В результате матрица приобретает диагональный вид:
,
далее, поделив строки матрицы на коэффициент , в столбце свободных членов получаем вектор решений системы уравнений.

planetcalc.ru

Решение матриц методом Гаусса, с примерами

Метод Гаусса используется для решения систем линейных уравнений и для нахождения обратной матрицы. Начнем с нахождения обратной матрицы.

Алгоритм нахождения обратной матрицы методом Гаусса

1. Пусть задана квадратная матрица

   

припишем к столбцам матрицы справа столбцы единичной матрицы того же порядка. Получим матрицу

   

2. С помощью элементарных преобразований строк приведем матрицу к матрице, в левой части которой будет стоять единичная матрица:

   

3. Полученная таким образом матрица, стоящая в правой части матрицы , и будет обратной матрицей к матрице

   

Алгоритм применения метода Гаусса для решения СЛУ

Пусть задана система линейных уравнений

   

Записывается матрица – расширенная матрица этой системы:

   

Над строками матрицы производятся элементарные преобразования: разрешается изменять порядок строк, умножать строки на любые отличные от нуля числа и прибавлять к любой строке матрицы любую другую её строку, умноженное на произвольное число. В результате таких элементарных преобразований основная матрица системы должна быть приведена к нижнему треугольному виду

   

Эта матрица эквивалентна системе линейных уравнений

   

Из этой системы последовательно снизу вверх выражаются все неизвестные переменные.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Решение системы линейных уравнений методом Гаусса-Жордана

метод Гаусса–Жордана — один из наиболее известных и широко применяемых методов решения систем линейных уравнений. Матричный метод и метод Крамера обладают тем недостатком,
что они не дают ответа в том случае, когда detA = 0, а определяют лишь единственное решение при detA неравном 0. Еще одним недостатком является то, что объем математических вычислений
в рамках этих методов резко возрастает с ростом числа уравнений. Метод Гаусса практически свободен от этих недостатков.

Алгоритм метода Гаусса

1. На основании системы линейных уравнений составляем расширенную матрицу системы;
2. Приводим матрицу к «треугольному» виду;
3. Определяем ранги основной и расширенной матриц, и на основании этого делаем вывод о совместности системы и количестве допустимых решений;
4. В случае, если система имеет единственное решение производим обратную подстановку и находим его, если система имеет множество решений: выражаем базисные переменные через
   переменные которые могут принимать произвольные значения;

Комментарий к шагу 2 Метода Гаусса. Треугольной называют матрицу, в которой все элементы расположенные ниже главной диагонали равны нулю.

Для приведения исходной расширенной матрицы к треугольному виду используем следующие два свойства определителей:

Свойство 1. Определитель не изменит свое значение, если ко всем элементам какой-либо строки (столбца) матрицы прибавить соответствующие элементы параллельной строки (столбца), умноженные на произвольное одно и то же число.

Свойство 2. При перестановке двух любых столбцов или строк матрицы ее определитель меняет знак на противоположный, а абсолютная величина определителя остается неизменной.

На основании этих свойств определителей составим алгоритм преобразования матрицы к треугольному виду:

1. Рассматриваем строку i(начиная с первой). Если, элемент aⁱ_i равен нулю, меняем местами i-ю и i+1-ю строки матрицы. Знак определителя при этом изменится на противоположный. Если a¹₁ отличен от нуля — переходим к следующему шагу;
2. Для каждой строки j, ниже i-й находим значение коэффициента K_j=a^j_i/aⁱ_i;
3. Пересчитываем элементы всех строк j, расположенных ниже текущей строки i, с использованием соответствующих коэффициентов по формуле: a^j_kнов.=a^j_k-K_j*aⁱ_k;
   После чего, возвращаемся к первому шагу алгоритма и рассматриваем следующую строку, пока не доберемся до строки i=n-1, где n — размерность матрицы A
4. В полученной треугольной матрице расчитываем произведение всех элементов главной диагонали Пaⁱ_i, которое и будет являтся определителем;

Другими словами, суть метода можно сформулировать следующим образом. Нам необходимо сделать нулевыми все элементы матрицы ниже главной диагонали. Сначала мы получаем нули в первом столбце.
Для этого мы последовательно вычитаем первую строку, домноженную на нужное нам число (такое, чтоб при вычитании мы получили ноль в первом элементе строки), из всех ниже лежащих строк.
Затем проделываем то же самое для второй строки, чтобы получить нули во втором столбце ниже главной диагонали матрицы. И так далее пока не доберемся до предпоследней строки.

Комментарий к шагу 3 Метода Гаусса. Рангом матрицы A размера m × n называется наивысший порядок отличного от нуля минора этой матрицы. Ранг матрицы A обозначается через r(A) = rangA = rankA.
Минором M (от латинского “minor” меньший) k-го порядка матрицы A называется определитель некоторой матрицы, составленной из элементов матрицы A, стоящих на пересечении произвольно выбранных k
строк и k сто

www.uchimatchast.ru

Решение уравнений методом Гаусса онлайн калькулятор

Карл Фридрих Гаусс — немецкий математик, механик, физик, астроном и геодезист. Он считается одним из величайших математиков всех времён, «королём математиков». И даже избирался иностранным почетным членом Петербургской академии наук. Для творчества Гаусса характерна органическая связь между теоретической и прикладной математикой, широта проблематики. Труды Гаусса оказали большое влияние на развитие алгебры, теории чисел, дифференциальной геометрии, математической физики, теории электричества и магнетизма, геодезии и многих разделов астрономии. Метод Гаусса позволяет максимально легко и быстро решить систему линейных алгебраических уравнений (СЛАУ). Успех данного метода заключается в последовательном исключении неизвестных из уравнений. Сегодня решить систему алгебраических уравнений онлайн методом Гаусса можно с помощью специальных решательов, но ниже мы разберем решение системы линейных уравнений, чтобы наглядно на примере увидеть все его достоинства.

Так же читайте нашу статью «Решить уравнение матричным способом онлайн решателем»

Допустим, дана система линейных уравнений:

\[\left\{\begin{matrix} 2\cdot x_1+4\cdot x_2+1\cdot x_3 = 36\\ 5\cdot x_1 + 2 \cdot x_2 +1 \cdot x_3 =47\\ 2\cdot x_1 + 3\cdot x_2 + 4 \cdot x_3 = 37 \end{matrix}\right.\]

Представим ее в матричной форме:

\[\begin{bmatrix} 2 & 4 & 1\\ 5 & 2 & 1\\ 2 & 3 & 4 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 36\\ 47\\ 37 \end{bmatrix}\]

Выберем строку с максимальным коэффициентом \[a_i1\] и меняем ее с первой.

\[\begin{bmatrix} 5 & 2 & 1\\ 2 & 4 & 1\\ 2 & 3 & 4 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 47\\ 36\\ 37 \end{bmatrix}\]

Нормируем уравнения относительно коэффициента при \[x_1\]:

\[\begin{bmatrix} 1 & \frac{2}{5} & \frac{1}{5}\\ 2 & \frac{4}{2} & \frac{1}{2}\\ 2 & \frac{3}{2} & \frac{4}{2} \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} \frac{47}{5}\\ \frac{36}{2}\\ \frac{37}{2} \end{bmatrix} \]

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 1 & 2 & 1\\ 1 & 1.5 & 2 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 9.6\\ 9.1 \end{bmatrix}\]

Вычитаем 1 уравнение из 2 и 3:

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1.6 & 0.3\\ 0 & 1.1 & 1.8 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 8.6\\ 9.1 \end{bmatrix}\]

Выбираем строку с наибольшим коэффициентом при \[a_i2\] (уравнение 1 не рассматривается) и перемещаем ее на место 2.

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1.6 & 0.3\\ 0 & 1.1 & 1.8 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 8.6\\ 9.1 \end{bmatrix}\]

Нормируем 2 и 3 уравнения относительно коэффициента при \[x_2\]

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1 & 0.1875\\ 0 & 1 & 1.636 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 5.375\\ 8.272 \end{bmatrix}\]

Вычитаем уравнение 2 из 3

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1 & 0.1875\\ 0 & 0 & 1.4489 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 5.375\\ 2.897 \end{bmatrix}\]

Нормируем уравнение 3 относительно коэффициента при \[x_3\]

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1 & 0.166\\ 0 & 0 & 1 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 5.333\\ 2 \end{bmatrix}\]

Откуда получаем \[x_3=2\]. Подставляем полученное значение в уравнения 2 и 1 получаем

\[x_2 = 5.333 — 0.1666 \cdot 2 = 5.333 — 0.333 =5\]

\[x_1+0.4 \cdot x_2 = 9.4 — 0.2 \cdot 2 = 9.4 — 0.4=9\]

Подставляя полученное значение \[x_2=5\] в уравнение 1, найдем

\[x_1 = 9 — 0.4 \cdot 5 = 9 — 2 = 7\]

Таким образом, решением системы уравнений будет вектор

\[x =\begin{bmatrix} 7 & 5 & 2 \end{bmatrix}^T\].

Где можно решить уравнение методом Гаусса онлайн?

Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

www.pocketteacher.ru