Решение высшей математики онлайн
‹— Назад
Если даны два отображения и , где , то имеет смысл «сквозное отображение» из в , заданное формулой , , которое называется композицией функций и и обозначается .
Таким образом, , при всех . Другое название композиции — сложная функция (так как сквозное отображение «сложено» из отображений и ).
Применяя композицию функций, которые сами могут получаться как композиции, мы можем получать сложные функции вида и более длинные композиции.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
mathserfer.narod.ru
§ 9. Арифметические операции над функциями. Композиция функций
Определение 1. Пусть функцииfиg заданы на множестве .Суммой функцийfиg называется
функция,
значение которой в точке
.Суммой функцийfиg называется
функция,
значение которой в точке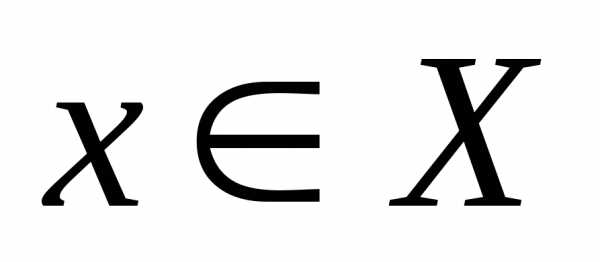 определяется как сумма значений функцийfиg в этой точке, то есть
определяется как сумма значений функцийfиg в этой точке, то есть.
Аналогично определяется разность
,
произведение
,
частное функций, если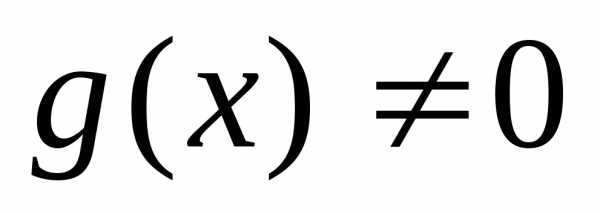 ,
,
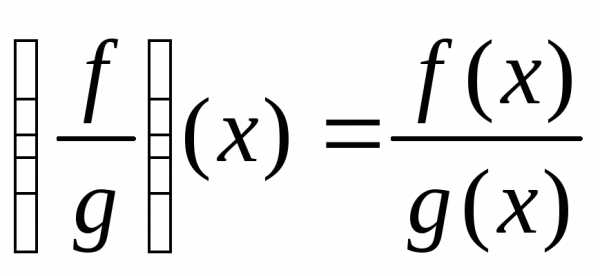 .
.
Определение 2. Пусть действительная функцияf задана на множествеХ, а действительная функцияg – на множестве. Тогда существует композиция отображений, которая является действительной функцией, заданной на множестве
Заметим, что сложную функцию
можно записать в виде цепочки функций.
Переменнуюу в этом случае обычно
называютпромежуточной переменной.
Заметим также, что термин «сложная
функция» характеризует не сложность
функции, а способ ее задания. Например,
функцияили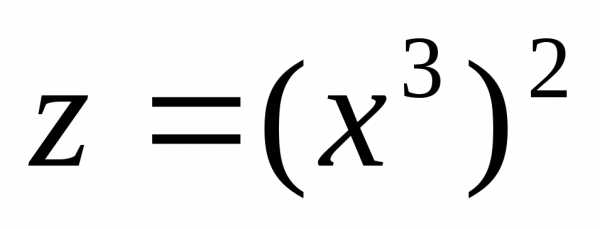 — сложная функция, а тождественная ей
функция
— сложная функция, а тождественная ей
функция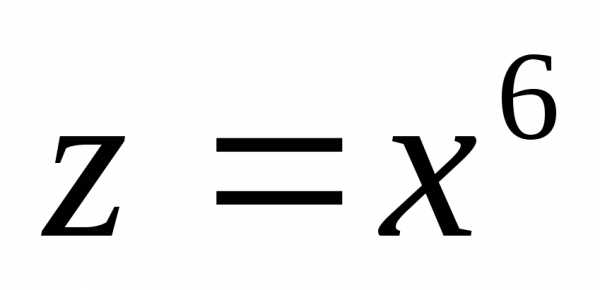 уже не является сложной.
уже не является сложной.
Пример 1. Если, то,.
Может получиться так, что множество 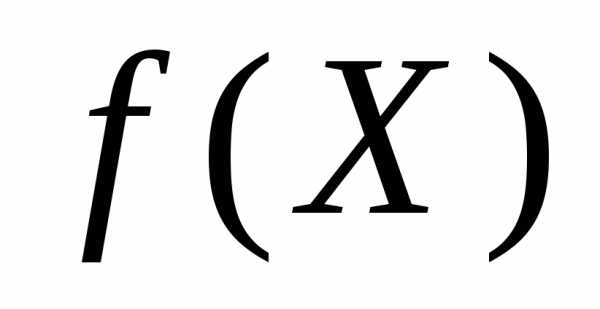 не является подмножеством множестваY. В этом случае сложная
функция определена лишь для тех
не является подмножеством множестваY. В этом случае сложная
функция определена лишь для тех
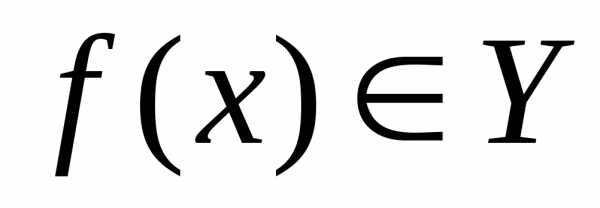 .
. Пример 2. Пусть.
Тогда.
Здесь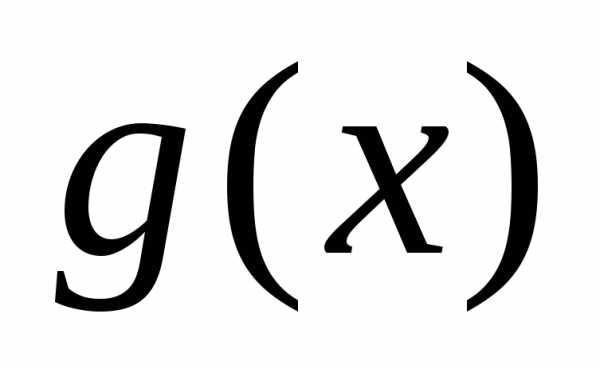 задана на множествезадана наи.
Сложная функция
задана на множествезадана наи.
Сложная функция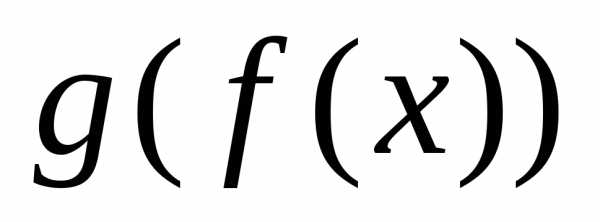 рассматривается
длях таких, что,
то есть.
рассматривается
длях таких, что,
то есть.
Пример 3. Функцииине определяют функции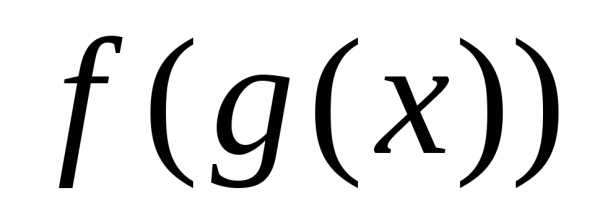 ,
так как
,
так как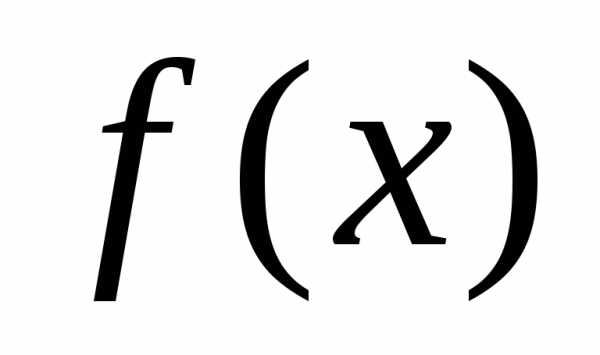 определена для
определена для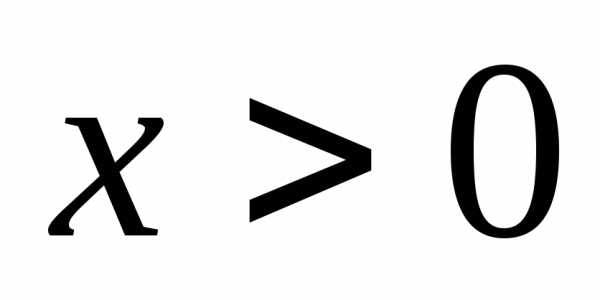 ,
а
,
а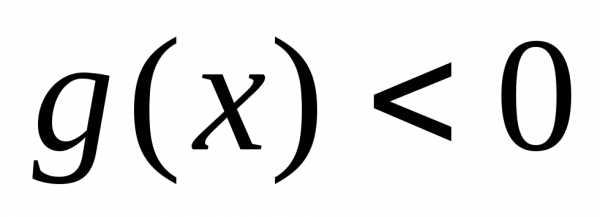 для всех
для всех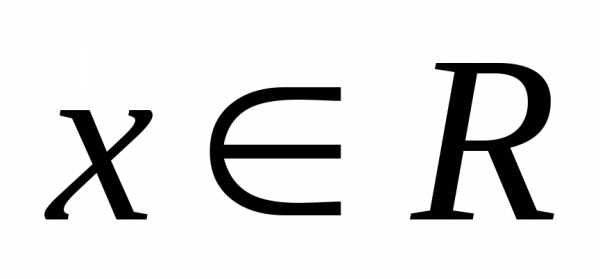 .
.
Пример 4. (Решить самостоятельно). Пустьи. Найти следующие функции и указать их области определения:.
§ 10. Ограниченные и неограниченные функции. Монотонные функции
Определение
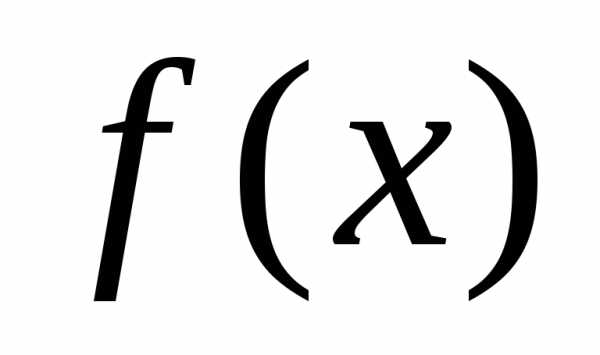 ,
заданная на множествеХ, называетсяограниченной сверху на этом
множестве, если существует числоМ,
такое, что.
Функция,
заданная на множествеХ, называетсяограниченной снизу на этом
множестве, если существует числоМ,
такое, что.
Функция
,
заданная на множествеХ, называетсяограниченной сверху на этом
множестве, если существует числоМ,
такое, что.
Функция,
заданная на множествеХ, называетсяограниченной снизу на этом
множестве, если существует числоМ,
такое, что.
Функция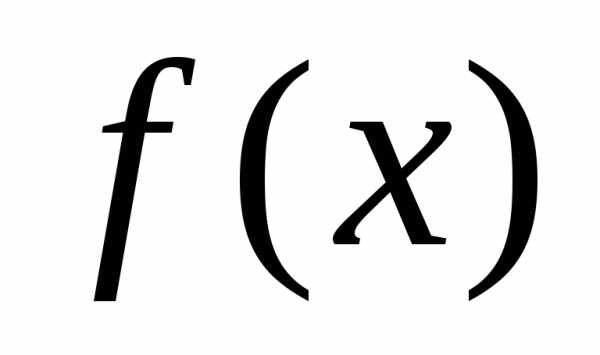 ,
заданная на множествеХ, называетсяограниченной на этом множестве,
если существуют числа
,
заданная на множествеХ, называетсяограниченной на этом множестве,
если существуют числа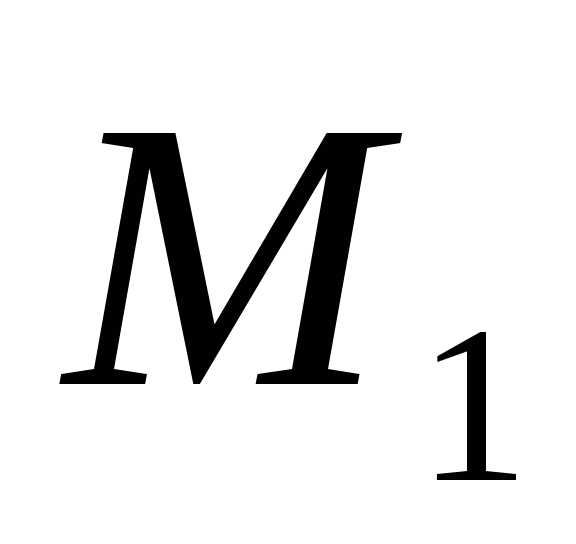 и
и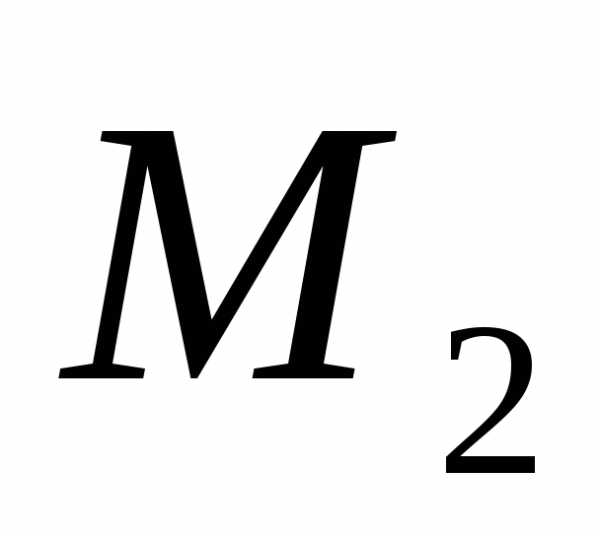 ,
такие, что.
,
такие, что. Иными словами, функция 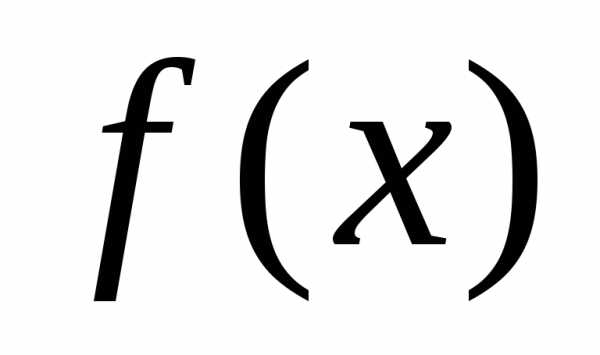 ограничена
на множествеХ, если на этом множестве
она ограничена и сверху, и снизу.
ограничена
на множествеХ, если на этом множестве
она ограничена и сверху, и снизу.
Например, функция
ограничена сверху на множествеR,
так как,
функция
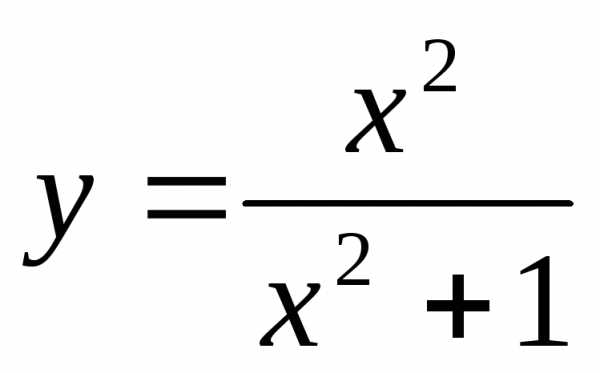 ограничена наR, так
как.
Ограниченными являются также функции
ограничена наR, так
как.
Ограниченными являются также функции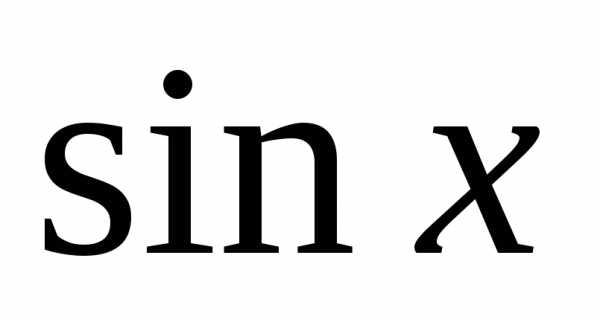 и
и ,
так как.
,
так как.Свойства ограниченных функций:
1) если функции fиgограничены на множествеХ, то и
функции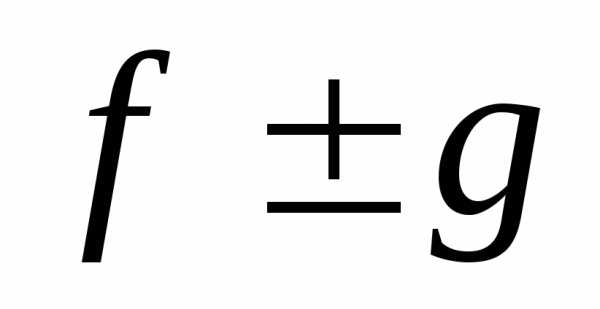 и
и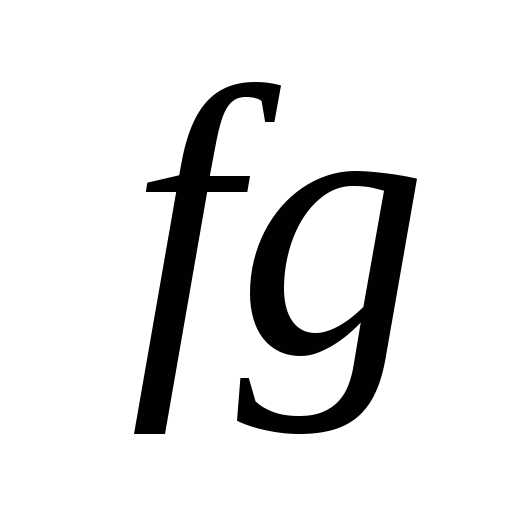 тоже ограничены на множествеХ;
тоже ограничены на множествеХ;
2) если функция 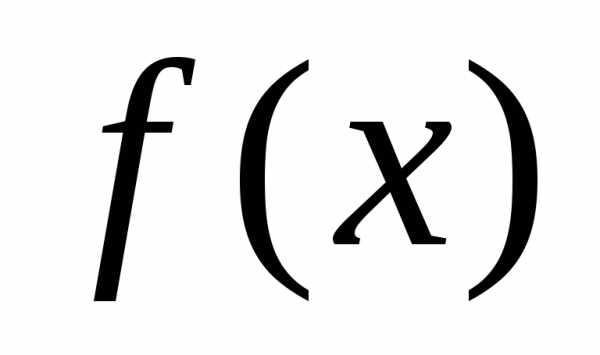 ограничена сверху, то функция
ограничена сверху, то функция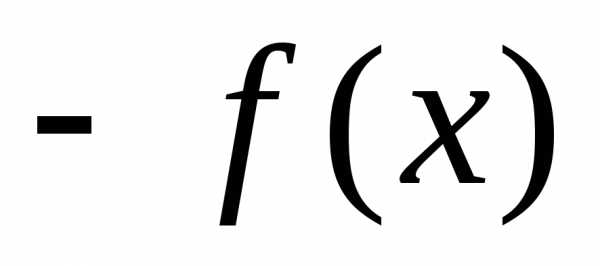 ограничена снизу;
ограничена снизу;
3) если функция 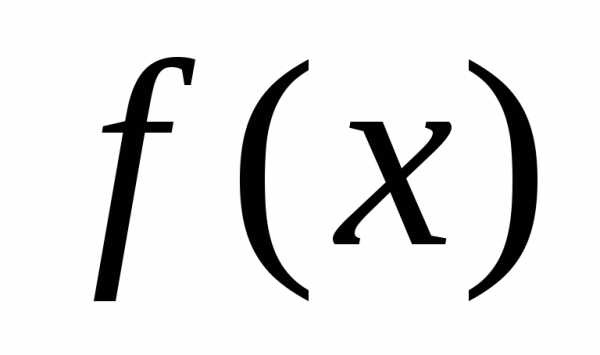
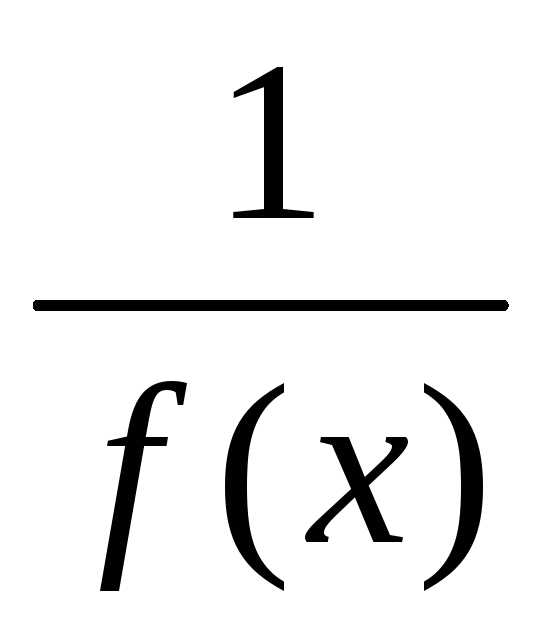 ограничена наХ.
ограничена наХ. Доказательство. 1) В силу ограниченности
функцийfиgна множествеХ найдутся числа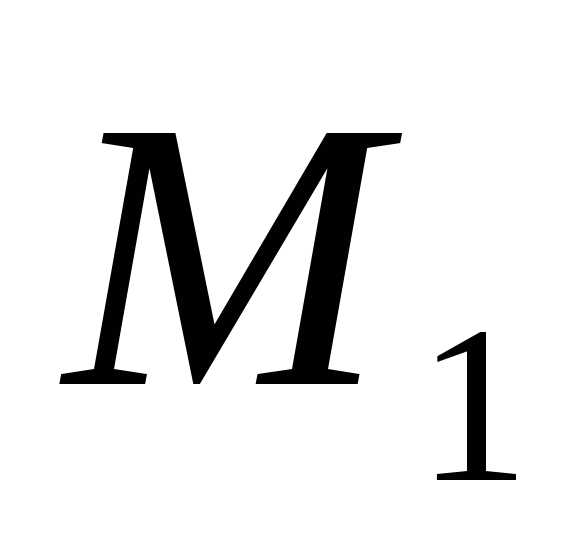 и
и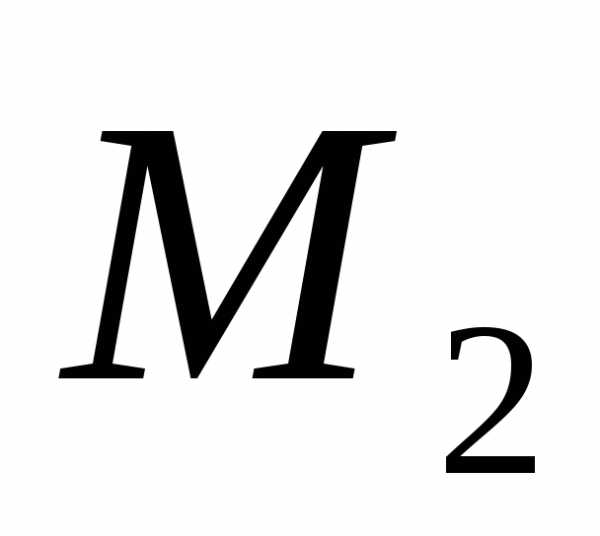 ,
,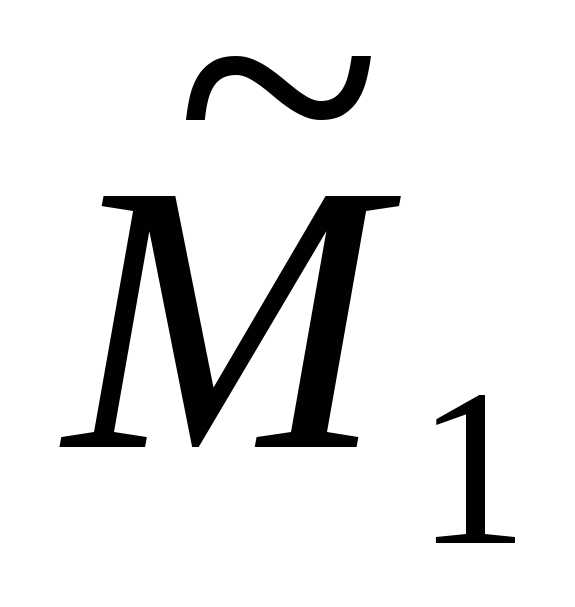 и
и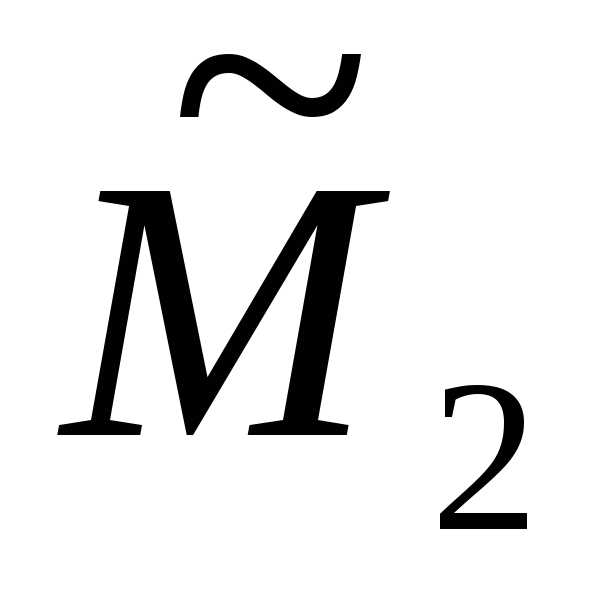 ,
такие, чтои.
А тогдаи
,
такие, чтои.
А тогдаи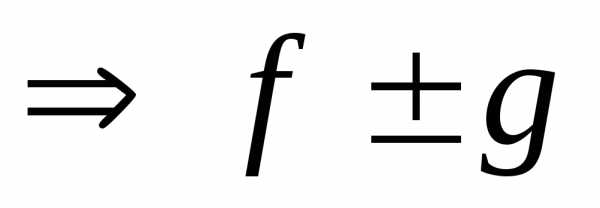 — ограниченные наХ функции. Чтобы
доказать ограниченность функции
— ограниченные наХ функции. Чтобы
доказать ограниченность функции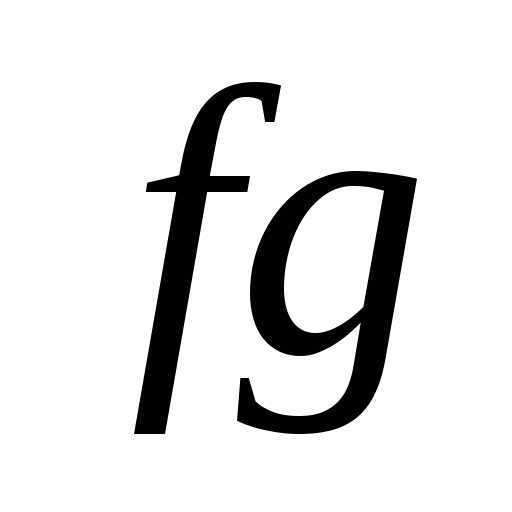 ,
положим.
Тогда имеют место неравенстваи,
из которых следует, что,
а это и означает ограниченность функции
,
положим.
Тогда имеют место неравенстваи,
из которых следует, что,
а это и означает ограниченность функции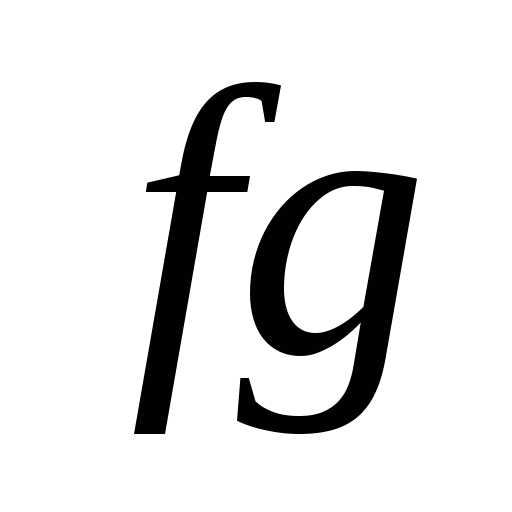
2) В силу ограниченности функции f сверху найдется числоМ, такое,
что.
Тогда,
что и означает ограниченность функции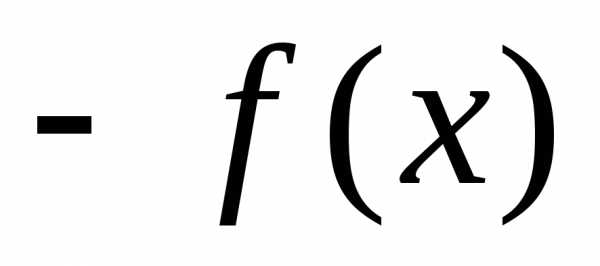 снизу.
снизу.
3) По условию
,
поэтомуограниченность функции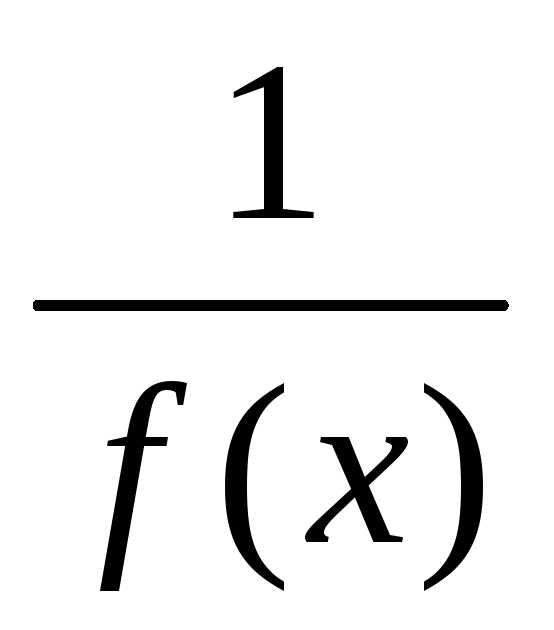 .
.
Например, функция 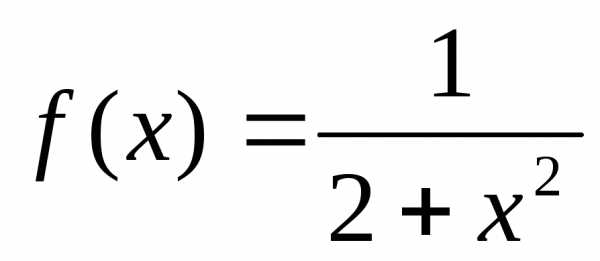 ограничена на множествеR действительных чисел, так как.
ограничена на множествеR действительных чисел, так как.
Чтобы дать определение неограниченной сверху или снизу функции, нужно сформулировать отрицание соответствующей части определения 1.
Определение 2. Функция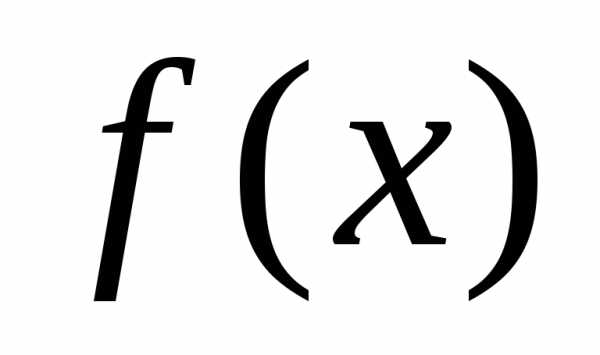 называетсянеограниченной сверху на множествеХ, если не существует
числаМ, такого, чтодля любого
называетсянеограниченной сверху на множествеХ, если не существует
числаМ, такого, чтодля любого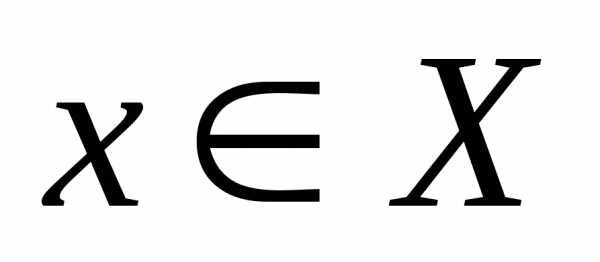
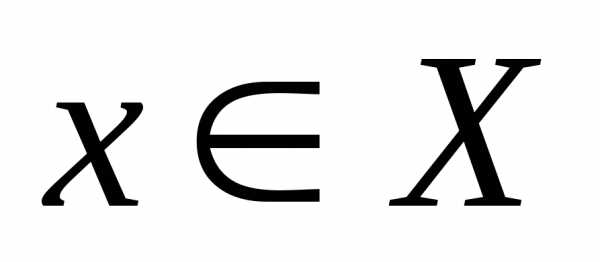 ,
такое, что.
,
такое, что. Функция 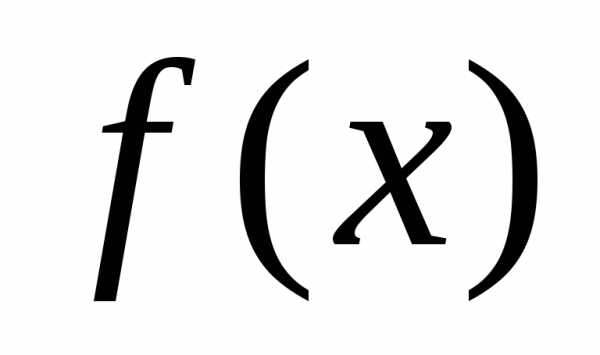 называетсянеограниченной снизу на
множествеХ, если для любого числаМнайдется число
называетсянеограниченной снизу на
множествеХ, если для любого числаМнайдется число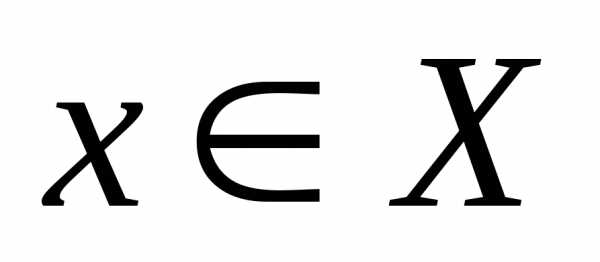 ,
такое, что.
,
такое, что.
Докажем, например, что функция 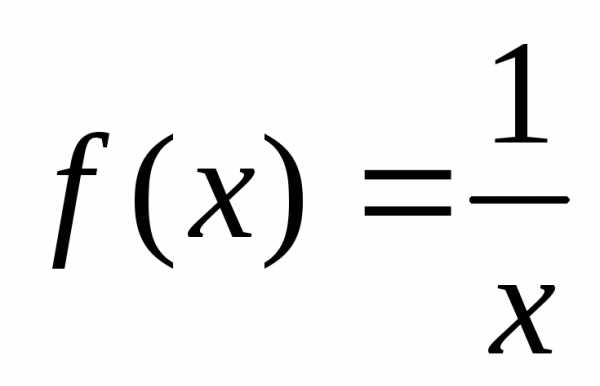 неограниченна на множестве
неограниченна на множестве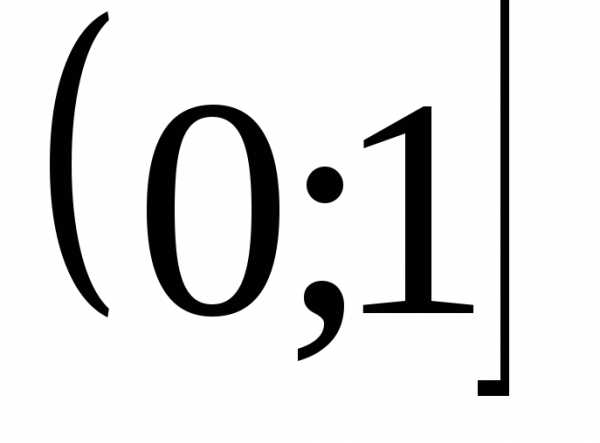 сверху. Возьмем произвольное число
сверху. Возьмем произвольное число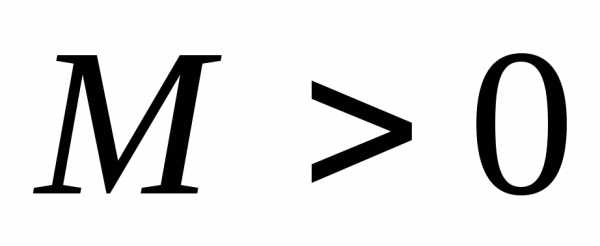 и покажем, что
и покажем, что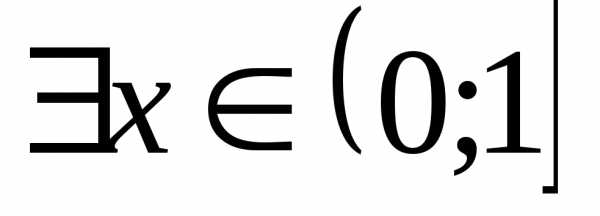 ,
такое, что
,
такое, что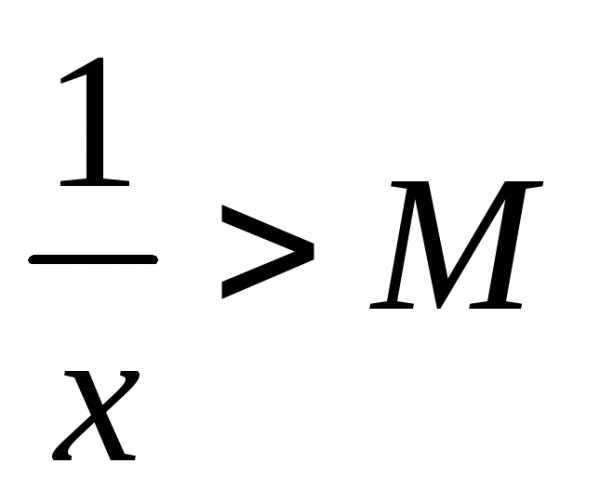 .
.
Для этого, очевидно, достаточно взять 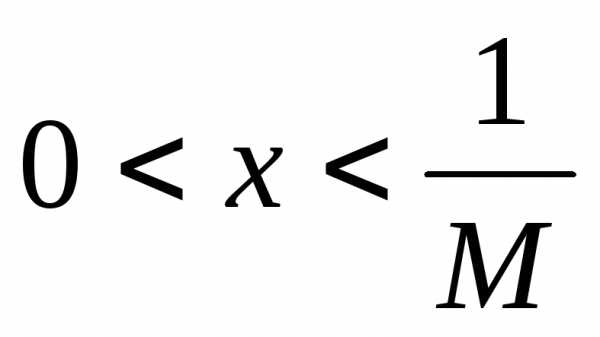
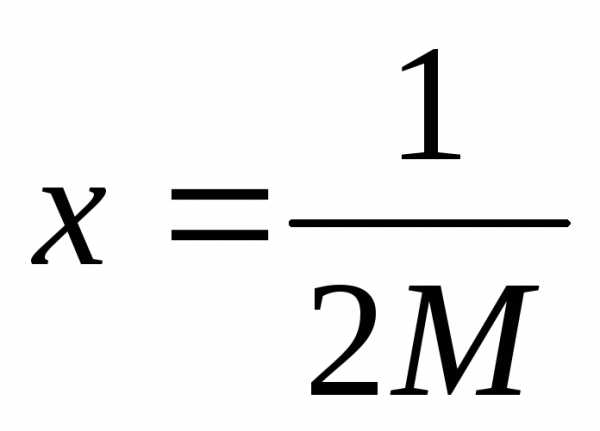 .
. Если функция 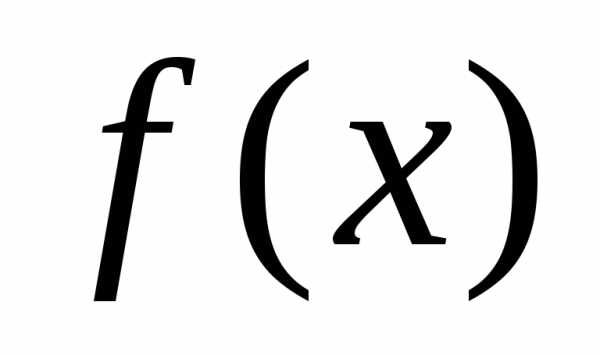 ограничена на множествеХ, то
множество
ограничена на множествеХ, то
множество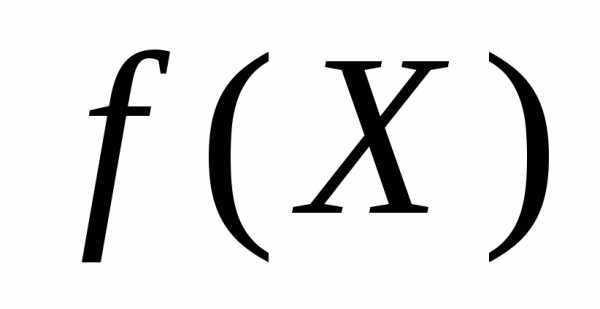 ограничено, поэтому имеет точную верхнюю
и точную нижнюю границы. Их обозначают
ограничено, поэтому имеет точную верхнюю
и точную нижнюю границы. Их обозначают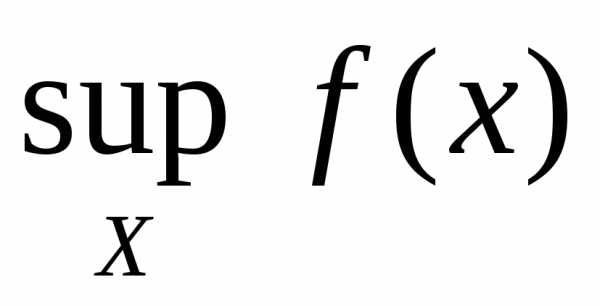 и
и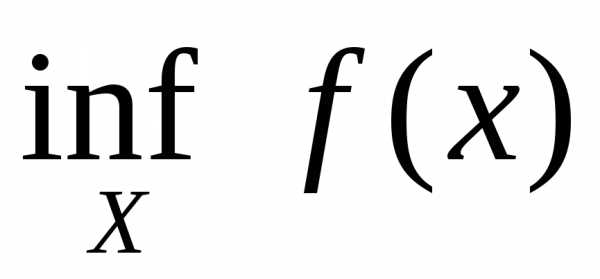 соответственно и называют точной
верхней границей и точной нижней границей
функции
соответственно и называют точной
верхней границей и точной нижней границей
функции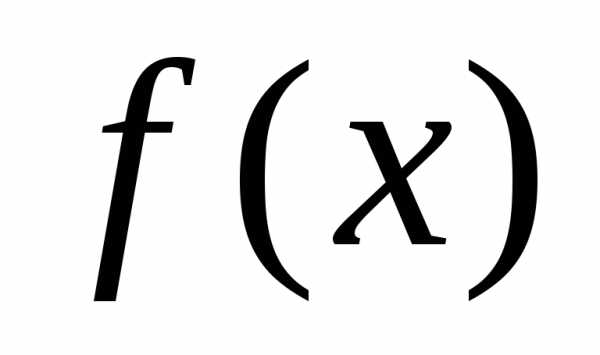 на множествеХ.
на множествеХ.
Определение 3. а) Функция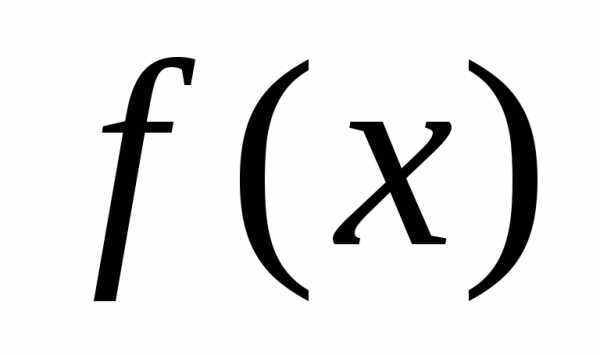 называетсявозрастающей на
множествеХ, если большему значению
аргумента соответствует большее значение
функции, т.е.,
таких, что
называетсявозрастающей на
множествеХ, если большему значению
аргумента соответствует большее значение
функции, т.е.,
таких, что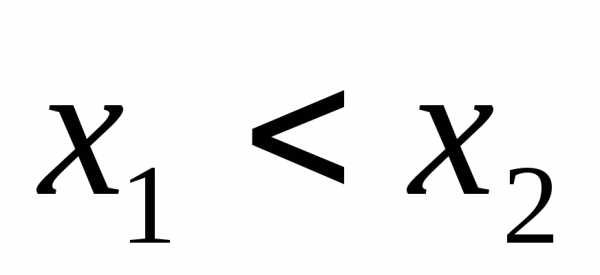
б) Функция 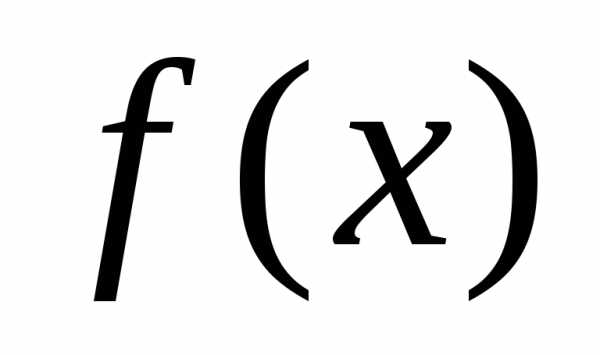 называетсяубывающей на множествеХ, если
называетсяубывающей на множествеХ, если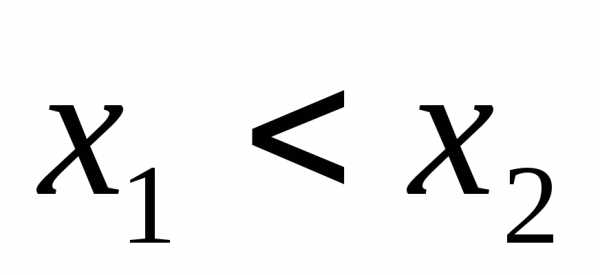
 .
.
в) Функция 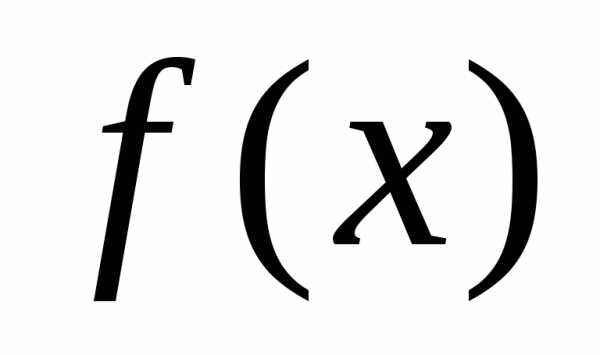 называетсянеубывающей на
множествеХ, если
называетсянеубывающей на
множествеХ, если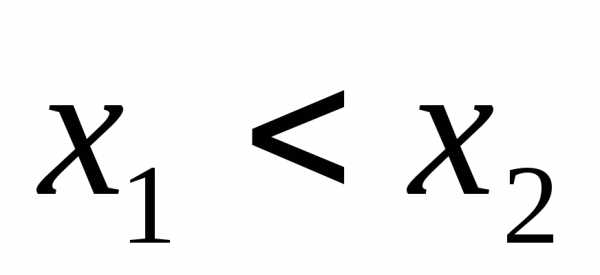
 .
.
г) Функция 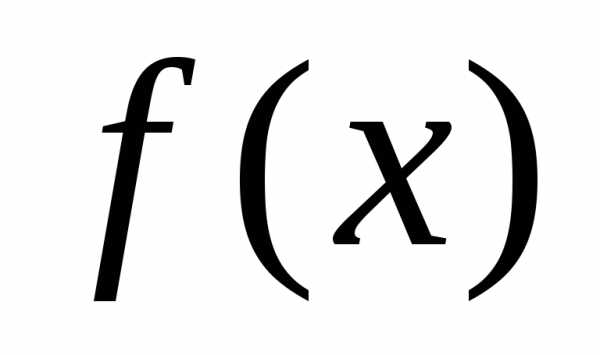 называетсяневозрастающей на
множествеХ, если
называетсяневозрастающей на
множествеХ, если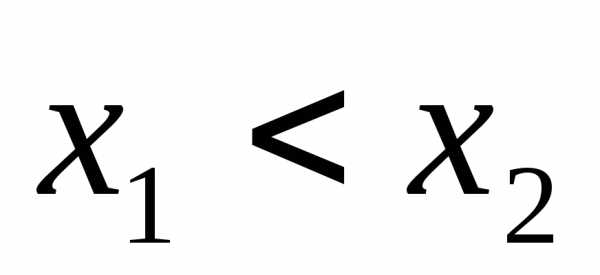
 .
.
Возрастающие, убывающие, неубывающие, невозрастающие функции называются монотонными, возрастающие и убывающие –строго монотонными функциями.
При исследовании функций на монотонность полезны следующие утверждения.
Теорема.а) Если функцииf иg возрастают (убывают) на множествеХ, то и функцияf+g возрастает (убывает) наХ.
б) Если на множествеХ, тонаХ.
в) Если функции fиg неотрицательны
на множествеХи возрастают (убывают)
на этом множестве, то их произведение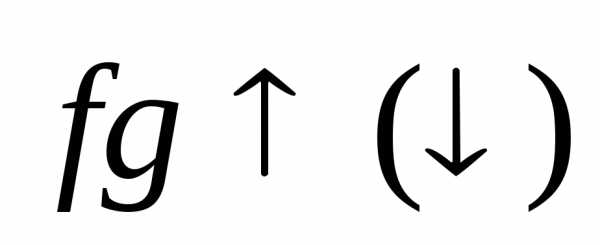 наХ.
наХ.
г) Если функция fположительна на множествеХи
возрастает (убывает), то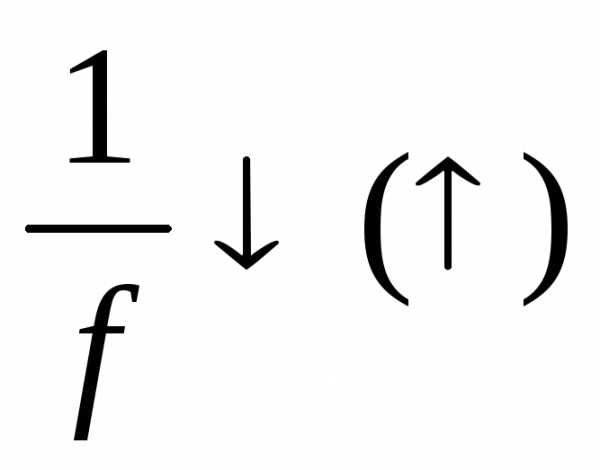 наХ.
наХ.
д) Если функция
на множествеХ, а функцияна множестве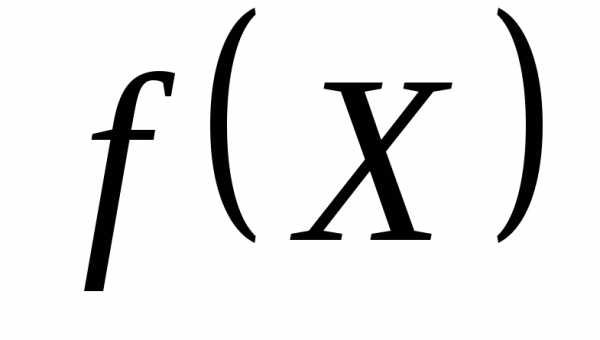 ,
то функция
,
то функция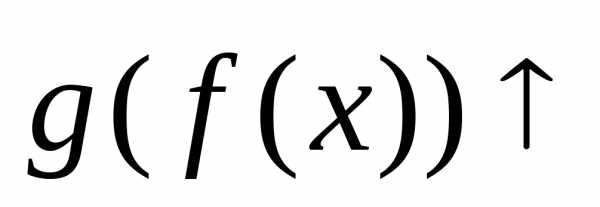 на множествеХ.
на множествеХ.
Доказательство. Докажем, например, а) и д).
а) Пусть функции f иg возрастают
на множествеХ и,
причем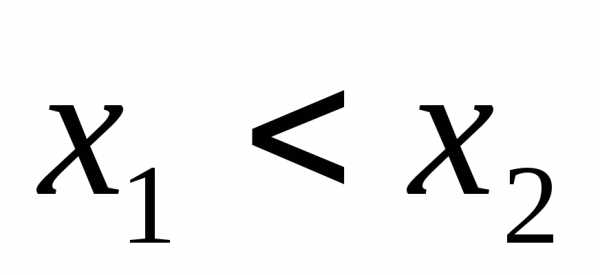 .
Тогдаи поскольку неравенства одинакового
смысла можно складывать, то,
т.е. функцияf+g возрастает.
.
Тогдаи поскольку неравенства одинакового
смысла можно складывать, то,
т.е. функцияf+g возрастает.
д) Пусть функция 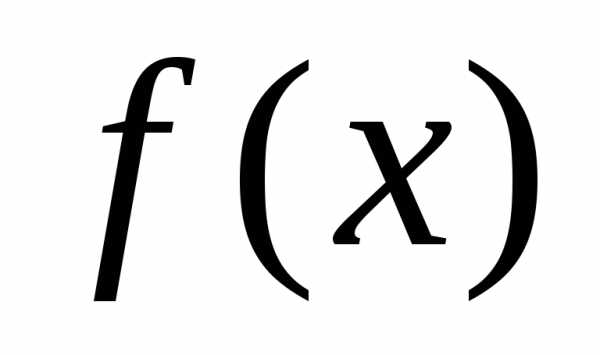 убывает на множествеХ, а функция
убывает на множествеХ, а функция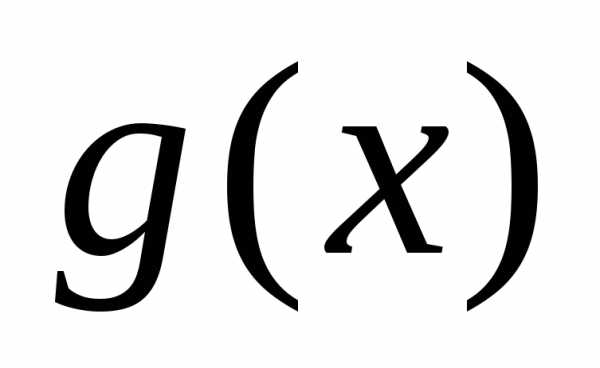 убывает на множестве
убывает на множестве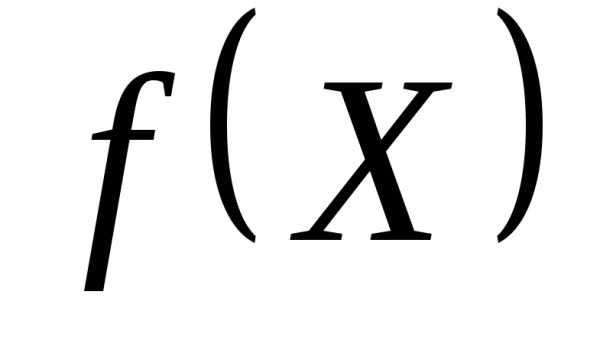 ,,
причем
,,
причем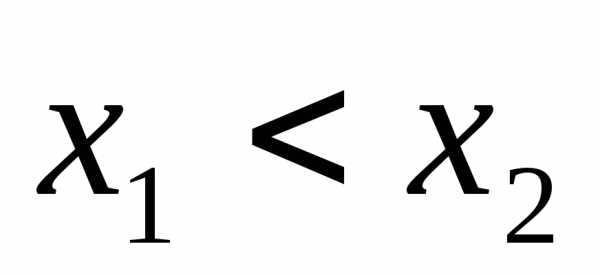 .
Тогдаи, так как,
т.е. функция
.
Тогдаи, так как,
т.е. функция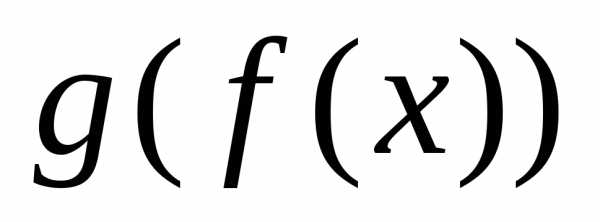 возрастает на множествеХ.
возрастает на множествеХ.
Остальные утверждения теоремы доказать самостоятельно.
Теорема доказана.
Отметим, что прибавление постоянной величины к функции и умножение функции на положительную постоянную величину не меняет характера монотонности.
Пример. Докажем, что функциии возрастают на промежутке
возрастают на промежутке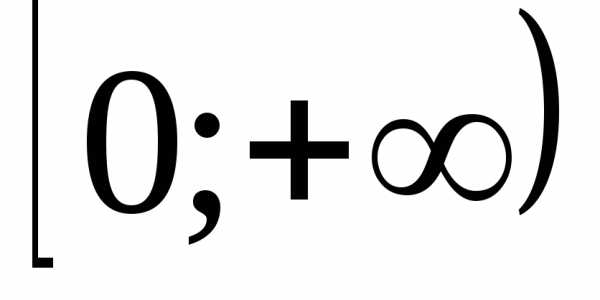 .
.
Доказательство. Функция возрастает
на промежутке
возрастает
на промежутке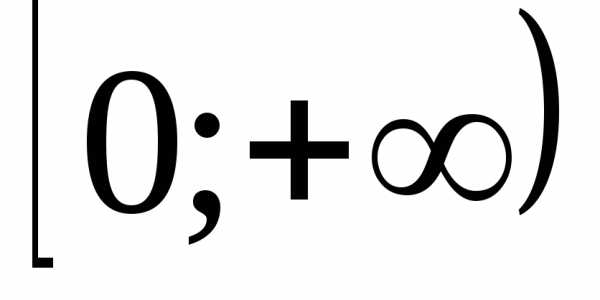 .
Тогда по свойству в)
.
Тогда по свойству в)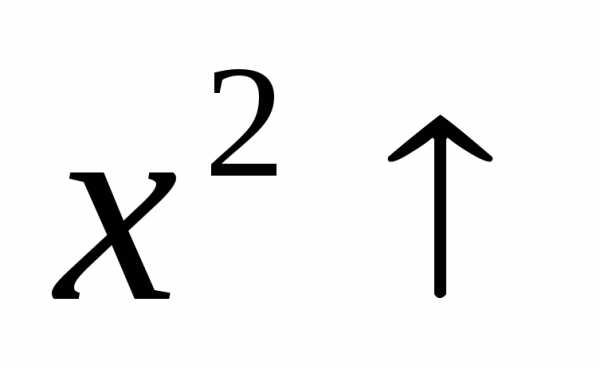 и
и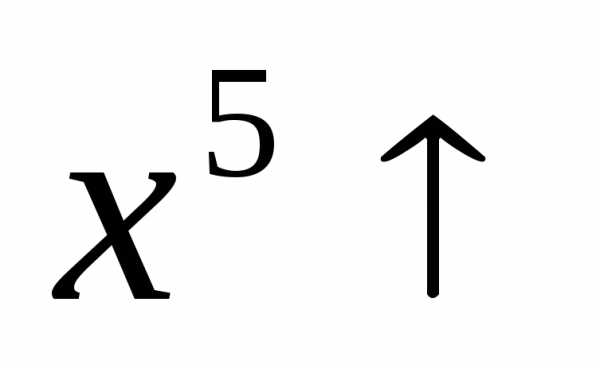 на
на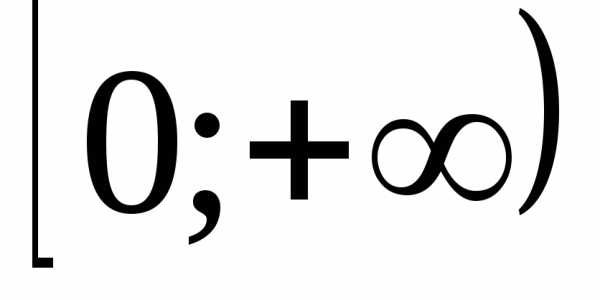 ,
,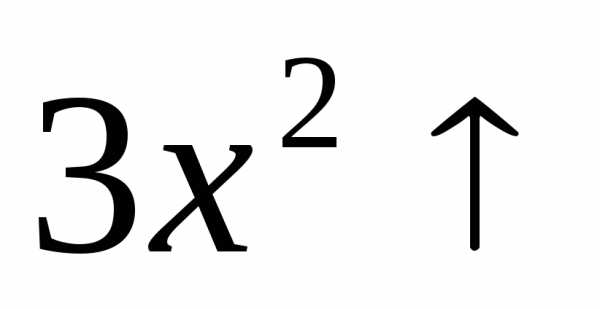 и
и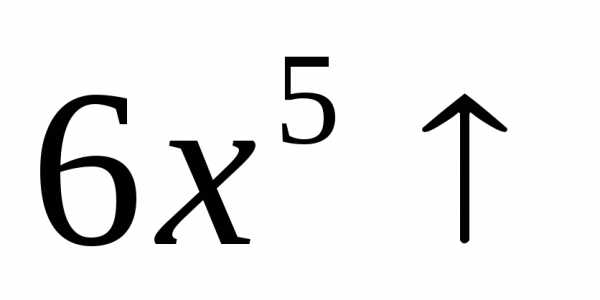 ,
поэтому по свойству а) возрастает и
функция
,
поэтому по свойству а) возрастает и
функция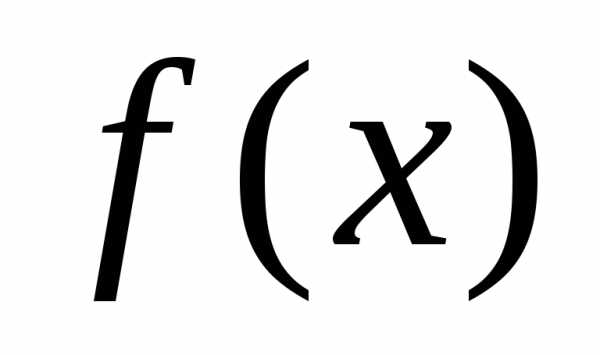 .
.
Для функции 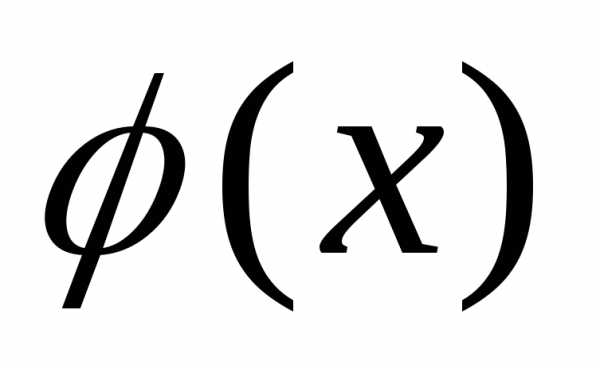 доказательство проведем методом от
противного. Пусть.
Предположим противное, т.е. что
доказательство проведем методом от
противного. Пусть.
Предположим противное, т.е. что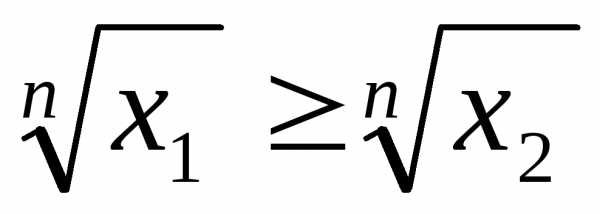 .
Тогда, в силу возрастания функции
.
Тогда, в силу возрастания функции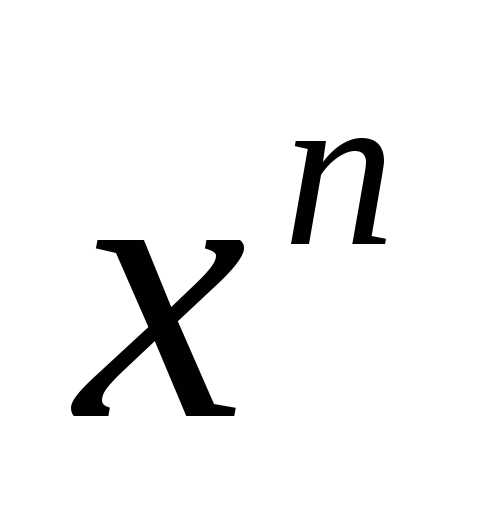 ,,
т.е.
,,
т.е.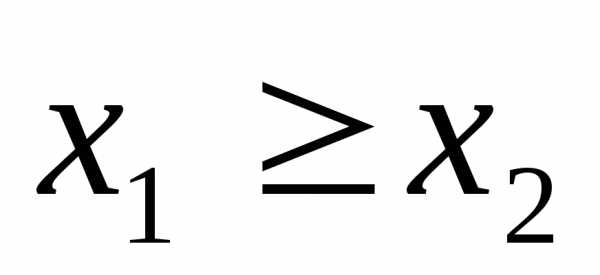 ,
что противоречит неравенству
,
что противоречит неравенству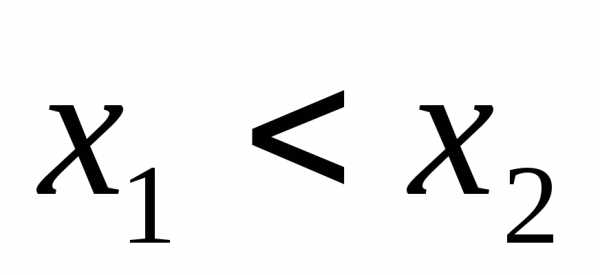 .
Из полученного противоречия следует,
что
.
Из полученного противоречия следует,
что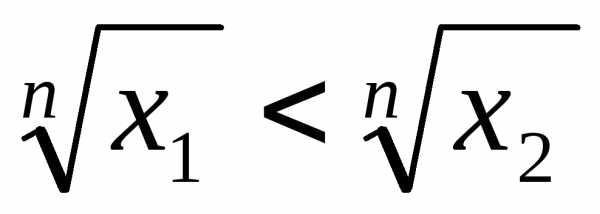 ,
т.е. функция
,
т.е. функция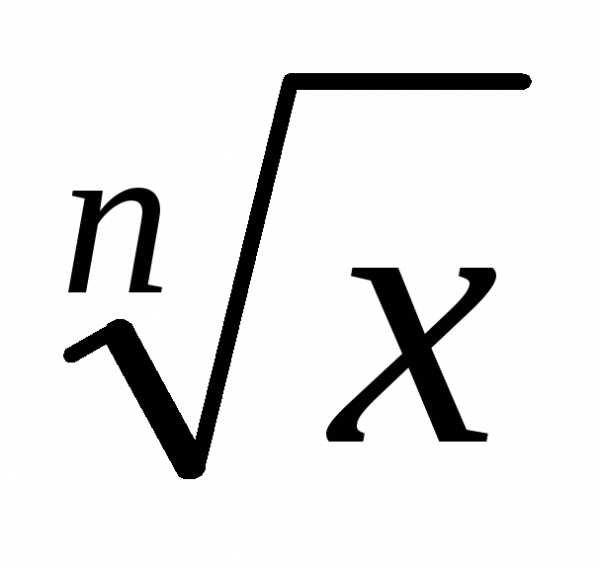 возрастает на промежутке
возрастает на промежутке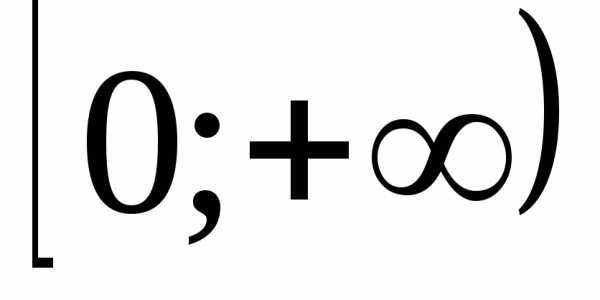 .
.
studfiles.net
Композиция функций и обратные отображения — Викиверситет
Если отображения f:X→Y{\displaystyle f:X\to Y} и g:Y→Z{\displaystyle g:Y\to Z} таковы, что g{\displaystyle g} определено на множестве значений f{\displaystyle f}, то можно построить новое отображение g∘f:X→Z{\displaystyle g\circ f:X\to Z} , значения которого (g∘f)∗(x)=g(f(x)){\displaystyle (g\circ f)*(x)=g(f(x))} .
Такое отображение называют композицией функции f{\displaystyle f} и отображения g{\displaystyle g}.
Свойства отображения функций.
1. h∘(g∘f)=(h∘g)∘f{\displaystyle h\circ (g\circ f)=(h\circ g)\circ f}.
Доказательство. h∘(g∘f)
ru.wikiversity.org
