Контрольная работа «Предел функции» для студентов 1 курса
Контрольная работа
«Предел функции»
Найти предел функции
1
а)
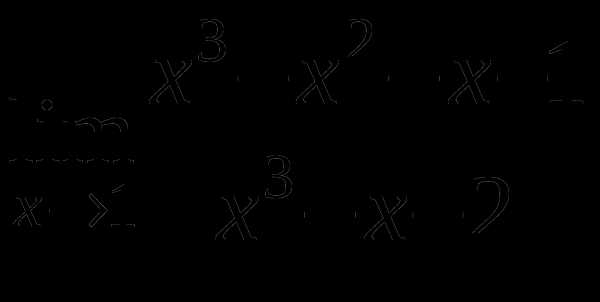
б)
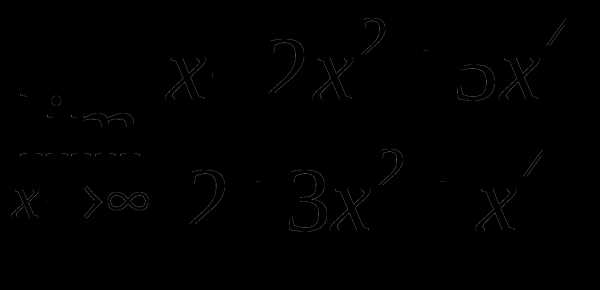
в)
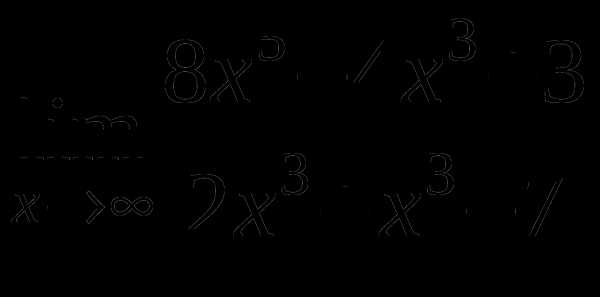
г)
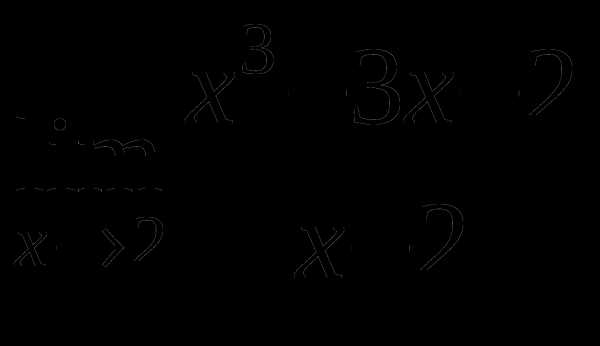
д)
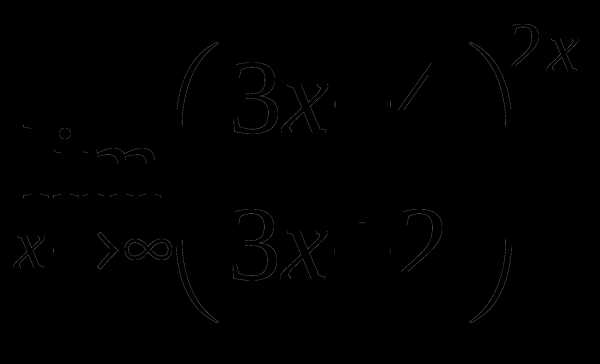
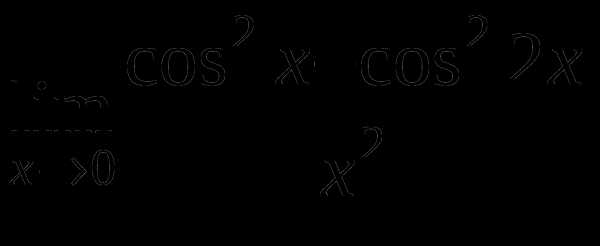
Найти предел функции
2
а)
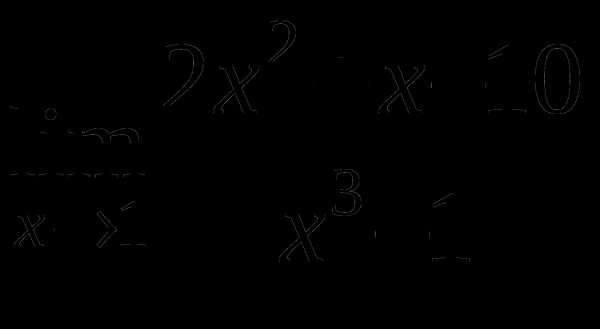
б)
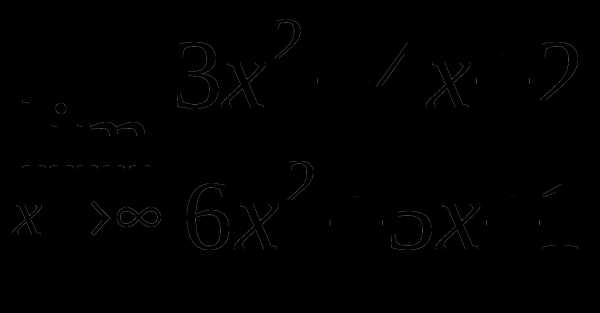
в)
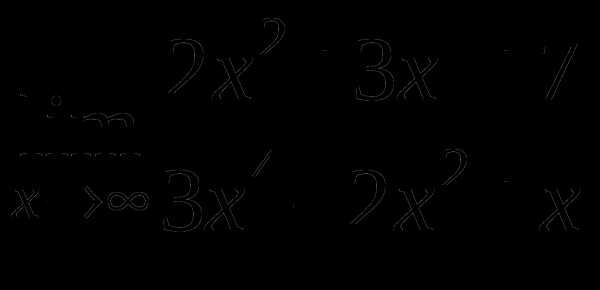
г)
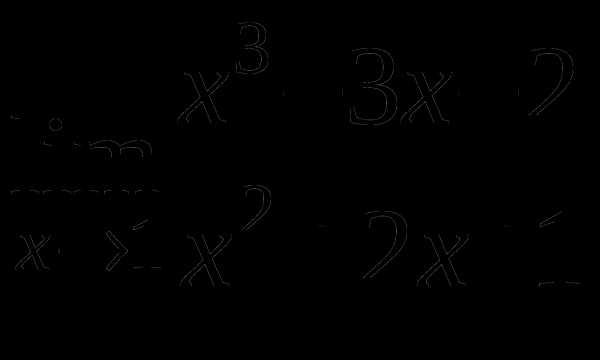
д)
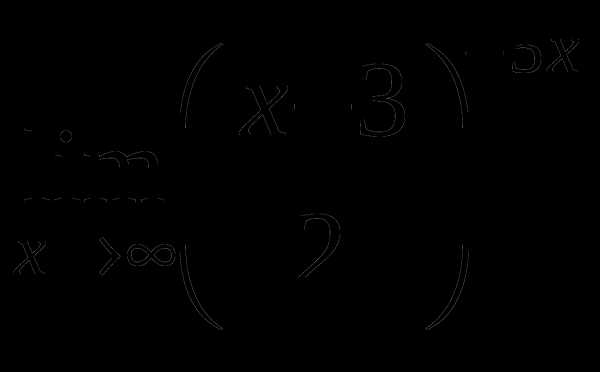
е)
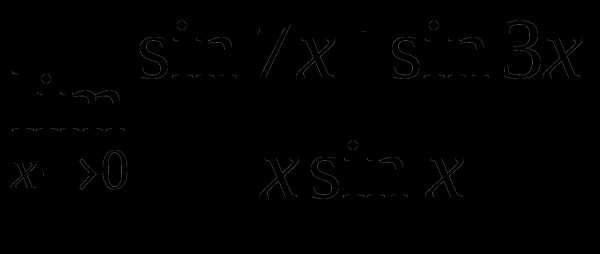
Найти предел функции
3
а)
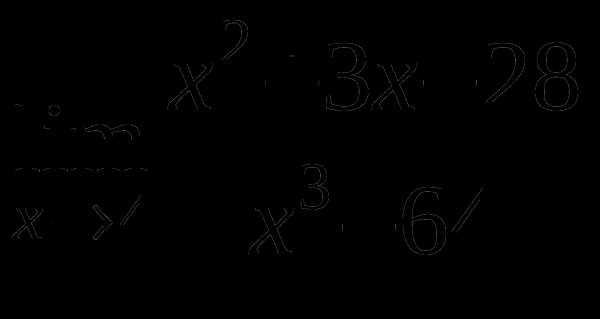
б)
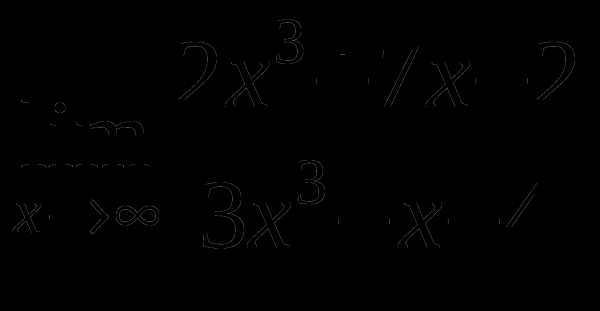
в)
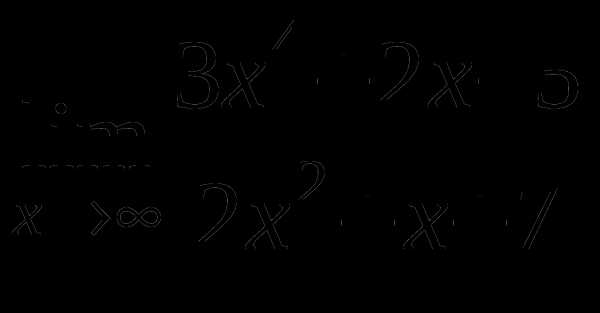
г)
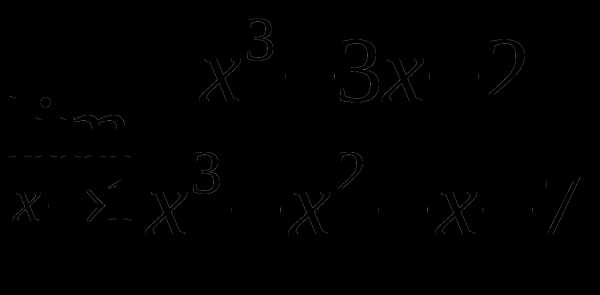
д)
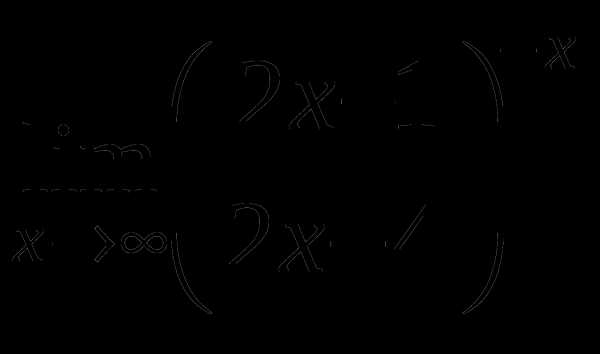
е)
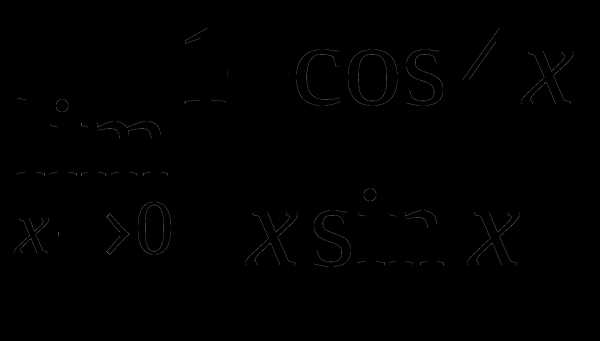
Найти предел функции
4
а)
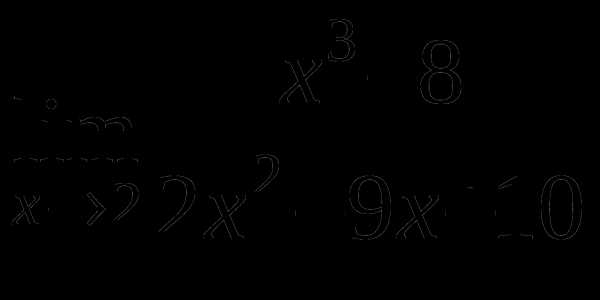
б)
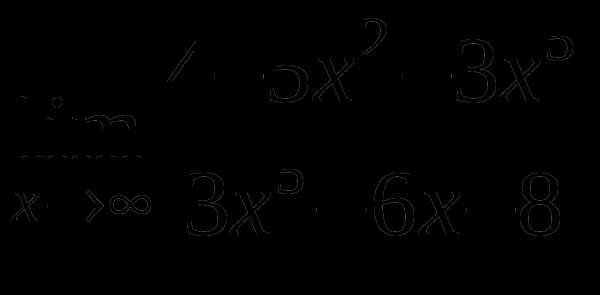
в)
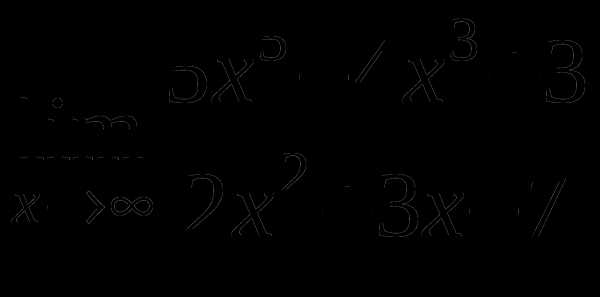
г)
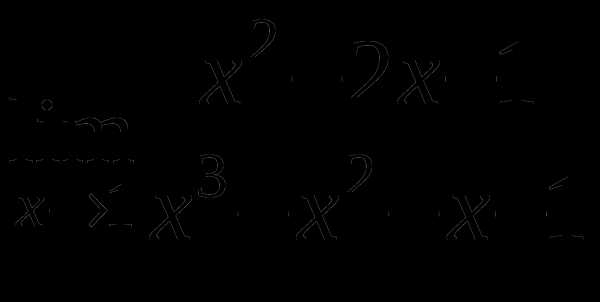
д)
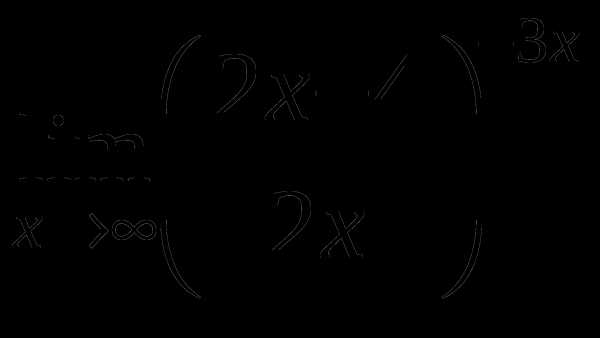
е)
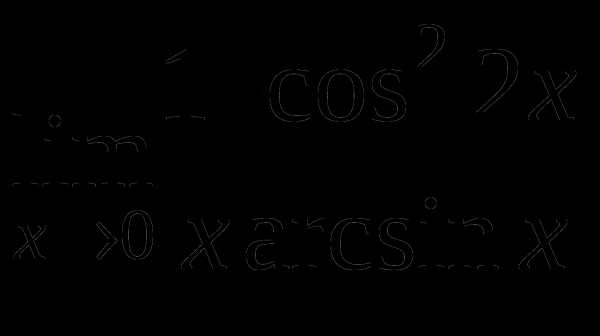
5
а)
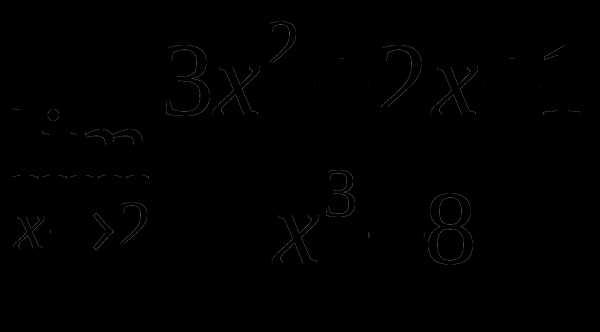
б)
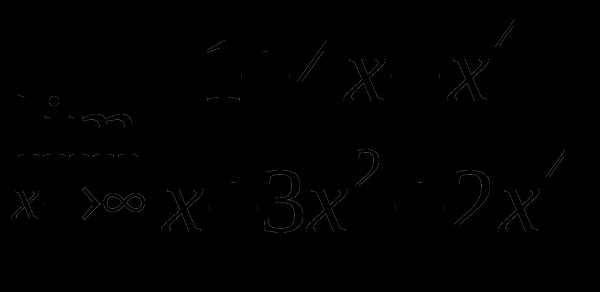
в)
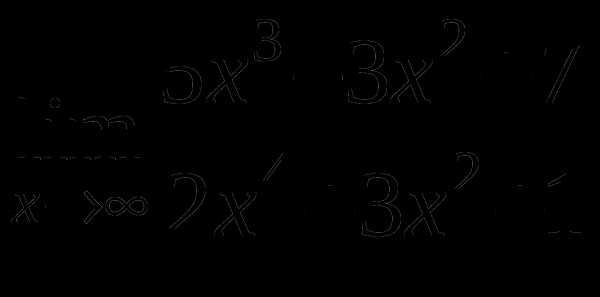
г)
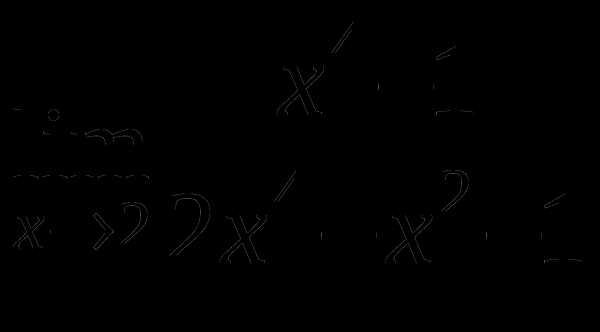
д)
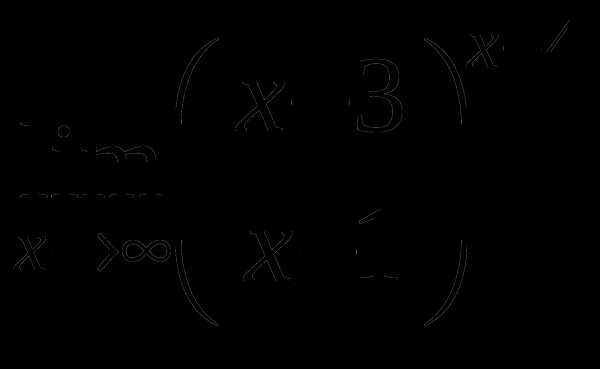
е)
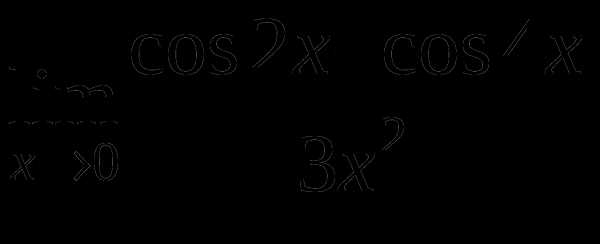
Найти предел функции
6
а)
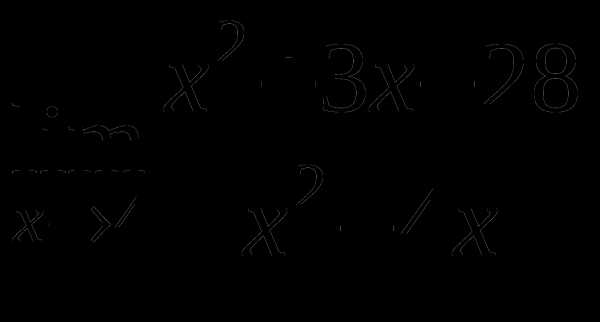
б)
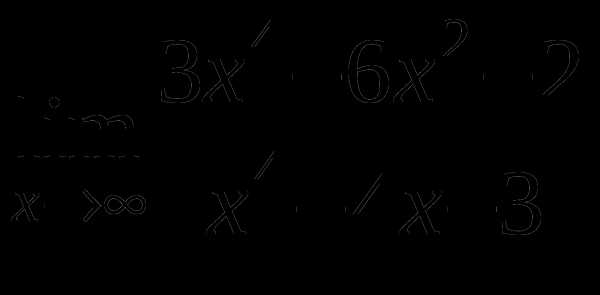
в)
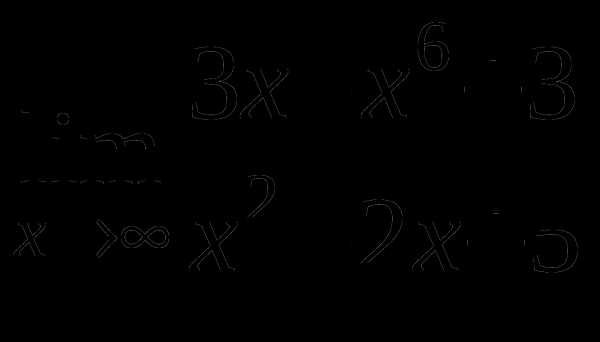
г)
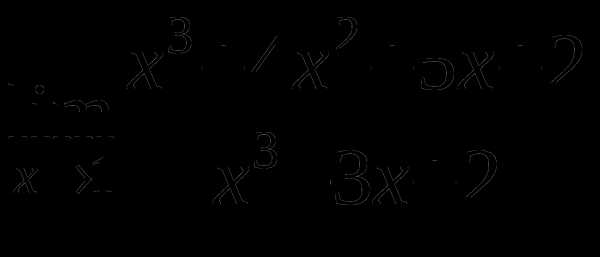
д)
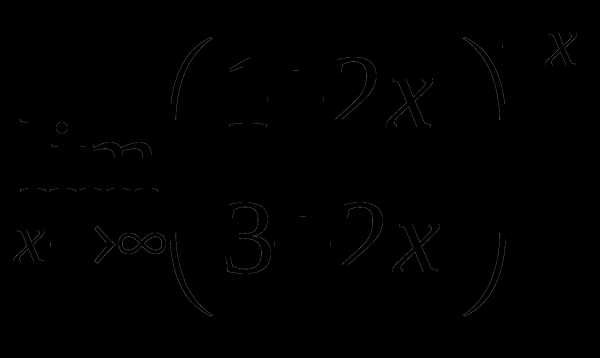
е)
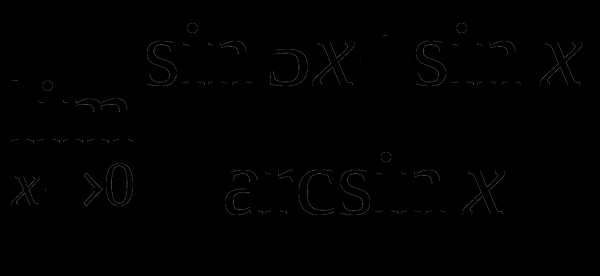
Контрольная работа № 5
Найти предел функции
7
а)
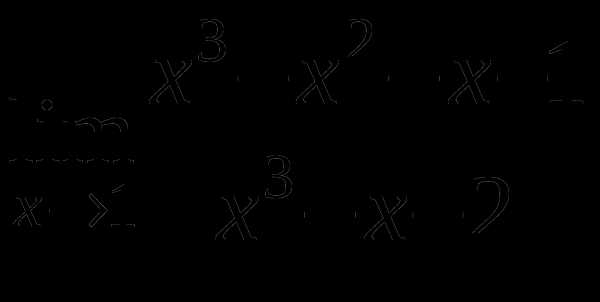
б)
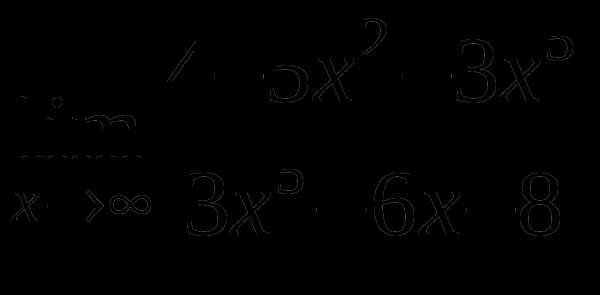
в)
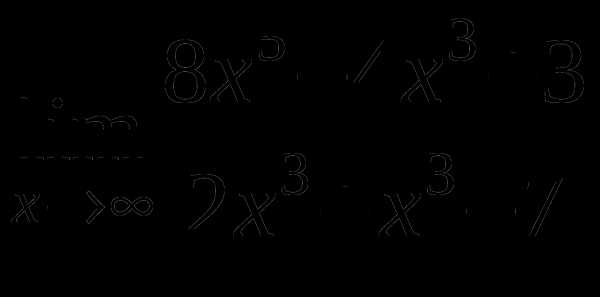
г)
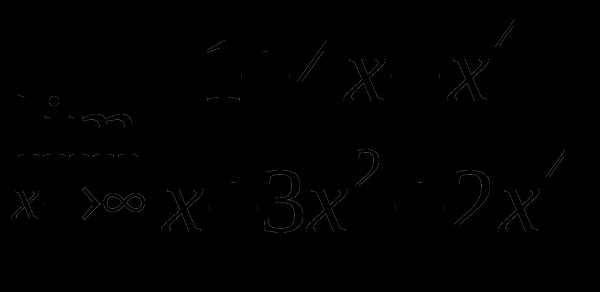
д)
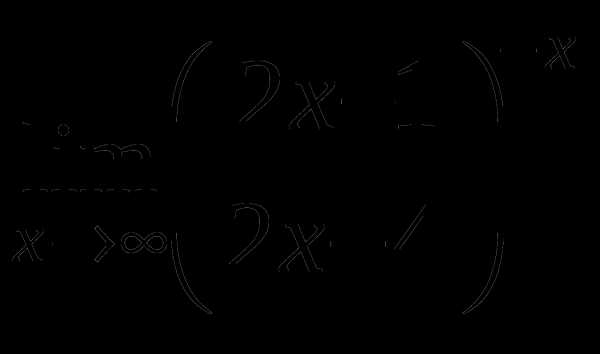
е)
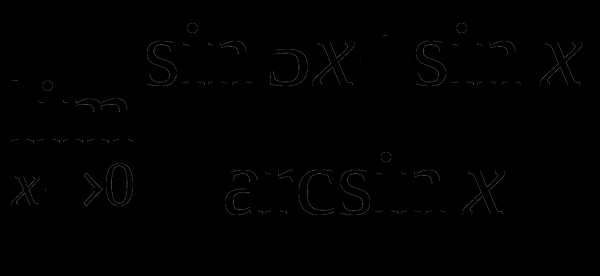
Найти предел функции
8
а)
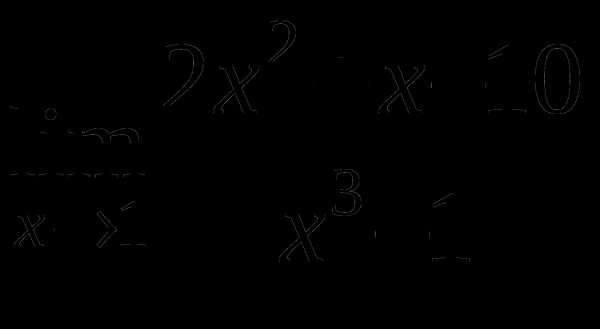
б)
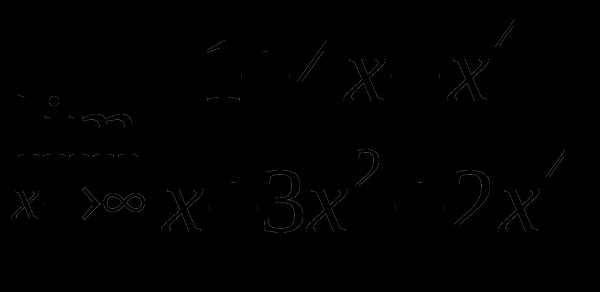
в)
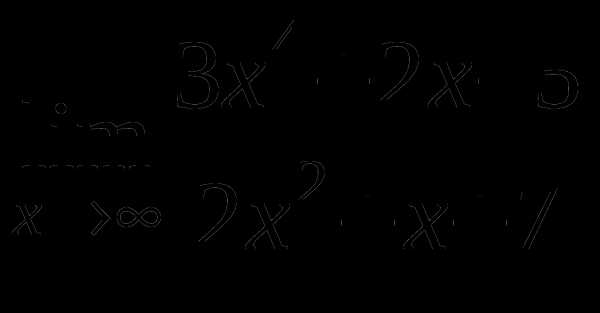
г)
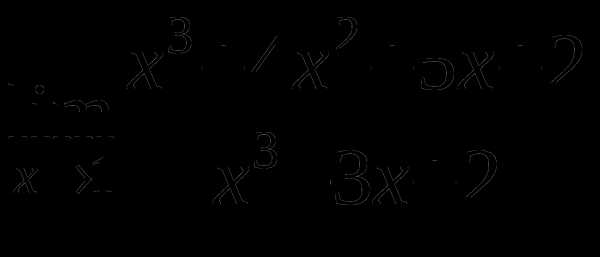
д)
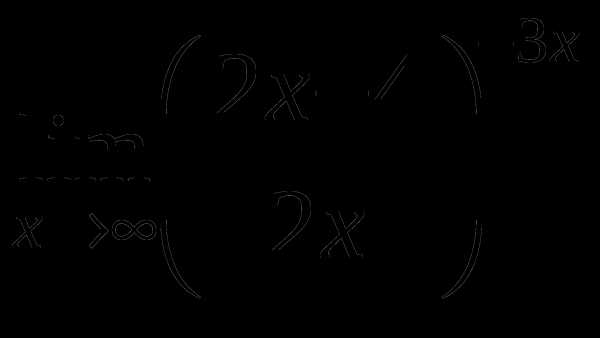
е)
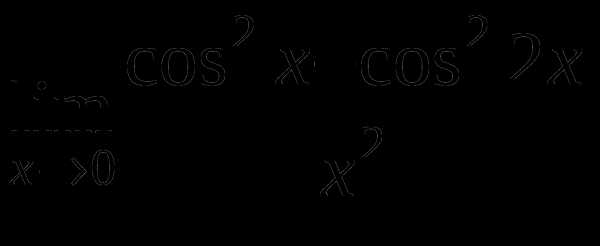
Найти предел функции
9
а)
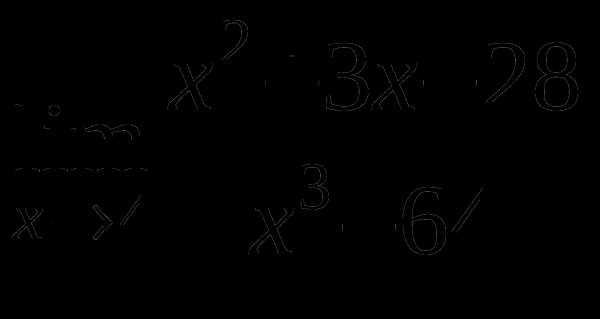
б)
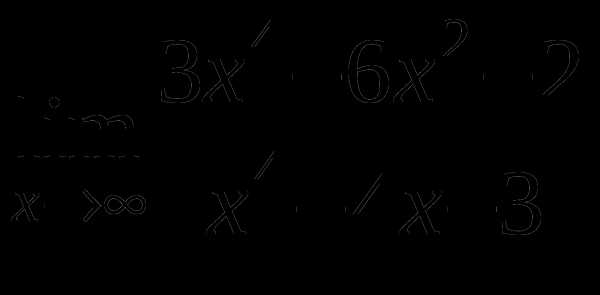
в)
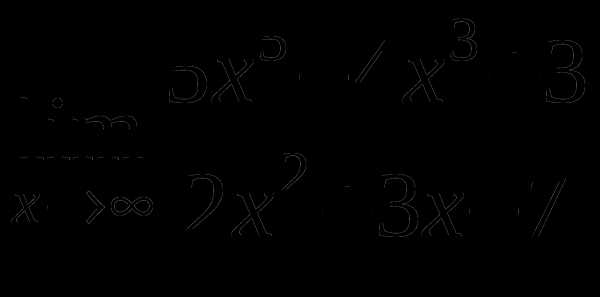
г)
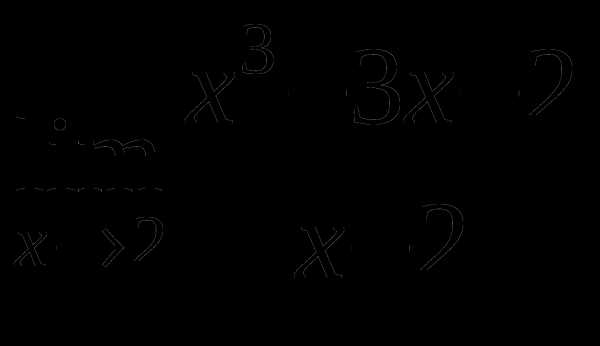
д)
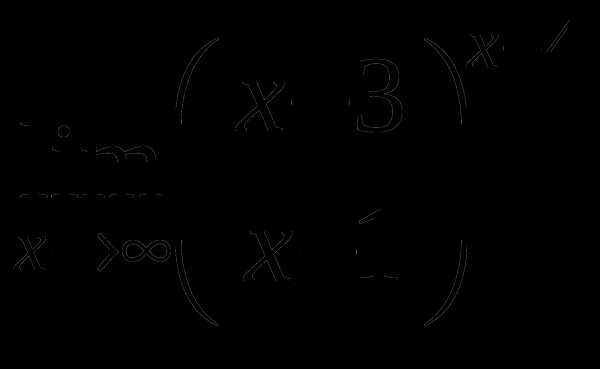
е)
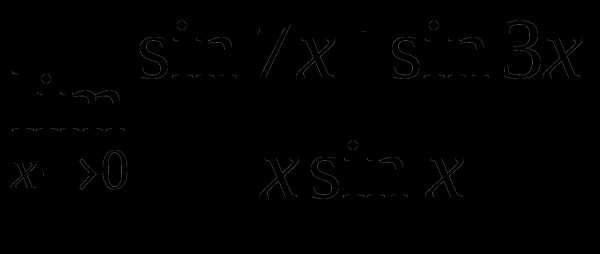
Контрольная работа № 5
Найти предел функции
10
а)
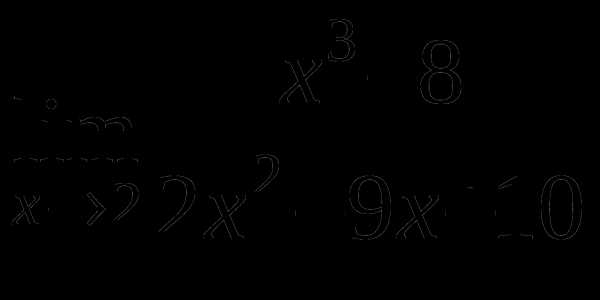
б)
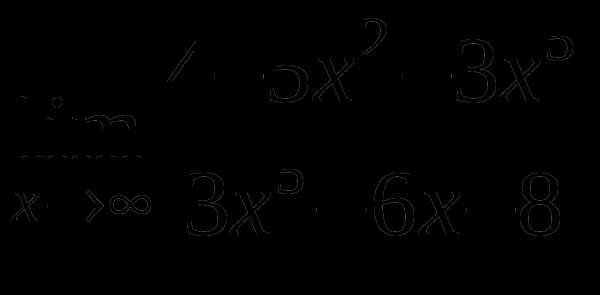
в)
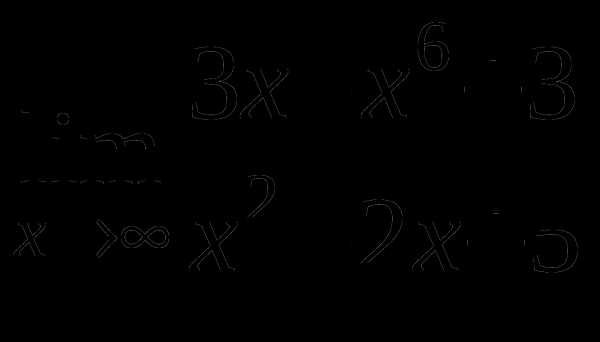
г)
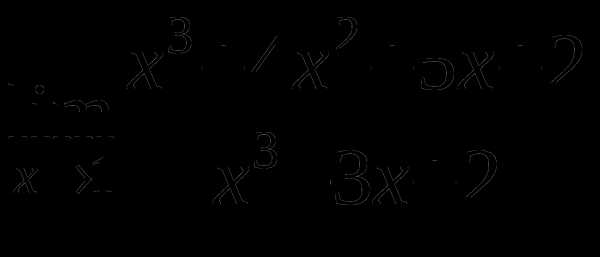
д)
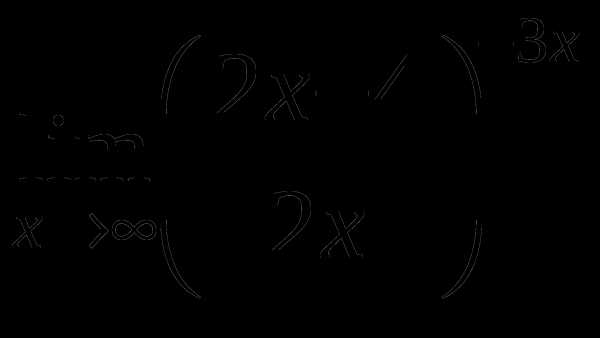
е)
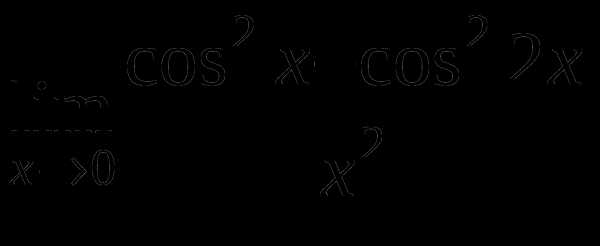
Найти предел функции
11
а)
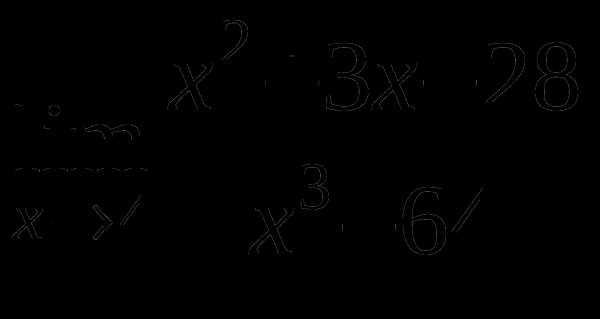
б)
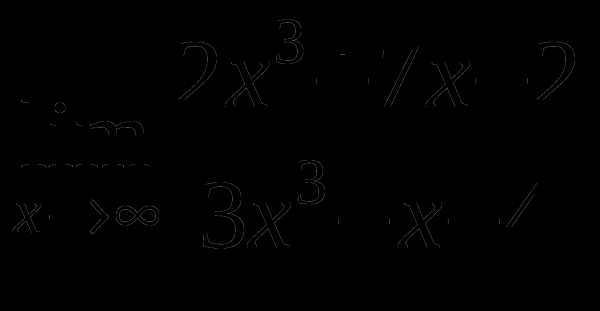
в)
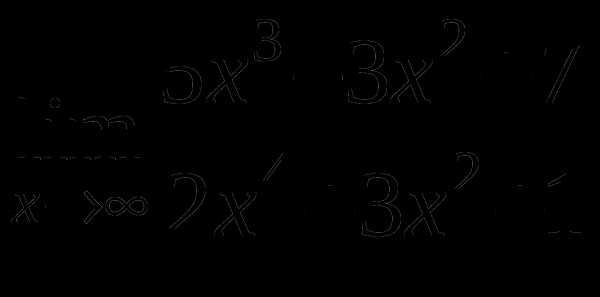
г)
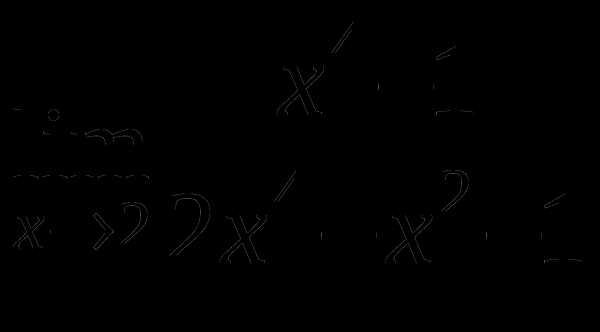
д)
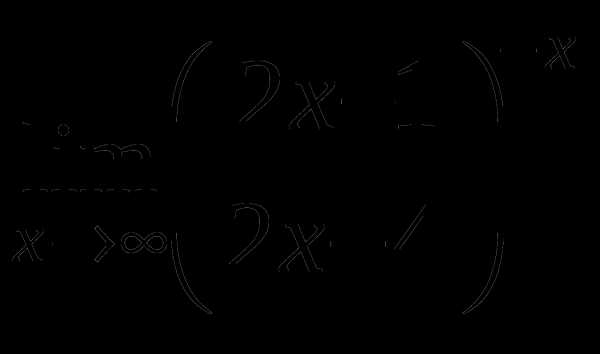
е)
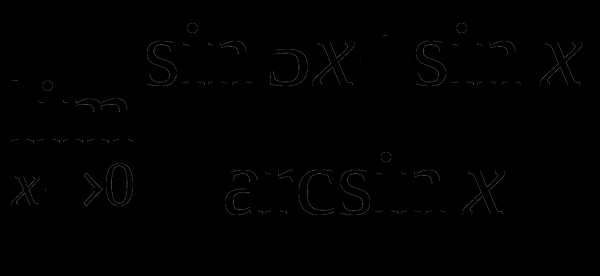
Найти предел функции
12
а)
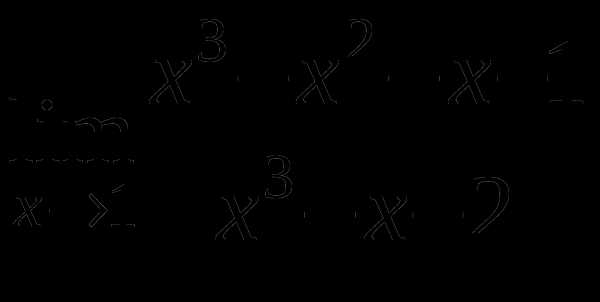
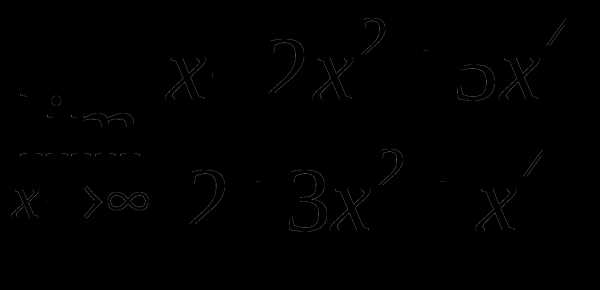
в)
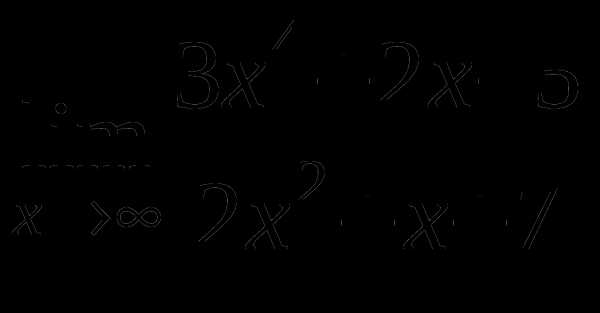
г)
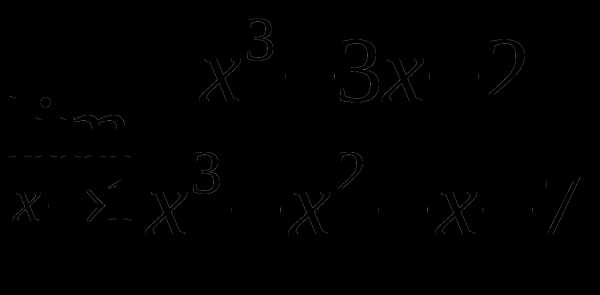
д)
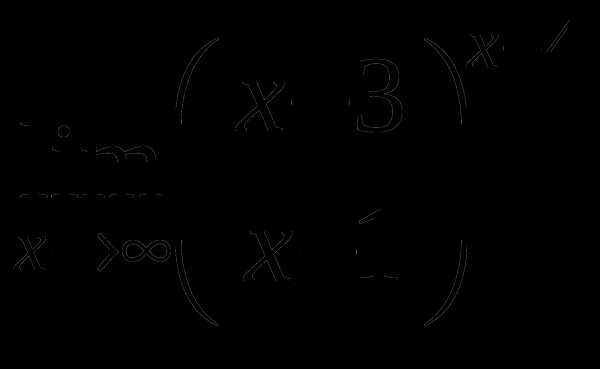
е)
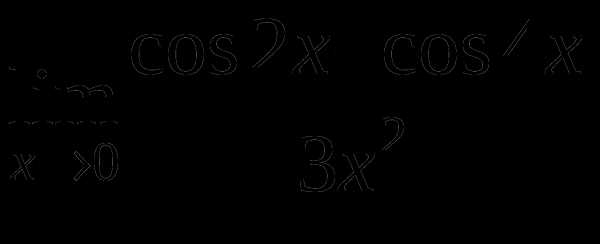
Контрольная работа № 5
Найти предел функции
13
а)
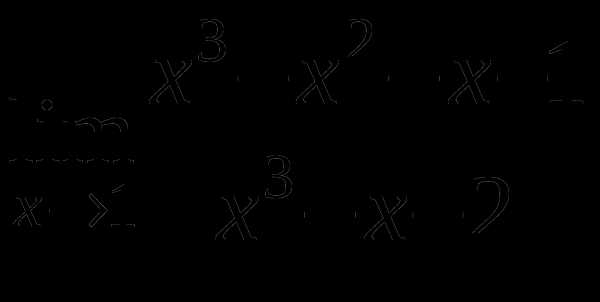
б)
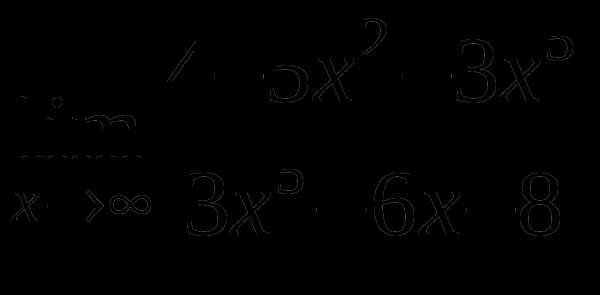
в)
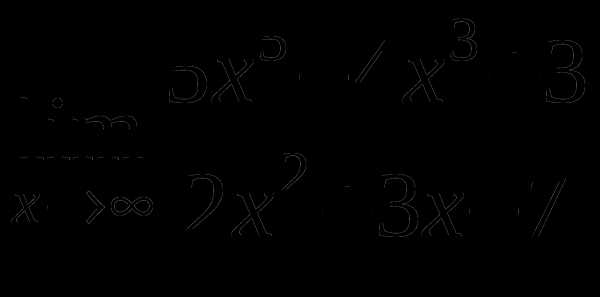
г)
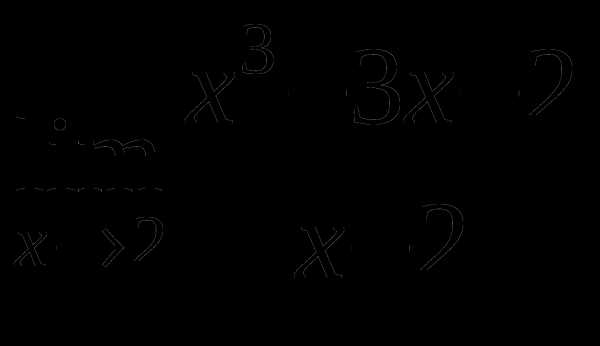
д)
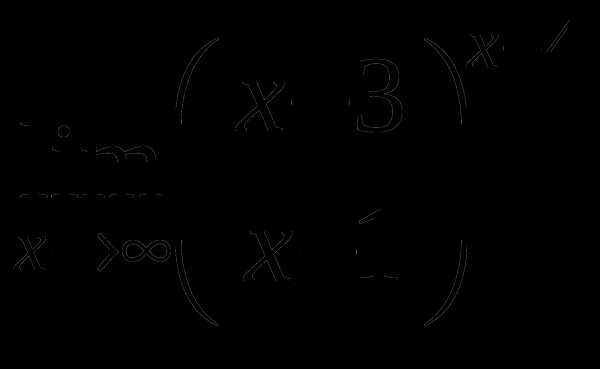
е)
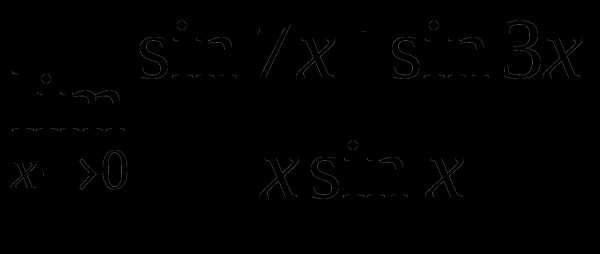
Найти предел функции
14
а)
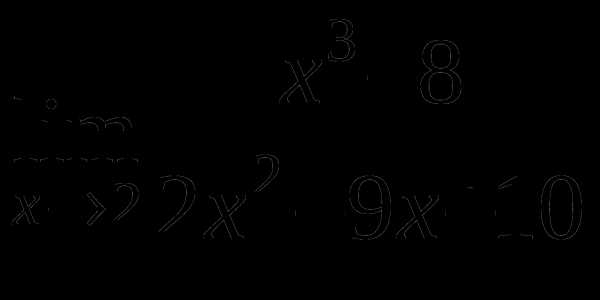
б)
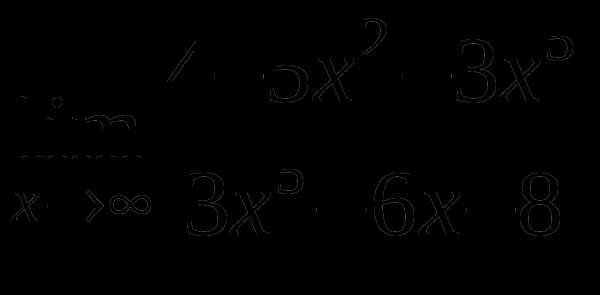
в)
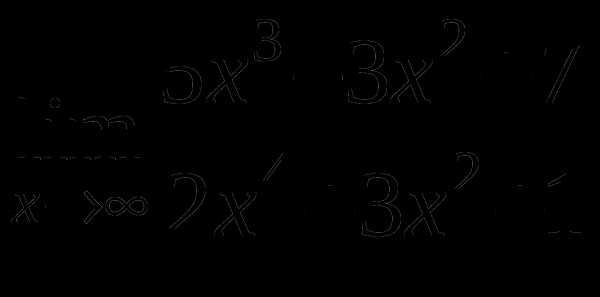
г)
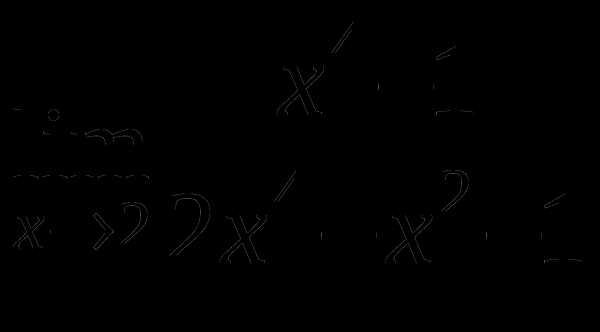
д)
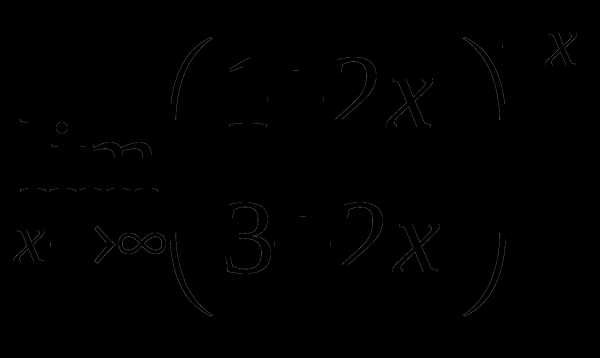
е)
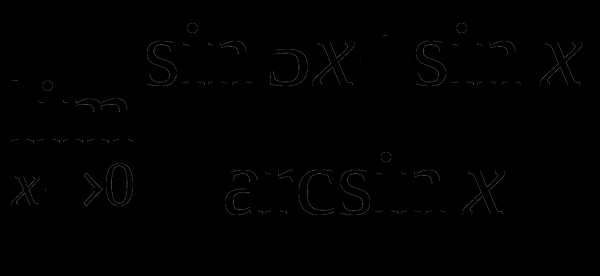
Найти предел функции
15
а)
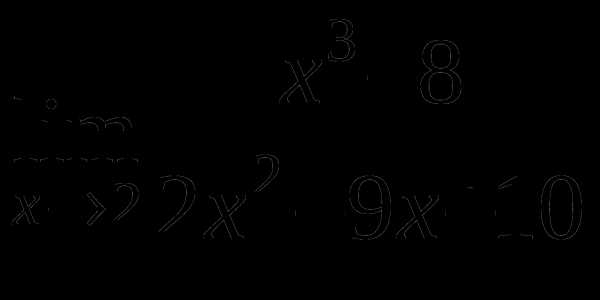
б)
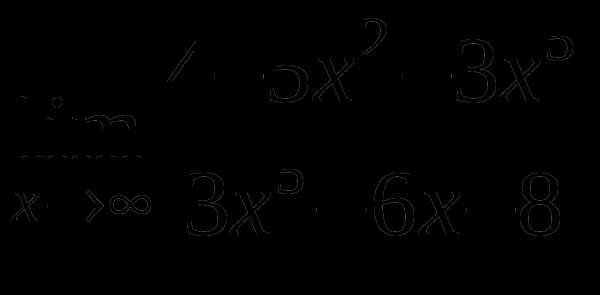
в)
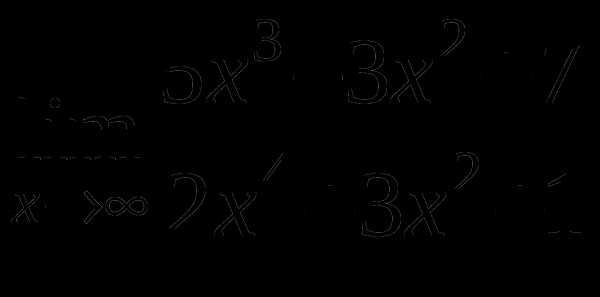
г)
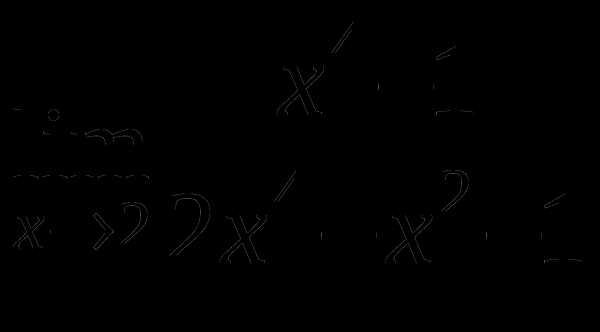
д)
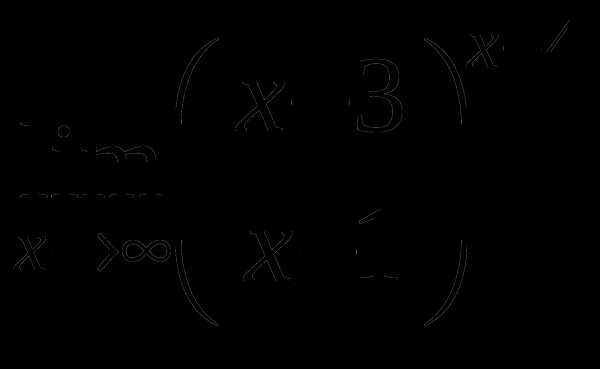
е)
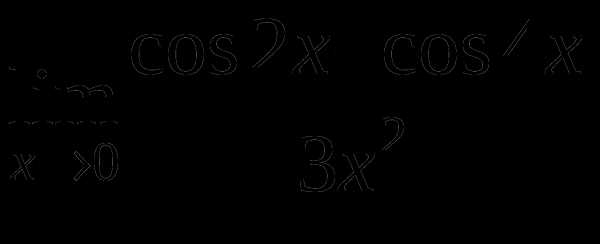
Контрольная работа № 5
Найти предел функции
16
а)
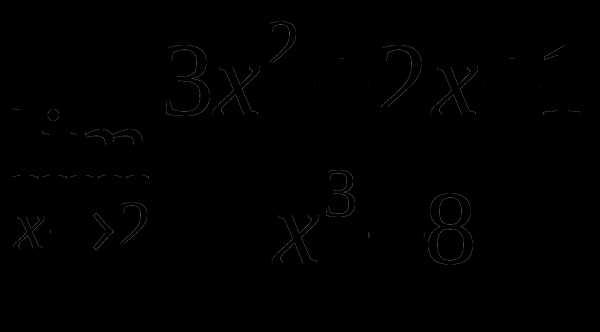
б)
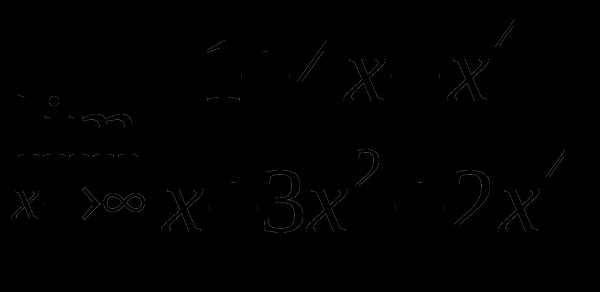
в)
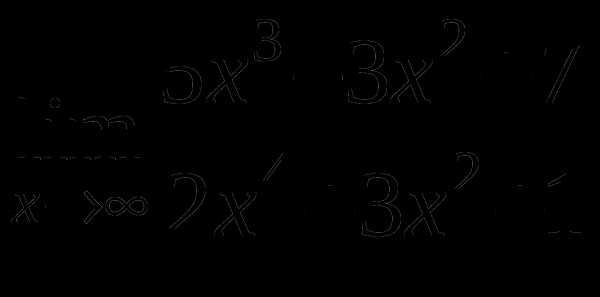
г)
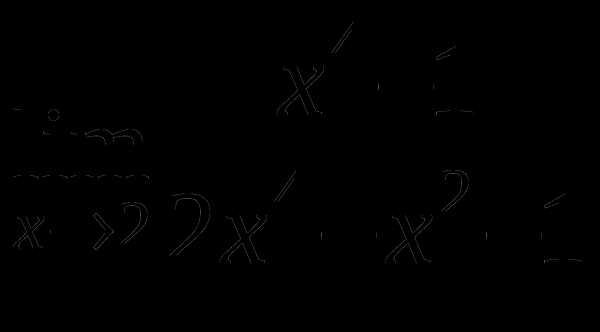
д)
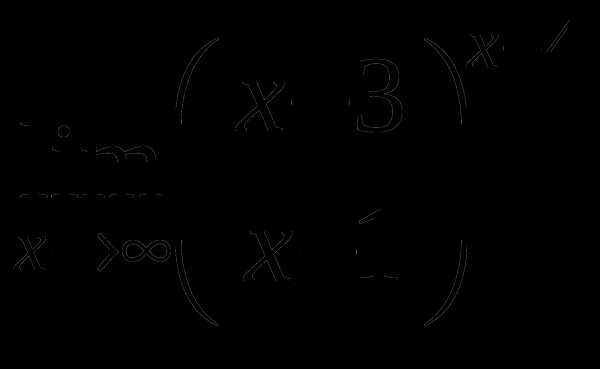
е)
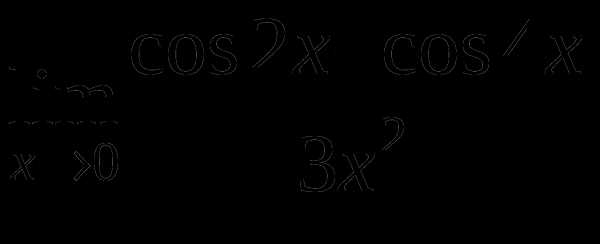
Найти предел функции
17
а)
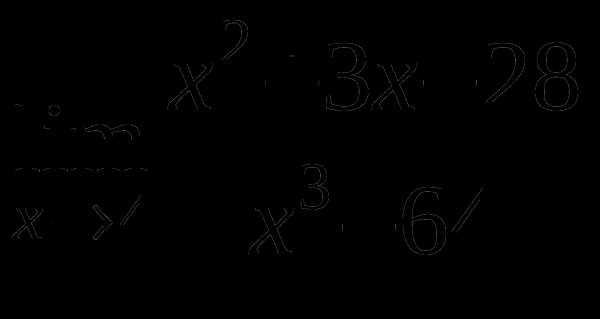
б)
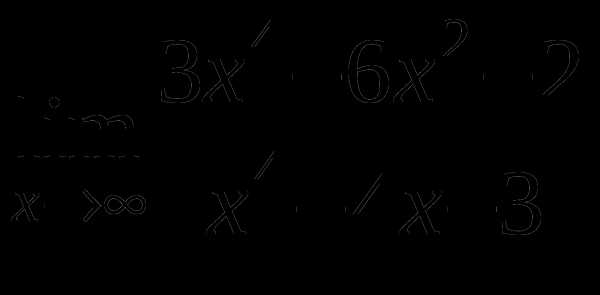
в)
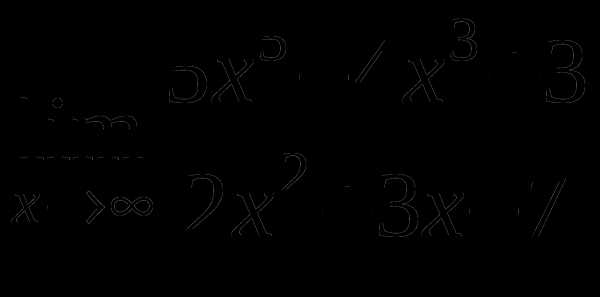
г)
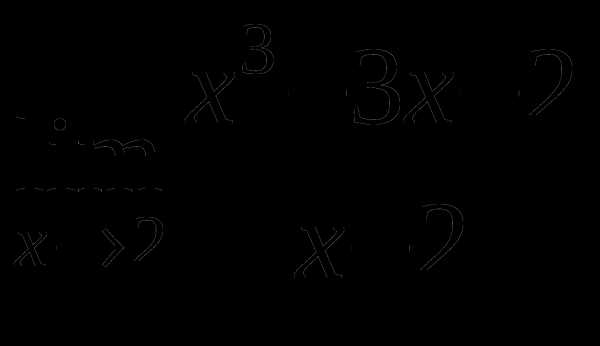
д)
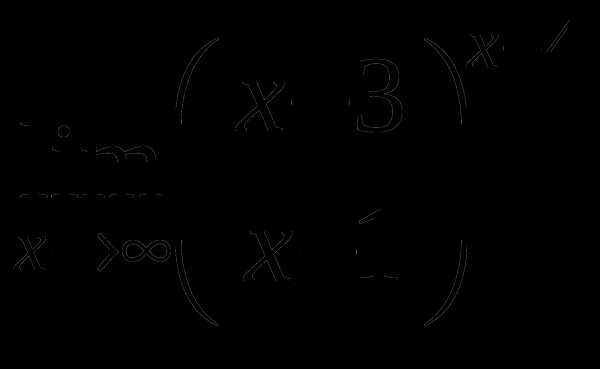
е)
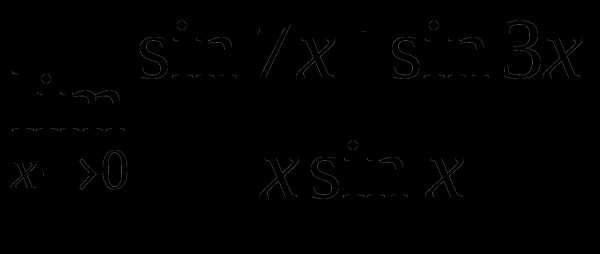
Найти предел функции
18
а)
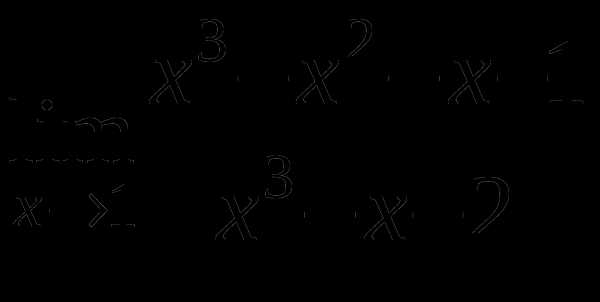
б)
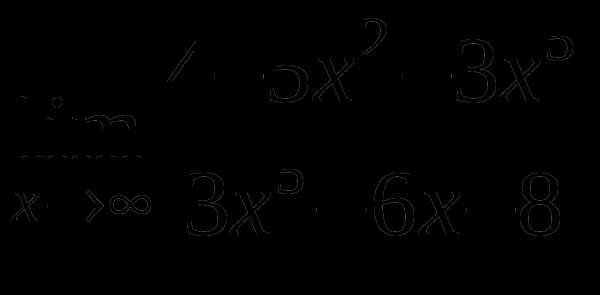
в)
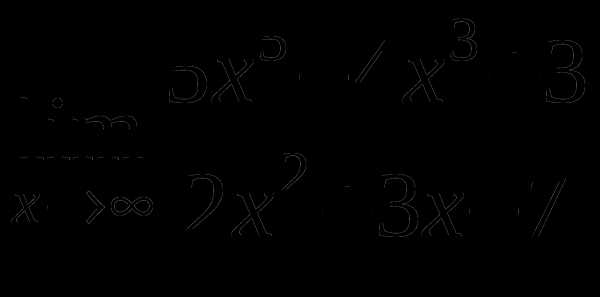
г)
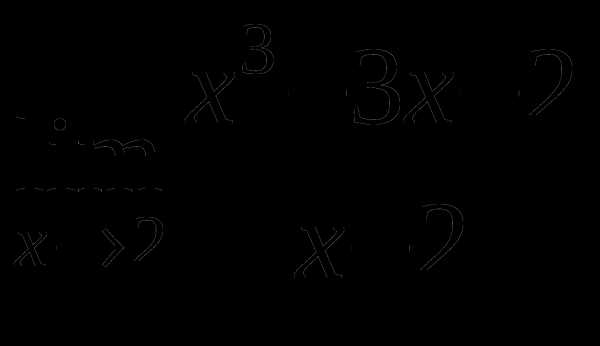
д)
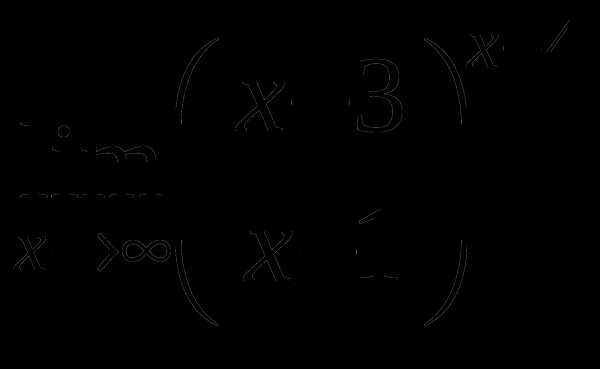
е)
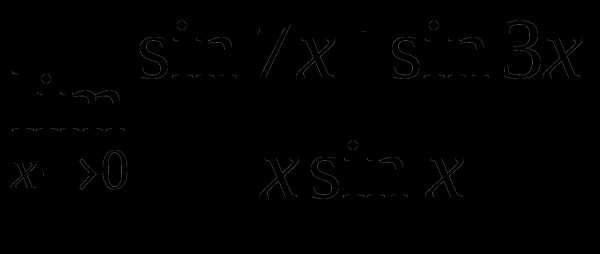
Контрольная работа № 5
Найти предел функции
19
а)
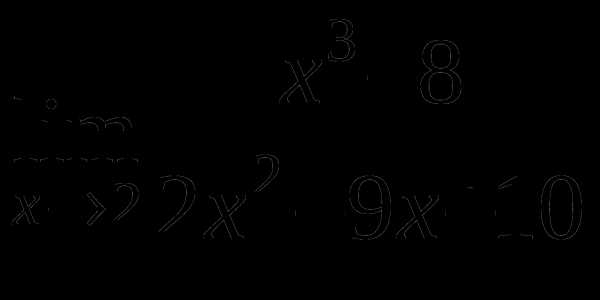
б)
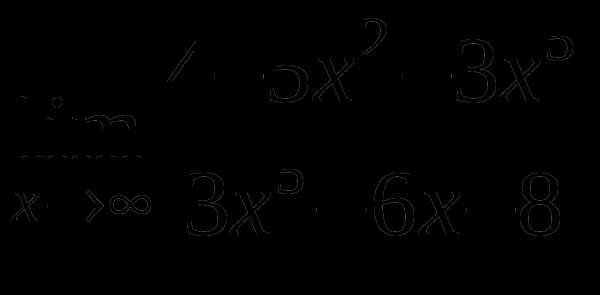
в)
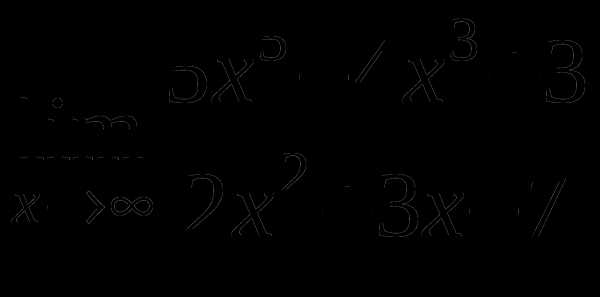
г)
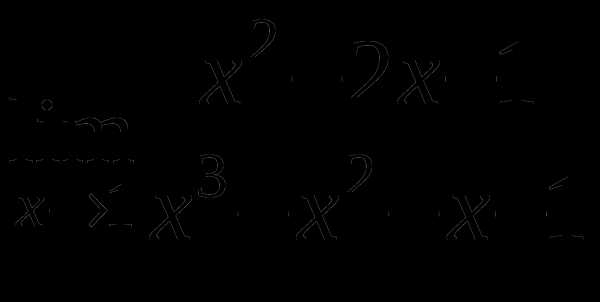
д)
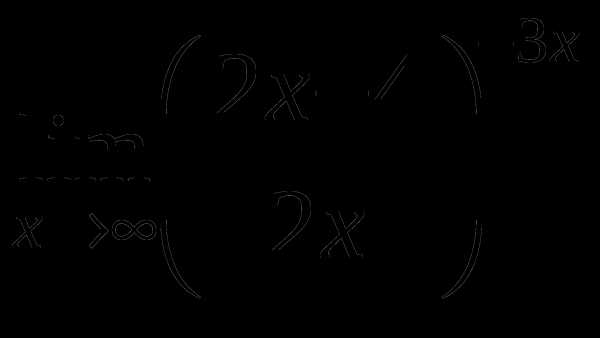
е)
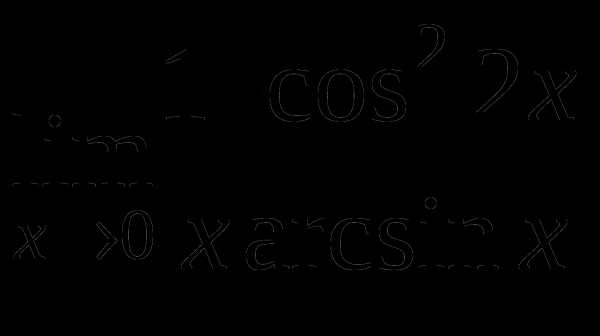
Найти предел функции
20
а)
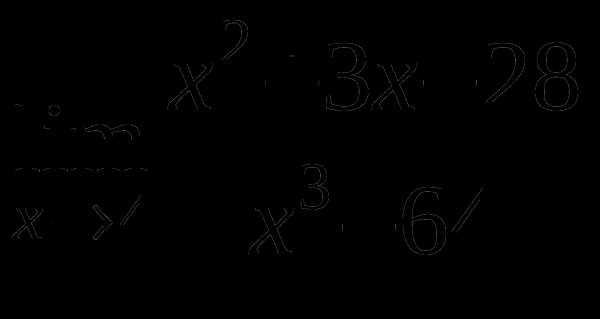
б)
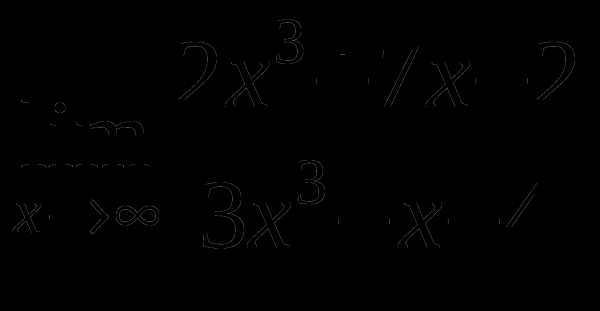
в)
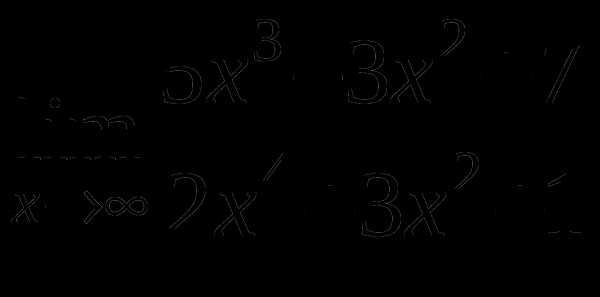
г)
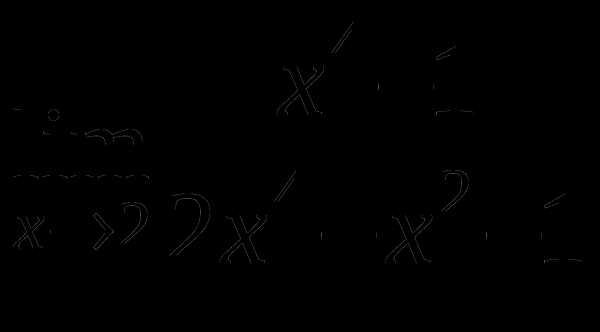
д)
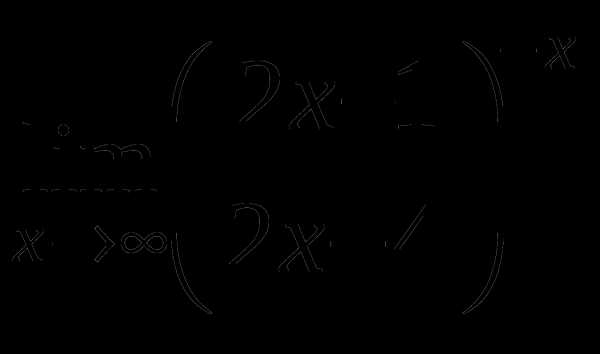
е)
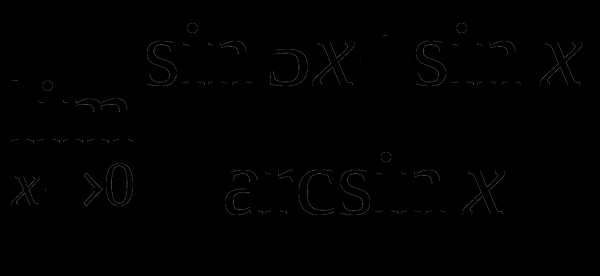
infourok.ru
Контрольная работа № 1 на тему «Пределы функции», ФГОС
Наименование: Контрольная работа №.1.
Учебная дисциплина: математика
Группы: РН-02, ТОЭ-02.
1 вариант.
Вычислить пределы функций:
1. 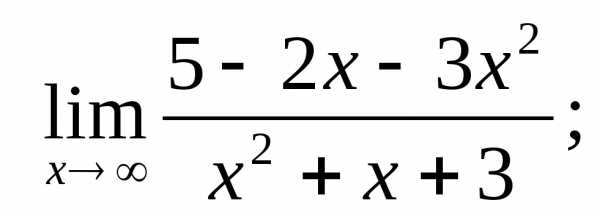
2. 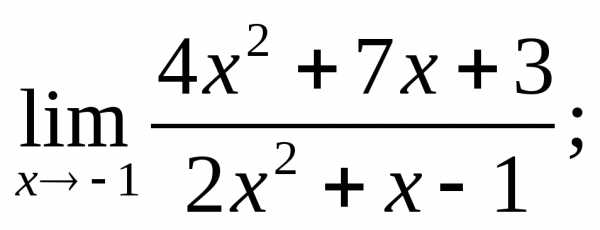
3.
4. 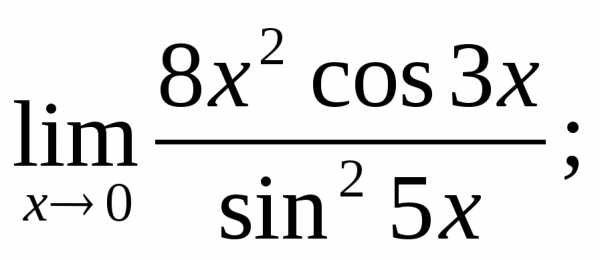
5. 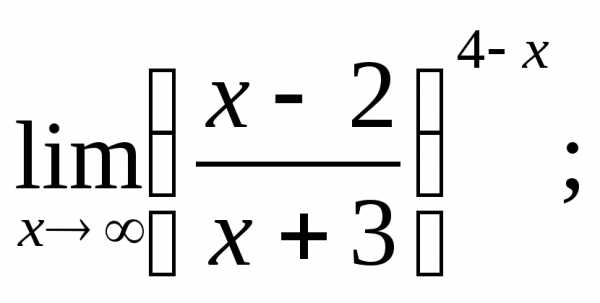
2 вариант.
Вычислить пределы функций:
1. 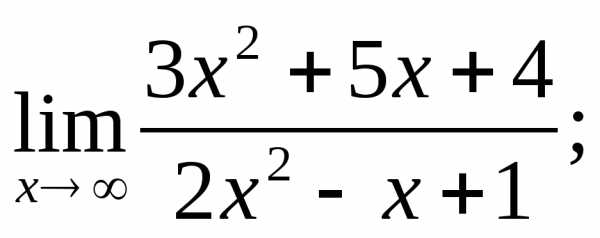
2. 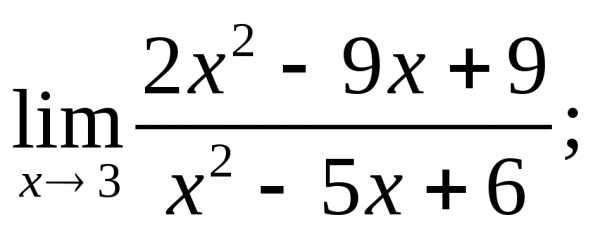
3.
4. 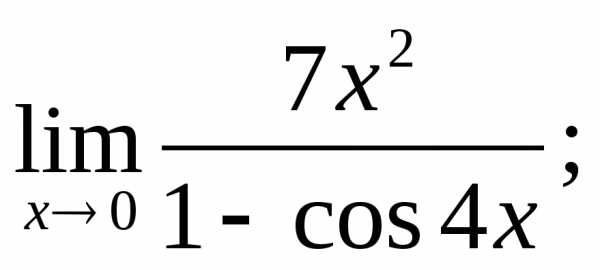
5. 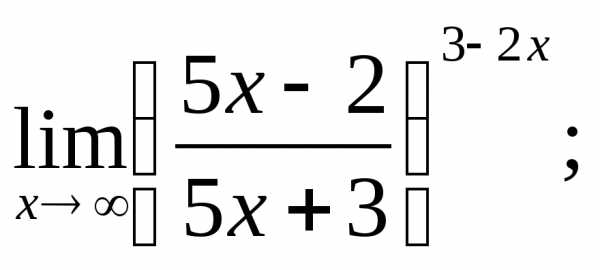
Наименование: Контрольная работа №.1.
Учебная дисциплина: математика
Группы: РН-02, ТОЭ-02.
3 вариант.
Вычислить пределы функций:
1. 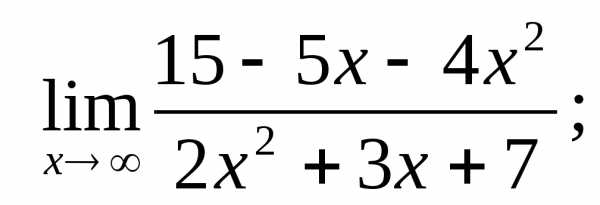
2. 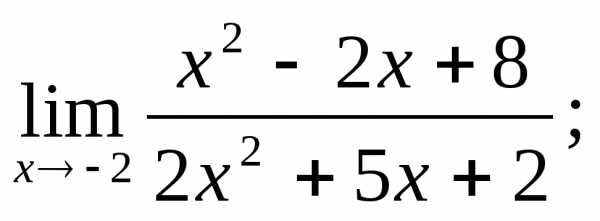
3. 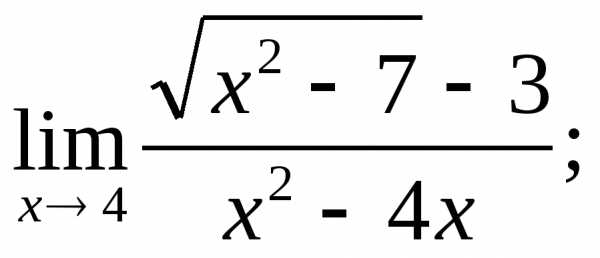
4. 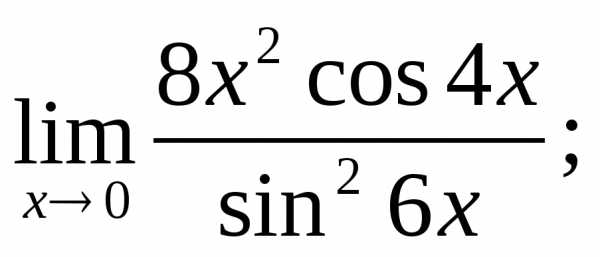
5. 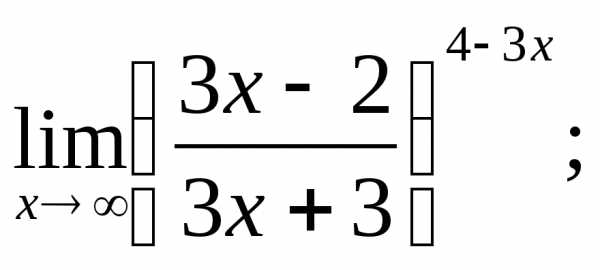
4 вариант.
Вычислить пределы функций:
1. 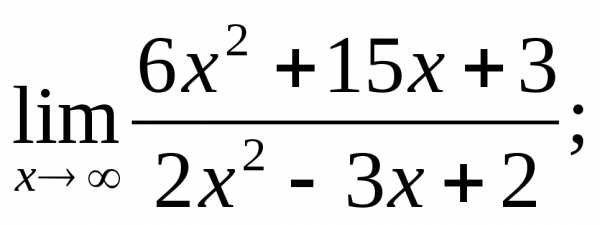
2. 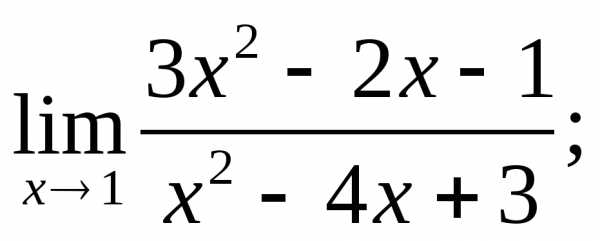
3. 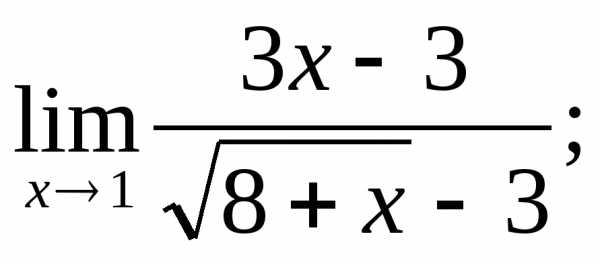
4. 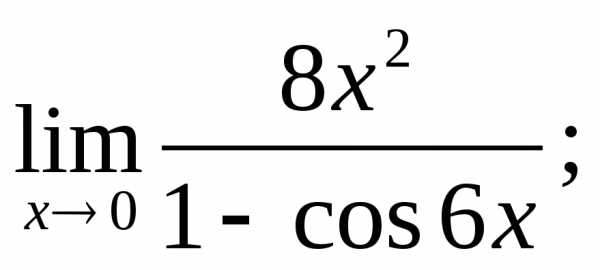
5. 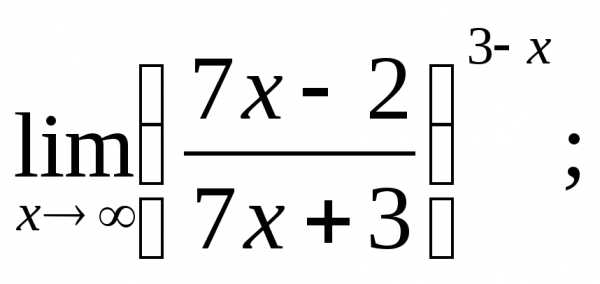
xn--j1ahfl.xn--p1ai
1 СЕМЕСТР. Контрольная работа 1 теме: «Предел функции».
Вопросы для экзамена 1-й курс (1-й семестр)
Вопросы для экзамена 1-й курс (1-й семестр) 1. Определения основных операций над множествами. 2. Законы дистрибутивности для операций над множествами. 3. Произведение множеств, простейшие свойства произведений
ПодробнееБалльно — рейтинговая система
7 «Архитектура» семестр Очная форма обучения. Бакалавры. I курс, семестр. Направление 7 «Архитертура». Дисциплина — «Математика» Содержание Содержание… Балльно — рейтинговая система… Самостоятельная
ПодробнееВсего 66 вопросов. 1 год обучения. Модули 1 2.
ВОПРОСЫ И ТИПОВЫЕ ЗАДАЧИ к итоговому экзамену по дисциплине «Математический анализ» Прикладная математика На устном экзамене студент получает два теоретических вопроса и две задачи Всего 66 вопросов год
ПодробнееI. Цель и задачи курса
Аннотация дисциплины «Математический анализ» Направления подготовки: 01.03.02 «Прикладная математика и информатика» Профиль подготовки: Системное программирование и компьютерные технологии» Квалификация
ПодробнееМатематика для направления торговое дело
Математика для направления 8..6 торговое дело Контрольные вопросы по курсу Математика семестр. п мерные векторы. п мерное векторное пространство.. Матрицы. Линейные операции над матрицами. Умножение матриц..
ПодробнееОГЛАВЛЕНИЕ. Предисловие… 15
ОГЛАВЛЕНИЕ Предисловие… 15 Глава I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 1. Матрицы… 16 1.1. Основные понятия… 16 1.2. Действия над матрицами… 17 2. Определители… 20 2.1. Основные понятия… 20 2.2. Свойства
ПодробнееМатематический анализ
1. Цель и задачи дисциплины Математический анализ Целью освоения дисциплины «Математический анализ» является формирование у будущих специалистов знаний и умения применять математический аппарат и математические
ПодробнееРАБОЧАЯ ПРОГРАММА дисциплины
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ» ИНСТИТУТ КИБЕРНЕТИКИ, ИНФОРМАТИКИ
ПодробнееМАТЕМАТИЧЕСКИЙ АНАЛИЗ
Государственное автономное образовательное учреждение высшего профессионального образования города Москвы «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ИНДУСТРИИ ТУРИЗМА ИМЕНИ ЮАСЕНКЕВИЧА» МАТЕМАТИЧЕСКИЙ АНАЛИЗ
ПодробнееМатематический анализ
Федеральное государственное образовательное учреждение высшего профессионального образования «ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ» (ФИНУНИВЕРСИТЕТ) Кафедра «Математика» ГАПостовалова
ПодробнееПредел. Непрерывность.
Функция. 1 1. Какие числа образуют множество действительных чисел? 2. Что называется числовой осью? 3. Что называется интервалом? 4. Определить понятие окрестности точки. 5. Что называется абсолютной величиной?
Подробнее1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
2 3 1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА В связи с возросшей ролью математики в современной науке и технике будущие экологи, инженеры нуждаются в серьезной математической подготовке. Изучение математики развивает
ПодробнееА Н Н О Т А Ц И Я Р А Б О Ч Е Й П Р О Г Р А М М Ы
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»
ПодробнееГлава 4. Функции одной переменной 69
ОГЛАВЛЕНИЕ Предисловие 3 Введение 5 Часть первая. Математический анализ функций одной переменной 10 Глава I. Вещественные числа 10 1. Множества. Обозначения. Логические символы 10 2. Вещественные числа
Подробнее1. Цели и задачи дисциплины
. Цели и задачи дисциплины Целями освоения дисциплины «Математический анализ» являются: — получение базовых знаний и формирование основных навыков по математическому анализу, необходимых для решения задач,
ПодробнееАННОТАЦИЯ РАБОЧЕЙ ПРОГРАММЫ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждениевысшего образования «УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
ПодробнееВопросы и задачи к экзамену 1 семестр
Направление: «Строительство» Вопросы и задачи к экзамену семестр. Матрицы: определение, виды. Действия с матрицами: транспонирование, сложение, умножение на число, умножение матриц. 2. Элементарные преобразования
ПодробнееТема 1. Предел и непрерывность функции
Уметь: Тема 1. Предел и непрерывность функции Вычислять пределы функций и числовых последовательностей, используя различные приемы, в том числе, замечательные пределы, проводить сравнение бесконечно малых
Подробнее2 ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
2 ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Учебная программа по дисциплине «Математический анализ» разработана для специальности «Прикладная информатика» шифр 1-31 03 07-03 высших учебных заведений. Целью изучения дисциплины
ПодробнееАлгебра и начала анализа, ХI
Алгебра и начала анализа, ХI АЛГЕБРА И НАЧАЛА АНАЛИЗА По Положению о государственной (итоговой) аттестации выпускников XI(XII) классов общеобразовательных учреждений Российской Федерации учащиеся сдают
ПодробнееМатематический анализ
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Воронежский государственный аграрный университет имени императора
ПодробнееЛ.В. Липагина, Е.В. Маевский, П.В. Ягодовский
Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ» (ФИНАНСОВЫЙ УНИВЕРСИТЕТ) Кафедра «Математика-1»
ПодробнееЛ.В. Липагина, Е.В. Маевский, П.В. Ягодовский
Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ» (ФИНАНСОВЫЙ УНИВЕРСИТЕТ) Кафедра «Математика-»
Подробнее3. Используемые методы обучения
3.2 МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПРЕПОДАВАТЕЛЯМ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ Семестр I Раздел 1. Векторная и линейная алгебра. Практическое занятие 1 1. Цель: Рассмотреть задачи на вычисление определителей второго
Подробнее1. ЦЕЛЬ И ЗАДАЧИ ДИСЦИПЛИНЫ
2 1. ЦЕЛЬ И ЗАДАЧИ ДИСЦИПЛИНЫ Целью дисциплины является формирование представлений о понятиях и методах математического анализа, его месте и роли в системе математических наук, использовании в естественных
ПодробнееМАТЕМАТИЧЕСКИЙ АНАЛИЗ
СЫКТЫВКАРСКИЙ ЛЕСНОЙ ИНСТИТУТ Кафедра высшей математики МАТЕМАТИЧЕСКИЙ АНАЛИЗ САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ Методические указания для подготовки дипломированных специалистов по направлению 654700 «Информационные
ПодробнееАбсолютная величина числа. 21, 27
МАТЕМАТИЧЕСКИЙ АНАЛИЗ Ориентировочный план семинаров, 1 семестр 1. Вещественные числа. 1.1. Аксиоматика вещественных чисел. «Школьное» представление о числе как модель поля действительных чисел. 33 1.2.
Подробнееdocplayer.ru
контрольная работа №2 1 курс 1 семестр
1
Контрольная работа №2
Задание 67
Найдите пределы последовательностей.
а) б)
в)
Решение
а) Имеем неопределенность типа , чтобы избавиться от нее проведем преобразование выражения:
Разделим числитель и знаменатель на n3:
=
б) Имеем неопределенность типа , чтобы избавиться от нее проведем преобразование выражения:
Разделим числитель и знаменатель на n3:
в) Здесь имеет место неопределенность вида . Преобразуем выражение и воспользуемся вторым замечательным пределом.
Ответ: а) 0; б) ; в) е — 2
Задание 77
Найдите производную заданных функций:
а) б)
Решение
а)
Воспользуемся правилом дифференцирования сложных функций
(vn)’ = n vn — 1 v ‘, где v = 2х3 + x в одном случае и v = — в другомслучае. Получаем:
Воспользуемся правилом дифференцирования сложной функций
(arctg u)′ = -, гдеu =. Получим
Воспользуемся правилом дифференцирования сложной функций
, где :
б)
Воспользуемся правилом дифференцирования сложной функций
, где в одном случае, и- в другом случае. Получим

Ответ: а) ; б)
Задание 87
Найдите предел функции :
1) не пользуясь правилом Лопиталя;
2) используя правило Лопиталя.
Решение
При непосредственной подстановке в выражение значения x = 1 получаем неопределенность. Чтобы избавиться от нее, преобразуем выражение и воспользуемся первым замечательным пределом .
Введем замену переменной:
x = t, x = 1 – t, ,t 0 при х 1.
Так как имеем неопределенность, воспользуемся правилом Лопиталя:
Ответ :
Задание 97
Дана функция .
1) вычислите все частные производные первого порядка;
2) найдите производную в точке М0 (2; 1; 1) по направлению вектора
;
3) найдите
Решение
1) Находим частные производные функции u= u(x,у):
2) Находим производную по направлению вектора :
Находим направляющие косинусы вектора :
cosα =
cosβ =
cosγ =
Находим значения частных производных в точке М0:
Находим производную по направлению вектора в точке М0 (2; 1; 1):
3) Находим градиент
Ответ: 1)
2) ; 3);
Задание 107
Дана функция . Вычислите значение ее частной производной четвертогопорядка в точке
Решение
Найдем частные производные:
Вычислим значение производной в точке:
Ответ: 36
Задание 107
Найдите неопределенные интегралы:
а) б)в)г)
Решение
а)Преобразуем подинтегральное выражение
Сделаем замену переменной: t = 2x, dt = 2dx, dx = dt/2.
Вернемся к переменной х:
б)
Найдем искомый интеграл методом замены переменной. Введем новую переменную t = sin5x. Тогда dt = 5cos5 dx, cos5 dx = dt/5 Имеем
Вернемся к переменной х:
в)
Применим метод интегрирования по частям, для чего воспользуемся формулой:
Положим u = =3х2 + 2х
Тогда = (3х2 + 2х ) =6x + 2; du = (6x + 2)dх = 2(3x + 1)
Повторным интегрированием по частям найдем интеграл .
3х + 1 = u, du 3dx
Тогда искомый интеграл
=
г)
Умножим числитель и знаменатель на сопряженное знаменателю выражение
:
Полученный интеграл представим в виде двух интегралов:
= ==
Аналогично найдем
= =
Получили
Ответ: а) ; б); в);
г)
studfiles.net
Мат. анализ. Контрольная работа №1 (0 вариант)
Контрольная работа №1
«Введение в математический анализ»
ВАРИАНТ 0
1.2.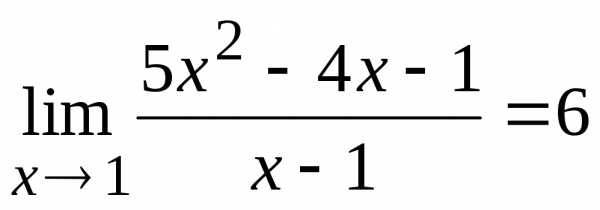
3.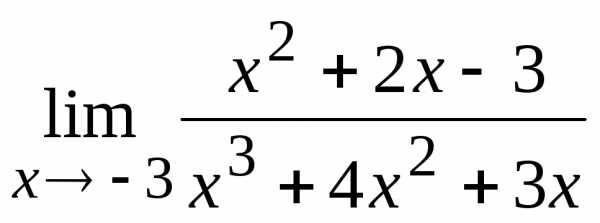 4.
4.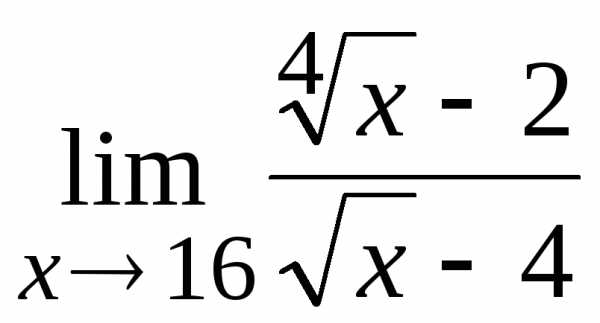 5.
5.
6.7.
8.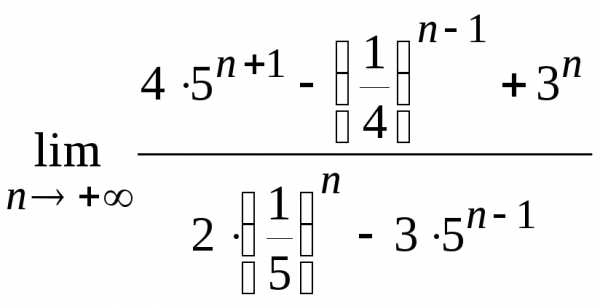 9.
9.
10.
Вычислить односторонние пределы
функции в точках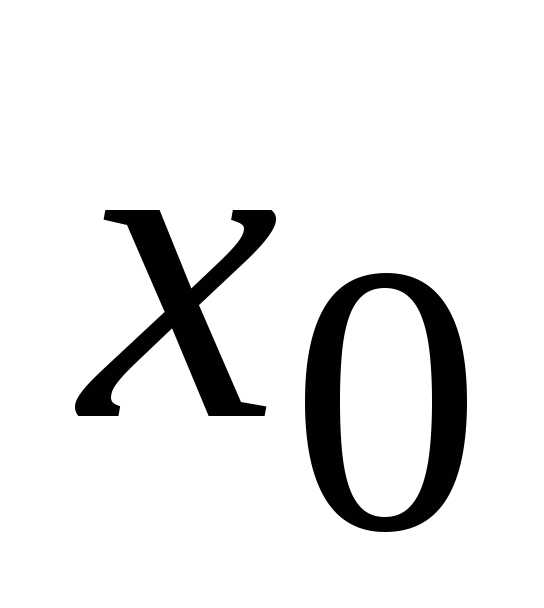 :
:
.
Нарисовать график функции в окрестности этих точек.
11. 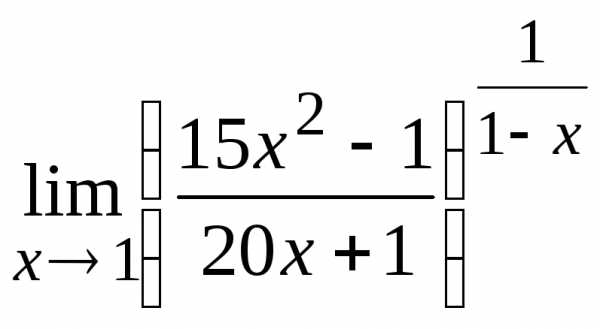 12.
12.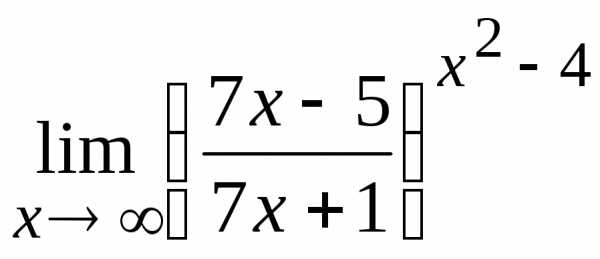
Примеры решения задач
Пример 1.
Доказать, пользуясь определением по Коши предела функции в точке, что .
Решение.
По определению предела функции в точке ( по Коши):
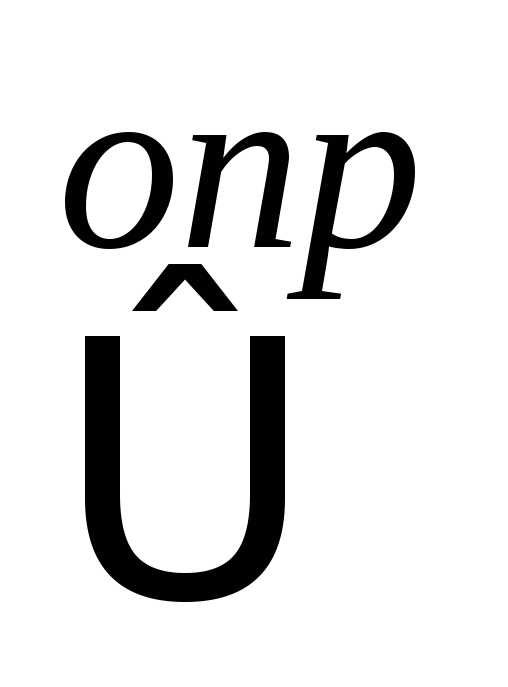 >0>0:x:
0<|x-1|<
>0>0:x:
0<|x-1|<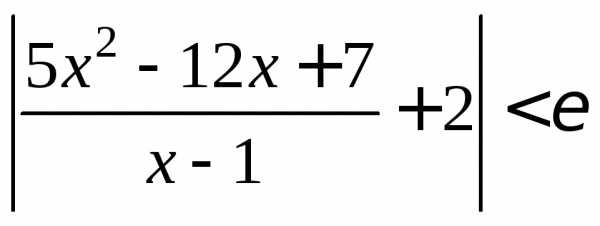 .
.
Выберем произвольное число >0.
Найдем для него число>0,
такое, что для всехх, удовлетворяющих
условию 0<|x-1|<выполнено неравенство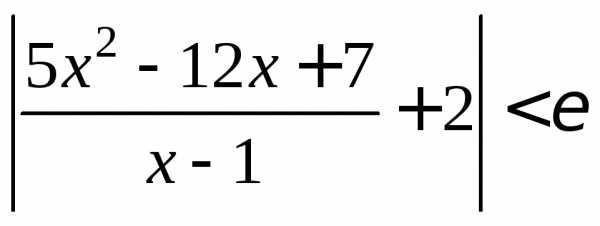 .
Преобразуем левую часть:
.
Преобразуем левую часть:
.
Значит, неравенство 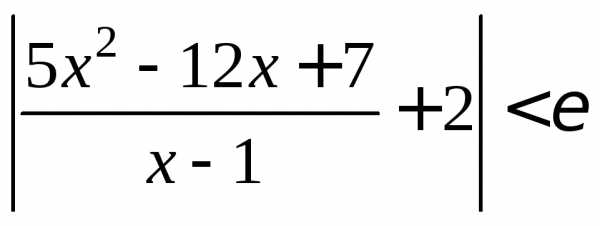 равносильно неравенству
равносильно неравенству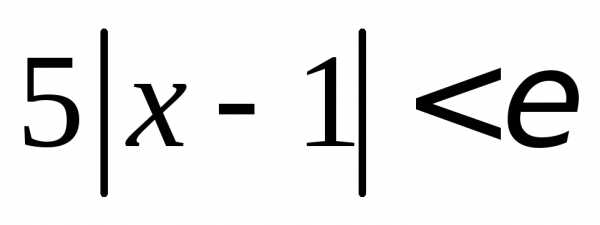 .
Отсюда
.
Отсюда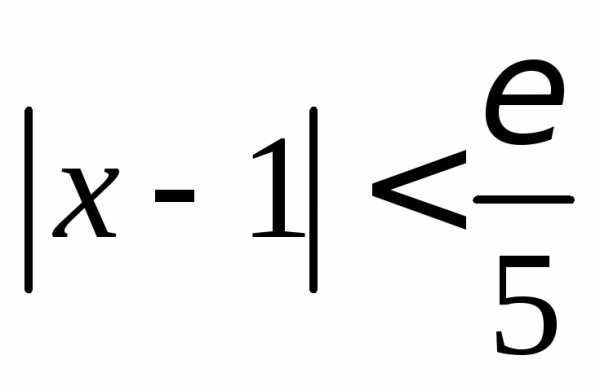 .
Поэтому в качестве можно взять число
.
Поэтому в качестве можно взять число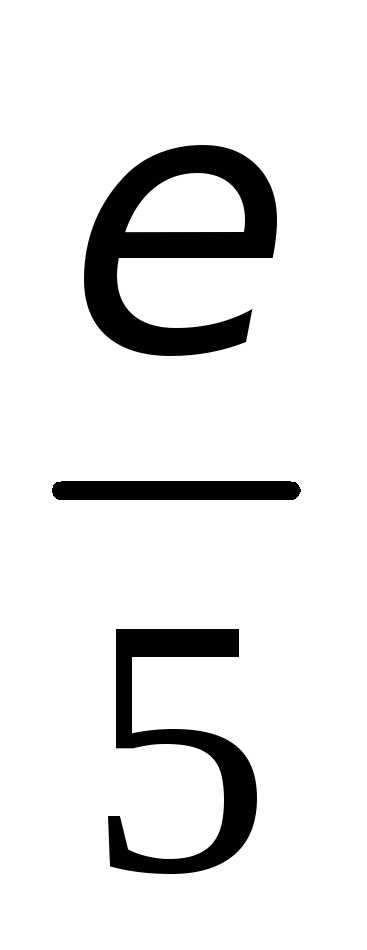 .
При таком из
условия 0<|x-1|<будет следовать неравенство
.
При таком из
условия 0<|x-1|<будет следовать неравенство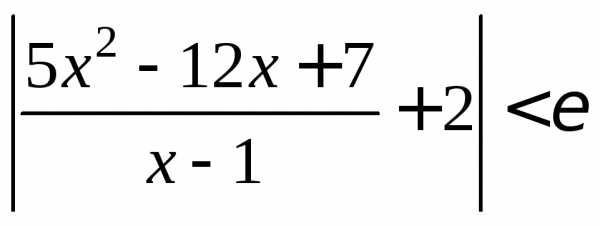 .
.
Таким образом, показано, что >0=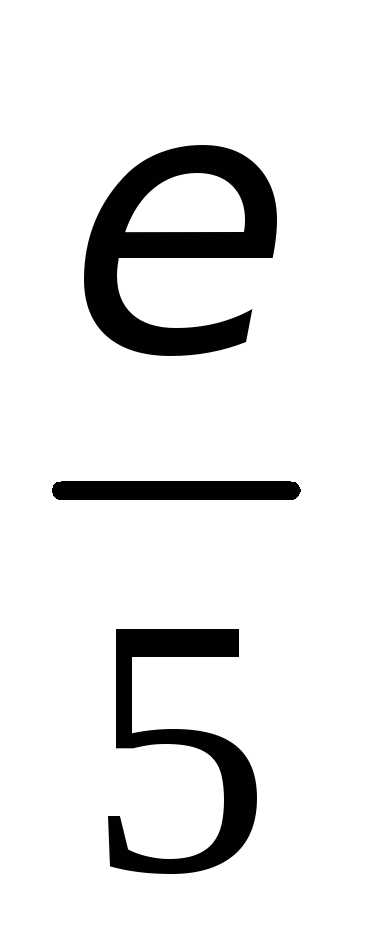 :x:
0<|x-1|<
:x:
0<|x-1|<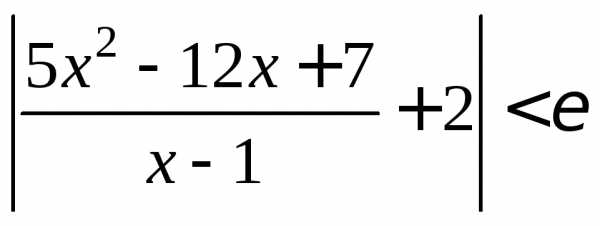 .
Это значит, что.
.
Это значит, что.
Пример 2.
Вычислить предел 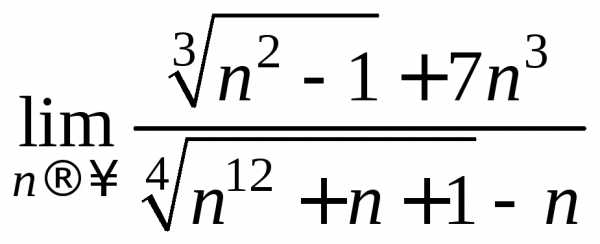 .
.
Решение.
Для раскрытия имеющейся здесь
неопределенности вида  применим следующий прием:разделим
числитель и знаменатель дроби на старшую
степень n. В
данном случае надо разделить наn3.
Получим
применим следующий прием:разделим
числитель и знаменатель дроби на старшую
степень n. В
данном случае надо разделить наn3.
Получим
.
Использовали тот факт, что величины 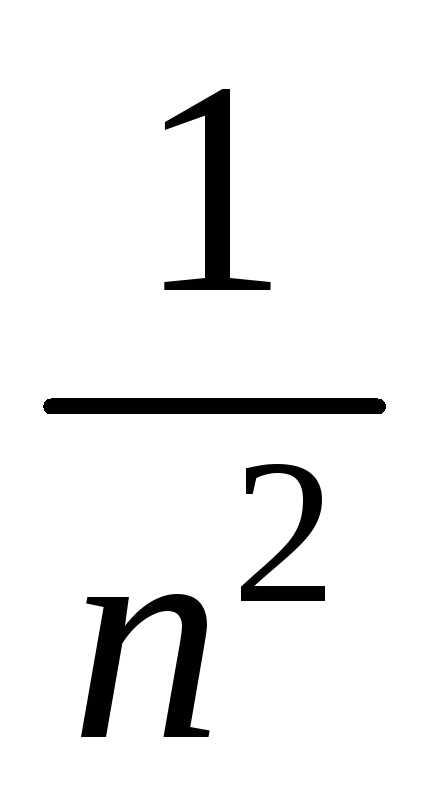 ,
,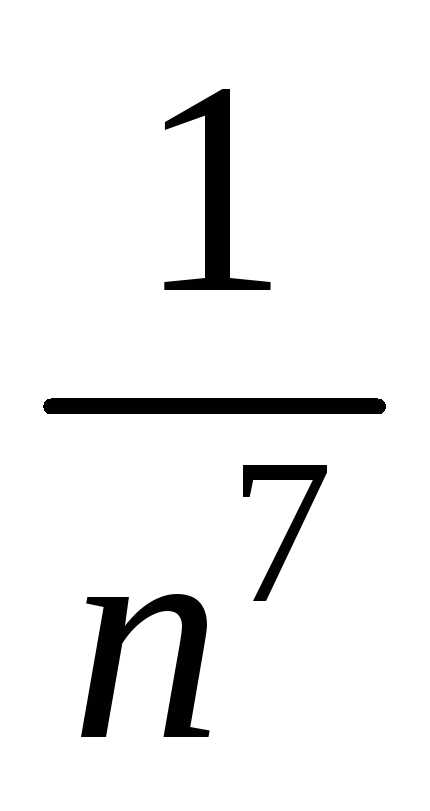 ,
,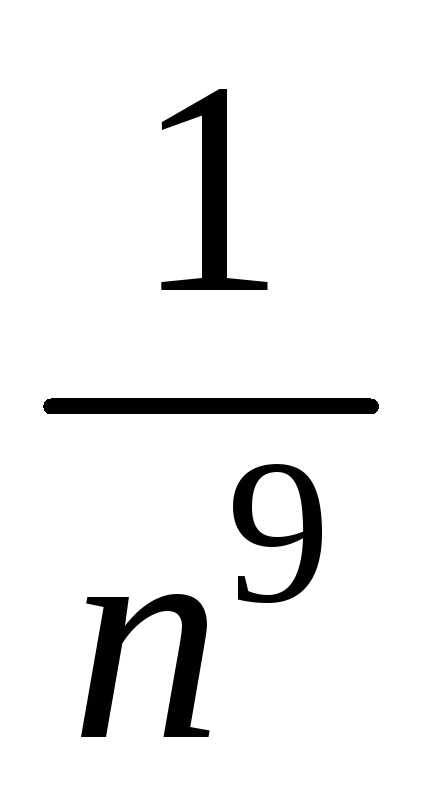 ,
,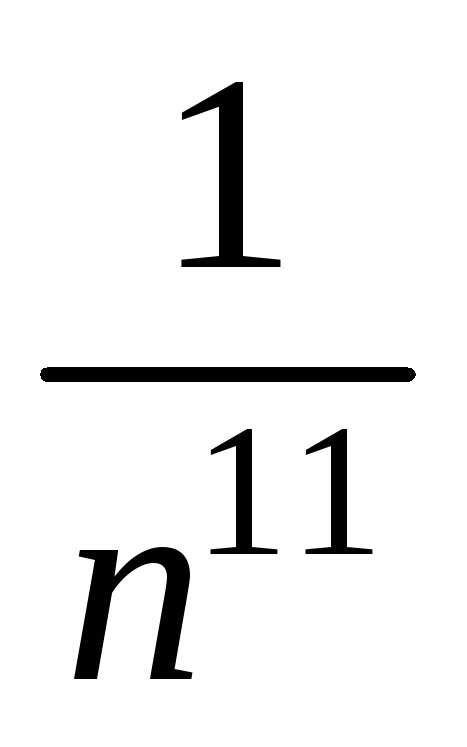 ,
,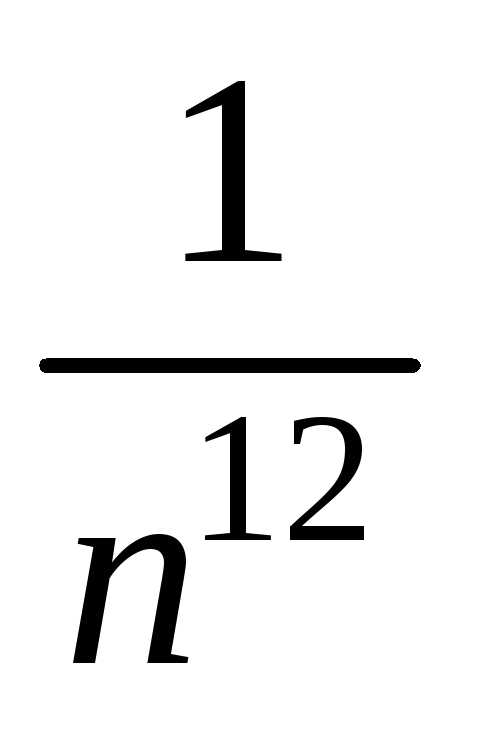 являются бесконечно малыми приn,
следовательно, их предел равен нулю.
являются бесконечно малыми приn,
следовательно, их предел равен нулю.
Пример 3.
Вычислить предел .
Решение.
В этом примере в скобке имеем
неопределенность вида -.
Чтобы избавиться от нее, применим
следующий прием:умножим и разделим
на выражение, сопряженное выражению в
скобках. В данном случае умножим наи в числителе получим разность квадратов.
Упростив, придем к неопределенности
вида ,
которую раскроем, как в предыдущем
примере, делением на старшую степеньn(на
,
которую раскроем, как в предыдущем
примере, делением на старшую степеньn(на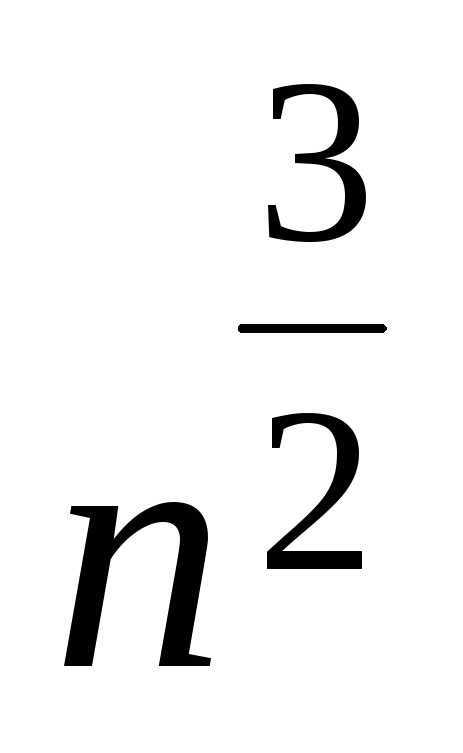 ).
).
====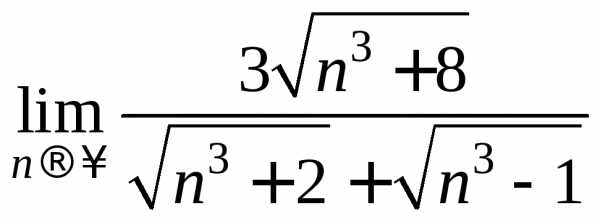 =
=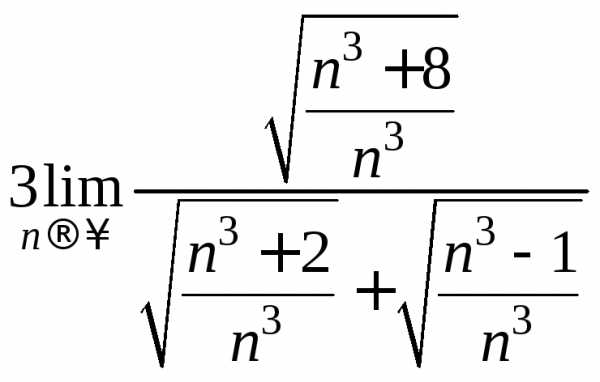 =
=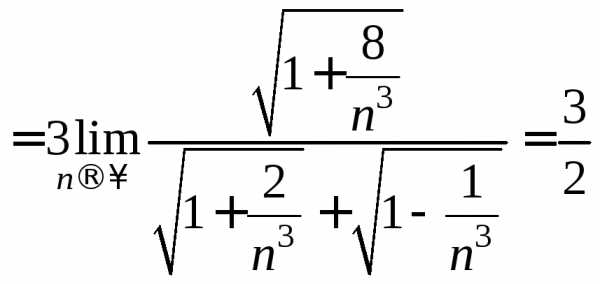 .
.
Пример 4.
Вычислить предел .
Решение.
В данном
примере используется определение
факториала натурального числа. Факториаломчислаn называется
произведение всех натуральных чисел
от 1 доnвключительно:n!=123n.
Например, 1!=1, 2!=12=2,
3!=123=6
и т. д. По определению 0!=1.
называется
произведение всех натуральных чисел
от 1 доnвключительно:n!=123n.
Например, 1!=1, 2!=12=2,
3!=123=6
и т. д. По определению 0!=1.
В пределах такого вида приходится выражать факториалы бóльших чисел через факториал меньшего числа. В данном случае меньшим числом является (3n-1). По определению факториала можем записать:
.
Значит, (3n+1)!=(3n-1)!(3n)(3n+1), а (3n)!=(3n-1)!(3n).
Выразим факториалы указанным образом через (3n-1)! и сократим дробь на (3n-1)! Затем раскроем скобки в числителе и знаменателе и разделим на старшую степеньn(наn3).
==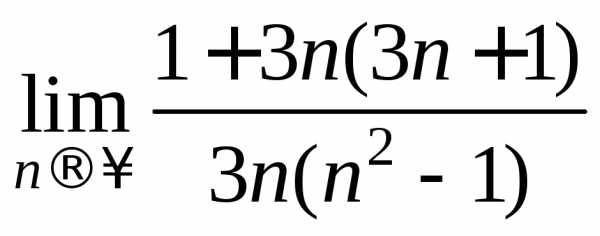 =
=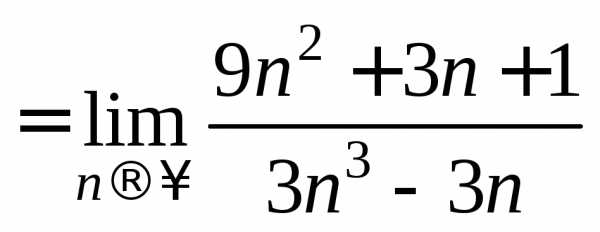 =
=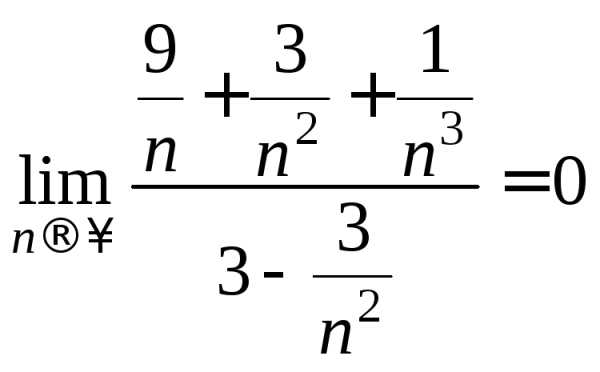 .
.
Пример 5.
Вычислить предел 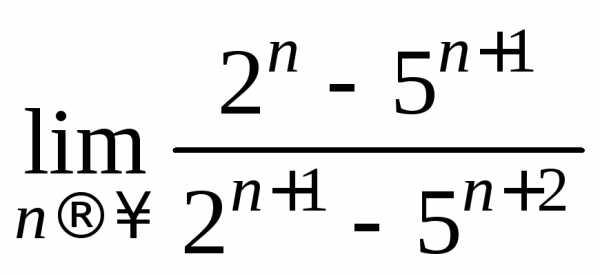 .
.
Решение.
Применим следующий прием: разделим числитель и знаменатель на старшую степень бóльшего по модулю числа. Заметим, что в данном примере можно делить на 5n+2или на 5n+1или на 5n. При этом используется известный предел:
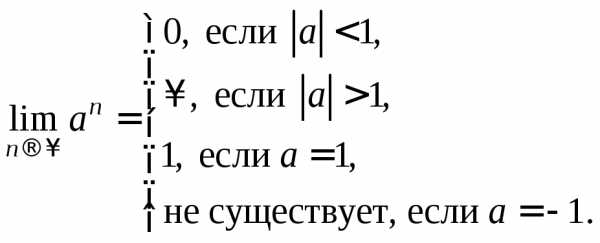
Удобнее делить числитель и знаменатель на 5n.
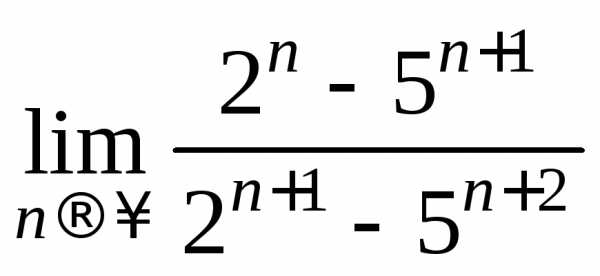 =
=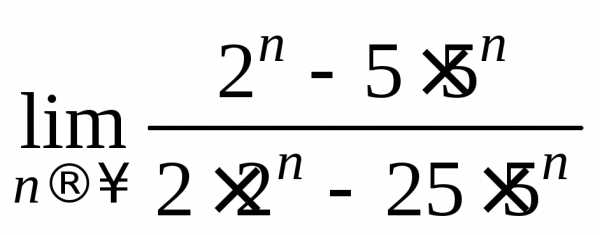 =
=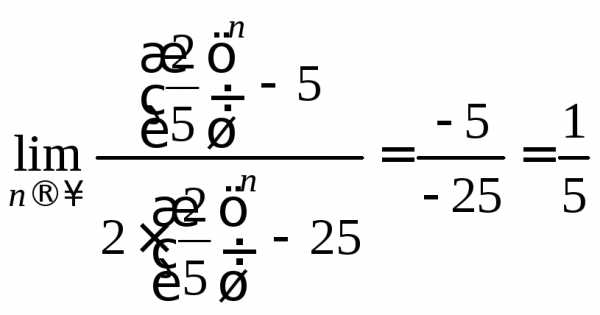 .
.
Пример 6.
Вычислить предел 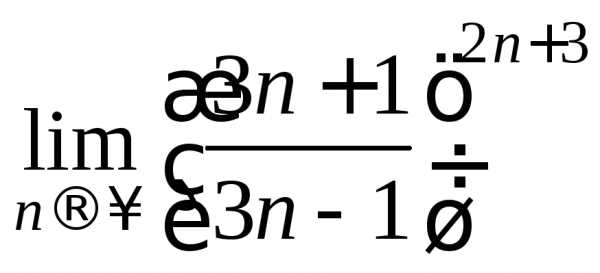 .
.
Решение.
Так как предел основания 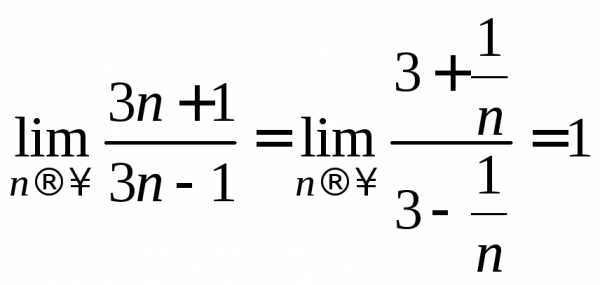 ,
а предел показателя степени,
то в данном случае имеем неопределенность
1. При вычислении
пределов такого вида используется
второй замечательный предел:
,
а предел показателя степени,
то в данном случае имеем неопределенность
1. При вычислении
пределов такого вида используется
второй замечательный предел: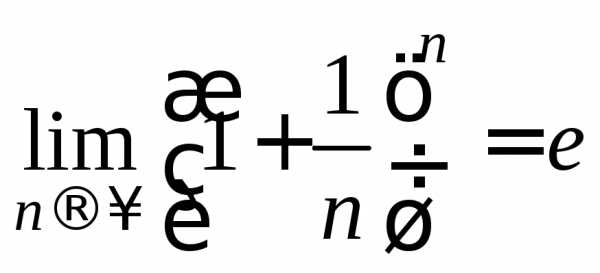 .
Вместоnздесь может
стоять любая бесконечно большая величина,
то есть
.
Вместоnздесь может
стоять любая бесконечно большая величина,
то есть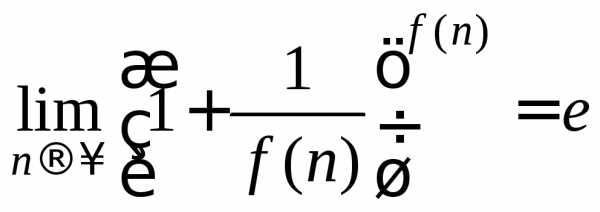 ,
где
,
где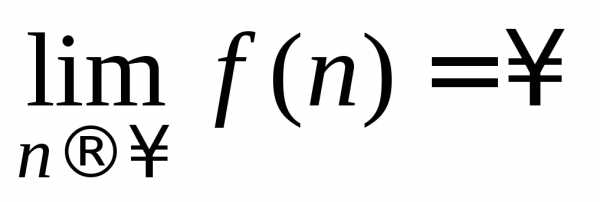 .
.
Выделим вначале в основании целую часть. Для этого получим в числителе выражение, равное знаменателю и разделим почленно числитель на знаменатель.
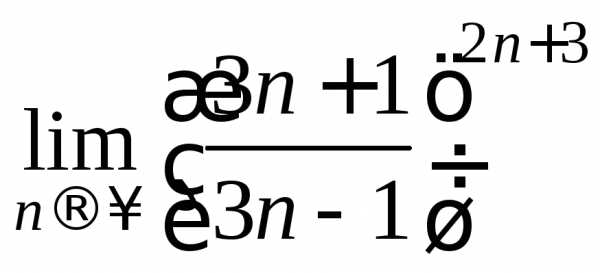 =
=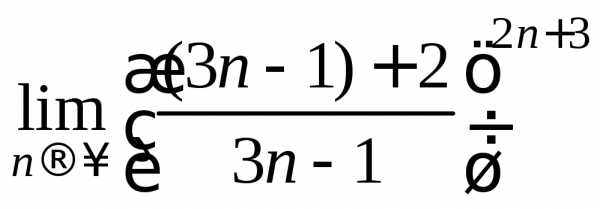 =
=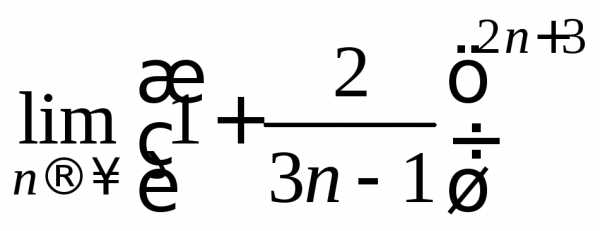 .
.
В нашем случае
.
В показателе выделим выражение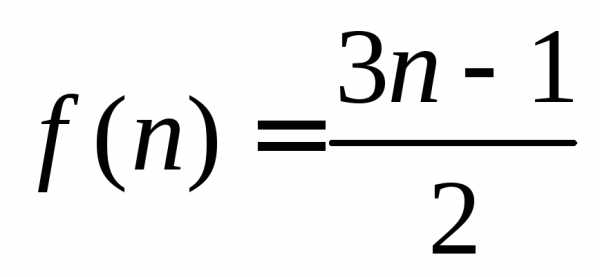 и затем используем свойство
и затем используем свойство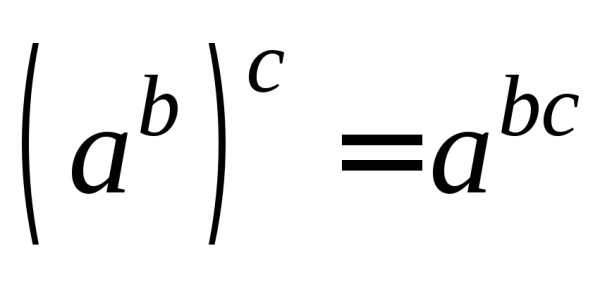 .
.
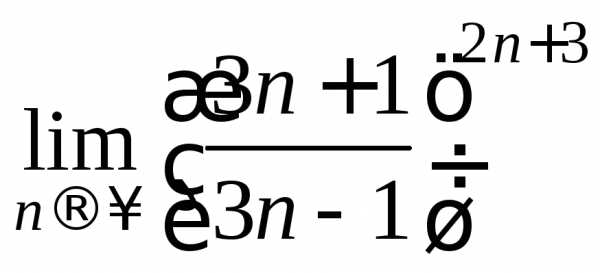 =
=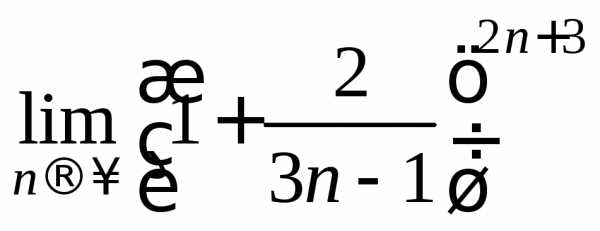 ==
==
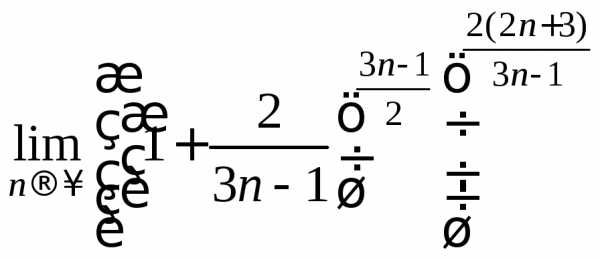 =.
=.
Пример 7.
Вычислить предел .
Решение.
Числитель и знаменатель данной дроби
стремятся к нулю при х10.
Для раскрытия имеющейся здесь
неопределенности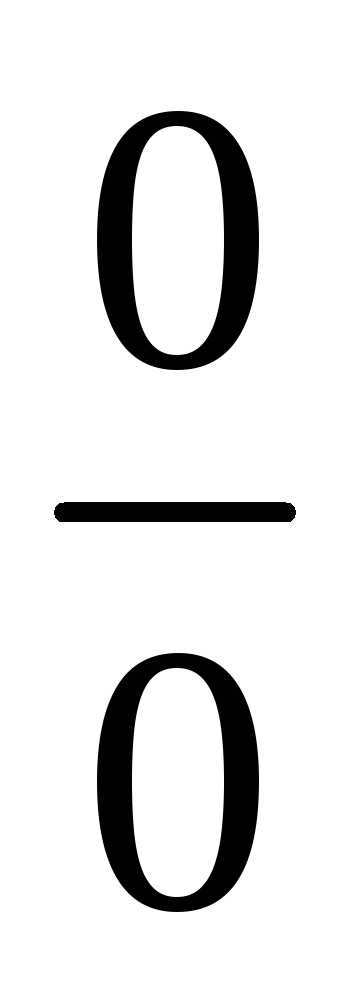 разложим числитель и знаменатель на
множители и разделим на выражение
(х-10). Для этого в числителе
применим формулу разности кубов:,
а в знаменателе вынесемх за скобки
и свернем квадрат разности:
разложим числитель и знаменатель на
множители и разделим на выражение
(х-10). Для этого в числителе
применим формулу разности кубов:,
а в знаменателе вынесемх за скобки
и свернем квадрат разности:
.
Числитель получившейся дроби стремится к 300, а знаменатель – к нулю, т. е. является бесконечно малой величиной. Значит, дробь является бесконечно большой величиной и
.
Пример 8.
Вычислить предел 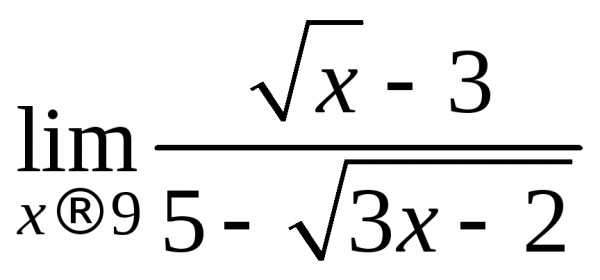 .
.
Решение.
В данном случае имеется неопределенность 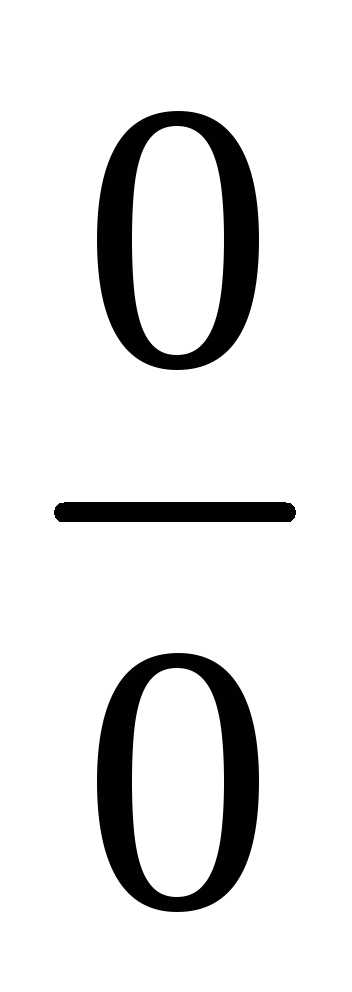 .
Умножим числитель и знаменатель дроби
на выражение, сопряженное числителю, и
на выражение, сопряженное знаменателю:
.
Умножим числитель и знаменатель дроби
на выражение, сопряженное числителю, и
на выражение, сопряженное знаменателю:
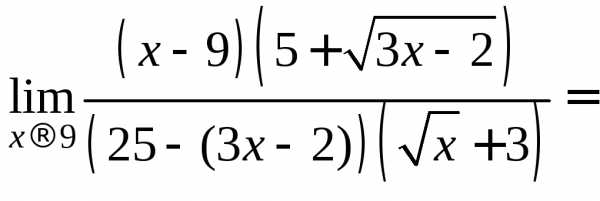
.
Пример 9.
Вычислить предел 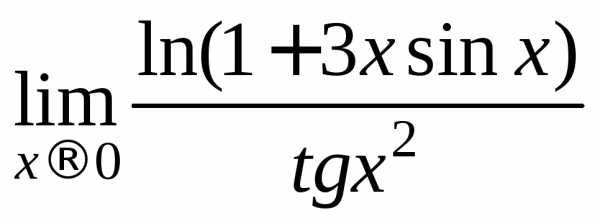 .
.
Решение.
Прих0sinx0,
3xsinx0,x20.
Значит, можно заменить числитель и
знаменатель дроби эквивалентными
бесконечно малыми:,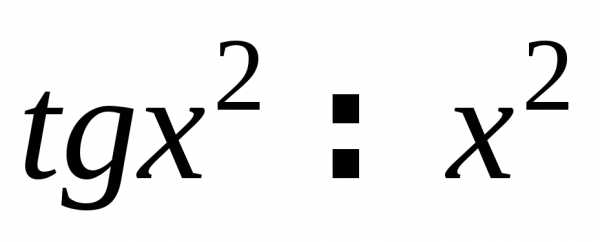 .
Тогда получим
.
Тогда получим
.
Пример 4.
Вычислить предел 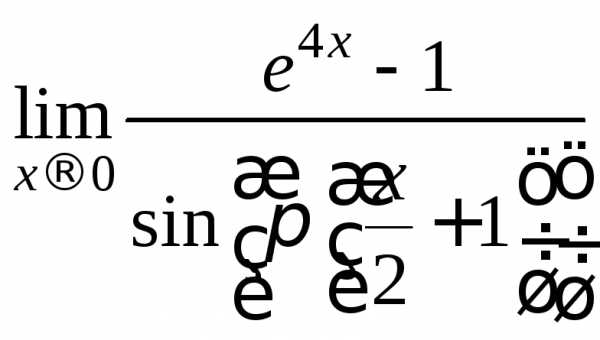 .
.
Решение.
В данном случае выражение, стоящее под
знаком синуса, не является бесконечно
малым: 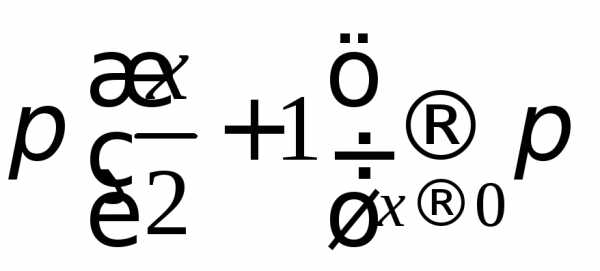 .
Поэтому вначале необходимо раскрыть в
этом выражении скобки и затем применить
формулу приведения:.
Получим
.
Поэтому вначале необходимо раскрыть в
этом выражении скобки и затем применить
формулу приведения:.
Получим
.
Теперь можно заменить числитель и
знаменатель эквивалентными бесконечно
малыми:
,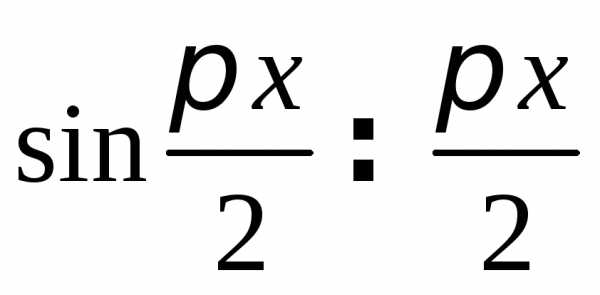 прих0. Тогда
прих0. Тогда
.
Пример 10.
Вычислить предел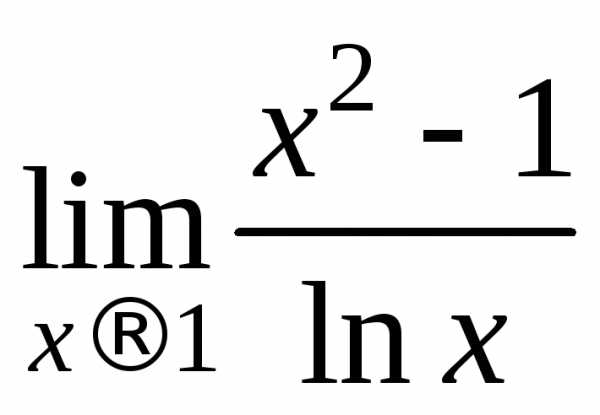 .
.
Решение.
Пример 11.
Вычислить предел 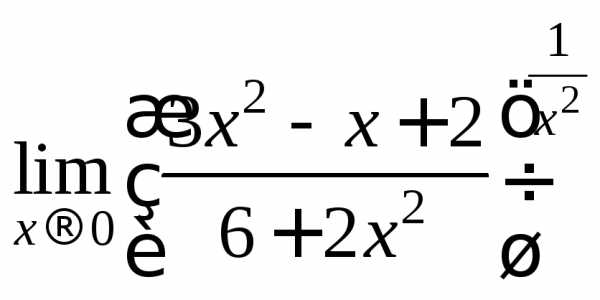 .
.
Решение.
Выражение, стоящее под знаком предела,
является показательно-степенной функцией 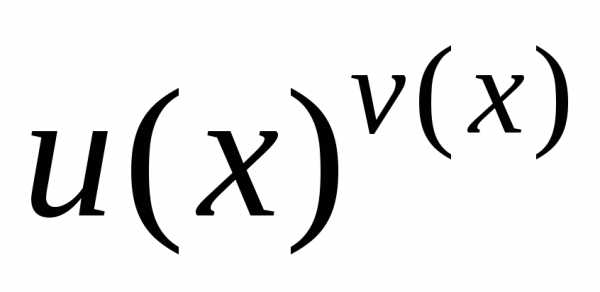 ,
где
,
где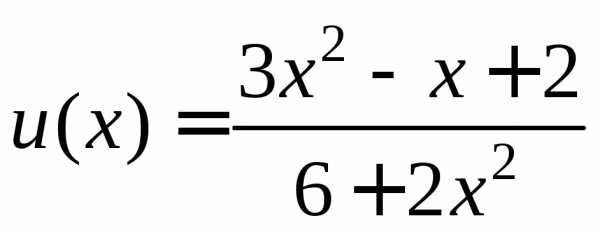 ,
,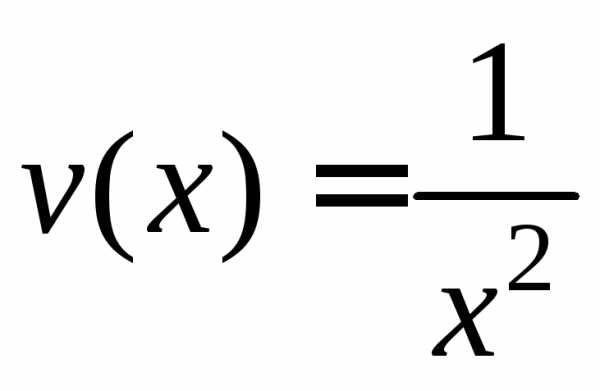 .
Вычислим пределы основания и степени:
.
Вычислим пределы основания и степени:
,.
Тогда используя правило предел степени равен степени пределов(в данном случае нет неопределенности), получим
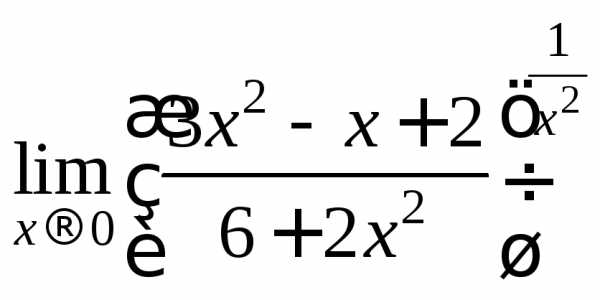 .
.
Пример 12.
Вычислить предел 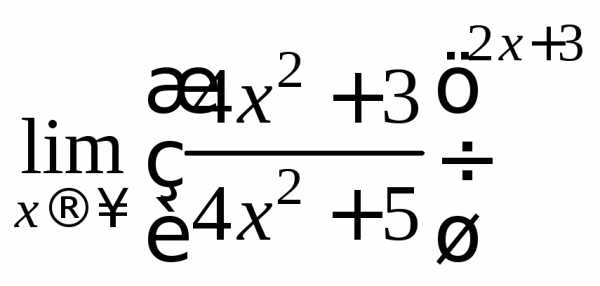 .
.
Решение.
В этом примере предел основания 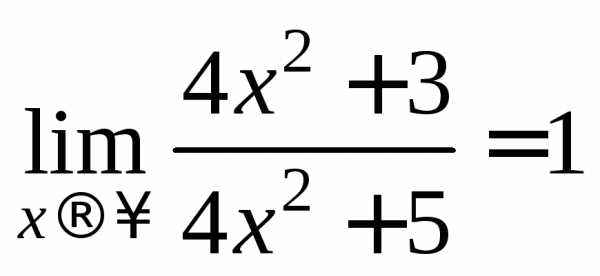 ,
предел показателя.
Значит, имеется неопределенность 1.
Воспользуемся вторым замечательным
пределом в следующей форме записи:
,
предел показателя.
Значит, имеется неопределенность 1.
Воспользуемся вторым замечательным
пределом в следующей форме записи: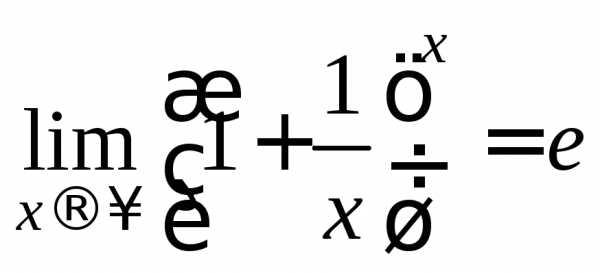 .
Выполним преобразования, как в примере
5 из задания 2:
.
Выполним преобразования, как в примере
5 из задания 2:
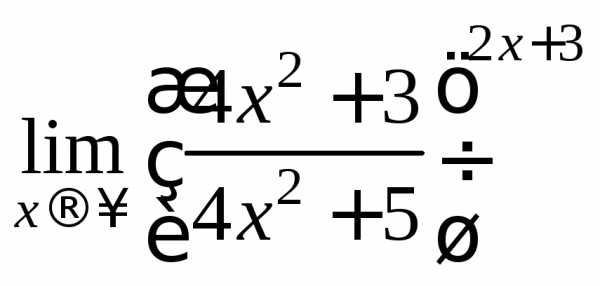
.
Пример 13.
Исследовать на непрерывность функцию 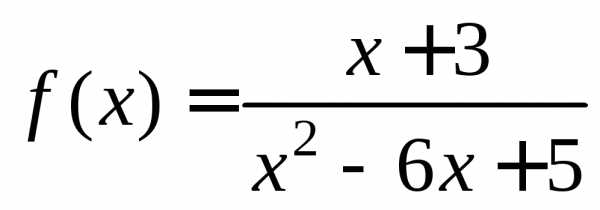 .
.
Решение.
Функция является элементарной как отношение двух многочленов, значит, она непрерывна во всех точках своей области определения. Областью определения является множество всех точек числовой прямой, за исключением тех, в которых знаменатель обращается в нуль. Найдем нули знаменателя: x2-6x+5=0x=1 иx=5.
Итак,
,
данная функция непрерывна на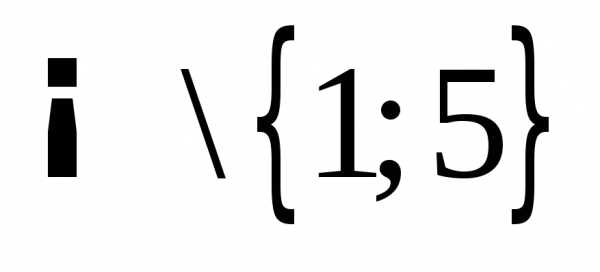 .
Точких=1 их=5 являются точками
разрыва. Исследуем характер разрыва.
Для этого найдем односторонние пределы
функции в точкахх=1 их=5.
.
Точких=1 их=5 являются точками
разрыва. Исследуем характер разрыва.
Для этого найдем односторонние пределы
функции в точкахх=1 их=5.
,
,
,
,
В точках х=1 их=5 функция имеет бесконечные односторонние пределы. Следовательно, эти точки являются точками разрыва второго рода.
studfiles.net
2 варианта контрольных по математическому анализу
Вариант 2
Задания для контрольной работы №1
1. Введение в анализ. Дифференциальное исчисление
1-10. Найти пределы функций.
2. 1) при A) , B) , C) ;
2) 3) ; 4)
Решение
1)
2) 3) ;
Использовали при
4)
11-20. Найти производные заданных функций.
12. А) ; Б)
В) Г) .
Решение
А)
Б)
В)
Г) .
21-30. Вычислить приближенное значение , заменив в точке приращение функции дифференциалом.
22.
Решение
Имеем , то есть
В нашем случае ,
Отсюда:
Поэтому ,
31-40. Исследовать функцию и построить ее график.
32.
Решение
Исследуем функцию, заданную формулой:
Область определения:
Найдём первую производную:
==
===
Первая производная:
Для нахождения критических точек приравняем первую производную к нулю и решим полученное уравнение.
, ,
Дискриминант отрицателен, значит уравнение не имеет корней.
Критические точки: нет
Найдём вторую производную:
Вторая производная это производная от первой производной.
==
=====
==
Вторая производная:
Для нахождения возможных точек перегиба приравняем вторую производную к нулю и решим полученное уравнение.
— нет решений.
Возможные точки перегиба: нет
Для нахождения точек пересечения с осью абсцисс приравняем функцию к нулю.
, ,
;
Точки пересечения с осью :
Пусть, .
Точки пересечения с осью :
Определим значения аргумента, при которых знаменатель функции обращается в ноль
X+3=0, x=-3. Вертикальные асимптоты: x=-3
Горизонтальные асимптоты: нет.
Для нахождения наклонных асимптот преобразуем исходное выражение. ==
Наклонные асимптоты: y=x.
Предел разности исходной функции и функции на бесконечности равен нулю.
Точки разрыва: x=-3.
Симметрия относительно оси ординат: нет
Функция f(x) называется четной, если f(-x)=f(x).
Симметрия относительно начала координат: нет
Функция f(x) называется нечетной, если f(-x)=-f(x).
Тестовые интервалы:
Результаты исследования функции занесем в таблицу.
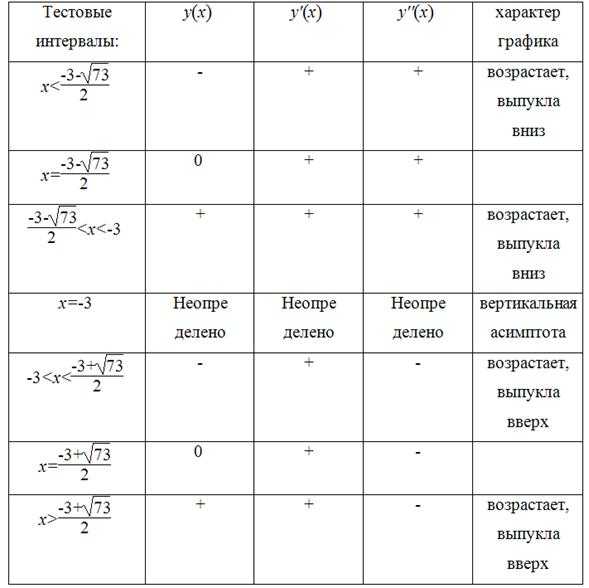
Относительные экстремумы: нет
Данные таблицы нанесем на координатную плоскость.
Используя результаты исследования функции, построим ее график.
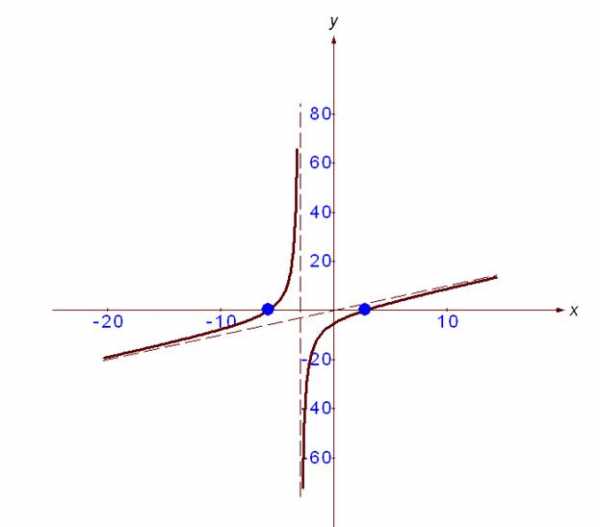
41-50. Найти неопределенные интегралы. Результаты проверить дифференцированием.
42. а) ; Б) ;
Решение
А) ;
Проверка: верно
Б) ;
Проверка: верно
51-60. Вычислить по формуле Ньютона-Лейбница определенный интеграл .
52.
Решение
61-70. Вычислить площадь фигуры, ограниченной параболой и прямой . Сделать чертеж.
62.
Решение
Изобразим фигуру, площадь которой нужно найти:
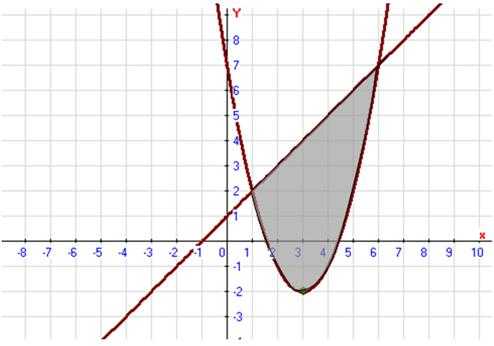
Найдём абсциссы точек пересечения данных линий, для этого решим систему уравнений:
,
По формуле . В нашем случае ,, , . Получим:
Ответ: (кв. ед)
Задания для контрольной работы № 2
1. Аналитическая геометрия
1-10. Даны вершины треугольника. Найти: 1) длину стороны AB; 2) внутренний угол A; 3) уравнение высоты, проведенной через вершину C; 4) уравнение медианы, проведенной через вершину С; 5) площадь треугольника АВС.
2. А(1;1), В (7;4), С (4;5)
Решение
Расстояние d между точками M1(x1; y1) и M2(x2; y2) определяется по формуле:
Угол между прямыми
Угол между векторами a1(X1;Y1), a2(X2;Y2) можно найти по формуле:
где a1a2 = X1X2 + Y1Y2
Найдем угол между векторами AB(6;3) и AC(3;4)
γ = arccos(0.89) = 26.570
Уравнение медианы треугольника
Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.
M(4;5/2)
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(4;5) и М(4;5/2), поэтому:
Каноническое уравнение прямой:
Или x — 4 = 0 или x = 4
Уравнение высоты через вершину C
Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
Y = -2x + 13 или y +2x -13 = 0
Площадь треугольника
Пусть точки A1(x1; y1), A2(x2; y2), A3(x3; y3) — вершины треугольника, тогда его площадь выражается формулой:
В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна.
Принимая A за первую вершину, находим:
По формуле получаем:
11-20. Решить систему линейных уравнений матричным способом
Решение
Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B — матрицу-столбец свободных членов: , Вектор B: BT=(8,5,3)
С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А*Х = B.
Если матрица А — невырожденная (ее определитель отличен от нуля, то она имеет обратную матрицу А-1. Умножив обе части уравнения на А-1, получим: А-1*А*Х = А-1*B, А-1*А=Е.
Это равенство называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А-1.
Система будет иметь решение, если определитель матрицы A отличен от нуля.
Найдем главный определитель.
∆=3•(5•4-3•2)-1•(4•4-3•2)+2•(4•2-5•2)=28
Итак, определитель 28 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения.
Пусть имеем невырожденную матрицу А:
Тогда:
Где Aij — алгебраическое дополнение элемента aij в определителе матрицы А, которое является произведением (-1)i+j на минор (определитель) N-1 порядка, полученный вычеркиванием I-й строки и J-го столбца в определителе матрицы А.
Транспонированная матрица к матрице A имеет вид:
Вычисляем алгебраические дополнения.
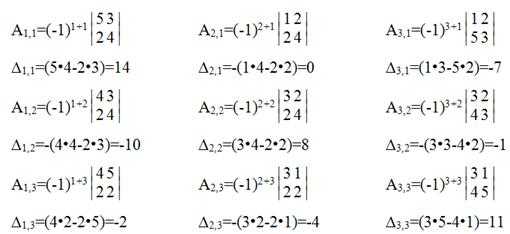
Из полученных алгебраических дополнений составим присоединенную матрицу:
Вычислим обратную матрицу:
Вектор результатов X X=A-1 • B,
XT=(2,1,-1)
X=56 / 28=2
У=28 / 28=1
Z=-28 / 28=-1
Ответ: x=2, у=1 , z=-1
Вариант 7
Задания для контрольной работы №1
1. Введение в анализ. Дифференциальное исчисление
1-10. Найти пределы функций.
7. 1) при A) , B) , C) ;
2) 3) ; 4)
Решение
1)
2) 3) ;
Использовали при
4)
11-20. Найти производные заданных функций.
17. А) ; Б)
В) Г) .
Решение
А) ;
Б) В)
Г) .
21-30. Вычислить приближенное значение , заменив в точке приращение функции дифференциалом.
27.
Решение
Имеем , то есть
В нашем случае ,
Отсюда:
Поэтому ,
31-40. Исследовать функцию и построить ее график.
37.
Решение
Исследуем функцию, заданную формулой:
Область определения:
Найдём первую производную:
==
===
Первая производная:
Для нахождения критических точек приравняем первую производную к нулю и решим полученное уравнение.
, ,
;
Критические точки:
Найдём вторую производную:
Вторая производная это производная от первой производной.
==
==
===
Вторая производная:
Для нахождения возможных точек перегиба приравняем вторую производную к нулю и решим полученное уравнение.
— нет решений.
Возможные точки перегиба: нет
Для нахождения точек пересечения с осью абсцисс приравняем функцию к нулю.
, ,
;
Точки пересечения с осью :
Точки пересечения с осью :
Пусть,
Определим значения аргумента, при которых знаменатель функции обращается в ноль
X+3=0, x=-3 Вертикальные асимптоты: x=-3
Горизонтальные асимптоты: нет.
Для нахождения наклонных асимптот преобразуем исходное выражение.
==
Наклонные асимптоты: y=4x-24 .
Предел разности исходной функции и функции 4x-24 на бесконечности равен нулю.
Точки разрыва: x=-3
Симметрия относительно оси ординат: нет
Функция f(x) называется четной, если f(-x)=f(x).
Симметрия относительно начала координат: нет
Функция f(x) называется нечетной, если f(-x)=-f(x).
Тестовые интервалы:
Результаты исследования функции занесем в таблицу.
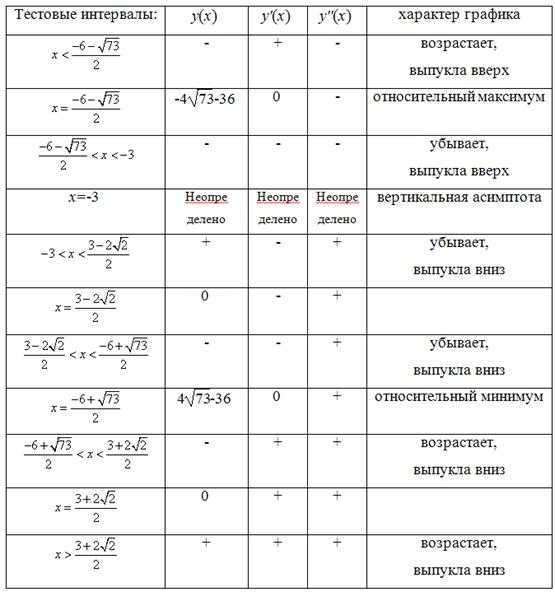
Относительные экстремумы:
Проходя через точку минимума, производная функции меняет знак с (-) на (+). Относительный минимум .
Проходя через точку максимума. производная функции меняет знак с (+) на (-). Относительный максимум .
Данные таблицы нанесем на координатную плоскость.
Используя результаты исследования функции, построим ее график.
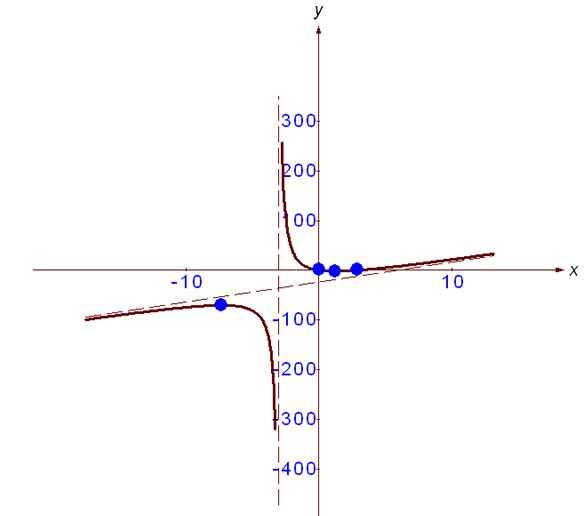
41-50. Найти неопределенные интегралы. Результаты проверить дифференцированием.
47. А) ; Б) ;
Решение
А) ;
Проверка: — верно
Б) Проверка: -верно
51-60. Вычислить по формуле Ньютона-Лейбница определенный интеграл .
57.
Решение
61-70. Вычислить площадь фигуры, ограниченной параболой и прямой . Сделать чертеж.
67.
Решение
Изобразим фигуру, площадь которой нужно найти:
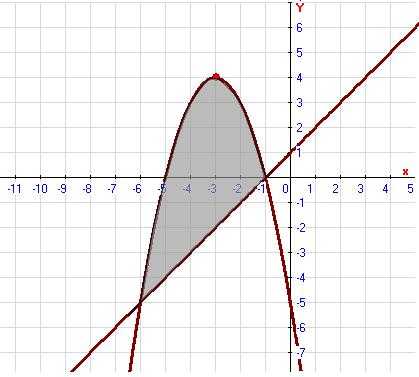
Найдём абсциссы точек пересечения данных линий, для этого решим систему уравнений:
,
По формуле . В нашем случае ,, , . Получим:
Ответ: (кв. ед)
Задания для контрольной работы № 2
1. Аналитическая геометрия
1-10. Даны вершины треугольника. Найти: 1) длину стороны AB; 2) внутренний угол A; 3) уравнение высоты, проведенной через вершину C; 4) уравнение медианы, проведенной через вершину С; 5) площадь треугольника АВС.
7. А (1;6), В (7;4), С (4;5)
Решение
Расстояние d между точками M1(x1; y1) и M2(x2; y2) определяется по формуле:
Угол между векторами a1(X1;Y1), a2(X2;Y2) можно найти по формуле:
Где a1a2 = X1X2 + Y1Y2
Найдем угол между векторами AB(6;-2) и AC(3;-1)
γ = arccos(1) = 00
Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(4;5) и М(4;5), поэтому:
Каноническое уравнение прямой:
Или x — 4 = 0 или x = 4
Уравнение высоты через вершину C
Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
Y = 3x -7 или y -3x +7 = 0
Площадь треугольника
Пусть точки A1(x1; y1), A2(x2; y2), A3(x3; y3) — вершины треугольника, тогда его площадь выражается формулой:
В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна.
Принимая A за первую вершину, находим:
По формуле получаем:
11-20. Решить систему линейных уравнений матричным способом
Решение
Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B — матрицу-столбец свободных членов: , Вектор B: BT=(6,9,10)
С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А*Х = B.
Если матрица А — невырожденная (ее определитель отличен от нуля, то она имеет обратную матрицу А-1. Умножив обе части уравнения на А-1, получим: А-1*А*Х = А-1*B, А-1*А=Е.
Это равенство называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А-1.
Система будет иметь решение, если определитель матрицы A отличен от нуля.
Найдем главный определитель.
∆=1•(1•2-5•4)-4•(2•2-5•3)+3•(2•4-1•3)=41
Итак, определитель 41 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения.
Пусть имеем невырожденную матрицу А:
Тогда:
Где Aij — алгебраическое дополнение элемента aij в определителе матрицы А, которое является произведением (—1)i+j на минор (определитель) N-1 порядка, полученный вычеркиванием I-й строки и J-го столбца в определителе матрицы А.
Транспонированная матрица к матрице A имеет вид:
Вычисляем алгебраические дополнения.
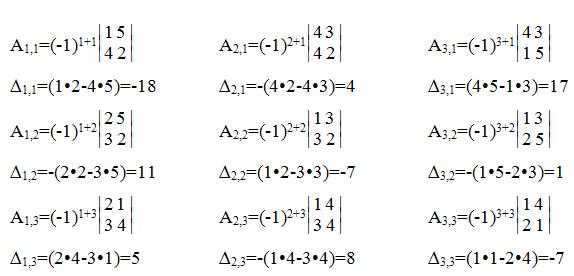
Из полученных алгебраических дополнений составим присоединенную матрицу:
Вычислим обратную матрицу:
Вектор результатов X X=A-1 • B
XT=(1,1,1)
X=41 / 41=1
Y=41 / 41=1
Z=41 / 41=1
Ответ: x=1, y=1, z=1
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Практика24.Контрольная_работа_на_тему_Предел функции
Практика 24. Контрольная работа на тему «Предел функции\
24.1.Теоретическая часть
Вариант 1.
Сформулировать определения
1. lim f(x) = Aпо Гейне;
x!a
2.lim f(x) = 1 ïî Êîøè;
x!+1
3.f(x) ограниченная функция;
4.Критерий Коши существования предела функции в точке. Условие Коши.
Вариант 2.
Сформулировать определения
1.f(x) не имеет предела приx ! a по Гейне;
2.f(x) бесконечно малая функция приx ! 1 ïî Êîøè;
3.f(x) неубывающая функция;
4.sup f(x) = M.
x2X
Вариант 3.
Сформулировать определения
1.f(x) имеет предел приx ! +1 по Гейне;
2.f(x) бесконечно большая функция приx ! a 0 ïî Êîøè;
3.f(x) неограниченная на множествеD;
4.(x) = o ( (x)) ïðè x ! a.
Вариант 4. Сформулировать определения
1.lim f(x) = b 0 ïî Êîøè;
x!a+0
2.f(x) невозрастающая функция;
3.inf f(x) = m;
x2X
4. f(x) èg(x) функции одного порядка приx ! a.
О. А. Кузенков, Е. А. Рябова | 2 |
|
|
24.2.Вариант 1.
Вычислить пределы:
|
|
|
| 2n p |
|
|
|
|
| ; | ||||||
1. | lim |
| 4n2 1 | |||||||||||||
|
|
|
|
|
|
|
|
|
|
| ||||||
| n!1 |
|
| pn2 + 3 n | ||||||||||||
2. | lim |
|
| n 10 |
|
| 3n+1 ; | |||||||||
n + 1 |
| |||||||||||||||
| n!1 |
|
|
|
|
| ||||||||||
3. | lim |
|
|
| x2 2x + 1 | |||||||||||
|
| x3 x2 x + 1 | ||||||||||||||
| x!1+0 | |||||||||||||||
| lim | p |
| p3 |
|
|
| ; | ||||||||
4. | cos x | cos x | ||||||||||||||
|
|
|
|
|
| |||||||||||
| x!0 |
|
|
| sin2 x |
|
|
|
|
| ||||||
5. | lim | tg( (1 + x=2)) | : | |||||||||||||
| ||||||||||||||||
| x!0 |
|
| ln(1 + x) | ||||||||||||
6. Нарисовать пример графика функции, удовлетворяющей предельному равенству
lim f(x) = 2 + 0:
x! 1
На рисунке отметить » и окрестности, дать определение по Коши.
7. Доказать по определению lim | 2x | = 2 + 0: | |
1 + x | |||
x! 1 |
|
О. А. Кузенков, Е. А. Рябова | 3 |
|
|
24.3.Вариант 2.
Вычислить пределы:
pp
1. | lim |
|
|
|
| n2 + 1 |
| n2 1 | ; | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |||
| n!1 |
|
| pn2 + n n 1 | |||||||||||
|
|
|
|
|
| n2 | + n |
| n | ||||||
| n!1 |
|
|
|
|
| |||||||||
| 2n2 | 5n |
|
| |||||||||||
2. | lim |
|
|
|
|
|
|
|
|
|
|
|
| ; |
|
|
| sin x |
|
|
|
|
|
| |||||||
3. | lim |
|
|
| 1=(x a) | ||||||||||
|
|
|
|
|
|
|
| ||||||||
sin a |
|
|
|
|
| ; |
| ||||||||
| x!a |
|
|
|
|
| |||||||||
pp
4. lim | 3 1 + 3×4 1 + x | ; | ||
|
|
| ||
x!+0 | 1 p1 x=2 | |||
5. lim
e4x1
x!0 sin( (x=2 + 1))
6. Нарисовать пример графика функции, удовлетворяющей предельному равенству
lim f(x) = 1 0:
x! 0
На рисунке отметить » и окрестности, дать определение по Коши.
7. Доказать по определению xlim0 | 2x = 1 0: |
! |
|
studfiles.net
