Корень кубический из числа – 3

Кубический корень

  Кубический корень. Как извлечь квадратный корень из большого числа без калькулятора мы уже разобрали. В этой статье рассмотрим как извлечь кубический корень (корень третьей степени). Оговорюсь, что речь идёт о натуральных числах. Как вы думаете, сколько времени нужно, чтобы устно вычислить такие корни как:

Совсем немного, а если потренируетесь  два-три раза минут по 20, то любой такой корень вы сможете извлечь за 5 секунд устно.

*Нужно отметить, что речь идёт о таких числах стоящих под корнем, которые являются результатом возведения в куб натуральных чисел от 0 до 100.

Мы знаем, что:

Так вот, число а, которое мы будем находить – это натуральное число от 0 до 100. Посмотрите на таблицу кубов этих чисел (результаты возведения в третью степень):

Вы без труда  сможете извлечь кубический корень из любого числа в этой таблице. Что нужно знать?

1. Это кубы чисел кратных десяти:

Я бы даже сказал, что это «красивые» числа, запоминаются они легко. Выучить несложно.

2. Это свойство чисел при произведении.  

Его суть заключается в том, что при возведении в третью степень какого-либо определённого числа, результат будет иметь особенность. Какую?

Например, возведём в куб 1, 11, 21, 31, 41 и т.д. Можно посмотреть по таблице.

1³ = 1,   11³ = 1331,   21³ = 9261,   31³ = 26791,   41³ = 68921   …

То есть, при возведении в куб числа с единицей на конце в результате  у нас всегда получится число с единицей в конце.

При возведении в куб числа с двойкой на конце в результате всегда получится число с восьмёркой в конце.

Покажем соответствие в табличке для всех чисел:

Знания представленных двух моментов вполне достаточно.

Рассмотрим примеры:

Извлечь кубический корень из 21952.

Данное число находится в пределах от 8000 до 27000. Это означает, что результат корня лежит в пределах от 20 до 30. Число 29952 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 28.

Извлечь кубический корень из 54852.

Данное число находится в пределах от 27000 до 64000. Это значит, что результат корня лежит в пределах от 30 до 40. Число 54852 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 38.

Извлечь кубический корень из 571787.

Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 571787 заканчивается на 7. Такой вариант возможен только тогда, когда в куб возводится число с тройкой в конце. Таким образом, результат корня равен 83.

Извлечь кубический корень из 614125.

Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 614125 заканчивается на 5. Такой вариант возможен только тогда, когда в куб возводится число с пятёркой в конце. Таким образом, результат корня равен 85.

Думаю, что вы теперь без труда сможете извлечь кубический корень из числа 681472.

Конечно, чтобы извлекать такие корни устно, нужна небольшая практика. Но восстановив две указанные таблички на бумаге, вы без труда в течение минуты, в любом случае, такой корень извлечь сможете.

После того, как нашли результат обязательно сделайте проверку (возведите его с третью степень). *Умножение столбиком никто не отменял 😉

На самом ЕГЭ задач с такими «страшненькими» корнями  нет. Например, в Задаче 27125 требуется извлечь кубический корень из 1728. Думаю, что это теперь для вас не проблема.

Если вы знаете какие-то интересные приёмы вычислений без калькулятора, присылайте, со временем опубликую. На этом всё. Успеха Вам!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Кубический корень. Извлечение кубического корня

Кубический корень из a, обозначающийся как ³√a или как a^1/3 — решение уравнения x³ = a (обычно подразумеваются вещественные решения).

Кубический корень — нечётная функция. В отличие от квадратного корня, кубический корень может быть извлечён и из отрицательных чисел.

Онлайн калькулятор для расчета кубического корня для положительных и отрицательных чисел.

Алгоритм извлечения кубического корня

Перед началом необходимо разделить число на тройки (целую часть — справа налево, дробную — слева направо). Когда Вы достигли десятичной запятой, в конце результата необходимо поставить десятичную запятую.

1. Найдите число, куб которого меньше первой группы цифр, но при её увеличении на 1 она становиться больше. Выпишите найденное число справа от данного числа. Под ним запишите число 3.
2. Запишите куб найденного числа под первой группой цифр и произведите вычитание. Результат после вычитания запишите под вычитаемым. Далее снесите следующую группу цифр.
3. Далее найденный промежуточный ответ заменим буквой a. Вычислите по формуле 300× a²× x+30× a × x²+x³ такое число x, что его результат меньше нижнего числа, но при увеличении на 1 становится больше. Запишите найденное x справа от ответа. Если достигнута необходимая точность, прекратите вычисления.
4. Запишите под нижним числом результат вычисления по формуле 300 × a² × x+30 × a × x²+x³ и произведите вычитание. Перейдите к пункту 3.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

2 часамин. срок

Узнать стоимость

Поделитесь с другими:

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

calcsbox.com

Простые и не очень способы того, как вычислить кубический корень :: SYL.ru

Сколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного. На самом деле разница не настолько велика. Особенно, если понять, что они только частные случаи общего корня n-ой степени.

Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений.

Что нужно знать о корне произвольной степени?

Во-первых, определение этого понятия. Корнем n-ой степени из некоторого «а» называется такое число, которое при возведении в степень n дает исходное «а».

Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет.

Когда же степень нечетная, то существует решение при любом значении «а». Оно вполне может быть и отрицательным.

Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь. Иногда это бывает очень удобным.

Например, «а» в степени 1/n как раз и будет корнем n-ой степени из «а». В этом случае основание степени всегда больше нуля.

Аналогично «а» в степени n/m будет представлено, как корень m-ой степени из «аⁿ».

В-третьих, для них справедливы все действия со степенями.

• Их можно перемножать. Тогда показатели степеней складываются.
• Корни можно разделить. Степени нужно будет вычесть.
• И возвести в степень. Тогда их следует перемножить. То есть ту степень, которая была, на ту, в которую возводят.

В чем сходства и различия квадратного и кубического корней?

Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение.

А о существенном отличии было сказано чуть выше. Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа. В то время, как вычислить кубический корень из отрицательной величины не составит труда.

Извлечение кубического корня на калькуляторе

Каждый человек хоть раз делал это для квадратного корня. А как быть если степень «3»?

На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.

А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у». То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=».

Извлечение кубического корня вручную

Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.

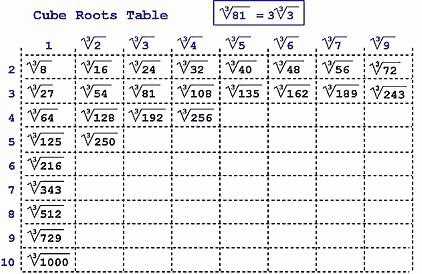
Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?

В противном случае нужно будет считать столбиком. Алгоритм не самый простой. Но если немного попрактиковаться, то действия легко запомнятся. И вычислить кубический корень больше не будет проблемой.

1. Мысленно разделить подкоренное выражение на группы по три цифры от десятичной запятой. Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
2. Определить число, куб которого меньше целой части подкоренного выражения. Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.
3. Выполнить вычитание.
4. К остатку приписать первую группу цифр после запятой.
5. В черновике записать выражение: а² * 300 * х + а * 30 * х² + х³. Здесь «а» — это промежуточный ответ, «х» является числом, которое меньше получившегося остатка с приписанными к нему числами.
6. Число «х» нужно записать после запятой промежуточного ответа. А значение всего этого выражения записать под сравниваемым остатком.
7. Если точности достаточно, то расчеты прекратить. В противном случае нужно возвращаться к пункту под номером 3.

Наглядный пример вычисления кубического корня

Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых.

Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее.

1. 15> 2³, значит под целой частью записана 8, а над корнем 2.
2. После вычитания из 15 восьми получается остаток 7. К нему нужно приписать три нуля.
3. а = 2. Поэтому: 2² * 300 * х +2 * 30 * х² + х³ < 7000, или 1200 х + 60 х² + х³< 7000.
4. Методом подбора получается, что х = 4. 1200 * 4 + 60 * 16 + 64 = 5824.
5. Вычитание дает 1176, а над корнем появилось число 4.
6. Приписать к остатку три нуля.
7. а = 24. Тогда 172800 х + 720 х² + х³< 1176000.
8. х = 6. Вычисление выражения дает результат 1062936. Остаток: 113064, над корнем 6.
9. Снова приписать нули.
10. а = 246. Неравенство получается таким: 18154800х + 7380х² + х³< 113064000.
11. х = 6. Расчеты дают число: 109194696, Остаток: 3869304. Над корнем 6.

Ответом получается число: 2, 466. Поскольку ответ должен быть дан до сотых, то его нужно округлить: 2,47.

Необычный способ извлечения кубического корня

Его можно использовать тогда, когда ответом является целое число. Тогда кубический корень извлекается разложением подкоренного выражения на нечетные слагаемые. Причем таких слагаемых должно быть минимально возможное число.

К примеру, 8 представляется суммой 3 и 5. А 64 = 13 + 15 + 17 + 19.

Ответом будет число, которое равно количеству слагаемых. Так корень кубический из 8 будет равен двум, а из 64 — четырем.

Если под корнем стоит 1000, то его разложением на слагаемые будет 91 + 109 + 93 + 107 + 95 + 105 + 97 + 103 + 99 + 101. Всего 10 слагаемых. Это и есть ответ.

www.syl.ru

Извлечение кубического корня в столбик

Я уже писала здесь, как можно извлекать в столбик квадратный корень. Однако практически такой же алгоритм, напоминающий деление столбиком (или арабский способ деления) работает и для извлечения корней более высоких степеней. Рассмотрим, как извлекать кубический корень с произвольной точностью, определяя на каждом шаге по одной цифре этого корня. Как и для квадратных корней, буду описывать алгоритм пошагово, и каждый шаг будет сопровождаться примером.

Итак, давайте для примера будем извлекать кубический корень из .

1. Разобьем цифры исходного числа на группы по три цифры в каждой. При этом разбиение начинаем от десятичной запятой, двигаясь влево и вправо.

Пример. В нашем случае разбиение выглядит таким образом: .

2. Извлечем кубический корень из первой слева группы цифр. Разумеется, точно корень может не извлекаться, поэтому возьмем наибольшее число, куб которого меньше числа, образованного данной группой цифр.

Пример. В нашем случае первая слева группа цифр , поэтому первая цифра кубического корня — . Действительно, , а вот уже равно .

3. Возводим найденное число в куб и вычитаем из первой слева группы цифр, к разности приписываем справа следующие три цифры (т.е. цифры следующей группы).

Пример. В нашем случае получаем:

   

4. Теперь нужно подобрать следующую цифру корня. Для этого квадрат числа, образованного уже имеющимися цифрами, умножаем на и выбираем цифру, при умножении на которую получится число, меньшее, чем число, образованное всеми цифрами разности, кроме двух последних, но достаточно близкое к нему. Однако следует иметь в виду, что если при очередном вычитании получилось отрицательное число, нужно последнюю вычисленную цифру уменьшить на единицу.

Пример. Имеем: , поэтому выбираем цифру (в самом деле, , а ).

5. Умножаем полученное ранее произведение на выбранную цифру, потом еще на , прибавляем к полученному числу квадрат выбранной цифры, умноженный на число, образованное уже найденными цифрами корня, домноженное на , после чего прибавляем еще куб выбранной цифры.

Пример. У нас получится
.

6. Из полученной на шаге 3 разности вычитаем число, полученное на шаге 5.

Пример. В нашем случае это будет .

7. Переходим к шагу 4.

Продолжаем данную последовательность шагов алгоритма до тех пор, пока корень не вычислен с требуемой точностью.

Пример. В нашем случае мы возводим в квадрат и умножаем его на : . Теперь подберем цифру, при умножении на которую числа получим близкое к , но меньшее его число. Эта цифра (). Теперь из числа (разность, полученная на предыдущем шаге и приписанная справа следующая группа цифр) нужно вычесть следующую сумму:

   

Тем самым, разность будет равна нулю, и корень, который оказался точным, извлечен — это .

Теперь приведу запись, которая при этом получается (разумеется, при реальных вычислениях все скорее всего будет не столь красиво и аккуратно ).

   

   

   

Алгоритм основан на формуле куба суммы: .

Для тех же, кому интересно извлечение корней высших степеней, даю ссылку (правда, материал на английском): http://en.wikipedia.org/wiki/Shifting_nth-root_algorithm.

hijos.ru

Кубический корень из числа

Практически каждый человек мечтает совершенствоваться, идти к чему-то более серьёзному и сложному. Все делают это по-своему. Одни ищут работу, на которой, со временем займут руководящие места, другие жаждут просто заработать побольше денег. Всегда считалось, что чем умнее человек, тем больших успехов он добьётся. Но есть и те, которые совершенствуют свой ум и оттачивают искусство вычисления. Кубический корень (его вычисление) – один из распространенных способов “привести мозги в порядок”.

Издревле считалось, что тренировка ума — это путь к обретению мудрости. Древние греки, которые достигли огромных высот в математике, говорили, что ”каждый человек рожден мудрецом, но не каждый его может отыскать внутри себя”. В последнее время стало очень популярно развивать умение проводить сложные, а иногда и громоздские вычисления в уме. Кубический корень, вычислить который не так просто, если число достаточно большое – один из способов. Существует несколько распространенных вариантов, как извлечь кубический корень из числа. Рассмотрим парочку.

Способ номер 1

Иногда можно встретить афиши, гласящие, что один человек проводит в уме сложнейшие вычисления, в том числе и вычисления кубического корня. Какое-то время, было непонятно, как это делается, но вот алгоритм вычисления известен, и каждый может блеснуть своими умениями.

Извлечение кубического корня проводится путем “отсечения от числа”. Сначала нужно запомнить одну простую закономерность: последние цифры и результат возведения в куб, для некоторых чисел, а именно 1, 4, 5, 6 и 9 одинаковы. Давайте рассмотрим конкретный пример. Предположим, нам нужно извлечь кубический корень из числа 85 184. Рассмотрим самую большую группу в данном числе – тысячи, это 85. Какое число, в кубе даст наиболее близкое значение к 85 но при этом не превзойдет его? Это число 4. Теперь рассмотрим оставшиеся числа 184. Заметьте, что оно заканчивается на 4. Единственное однозначное число, которое дает при возведении в 3-ю степень 4-ку в конце многозначного числа, это число 4. Выходит, что ответом на вопрос является число 44. Умножаем его на самого себя 2 раза (44x44x44) и получаем 85184.

Способ номер 2

Кубический корень можно извлечь и с помощью разложения числа в ряд Тейлора. Однако этот вариант намного сложнее, чем предыдущий. Нам понадобится чёткое знание формулы разложения, и все операции нужно будет вычислять уже не в уме, а на бумаге. Так как кубический корень — это возведение числа в степень 1/3, то проведем вычисления с возведением числа 5. Разложив это число в ряд Тейлора, получим ответ, с мизерной погрешностью. Однако вычислений пришлось проводить немало. Поэтому такой способ не самый выгодный с точки зрения экономии времени. Ведь если число очень большое, то потребуется приложить много усилий для решения

Есть конечно ещё один способ, калькулятор. На инженерных калькуляторах есть возможность одним нажатием кнопки извлечь корень кубический из числа. Как уже было сказано выше, способов извлечения кубического корня из числа очень много. И все время находятся энтузиасты, которые пробуют все новые и новые варианты. Сейчас, при желании, можно найти таблицы со значением кубических корней всех чисел. Вы можете сами, забавы ради или для «разминки мозгов», составить свою таблицу. Конечно, это дело не одного дня, однако подобное времяпрепровождение можно превратить в интересное и достаточно редкое хобби. Ведь счет, неважно какой, — это очень хорошая тренировка для ума. Самое главное — это не то, как и что вы считаете, а то делаете ли вы это вообще. Все люди уникальны, существуют уникумы, которые в уме производят все сложнейшие вычисления. Дар этот у них от природы. Все же остальные могут развивать в себе эти способности. Старайтесь, и быть может вы следующим, кто придумает очередной способ того, как вычислить кубический корень из числа.

fb.ru

Кубический корень из числа

Практически каждый человек мечтает совершенствоваться, идти к чему-то более серьёзному и сложному. Все делают это по-своему. Одни ищут работу, на которой, со временем займут руководящие места, другие жаждут просто заработать побольше денег. Всегда считалось, что чем умнее человек, тем больших успехов он добьётся. Но есть и те, которые совершенствуют свой ум и оттачивают искусство вычисления. Кубический корень (его вычисление) – один из распространенных способов “привести мозги в порядок”.

Издревле считалось, что тренировка ума — это путь к обретению мудрости. Древние греки, которые достигли огромных высот в математике, говорили, что ”каждый человек рожден мудрецом, но не каждый его может отыскать внутри себя”. В последнее время стало очень популярно развивать умение проводить сложные, а иногда и громоздские вычисления в уме. Кубический корень, вычислить который не так просто, если число достаточно большое – один из способов. Существует несколько распространенных вариантов, как извлечь кубический корень из числа. Рассмотрим парочку.

Способ номер 1

Иногда можно встретить афиши, гласящие, что один человек проводит в уме сложнейшие вычисления, в том числе и вычисления кубического корня. Какое-то время, было непонятно, как это делается, но вот алгоритм вычисления известен, и каждый может блеснуть своими умениями.

Извлечение кубического корня проводится путем “отсечения от числа”. Сначала нужно запомнить одну простую закономерность: последние цифры и результат возведения в куб, для некоторых чисел, а именно 1, 4, 5, 6 и 9 одинаковы. Давайте рассмотрим конкретный пример. Предположим, нам нужно извлечь кубический корень из числа 85 184. Рассмотрим самую большую группу в данном числе – тысячи, это 85. Какое число, в кубе даст наиболее близкое значение к 85 но при этом не превзойдет его? Это число 4. Теперь рассмотрим оставшиеся числа 184. Заметьте, что оно заканчивается на 4. Единственное однозначное число, которое дает при возведении в 3-ю степень 4-ку в конце многозначного числа, это число 4. Выходит, что ответом на вопрос является число 44. Умножаем его на самого себя 2 раза (44x44x44) и получаем 85184.

Способ номер 2

Кубический корень можно извлечь и с помощью разложения числа в ряд Тейлора. Однако этот вариант намного сложнее, чем предыдущий. Нам понадобится чёткое знание формулы разложения, и все операции нужно будет вычислять уже не в уме, а на бумаге. Так как кубический корень — это возведение числа в степень 1/3, то проведем вычисления с возведением числа 5. Разложив это число в ряд Тейлора, получим ответ, с мизерной погрешностью. Однако вычислений пришлось проводить немало. Поэтому такой способ не самый выгодный с точки зрения экономии времени. Ведь если число очень большое, то потребуется приложить много усилий для решения

Есть конечно ещё один способ, калькулятор. На инженерных калькуляторах есть возможность одним нажатием кнопки извлечь корень кубический из числа. Как уже было сказано выше, способов извлечения кубического корня из числа очень много. И все время находятся энтузиасты, которые пробуют все новые и новые варианты. Сейчас, при желании, можно найти таблицы со значением кубических корней всех чисел. Вы можете сами, забавы ради или для «разминки мозгов», составить свою таблицу. Конечно, это дело не одного дня, однако подобное времяпрепровождение можно превратить в интересное и достаточно редкое хобби. Ведь счет, неважно какой, — это очень хорошая тренировка для ума. Самое главное — это не то, как и что вы считаете, а то делаете ли вы это вообще. Все люди уникальны, существуют уникумы, которые в уме производят все сложнейшие вычисления. Дар этот у них от природы. Все же остальные могут развивать в себе эти способности. Старайтесь, и быть может вы следующим, кто придумает очередной способ того, как вычислить кубический корень из числа.

autogear.ru