Круги Эйлера: примеры и возможности
Математика по своей сути наука абстрактная, если отойти от элементарных понятий. Так, на паре-тройке яблок можно наглядно изобразить основные операции, что лежат в основе математики, но, как только плоскость деятельности расширяется, этих объектов становится недостаточно. Кто-нибудь пробовал изобразить на яблоках операции над бесконечными множествами? В том-то и дело, что нет. Чем сложнее становились понятия, которыми оперирует математика в своих суждениях, тем проблематичнее казалось их наглядное выражение, которое было бы призвано облегчить понимание. Однако, на счастье как современных студентов, так и науки в целом, были выведены круги Эйлера, примеры и возможности которых мы рассмотрим ниже.
Немного истории
17 апреля 1707 года мир подарил науке Леонарда Эйлера — замечательного ученого, чей вклад в математику, физику, кораблестроение и даже теорию музыки не переоценить.
 Труды его признаны и востребованы по сей день во всем мире, несмотря на то что наука не стоит на месте. Особо занимательным является тот факт, что господин Эйлер принял непосредственное участие в становлении российской школы высшей математики, тем более что волею судеб он дважды возвращался в наше государство. Ученый обладал уникальной способностью выстраивать прозрачные в своей логике алгоритмы, отсекая все лишнее и в кратчайшие сроки переходя от общего к частному. Не станем перечислять все его заслуги, так как это займет немалое количество времени, и обратимся непосредственно к теме статьи. Именно он предложил использовать графическое изображение операций над множествами. Круги Эйлера решение любой, даже самой сложно составленной задачи, способны изобразить наглядно.
Труды его признаны и востребованы по сей день во всем мире, несмотря на то что наука не стоит на месте. Особо занимательным является тот факт, что господин Эйлер принял непосредственное участие в становлении российской школы высшей математики, тем более что волею судеб он дважды возвращался в наше государство. Ученый обладал уникальной способностью выстраивать прозрачные в своей логике алгоритмы, отсекая все лишнее и в кратчайшие сроки переходя от общего к частному. Не станем перечислять все его заслуги, так как это займет немалое количество времени, и обратимся непосредственно к теме статьи. Именно он предложил использовать графическое изображение операций над множествами. Круги Эйлера решение любой, даже самой сложно составленной задачи, способны изобразить наглядно.В чем же суть?
На практике круги Эйлера, схема которых изображена ниже, могут применяться не только в математике, так как понятия «множества» присущи не только данной дисциплине. Так, они с успехом применяются и в менеджменте.
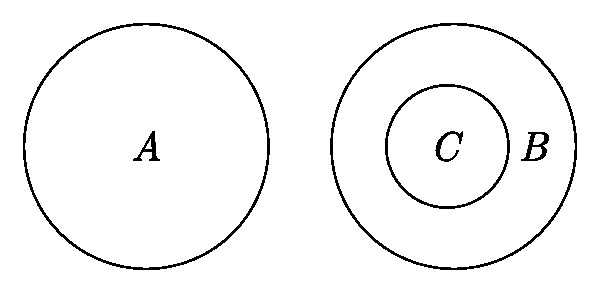
Схема выше показывает отношения множеств А (иррациональные числа), В (рациональные числа) и С (натуральные числа). Круги показывают, что множество С включено в множество В, тогда как множество А с ними никак не пересекается. Пример простейший, но наглядно объясняет специфику «взаимоотношений множеств», которые слишком абстрактны для реального сравнения хотя бы в силу их бесконечности.
Алгебра логики
Данная область математической логики оперирует высказываниями, которые могут носить как истинный, так и ложный характер. Например, из элементарного: число 625 делится нацело на 25, число 625 делится нацело на 5, число 625 является простым. Первое и второе утверждения – истина, тогда как последнее – ложь. Конечно, на практике все сложнее, но суть показана ясно. И, конечно же, в решении опять участвуют круги Эйлера, примеры с их использованием слишком удобны и наглядны, чтобы их игнорировать.
Немного теории:
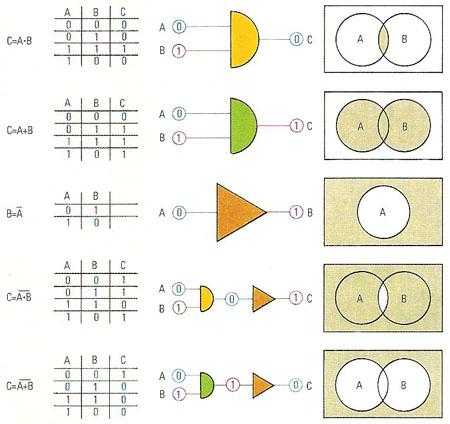
- Пусть множества А и В существуют и не являются пустыми, тогда для них определены следующие операции пересечения, объединения и отрицания.
- Пересечение множеств А и В состоит из элементов, что принадлежат одновременно как множеству А, так и множеству В.
- Объединение множеств А и В состоит из элементов, что принадлежат множеству А или множеству В.
- Отрицание множества А — это множество, что состоит из элементов, которые не принадлежат множеству А.

Все это изображают опять же круги Эйлера в логике, так как с их помощью каждая задача, вне зависимости от степени сложности, становится очевидной и наглядной.
Аксиомы алгебры логики
Положим, что 1 и 0 существуют и определены во множестве А, тогда:
- отрицание отрицания множества А есть множество А;
- объединение множества А с не_А есть 1;
- объединение множества А с 1 есть 1;
- объединение множества А с самим собой есть множество А;
- объединение множества А с 0 есть множество А;
- пересечение множества А с не_А есть 0;
- пересечение множества А с самим собой есть множество А;
- пересечение множества А с 0 есть 0;
- пересечение множества А с 1 есть множество А.
Основные свойства алгебры логики
Пусть множества А и В существуют и не являются пустыми, тогда:
- для пересечения и объединения множеств А и В действует переместительный закон;
- для пересечения и объединения множеств А и В действует сочетательный закон;
- для пересечения и объединения множеств А и В действует распределительный закон;
- отрицание пересечения множеств А и В есть пересечение отрицаний множеств А и В;
- отрицание объединения множеств А и В есть объединение отрицаний множеств А и В.
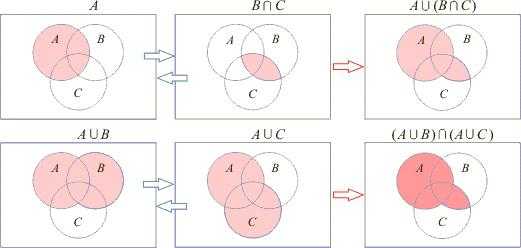
Ниже показаны круги Эйлера, примеры пересечения и объединения множеств А, В и С.
Перспективы
Работы Леонарда Эйлера обоснованно считаются базой современной математики, однако сейчас их с успехом применяют в областях человеческой деятельности, что появились относительно недавно, взять хотя бы корпоративное управление: круги Эйлера, примеры и графики описывают механизмы моделей развития, будь то российская или англо-американская версия.
fb.ru
Презентация по математике «Множества. Операции над множествами. Круги Эйлера»
Презентация на тему: Множества. Операции над множествами. Круги ЭйлераСкачать эту презентацию
Скачать эту презентацию
№ слайда 1 Описание слайда:
Описание слайда:На языке мудрости ЗНАТЬ – это значит УМЕТЬ, а ПОНИМАТЬ – это значит ДЕЙСТВОВАТЬ.
№ слайда 2 Описание слайда:
Описание слайда:Тема урока: Множества. Операции над множествами. Круги Эйлера.
№ слайда 3 Описание слайда:
Описание слайда:Цель урока: обобщить и систематизировать знания студентов по теме: «Множества. Операции над множествами. Круги Эйлера.»
 Описание слайда:
Описание слайда:МНОЖЕСТВО ЭЛЕМЕНТ МНОЖЕСТВА ВИДЫ МНОЖЕСТВ ОТНОШЕНИЯ МЕЖДУ МНОЖЕСТВАМИ ОБЪЕДИНЕНИЕ МНОЖЕСТВ ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ НАХОДИТЬ ОБЪЕДИНЕНИЕ МНОЖЕСТВ НАХОДИТЬ ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ ИЗОБРАЖАТЬ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА-ВЕННА РЕШАТЬ ЗАДАЧИ С ИСПОЛЬЗОВАНИЕМ ИМЕЮЩИХСЯ ЗНАНИЙ
№ слайда 5 Описание слайда:
Описание слайда:основатель теории множеств Георг Кантор (1845 -1918 гг.) – немецкий математик «Множество есть многое, мыслимое нами как единое»
№ слайда 6 Описание слайда:
Описание слайда:Понятие теории множеств Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно было введено в математику немецким ученым Георгом Кантором (1845-1918).Следуя Кантору, понятие «множество» можно определить так: Множество-совокупность объектов, обладающих определенным свойством, объединенных в единое целое.
№ слайда 7 Описание слайда:
Описание слайда:Множество – совокупность объектов, обладающих определенным свойством, объединенных в единое целое. Объекты, из которых образовано множество, называются элементами множества. Множества принято обозначать прописными буквами латинского алфавита: А, В, С, D,…, Z е в d а с z Элементы множества принято обозначать строчными буквами латинского алфавита: а, b, c,…, z.
№ слайда 8 Описание слайда:
Описание слайда:множество людей на Солнце множество прямых углов равностороннего треугольника множество точек пересечения двух параллельных прямых Пустое множество-множество, не содержащее ни одного элемента.
 Описание слайда:
Описание слайда:КОЛЛЕКЦИЯ МАРОК НАБОР КАРАНДАШЕЙ СТАЯ ПТИЦ ЧАЙНЫЙ СЕРВИЗ БУКЕТ ЦВЕТОВ СТАДО КОРОВ
№ слайда 10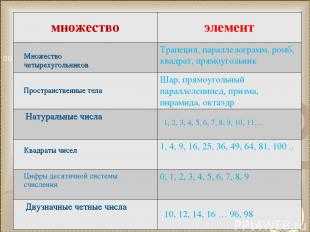 Описание слайда:
Описание слайда:Множество четырехугольников Пространственные тела 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11… Квадраты чисел Цифры десятичной системы счисления 10, 12, 14, 16 … 96, 98 множество элемент Трапеция, параллелограмм, ромб, квадрат, прямоугольник Шар, прямоугольный параллелепипед, призма, пирамида, октаэдр Натуральные числа 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 .. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Двузначные четные числа
№ слайда 11 Описание слайда:
Описание слайда:Обозначения числовых множеств N – множество натуральных чисел; Z – множество целых чисел; Q – множество рациональных чисел; R – множество действительных чисел.
№ слайда 12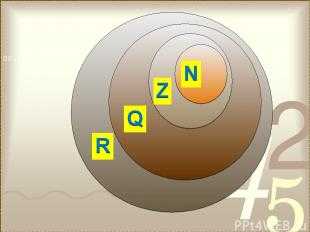 Описание слайда: № слайда 13
Описание слайда: № слайда 13  Описание слайда:
Описание слайда:Стандартные обозначения
№ слайда 14 Описание слайда:
Описание слайда:Запишите множества букв слов КОНИ И КИНО ВИДЫ МНОЖЕСТВ Равные множества {К, О, Н, И} {К, И, Н, О}
№ слайда 15
А = {2; 3; 5; 7; 11; 13}; {х | 5< х
№ слайда 16 Описание слайда:
Описание слайда:{1; 4; 9; 16; 25; …}; {10; 20; 30; 40; 50; …}; ВИДЫ МНОЖЕСТВ Бесконечные множества
№ слайда 17 Описание слайда:
Описание слайда:Среди перечисленных ниже множеств укажите конечные и бесконечные множества: а) множество чисел, кратных 13; б) множество делителей числа 15; в) множество деревьев в лесу; г) множество натуральных чисел; д) множество рек Ростовской области; е) множество корней уравнения х + 3 = 11; ж) множество решений неравенства х + 1 < 3.
№ слайда 18 Описание слайда:
Описание слайда:Задайте множество цифр, с помощью которых записывается число: а) 3254; б) 8797; в) 11000; г) 555555. Охарактеризуйте множество А: а) А = {1, 3, 5, 7, 9}; б) А = {- 2, — 1, 0, 1, 2}; в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99}.
№ слайда 19 Описание слайда:
Описание слайда:Даны множества: М = {5, 4, 6}; Р = {4, 5, 6}; Т = {5, 6, 7}; S = {4, 6}. Какое из утверждений неверно? а) М = Р б) Р ≠ S в) М ≠ Т г) Р = Т
№ слайда 20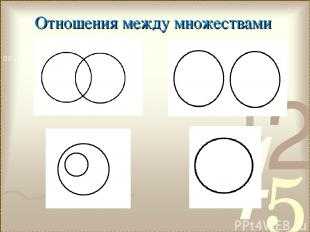 Описание слайда:
Описание слайда:Отношения между множествами
№ слайда 21 Описание слайда: № слайда 22
Описание слайда: № слайда 22 
 Описание слайда: № слайда 24
Описание слайда: № слайда 24 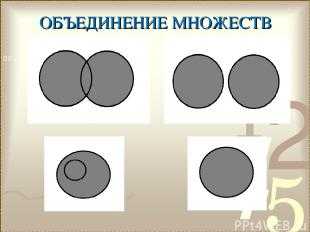 Описание слайда:
Описание слайда:ОБЪЕДИНЕНИЕ МНОЖЕСТВ
№ слайда 25 Описание слайда: № слайда 26
Описание слайда: № слайда 26 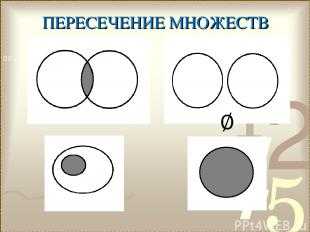 Описание слайда:
Описание слайда:ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
№ слайда 27 Описание слайда:
Описание слайда:Даны множества: А = {2; 3; 8}; В = {2; 3; 8; 11}; С = {5; 11}. Найдите: 1) АUВ; 2) АUС; 3) СUВ.
№ слайда 28 Описание слайда:
Описание слайда:Даны множества: А = {a, b, c, d}; B = {c, d, e, f}; C = {c, e, g, k}. Найдите: (АUВ)UС.
№ слайда 29 Описание слайда:
Описание слайда:Даны множества: А – множество всех натуральных чисел, кратных 10; В = {1; 2; 3;…, 41}. Найдите А∩В.
№ слайда 30 Описание слайда:
Описание слайда:k Решение задачи с помощью кругов Эйлера Леона рд Э йлер (1707-1783 гг.) — швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.
№ слайда 31
поют 17 танцуют 19 Всего 30 17+19=36, всего 30 36-30=6 6 11 13 В классе 30 человек, каждый из которых поёт или танцует. Известно, что поют 17 человек, а танцевать умеют 19 человек. Сколько человек поёт и танцует одновременно?
№ слайда 32 Описание слайда:
Описание слайда:Решение Пусть А — это множество учеников, умеющих петь. Количество элементов в нём по условию равно n = 17. Пусть В — множество учеников, умеющих танцевать. Количество элементов в нём — m = 19. Множество совпадает со всем классом, т.к. каждый ученик в классе поёт или танцует. — это множество тех учеников класса, которые поют и танцуют одновременно. Пусть их количество равно k. Согласно формуле доказанной выше n + m- k = 17+ 19- k = 30 k = 6. Ответ: 6 учеников в классе поют и танцуют одновременно.
№ слайда 33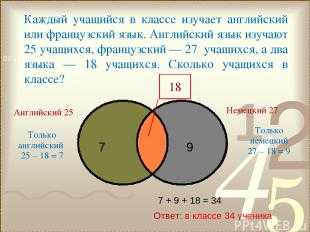 Описание слайда:
Описание слайда:Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27 учащихся, а два языка — 18 учащихся. Сколько учащихся в классе? Ответ: в классе 34 ученика Английский 25 Немецкий 27 Только английский 25 – 18 = 7 Только немецкий 27 – 18 = 9 7 + 9 + 18 = 34 18 7 9
№ слайда 34 Описание слайда:
Описание слайда:Расположите 4 элемента в двух множествах так, чтобы в каждом из них было по 3 элемента
№ слайда 35 Описание слайда:
Описание слайда:Множества А и В содержат соответственно 5 и 6 элементов, а множество А ∩ В – 2 элемента. Сколько элементов в множестве А U В? Объединение содержит 9 элементов
 Описание слайда:
Описание слайда:Каждая семья, живущая в нашем доме, выписывает или газету, или журнал, или и то и другое вместе. 75 семей выписывают газету, а 27 семей выписывают журнал и лишь 13 семей выписывают и журнал, и газету. Сколько семей живет в нашем доме? * Всего: 14 + 13 + 62 =89
№ слайда 37 Описание слайда:
Описание слайда:На школьной спартакиаде каждый из 25 учеников 9-го класса выполнил норматив или по бегу, или по прыжкам в высоту. Оба норматива выполнили 7 человек, а 11 учеников выполнили норматив по бегу, но не выполнили норматив по прыжкам в высоту. Сколько учеников выполнили норматив: а) по бегу; б) по прыжкам в высоту; в) по прыжкам при условии, что не выполнен норматив по бегу?
№ слайда 38 Описание слайда:
Описание слайда:Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 – и значки, и марки. Остальные не увлекаются коллекционированием. Сколько школьников не увлекаются коллекционированием? *
№ слайда 39 Описание слайда:
Описание слайда:Каждый из учеников 9-го класса в зимние каникулы ровно два раза был в театре, посмотрев спектакли А, В или С. При этом спектакли А, В, С видели соответственно 25, 12 и 23 ученика. Сколько учеников в классе?
№ слайда 40 Описание слайда:
Описание слайда:В воскресенье 19 учеников нашего класса побывали в планетарии, 10 – в цирке и 6 – на стадионе. Планетарий и цирк посетили 5 учеников; планетарий и стадион — 3; цирк и стадион — 1. Сколько учеников в нашем классе, если никто не успел посетить все три места, а три ученика не посетили ни одного места?
№ слайда 41 Описание слайда:
Описание слайда:САМООЦЕНКА 10 – хорошо знаю весь фактический материал, и участвовал в организации группы; 9 – хорошо знаю свой вопрос, и участвовал в работе на уроке; 8 – хорошо знаю весь фактический материал; 7 – хорошо знаю свой вопрос; 6 – знаю свой вопрос; 5 – знаю свой вопрос, но был пассивен; 4 – плохо знаю свой вопрос, но был активен в обсуждении других вопросов; 3 – плохо знаю свой вопрос, и был пассивен; 1,2 – не знаю свой вопрос, и был пассивен.
№ слайда 42 Описание слайда:
Описание слайда:Подведение итогов занятия — оценка степени реализации поставленных целей; — оценка работы студентов; — самооценка работы студентов в группах.
№ слайда 43 Описание слайда:
Описание слайда:Домашнее задание М.С. Спирина, «Дискретная математика» §§1.1.-1.2, с.14-20.
№ слайда 44 Описание слайда:
Описание слайда:Спасибо за работу на уроке, урок окончен!
ppt4web.ru
Круги Эйлера. Алгебра множеств. — КиберПедия
Для наглядного изображения соотношений между подмножествами некоторого универсального множества U используются круги Эйлера. Множество U обычно представляется множеством точек прямоугольника, а его подмножества изображаются кругами или другими простыми областями внутри этого прямоугольника. Непересекающиеся множества изображаются непересекающимися областями, а подмножествам соответствуют области, целиком располагающиеся внутри другой области. Дополнение множества А (до U), т.е. множество , изображается той частью прямоугольника, которая вне круга, изображающего .
Рассмотрим операции над множествами с помощью диаграмм Эйлера-Венна.
A ÇB A ÈB
Пусть А, В, СÎU, тогда имеют место следующие соотношения:
| 1a AÈB=BÈA | 1b AÇB=BÇA (коммутативность) |
| 2a AÈ(BÈC)=(AÈB)ÈC | 2b AÇ(BÇC)=(AÇB)ÇC (ассоциативность) |
| 3a AÇ(BÈC)=(AÇB)È(AÇC) | 3b AÈ(BÇC)=(AÈB)Ç(BÈC) (дистрибутивность) |
Законы поглощения:
| 4a (AÇB)ÈB=B | 4b (AÈB)ÇB=B |
| 5a (AÇ )ÈB=B | 5b (AÈ )ÇB=B |
Дополнительные свойства:
Мощность множества.
Конечные множества можно сравнивать по количеству элементов, содержащихся в них. Для сравнения по насыщенности бесконечных множеств используется принцип сравнения. Между множеством точек гипотенузы прямоугольного треугольника и множеством точек катета можно установить соответствие таким образом, что каждой точке гипотенузы будет соответствовать точка катета и при этом разным точкам гипотенузы соответствуют разные точки катета. Соответствие устанавливается с помощью прямой, проведенной параллельно другому катету через взятую на гипотенузе точку М.
Определение. Говорят, что между элементами А и В установлено взаимно однозначное соответствие, если указано правило, по которому каждому элементу аÎА сопоставлен один элемент вÎВ, называемый образом а, причем выполнены следующие два условия: 1) любые два различные элемента из А имеют различные образы; 2) каждый элемент из В является образом некоторого элемента из А.
Определение. Два множества А и В называются эквивалентными или имеющими одинаковую мощность (обозначается А ~ В), если между их элементами может быть установлено взаимно однозначное соответствие.
Примеры эквивалентных бесконечных множеств:
1. Множество N всех натуральных чисел и множество N1 всех целых отрицательных чисел эквивалентны: nÎN, -nÎN1, N~N1
2. Множество N эквивалентно множеству P положительных четных чисел:
nÎN, 2nÎP, N~P.
3. Множество действительных чисел и множество чисел интервала G=( ; — )
эквивалентны между собой. Эквивалентность этих множеств легко проверить с помощью соответствия у=tgx (xÎG,yÎR).
4. Любые два отрезка эквивалентны между собой. Взаимно однозначное соответствие между точками отрезков ОА и ОВ устанавливается с помощью прямых,
проводимых параллельно отрезку АВ. Способ установления взаимно однозначного соответствия между элементами (точками) показан на рисунке.
Два множества, порознь эквивалентные третьему, эквивалентны между собой: Если А~B и B~C, то А~B. Поэтому любой отрезок эквивалентен, например, отрезку [0;1].
Множества, эквивалентные множеству всех вещественных чисел из отрезка [0;1] называют множеством мощности континуум (сокращенно мощности С). Значит, множество чисел любого числового отрезка имеет мощность С. В частности, множество всех вещественных чисел R~( ; — )~[0;1] имеет мощность С.
cyberpedia.su
Материал по математике «Круги Эйлера»
Круги Эйлера
Цель: показать, что применение кругов Эйлера придает задачам наглядность и простоту; круги Эйлера с успехом применяются в логических задачах для изображения множеств истинности высказываний.
1. Введение
Леонард Эйлер (1707 — 1783).
Эйлеру повезло: он родился в маленькой тихой Швейцарии, куда изо всей Европы приезжали мастера и ученые, не желавшие тратить дорогое рабочее время на гражданские смуты или религиозные распри. Так переселилась в Базель из Голландии семья Бернулли: уникальное созвездие научных талантов во главе с братьями Якобом и Иоганном. По воле случая юный Эйлер попал в эту компанию и вскоре сделался достойным членом базельского питомника гениев.
Эйлер принадлежит к числу гениев, чьё творчество стало достоянием всего человечества. До сих пор школьники всех стран изучают тригонометрию и логарифмы в том виде, какой придал им Эйлер. Студенты проходят высшую математику под руководством, первыми образцами которых явились классические монографии Эйлера. Он был, прежде всего, математиком, но он знал, что почвой, на которой расцветает математика, является практическая деятельность. Он оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. Трудно даже перечислить все отрасли, в которых трудился великий учёный.
Его называли идеальным математиком 18 века.
Леонард Эйлер написал более 850 научных работ. В одной из них и появились круги. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный прием использовал ученый Джон Венн — британский логик и философ; основные труды в области логики классов; и этот приём назвали «диаграммы Венна», который используется во многих областях: теория множеств, теория вероятностей, логика, статистика, компьютерные науки.
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов, и они получили название «круги Эйлера-Венна».
Этот метод даёт более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах.
В нашем учебнике по математике множество всех действительных чисел Эйлер изображено с помощью этих кругов: N — Множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество вех действительных чисел.
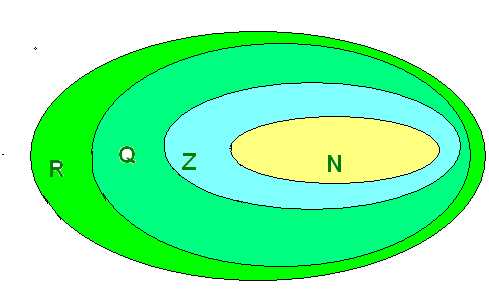
2. Решение задач с помощью кругов Эйлера
Задача 1. В гостях на уроке математики присутствовало 3 математика, директор и завуч. Из них преподаёт только математику один человек. Возможно ли это, если да, то показать это с помощью кругов Эйлера-Венна.
Задача 2. Интересная задача родилась при изучении простых чисел. Даны множества: натуральны, четные и простые числа. Найти пересечение этих множеств.
Ответ: 2.
Задача 3. Все мои друзья занимаются каким-нибудь видом спорта. 16 из них увлекаются футболом, а 12 — баскетболом. И только двое увлекаются и тем и другим видом спорта. Угадайте, сколько у меня друзей?
Решение: Обратимся к кругам Эйлера:
Изобразим два множества (можно вводить обозначения их не только кругами), так как два вида спорта. В одном я буду фиксировать друзей, которые увлекаются футболом, а в другом — баскетболом. Поскольку некоторые из моих друзей увлекаются и тем и другим видом спорта, то квадраты нарисую так, чтобы у них была общая часть (пересечение). В этой общей части ставим цифру 2. В оставшейся части «футболистов» круга ставим цифру 14 (16 − 2= 14). В свободной части «баскетболистов» круга ставим цифру10 (12 − 2 = 10). А теперь рисунок сам подсказывает, что всего у меня 14 + 2 + 10 = 26 друзей.
Ответ: 26 друзей.
Задача 4.
Дано множество: А = {–16; 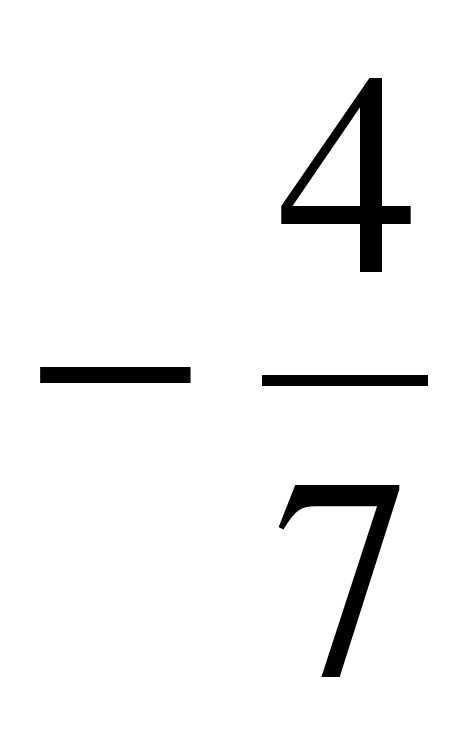 ; –0,3; 9; 1
; –0,3; 9; 1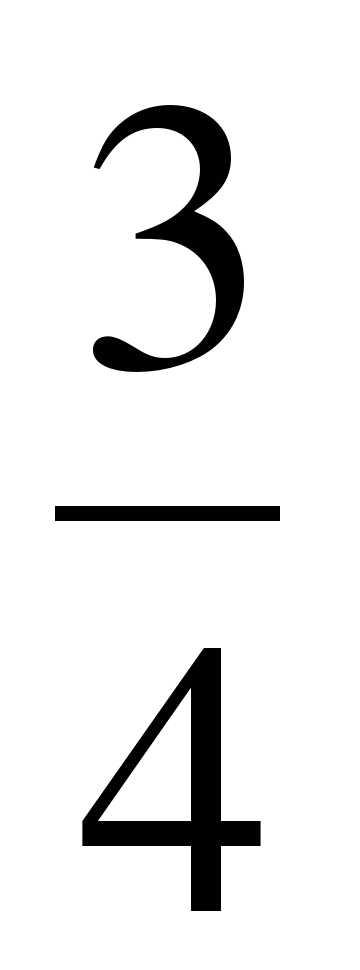 ; 0; –5; 2; 4,8}. Составьте из элементов этого множества подмножества: 1) В – отрицательных рациональных чисел; 2) С – натуральных чисел; 3) D – целых чисел; 4) Е – целых отрицательных чисел. Постройте круги Эйлера-Венна множеств A, B, C, D и E.
; 0; –5; 2; 4,8}. Составьте из элементов этого множества подмножества: 1) В – отрицательных рациональных чисел; 2) С – натуральных чисел; 3) D – целых чисел; 4) Е – целых отрицательных чисел. Постройте круги Эйлера-Венна множеств A, B, C, D и E.
Задача 5.
Выберите из множества А = {1,5; –7; 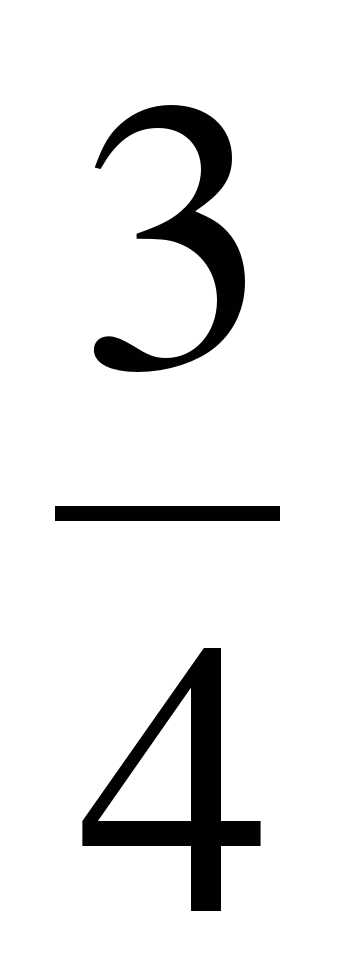 ; 0; 9; –2
; 0; 9; –2 ; 68} подмножество: 1) В – натуральных чисел; 2) С – целых чисел; 3) D – рациональных чисел. Постройте круги Эйлера-Венна множеств. А, В, С и D и отметьте на ней элементы множества А.
; 68} подмножество: 1) В – натуральных чисел; 2) С – целых чисел; 3) D – рациональных чисел. Постройте круги Эйлера-Венна множеств. А, В, С и D и отметьте на ней элементы множества А.
Задача 6
Дано множество: А = {–2; 0,8; 15; 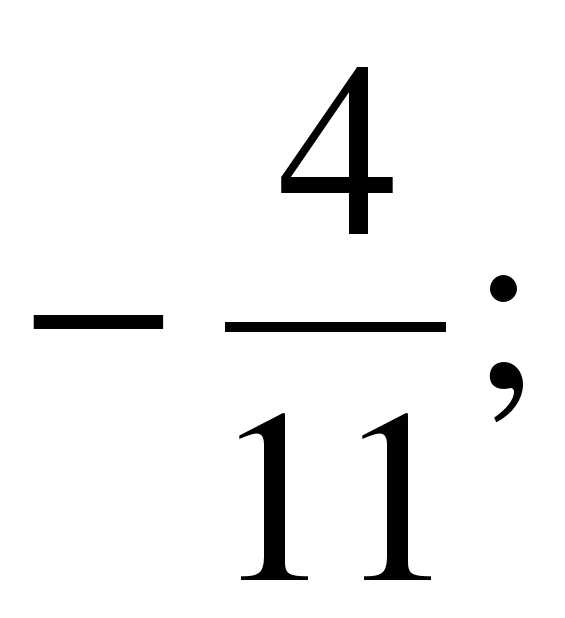 –36; 0;
–36; 0; 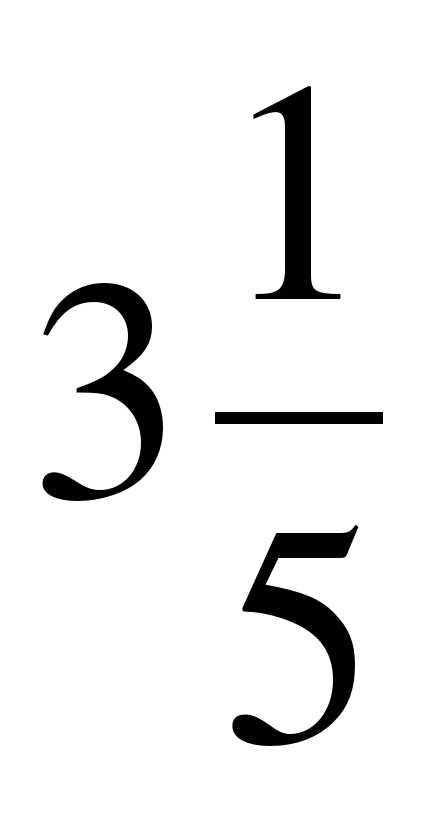 ; 4}. Нарисуйте круги Эйлера-Венна множеств N, Z, Q и отметьте на ней элементы множества А.
; 4}. Нарисуйте круги Эйлера-Венна множеств N, Z, Q и отметьте на ней элементы множества А.
Задача 7.
Выберите из множества А = {5; 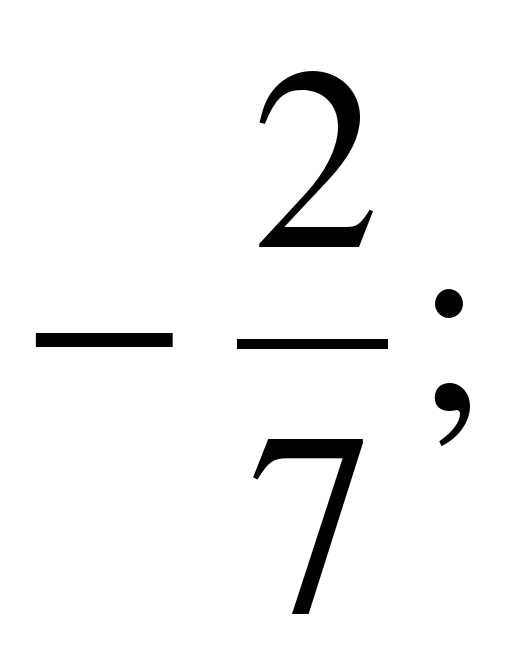 0; –12; –7,8;
0; –12; –7,8; 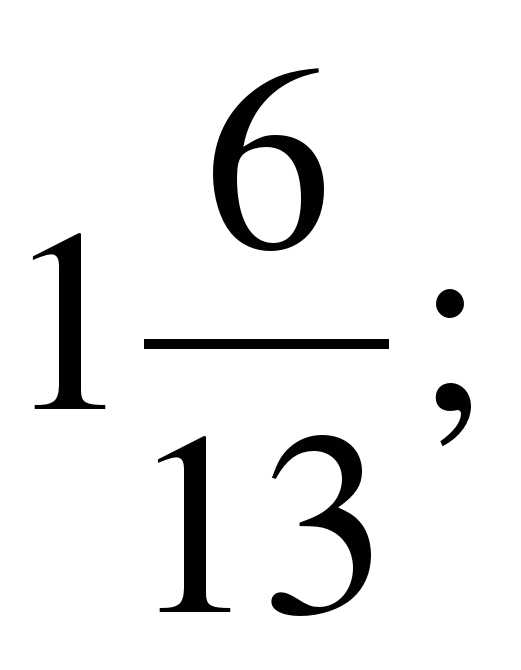 –0,95; 8,6; 21;
–0,95; 8,6; 21; 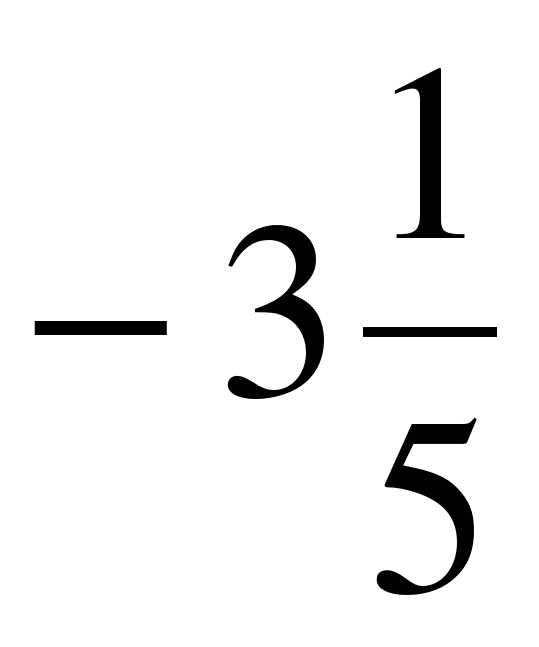 } подмножество: 1) В – положительных чисел; 2) С – отрицательных чисел; 3) D – целых чисел; 4) Е – натуральных чисел; 5) F – неотрицательных целых чисел; 6) К – отрицательных дробных чисел. Постройте круги Эйлера-Венна множеств A, B, C и D. Обведите на ней красным карандашом множество Е, зеленым – множество F, а желтым – множество К.
} подмножество: 1) В – положительных чисел; 2) С – отрицательных чисел; 3) D – целых чисел; 4) Е – натуральных чисел; 5) F – неотрицательных целых чисел; 6) К – отрицательных дробных чисел. Постройте круги Эйлера-Венна множеств A, B, C и D. Обведите на ней красным карандашом множество Е, зеленым – множество F, а желтым – множество К.
Задача 8.
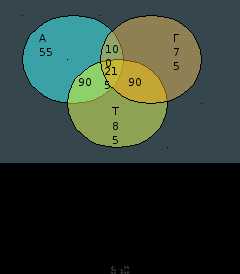
Экзамен по математике содержал 3 задачи: по алгебре, по геометрии и тригонометрии. Из 650 студентов по алгебре решили 400 студентов, по геометрии – 480, по тригонометрии 420 человек. Задачи только по алгебре и геометрии решили 100 человек, только по геометрии и тригонометрии – 90 человек. Сколько студентов решили только одну задачу?
Решение: А – задачи по алгебре, Г – задачи по геометрии, Т – задачи по тригонометрии. По условию: АГ = 100, АТ – 90, Т – 85, Г = 75.
Нам надо найти количество студентов решивших одну задачу, т.е. m (А)+ m (Т) + m (Г), где неизвестно лишь m (А) – количество студентов решивших только алгебру. Из условия геометрию решили 480, следовательно, m (АТГ) = 480 m (Г) – m (АГ) – m (ГТ) = 480-75-100-90 = 215 – количество человек, которые решили все три задачи. Из условия тригонометрию решили 420, следовательно: m (А) = 400 – m (АГ) – m (АТГ) – m (АТ) = 400 – 100 – 215 – 30 = 55 – количество абитуриентов решили только алгебру.
Проверка: итак m (А) + m (Т) + m (Г) = 55 + 85 + 75 = 215 – количество человек, которые решили только 1 задачу. Так как всего 650 студентов, то должно выполниться равенство: 215 + 100 + 30 + 90 + 215 = 650 – верно!
Ответ: 215 человек, которые решили только 1 задачу.
Задача 9.
Учитель математики прочитала нам задачу из раздела круги Эйлера-Венна: по дороге шли два отца и два сына. А всего три человека. Возможна ли такая ситуация и как показать это с помощью кругов Эйлера-Венна?
Решение:
Отмечу 2 множества: сыновья и отцы. Зная, какие родственные узы бывают, я делаю вывод, что по дороге шел мальчик со своим отцом и дедушкой.
Ответ: По дороге: папа с сыном и своим отцом.
Задача 10: За праздничным столом собрались родственники. Папа объявил, что сегодня у нас в гостях 4 поколения, среди которых 4 мамы, 2 деда и 3 папы, 3 бабушки, 5 детей, а всего 9 человек. Известно, что среди нас 1 прабабушка и только 1 женщина является и мамой, дочкой и внучкой. Как решить данную задачу. Кто собрался за праздничным столом?
Р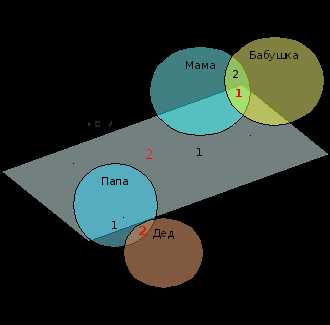 ешение:
ешение:
Ответ: К своей дочери (у неё 2 детей) пришли в гости папа, мама и её бабушка по линии мамы. В гости к её мужу приехали папа и мама.
Сложные задачи
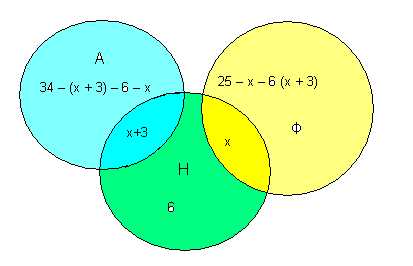
Задача 1. В восьмом классе учится 40 человек. Каждый из них изучает не менее одного иностранного языка: английский (А), немецкий (Н), французский (Ф). 34 человека изучают хотя бы один из двух языков: английский, немецкий. 25 человек — хотя бы один из языков: немецкий, французский. 6 человек только немецкий. Одновременно два языка — английский и немецкий — изучают на 3 человека больше, чем французский и немецкий языки. Сколько человек изучает каждый из языков и сколько изучает одновременно каждую пару языков?
Решение. При решении данной задачи недостаточно метода «Круги Эйлера-Венна». Удобно применить составление уравнения по условию задачи, а круги Эйлера-Венна в данной задаче наглядно показывают решение.
А
хотя бы 1
+ Н = 34Ф + Н = 25
Н = 6
По условию: А + Н = на 3 человека , чем Ф + Н = х изучают одновременно 2 языка.
Составим и решим уравнение:
34 – х – 3 – 6 – х + х + 3 + 6 + х +25 – х – 6 – х – 3 = 40
– 2х = 40 – 34 + 3 – 25
– 2х = –10
х = 5
Ф + Н = 5 человек.
А + Н = 8 человек.
А = 34 – 8 – 6 – 5 =15 человек.
Н = 6 человек.
Ф =25 – 5 – 6 –8 = 6 человек.
Ответ: всего 40 человек.
Пример задачи из жизни, которую я нашел в литературе. Данная задача показывает, что с помощью кругов Эйлера-Венна можно решать не только задачи по математике.
Задача 2. Министерство послало в один из лицеев инспектора для проверки, как в нем ведется преподавание иностранных языков. Сотрудник министерства в отчете записал, что в лицее учатся 100 детей. Каждый изучает по крайней мере один из трех языков: французский, немецкий или испанский. Причем все три языка изучают 5 человек; немецкий и испанский 10; французский и испанский 8; немецкий и французский 20; испанский 30, немецкий 23, французский 50. Инспектор, представивший отчет, был уволен. Почему?
Решение: Начнем, как всегда, с обозначений. Назовем Ф множество учащихся, изучающих французский язык, Н – множество учащихся, изучающих немецкий язык, И – тех, кто изучает испанский. В отчете сказано, что каждый из 100 лицеистов изучает хотя бы один из трех языков.
Проверим, соответствует ли это утверждение остальным данным отчета. Их можно записать так: Ф = 50, Н = 23, И = 30, Ф ∩ Н = 20, Ф ∩ И = 8, Н ∩ И = 10, Ф ∩ Н ∩ И = 5. Поскольку множество всех лицеистов есть объединение множеств Ф, Н и И, мощность которого равна 100, то 100 = Ф + Н + И – ( Ф ∩ Н + Ф ∩ И ) + Н ∩ И + Ф ∩ Н ∩ И. Подставим соответствующие значения и получим 50 + 23 + 30 – 20 – 8 – 10 + 5 = 70. Противоречие: 100 ≠ 70. Попробуем из отчета инспектора понять, сколько учеников изучают только немецкий язык. Как следует из рис.5, мощность данного множества равна Н – Н ∩ Ф – Н ∩ И + Н ∩ И ∩ Ф. Подставив соответствующие значения в последнюю формулу, получим 23 – 20 – 10 + 5 = – 2. Опять абсурд! Вывод очевиден – проверка была произведена плохо или совсем не проводилась. Не исключено, что инспектор взял произвольные числа.
videouroki.net
Круги Эйлера Вики
Пример кругов Эйлера. Буквами обозначены, например, свойства: B{\displaystyle B} — живое существо, A{\displaystyle A} — человек, C{\displaystyle C} — неживая вещьДиагра́ммы Э́йлера (круги́ Э́йлера) — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Первое их использование приписывают Леонарду Эйлеру (подробней см. ниже). Используется в математике, логике, менеджменте и других прикладных направлениях. Не следует их путать с диаграммами Эйлера — Венна (о различии между ними см. ниже).
Диаграммы Эйлера также называют кругами Эйлера. При этом «круги» — это условный термин, вместо кругов могут быть любые фигуры.
На диаграммах Эйлера множества изображаются кругами (или другими фигурами). Причём непересекающиеся множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами. Например, диаграмма на рисунке показывает, что множество A является подмножеством B, а B не пересекается с C.
История[ | код]
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.[1]
Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Венн предложил свою схему изображения отношения между множествами, которая теперь называется диаграммами Эйлера — Венна. Первоначально круги Эйлера возникли на основе идей силлогистики Аристотеля. Диаграммы Венна были созданы для решения задач математической логики. Их основная идея разложения на конституенты возникла на основе алгебры логики[2].
Связь диаграмм Эйлера и Венна[ | код]
Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествами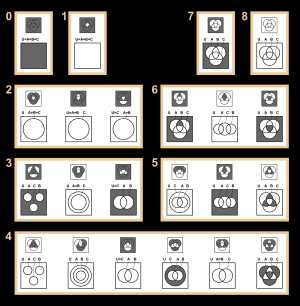 22 (из 256) существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу)
22 (из 256) существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу)Диаграммы Эйлера — Венна в отличие от диаграмм Эйлера изображают все 2n{\displaystyle 2^{n}} комбинаций n{\displaystyle n} свойств, то есть конечную булеву алгебру. При n=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
На рис. ниже даны диаграммы Венна и Эйлера для 3 множеств однозначных натуральных чисел:
- A={1,2,5}{\displaystyle A=\{1,\,2,\,5\}}
- B={1,6}{\displaystyle B=\{1,\,6\}}
- C={4,7}{\displaystyle C=\{4,\,7\}}
диаграмма Эйлера
диаграмма Венна
Иногда, если какая-то комбинация свойств соответствует пустому множеству, то эту комбинацию закрашивают. На рисунке справа даны 22 существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу). Некоторые из диаграмм Эйлера не типичны, а некоторые даже эквивалентны диаграммам Венна. Черные области указывают на то, что в них нет элементов (пустые множества).
Примеры[ | код]
На рисунке внизу дана Диаграмма Эйлера, иллюстрирующая тот факт, что множество существ с 4 конечностями является подмножеством животных, которое не пересекается с множеством минералов.
Диаграмма ЭйлераСм. также[ | код]
Примечания[ | код]
- ↑ Leibniz G. W. Opuscules et fragments inédits de Leibniz. — Paris, 1903. — p. 293—321.
- ↑ Кузичев, 1968, с. 25.
Литература[ | код]
- Кузичев А. С. Диаграммы Венна. История и применения. — М.: Наука, 1968. — 249 с.
ru.wikibedia.ru
Понятие множества. Круги Эйлера. Операции над множествами
Математика Понятие множества. Круги Эйлера. Операции над множествамипросмотров — 215
46.
Лекция 9. Теоретико-множественные понятия в математике
9.1. Понятие множества. Круги Эйлера. Операции над множествами
9.2. Отношения и отображения как соответствия между элементами множеств. Мощность множества
9.3. Множество действительных чисел и его основные подмножества
9.4. Окрестность точки, элементы топологии
Множество – совокупность, набор каких-либо предметов (объектов) произвольной природы, объединенных по какому –либо общему для них признаку (множество студентов данной группы, множество цветных телевизоров в гостинице, множество чисел первого десятка, множество точек на прямой и т. д.).Немецкий математик Г.Кантор считал, что «множество есть многое, мыслимое нами как единое».Понятие множества, точки, числа приходится принимать без определения.
Объекты, из которых состоит множество, называют его элементами. В случае если элементами множества являются числа, то оно принято называть числовым множеством. Множестваобозначаются большими буквами латинского алфавита А, В, С,…, а их элементы- малыми буквами этого алфавита. В случае если элемент х принадлежит множеству А, то пишут х А, если же х не принадлежит множеству А, то пишут х А.
Множества можно задать двумя способами:
1) перечислить его элементы;
2) описать его элементы с помощью характеристического свойства.
Множество, не имеющее элементов, называют пустым и обозначают Ø.
Примеры пустых множеств:
1) Множество действительных чисел, являющихся корнями уравнения
х2 +1=0.
2) Множество треугольников, сумма углов которых ≠ 180.
3) Множество решений системы уравнений
3х +4у =7
6х +8у = 10
Множества бывают конечными и бесконечными. К примеру, множество А= { 0,1,2,3,4,5,6,7,8,9 } всех цифр — конечное, а множество всех целых чисел, составленных из этих цифр — бесконечное.
Одно и то же множество может быть задано разными характеристическими свойствами: множество А ={ 2,4 } можно определить как множество четных чисел, удовлетворяющих неравенству А = { х: 1 < x < 5, х- четное} и как множество корней квадратного уравнения х2 – 6 х + 8 = 0: А = { х: х2 – 6 х + 8 = 0 }
Примеры множеств в геометрии, описываемых
характеристическими свойствами:
биссектриса угла – геометрическое место точек плоскости, лежащих
внутри угла и равноудаленных от его сторон;
окружность— геометрическое место точек плоскости, равноудаленных от фиксированной точки – центра окружности.
Множество, содержащее все те элементы, которые встречаются в контексте проводимых рассуждений, принято называть универсальным и обозначается Е.
Два множества А и В считаются равными, если они состоят из одних и тех же элементов: А = В ↔ для любого х ( х А ↔ х В).
Множество А принято называть подмножеством множества В : А С В , если
из того, что х А следует, что х В.
В случае если А С В и В С А, то множества А и В равны : А=В.
Для обозначения множеств удобно использовать круги Эйлера, диаграммы Венна, диаграммы Эйлера – Венна — ϶ᴛᴏ замкнутые линии, внутри которых расположены элементы данного множества, а снаружи – элементы, не принадлежащие множеству.
А С В
Пусть Е – какое-либо множество, рассмотрим всевозможные его подмножества. В этом случае Е является универсальным множеством.
1) Пусть Е – какое-либо множество книг, его подмножества: научные книги, художественные книги, книги по искусству, учебники.
2) Е = { а, в, с } и его подмножества: { Ø, { а,в,с }, {а}, {в}, {с}, {а,в}, {в,с}, {а,с} }, количество таких подмножеств 23 = 8.
В случае если Е – универсальное множество, состоящее из n элементов, то число его подмножеств 2n.
Операции над множествами
1) Объединением( или суммой ) множеств А и В принято называть множество С = А В , составленное из всех элементов, принадлежащих хотя бы одному из этих множеств, ᴛ.ᴇ. из элементов, входящих либо в А, либо в В (не исключается возможность одновременной принадлежности и к множеству А и к множеству В). Знак принято называть знаком объединения.
А В А B C
2) Пересечением (или произведением) множеств А и В принято называть множество С = А ∩ В, состоящее из элементов, принадлежащих и множеству А, и множеству В одновременно. Знак ∩ принято называть знаком пересечения.
А ∩ В А ∩ В ∩ С А ∩ В=А
3) Разностью множеств А и В принято называть множество С = А \ В, состоящее из элементов множества А, не входящих во множество В.А \ В А\ В А\ В=А
Результат применения операций к множествам изображается на кругах Эйлера.
Пусть Е – универсальное множество, А С Е.
Множество Ā = Е \ А принято называть дополнением до множества А.
а) Е – множество студентов в группе, А – юноши, Ā – девушки.
б) Е – множество прямоугольников, А – множество квадратов, Ā – множество прямоугольников с разными (неравными) сторонами.
в) Е – множество целых чисел, А = {множество четных чисел}, Ā = { множество нечетных чисел }.
Пример: пусть А – множество натуральных делителей числа 72, а В – множество натуральных делителей числа 54:
А = { 1; 2; 3; 4; 6, 8, 9, 12, 18, 24, 36, 72}, В = {1, 2, 3, 6, 9, 18, 27, 54}.
Тогда: А U В = {1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72 },
А ∩ В = {1, 2, 3, 6, 9, 18 }, А \ В = { 8, 4, 12, 24, 36, 72}.
4) Декартовым произведением множеств А и В принято называть множество
А х В всех упорядоченных пар элементов (а, b), где а Є А, b Є В.
В случае если множество А = {1,2 }, а множество В = {1, 2, 3}, тогда
А х В = { (1, 2), (1, 1), (1 ,3), (2, 1), (2, 2), (2, 3)},
В х А = { (1, 1), (1, 2), (2, 1), (2, 2), (3, 1), (3, 2)}
В В
АхВ ВхА
А А
Основные законы операций над множествами
1) А В = В А, А ∩ В = В ∩ А (переместительный),
2) (А B) C = A ( B C) , (А ∩ В) ∩ C= A ∩ (B∩C) (сочетательный),
3) А Ø = А, А ∩ Ø = Ø, Ø \ А = Ø, А \ А = Ø, Ø играет роль нуля в алгебре, но Ø \ А = Ø не имеет аналога в алгебре.
4) Ẫ = А, А Ā = E, A ∩ Ā = Ø, E \ A = Ā, A \ E = Ø, А A = A,
A ∩ A = A, A E = E, A ∩ E = A.
| Законы Моргана |
A ∩ (B C) = (A ∩ B) (A ∩ C)
oplib.ru