Квадратное неравенство
Квадратное неравенство – «ОТ и ДО». В этой статье мы с вами рассмотрим решение квадратных неравенств что называется до тонкостей. Изучать материал статьи рекомендую внимательно ничего не пропуская. Осилить статью сразу не получится, рекомендую сделать это за несколько подходов, информации много.
Содержание:
Вступление. Важно!
Алгоритм решения квадратного неравенства. Метод интервалов. Примеры.
Использование графика квадратичной функции. Рекомендую!
Решение квадратного неравенства. Все случаи…
Вступление. Важно!
Рекомендую повторить формулы для решения квадратного уравнения и научиться быстро его решать. Без этого о решении квадратных неравенств речи быть не может.
Квадратное неравенство – это неравенство вида:
Если взять квадратное уравнение и заменить знак равенства на любой из указанных выше, то получится квадратное неравенство. Решить неравенство — это значит ответить на вопрос, при каких значениях х данное неравенство будет верно. Примеры:
10x2– 6x+12 ≤ 0
2x2+ 5x –500 > 0
– 15x2– 2x+13 > 0
8x2– 15x+45≠ 0
Квадратное неравенство может быть задано в неявном виде, например:
10x2– 6x+14x2 –5x +2≤ 56
2x2 > 36
8x2<–15x2– 2x+13
0> – 15x2– 2x+13
В этом случае необходимо выполнить алгебраические преобразования и привести его к стандартному виду (1).
*Коэффициенты могут быть и дробными и иррациональными, но в школьной программе такие примеры редкость, а в заданиях ЕГЭ не встречаются вообще. Но вы не пугайтесь, если, например, встретите:
Это тоже квадратное неравенство.
Сначала рассмотрим простой алгоритм решения, не требующий понимания того, что такое квадратичная функция и как её график выглядит на координатной плоскости относительно осей координат. Если вы способны запоминать информацию крепко и надолго, при этом регулярно подкрепляете её практикой, то алгоритм вам поможет. Так же если вам, как говорится, нужно решить такое неравенство «наразок», то алгоритм вам в помощь. Следуя ему вы без труда осуществите решение.
Если же вы учитесь в школе, то настоятельно рекомендую вам начать изучение статьи со второй части, где рассказывается весь смысл решения (смотрите ниже с пункта – использование графика квадратичной функции). Если будет понимание сути, то не учить, не запоминать указанный алгоритм будет не нужно, вы без труда быстро решите любое квадратное неравенство.
Конечно, следовало бы сразу начать разъяснение именно с графика квадратичной функции и oбъяснения самого смысла, но решил «построить» статью именно так.
Ещё один теоретический момент! Посмотрите формулу разложения квадратного трёхчлена на множители:
где х1 и х2 — корни квадратного уравнения ax2+bx+c=0
*Для того, чтобы решить квадратное неравенство, необходимо будет квадратный трёхчлен разложить на множители.
Представленный ниже алгоритм называют ещё методом интервалов. Он подходит для решения неравенств вида f(x)>0, f(x)<0, f(x)≥0 и f(x)≤0. Обратите внимание, что множителей может более двух, например:
(х–10)(х+5)(х–1)(х+104)(х+6)(х–1)<0
Алгоритм решения. Метод интервалов. Примеры.
Дано неравенство ax2 + bx + с > 0 (знак любой).
1. Записываем квадратное уравнение ax2 + bx + с = 0 и решаем его. Получаем х1 и х2 – корни квадратного уравнения.
2. Подставляем в формулу (2) коэффициент a и корни. Записываем неравенство в виде:
a (x – x1)(x – x2)>0
3. Определяем интервалы на числовой прямой (корни уравнения делят числовую ось на интервалы):
4. Определяем «знаки» на интервалах (+ или –) путём подстановки произвольного значения «х» из каждого полученного интервала в выражение:
a (x – x1)(x – x2)
и отмечаем их.
5. Остаётся лишь выписать интересующие нас интервалы, они отмечены:
— знаком «+», если в неравенстве стояло «>0» или «≥0».
— знаком «–», если в неравенстве было «<0» или «≤0».
Далее записываем ответ.
ОБРАТИТЕ ВНИМАНИЕ!!! Сами знаки в неравенстве могут быть:
строгими – это «>», «<» и нестрогими – это «≥», «≤».
Как это влияет на результат решения?
При строгих знаках неравенства границы интервала НЕ ВХОДЯТ в решение, при этом в ответе сам интервал записывается в виде (x1;x2) – скобки круглые.
При нестрогих знаках неравенства границы интервала ВХОДЯТ в решение, и ответ записывается в виде [x1;x2] – скобки квадратные.
*Это касается не только квадратных неравенств. Квадратная скобка означает, что сама граница интервала включена в решение.
На примерах вы это увидите. Давайте разберём несколько, чтобы снять все вопросы по этому поводу. В теории алгоритм может показаться несколько сложным, на самом деле всё просто.
ПРИМЕР 1: Решить x2– 60x+500 ≤ 0
Решаем квадратное уравнение x2–60x+500=0
D = b2–4ac = (–60)2–4∙1∙500 = 3600–2000 = 1600
Находим корни:
Подставляем коэффициент a и корни в формулу (2), получаем:
x2–60x+500 = (х–50)(х–10)
Записываем неравенство в виде (х–50)(х–10) ≤ 0
Корни уравнения делят числовую ось на интервалы. Покажем их на числовой прямой:
Мы получили три интервала (–∞;10), (10;50) и (50;+∞).
Определяем «знаки» на интервалах, делаем это путём подстановки в выражение (х–50)(х–10) произвольных значений их каждого полученного интервала и смотрим соответствие полученного «знака» знаку в неравенстве (х–50)(х–10) ≤ 0:
при х=2 (х–50)(х–10) = 384 > 0 неверно
при х=20 (х–50)(х–10) = –300 < 0 верно
при х=60 (х–50)(х–10) = 500 > 0 неверно
Решением будет являться интервал [10;50].
При всех значениях х из этого интервала неравенство будет верным.
*Обратите внимание, что мы поставили квадратные скобки.
При х = 10 и х = 50 неравенство также будет верно, то есть границы входят в решение.
Ответ: x∊[10;50]
Ещё раз:
— Границы интервала ВХОДЯТ в решение неравенства тогда, когда в условии стоит знак ≤ или ≥ (нестрогое неравенство). При этом на эскизе принято полученные корни отображать ЗАШТРИШОВАННЫМ кружком.
— Границы интервала НЕ ВХОДЯТ в решение неравенства тогда, когда в условии стоит знак < или > (строгое неравенство). При этом на эскизе принято корень отображать НЕЗАШТРИХОВАННЫМ кружком.
ПРИМЕР 2: Решить x2+ 4x–21 > 0
Решаем квадратное уравнение x2+ 4x–21 = 0
D = b2–4ac = 42–4∙1∙(–21) =16+84 = 100
Находим корни:
Подставляем коэффициент a и корни в формулу (2), получаем:
x2+ 4x–21 = (х–3)(х+7)
Записываем неравенство в виде (х–3)(х+7) > 0.
Корни уравнения делят числовую ось на интервалы. Отметим их на числовой прямой:
*Неравенство нестрогое, поэтому обозначения корней НЕзаштрихованы. Получили три интервала (–∞;–7), (–7;3) и (3;+∞).
Определяем «знаки» на интервалах, делаем это путём подстановки в выражение (х–3)(х+7) произвольных значений их этих интервалов и смотрим соответствие неравенству (х–3)(х+7)> 0:
при х= –10 (–10–3)( –10 +7) = 39 > 0 верно
при х= 0 (0–3)(0 +7) = –21 < 0 неверно
при х=10 (10–3)(10 +7) = 119 > 0 верно
Решением будут являться два интервала (–∞;–7) и (3;+∞). При всех значениях х из этих интервалов неравенство будет верным.
*Обратите внимание, что мы поставили круглые скобки. При х = 3 и х = –7 неравенство будет неверным – границы не входят в решение.
Ответ: x∊(–∞;–7) U (3;+∞)
ПРИМЕР 3: Решить –x2–9x–20 > 0
Решаем квадратное уравнение –x2–9x–20 = 0.
a = –1 b = –9 c = –20
D = b2–4ac = (–9)2–4∙(–1)∙ (–20) =81–80 = 1.
Находим корни:
Подставляем коэффициент a и корни в формулу (2), получаем:
–x2–9x–20 =–(х–(–5))(х–(–4))= –(х+5)(х+4)
Записываем неравенство в виде –(х+5)(х+4) > 0.
Корни уравнения делят числовую ось на интервалы. Отметим на числовой прямой:
*Неравенство строгое, поэтому обозначения корней незаштрихованы. Получили три интервала (–∞;–5), (–5; –4) и (–4;+∞).
Определяем «знаки» на интервалах, делаем это путём подстановки в выражение –(х+5)(х+4) произвольных значений их этих интервалов и смотрим соответствие неравенству –(х+5)(х+4)>0:
при х= –10 – (–10+5)( –10 +4) = –30 < 0 неверно
при х= –4,5 – (–4,5+5)(–4,5+4) = 0,25 > 0 верно
при х= 0 – (0+5)(0 +4) = –20 < 0 неверно
Решением будут являться интервал (–5;–4). При всех значениях «х» принадлежащих ему неравенство будет верным.
*Обратите внимание, что границы не входят в решение. При х = –5 и х = –4 неравенство будет неверным.
ЗАМЕЧАНИЕ!
При решении квадратного уравнения у нас может получится один корень или корней не будет вовсе, тогда при использовании данного метода вслепую могут возникнуть затруднения в определении решения.
Небольшой итог! Метод хорош и использовать его удобно, особенно если вы знакомы с квадратичной функцией и знаете свойства её графика. Если нет, то прошу ознакомиться, приступим к следующему разделу.
Использование графика квадратичной функции. Рекомендую!
Квадратичная это функция вида:
Её графиком является парабола, ветви параболы направлены вверх, либо вниз:
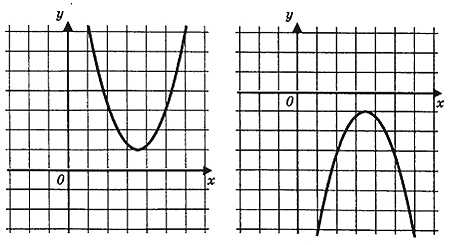
График может быть расположен следующим образом: может пересекать ось х в двух точках, может касаться её в одной точке (вершиной), может не пересекать. Об этом подробнее в дальнейшем.
Теперь рассмотрим этот подход на примере. Весь процесс решения состоит из трёх этапов. Решим неравенство x2+2x –8 >0.
Первый этап
Решаем уравнение x2+2x–8=0.
D = b2–4ac = 22–4∙1∙(–8) = 4+32 = 36
Находим корни:
Получили х1=2 и х2 = – 4.
Второй этап
Строим параболу у= x2+2x–8 по точкам:
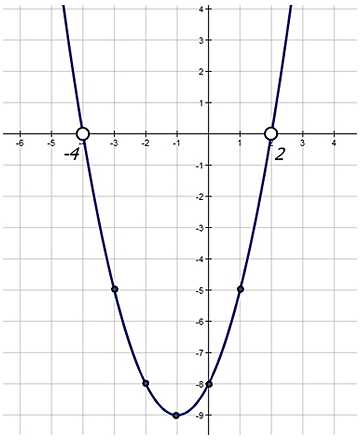
Точки – 4 и 2 это точки пересечения параболы и оси ох. Всё просто! Что сделали? Мы решили квадратное уравнение x2+2x–8=0. Посмотрите его запись в таком виде:
0 = x2+2x – 8
Ноль у нас это значение «у». При у = 0, мы получаем абсциссы точек пересечения параболы с осью ох. Можно сказать, что нулевое значение «у» это есть ось ох.
Теперь посмотрите при каких значениях х выражение x2+2x – 8 больше (или меньше) нуля? По графику параболы это определить несложно, как говорится, всё на виду:
1. При х < – 4 ветвь параболы лежит выше оси ох. То есть при указанных х трёхчлен x2+2x –8 будет положительным.
2. При –4 < х < 2 график ниже оси ох. При этих х трёхчлен x2+2x –8 будет отрицательным.
3. При х > 2 ветвь параболы лежит выше оси ох. При указанных х трёхчлен x2+2x –8 будет положительным.
Третий этап
По параболе нам сразу видно, при каких х выражение x2+2x–8 больше нуля, равно нулю, меньше нуля. В этом заключается суть третьего этапа решения, а именно увидеть и определить положительные и отрицательные области на рисунке. Сопоставляем полученный результат с исходным неравенством и записываем ответ. В нашем примере необходимо определить все значения х при которых выражение x2+2x–8 больше нуля. Мы это сделали во втором этапе.
Остаётся записать ответ.
Ответ: x∊(–∞;–4) U (2;∞).
Подведём итог: вычислив в первом шаге корни уравнения, мы можем отметить полученные точки на оси ох (это точки пересечения параболы с осью ох). Далее схематично строим параболу и уже можем увидеть решение. Почему схематично? Математически точный график нам не нужен. Да и представьте, например, если корни получатся 10 и 1500, попробуй-ка построй точный график на листе в клетку с таким разбегом значений. Возникает вопрос! Ну получили мы корни, ну отметили их на оси ох, а зарисовать расположение самой парабола – ветвями вверх или вниз? Тут всё просто! Коэффициент при х2 вам подскажет:
— если он больше нуля, то ветви параболы направлены вверх.
— если меньше нуля, то ветви параболы направлены вниз.
В нашем примере он равен единице, то есть положителен.
*Примечание! Если в неравенстве будет стоять знак нестрогий, то есть ≤ или ≥, то корни на числовой прямой следует заштриховать, этим условно обозначается, что сама граница интервала входит в решение неравенства. В данном случае корни не заштрихованы (выколоты), так как неравенство у нас строгое (стоит знак «>»). При чем в ответе, в данном случае, ставятся круглые скобки, а не квадратные (границы не входят в решение).
Написано много, кого-то запутал, наверное. Но если вы решите минимум 5 неравенств с использованием парабол, то восхищению вашему предела не будет. Всё просто!
Итак, кратко:
1. Записываем неравенство, приводим к стандартному.
2. Записываем квадратное уравнение и решаем его.
3. Рисуем ось ох, отмечаем полученные корни, схематично рисуем параболу, ветвями вверх, если коэффициент при х2 положителен, или ветвями вниз, если он отрицателен.
4. Определяем визуально положительные или отрицательные области и записываем ответ по исходному неравенству.
Рассмотрим примеры.
ПРИМЕР 1: Решить x2–15x+50 > 0
Первый этап.
Решаем квадратное уравнение x2–15x+50=0
D = b2–4ac = (–15)2–4∙1∙50 = 225–200 = 25
Находим корни:
Второй этап.
Строим ось ох. Отмечем полученные корни. Так как неравенство у нас строгое, то заштриховывать их не будем. Схематично строим параболу, расположена она ветвями вверх, так как коэффициент при х2 положительный:
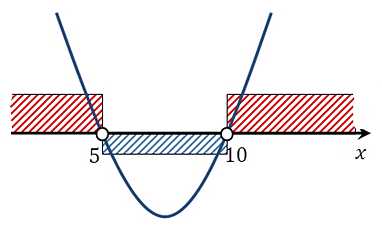
Третий этап.
Определяем визуально положительные и отрицательные области, здесь мы их отметили разными цветами для наглядности, можно этого и не делать.
Записываем ответ.
Ответ: x∊(–∞;5) U (10;∞).
*Знак U обозначает объёдинение решение. Образно можно выразиться так, решением является «этот» И « ещё этот» интервал.
ПРИМЕР 2: Решить –x2+x+20 ≤ 0
Первый этап.
Решаем квадратное уравнение –x2+x+20=0
D = b2–4ac = 12–4∙(–1)∙20 = 1+80 = 81
Находим корни:
Второй этап.
Строим ось ох. Отмечем полученные корни. Так как неравенство у нас нестрогое, то заштрихуем обозначения корней. Схематично строим параболу, расположена она ветвями вниз, так как коэффициент при х2 отрицательный (он равен –1):
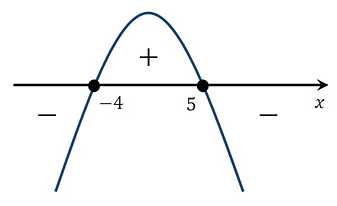
Третий этап.
Определяем визуально положительные и отрицательные области. Сопоставляем с исходным неравенством (знак у нас ≤ 0). Неравенство будет верно при х ≤ – 4 и х ≥ 5.
Записываем ответ.
Ответ: x∊(–∞;–4] U [5;∞).
*Указаны квадратные скобки – это обозначает, что границы интервала входят в решение. Ось оу мы на эскизах не указали, так как она в данной ситуации не играет никакой роли, то есть при построении эскиза ось оу строить необязательно.
Теперь ещё один важный момент! Мы рассмотрели примеры, в которых при решении квадратного уравнения получается два корня, то есть парабола пересекает ось ох в двух точках. Процесс решения понятен. Но возникают вопросы: а если при решении квадратного уравнения получится один корень или вообще не будет корней (дискриминант отрицательный), то как это осмыслить и как определить есть ли решение?
Некоторые ответы очевидны:
— Если получится один корень (дискриминант равен нулю), то парабола будет касаться оси ох в одной точке, а именно своей вершиной.
— Если решения квадратного уравнения нет (дискриминант отрицательный), то парабола вообще не будет касаться оси ох.
Тогда возникает вопрос, что делать в этих ситуациях и как определять ответ?
И вот тут прошу вас обратить внимание на один ключевой момент, который уже оговаривался в этой статье! В неравенстве при х2 у нас может стоять положительный или отрицательный коэффициент. При положительном коэффициенте ветви параболы направлены вверх, при отрицательном вниз. А теперь переходим к следующему разделу статьи.
Решение квадратного неравенства. Все случаи!
Ниже для вас представлены все варианты расположения парабол, которые могут иметь место при решении квадратных неравенств:
Первая группа графиков
(коэффициент а > 0, то есть ветви параболы направлены вверх)
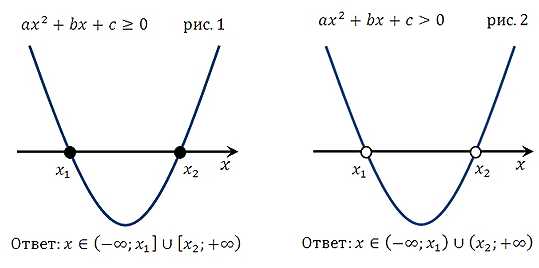
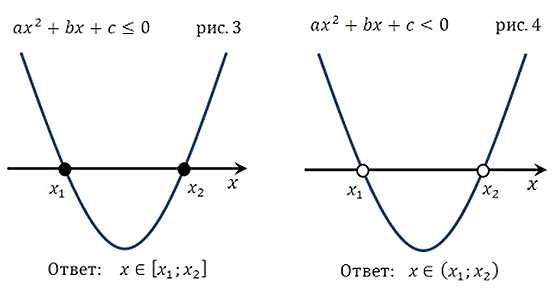

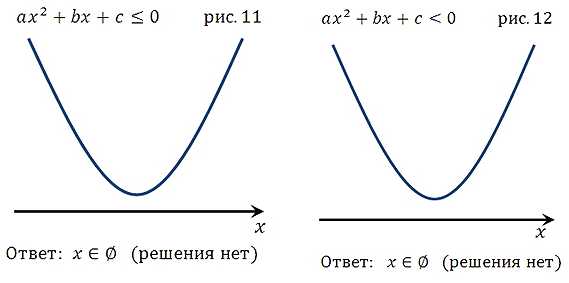
Вторая группа графиков
(коэффициент а < 0, то есть ветви параболы направлены вниз)
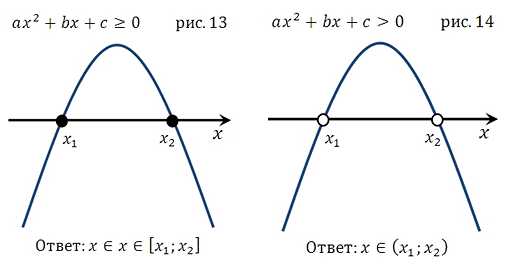
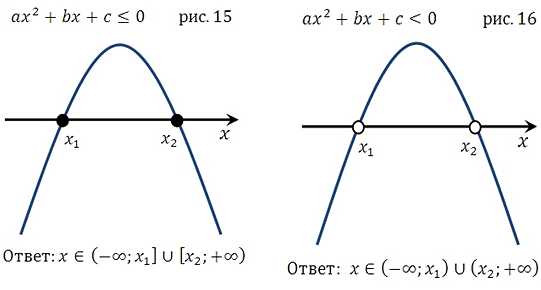
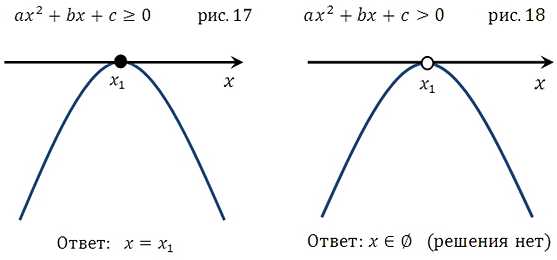
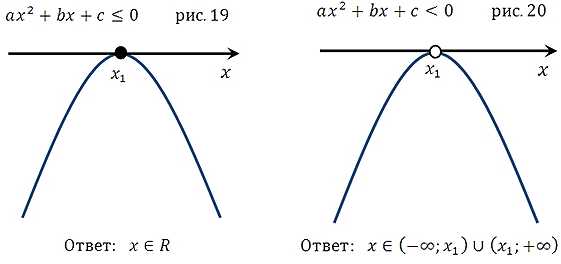
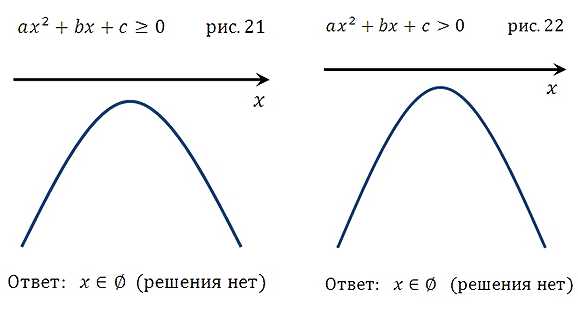
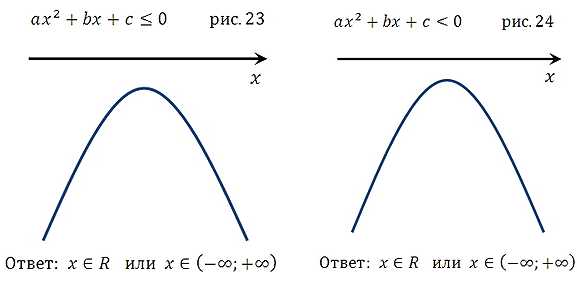
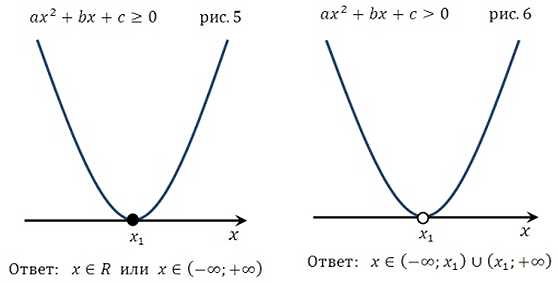
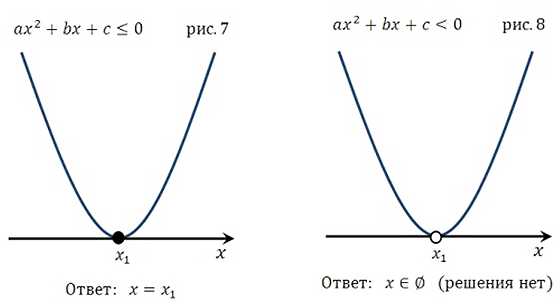
Что касается оговоренных выше вопросов по поводу случая, когда квадратное уравнение не имеет решения, обратите внимание на рисунки 9,10,11,12, 21,22,23,24 и всё поймёте. Подробнее:
Например, при решении квадратного уравнения вы обнаружили, что дискриминант отрицательный, то есть коней нет. Что это означает? А то, что ветви параболы не пересекают ось ох, то есть она расположена либо выше оси ох и её ветви направлены вверх, либо ниже оси и её ветви направлены вниз. И тут нам необходимо разобраться куда в вашем случае направлены ветви. Смотрим на коэффициент при х2:
— если он положительный, то схематично рисуем параболу выше оси ох с ветвями направленными вверх.
— если он отрицательный, то схематично рисуем параболу ниже оси ох с ветвями направленными вниз.
Далее только остаётся сопоставить наш рисунок с данным неравенством и учитывая знак в нём просто записать ответ. Всё!!!
Пример: х2 +2х+16 < 0
Решаем квадратное уравнение x2+2x+16=0
D = b2–4ac = 22–4∙2∙16 = 4–128 = –124
Дискриминант отрицательный, коней нет. Значит парабола не пересекает ось ох.
Коэффициент при х2 положительный (равен 1), значит парабола расположена следующим образом – её ветви направлены вверх и расположена она выше оси ох (как на рис. 12).
Нам необходимо записать значения х, при которых х2 +2х+16 отрицательно. Таких «х» нет, это видно по графику (рис 12).
Ответ: x∊∅ (решения нет).
*Если бы знак в этом неравенстве был «>», то решением были бы все действительные числа (рис. 10).
Теперь завершающий момент который стороной никак обойти нельзя, мы ещё не рассматривали решение неравенства вида:
Тут всё просто. Если вы детально изучили материал изложенный выше в статье и пропустили информацию, что называется, через себя, то здесь на эти вопросы вы ответите без труда.
Возможны три случая, если при решении aх2+bх+c = 0 получаем:
1. Два корня, то решением неравенства будет x∊(–∞;х1) U (х1;х2) U (х2;+∞).
2. Один корень, то решением будет x∊(–∞;х) U (х;+∞).
3. Нет корней, то решением будет вся числовая ось x∊(–∞;+∞).
Получить материал статьи в PDF
Понравилась статья — делитесь с коллегами и друзьями, социальные кнопки к вашим услугам. Также можете скачанный файл свободно распространять в сети.
На этом всё, благодарю за внимание. Ёмкая получилась статейка.
С уважением, Александр крутицких
P.S: Буду благодарен Вам, если расскажите о сайте в социальных сетях.
matematikalegko.ru
Квадратные неравенства
Определение квадратного неравенства
Определение 1
Квадратным неравенством называют неравенство вида
$ax^2+bx+c > 0$ (знак неравенства может быть также $
где $a$, $b$, $c$ – действительные числа и $a \ne 0$,
$x$ – переменная.
Замечание 1
Квадратным неравенство называется т.к. переменная возведена в квадрат. Также квадратные неравенства называют неравенствами второй степени.
Пример 1
Пример.
$7x^2-18x+3 0$, $11z^2+8 \le 0$ – квадратные неравенства.
Как видно из примера, не все элементы неравенства вида $ax^2+bx+c > 0$ присутствуют.
Например, в неравенстве $\frac{5}{11} y^2+\sqrt{11} y>0$ нет свободного члена (слагаемое $с$), а в неравенстве $11z^2+8 \le 0$ нет слагаемого с коэффициентом $b$. Такие неравенства также являются квадратными, но их еще называют неполными квадратными неравенствами. Это лишь означает, что коэффициенты $b$ или $с$ равны нулю.
Методы решения квадратных неравенств
При решении квадратных неравенств используют такие основные методы:
- графический;
- метод интервалов;
- выделения квадрата двучлена.
Графический способ
Замечание 2
Графический способ решения квадратных неравенств $ax^2+bx+c > 0$ (или со знаком $
Данные промежутки и являются решением квадратного неравенства.
Метод интервалов
Замечание 3
Метод интервалов решения квадратных неравенств вида $ax^2+bx+c > 0$ (знак неравенства может быть также $
Решениями квадратного неравенства со знаком $«»$ – положительные промежутки, со знаками $«≤»$ и $«≥»$ – отрицательные и положительные промежутки (соответственно), включая точки, которые отвечают нулям трехчлена.
Выделение квадрата двучлена
Метод решения квадратного неравенства выделением квадрата двучлена заключается в переходе к равносильному неравенству вида $(x-n)^2 > m$ (или со знаком $
Неравенства, которые сводятся к квадратным
Замечание 4
Зачастую при решении неравенств их нужно привести к квадратным неравенствам вида $ax^2+bx+c > 0$ (знак неравенства может быть также $ неравенствами, которые сводятся к квадратным.
Замечание 5
Самым простым способом приведения неравенств к квадратным может быть перестановка в исходном неравенстве слагаемых или перенос их, например, из правой части в левую.
Например, при переносе всех слагаемых неравенства $7x > 6-3x^2$ из правой части в левую получается квадратное неравенство вида $3x^2+7x-6 > 0$.
Если переставить в левой части неравенства $1,5y-2+5,3x^2 \ge 0$ слагаемые в порядке убывания степени переменной $у$, то это приведет к равносильному квадратному неравенству вида $5,3x^2+1,5y-2 \ge 0$.
При решении рациональных неравенств часто используют приведение их к квадратным неравенствам. При этом необходимо перенести все слагаемые в левую часть и преобразовать получившееся выражение к виду квадратного трехчлена.
Пример 2
Пример.
Привести неравенство $7 \cdot (x+0,5) \cdot x > (3+4x)^2-10x^2+10$ к квадратному.
Решение.
Перенесем все слагаемые в левую часть неравенства:
$7 \cdot (x+0,5) \cdot x-(3+4x)^2+10x^2-10 > 0$.
Используя формулы сокращенного умножения и раскрывая скобки, упростим выражение в левой части неравенства:
$7x^2+3,5x-9-24x-16x^2+10x^2-10 > 0$;
$x^2-21,5x-19 > 0$.
Полученное квадратное неравенство далее можно решить одним из указанных выше способов.
Ответ: $x^2-21,5x-19 > 0$.
spravochnick.ru
Решение квадратных неравенств. Видеоурок. Алгебра 9 Класс
Тема: Рациональные неравенства и их системы
Урок: Решение квадратных неравенств
Определение: Квадратное неравенство – это неравенство вида
В случае если a=0, мы получаем линейное неравенство.
Вспомним терминологию.
x — независимая переменная. Необходимо найти множество всех x, при которых неравенство выполняется.
a,b,c – конкретные числа, параметры;
квадратный трехчлен;
квадратичная функция.
Решение квадратного неравенства целиком основано на свойствах квадратичной функции.
Вспомним и изучим эти свойства на примерах.
Решить неравенства:
a.
Рассмотрим функцию Построим и прочтем ее график.
Графиком квадратичной функции является парабола, шаблон — парабола сдвинутая относительно начала координат.
Определим координаты вершины.
Схематически изобразим график функции. Ветви параболы направлены вверх, т.к. .
Теперь прочтем полученный график.
Функция определена при . Основное свойство данной функции заключается в том, что при всех Более того,
Ответ:
Мы рассмотрели случай, когда график функции не пересекает ось ox.
b.
Рассмотрим функцию
Найдем корни квадратного трехчлена
D=8-8=0, значит
Схематически построим график функции
Корень x=1;
графиком является парабола, значит ветви направлены вверх.
Прочитаем график.
На промежутке функция положительна. На промежутке функция также положительна. При
Ответ:
Мы рассмотрели случай, когда кривая касается оси ox в одной точке.
c.
Найдем корни квадратного трехчлена Воспользуемся теоремой Виета.
Схематически изобразим график функции
Это парабола, ветви направлены вверх, т.к.
Прочитаем график. На промежутке функция положительна.
На промежутке функция отрицательна.
В точках пересечения с осью ox функция равна нулю.
Ответ:
Мы продемонстрировали методику решения квадратных неравенств для трех случаев:
1. Соответствующий квадратный трехчлен не имеет корней.
2. Квадратный трехчлен имеет один корень.
3. Квадратный трехчлен имеет два корня.
Сформулируем важнейшее свойство квадратичной функции для случая, когда соответствующий квадратный трехчлен имеет два корня.
Функция сохраняет свой знак вне интервала корней трехчлена. Функция сохраняет свой знак внутри интервала корней трехчлена. Функция меняет свой знак при переходе аргумента через корень.
Эти простейшие свойства, которые мы повторили, лежат в основе решения квадратных неравенств.
Продолжим решение неравенств.
1.
Рассмотрим функцию
Найдем корни трехчлена Один из корней легко определить методом подбора. Возьмем Проверяем: корень подходит.
Второй корень найдем по теореме Виета.
Построим эскиз графика функции. Графиком является парабола, ветви направлены вверх.
Отметим знаки на интервалах знакопостоянства и выберем интервалы, удовлетворяющие нашим условиям.
Ответ:
Мы продемонстрировали на примере применение методики решения квадратных неравенств. Один из корней мы нашли методом подбора, рассмотрим еще один подобный пример.
2.
Рассмотрим уравнение Можно ли угадать корень такого уравнения? Очевидно, что один из корней Второй корень найдем по теореме Виета.
Графиком функции является парабола, ветви направлены вверх. Построим эскиз графика.
Вне интервала корней функция положительна, внутри интервала – отрицательна. Нашему условию удовлетворяет промежуток внутри интервала корней.
Ответ:
Рассмотрим сопутствующую задачу: найти все целочисленные решения неравенства.
Точки пересечения графика с осью ox выколотые, не являются решениями. В рассматриваемом интервале только одно целочисленное решение,
Ответ:
Бывают неполные квадратные неравенства, вот одно из них:
3.
Рассмотрим функцию
Построим график, ветви параболы направлены вверх.
Нашему условию удовлетворяет интервал вне корней.
Ответ:
Мы рассмотрели квадратные неравенства, методику их решения, и проиллюстрировали ее на конкретных примерах.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на интернет-ресурсы
1. Портал Естественных Наук (Источник).
2. Центр образования «Технология обучения» (Источник).
3. Электронный учебно-методический комплекс для подготовки 10-11 классов к вступительным экзаменам по информатике, математике, русскому языку (Источник).
4. Виртуальный репетитор (Источник).
5. Раздел College.ru по математике (Источник).
Рекомендованное домашнее задание
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил.№№ 5; 6; 7.
interneturok.ru
2.2.1 Квадратные неравенства
Видеоурок 1: Решение квадратных неравенствВидеоурок 2: Решение неравенств методом интервалов
Лекция: Квадратные неравенства
Равносильные неравенства
Под решением неравенства понимают нахождение такого значения или промежутка значений, при котором сохраняется знак неравенства.
Так бывают такие неравенства, в которых не существует решений. Однако, это необходимо доказать.
Как и в случае с уравнениями и системами уравнений, при решении неравенств сталкиваются с равносильными неравенствами. Неравенства называются равносильными, если они имеют одинаковые решения или не имеют их вообще.
Итак, в каких случаях можно получить равносильные неравенства:
1. При перенесении слагаемого из одной части неравенства в другую, неравенство будет равносильным, если изменить знак слагаемого.
2. Если правую и левую часть неравенства умножить или разделить на любое положительное число или выражение, то знак неравенства останется прежним, а неравенство получится равносильным.
3. Если правую и левую часть неравенства умножить или разделить на любое отрицательное число или выражение, то необходимо изменить знак неравенства. В таком случае получится равносильное неравенство.
Способы решения неравенств
Самым популярным способом решения всех неравенств является метод интервалов.
Чтобы решить неравенство, таким образом, необходимо любое неравенство разложить с одной стороны на множители, а в другой части неравенства получить нуль.
Обратите внимание, в отличие от уравнения, если вы получили множители в знаменателе, то нельзя от них избавляться. Следует заменить деление умножением, с учетом ОДЗ.
Алгоритм решения неравенств методом интервалов:
1. Итак, если Вы получили неравенство, содержащее функцию:
То необходимо найти ОДЗ. Напоминаем, что если в неравенстве содержится корень, то значение под знаком корня не может принимать отрицательное значение. Если некоторый множитель находится в знаменателе, то он не может принимать отрицательное значение.
2. Следующим шагом необходимо найти нули функции. Для этого функцию приравнивают к нулю.
3. Полученные значения нулей следует нанести на числовую прямую. Если неравенство строгое или полученные нули не попадают в ОДЗ, то точки наносятся пустыми кружочками. Если же неравенство не строгое, то кружочки зарисовываем. Пустая точка означает, что данное значение переменной не является решением неравенства.
4. После нанесения точек на прямую необходимо узнать знак, который принимает функция в целом в данном промежутке. А затем расставить знаки над каждым промежутком.
5. После этого все промежутки, которые удовлетворяют знаку неравенства, записать в качестве решения с учетом крайних точек.
Квадратичные неравенстваЕсли неравенство имеет вид: ax2 + bx + c >0 (<, ≤, ≥), то данное неравенство называется квадратичным.
Прежде, функцию, содержащуюся в неравенстве, необходимо приравнять к нулю и найти корни данного уравнения.
После этого неравенство раскладывается на множители и решается так, как описано выше.
cknow.ru
| Техническая информация тут | Адрес этой страницы (вложенность) в справочнике dpva.ru:
| ||||||||||||||||
dpva.ru
Квадратные неравенства
Общий вид квадратного неравенства после переноса всех выражений на одну сторону неравенства представляет собой одну из следующих форм:
$ax^2+bx+c > 0$ , либо $ax^2+bx+c \geq 0$ либо $ax^2+bx+c
Когда $a \neq 0$ , а также $b, c \in \mathbb{R}$
Решением каждого неравенства указанного выше, является нахождение всех действительных чисел, которыми можно заменить $x$ так, чтобы неравенство было верным.
Например, если мы заявляем, что $x = 1$ является одним из корней неравенства $x^2 — \frac{1}{2} > 0$. Подставив 1 вместо всех переменных $x$ в неравенстве, мы получим, что $1^2 — \frac{1}{2} > 0 \rightarrow \frac{1}{2} > 0$ ,
что всегда верно. Поэтому $x = 1$ является одним из решений данного неравенства.
Теперь мы научимся решать неравенства (1).
Во-первых, мы рассмотрим уравнение с двумя переменными, $y = ax^2+bx+c$, и предположим, что $ax^2+bx+c$ равно нулю. Тогда:
$ax^2+bx+c = 0 \rightarrow a(x^2+\frac{b}{a}x+\frac{c}{a}) = 0 \rightarrow^{a \neq 0} x^2+\frac{b}{a}x+\frac{c}{a} = 0 \rightarrow$
$x^2+\frac{b}{a}x+\frac{c}{a}+\frac{b^2}{4a^2}-\frac{b^2}{4a^2} = 0 \rightarrow (x + \frac{b}{2a})^2 — \frac{b^2 — 4ac}{4a^2} = 0 \rightarrow$
$(x + \frac{b}{2a})^2 = \frac{b^2 — 4ac}{4a^2} \rightarrow x + \frac{b}{2a} = \pm \sqrt{\frac{b^2 — 4ac}{4a^2}} \rightarrow x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 — 4ac}}{2a} \rightarrow $
$x = \frac{-b}{2a} \pm \frac{\sqrt{b^2 — 4ac}}{2a} \rightarrow x = \frac{-b \pm \sqrt{b^2 — 4ac}}{2a}$
Из этого следует, что график квадратного уравнения пересекает ось x в точке $x_1 = \frac{-b + \sqrt{b^2 — 4ac}}{2a}$ и $x_2 = \frac{-b — \sqrt{b^2 — 4ac}}{2a}$
Эти нули разделяют числовую прямую на три интервала:
$(-\infty, x_1)$ , $[x_1,x_2]$ , $(x_2,+\infty)$,
допуская, что $x_1
Теперь пусть $\Delta = b^2 — 4ac$.
Мы можем рассмотреть три указанных ниже случая:
- $\Delta > 0$
- $\Delta = 0$
- $\Delta
- Случай 1:
- Если $\Delta > 0$,
тогда $ax^2+bx+c$ имеет два различных корня $(x_1 \neq x_2)$.
Теперь, если $a>0$, то его график получается таким, как на «Рисунке а».
Если $a»Рисунке b»
www.math10.com
5.2. Квадратные неравенства
Определение
5.5. Квадратными неравенствами называются
неравенства вида
,,
где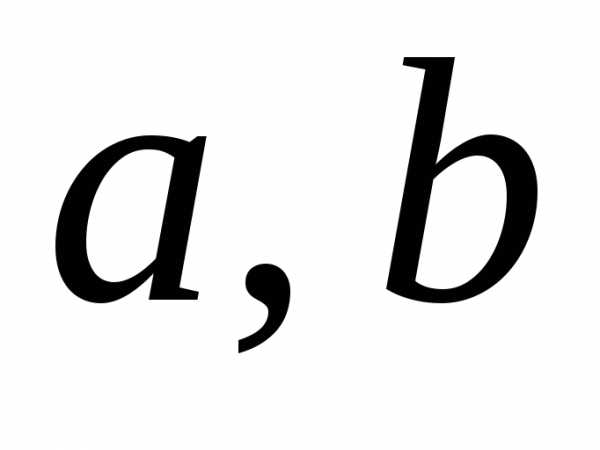 и
и
 ,
,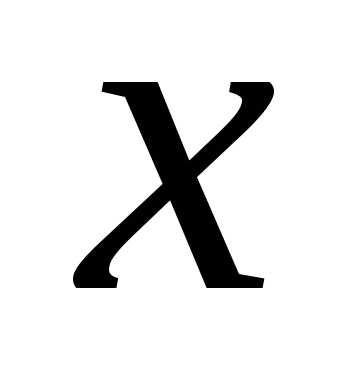 – переменная, при этом
– переменная, при этом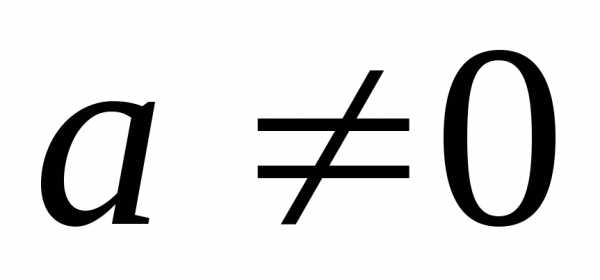 .
.
Выделяют два основных метода решения квадратных неравенств – графический и аналитический.
1. Графический метод. Решение определяется в зависимости от расположения графика (таблица 5.1).
Таблица 5.1.
нет решений | нет решений |
| |
нет решений |
|
| |
нет решений | нет решений |
| |
нет решений |
|
| |
2. Аналитический
метод. Если 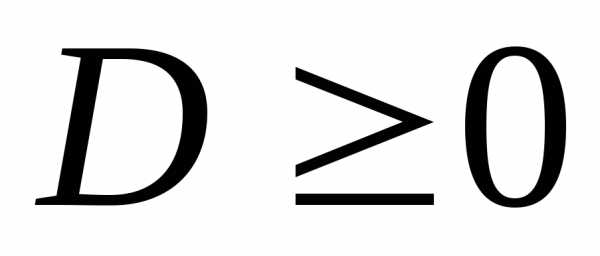 ,
то квадратный трехчлен раскладывают
на множители и полученное равносильное
неравенство решают методом интервалов
(см. пункт 5.3).
,
то квадратный трехчлен раскладывают
на множители и полученное равносильное
неравенство решают методом интервалов
(см. пункт 5.3).
5.3. Рациональные и дробно-рациональные неравенства. Метод интервалов для рациональных неравенств
Важнейшим методом
решения неравенств является метод
интервалов.
Данный метод основан на том, что двучлен 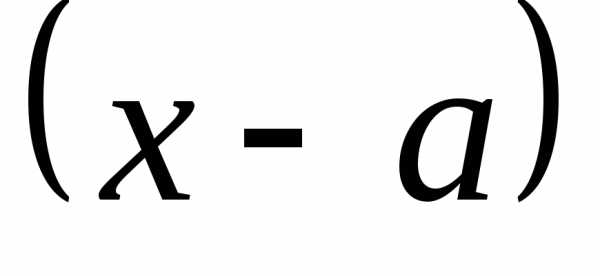 положителен при
положителен при и отрицателен при
и отрицателен при ,
то есть меняет знак при переходе через
точку
,
то есть меняет знак при переходе через
точку .
.
Кроме того полезно использовать следующие правила:
двучлен
 внечетной степени ведет себя так же, как
внечетной степени ведет себя так же, как  ;
;двучлен
 вчетной степени не
меняет знак
при переходе через точку
вчетной степени не
меняет знак
при переходе через точку  ;
;квадратный трехчлен при
 ,
, ,
поэтому он может быть опущен при решении
любого неравенства;
,
поэтому он может быть опущен при решении
любого неравенства;при переходе через точку
 может изменить знак только множитель
вида
может изменить знак только множитель
вида ,
а выражение
,
а выражение ,
где
,
где ,
при переходе через точку
,
при переходе через точку знак не меняет.
знак не меняет.
Пример 5.1. Решить неравенство .
Решение. Для решения строгого неравенства наносим на числовую ось нули функции кружочками («дырками»). Далее расставляем знаки, используя приведенные выше правила:
Тогда решение неравенства имеет вид: .
Ответ: .
Пример 5.2. Решить неравенство .
Решение. Напомним, что по определению,
.
Для решения нестрогих неравенств наносим нули функции на числовую ось точками. Затем расставляем знаки в промежутках:
Решение примет вид: .
Ответ: .
Определение
5.6. Неравенства
вида 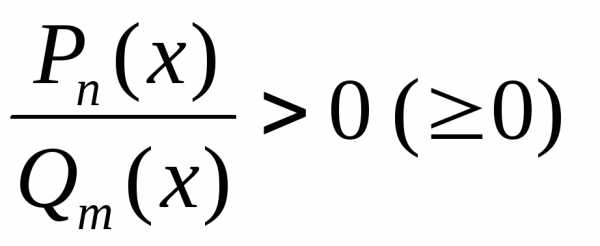 ,
,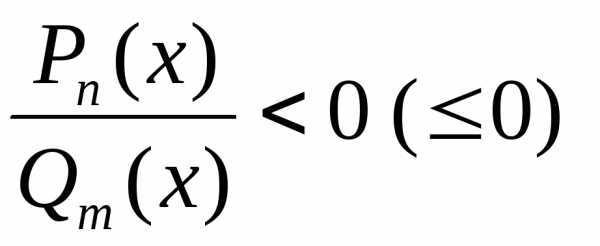 ,где
,где 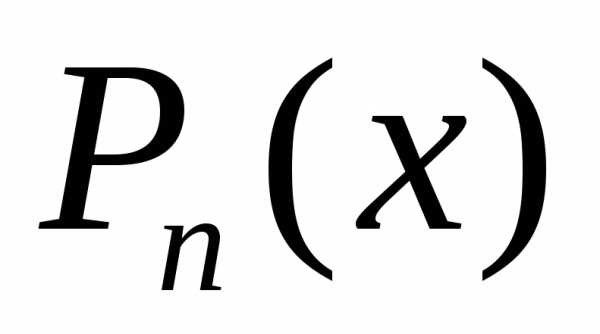 ,
,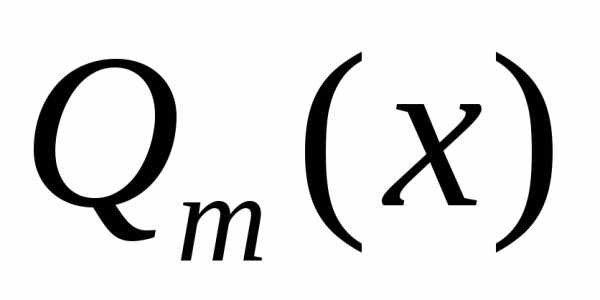 — многочлены, называютсярациональными.
— многочлены, называютсярациональными.
Для решения рациональных неравенств необходимо предварительно сделать следующие преобразования:
1. все члены неравенства перенести в одну сторону и привести дроби к общему знаменателю;
2. выражения, стоящие в числители и знаменатели разложить на множители;
3. определить нули числителя и знаменателя;
4. применить метод интервалов.
Замечание 5.1. Метод интервалов применяется к дроби точно так же, как и к многочленам. Для нестрого же неравенства имеем:
.
При решении нестрогих рациональных неравенств нули числителя наносятся на числовую ось точками, а нули знаменателя (и нули числителя, если они равны нулям знаменателя) – «дырками».
Пример 5.3. Решить
неравенство 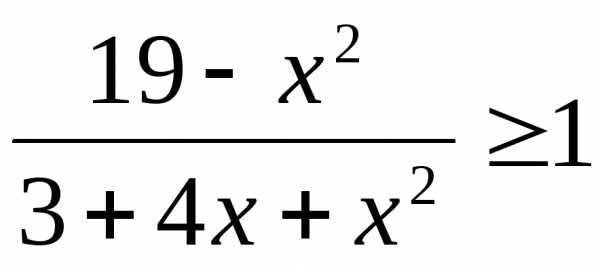 .
.
Решение.
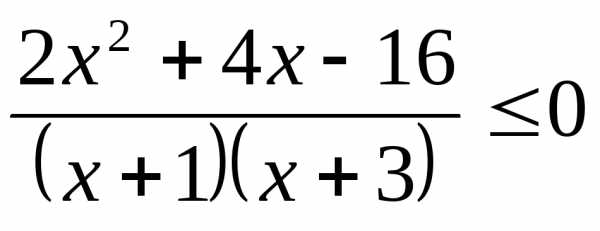 ,
, 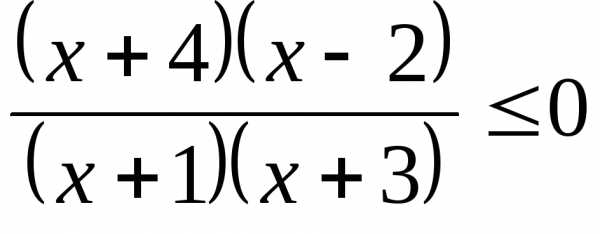
Ответ: .
Пример 5.5. Найти
сумму целых решений неравенства 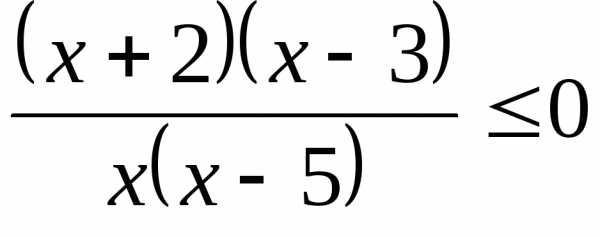 .
.
Решение. Решим неравенство методом интервалов:
тогда .Целыми решениями являются числа: -2, -1. 3. 4. Их сумма равна 4.
Ответ: 4.
studfiles.net

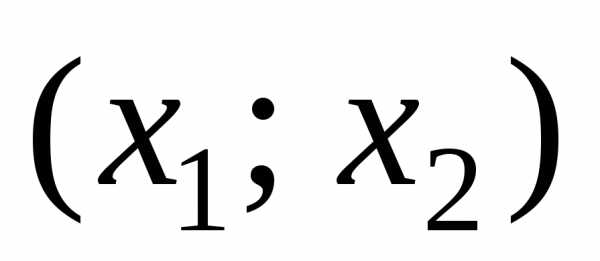
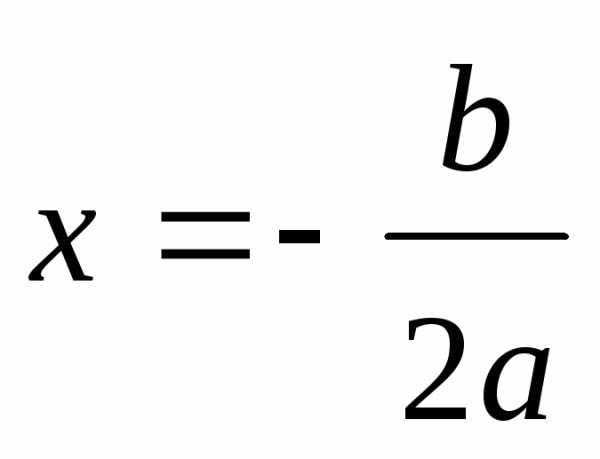
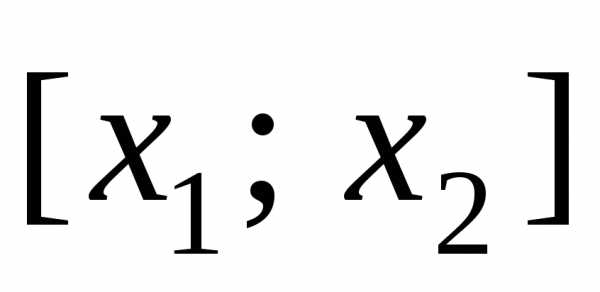

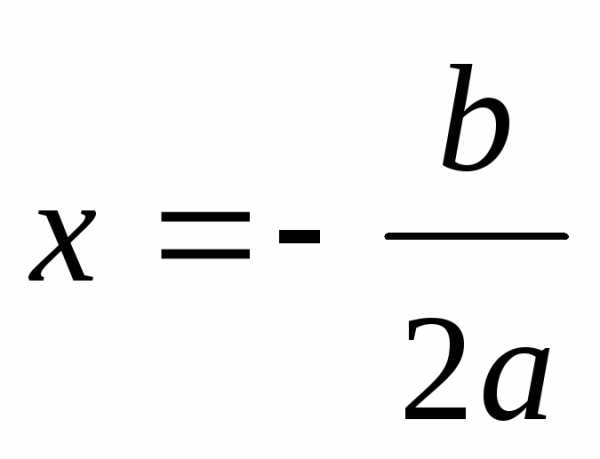
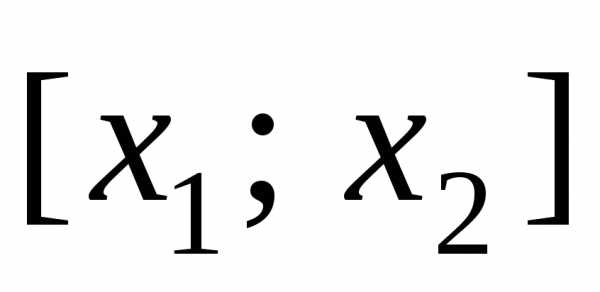
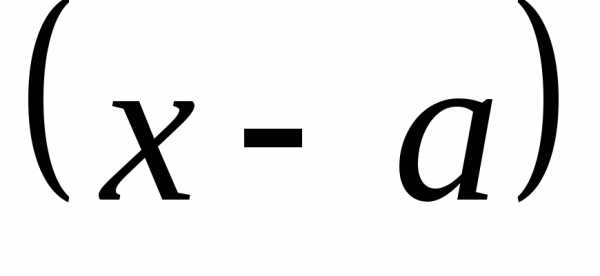 внечетной степени ведет себя так же, как
внечетной степени ведет себя так же, как  ;
;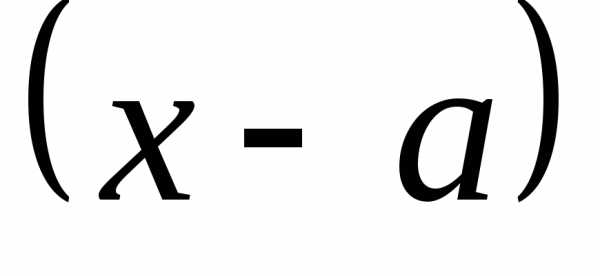 вчетной степени не
меняет знак
при переходе через точку
вчетной степени не
меняет знак
при переходе через точку  ;
; ,
,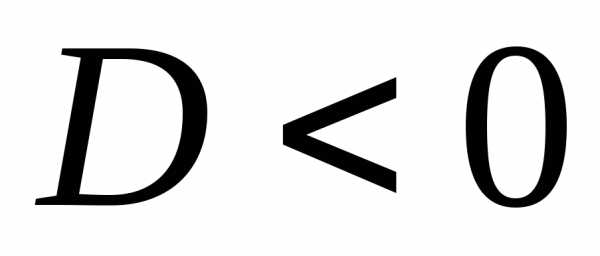 ,
поэтому он может быть опущен при решении
любого неравенства;
,
поэтому он может быть опущен при решении
любого неравенства; может изменить знак только множитель
вида
может изменить знак только множитель
вида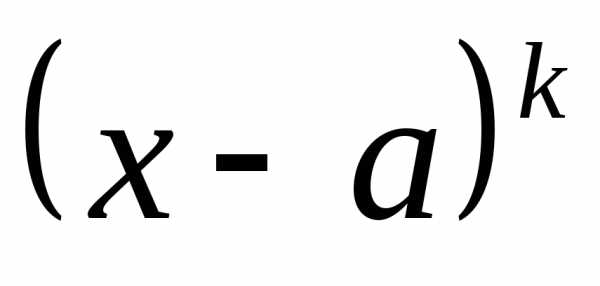 ,
а выражение
,
а выражение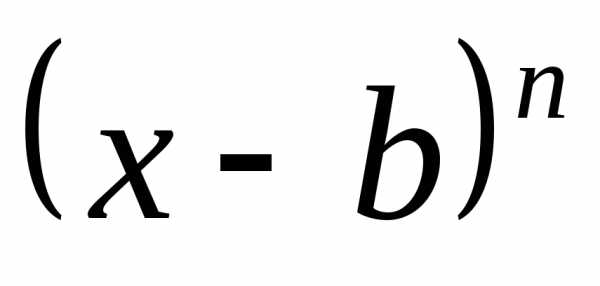 ,
где
,
где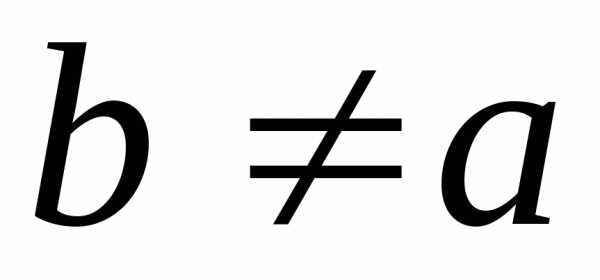 ,
при переходе через точку
,
при переходе через точку знак не меняет.
знак не меняет.