Квадратные уравнения с параметром | Александр Будников
Задачи с параметрами. Простейшие задачи на квадратный трёхчлен.
Сегодня мы рассмотрим задачи на квадратный трёхчлен, про который, в зависимости от параметра, надо будет что-то выяснить. Это «что-то» может быть самым разнообразным, насколько только хватит фантазии у составителей задачи. Это самый простой тип задач с параметрами. И, если на ЕГЭ вам попалась такая – считайте, что вам повезло!
Но, прежде чем приступать к разбору самих задач, ответьте сами себе на такие простые вопросы:
— Что такое квадратное уравнение, как оно выглядит и как решается?
— Что такое дискриминант и куда его пристроить?
— Что такое теорема Виета и где её можно применить?
Если вы верно отвечаете на эти простые вопросы, то 50% успеха в решении параметрических задач на квадратный трёхчлен вам обеспечены! А остальные 50% — это обычная алгебра и арифметика: раскрытие скобок, приведение подобных, решение уравнений, неравенств и систем и т.д.
Итак, приступим!
Для начала рассмотрим совсем безобидную задачку. Для разминки. 🙂
Пример 1
Приступаем к решению. Во-первых, чтобы в будущем не накосячить в коэффициентах, всегда полезно выписать их отдельно. Прямо в столбик. Вот так:
a = 1
b = -(a-1)
c = a-2
Да-да! Часть коэффициентов в уравнении (а именно – b и с) зависит от параметра. В этом как раз и состоит вся фишка таких задач. А теперь снова въедливо перечитываем условие. Ключевой зацепкой в формулировке задания являются слова «единственный корень». И когда же квадратное уравнение имеет единственный корень? Подключаем наши теоретические знания о квадратных уравнениях. Только в одном единственном случае – когда его дискриминант равен нулю.
Так и пишем:
D = 0
Осталось составить выражение для дискриминанта и приравнять его к нулю. Поехали!
Теперь надо приравнять наш дискриминант к нулю:
Можно, конечно, решать это квадратное уравнение через дискриминант, а можно немного схитрить. На что у нас похожа левая часть, если как следует присмотреться? Она у нас похожа на квадрат разности (a-3)2!
Респект внимательным! Верно! Если заменить наше выражение слева на (a-3)2, то уравнение будет решаться в уме!
(a — 3)2 = 0
a —
a = 3
Вот и всё. Это значит, что единственный корень наше квадратное уравнение с параметром будет иметь только в одном единственном случае – когда значение параметра «а» равно тройке.)
Ответ: 3
Это был разминочный пример. Чтобы общую идею уловить.) Теперь будет задачка посерьёзнее.
Пример 2
Вот такая задачка. Начинаем распутывать. Первым делом выпишем наше квадратное уравнение:
0,5x2 — 2x + 3a + 1,5 = 0
Самым логичным шагом, было бы умножить обе части на 2. Тогда у нас исчезнут дробные коэффициенты и само уравнение станет посимпатичнее. Умножаем:
Выписываем в столбик наши коэффициенты a, b, c:
a = 1
b = -4
c = 6a+3
Видно, что коэффициенты a и b у нас постоянны, а вот свободный член с зависит от параметра «а»! Который может быть каким угодно – положительным, отрицательным, целым, дробным, иррациональным – всяким!
А теперь, чтобы продвинуться дальше, вновь подключаем наши теоретические познания в области квадратных уравнений и начинаем рассуждать. Примерно так:
«Для того чтобы сумма кубов корней была меньше 28, эти самые корни, во-первых, должны существовать. Сами по себе. В принципе. А корни у квадратного уравнения существуют, тогда и только тогда, когда его дискриминант неотрицательный. Кроме того, в задании говорится о двух различных корнях. Эта фраза означает, что наш дискриминант обязан быть не просто неотрицательным, а строго положительным!»
Если вы рассуждаете таким образом, то вы движетесь правильным курсом! Верно.) Составляем условие положительности для дискриминанта:
D = (-4)2 — 4·1·(6a+3) = 16-24a-12 = 4-24a
4-24a > 0
-24a > -4
a < 1/6
Полученное условие говорит нам о том, что два различных корня у нашего уравнения будет не при любых значениях параметра «а», а только при тех, которые меньше одной шестой! Это глобальное требование, которое должно выполняться железно. Неважно, меньше 28 наша сумма кубов корней или больше. Значения параметра «а», большие или равные 1/6, нас заведомо не устроят. Гуд.) Соломки подстелили. Движемся дальше.
Теперь приступаем к загадочной сумме кубов корней. По условию она у нас должна быть меньше 28. Так и пишем:
Значит, для того чтобы ответить на вопрос задачи, нам надо совместно рассмотреть два условия:
А дальше начинаем отдельно работать с этой самой суммой кубов. Есть два способа такой работы: первый способ для трудолюбивых и второй способ – для внимательных.
Способ для трудолюбивых заключается в непосредственном нахождении корней уравнения через параметр. Прямо по общей формуле корней. Вот так:
Теперь составляем нужную нам сумму кубов найденных корней и требуем, чтобы она была меньше 28:
А дальше – обычная алгебра: раскрываем сумму кубов по формуле сокращённого умножения, приводим подобные, сокращаем и т.д. Если бы корни нашего уравнения получились покрасивее, без радикалов, то такой «лобовой» способ был бы неплох. Но проблема в том, что наши корни выглядят немного страшновато. И подставлять их в сумму кубов как-то неохота, да. Поэтому, для того чтобы избежать этой громоздкой процедуры, я предлагаю второй способ – для внимательных.
Для этого раскрываем сумму кубов корней по соответствующей формуле сокращенного умножения. Прямо в общем виде:
А дальше проделываем вот такой красивый фокус: во вторых скобках выражаем сумму квадратов корней через сумму корней и их произведение. Вот так:
Итого:
Казалось бы, и что из этого? Сейчас интересно будет! Давайте, посмотрим ещё разок на наше уравнение. Как можно внимательнее:
Чему здесь равен коэффициент при x2? Правильно, единичке! А как такое уравнение называется? Правильно, приведённое! А, раз приведённое, то, стало быть, для него справедлива теорема Виета:
Вот и ещё одна теорема нам пригодилась! Теперь, прямо по теореме Виета, подставляем сумму и произведение корней в наше требование для суммы кубов:
Осталось раскрыть скобки и решить простенькое линейное неравенство:
4·(16-18a-9) < 28
64–72a+36 < 28
-72a < 28-64+36
-72a < 0
a > 0
Вспоминаем, что ещё у нас есть глобальное требование a < 1/6. Значит, наше полученное множество a > 0 необходимо пересечь с условием a < 1/6. Рисуем картинку, пересекаем, и записываем окончательный ответ.
Ответ:
Да. Вот такой маленький интервальчик. От нуля до одной шестой… Видите, насколько знание теоремы Виета, порой, облегчает жизнь!
Вот вам небольшой практический совет: если в задании говорится о таких конструкциях, как сумма, произведение, сумма квадратов, сумма кубов корней, то пробуем применить теорему Виета. В 99% случаев решение значительно упрощается.
Это были довольно простые примеры. Чтобы суть уловить. Теперь будут примеры посолиднее.
Например, такая задачка из реального варианта ЕГЭ:
Пример 3
Что, внушает? Ничего не боимся и действуем по нашему излюбленному принципу: «Не знаешь, что нужно, делай что можно!»
Опять аккуратно выписываем все коэффициенты нашего квадратного уравнения:
a = 1
b = -6
c = a2-4a
А теперь вчитываемся в условие задачи и находим слова «модуль разности корней уравнения». Модуль разности нас пока не волнует, а вот слова «корней уравнения» примем во внимание. Раз говорится о корнях (неважно, двух одинаковых или двух различных), то наш дискриминант обязан быть неотрицательным! Так и пишем:
D ≥ 0
Что ж, аккуратно расписываем наш дискриминант через параметр а:
D = (-6)2 – 4·1·(12 + a2-4a) = 36 — 48 — 4а2 + 16а = -4а2+16а-12.
А теперь решаем квадратное неравенство. По стандартной схеме, через соответствующее квадратное уравнение и схематичный рисунок параболы:
Значит, для того чтобы у нашего уравнения в принципе имелись хоть какие-то корни, параметр а должен находиться в отрезке [-1; 3]. Это железное требование. Хорошо. Запомним.)
А теперь приступаем к этому самому модулю разности корней уравнения. От нас хотят, чтобы вот такая штука
принимала бы наибольшее значение. Для этого, ничего не поделать, но теперь нам всё-таки придётся находить сами корни и составлять их разность: x1 – x2. Теорема Виета здесь в этот раз бессильна.
Что ж, считаем корни по общей формуле:
Дальше составляем модуль разности этих самых корней:
Теперь вспоминаем, что корень квадратный – величина заведомо неотрицательная. Стало быть, без ущерба для здоровья, модуль можно смело опустить. Итого наш модуль разности корней выглядит так:
И эта функция f(a) должна принимать наибольшее значение. А для поиска наибольшего значения у нас есть такой мощный инструмент, как производная! Вперёд и с песнями!)
Дифференцируем нашу функцию и приравниваем производную к нулю:
Получили единственную критическую точку a = 2. Но это ещё не ответ, так как нам ещё надо проверить, что найденная точка и в самом деле является точкой максимума! Для этого исследуем знаки нашей производной слева и справа от двойки. Это легко делается простой подстановкой (например, а = 1,5 и а = 2,5).
Слева от двойки производная положительна, а справа от двойки – отрицательна. Это значит, что наша точка a = 2 и вправду является точкой максимума. Заштрихованная зона на картинке означает, что нашу функцию мы рассматриваем только на отрезке [1; 3]. Вне этого отрезка нашей функции f(a) попросту не существует. Потому, что в заштрихованной области наш дискриминант отрицательный, и разговоры о каких-либо корнях (и о функции тоже) бессмысленны. Это понятно, думаю.
Всё. Вот теперь наша задача полностью решена.
Ответ: 2.
Здесь было применение производной. А бывают и такие задачи, где приходится решать уравнения либо неравенства с так ненавистными многими учениками модулями и сравнивать некрасивые иррациональные числа с корнями. Главное – не бояться! Разберём похожую злую задачку (тоже из ЕГЭ, кстати).
Пример 4
Итак, приступаем. Первым делом замечаем, что параметр а ни в коем случае не может быть равен нулю. Почему? А вы подставьте в исходное уравнение вместо а нолик. Что получится?
Получили линейное уравнение, имеющее единственный корень x=2. А это уже совсем не наш случай. От нас хотят, чтобы уравнение имело два различных корня, а для этого нам необходимо, чтобы оно, как минимум, было хотя бы квадратным.)
Итак, а ≠ 0.
При всех остальных значениях параметра наше уравнение будет вполне себе квадратным. И, следовательно, чтобы оно имело два различных корня, необходимо (и достаточно), чтобы его дискриминант был положительным. То есть, первое наше требование будет D > 0.
А далее по накатанной колее. Считаем дискриминант:
D = 4(a-1)2 – 4a(a-4) = 4a2-8a+4-4a2+16a = 4+8a
Вот так. Значит, наше уравнение имеет два различных корня тогда и только тогда, когда параметр a > -1/2. При прочих «а» у уравнения будет либо один корень, либо вообще ни одного. Берём на заметку это условие и движемся дальше.
Далее в задаче идёт речь о расстоянии между корнями. Расстояние между корнями, в математическом смысле, означает вот такую величину:
Зачем здесь нужен модуль? А затем, что любое расстояние (что в природе, что в математике) – величина неотрицательная. Причём здесь совершенно неважно, какой именно корень будет стоять в этой разности первым, а какой вторым: модуль – функция чётная и сжигает минус. Точно так же, как и квадрат.
Значит, ответом на вопрос задачи является решение вот такой системы:
Теперь, ясен перец, нам надо найти сами корни. Здесь тоже всё очевидно и прозрачно. Аккуратно подставляем все коэффициенты в нашу общую формулу корней и считаем:
Отлично. Корни получены. Теперь начинаем формировать наше расстояние:
Наше расстояние между корнями должно быть больше трёх, поэтому теперь нам надо решить вот такое неравенство:
Неравенство – не подарок: модуль, корень… Но и мы всё-таки уже решаем серьёзную задачу №18 из ЕГЭ! Делаем всё что можно, чтобы максимально упростить внешний вид неравенства. Мне здесь больше всего не нравится дробь. Поэтому первым делом я избавлюсь от знаменателя, умножив обе части неравенства на |a|. Это можно сделать, поскольку мы, во-первых, в самом начале решения примера договорились, что а ≠ 0, а во-вторых, сам модуль – величина неотрицательная.
Итак, смело умножаем обе части неравенства на положительное число |a|. Знак неравенства сохраняется:
Вот так. Теперь в нашем распоряжении имеется иррациональное неравенство с модулем. Ясное дело, для того чтобы решить его, надо избавляться от модуля. Поэтому придётся разбивать решение на два случая – когда параметр а, стоящий под модулем, положителен и когда отрицателен. Другого пути избавиться от модуля у нас, к сожалению, нет.
Итак!
Случай 1 (a>0, |a|=a)
В этом случае наш модуль раскрывается с плюсом, и неравенство (уже без модуля!) принимает следующий вид:
Неравенство имеет структуру: «корень больше функции». Такие иррациональные неравенства решаются по следующей стандартной схеме:
Отдельно рассматривается случай а), когда обе части неравенства возводятся в квадрат и правая часть неотрицательна и отдельно – случай б), когда правая часть всё-таки отрицательна, но зато сам корень при этом извлекается.) И решения этих двух систем объединяются.
Тогда, в соответствии с этой схемой, наше неравенство распишется вот так:
А теперь можно существенно упростить себе дальнейшую работу. Для этого вспомним, что в случае 1 мы рассматриваем только a>0. С учётом этого требования, вторую систему можно вообще вычеркнуть из рассмотрения, поскольку, второе неравенство в ней (3a<0) эквивалентно неравенству a<0, а условия a>0 и a<0 – это два взаимно исключающих требования.
Упрощаем нашу совокупность с учётом главного условия a>0:
Вот так. А теперь решаем самое обычное квадратное неравенство:
Нас интересует промежуток между корнями. Стало быть,
Отлично. Теперь этот промежуток пересекаем со вторым условием системы a>0:
Есть. Таким образом, первым кусочком ответа к нашему неравенству (а пока не ко всей задаче!) будет вот такой интервал:
Всё. Случай 1 разложен по полочкам. Переходим к случаю 2.
Случай 2 (a<0, |a|=-a)
В этом случае наш модуль раскрывается с минусом, и неравенство принимает следующий вид:
Опять имеем структуру: «корень больше функции». Применяем нашу стандартную схему с двумя системами (см. выше):
С учётом общего требования a<0, мы снова, как и в предыдущем случае, проводим максимальные упрощения: вычёркиваем вторую систему в силу противоречивости двух требований -3а < 0 и нашего общего условия a<0 для всего случая 2.
А дальше снова решаем обычное квадратное неравенство:
И опять сокращаем себе работу. Ибо оно у нас уже решено в процессе разбора случая 1! Решение этого неравенства выглядело вот так:
Осталось лишь пересечь этот интервал с нашим новым условием a<0.
Пересекаем:
Вот и второй кусочек ответа готов:
Кстати сказать, как я узнал, что ноль лежит именно между нашими иррациональными корнями? Легко! Очевидно, что правый корень заведомо положителен. А что касается левого корня, то я просто в уме сравнил иррациональное число
с нулём. Вот так:
А теперь объединяем оба найденных интервала. Ибо мы решаем совокупность (а не систему):
Готово дело. Эти два интервала – это пока ещё только решение неравенства
Кто забыл, данное неравенство отвечает у нас за расстояние между корнями нашего уравнения. Которое должно больше 3. Но! Это ещё не ответ!
Ещё у нас есть условие положительного дискриминанта! Неравенство a>-1/2, помните? Это значит, что данное множество нам ещё надо пересечь с условием a>-1/2. Иными словами, теперь мы должны пересечь два множества:
Но есть одна проблемка. Мы не знаем, как именно расположено на прямой число -1/2 относительно левого (отрицательного) корня. Для этого нам придётся сравнить между собой два числа:
Поэтому сейчас берём черновик и начинаем сравнивать наши числа. Примерно так:
Это значит, что дробь -1/2 на числовой прямой находится левее нашего левого корня. И картинка к окончательному ответу задачи будет какая-то вот такая:
Всё, задача полностью решена и можно записывать окончательный ответ.
Ответ:
Ну как? Уловили суть? Тогда решаем самостоятельно.)
1. Найдите все значения параметра b, при которых уравнение
ax2 + 3x +5 = 0
имеет единственный корень.
2. Найдите все значения параметра а, при каждом из которых больший корень уравнения
x2 – (14a-9)x + 49a2 – 63a + 20 = 0
меньше 9.
3. Найдите все значения параметра а, при каждом из которых сумма квадратов корней уравнения
x2 – 4ax + 5a = 0
равна 6.
4. Найдите все значения параметра а, при каждом из которых уравнение
x2 + 2(a-2)x + a + 3 = 0
имеет два различных корня, расстояние между которыми больше 3.
Ответы (в беспорядке):
abudnikov.ru
Квадратные уравнения с параметрами
Тема занятия «КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРАМИ»
Цели занятия:
Образовательная: углубить ранее полученные знания об уравнениях с параметрами, закрепить навыки решения уравнений;
Воспитательная: воспитывать навыки учебного труда, умение работать в группах;
Развивающая: развивать логическое мышление, формировать потребность к приобретению знаний.
Опрос:
Вспомним условия расположения корней уравнения,при условии , что оба корня положительные, отрицательные, разных знаков.

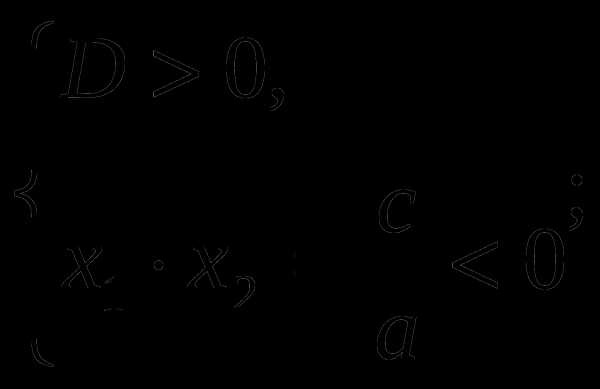

Рассмотрим примеры решения квадратных уравнений с параметрами.
ПРИМЕР 1.
Решить уравнение
Решение:
1.Если 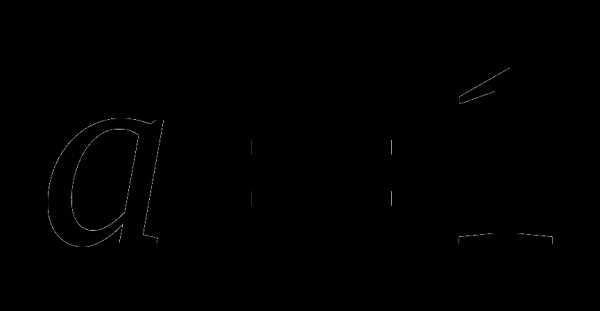 , то мы имеем линейное уравнение:
, то мы имеем линейное уравнение:

2.Если  найдём дискриминант D квадратного уравнения :
найдём дискриминант D квадратного уравнения :
а)Если , то
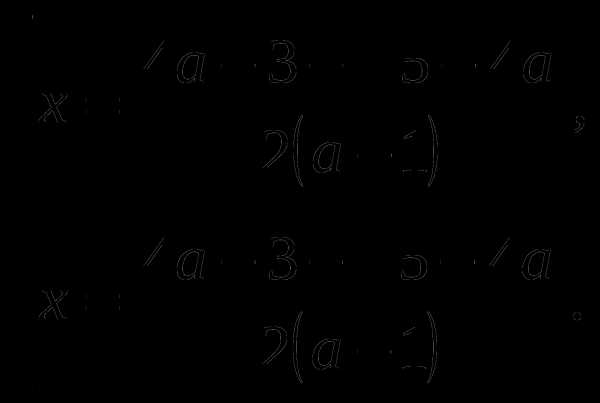
б)Если т.е.  то
то 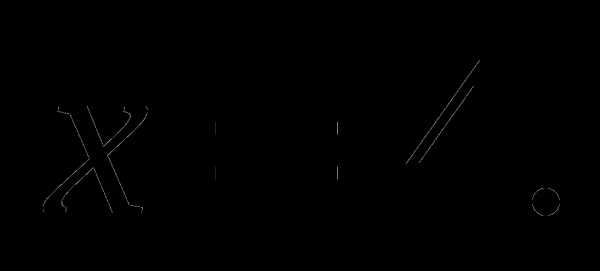
в)Если то действительных корней нет .
Ответ:  если
если 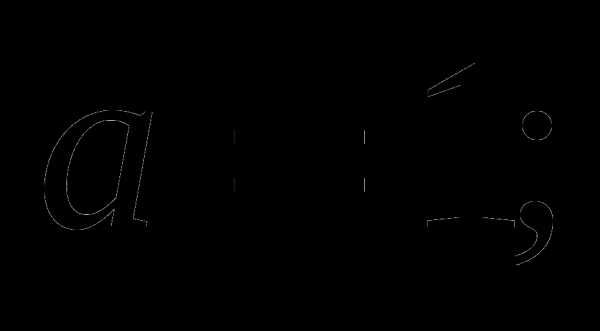
 если
если 
 если
если 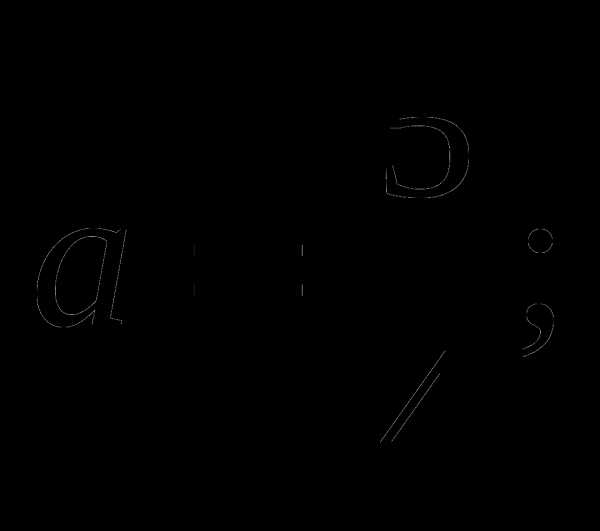
решений нет, если 
ПРИМЕР 2.
Решить уравнение 
Решение:
Уравнение  равносильно системе:
равносильно системе:

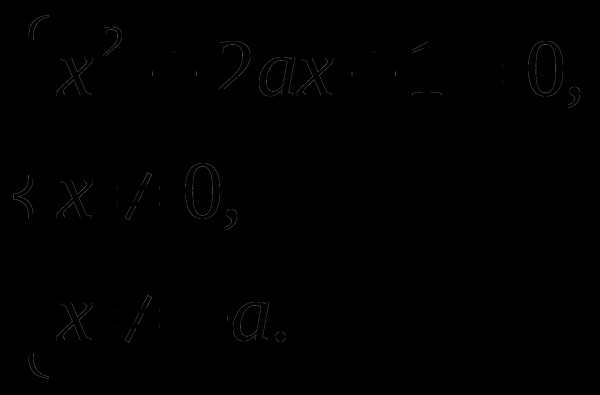
Решим уравнение 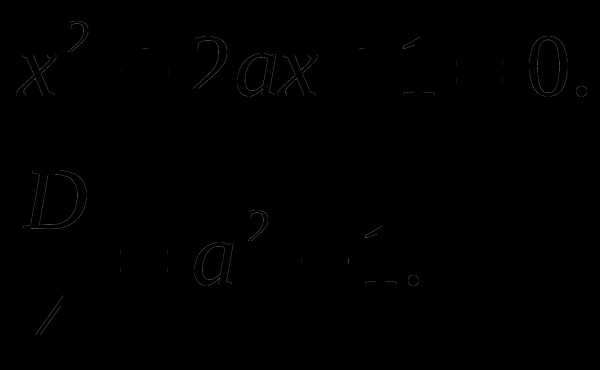
1.Если  т.е.
т.е.  имеем :
имеем :
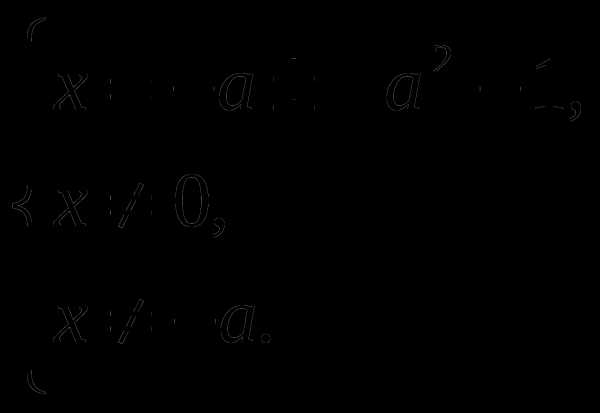
Условие  выполнено, т.к.
выполнено, т.к.

Выясним, при каких значениях  Для этого решим уравнения :
Для этого решим уравнения :
 и
и
Понятно, что при всех отрицательных значениях параметра  равенство в первом уравнении невозможно, при
равенство в первом уравнении невозможно, при  возведя в квадрат обе части равенства , мы получим что невозможно.
возведя в квадрат обе части равенства , мы получим что невозможно.
Второе из рассматриваемых уравнений невозможно при положительных значениях  ,а при
,а при  имеем , как и в первом случае , неверное равенство
имеем , как и в первом случае , неверное равенство
Таким образом , если 
2.Если  то
то
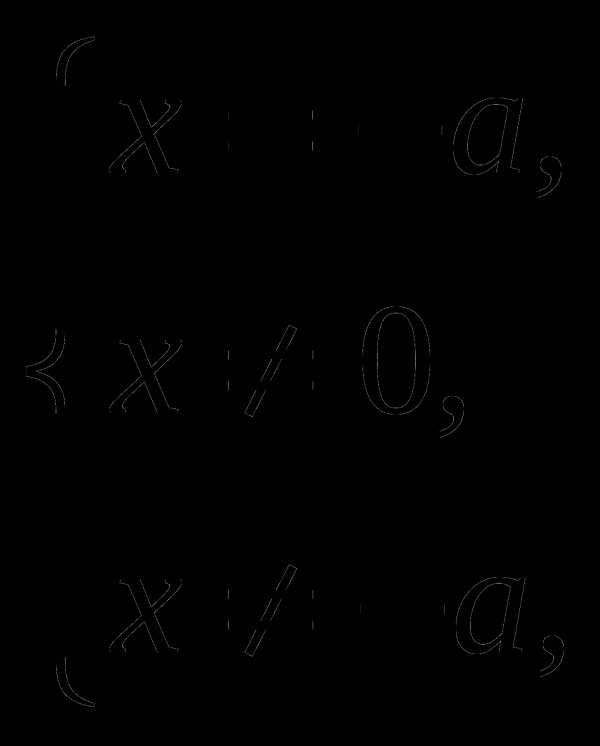
Т.е. в данном случае уравнение не имеет решений.
3.Если  то дискриминант квадратного уравнения отрицательный и, таким образом, нет действительных корней.
то дискриминант квадратного уравнения отрицательный и, таким образом, нет действительных корней.
Ответ: если
решений нет, если 
ПРИМЕР 3.
Определить количество корней уравнения в зависимости от  :
:
Решение:
Обозначим Тогда исходное уравнение имеет вид
или .
Количество корней зависит от знака D1 .
D1=
1.Если  то данное уравнение не имеет корней.
то данное уравнение не имеет корней.
2.При  уравнение имеет единственный корень:
уравнение имеет единственный корень:  Итак,
Итак,
Это уравнение не имеет корней.
3.Если  то корни уравнения
то корни уравнения
Итак ,необходимо выяснить , сколько корней имеет совокупность уравнений:


В первом уравнении дискриминант отсюда следует, что оно не имеет решений при любых значениях параметра 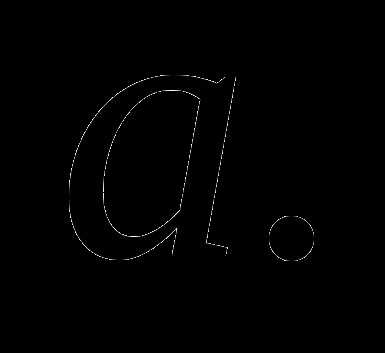
Во втором уравнении
1)Если т.е. 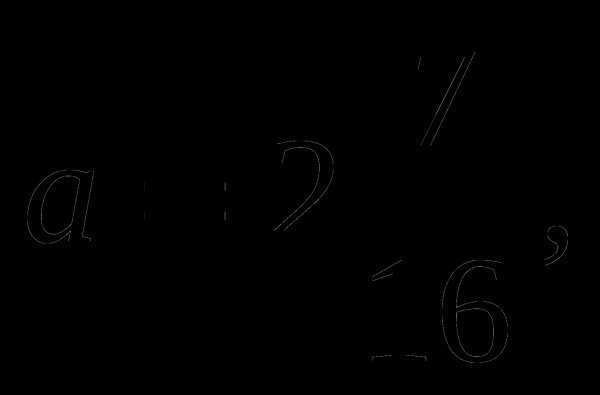 то данное уравнение имеет один корень.
то данное уравнение имеет один корень.
2)Если т.е. 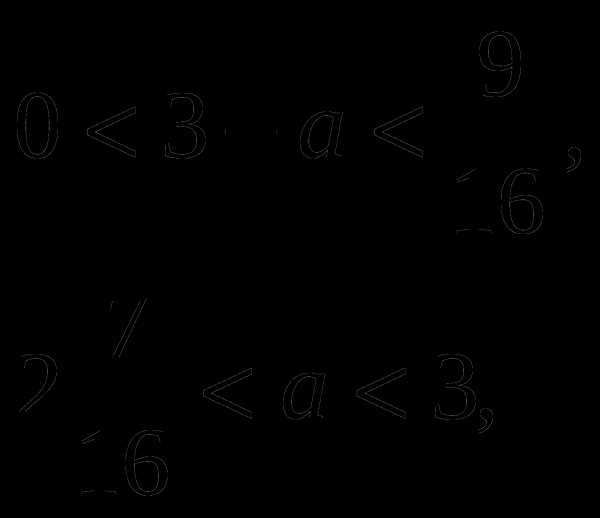
Уравнение не имеет действительных корней.
3)Если т.е. уравнение имеет два корня .
Ответ: Два корня , если 
один корень, если 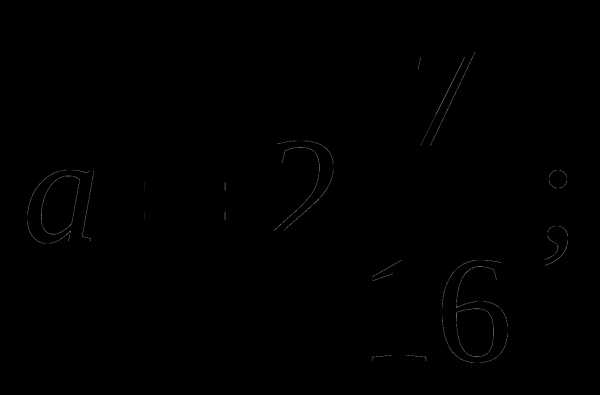
действительных корней нет, если 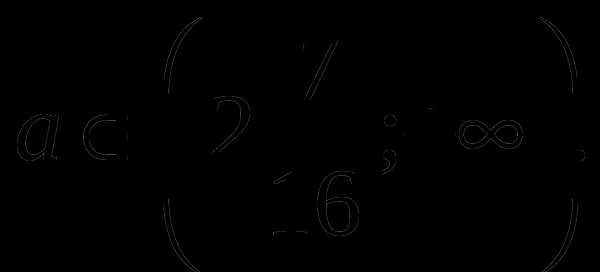
ПРИМЕР 4.
При каких значениях параметра  уравнение
уравнение
имеет единственное решение?
Решение:
Данное уравнение равносильно системе :

Найдём дискриминант квадратного уравнения :
Если  , уравнение имеет один корень
, уравнение имеет один корень  что удовлетворяет условию
что удовлетворяет условию

При  получим:
получим:


Уравнение имеет одно решение , если  т. е. при
т. е. при 
Ответ: Уравнение имеет один корень, если
ПРИМЕР 5.
При каких значениях параметра  уравнение имеет
уравнение имеет
два разных действительных корня?
Решение:
Данное биквадратное уравнение сводится к совокупности уравнений:
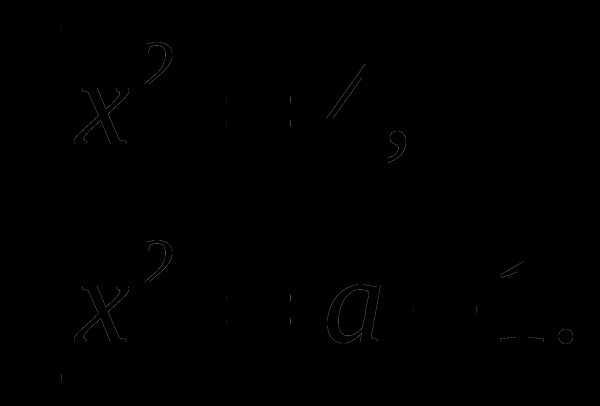
Уравнение имеет два разных корня, если
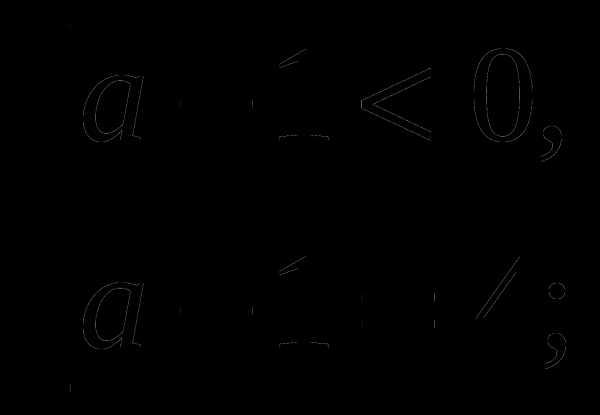
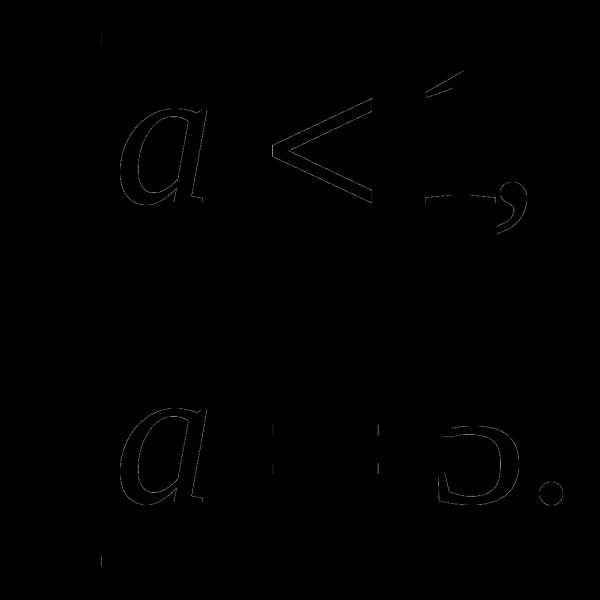
Ответ: уравнение имеет два разных корня , если
ПРИМЕР 6.
При каких значениях параметра  уравнение
уравнение
 имеет единственное решение ?
имеет единственное решение ?
Решение:
Данное уравнение равносильно системе :
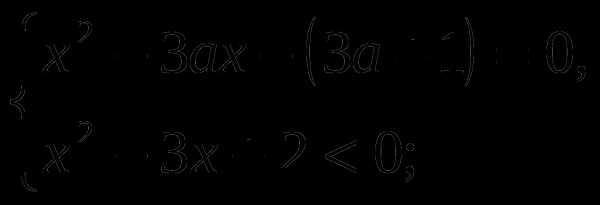
 система будет иметь одно решение ,если
система будет иметь одно решение ,если
т.е. при 
Ответ: уравнение имеет единственное решение при 
ПРИМЕР 7.
Сколько решений имеет уравнение в зависимости от значения параметра  ?
?
Решение:
Данное уравнение равносильно системе :
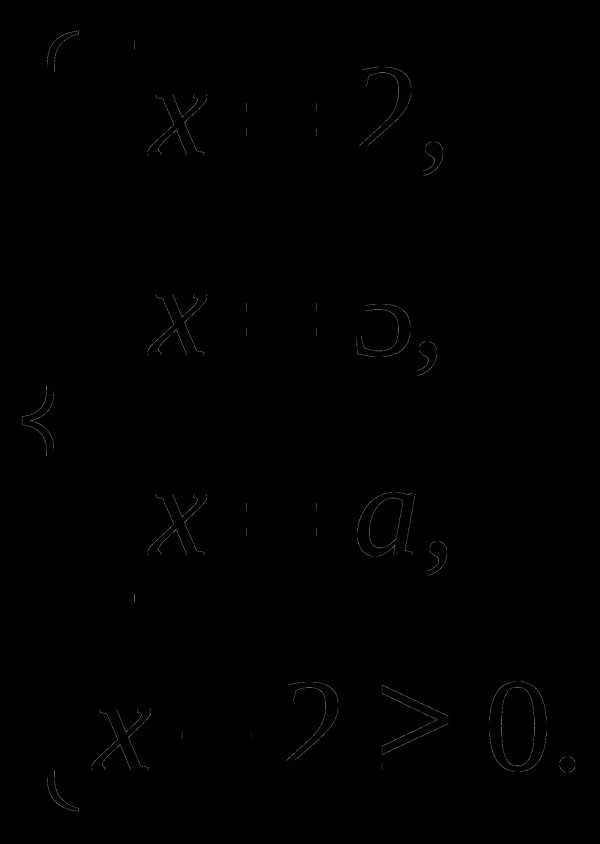
При 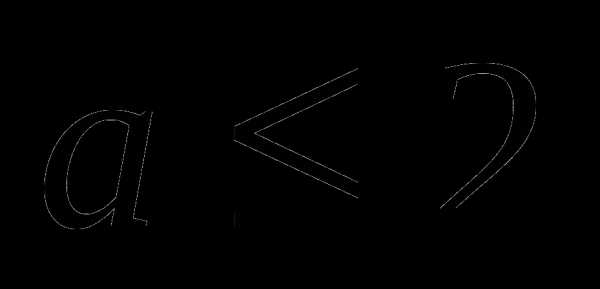 или
или  уравнение имеет два решения, в других случаях – три.
уравнение имеет два решения, в других случаях – три.
Ответ: два решения , если
три решения, если
ПРИМЕР 8.
При каких значениях параметра  уравнение
уравнение
имеет единственное решение ?
Решение:
Данное уравнение равносильно системе :
Решив квадратное уравнение , имеем :
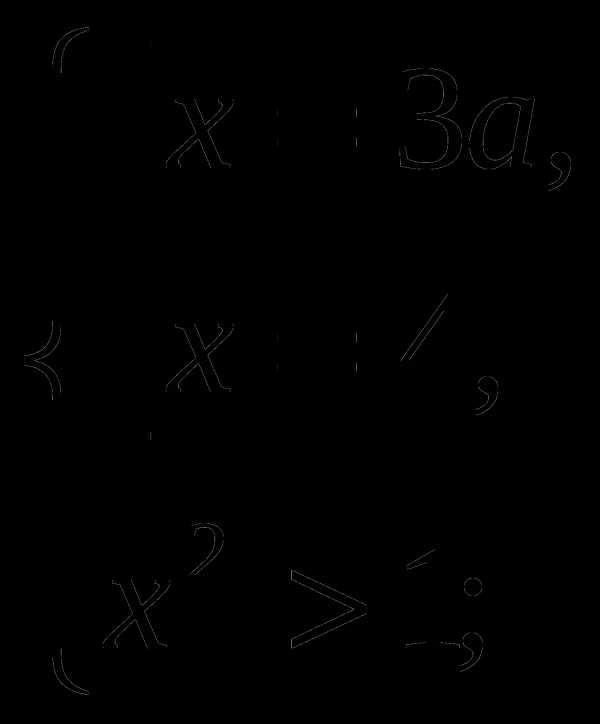
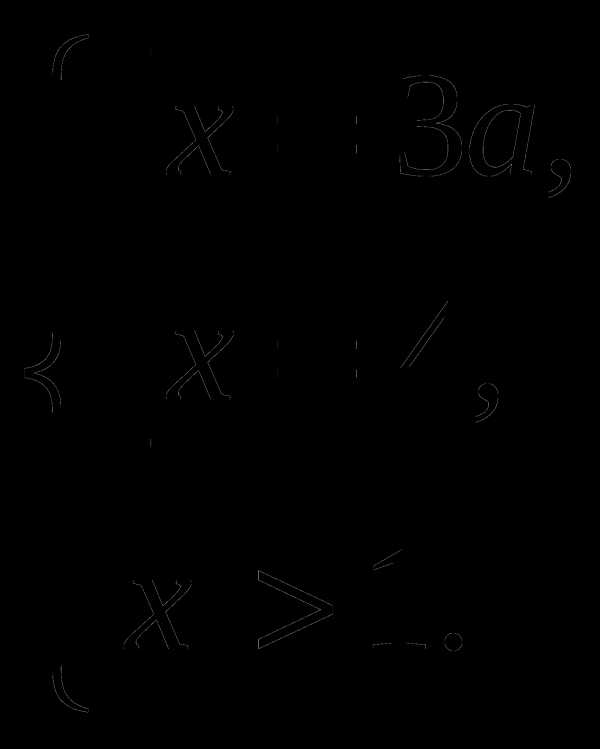
Система имеет единственное решение, если 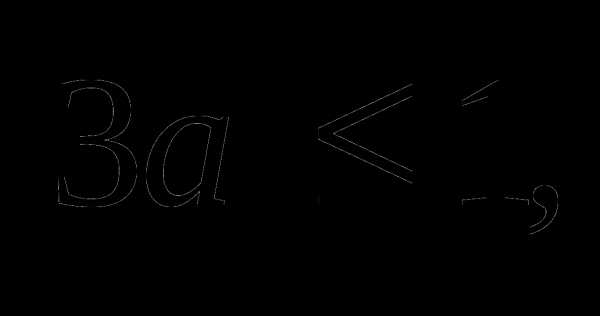 т.е.
т.е. 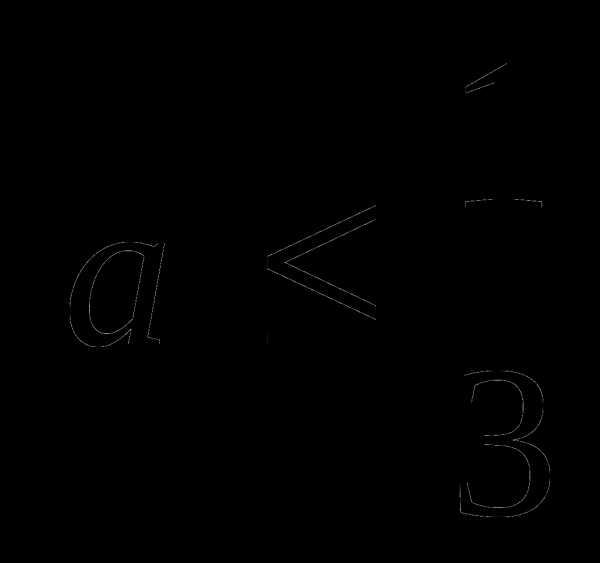 или, когда
или, когда 
Ответ: уравнение имеет единственное решение, если 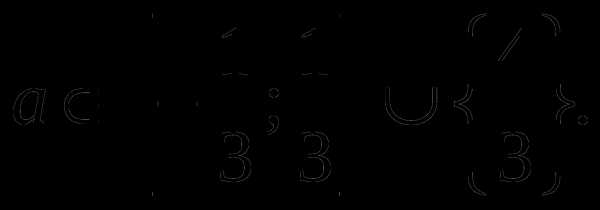
ПРИМЕР 9.
При каких значениях параметра  уравнение
уравнение
имеет единственное решение?
Решение:
1.Если то мы получим линейное уравнение 
При 
При  решений нет .
решений нет .
2.При дискриминант D должен равняться нулю, т.е.

Случай  уже рассмотрен .
уже рассмотрен .
Ответ:уравнение имеет единственное решение при 
ПРИМЕР 10.
При каких значениях параметра  сумма корней уравнения
сумма корней уравнения
равна 2?
Решение:
Чтобы уравнение имело корни ,
По теореме Виета,
Таким образом, имеем систему:


Ответ: при 
ПРИМЕР 11.
При каких значениях параметра  уравнение
уравнение
имеет два разных положительных корня ?
Решение:
Для того, чтобы квадратное уравнение имело два разных действительных корня, необходимо, чтобы дискриминант
По теореме Виета:

Таким образом, имеем систему неравенств :
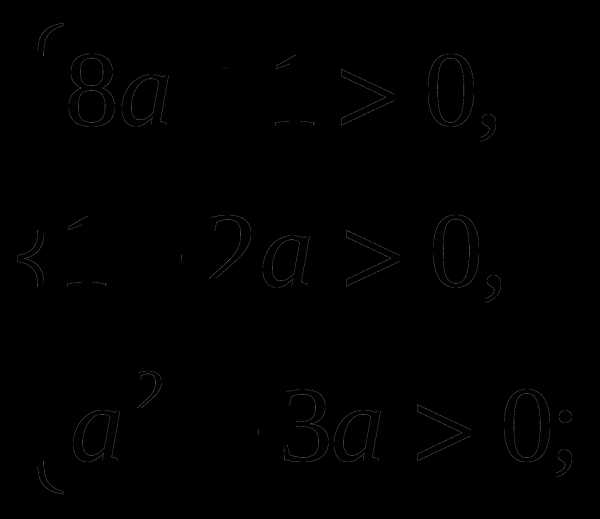



Ответ: уравнение имеет два разных положительных корня,
если  .
.
ПРИМЕР 12.
При каких значениях параметра  один корень уравнения
один корень уравнения
меньше, чем -2 , три других- больше -1 ?
Решение:
В условии задачи идёт речь о четырёх корнях , т.е. 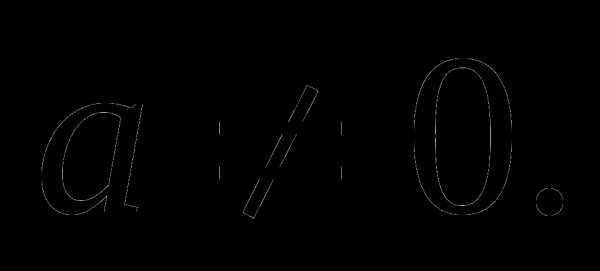 Пусть
Пусть 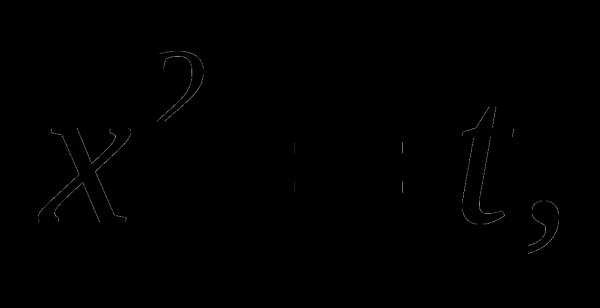 тогда
тогда
данное уравнение примет вид
.
Чтобы данное уравнение имело четыре действительных корня , которые удовлетворяют условию задачи , необходимо, чтобы корни уравнения относительно t удовлетворяли условиям:
Итак имеем систему неравенств :
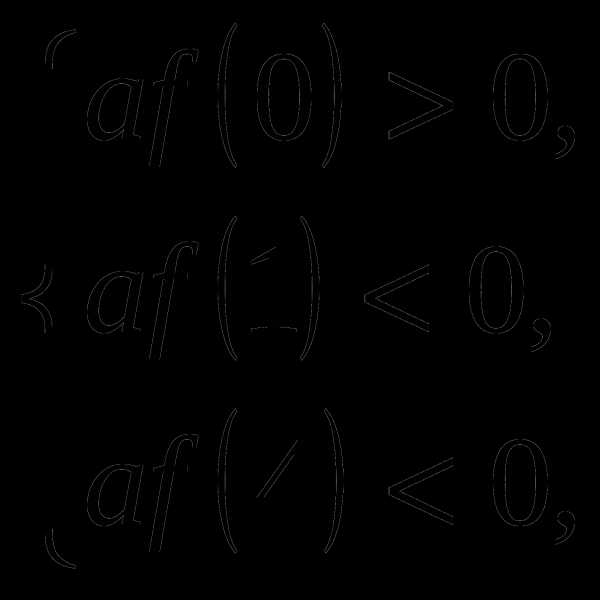 где
где
Ответ: при 
ПРИМЕР 13.
При каких значениях параметра  уравнение имеет
уравнение имеет
единственный корень ? Найти его.
Решение:
а)  тогда
тогда 
б)  тогда
тогда 

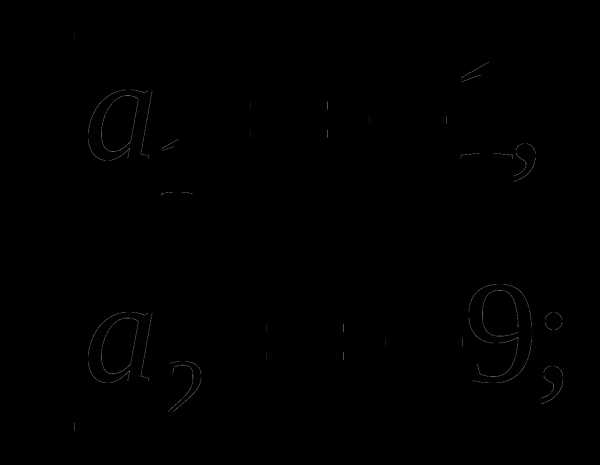

 Ответ: при
Ответ: при 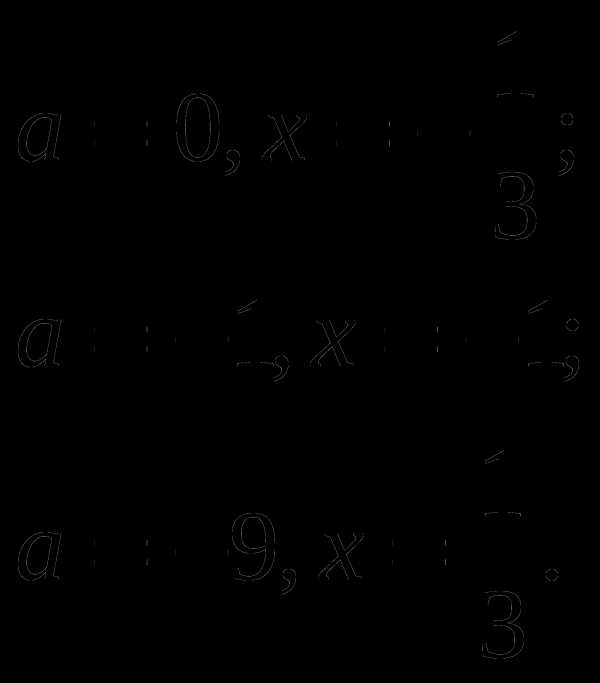
ПРИМЕР 14.
Определить количество целых значений параметра  из промежутка
из промежутка 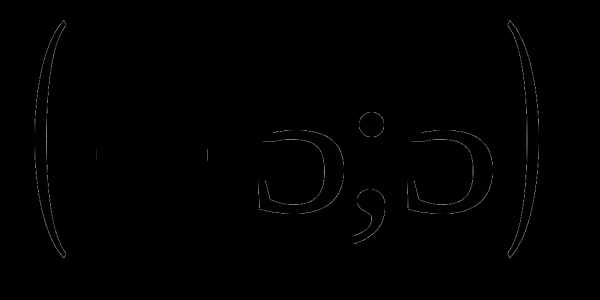 ,
,
при которых квадратное уравнение имеет два разных корня.
Решение:
Для того , чтобы квадратное уравнение имело два разных корня, необходимо, чтобы 
Ответ: 4.
ПРИМЕР 15.
При каком наименьшем целом значении  уравнение
уравнение
имеет четыре решения ?
Решение :
Построим в одной системе координат графики функций и

Видим, что при эти графики имеют четыре точки пересечения.
Ответ:
ПРИМЕР 16.
Найдите количество целых значений  , при которых сумма корней уравнения принадлежит промежутку
, при которых сумма корней уравнения принадлежит промежутку  .
.
Решение:
 Сумма корней уравнения равна
Сумма корней уравнения равна 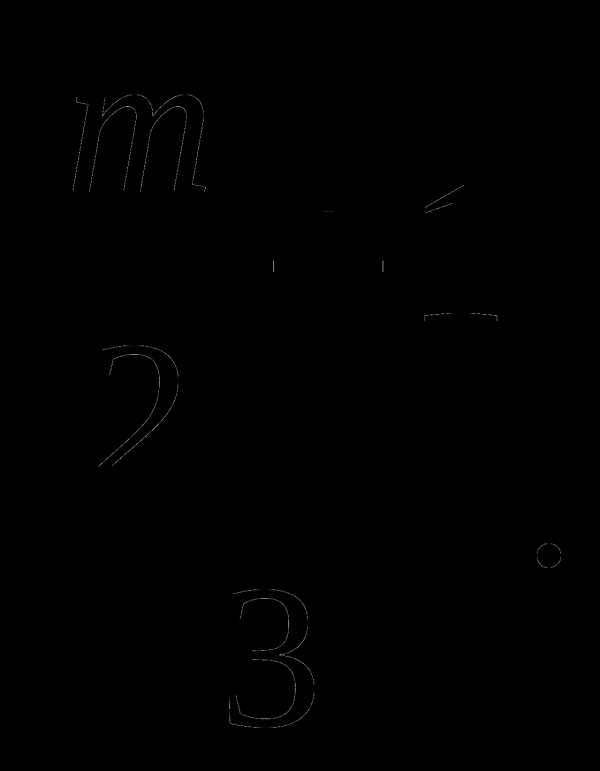
Итак , 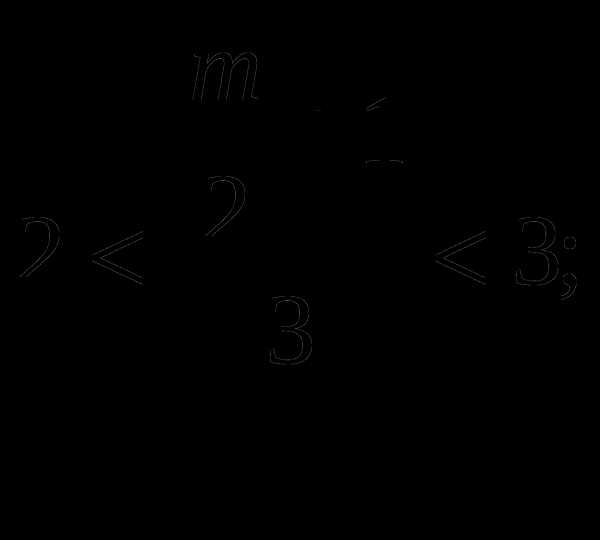
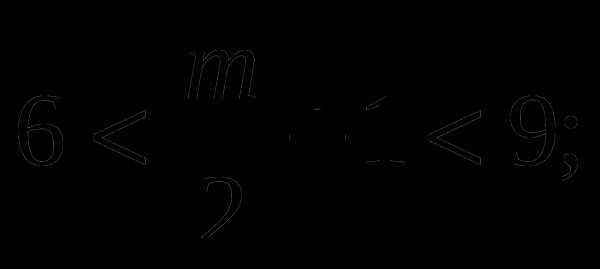


Целые числа, которые удовлетворяют условию 11, 12,13, 14,15.
Ответ: пять.
ПРИМЕР 17.
Найдите количество целых значений  , при которых произведение корней уравнения принадлежит промежутку
, при которых произведение корней уравнения принадлежит промежутку 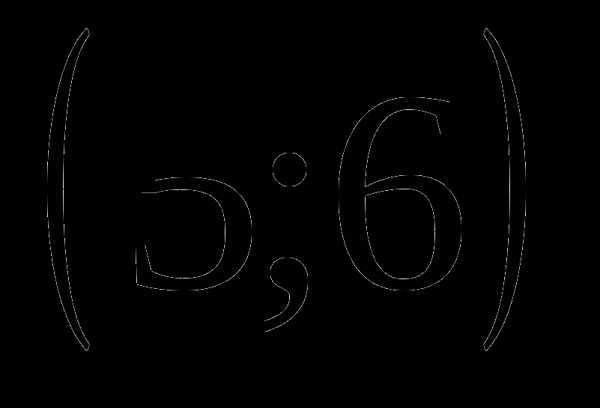 .
.
Решение:
Произведение корней уравнения равно 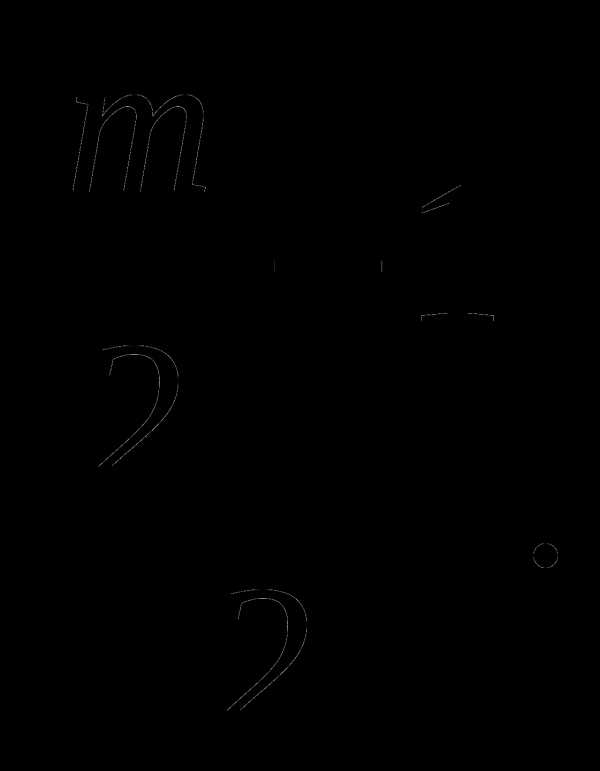
Итак, 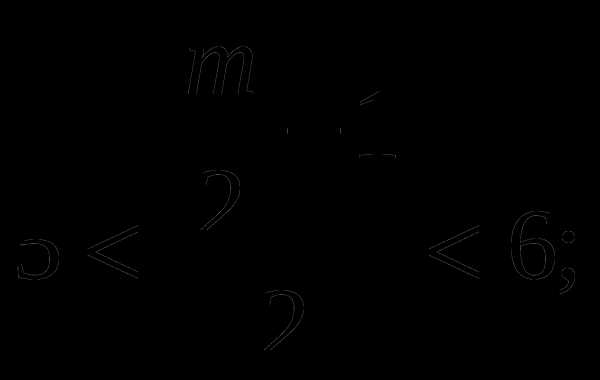

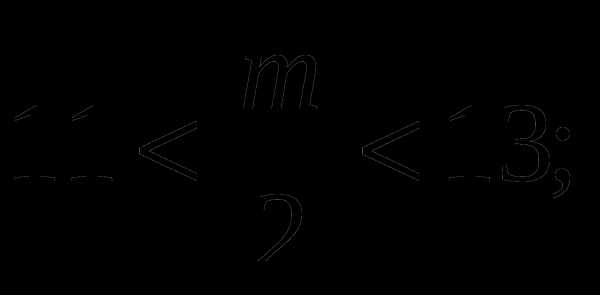
Целые числа , которые удовлетворяют условию это 23, 24, 25.
Ответ:три.
ПРИМЕР 18.
При каком наименьшем натуральном значении параметра  корни уравнения являются рациональными числами?
корни уравнения являются рациональными числами?
Решение:
Для того ,чтобы корни уравнения были рациональными числами, необходимо, чтобы выражение  было полным квадратом ,т.е.
было полным квадратом ,т.е.
будет полным квадратом при наименьшем натуральном значении

Ответ: при 
ПРИМЕР 19.
При каком значении параметра  квадратное уравнение
квадратное уравнение
имеет корни, равные по абсолютной величине и противоположные по значению ?
Решение:
разделим на 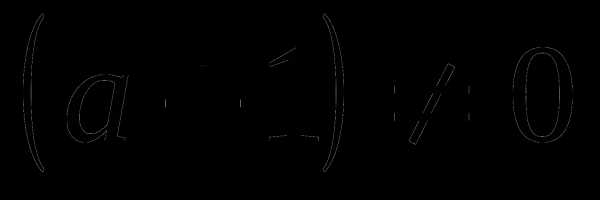
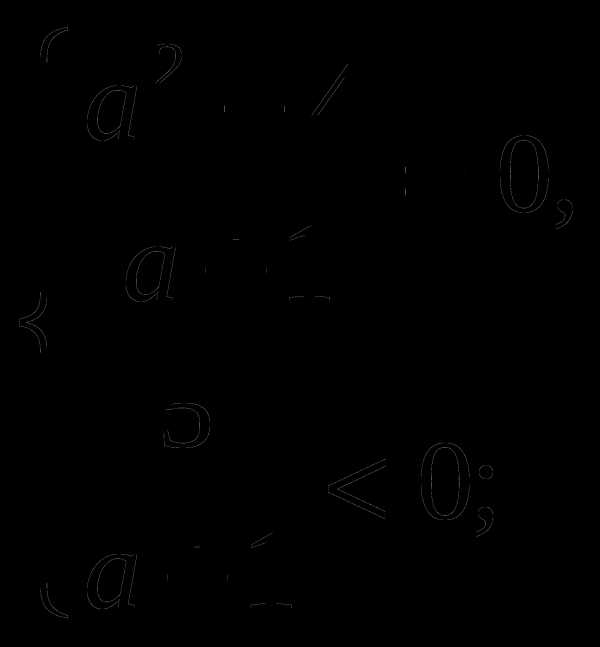

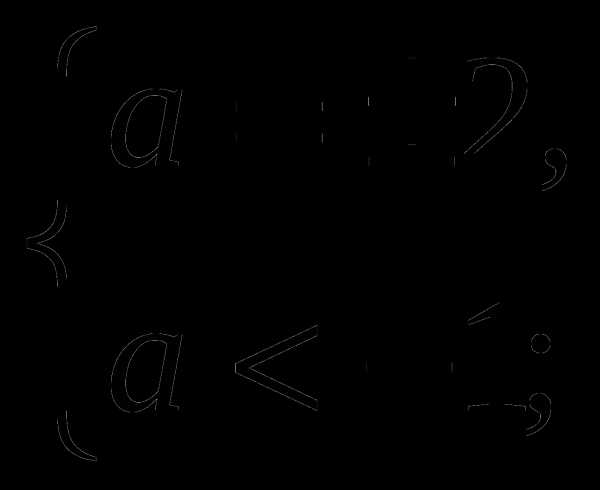

Ответ: при 
ПРИМЕР 20.
При каком наибольшем целом значении параметра  корни уравнения
корни уравнения
находятся по разные стороны промежутка  ?
?
Решение:
Запишем левую часть уравнения как функцию
Нарисуем график этой функции ( схематично).
Мы видим, что корни уравнения находятся по разные стороны промежутка
 , если выполняются условия:
, если выполняются условия:
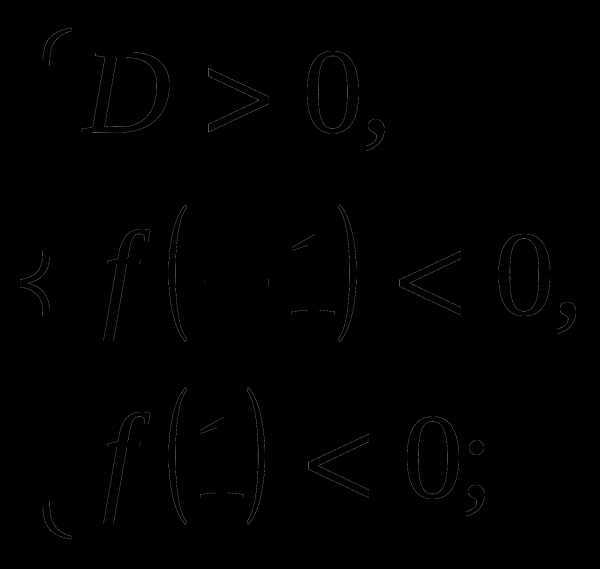
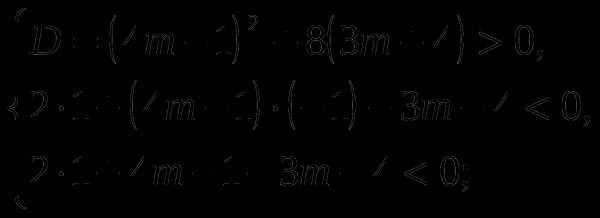


Ответ: 
ПРИМЕР 21.
При каком значении параметра  сумма квадратов корней уравнения
сумма квадратов корней уравнения
равна 12?
Решение:
По теореме Виета:
infourok.ru
Урок «Решение квадратных уравнений с параметром»
Министерство образования и науки Самарской области
Государственное автономное образовательное учреждение дополнительного профессионального образования (повышения квалификации) специалистов
САМАРСКИЙ ОБЛАСТНОЙ ИНСТИТУТ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ
И ПЕРЕПОДГОТОВКИ РАБОТНИКОВ ОБРАЗОВАНИЯ
Итоговая работа
На курсах повышения квалификации
«Методические особенности обучения решению задач с параметром в условиях перехода к новым образовательным стандартам».
По ИОЧ ВБ 13.03.2017г-17.03.2017г
по теме:
« Квадратные уравнения с параметрами»
Выполнила:
Тихонова Надежда Викторовна,
Преподаватель математики
БГПОУ Сызранский «политехнический колледж»
Сызрань 2017 г.
. КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРАМИ
Уравнение вида ax2+bx+c=0, где a, b, c – числа, причем а≠0 называется
квадратным уравнением.
а – первый коэффициент, b – второй коэффициент, с – свободный член.
Например:
а) 2х2– 3х + 0,7 = 0
б) -0,9 х2+ 8 – 2 1/6х=0
Найти a, b, c?
Решим уравнение ax2+bx+c=0
а) если а=0, то уравнение имеет вид bx+c=0. Тогда x=-c|b
б) если а≠0, то уравнение имеет:
1) 2 различных корня х1≠х2, если Д>0,
2) 2 равных корня х1=х2, если Д=0
3) не имеет корней, если Д<0.
Рассмотрим примеры.
Пример №1. При каких значениях уравнение имеет 2 корня?
2х2+6х+b=0
Уравнение квадратное.
Найдем Д=36-4*2*b=36-8b. По условию задачи уравнение имеет 2 корня,
значит Д>0.
Решим неравенство 36-8b>0
-8b>-36
b<4,5.
Ответ: при b<4,5.
Пример № 2. При каких значениях имеет один корень?
3х2-6х+2v=0
Уравнение квадратное. Д=36-4*3*2v=36-24v.
Так как уравнение имеет один корень, то Д=0.
36-24v=0
24v=36
V=1,5.
Пример № 3. При каких t уравнение не имеет корней?
2×2-15x+t=0
Уравнение квадратное. Д=225-4*2t=225-8 t По условию Д<0, то
225-8t<0
-8t<-225
t>281/8.
Ответ: при t>281/8/
Пример № 4.
При каких значениях m равно один из корней уравнения равен нулю. х2 – 2х + 2m – 3 = 0
Решение: Если х = 0, то имеем:
02 – 2 .0 + 2m – 3 = 0
2m = 3
m = 1,5
Проверим, не равняется ли второй корень уравнения нулю.
х = 0
х = 2
х2 – 2х = 0
Ответ: m = 1,5
При решении квадратного уравнения с параметрами контрольными будут те значения параметра, при которых коэффициент при х2 обращается в 0. Дело в том, что если этот коэффициент равен нулю, то уравнение превращается в линейное и решается по соответствующему алгоритму; если же этот коэффициент отличен от нуля, то имеем квадратное уравнение, которое решается по иному алгоритму. Дальнейшее решение зависит от дискриминанта.
Пример №.5
Решить уравнение х2 – (2р + 1)х + (р2 + р – 2) = 0
Решение: Здесь коэффициент перед х2 отличен от нуля, значит данное уравнение при любых значениях параметра является квадратным. Найдем дискриминант:
D = (2р + 1)2 – 4∙1(р2 + р – 2) = (4р2 + 4р + 1) – (4р2 + 4р – 8) = 4р2 + 4р + 1 – – 4р2 – 4р + 8 = 9
D > 0, значит квадратное уравнение имеет два решения
х1 = р + 2
х2 = р – 1
Ответ: при любых значениях р х1 = р + 2; х2 = р – 1
Пример № 6.
Решить уравнение рх2 +( 1 – р)х – 1 = 0
Решение: Мы не можем утверждать, что данное уравнение является квадратным. Рассмотрим контрольные (точки) значения р = 0, имеем два случая.
Если р=0, то получается уравнение вида 0∙х2 + х – 1 = 0, которое является линейным и имеет корень х = 1
Если р ≠0, то уравнение является квадратным, можно применять формулы корней квадратного уравнения.
D = (1 – р)2 – 4∙.р .(-1) = 1 – 2р + р2 + 4р = (1+ р)2
х1 = 1
х2 = –
Ответ: при р = 0 х = 1; при р ≠0 х1 = 1 х2 = –
Пример № 7
Решить уравнение: (а – 1)х 2 + 2(2а + 1)х + (4а + 3) = 0
Решение: здесь контрольными будут те значения параметра, при которых коэффициент при х2 обращается в 0.
Если а – 1 = 0, а = 1, уравнение имеет вид 0∙ х2 + 6х + 7 = 0 и является линейным. Корнем этого уравнения является х =
Если а–1 ≠ 0, а ≠ 0, уравнение является квадратным. Найдем его дискриминант.
D = (2∙(2а + 1))2 – 4(а – 1)(4а + 3) = 4(4а2 + 4а + 1) – 4(4а2 – а – 3) = 4(5а + 4)
Дальнейшие рассуждения зависят от значения дискриминанта.
Если D < 0, то квадратное уравнение не имеет корней; если D = 0, то уравнение имеет один корень, если D > 0, то уравнение имеет два корня.
Дискриминант обращается в нуль при а = – (можно сказать, что это – второе контрольное значение параметра; при переходе через него происходит качественное изменение уравнения – меняется число корней уравнения).
Если а < – , то D < 0 и следовательно, квадратное уравнение не имеет корней.
Если а > – , то если D > 0 и, значит квадратное уравнение имеет два корня:
х1 =
х2 =
Если а = – , то D = 0, то уравнение имеет единственное решение
х =
Ответ: при а = 1, х = – ;
при а = –, х = ;
при а < –, корней нет;
при а > –, х1 =
х2 =
Иногда задания сформулированы так, что искать корни нет необходимости.
Пример №8
При каких значениях m ровно один из корней х2+(m+3)х +|m| – 3 = 0
уравнения равен нулю.
Решение. Если нуль является корнем уравнения, квадратный трехчлен х2+(m+3)х +|m| – 3 при х = 0 обращается в нуль. 02+(m+3) .0 +|m| – 3 = 0
|m| – 3 = 0 m1 = 3 m2 = –3
Найдем второй корень при найденных значениях m.
Если m=3, то уравнение принимает вид х2+6х = 0; х1 = 0 х2 = –6
Если m= –3, то уравнение принимает вид х2 = 0, которое имеет два кратных корня, равных нулю.
Ответ: при m = 3
Пример №9
Сколько корней имеет уравнение 3х (х – 1) 2 = kх в зависимости от значения параметра k ?
Решение: 3х (х – 1) 2 = kх
3х (х – 1) 2 – kх = 0
х (3(х – 1) 2 – k) = 0
Один корень есть всегда – х0 = 0
Исследуем 3х 2 – 6х + 3 – k = 0
D = 32 – 3(3 – k) = 3k
а) Если k = 0, существует один корень х = 1;
б) Если k > 0, существуют два корня х1 = х2 = , но необходимо исследовать случай, когда один из корней равен 0. Это так, если k = 3;
в) Если k < 0, корней нет.
Ответ: уравнение 3х (х – 1) 2 = kх имеет при
1) k > 0
k ≠ 3 три корня;
2) k = 0 два корня
3) k = 3 два корня
4) k < 0 один корень.
xn--j1ahfl.xn--p1ai
Методическое пособие «Решение квадратных уравнений с параметрами»
МИНИСТЕРСТВО ОБОРОНЫ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ КАЗЁННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ОРЕНБУРГКОЕ ПРЕЗИДЕНТСКОЕ КАДЕТСКОЕ УЧИЛИЩЕ»
РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С ПАРАМЕТРАМИ
(методическое пособие для воспитанников и преподавателей)
Составила преподаватель математики
высшей квалификационной категории
Зевина Елена Петровна
2013г.
УДК 372.
Зевина Е.П.: РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С ПАРАМЕТРАМИ.
Методическое пособие для воспитанников и преподавателей.
– Оренбург: ФГКОУ Оренбургское ПКУ, 2013. –32с.
В пособии представлен опыт практической деятельности преподавателя училища по методике обучения решению квадратных уравнений с параметрами.
Методическое пособие содержит задачи с параметрами, при решении которых возникают наибольшие затруднения во время обучения. Методами решения таких задач уделяется минимум внимания, и целью данного пособия является помощь учащимся в устранении данного пробела.
Данное методическое пособие составлено по итогам многолетней практики работы и подготовки учащихся к сдаче экзамена по математике в формате ЕГЭ и ГИА.
Рассмотрено на заседании методического совета ФГКОУ Оренбургское ПКУ.
ФГОУ «Оренбургское президентское кадетское училище», 2013
Содержание
Введение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
§1. Квадратные уравнения с параметром . . . . . . . . . . . . . . . . . . . . . . . . 5
Понятие уравнения с параметром . . . .. . . . . . . . . . . . . . . . . . . . . . . 5
Квадратные уравнения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Теорема Виета . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . 6
§2. Примеры решения квадратных уравнений с параметром . . . . . . . . . 7
§3. Задачи для самостоятельной работы по решению квадратных
уравнений с параметром . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
§4. Решение уравнений с параметром, приводимых к квадратным. . . .15
§5. Задачи для самостоятельной работы по решению уравнений,
приводимых к квадратным . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .17
§6. Задачи, связанные с расположением корней квадратного трехчлена.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
§7. Задачи для самостоятельного решения, связанные с
расположением корней квадратного трехчлена . . . . . . . . . . . . . . . . . . 25
Заключение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
Список использованной литературы . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
Введение
У большинства выпускников и абитуриентов задачи с параметрами вызывают серьезные затруднения (как решать задачу и как довести решение до правильного ответа). Трудности при решении таких задач обусловлены во-первых: решением не по шаблону, во- вторых: рассмотрением различных случаев, в которых методы решения существенно отличаются друг от друга; в-третьих: хорошими знаниями свойств функций и правильным выделением тех свойств, которые нужно применить.
Предлагаемое пособие построено так, чтобы учащиеся самостоятельно могли понять логику решения задач с параметрами, и научились их решать.
Пособие разбито на параграфы, в конце которых приведены упражнения для самостоятельного решения. Разобраны примеры, которые расположены в последовательности «от простого к сложному», при этом предполагается, что учащийся имеет хорошие знания по математике и изучает пособие последовательно.
Пособие может быть использовано как для самостоятельной подготовки к вступительным экзаменам, так и в качестве пособия на индивидуальных и групповых занятиях.
Функции вида , где – квадратный трехчлен, в школьном курсе математики придается большое значение. Для нее строго доказываются все свойства, нужные в теории и для решения задач. Безукоризненное знание необходимых свойств квадратного трехчлена требуется от каждого абитуриента, так как квадратный трехчлен с параметром часто включается в варианты письменных работ и в тесты для собеседования на вступительных экзаменах в ВУЗы. Как правило, большая часть абитуриентов с этими задачами не справляется. Значит, им надо уделять больше внимания на факультативных занятиях в школе, на страницах печати.
§1. Квадратные уравнения с параметром
1.1 Понятие уравнения с параметром
Определение. Пусть задано уравнение , если ставится задача, для каждого действительного значения решить уравнение относительно , то это уравнение называют уравнением с переменной и параметром .
Решить уравнение с параметром – это значит, для каждого действительного значения найти значение , удовлетворяющее данному уравнению.
Назовем контрольными значениями параметра (КЗП) те его значения, при которых обращается в нуль: 1) старший коэффициент в уравнении или неравенстве; 2) знаменатель дроби; 3) дискриминант квадратного уравнения.
1.2 Квадратные уравнения
Определение. Квадратным уравнением называют уравнение вида
,
(1)
где – переменная, и , , – некоторые действительные числа или выражения, зависящие от параметров.
Левая часть уравнения является квадратным трехчленом, то есть многочленом второй степени.
Корни квадратного уравнения (1) находят по формуле
.
(2)
Выражение называют дискриминантом квадратного уравнения (1).
В случае, когда второй коэффициент квадратного уравнения четное число , корни удобно находить по формуле
.
(3)
Число корней квадратного уравнения зависит от дискриминанта:
если , то уравнение имеет два различных действительных корня;
если , то уравнение имеет два равных действительных корня
или один корень, но двойной кратности.
если , то уравнение не имеет действительных корней.
При решении неполного квадратного уравнения , где удобно пользоваться разложением на множители левой части уравнения:
.
1.3 Теорема Виета
При решении полных квадратных уравнений применяют теорему Виета: если и – корни квадратного уравнения , где , то справедливы формулы для суммы и произведения этих корней:
, .
(4)
Формулы (4) называют формулами Виета.
Верно и обратное утверждение: если числа и удовлетворяют равенствам (4), то эти числа являются корнями квадратного уравнения.
Формулы Виета верны и для приведенного квадратного уравнения . В этом случае они приобретают вид:
, .
Квадратный трехчлен можно разложить на линейные множители:
если , то ;
если , то .
§2. Примеры решения квадратных уравнений с параметром
Пример 1. Найти все значения параметра а, для которых квадратное уравнение
имеет два различных корня;
не имеет корней;
имеет один корень.
Решение. Так как по условию старший коэффициент , то уравнение является квадратным. Найдем его дискриминант: .
Контрольными значениями параметра будут те значения, при которых дискриминант равен нулю.
КЗП: или .
Далее определим знак дискриминанта, а для этого заметим, что он представляет собой квадратичную функцию, графиком которой является парабола, причем ветви её направлены вверх.
Знак : 1) + 2) 3) 2) + 1)
– 4 – 4 а
Возможны три случая.
1) Если , то и уравнение имеет два различных действительных корня
.
Если или , то и уравнение имеет один двукратный корень , причем если , то , а если , то .
3) Если , то и уравнение не имеет действительных корней.
Ответ: при ;
при корней нет;
при ;
при .
Пример 2. Решить уравнение .
Решение. Поскольку старший коэффициент данного уравнения зависит от параметр , то это уравнение нельзя считать квадратным. Поэтому найдем первое контрольное значение параметра, приравняв старший коэффициент к нулю.
КЗП: .
Если , то исходное уравнение принимает вид:
,
то есть становится линейным и его корнем является .
infourok.ru
«Квадратные уравнения с параметрами»
Введение.
В заданиях ЕГЭ и ОГЭ по математике широкое распространение получили задачи, содержащие параметры. Решение задач с параметрами носит учебно-исследовательский характер, они играют важную роль в формировании логического мышления.
Как известно, решению задач с параметрами в школе уделяется очень мало времени. Поэтому решение задач с параметрами всегда вызывает большие трудности . Трудно рассчитывать на то, что учащиеся, подготовка которых не содержала «параметрическою терапию», смогут в жесткой атмосфере конкурсного экзамена успешно справиться с подобными задачами, следовательно, учащиеся должны специально готовиться к «встрече с параметрами».
В следующем году мы будем сдавать ОГЭ, а через два года ЕГЭ. Подготовку к этому ответственному экзамену мы начали в этом году, когда изучили методы решения линейных и квадратных уравнений .
Гипотеза исследования: если освоить методы решения квадратных уравнений с параметрами, то это позволит в дальнейшем овладеть приемами и способами решения более сложных задач с параметрами, тем самым обеспечит качественную подготовку к ЕГЭ.
Актуальность работы: усвоение методов решения квадратных уравнений с параметрами будет хорошим подспорьем при сдаче ОГЭ и ЕГЭ.
Цель работы: научиться решать квадратные уравнения с параметрами.
Задачи:
Изучить методы решения квадратных уравнений с параметрами;
Познакомить одноклассников с методами решения квадратных уравнений с параметрами на факультативе при подготовке к ОГЭ.
Объект исследования: уравнения с параметрами.
Предмет исследования: квадратные уравнения с параметрами.
1. Алгебраические методы решения уравнений второй степени с параметром.
Что такое параметр?
Как это ни покажется странным, задачи с параметрами мы решаем чуть ли не ежедневно, при этом в большинстве своем не зная, что такое параметр. Например, придя в магазин покупать какой-либо товар, мы смотрим на его цену. Если цена будет очень высокой, мы не купим его. Если цена будет вполне приемлемой, мы принимаем решение купить товар. Но если цена товара резко уменьшилась (например, в результате распродажи), мы можем купить несколько единиц этого товара. Таким образом, если рассматривать цену товара как параметр, то от значений этого параметра будет зависеть, купим или не купим мы этот товар, а если и купим, то сколько единиц.
Та же самая картина имеет место и в математике при решении уравнений. При одних значениях коэффициентов уравнение может вообще не иметь решений, при других — одно решение, при третьих – бесконечно многих решений. Например, в школьном курсе алгебры мы часто встречались с ситуацией, когда квадратное уравнение в зависимости от значений коэффициентов имело два решения, одно решение или не имело решений вовсе.
ПАРАМЕТР (от греч. parametron — отмеривающий) в математике, величина, числовые значения которой позволяют выделить определенный элемент из множества элементов того же рода. (Большой Энциклопедический словарь (БЭС)).
Определение 1. Параметром называется независимая переменная величина, входящая в условие задачи или появляющаяся в процессе ее решения, «управляющая» решением задачи.1
Определение 2. Задача, условие которой содержит или в ходе решения которой появляется хотя бы одна независимая переменная, удовлетворяющая определению понятия «параметр», называется задачей с параметром.1
Если в уравнении (неравенстве) коэффициенты при некоторых величинах зависят от некоторой переменной или нескольких переменных, то эта переменная или переменные называются параметрами, а уравнения или неравенство параметрическим.
Решить уравнение или неравенство с параметрами означает:
Определить, при каких значениях параметров существуют решения;
Для каждой допустимой системы значений параметров найти соответствующее множество решений.
1.2. Квадратные уравнения. Теория.
Уравнение вида ах2+bх+с=0, а0, где a,b,c – некоторые действительные числа или выражения, зависящие от параметров, называется квадратным. Левая его часть является квадратным трехчленом, то есть многочленом второй степени. Корни квадратного уравнения ах2+bх+с=0, а0 находятся по формуле
Выражение D = называется дискриминантом квадратного уравнения ах2+bх+с=0, а0.
Если D > 0, то уравнение имеет два различных действительных корня;
Если D = 0, то уравнение имеет два совпадающих действительных корня;
Если D < 0, то уравнение не имеет действительных корней.
В случае, когда второй коэффициент квадратного уравнения четен, то есть
b = 2k, корни удобно находить по формуле
Неполные квадратные уравнения, то есть такие, в которых b = 0 или
c = 0, удобно решать методом разложения на множители левой части уравнения.
Если уравнение имеет два различных корня х1 и х2, то его левая часть раскладывается на множители следующим образом:
ах2+bх+с = а(х — х1)(х — х2).
Если уравнение имеет единственный корень х0, то его левая часть является полным квадратом:
ах2+bх+с = а(х – х0)2.
Уравнение вида ах2+bх+с=0 при а = 0 приводится к уравнению степени не выше первой. То есть случай а = 0 при необходимости следует рассматривать отдельно.
2.Примеры решения уравнений с параметром.
Пример№1
Найти все значения параметра а, при которых уравнение
ах2 -(2а+6)х + 3а+3=0 имеет единственный корень.
Решение:
а=о, х= . х= 0,5
а≠0
Д= (2а+6)2 -4а(3а+3)= -4(2а2 -3а-9)=0
2а2 -3а-9=0
а1= 3 , а2= -1,5
Ответ: 0; 3; -1,5
Пример №2
Найти значения параметра а, при котором уравнение
(а-2)х2 +(3а+1)х + 2а -7 =0 имеет один корень х>1.
Рассмотрим квадратичную функцию у= ах2+ вх+с
α — число
Д<0Д= 0
Д>0
α
α
f(α)
α
хв<α
хв = α
хв > α
хв<α
хв = α
3) хв > α
хв<α
хв = α
3) хв > α
хв<α+
?
—
хв > α
+
Решение:
Если Д<0, то корней нет.
Если Д=0, то не более одного корня.
Если Д>0 ,то не более двух корней.
а=2 , 7х-3 =0 , х= 3/7 , 3/7<1 не подходит по условию.
а≠2
1
1
Хв > 1
Д= а2 +50а- 55= 0
а= -25 ± не подходит по условию, т.к.
хв = >1 , <0, 3/5<х<2
(а-2)f(1)<0
(а-2)(а-2+3а+1+2а-7)<0
(а-2)(6а-8)<0 + 4/3 — 2 +
4/3<а<2
Рассмотрим частный случай, когда парабола проходит через единицу
1
f(1)=0 , а= 4/3 , -2х2 +15х -13=0, х1 =1, х2 = 6,5
Ответ : 4/3≤ а<2
Пример №3 ?
Рассмотрим функцию f(х)= ах2 +вх+с , а≠0 , α< х<β
α β
α β
хв<α
α<хв<β
Хв>β
4
1 2 3 5
6
α β
Особо рассмотреть случаи f(α)=0 и f(β)=03.Заключение.
Задачи с параметрами очень разнообразны и охватывают практически весь школьный курс. Нам очень многое еще придется изучить, но эта работа была очень полезной для нас. Я получила практические навыки решения квадратных уравнений с параметрами. Я поднялась на одну ступеньку выше в своем понимании методов решения математических задач.
Решение задач с параметрами развивает логическое мышление, учит думать нестандартно, анализировать, сравнивать, обобщать.
В моих планах изучение задач связанных с расположением корней квадратного трехчлена, решение квадратных неравенств с параметрами.
Я надеюсь, что навыки решений задач с параметрами помогут мне в подготовке к ЕГЭ по математики.
infourok.ru
Уравнения с параметром
Разделы: Математика
Справочный материал
Уравнение вида f(x; a) = 0 называется уравнением с переменной х и параметром а.
Решить уравнение с параметром а – это значит, для каждого значения а найти значения х, удовлетворяющие этому уравнению.
Пример 1. ах = 0
- Если а = 0, то 0х = 0
х – любое действительное число - Если а 0, то х =
х = 0
Пример 2. ах = а
- Если а = 0, то 0х = 0
х – любое действительное число - Если а 0, то х =
х = 1
Пример 3.
х + 2 = ах
х – ах = -2
х(1 – а) = -2
Если 1 – а = 0, т.е. а = 1, то х0 = -2 корней нет
Если 1 – а 0, т.е. а 1, то х =
Пример 4.
(а2 – 1) х = 2а2 + а – 3
(а – 1)(а + 1)х = 2(а – 1)(а – 1,5)
(а – 1)(а + 1)х = (1а – 3)(а – 1)
Если а = 1, то 0х = 0
х – любое действительное число
Если а = -1, то 0х = -2
Корней нет
Если а 1, а -1, то х = (единственное решение).
Это значит, что каждому допустимому значению а соответствует единственное значение х.
Например:
если а = 5, то х = = ;
если а = 0, то х = 3 и т. д.
Дидактический материал
1. ах = х + 3
2. 4 + ах = 3х – 1
3. а = +
4. + 3(х+1)
5. = –
6. =
Ответы:
- При а 1 х =;
при а = 1 корней нет.
- При а 3 х = ;
при а = 3 корней нет.
- При а 1, а -1, а 0 х = ;
при а = 1 х – любое действительное число, кроме х = 1
при а = -1, а = 0 решений нет.
- При а 2, а 0 х = ;
при а = 0, а = 2 решений нет.
- При а -3, а -2, а 0, 5 х =
при а = -3, а = 0, 5, а = -2 решений нет
- При а + с 0, с 0 х = ;
при а = —с, с = 0 решений нет.
Квадратные уравнения с параметром
Пример 1. Решить уравнение
(а – 1)х2 = 2(2а + 1)х + 4а + 3 = 0
При а = 1 6х + 7 = 0
х = –
В случае а 1 выделим те значения параметра, при которых Д обращается в нуль.
Д = (2(2а + 1))2 – 4(а – 1)(4а + 30 = 16а2 + 16а + 4 – 4(4а2 + 3а – 4а – 3) = 16а2 + 16а + 4 – 16а2 + 4а + 12 = 20а + 16
20а + 16 = 0
20а = -16
a =
a =
Если а < -4/5, то Д < 0, уравнение имеет действительный корень.
Если а > -4/5 и а 1, то Д > 0,
х =
Если а = 4/5, то Д = 0,
х = – = –
Пример 2. При каких значениях параметра а уравнение
х2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?
Д = 4(а + 1)2 – 4(9а – 5) = 4а2 – 28а + 24 = 4(а – 1)(а – 6)
4(а – 1)(а – 6) > 0
по т. Виета: х1 + х2 = -2(а + 1)
х1х2 = 9а – 5
По условию х1 < 0, х2 < 0 то –2(а + 1) < 0 и 9а – 5 > 0
| В итоге | 4(а – 1)(а – 6) > 0 — 2(а + 1) < 0 9а – 5 > 0 |
а < 1: а > 6 а > — 1 а > 5/9 |
(Рис. 1) < a < 1, либо a > 6 |
Пример 3. Найдите значения а, при которых данное уравнение имеет решение.
х2 – 2(а – 1)х + 2а + 1 = 0
Д = 4(а – 1)2 – 4(2а + 10 = 4а2 – 8а + 4 – 8а – 4 = 4а2 – 16а
4а2 – 16 0
4а(а – 4) 0
а(а – 4)) 0
а(а – 4) = 0
а = 0 или а – 4 = 0
а = 4
(Рис. 2)
Ответ: а 0 и а 4
Дидактический материал
1. При каком значении а уравнение ах2 – (а + 1) х + 2а – 1 = 0 имеет один корень?
2. При каком значении а уравнение (а + 2) х2 + 2(а + 2)х + 2 = 0 имеет один корень?
3. При каких значениях а уравнение (а2 – 6а + 8) х2 + (а2 – 4) х + (10 – 3а – а2) = 0 имеет более двух корней?
4. При каких значениях а уравнение 2х2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х2 – 7х + 6 = 0?
5. При каких значениях а уравнения х2 +ах + 1 = 0 и х2 + х + а = 0 имеют хотя бы один общий корень?
Ответы:
1. При а = — 1/7, а = 0, а = 1
2. При а = 0
3. При а = 2
4. При а = 10
5. При а = — 2
Показательные уравнения с параметром
Пример 1.Найти все значения а, при которых уравнение
9х – (а + 2)*3х-1/х +2а*3-2/х = 0 (1) имеет ровно два корня.
Решение. Умножив обе части уравнения (1) на 32/х, получим равносильное уравнение
32(х+1/х) – (а + 2)*3х+1/х + 2а = 0 (2)
Пусть 3х+1/х = у, тогда уравнение (2) примет вид у2 – (а + 2)у + 2а = 0, или
(у – 2)(у – а) = 0, откуда у1 =2, у2 = а.
Если у = 2, т.е. 3х+1/х = 2 то х + 1/х = log32 , или х2 – хlog32 + 1 = 0.
Это уравнение не имеет действительных корней, так как его Д = log232 – 4 < 0.
Если у = а, т.е. 3х+1/х = а то х + 1/х = log3а, или х2 – хlog3а + 1 = 0. (3)
Уравнение (3) имеет ровно два корня тогда и только тогда, когда
Д = log232 – 4 > 0, или |log3а| > 2.
Если log3а > 2, то а > 9, а если log3а < -2, то 0 < а < 1/9.
Ответ: 0 < а < 1/9, а > 9.
Пример 2. При каких значениях а уравнение 22х – (а – 3) 2х – 3а = 0 имеет решения?
Для того чтобы заданное уравнение имело решения, необходимо и достаточно, чтобы уравнение t2 – (a – 3) t – 3a = 0 имело хотя бы один положительный корень. Найдем корни по теореме Виета: х1 = -3, х2 = а = >
а – положительное число.
Ответ: при а > 0
Дидактический материал
1. Найти все значения а, при которых уравнение
25х – (2а + 5)*5х-1/х + 10а * 5-2/х = 0 имеет ровно 2 решения.
2. При каких значениях а уравнение
2(а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?
3. При каких значениях параметра а уравнение
4х — (5а-3)2х +4а2 – 3а = 0 имеет единственное решение?
Ответ:
- 0 < а < 1/50, а > 25/2
- при а = 1, а = -2,2
- 0 < а 3/4 и а = 1
Логарифмические уравнения с параметром
Пример 1. Найти все значения а, при которых уравнение
log4x(1 + ах) = 1/2 (1)
имеет единственное решение.
Решение. Уравнение (1) равносильно уравнению
1 + ах = 2х при х > 0, х 1/4 (3)
х = у
ау2 –у + 1 = 0 (4)
| Если а = 0, то – | 2у + 1 = 0 2у = 1 у = 1/2 х = 1/2 х = 1/4 |
Не выполняется (2) условие из (3).
Пусть а 0, то ау2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а 0, т.е. при а 1.
Если Д = 0 (а = 1), то (4) имеет единственный положительный корень х = 1, удовлетворяющий условиям (3).
Пусть Д > 0 (а < 1), тогда уравнение (4) имеет два различных корня. Так как у = х 0, то в случае Д > 0 уравнение (4) имеет действительные корни разных знаков. Это условие выполняется тогда и только тогда, когда Д > 0 и 1/а < 0, т.е. при а < 0.
Пример 2. Найти все значения а, при которых уравнение
log5(x = 2-a ) – log1/5(a-1-x) = log259 имеет решение.
Решение. log5(x + 2-a) –log5(f – 1 – x) = log53
(1) х + 2 – а = 3(а – 1 – х), если
(2) а – 1 > х
Выражая х из (1) и подставляя в (2), получаем неравенство
2 – а > 1 – а (3)
Чтобы решить неравенство (3), построим графики функций у = 2 – а и у = 1 – а.
Рис. 3
Решения неравенства (3) образуют промежуток (а0; 2), где а0 < 0 и а0 – корень уравнения 2 – а = 1 – а.
Тогда 2 – а = (1– а)2
а2 – а – 1 = 0
а0 =
Ответ: < a 2
Дидактический материал
- Найдите, при каких значениях а уравнение log 3 (9x + 9a3)= x имеет ровно два корня.
- Найдите, при каких значениях а уравнение log 2 (4x – a) = x имеет единственный корень.
- При каких значениях а уравнение х – log 3 (2а – 9х) = 0 не имеет корней.
Ответы:
- при а < 1/3 36
- при а = -1/4
- при а < -1/8
Литература
16.06.2009
urok.1sept.ru
Квадратные уравнения с параметром. Видеоурок. Алгебра 8 Класс
На данном уроке будет рассмотрена тема: «Квадратные уравнения с параметром». Вы рассмотрите общую постановку решения задач с параметром и решите конкретную задачу с параметром двумя способами.
Тема: Неравенства
Урок: Квадратные уравнения с параметром
Решить задачу с параметром – значит перебрать все значения параметра и для каждого указать ответ. Для квадратных уравнений наличие корней зависит от дискриминанта
Пример №1 – решить уравнение с параметром
Решить уравнение:
I-ый способ.
Считаем, что – величина постоянная, и находим корни уравнения:
. Корни существуют, если . Решаем это линейное неравенство: При этих значениях параметра, то есть когда дискриминант положителен или равен нулю, корни есть. Причем, когда дискриминант равен нулю, уравнение имеет единственный корень. Когда дискриминант отрицателен – корней нет.
Ответ: 1. при любом решений нет; 2. при уравнение имеет единственное решение: ; 3. при любом значении уравнение имеет два различных корня:
Частные случаи:
Найти значения параметра а, при котором уравнение имеет одно решение.
Ответ: при корни есть, уравнение имеет единственное решение: .
Найти значения параметра а, при котором уравнение не имеет решения.
Ответ: при любом решений нет.
Решим пример №1 графически (II способ):
или
Алгоритм:
Рис. 1. График квадратной функции
1. Построим график функции, стоящей в левой части (Рис. 1).
2. Корнями этой функции является
3. График этой функции – парабола, ветви которой направлены вверх. Вершина параболы находится по формуле: ; . Подставляем . Вершина параболы ().
1. Рассечь построенный график семейством прямых: (Рис. 2).
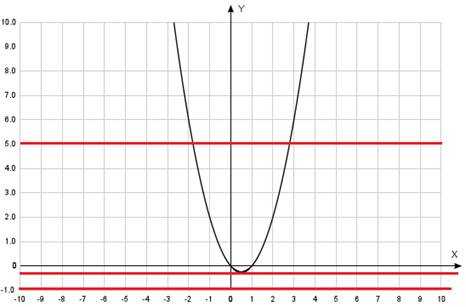
Рис. 2. Рассечение графика функции семейство
interneturok.ru
