математика в формулах и таблицах
19
Сибирский государственный университет телекоммуникаций и информатики
В.И. Агульник, Б.П. Зеленцов
в формулах и таблицах
Справочное пособие
Новосибирск
2000 г.
В.И.Агульник, Б.П.Зеленцов.
Математика в формулах и таблицах. Справочное пособие
Справочное пособие содержит формулы, таблицы, графики по математике, охватывающие основные разделы элементарной математики — алгебры и геометрии. Оно предназначено для абитуриентов при подготовке к вступительным экзаменам, а также для студентов дневного и заочного обучения при изучении высшей математики и других дисциплин.
Кафедра высшей математики
Рецензент: И.И.Резван
Утверждено редакционно-издательским советом СибГУТИ в качестве учебного пособия.
Сибирский государственный университет телекоммуникаций и информатики, 2000 г.
В.И.Агульник, Б.П.Зеленцов, 2000 г.
ОГЛАВЛЕНИЕ
ЧИСЛА, ДРОБИ, МОДУЛИ…………………………………
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ …………
СТЕПЕНИ И КОРНИ ……………………………………….
КВАДРАТНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА ………
ПРОГРЕССИИ ………………………………………………
ЛОГАРИФМЫ ………………………………………………
ТРИГОНОМЕТРИЯ ………………………………………
ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ ……………
ПЛАНИМЕТРИЯ …………………………………………
СТЕРЕОМЕТРИЯ …………………………………………
ЛИТЕРАТУРА …………………………………………………
1. ЧИСЛА, ДРОБИ, МОДУЛИ
n N — множество
натуральных чисел  {1,
2, 3, …}
{1,
2, 3, …}
d = НОД (n, m) — наибольший общий делитель n и m
k = НОК (n, m) — наименьшее общее кратное n и m
Z = множество целых чисел
Q = -множество рациональных чисел (дробей)
R – множество действительных чисел
Арифметические операции с дробями:
;  ;
; 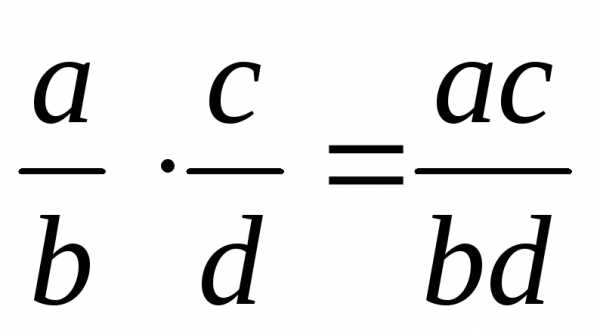 ;
;
 ;
;  ;
; ;
;
Пропорция  ;
;
Модуль числа. Определение: ;
Свойства модуля:
 ;
;  ; ;
; ;
a
a+b
a-b
 ;x
;x;
a
a+b
a-b
x2. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
; ;
;
;
;
; ;
3. СТЕПЕНИ И КОРНИ
 ;
;  ; ;;
; ;;
;  ;
; ;
;  ;
;
; ;  ;
;
4. КВАДРАТНЫЕ УРАВНЕНИЯ
; 
Корни уравнения:  ,
где
,
где —
дискриминант.
—
дискриминант.
Формулы Виета:  ;
; .
.
Разложение квадратного трехчлена на множители:
.
Приведенное
уравнение: ;  .
.
Квадратное неравенство:
Если D>0
, a>0, 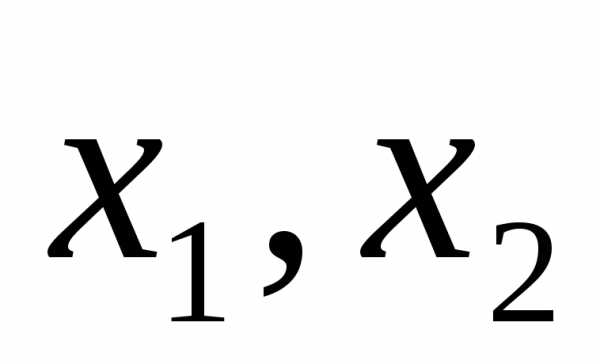 -корни
квадратного
трехчлена,
-корни
квадратного
трехчлена,  ,
то
,
то
;
.
5. ПРОГРЕССИИ
Арифметическая прогрессия:
Общий член:
,,
где
Сумма членов .
Геометрическая прогрессия
Общий член:
, где  — знаменатель
прогрессии;
— знаменатель
прогрессии;
Сумма членов .
Сумма геометрической
прогрессии (при  ):
):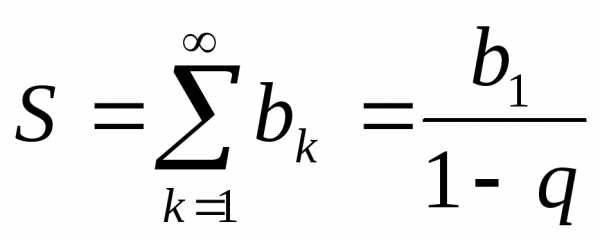 .
.
Некоторые суммы:
; ;
;
; ;
6. ЛОГАРИФМЫ
Логарифм числа  по
основанию
по
основанию :
:
.
Основное
логарифмическое тождество:  .
.
Свойства логарифмов:
; ;
 ; ;.
; ;.
Десятичные
логарифмы  :.
:.
Натуральные логарифмы :.
Логарифмические неравенства:
.
Показательные неравенства:
.
7. ТРИГОНОМЕТРИЯ
7.1. Основные соотношения
;
 ;
;  ;
;
 ;
;  ;;
;;
 ;
; 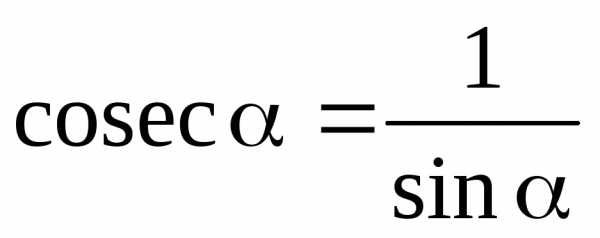 ;
;
7.2. Перевод из радианной меры углов в градусную и обратно:
 ;
; 
7.3. Основные значения тригонометрических функций
7.4. Знаки тригонометрических функций
7.5. Формулы сложения
; ;
; ;
; ;
; ;
7.6. Формулы двойных углов
;
;
 ;
;  ;
;
7.7. Формулы тройных углов
; ;
 ; ;
; ;
7.8. Формулы половинных углов
 ;
;  ;
;
;  ;
;
;
Универсальная тригонометрическая подстановка, используемая для решения тригонометрических уравнений:
 ;
;  ;
;  ;
;  ;
;
7.9. Формулы приведения

sin
– sin
cos
sin
– cos
sin
cos
cos
sin
– cos
sin
cos
tg
–tg
ctg
tg
ctg
tg
ctg
–ctg
tg
ctg
tg
ctg
7.10. Формулы преобразования суммы и разности
; ;
; ;
, где ;
; ;
; .
7.11. Формулы преобразования произведения
; ;
.
7.12. Обратные тригонометрические функции
;
;
;
.
7.13. Простейшие тригонометрические уравнения
1) ;  ;.
;.
Частные случаи: ;;
; 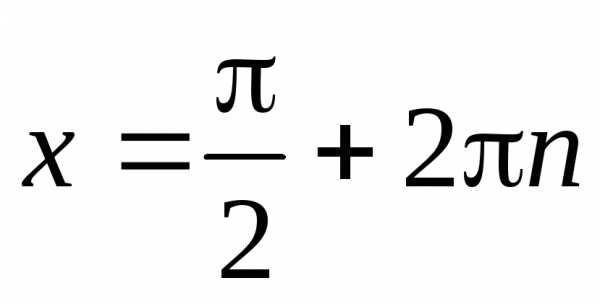 ;
;
;  .
.
2)
; ;.
;.
Частные случаи: ; ;
;
;  ;
;
; .
3)  ,;.
,;.
4) ;;.
8. Графики основных элементарных функций
Парабола
Гипербола
Y
Y
y0
x0
x0
X
X
y0
Логарифмическая кривая
Экспонента
Y
a>1
0<a<1
Y
a>1
1
X
0<a<1
y = log a x
y = ax
X
Синусоида
Y
1
/2
-
2
X
y = sin x
y = cos x
Y
Тангенсоида
/2
0
X
y = ctg x
y = tg x
10. ПЛАНИМЕТРИЯ
Треугольник
10.1.1. Основные соотношения
A,B,C – вершины aa,b,c – стороны ,, — углы
— неравенства треугольника; ;
теорема проекций
теорема синусов
теорема косинусов
10.1.2. Замечательные линии и точки в теугольнике
ma, mb, mc — медианы
ha, hb, hc — высоты
la, lb , lc — биссектрисы
p —
полупериметр, 
r — радиус вписанной окружности
R – радиус описанной окружности
; ;
 ;
;  ;
;
10.1.3. Формулы площади треугольника


studfiles.net
Формулы элементарной математикИ
Степени и корни
Если  ,
, ,
то:
,
то:
;; ;
; ,
, ;
; 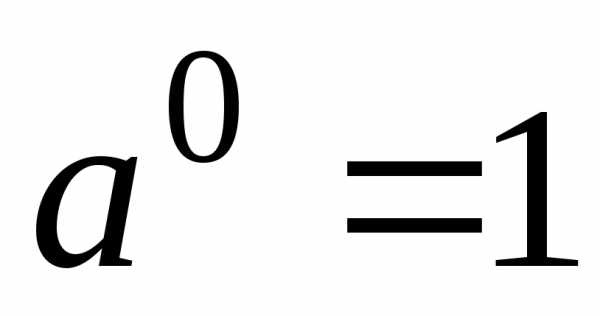 ;
;
 ,
, ;,
;, ;
;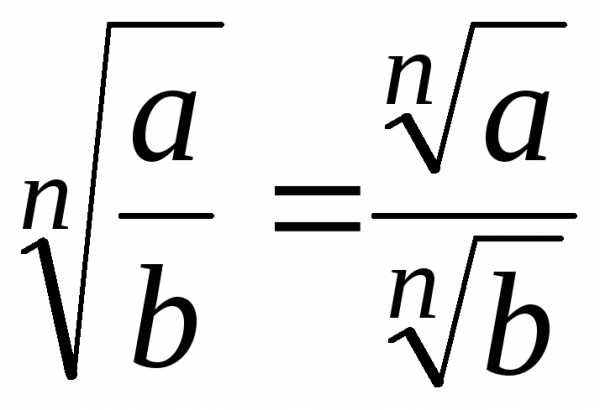 ,
, .
.
Формулы сокращенного умножения
– квадрат суммы или разности;
– разность квадратов;
– куб суммы;
– сумма кубов;
– куб разности;
– разность кубов;
3. Квадратное уравнение
Если  и
и — корни квадратного уравнения,
то
— корни квадратного уравнения,
то
;.
4. Логарифмы
Если
, ,
, ,
,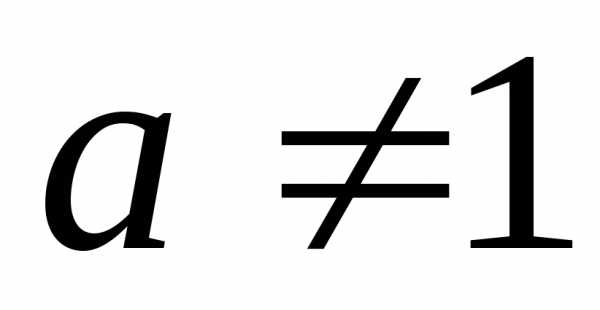 ,
то:
,
то:
– определение логарифма;
 – основное логарифмическое тождество;
– основное логарифмическое тождество;– логарифм произведения;
– логарифм частного;
– логарифм степени;
 – формула перехода;
– формула перехода; ,;
8)
,;
8) ;
9)
;
9) .
.
5. Основные тригонометрические тождества
1)
2) 3)
3)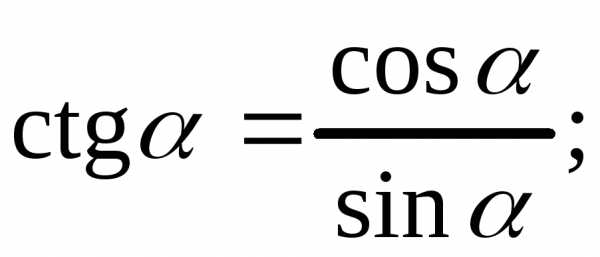
4)  5) 6)
5) 6)
6. Значения тригонометрических функций некоторых аргументов
7. Формулы двойного угла
1) 2)
3)  4)
4) 5)
5)
8. Формулы понижения степени
1) 2)
9. Преобразование произведения тригонометрических функций в сумму
1)
2)
3)
Приложение 2
Таблица тригонометрических функций sinx,cosx.
Угол, | sin x | cos x | Угол, | sin x | cos x | Угол, | sin x | cos x |
град | град | град | ||||||
0 | 0 | 1,0000 | ||||||
1 | 0,0175 | 0,9998 | 31 | 0,5150 | 0,8572 | 61 | 0,8746 | 0,4848 |
2 | 0,0349 | 0,9994 | 32 | 0,5299 | 0,8480 | 62 | 0,8829 | 0,4695 |
3 | 0,0523 | 0,9986 | 33 | 0,5446 | 0,8387 | 63 | 0,8910 | 0,4540 |
4 | 0,0698 | 0,9976 | 34 | 0,5592 | 0,8290 | 64 | 0,8988 | 0,4384 |
5 | 0,0872 | 0,9962 | 35 | 0,5736 | 0,8192 | 65 | 0,9063 | 0,4226 |
6 | 0,1045 | 0,9945 | 36 | 0,5878 | 0,8090 | 66 | 0,9135 | 0,4067 |
7 | 0,1219 | 0,9925 | 37 | 0,6018 | 0,7986 | 67 | 0,9205 | 0,3907 |
8 | 0,1392 | 0,9903 | 38 | 0,6157 | 0,7880 | 68 | 0,9272 | 0,3746 |
9 | 0,1564 | 0,9877 | 39 | 0,6293 | 0,7771 | 69 | 0,9336 | 0,3584 |
10 | 0,1736 | 0,9848 | 40 | 0,6428 | 0,7660 | 70 | 0,9397 | 0,3420 |
11 | 0,1908 | 0,9816 | 41 | 0,6561 | 0,7547 | 71 | 0,9455 | 0,3256 |
12 | 0,2079 | 0,9781 | 42 | 0,6691 | 0,7431 | 72 | 0,9511 | 0,3090 |
13 | 0,2250 | 0,9744 | 43 | 0,6820 | 0,7314 | 73 | 0,9563 | 0,2924 |
14 | 0,2419 | 0,9703 | 44 | 0,6947 | 0,7193 | 74 | 0,9613 | 0,2756 |
15 | 0,2588 | 0,9659 | 45 | 0,7071 | 0,7071 | 75 | 0,9659 | 0,2588 |
16 | 0,2756 | 0,9613 | 46 | 0,7193 | 0,6947 | 76 | 0,9703 | 0,2419 |
17 | 0,2924 | 0,9563 | 47 | 0,7314 | 0,6820 | 77 | 0,9744 | 0,2250 |
18 | 0,309 | 0,9511 | 48 | 0,7431 | 0,6691 | 78 | 0,9781 | 0,2079 |
19 | 0,3256 | 0,9455 | 49 | 0,7547 | 0,6561 | 79 | 0,9816 | 0,1908 |
20 | 0,3420 | 0,9397 | 50 | 0,7660 | 0,6428 | 80 | 0,9848 | 0,1736 |
21 | 0,3584 | 0,9336 | 51 | 0,7771 | 0,6293 | 81 | 0,9877 | 0,1564 |
22 | 0,3746 | 0,9272 | 52 | 0,7880 | 0,6157 | 82 | 0,9903 | 0,1392 |
23 | 0,3907 | 0,9205 | 53 | 0,7986 | 0,6018 | 83 | 0,9925 | 0,1219 |
24 | 0,4067 | 0,9135 | 54 | 0,8090 | 0,5878 | 84 | 0,9945 | 0,1045 |
25 | 0,4226 | 0,9063 | 55 | 0,8192 | 0,5736 | 85 | 0,9962 | 0,0872 |
26 | 0,4384 | 0,8988 | 56 | 0,8290 | 0,5592 | 86 | 0,9976 | 0,0698 |
27 | 0,4540 | 0,8910 | 57 | 0,8387 | 0,5446 | 87 | 0,9986 | 0,0523 |
28 | 0,4695 | 0,8829 | 58 | 0,8480 | 0,5299 | 88 | 0,9994 | 0,0349 |
29 | 0,4848 | 0,8746 | 59 | 0,8572 | 0,5150 | 89 | 0,9998 | 0,0175 |
30 | 0,5000 | 0,8660 | 60 | 0,8660 | 0,5000 | 90 | 1 | 0,0000 |
При ложение 3
Таблица тригонометрических функций tgx.
Угол, | Угол, | tg x | Угол, | Угол, | tg x | Угол, | Угол, | tg x |
град. | рад. | град. | рад. | град. | рад. | |||
0 | 0 | 0 | ||||||
1 | 0,02 | 0,0175 | 31 | 0,54 | 0,6009 | 61 | 1,06 | 1,8040 |
2 | 0,03 | 0,0349 | 32 | 0,56 | 0,6249 | 62 | 1,08 | 1,8807 |
3 | 0,05 | 0,0524 | 33 | 0,58 | 0,6494 | 63 | 1,10 | 1,9626 |
4 | 0,07 | 0,0699 | 34 | 0,59 | 0,6745 | 64 | 1,12 | 2,0503 |
5 | 0,09 | 0,0875 | 35 | 0,61 | 0,7002 | 65 | 1,13 | 2,1445 |
6 | 0,10 | 0,1051 | 36 | 0,63 | 0,7265 | 66 | 1,15 | 2,2460 |
7 | 0,12 | 0,1228 | 37 | 0,65 | 0,7536 | 67 | 1,17 | 2,3559 |
8 | 0,14 | 0,1405 | 38 | 0,66 | 0,7813 | 68 | 1,19 | 2,4751 |
9 | 0,16 | 0,1584 | 39 | 0,68 | 0,8098 | 69 | 1,20 | 2,6051 |
10 | 0,17 | 0,1763 | 40 | 0,70 | 0,8391 | 70 | 1,22 | 2,7475 |
11 | 0,19 | 0,1944 | 41 | 0,72 | 0,8693 | 71 | 1,24 | 2,9042 |
12 | 0,21 | 0,2126 | 42 | 0,73 | 0,9004 | 72 | 1,26 | 3,0777 |
13 | 0,23 | 0,2309 | 43 | 0,75 | 0,9325 | 73 | 1,27 | 3,2709 |
14 | 0,24 | 0,2493 | 44 | 0,77 | 0,9657 | 74 | 1,29 | 3,4874 |
15 | 0,26 | 0,2679 | 45 | 0,79 | 1,0000 | 75 | 1,31 | 3,7321 |
16 | 0,28 | 0,2867 | 46 | 0,80 | 1,0355 | 76 | 1,33 | 4,0108 |
17 | 0,30 | 0,3057 | 47 | 0,82 | 1,0724 | 77 | 1,34 | 4,3315 |
18 | 0,31 | 0,3249 | 48 | 0,84 | 1,1106 | 78 | 1,36 | 4,7046 |
19 | 0,33 | 0,3443 | 49 | 0,86 | 1,1504 | 79 | 1,38 | 5,1446 |
20 | 0,35 | 0,3640 | 50 | 0,87 | 1,1918 | 80 | 1,40 | 5,6713 |
21 | 0,37 | 0,3839 | 51 | 0,89 | 1,2349 | 81 | 1,41 | 6,3138 |
22 | 0,38 | 0,4040 | 52 | 0,91 | 1,2799 | 82 | 1,43 | 7,1154 |
23 | 0,40 | 0,4245 | 53 | 0,93 | 1,3270 | 83 | 1,45 | 8,1443 |
24 | 0,42 | 0,4452 | 54 | 0,94 | 1,3764 | 84 | 1,47 | 9,5144 |
25 | 0,44 | 0,4663 | 55 | 0,96 | 1,4281 | 85 | 1,48 | 11,430 |
26 | 0,45 | 0,4877 | 56 | 0,98 | 1,4826 | 86 | 1,50 | 14,301 |
27 | 0,47 | 0,5095 | 57 | 0,99 | 1,5399 | 87 | 1,52 | 19,081 |
28 | 0,49 | 0,5317 | 58 | 1,01 | 1,6003 | 88 | 1,54 | 28,636 |
29 | 0,51 | 0,5543 | 59 | 1,03 | 1,6643 | 89 | 1,55 | 57,290 |
30 | 0,52 | 0,5774 | 60 | 1,05 | 1,7321 | 90 | 1,57 |
studfiles.net
Величайшая формула математики | Математика, которая мне нравится
Без дальнейших церемоний, вот она:
Ее обычно называют тождеством Эйлера в честь великого швейцарского математика Леонарда Эйлера (1707 — 1783). Ее можно увидеть на футболках и кофейных кружках, и несколько опросов среди математиков и физиков удостоили ее такого названия, как “величайшее уравнение” (Crease, Robert P., “The greatest equations ever”).
Ощущение красоты и элегантности тождества происходит из того, что оно сочетает в простой форме пять самых важных чисел математических констант: — основание натурального логарифма, — квадратный корень из и . Глядя на него внимательно, большинство людей задумываются о показателе: что значит возвести число в мнимую степень? Терпение, терпение, мы до этого доберемся.
Чтобы объяснить, откуда возникает эта формула, мы должны сначала получить более общую формулу, найденную Эйлером, а затем показать, что наше равенство является всего лишь частным случаем этой формулы. Общая формула удивительна сама по себе и имеет множество замечательных приложений в математике, физике и технике.
Первый шаг в нашем путешествии — понять, что большинство функций в математике может быть представлено в виде бесконечной суммы по степеням аргумента. Это пример:
Здесь измеряется в радианах, а не в градусах. Мы можем получить хорошее приближение для конкретного значения , используя только несколько первых членов ряда. Это пример ряда Тейлора, и довольно легко вывести эту формулу, используя математический анализ. Здесь я не предполагаю знание математического анализа, поэтому прошу читателя принять ее на веру.
Соответствующая формула для косинуса:
Наконец,
Число — константа, равная , и Эйлер был первым, кто признал его фундаментальное значение в математике и вывел последнюю формулу (две предыдущие были найдены Исааком Ньютоном). О числе написаны книги (например, Maor, E. (1994). e, the story of a number. Princeton University Press), можно также прочитать о нем здесь.
Примерно в 1740 году Эйлер посмотрел на эти три формулы, расположенные приблизительно так, как мы их здесь видим. Сразу видно, что каждое слагаемое в третьей формуле также появляется в любой предыдущей. Тем не менее, половина членов в первых равенствах являются отрицательными, в то время как каждый член в последнем положителен. Большинство людей так бы это и оставили, но Эйлер увидел во всем этом закономерность. Он первый сложил первые две формулы:
Обратите внимание на последовательность знаков в этом ряду: , она повторяется группами по 4. Эйлер заметил, что эта же последовательность знаков получается, когда мы возводим мнимую единицу в целые степени:
Это означало, что можно заменить в последней формуле на и получить:
Теперь знаки соответствуют знакам в предыдущей формуле, и новый ряд совпадает с предыдущим, за исключением того, что члены разложения умножаются на . То есть получаем в точности
Это удивительный и таинственный результат, он свидетельствует о существовании тесной связи между числом и синусами и косинусами в тригонометрии, хотя было известно только из задач, не связанных с геометрией или треугольниками. Кроме ее элегантности и странности, однако, было бы трудно переоценить важность этой формулы в математике, которая увеличивалась с момента ее открытия. Она появляется везде, и не так давно вышла книга примерно в 400 страниц (Nahin P. Dr. Euler’s Fabulous Formula, 2006), посвященная описанию некоторых приложений этой формулы.
Обратите внимание, что старый вопрос о мнимых показателях в настоящее время решен: для возведения в мнимую степень просто поставьте мнимое число в формулу Эйлера. Если основание – число, отличное от , требуется только ее незначительная модификация.
Теперь вернемся к волшебному равенству. Мы можем подставить в него любое вещественное число , и в результате получим некоторое комплексное число. Один возможный выбор для — это . Вспомним из тригонометрии, что радиан — это 180 градусов. Косинус 180 градусов равен , а синус равен .
Поэтому
, или
Все это дает понятие о мощи и творческих способностях Леонарда Эйлера, и о том, почему его иногда называют выдающимся умом восемнадцатого века. Я буду еще писать о нем и некоторых его результатах в серии Euler’s Greatest Hits.
Перевод статьи Larry Phillips, The Greatest Formula in Mathematics, http://brightstartutors.com/blog/2010/01/29/the-greatest-formula-in-mathematics.
hijos.ru
Формулы — высшая математика
Справочник по формулам высшей математики — очень компактный и превосходный по основам простой и высшей математики. Он охватывает очень многие разделы, где дает не только список различных формул, но и объяснения к ним.
Справочник содержит формулы высшей математики:
по элементарной геометрии (стереометрия, планиметрия и геометрические преобразования), по математическому анализу (алгебраические преобразования, тригонометрия, гиперболические функции, элементы комбинаторики, множества и действительные числа, функции),
по уравнениям и неравенствам (линейные, квадратные, показательные, логарифмические, тригонометрические, простейшие уравнения и неравенства и методы приближенного решений уравнения вида f(x) = 0),
по аналитической геометрии (преобразование декартовых прямоугольных координат на плоскости, системы координат в пространстве и на плоскости, плоскость, прямая на плоскости и в пространстве, линии и поверхности второй степени, простейшие задачи аналитической геометрии),
по высшей алгебре (комплексные числа, определители, многочлены, матричное исчисление, евклидовы и линейные пространства и их преобразования, квадратичные формы, системы линейных уравнений),
по дифференциальному, интегральному и тензорному исчислению (числовые, степенные ряды и пределы, формула Тейлора, определенные и неопределенные интегралы, а также несобственные, зависящие от параметра, тензоры, действия над тензорами и тензорный анализ),
по комплексному анализу (ряд Фурье, комплексные функции, операционное исчисление),
по элементам теории поля (векторное и скалярное поле),
по дифференциальному уравнению и геометрии (вектор, поверхности, пространственные и плоские линии, нелинейные и линейные дифференциальные уравнения, также в частных производных),
по теории вероятности (случайные величины и события),
по математической логике (предикаты, алгебра и исчисления высказываний, множества и отображения) и по многим другим разделам математики.
Пригодится студентам любых факультетов и вузов, где изучается высшая математика.
www.for-stydents.ru
Математические формулы – жизнь среди чисел
Решение задачи зависит от правильного подхода и умения применять знания. Математические формулы – это плод многолетних трудов массы ученых, современным же людям остается найти в массе комбинаций ту самую, единственно подходящую.
Математика – наука, которая кажется незаметной, но она сопровождает нас всю сознательную жизнь. С числами и формулами нас знакомят в школе, а жизнь находит применение базовым знаниям.
Не каждый человек имеет способности к математике, но нормативы и контрольные, экзамены и тестирования приходится сдавать практически всем. Сложные и простые задачи приходится решать ежедневно, тем более студентам и школьникам. Решение дается не всегда просто, ведь строгие педагоги спешат дать знания и проверить степень усвоения материала.
Математические формулы – простой ключ к решению задач
Обширная и интересная наука все развивается, усложняясь и представляя новые решения старых вопросов. Ученые веками изучали закономерности и выводили формулы, доказывали теоремы и рассуждали о смысле аксиомы. Огромные труды, многовековые познания современные студенты должны освоить в короткий промежуток времени. Это невозможно.
Все осознают, что объять необъятные познания в области науки невозможно, поэтому курс математики и подразделов данной науки дает лишь поверхностное понимание законов и правил, лишь самые востребованные знания.
С первого класса и до конца жизни человек изучает формулы по математике, иногда даже не осознавая того. Их настолько много, что запомнить весь массив не удастся никогда. На выручку идут специальные сборники, классифицированные по различным характеристикам, в которых также нужно уметь ориентироваться. Применение правильной формулы дает простое решение задачи.
Как найти ключ к решению?
Еще раз следует отметить, что формул много, поэтому справочная информация выручит в трудный момент. Математические формулы разделяются соответственно разделам обширной науки, и состоят из определенного количества параметров, зная часть из которых, можно найти решение.
Умение оперировать познаниями в математике необходимо, поэтому мы собрали самые часто используемые формулы для вас, ссылки на которые есть в разделе Полезные материалы для изучения математики.
Применение математических формул
Математику невозможно вычленить из смежных наук – физики, информатики и т.п. Применение формул иногда настолько неожиданно, что трудно поверить, что этот результат возможен лишь благодаря «скучной» науке под названием «математика», также смотрите где найти формулы по геометрии.
Математические формулы в процессе эволюции своего назначения претерпевали изменения, и связано это было с изменением понимания назначения самих формул. Числа давно уже перестали быть просто числами, а стали делиться на элиту в виде простых чисел, и на все остальные цифры. Когда любое число стало возможным представить в виде двух простых, а их, в свою очередь, представить кодированными символами, то и методы действий над ними тоже немного изменились.
Не секрет, что каждый человек, работающий в сфере чисел, имеет свои наработки и взгляды на алгебраические формулировки. Суть в том, что как раз из этого и возникают предпосылки к возникновению новых формул и трактовок к их пониманию.
Как бы ни были нам в прошлом дики массивы чисел, сейчас это норма, и массивы массивов только помогают в развитии других аспектов математических формул, например, в криптографии.
Студенческие годы пройдут, и экзамены будет устраивать сама жизнь. Научитесь оперировать исходными данными и применять формулы. Эти навыки позволят успешно развивать свою жизнь, правильно распоряжаясь своими ресурсами, более подробнее смотрите на сайте educon.by.
www.vash-remontik.ru


 – основное логарифмическое тождество;
– основное логарифмическое тождество; – формула перехода;
– формула перехода; ,;
8)
,;
8) ;
9)
;
9)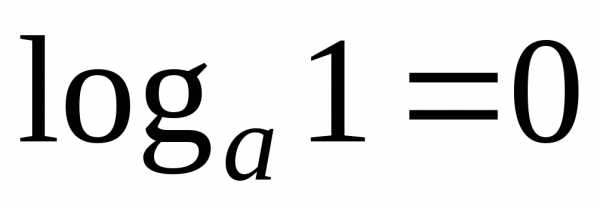 .
.