Сайт преподавателей информатики КМТТМП — Примеры и задачи для самостоятельного решения.
I. Сложение матриц
Рассмотрим пример сложения двух матриц размером 2х3.
Пример 1.
Даны две матрицы одинакового размера.
Найти сумму А+В двух матриц.
Решение.
Пример 2.
Пусть даны матрицы:
Решение.

II. Умножение матрицы на число
Пусть
Найти результат умножения матрицы А на число 4.
III. Вычитание матриц
Пример 3.
Даны две матрицы одинакового размера 4х4
Найти разность двух матриц
Решение.

Примеры для самостоятельного решения
Пример 4.
Найти сумму двух матриц А и В в каждом из следующих случаев:
Пример 5.
Найти матрицу: С=-5А+2В
IV. Транспонирование матриц
Транспонирование матриц – переход от матрицы А к матрице, в которой строки и столбцы поменялись местами с сохранением порядка.
Пример 5.
Составить транспонированную матрицу, полученную из А:
Решение:
Поменяем местами строки и столбцы, сохраняя порядок:
Примеры для самостоятельного решения:
Пример 6.
Составить из исходной матрицы транспонированную матрицу:
II. Умножение матриц
Пример 7.
Решение:
Пример 8.
Найти произведение двух матриц:
Решение:
В первом случае найдем произведение:

Во втором случае найдем произведение:

Пример 9.
Вычислить значение многочлена f(x)=2x2-5x+3 от матрицы:
Решение.
В многочлен f(x) подставим вместо х матрицу А, вместо числа 3 используем матрицу 3Е, где Е – единичная матрица 2-го порядка.
Теперь получим окончательный результат
Примеры для самостоятельного решения
I. Найти произведение матриц:
II. Найти значение многочлена от матрицы А:
2. Действия над матрицами
Равенство матриц
Две матрицы A иB равны между собой, если они одинакового размера и их соответствующие элементы равны, т.е.
A =B, еслиaij =bij (i = 1,2,…,m;j = 1,2,…,n).
Сложение матриц
Складывать можно только матрицы одинакового размера по правилу
A = {aij }m×n , B= {bij }m×n ,C= {cij }m×n ,
C = A+ B= {aij + bij }m×n .
Пример:
| 1 | 2 | 3 | 1 | 3 | 0 | 1+ 1 2+ 3 3+ 0 | 2 | 5 | 3 |
| ||||||||
| 0 | 2 | 1 |
|
| 0 |
|
|
| 0 + 0 2 | − 2 |
|
|
| 0 | 0 | 12 |
| |
A = |
| , B = | −2 11 | . C= A+ B= | 1+ 11 | = | . | ||||||||||||
| 1 | 2 | 4 |
|
|
|
| 4 |
|
|
| + 0 | 4 + 4 |
|
|
|
| 8 |
|
|
| 10 0 |
| 1+ 10 2 |
| 11 2 |
| ||||||||||||
Свойства сложения матриц
A + B= B+ A;
A + (B+ C) = (A+ B) + C= A+ B+ C.
Умножение матрицы на число
Чтобы умножить матрицу на число α надо умножить на это число каждый элемент матрицы.
A = {aij }m×n , B= α iA, B= {bij }m×n = {α iaij } .
Пример:
| 1 | 2 | 4 |
| 3i1 | 3i2 | 3i4 | 3 6 | 9 |
| ||||
| 0 | 2 | 1 |
|
| 3i0 | 3i2 | 3i1 |
|
| 0 | 6 | 3 |
|
A = |
| , B = 3*A = |
| = | . | |||||||||
| 1 | 2 | 4 |
|
| 3i1 | 3i2 | 3i4 |
|
| 3 | 6 | 12 |
|
|
|
|
|
|
| |||||||||
Свойства умножения матриц
α i( A +B) =α iA +α iB , (α +β )iA =α iA +β iA ,
(αiβ)iA = αi(βiB) .
Вычитание матриц
| A −B =A +(−1)iB |
|
|
| ||||
1 | 2 | 3 |
| 1 | 2 | 0 |
|
|
A = 0 2 1 ,B = 0 | −2 11 . |
| ||||||
1 | 2 | 4 | 10 0 4 |
|
| |||
1−1 2− 3 | 3 − 0 | 0 | −1 3 |
| ||||
C =A −B =0 −0 2 +2 | 1−11 | = 0 | 4 | −10 . | ||||
1−10 2− 0 | 4 − 4 | −9 2 | 0 |
| ||||
Произведение двух матриц
Умножать можно только те матрицы, для которых число столбцов в первой матрицы равно числу строк во второй матрицы. Произведением двух матриц
| a11 | a12 | … | a1n |
|
|
|
|
|
|
|
| ||
a | 21 | a | … | a |
|
| b | b | … | b | … | b |
|
| 22 |
| 2n |
| 11 | 12 |
| 1 j |
| 1 p |
| ||
|
|
| … … |
|
| b | b | … | b | … | b |
| |
… … |
|
| 21 | 22 |
| 2 j |
| 2 p | |||||
A = |
| ai2 | … | ain | , | B = |
|
|
|
|
|
|
|
ai1 |
|
| … … … … … … |
| |||||||||
… … | … | … |
|
|
| bn2 | … | bnj | … | bnp | |||
| bn1 |
| |||||||||||
|
| a | … | a |
|
|
|
|
|
|
|
| n× p |
a | m1 |
|
|
|
|
|
|
|
|
| |||
| m2 |
| mn m×n |
|
|
|
|
|
|
|
| ||
называется матрица
| c11 | c12… | c1p |
| ||
| c | c | … | c |
| , |
| C = 21 | 22 | c |
| 2 p | |
| … | … | … |
| ||
| cm1 |
| ij | cmp |
| |
| cm2 … |
| ||||
|
|
|
|
| m× p |
|
у которой элемент cij находится по формуле |
|
|
|
| ||
n |
|
|
|
|
|
|
cij= ∑aik*bkj= ai1 *b1 j+ …+ain*bnj, | i = 1, 2,…,m;j = 1, 2,…,p, | |||||
k =1 |
|
|
|
|
|
|
т.е. элемент матрицы cij | , стоящий на пересечении i | – строки и j -столбцаравен сумме | ||||
произведений элементов i | – строки матрицы A на соответствующие элементыj -столбца | |||||
матрицы B . В результате умножения матрицыA на матрицуB получится матрицаC число строк , которой равно числу строк матрицыA , а число столбцов равно числу столбцов матрицы
B .
Пример: Перемножить матрицы A иB .
A | 2 | 3 |
| , | 1 | 2 | 3 |
|
|
|
= | 4 |
| B = |
|
| . |
| |||
| 1 | 2×2 |
| 4 5 6 | 2×3 |
| ||||
2i1+ 3i4 2i2+ | 3i5 2i3 | + 3i6 | 14 19 24 |
| ||||||
C = AiB= |
|
|
|
|
|
|
| = |
| . |
1i1+ 4i4 1i2+ 4i5 1i3+ 4i6 |
| 17 22 27 |
| |||||||
Если AiB = BiA , то матрицы коммутативная.
2.1. Равенство матриц
Две матрицы A иB равны между собой, если они одинакового размера и их соответствующие элементы равны, т.е.
A =B, еслиaij =bij (i = 1,2,…,m;j = 1,2,…,n).
2.2. Сложение матриц
Складывать можно только матрицы одинакового размера по правилу
A = {aij }m×n , B= {bij }m×n ,C= {cij }m×n ,
C = A+ B= {aij + bij }m×n .
Пример:
| 1 | 2 | 3 | 1 | 3 | 0 | 1+ 1 2+ 3 3+ 0 | 2 | 5 | 3 |
| ||||||||
| 0 | 2 | 1 |
|
| 0 |
|
|
|
| 0 + 0 2 | − 2 |
|
|
| 0 | 0 | 12 |
|
A = |
| , B = | −2 11 | . C= A+ B= | 1+ 11 | = | . | ||||||||||||
| 1 | 2 | 4 |
|
|
|
| 4 |
|
|
| + 0 | 4 + 4 |
|
|
|
| 8 |
|
|
| 10 0 |
| 1+ 10 2 |
| 11 2 |
| ||||||||||||
Свойства сложения матриц
A + B= B+ A;
A + (B+ C) = (A+ B) + C= A+ B+ C.
2.3. Умножение матрицы на число
Чтобы умножить матрицу на число α надо умножить на это число каждый элемент матрицы.
A = {aij }m×n , B= α iA, B= {bij }m×n = {α iaij } .
Пример:
| 1 | 2 | 4 |
|
| 3i1 | 3i2 | 3i4 | 3 6 | 9 |
| ||||
| 0 | 2 | 1 |
| , |
| 3i0 | 3i2 | 3i1 |
|
| 0 | 6 | 3 |
|
A = |
| B = 3* A= |
| = | . | ||||||||||
| 1 | 2 | 4 |
|
|
| 3i1 | 3i2 | 3i4 |
|
| 3 | 6 | 12 |
|
|
|
|
|
|
|
| |||||||||
Свойства умножения матриц
α i( A +B) =α iA +α iB , (α +β )iA =α iA +β iA,
(αiβ)iA = αi(βiB) .
2.4. Вычитание матриц
| A −B =A +(−1)iB |
|
|
| ||||
1 | 2 | 3 |
| 1 | 2 | 0 |
|
|
A = 0 2 1 ,B = 0 | −2 11 . |
| ||||||
1 | 2 | 4 | 10 0 4 |
|
| |||
1−1 2− 3 | 3 − 0 | 0 | −1 3 |
| ||||
C =A −B =0 −0 2 +2 | 1−11 | = 0 | 4 | −10 . | ||||
1−10 2− 0 | 4 − 4 | −9 2 | 0 |
| ||||
2.5. Произведение двух матриц
Умножать можно только те матрицы, для которых число столбцов в первой матрицы равно числу строк во второй матрицы. Произведением двух матриц
a11 | a12 | … | a1n |
|
|
|
|
|
|
|
|
| |||
a | 21 | a | … | a |
|
| b | b |
| … | b | … | b |
| |
| 22 |
| 2n |
|
| 11 | 12 |
| 1 j |
| 1 p |
| |||
|
|
| … … |
|
|
| b | b |
| … | b | … | b |
| |
… … |
|
|
| 21 | 22 |
| 2 j |
| 2 p | ||||||
A = |
| ai2 | … | ain |
| , B = |
|
|
|
|
|
|
|
| |
ai1 |
|
|
| … … … … … … |
| ||||||||||
… … | … … |
|
|
|
| bn2 | … | bnj | … | bnp | |||||
|
| bn1 |
| ||||||||||||
|
| a | … | a |
|
|
|
|
|
|
|
|
|
| n× p |
a | m1 |
|
|
|
|
|
|
|
|
|
|
| |||
| m2 |
| mn | m×n |
|
|
|
|
|
|
|
|
| ||
называется матрица |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| c11 | c12… | c1p |
|
|
|
|
|
| ||
|
|
|
| C = | c | c | … | c |
| , |
|
|
|
| |
|
|
|
|
| 21 | 22 | c | 2 p |
|
|
|
|
| ||
|
|
|
|
| … | … | … |
|
|
|
|
| |||
|
|
|
|
| cm1 |
| ij |
|
|
|
|
|
|
| |
|
|
|
|
| cm2 … | cmp |
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
| m× p |
|
|
|
| |
у которой элемент cij находится по формуле
n
cij = ∑aik *bkj = ai1 *b1 j + …+ain *bnj ,i = 1, 2,…,m;j = 1, 2,…,p,
k =1
т.е. элемент матрицы cij , стоящий на пересеченииi – строки иj -столбцаравен сумме произведений элементовi – строки матрицыA на соответствующие элементыj -столбца
матрицы B . В результате умножения матрицыA на матрицуB получится матрицаC число строк , которой равно числу строк матрицыA , а число столбцов равно числу столбцов матрицы
B .
Пример: Перемножить матрицы A иB .
2 | 3 |
| , | 1 2 3 |
| ||
A = | 1 | 4 |
| B = | 4 5 6 | . | |
| 2×2 |
|
| 2×3 | |||
C = AiB = 2i1+ 3i4 2i2+ 3i5 2i3+ 3i6 |
| = 14 | 19 | 24 | . |
1i1+ 4i4 1i2+ 4i5 1i3+ 4i6 |
| 17 | 22 | 27 |
|
Если AiB = BiA , то матрицы коммутативная.
studfiles.net
I. Матрицы и определители 2
Лекция 1. Матрицы и определители, их характеристики 2
1.1. Понятие матрицы 4
1.2. Определители второго, третьего, n-го порядка 6
1.3. Свойства определителей 8
1.4. Разложение определителя по элементам строки или столбца 10
1.5. Вычисление определителей n-го порядка (2 метода) 12
1.6. Задания для самопроверки 15
Лекция 2. Алгебра матриц 16
2.1. Основные операции над матрицами и их свойства 17
2.2. Обратная матрица 20
2.3. Решение матричных уравнений 23
2.4. Невырожденные системы n линейных уравнений с n неизвестными 24
2.5. Задания для самопроверки 29
Ответы к примерам для самопроверки 30
I. Матрицы и определители |
Лекция 1. Матрицы и определители, их характеристики
Содержание
1. Понятие матрицы.
2. Определители второго, третьего, n-го порядка.
3. Свойства определителей.
4. Разложение определителя по элементам строки или столбца.
5. Вычисление определителей n-го порядка (2 метода).
6. Задания для самопроверки
Определения | Теоремы и свойства |
| Свойства определителей
|
1.1. Понятие матрицы
Звуковое сопровождение лекции
Определение
Матрицей размера 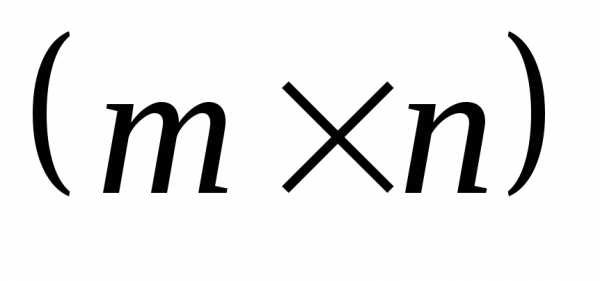 называется прямоугольная таблица чисел
называется прямоугольная таблица чисел ,
где– номер строки,– номер столбца, таких, на пересечении
которых расположены числа
,
где– номер строки,– номер столбца, таких, на пересечении
которых расположены числа ,
,
 .
.
Пример
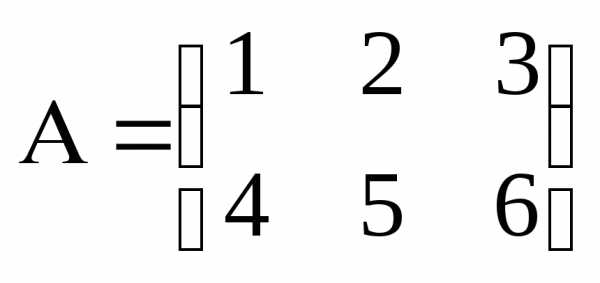 –матрица
размера
–матрица
размера 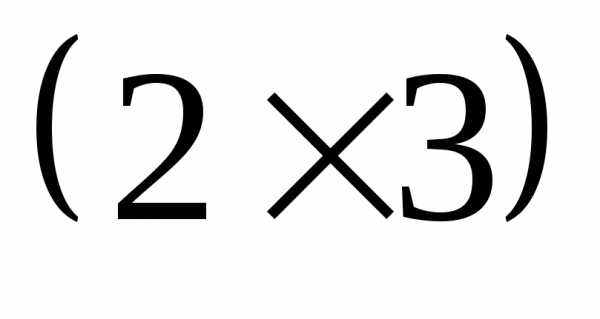 .
.
Определение
Если  ,
матрица называетсяквадратной порядка
,
матрица называетсяквадратной порядка 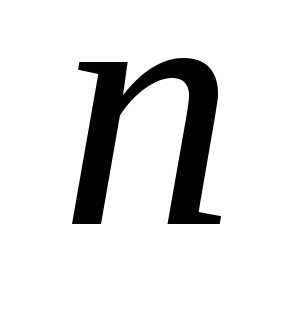 .
.
Пример
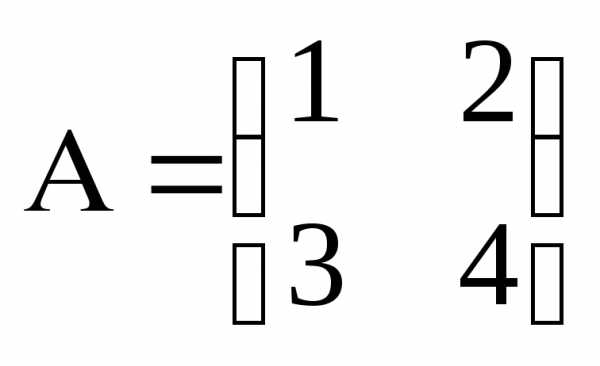 –квадратная
матрица второго порядка.
–квадратная
матрица второго порядка.
Определение
Главная и побочная диагональ квадратной матрицы –
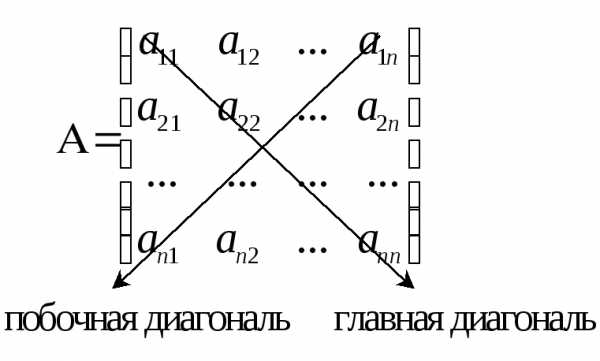
Частные случаи квадратных матриц
а) треугольная матрица – выше или ниже главной диагонали все элементы равны нулю.
Пример
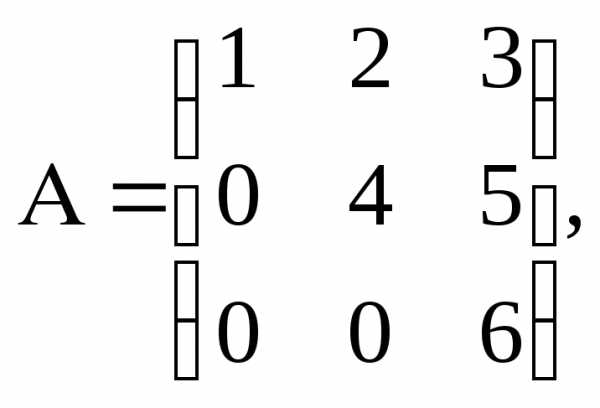
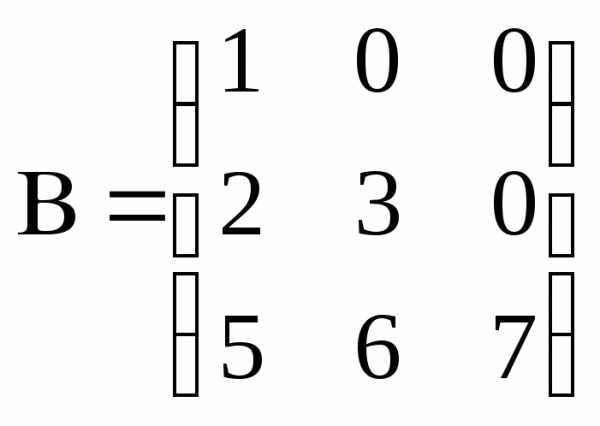 ;
;
б) диагональная матрица – выше и ниже главной диагонали – нули, на главной диагонали произвольные числа.
Пример
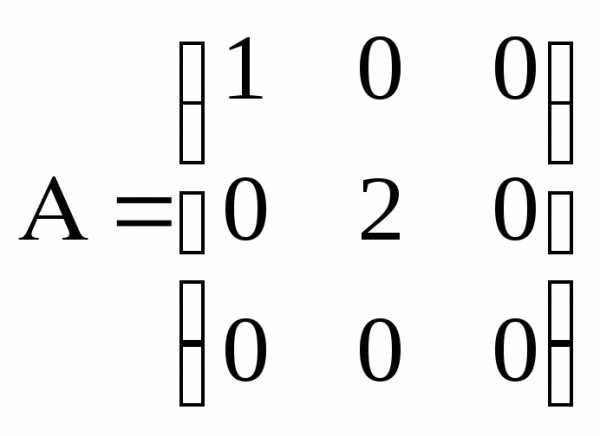 ;
;
в) единичная матрица – диагональная матрица, на главной диагонали которой – единицы.
Пример
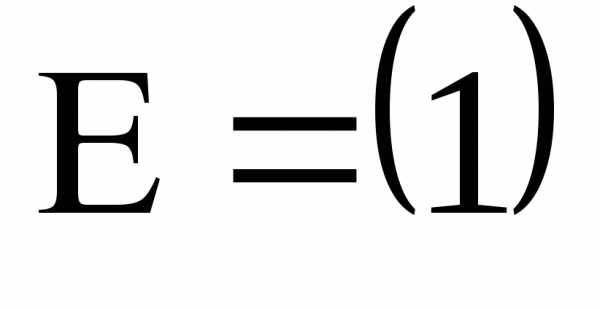 –единичная
матрица первого порядка.
–единичная
матрица первого порядка.
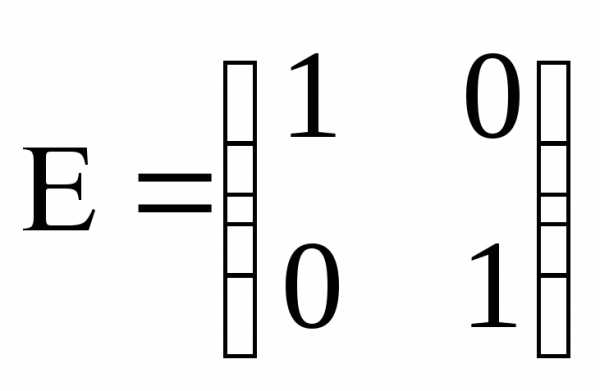 –единичная
матрица второго порядка.
–единичная
матрица второго порядка.
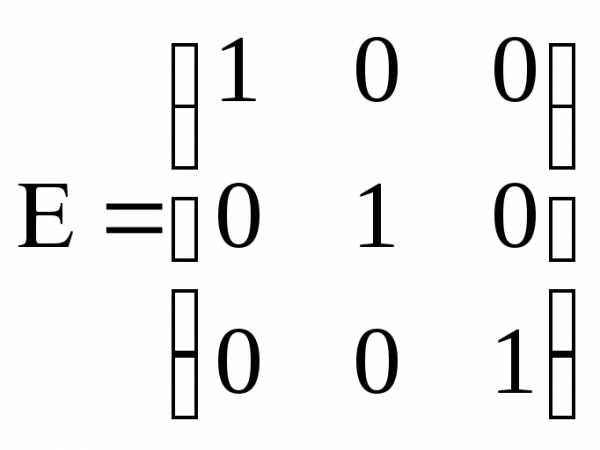 –единичная
матрица третьего порядка.
–единичная
матрица третьего порядка.
Таким
образом 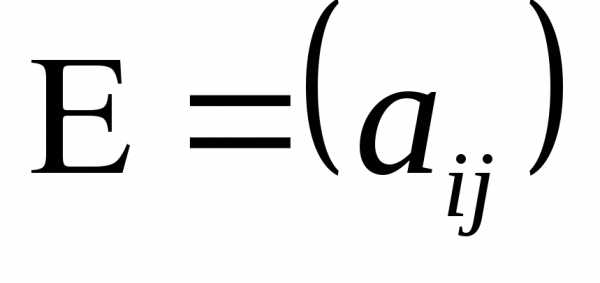 ,
,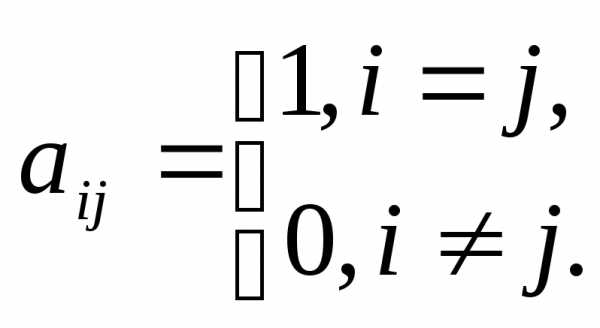
Определение
Транспонированная
матрица – матрица  ,
построенная из матрицы
,
построенная из матрицы ,
путем замены строк на столбцы и наоборот
(строки и столбцы меняются ролями).
,
путем замены строк на столбцы и наоборот
(строки и столбцы меняются ролями).
Пример

Пример
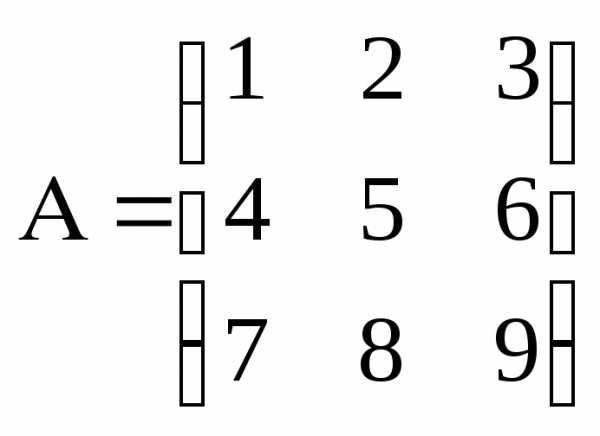 ,
, 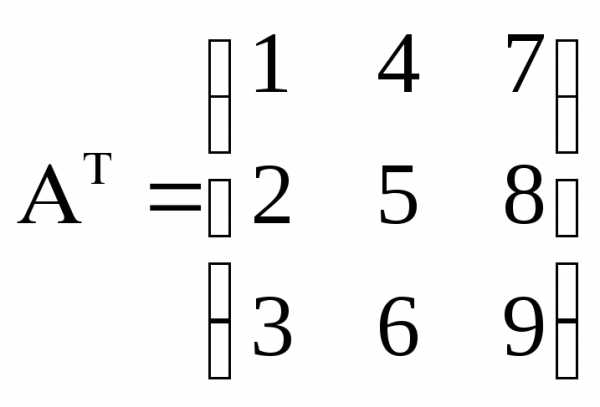 .
.
studfiles.net
Матрицы, основные действия над матрицами
Определение.Таблица вида

называется mn матрицей или, сокращенно, A=(aij), где i=1,…,m — номер строки, j=1,…,n-номер столбца, аij-элементы матрицы А.
Определение. Матрица, у которой число строк равно числу столбцов, называется квадратной.
Определение. Квадратная матрица, у которой все элементы, кроме главной диагонали, равны нулю, называется диагональной.
Определение. Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной и обозначается буквой Е.
Пример 1.1
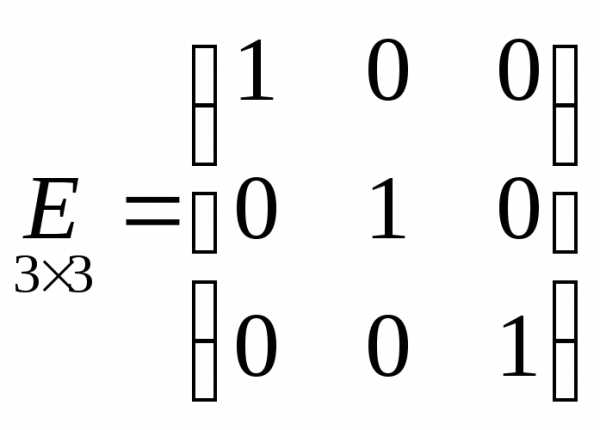 —
единичная матрица третьего порядка,
—
единичная матрица третьего порядка,
Определение. Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.
Пример 1.2

Определение. Матрица, все элементы которой равны нулю, называется нулевой и обозначается
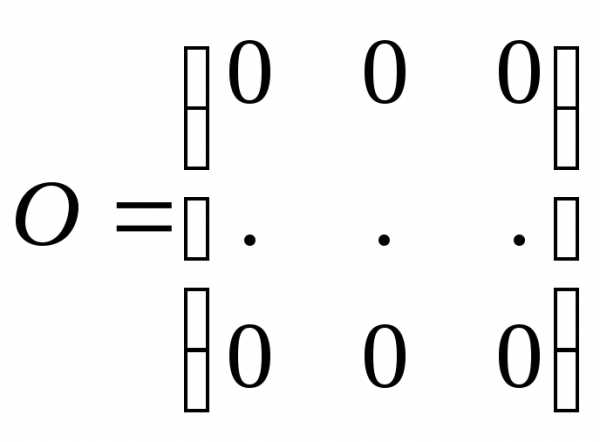 .
.
В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в арифметике.
Определение. Матрица, содержащая один столбец или одну строку, называется вектором-столбцом или вектором-строкой соответственно.
Пример 1.3
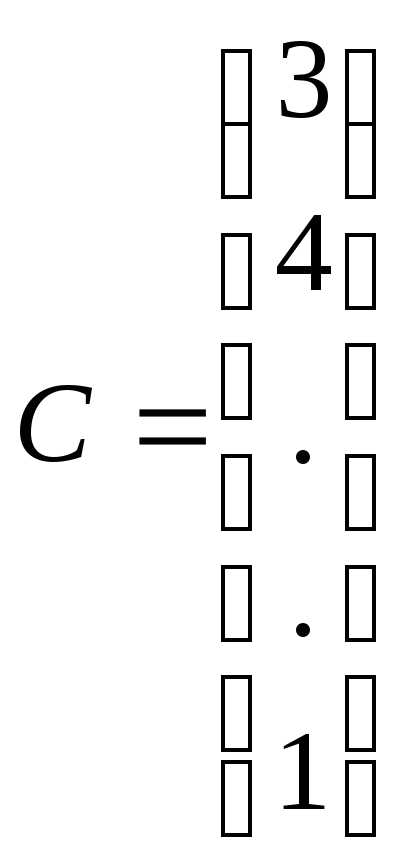 — вектор-столбец,
— вектор-столбец,
— вектор-строка.
Определение. Матрица, полученная
из данной заменой каждой её строки
столбцом с тем же номером, называется
матрицей транспонированной к данной и
обозначается .
.
Пример 1.4
Дано: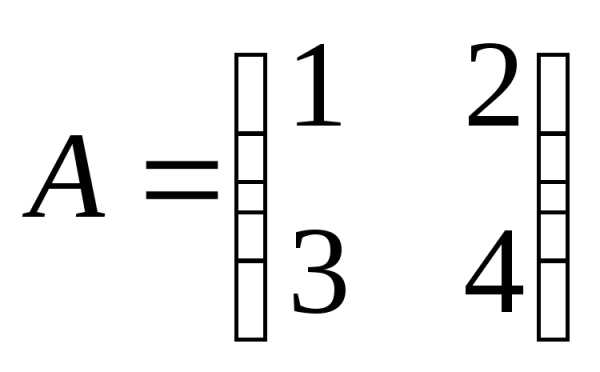 .
Найти
.
Найти .
.
Решение.
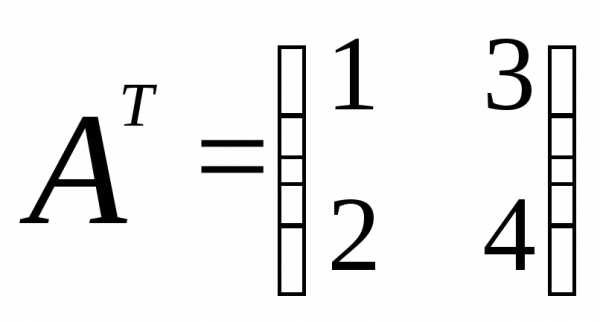 .
.
Действия над матрицами
1. Операция сложения матриц
Операция сложения матриц вводится только для матриц одинаковых размеров.
Определение. Суммой двух матриц
иназывается матрицатакая, что( )=
)=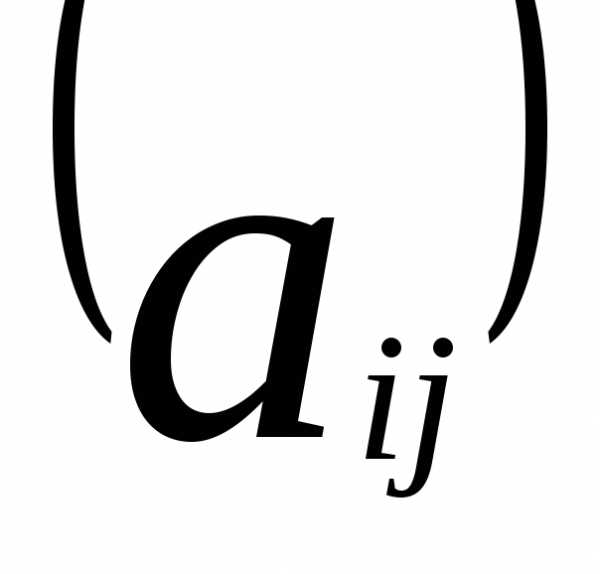 +(
+(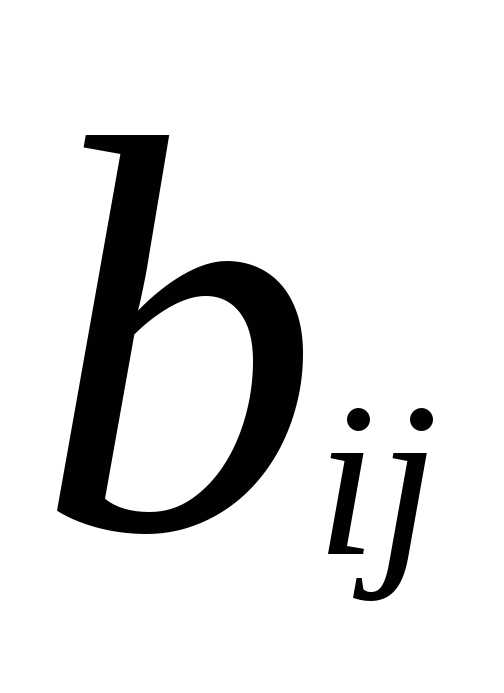 ),
где i=1,…,m; j=1,…,n.
),
где i=1,…,m; j=1,…,n.
Пример 1.5.
Произвести сложение матриц A= и
B=
и
B=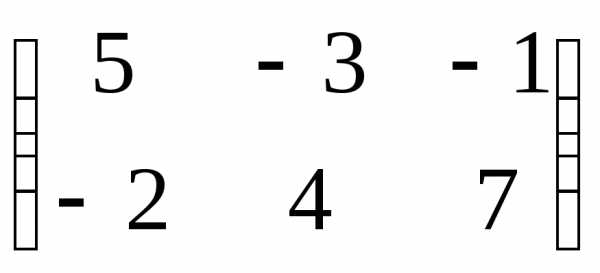
Решение.
 +
+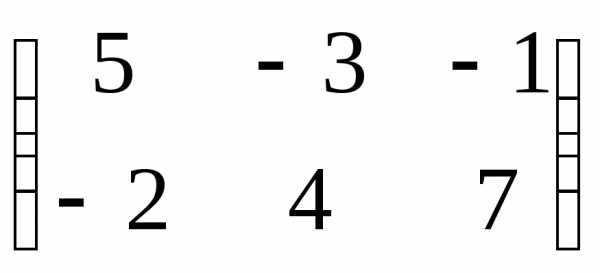 =
= .
.
2. Операция разности матриц
Аналогично определяется разность матриц.
3. Операция произведения матриц
Операция произведения матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Определение. Произведением матрицына матрицуназывается матрицатакая, что =,
где i=1,…,m; k=1,…,p, т. е. элемент i-ой строки
и k-го столбца матрицы произведения С
равен сумме произведений элементов
i-ой строки матрицы А на соответствующие
элементы k-го столбца матрицы В.
=,
где i=1,…,m; k=1,…,p, т. е. элемент i-ой строки
и k-го столбца матрицы произведения С
равен сумме произведений элементов
i-ой строки матрицы А на соответствующие
элементы k-го столбца матрицы В.
Пример 1.6
Произвести умножение матриц  и
и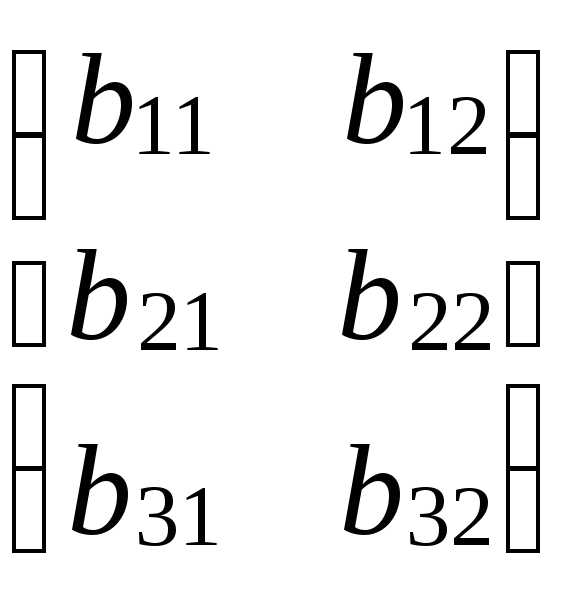 .
.
Решение.
4. Произведение матрицы на число
Произведение матрицы на число k называется матрицатакая, чтоbij= kаij(i=1,…,m; j=1,…,n).
Пример 1.7
Произвести умножение матрицы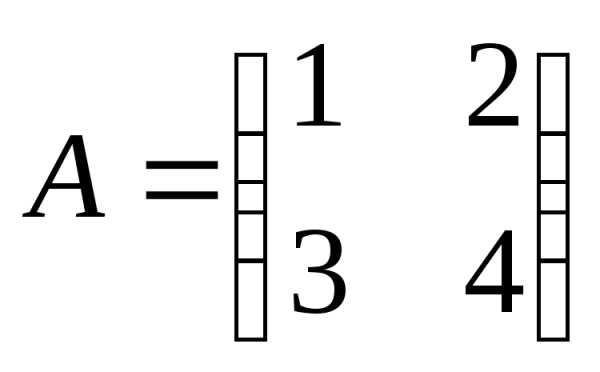 на
число k=2.
на
число k=2.
Решение.
5. Возведение матрицы в натуральную степень
Возведение в натуральную степень
квадратной матрицы А происходит по
правилу:
,
причем по определению 1)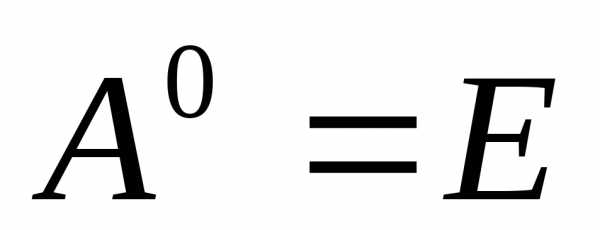 ,2)
,2)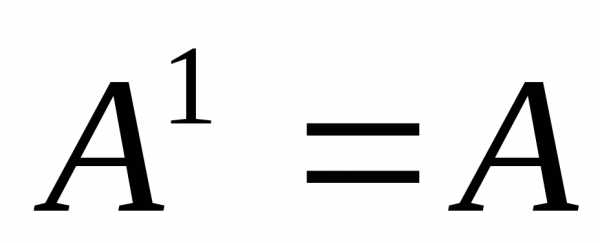 .
.
Пример 1.8
Вычислить: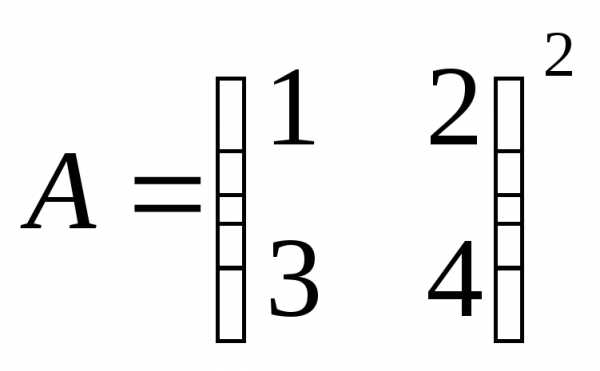 .
.
Решение.
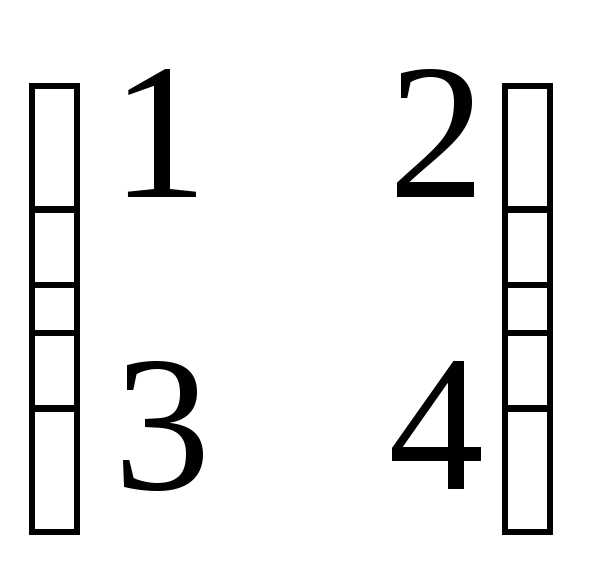
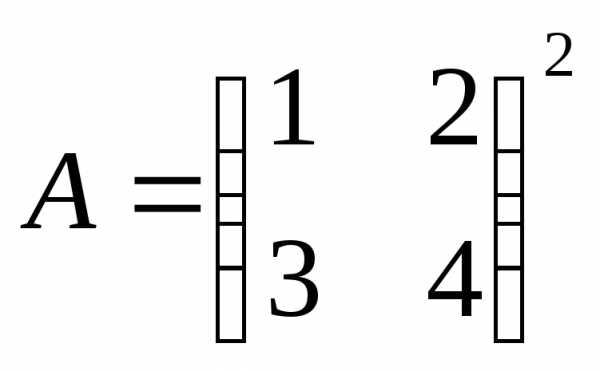 =
=
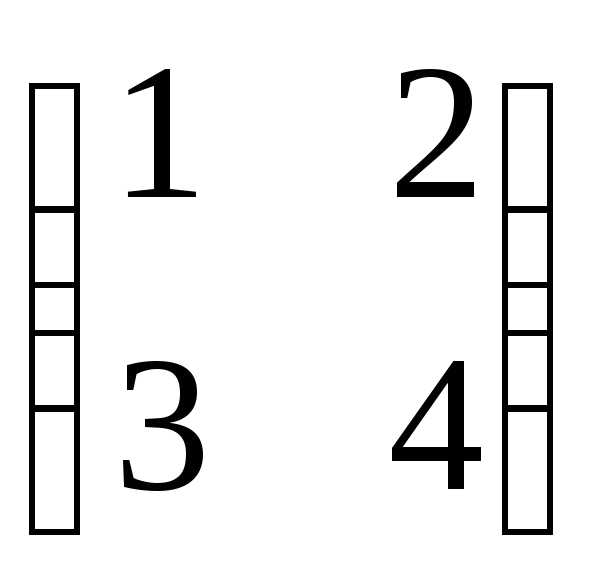 ==
==
Определение. Матрица -А=(-1)А называется противоположной.
Определение. Две матрицы называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований, к которым относятся:
перестановка местами двух параллельных рядов матрицы;
умножение всех элементов рада матрицы на число, отличное от нуля;
прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число.
Определители. Ранг матрицы.
Определение.Определитель-число,
характеризующее квадратную матрицу и
обозначается, например определитель
матрицы А, следующим образом: или
или ,
илиdetA.
,
илиdetA.
Пример 2.1
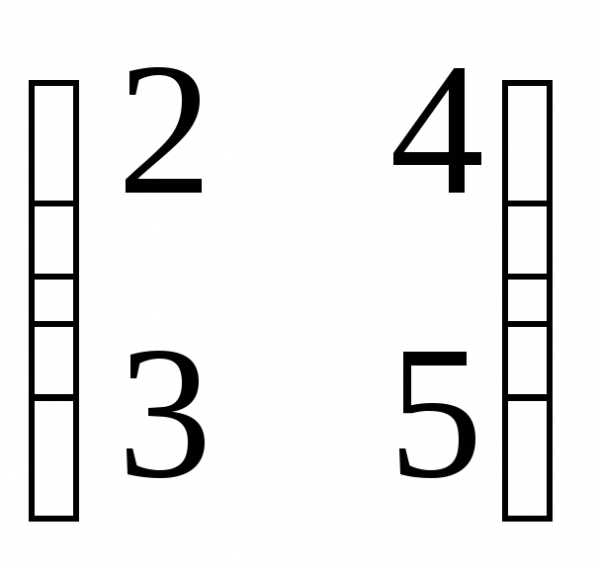
Найти определитель матрицы В, если:
В=
 ,
тогда определитель
,
тогда определитель
В=
 ,
тогда определитель
,
тогда определитель
Таким образом, получаем формулу для нахождения определителя второго порядка:
Если А=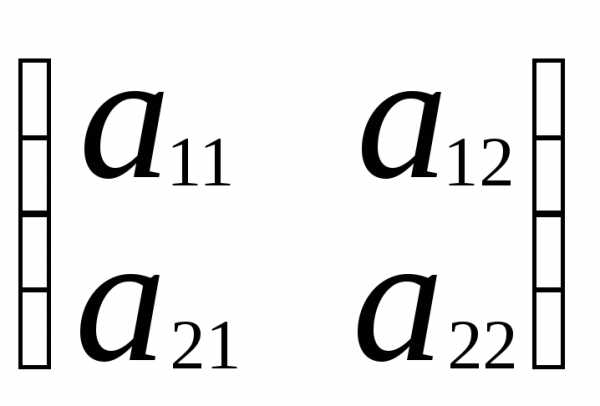 ,
то
,
то =
=
Определение. Минором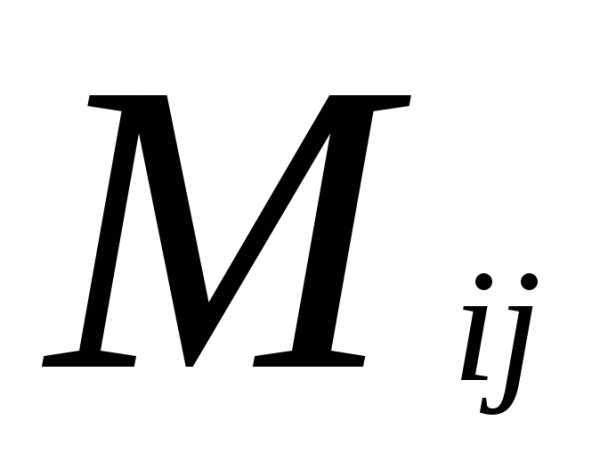 элемента
элемента матрицыn-го порядка называется
определитель матрицы (n-1)-го
порядка, полученного из матрицы А
вычеркиваниемi-ой строки
иj-го столбца.
матрицыn-го порядка называется
определитель матрицы (n-1)-го
порядка, полученного из матрицы А
вычеркиваниемi-ой строки
иj-го столбца.
Пример 2.2
Дано: А=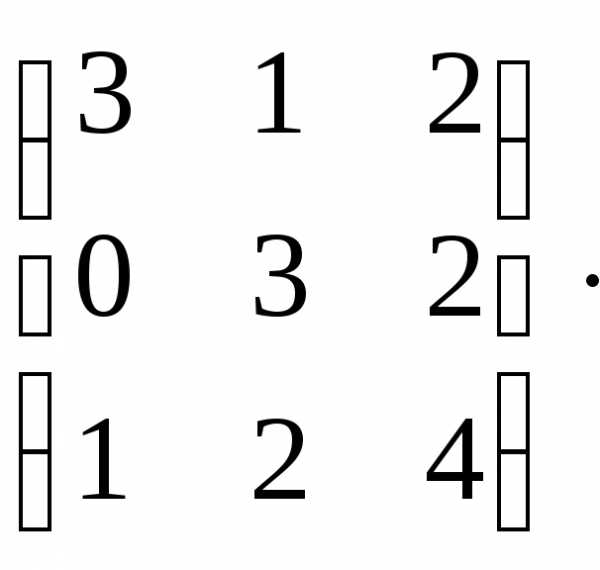 Найти все миноры матрицы А.
Найти все миноры матрицы А.
Решение.
Вычеркиваем первую строку и первый
столбец: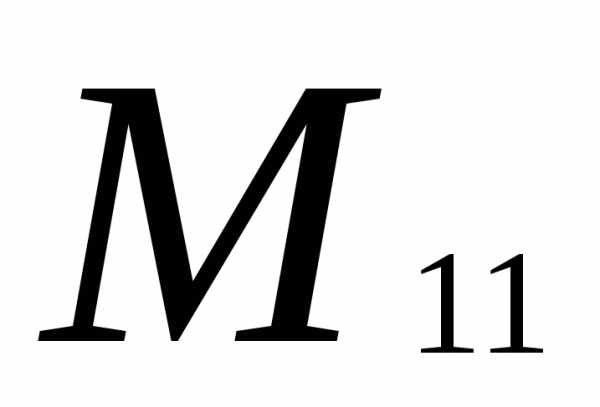 =
=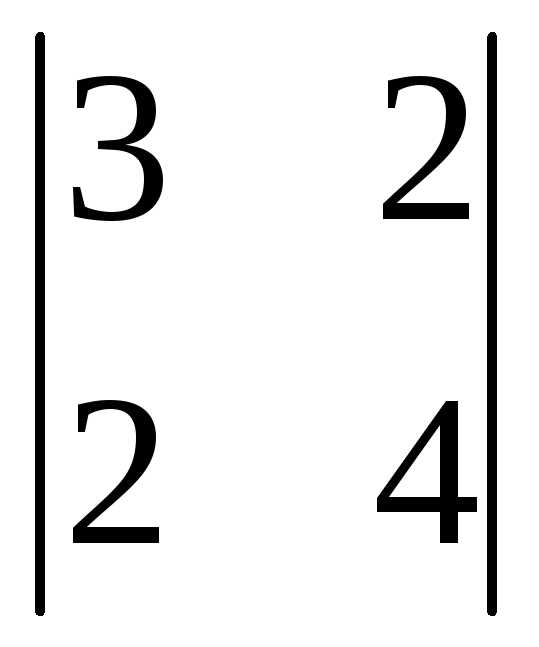 =12-4=8
=12-4=8
Вычеркиваем первую строку и второй
столбец: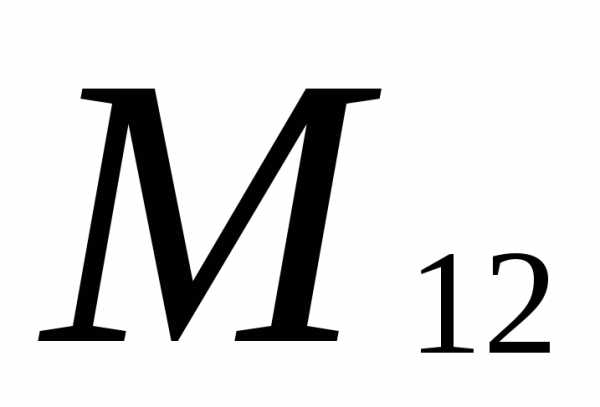 =
=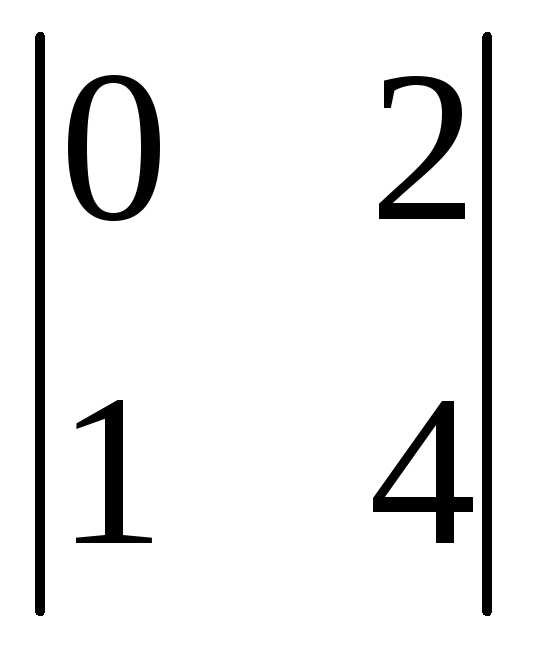 =0-2=
-2
=0-2=
-2
Вычеркиваем первую строку и третий
столбец: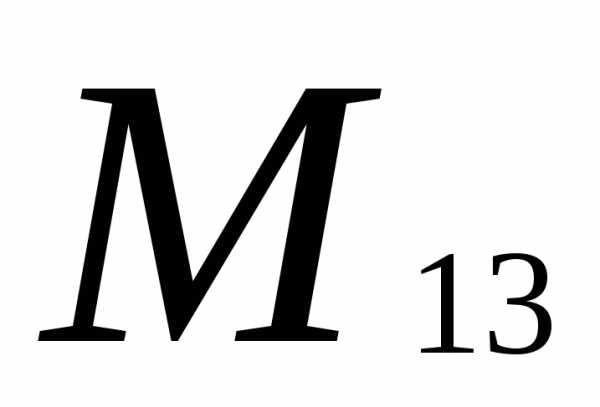 =
=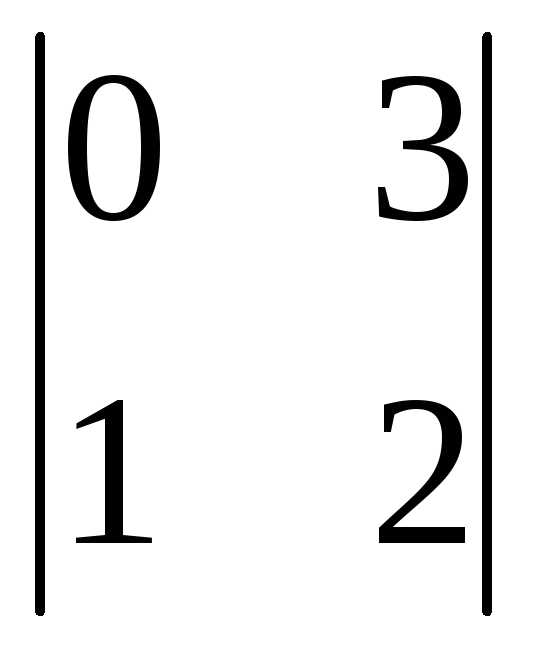 =
0-3= -3
=
0-3= -3
Вычеркиваем вторую строку и первый
столбец: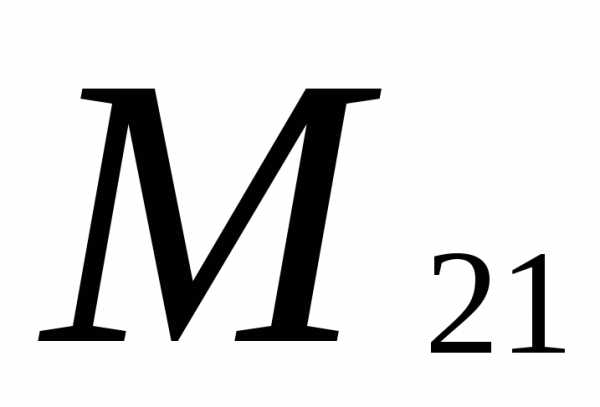 =
=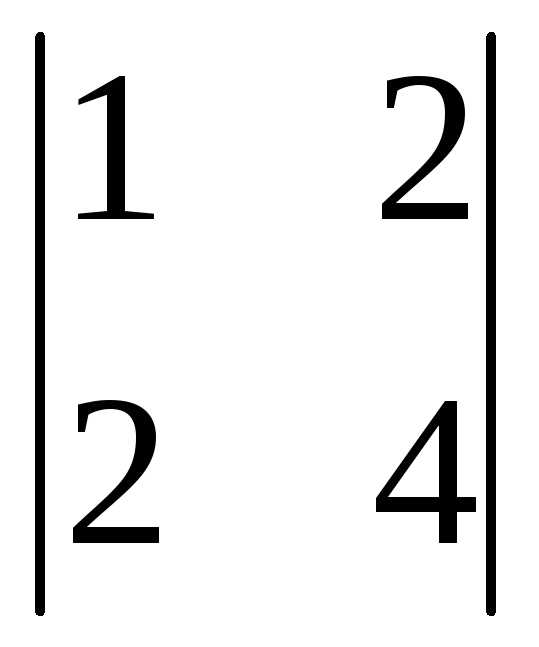 =
4-4=0
=
4-4=0
Вычеркиваем вторую строку и второй
столбец: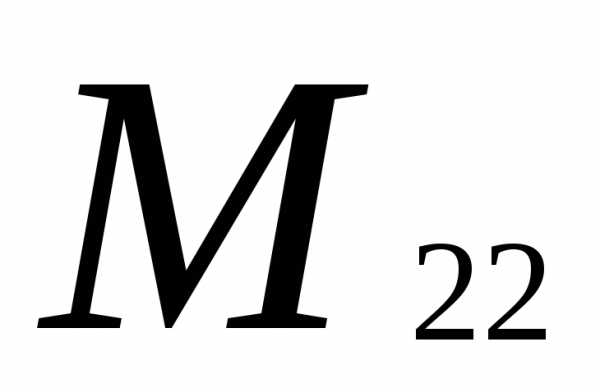 =
= =
12-2=10
=
12-2=10
Вычеркиваем вторую строку и третий
столбец: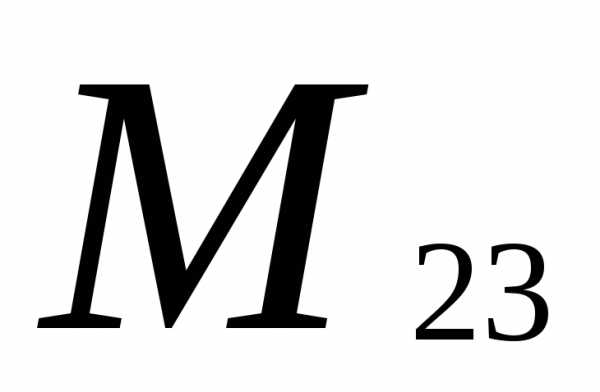 =
=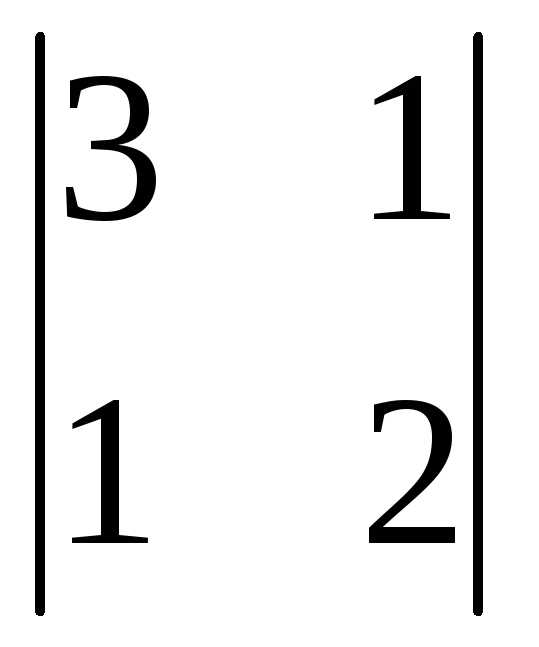 =
6-1=5
=
6-1=5
Вычеркиваем третью строку и первый
столбец: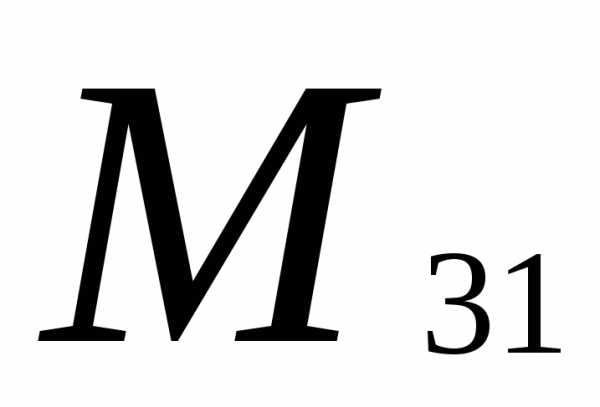 =
= =
2-6= -4
=
2-6= -4
Вычеркиваем третью строку и второй
столбец: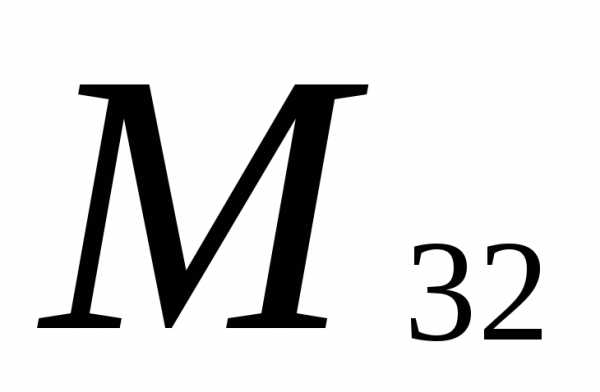 =
= =
6-0=6
=
6-0=6
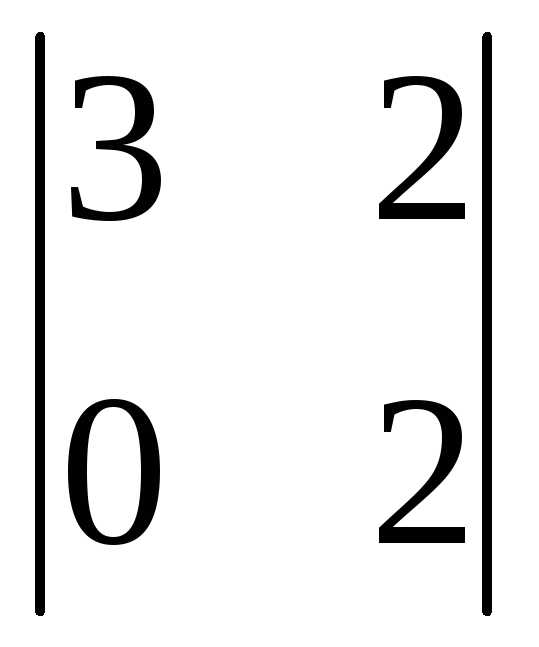
Вычеркиваем третью строку и третий
столбец: =
=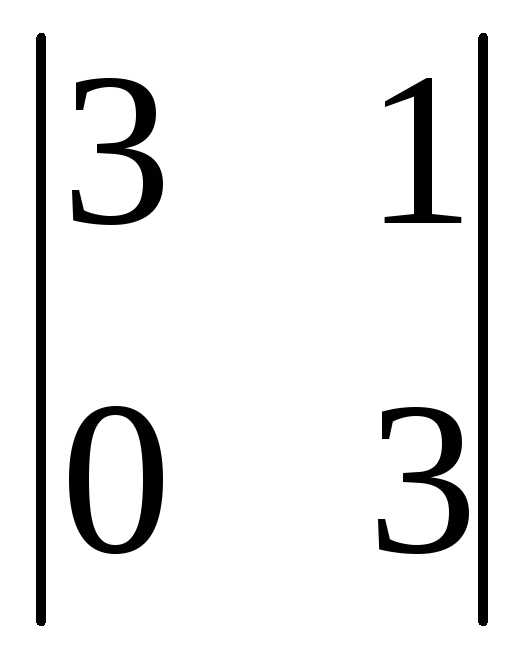 =
9-0=9.
=
9-0=9.
Определение. Алгебраическим
дополнением элемента
элемента матрицыn-го порядка называется
его минор, взятый со знаком (-1)i+j,
т. е.
матрицыn-го порядка называется
его минор, взятый со знаком (-1)i+j,
т. е.  =(-1)i+j
=(-1)i+j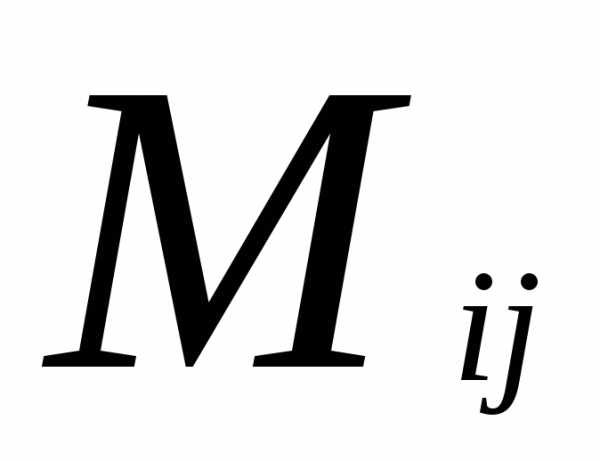 .
.
Пример 2.3
Дано: А=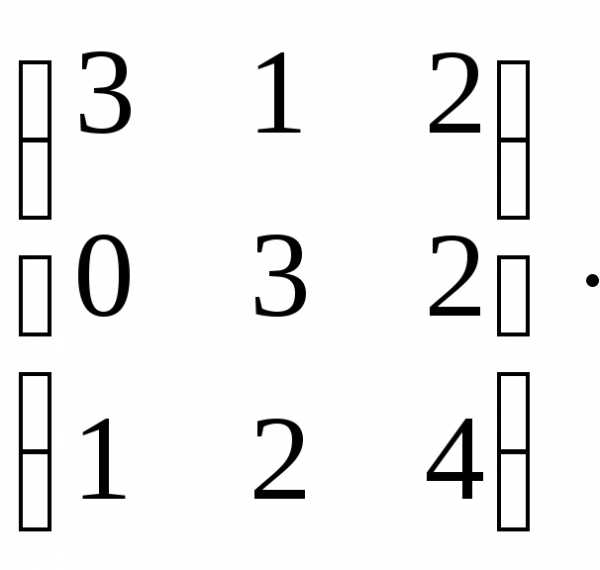 Найти алгебраическое дополнение каждого
элемента матрицы А.
Найти алгебраическое дополнение каждого
элемента матрицы А.
Решение.
Вычеркиваем первую строку и первый
столбец: =
(-1)1+1
=
(-1)1+1 =12-4=8
=12-4=8
Вычеркиваем первую строку и второй
столбец: =
(-1)1+2
=
(-1)1+2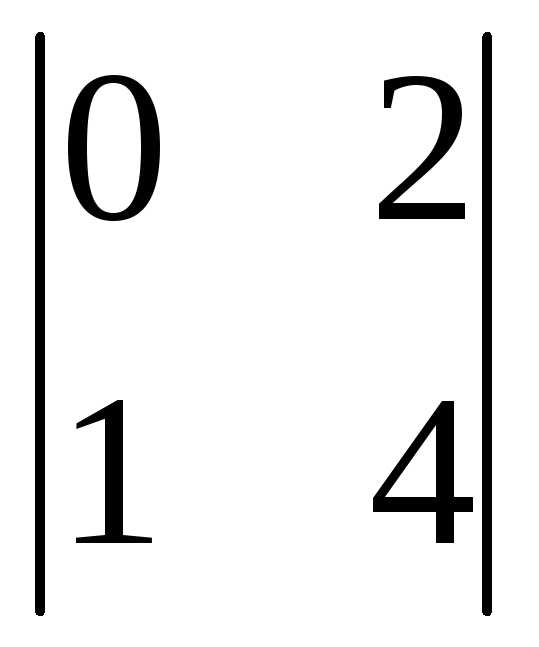 =
-(0-2)= 2
=
-(0-2)= 2
Вычеркиваем первую строку и третий
столбец: =
(-1)1+3
=
(-1)1+3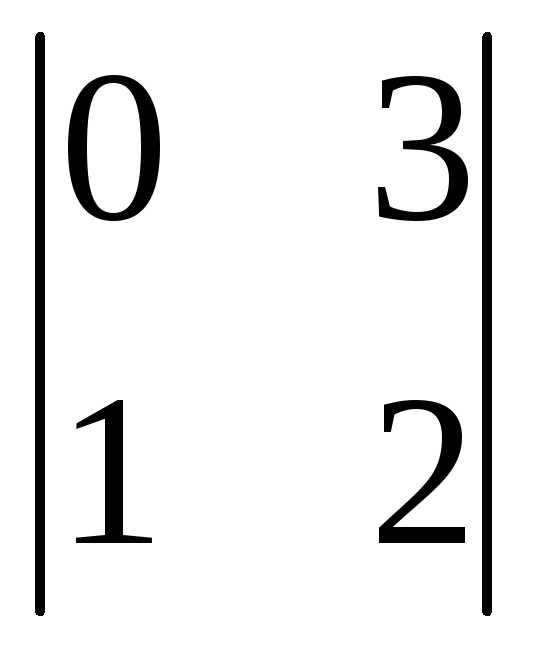 =
0-3= -3
=
0-3= -3
Вычеркиваем вторую строку и первый
столбец: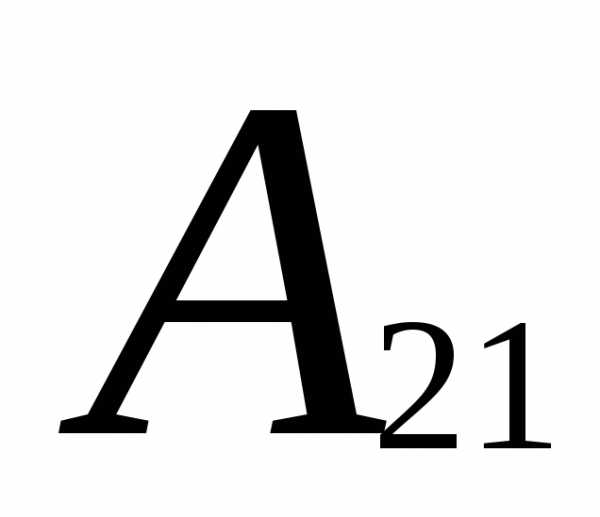 =
(-1)2+1
=
(-1)2+1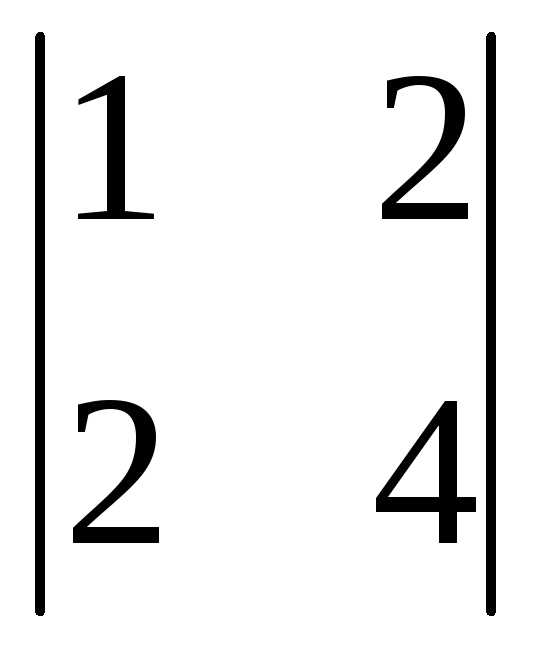 =
-(4-4)=0
=
-(4-4)=0
Вычеркиваем вторую строку и второй
столбец: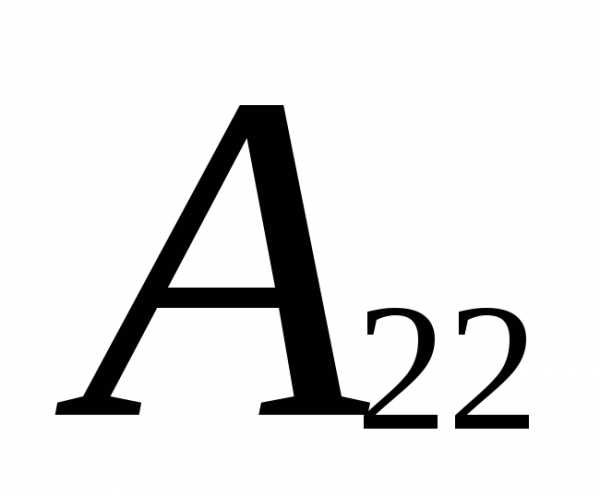 =
(-1)2+2
=
(-1)2+2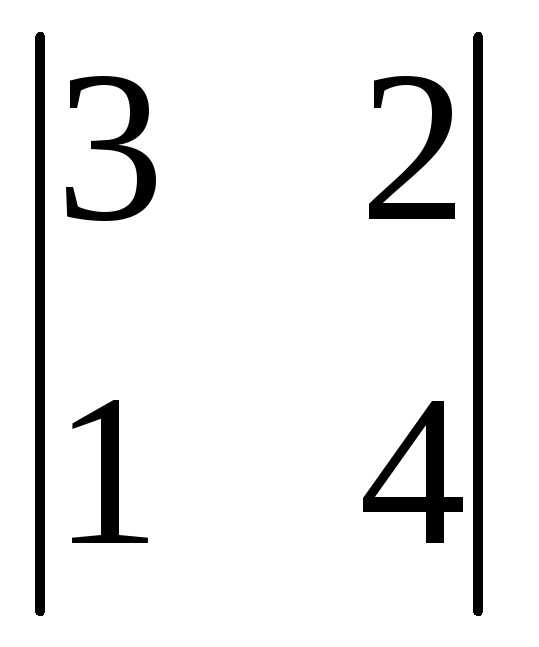 =
12-2=10
=
12-2=10
Вычеркиваем вторую строку и третий
столбец: =
(-1)2+3
=
(-1)2+3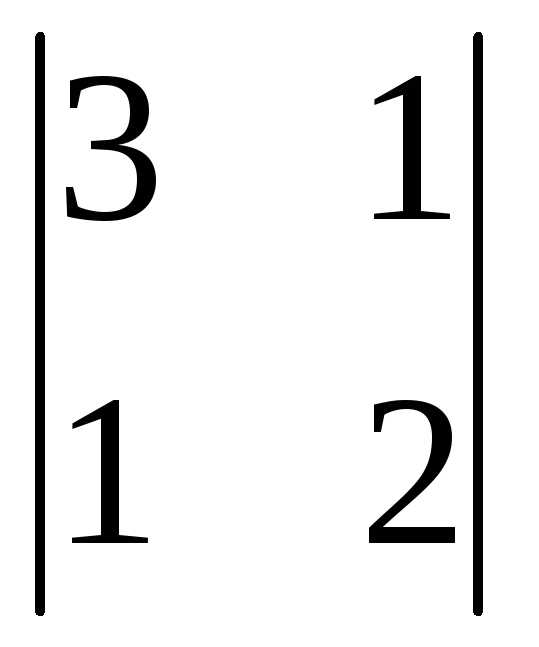 =
-(6-1)= -5
=
-(6-1)= -5
Вычеркиваем третью строку и первый
столбец: =
(-1)3+1
=
(-1)3+1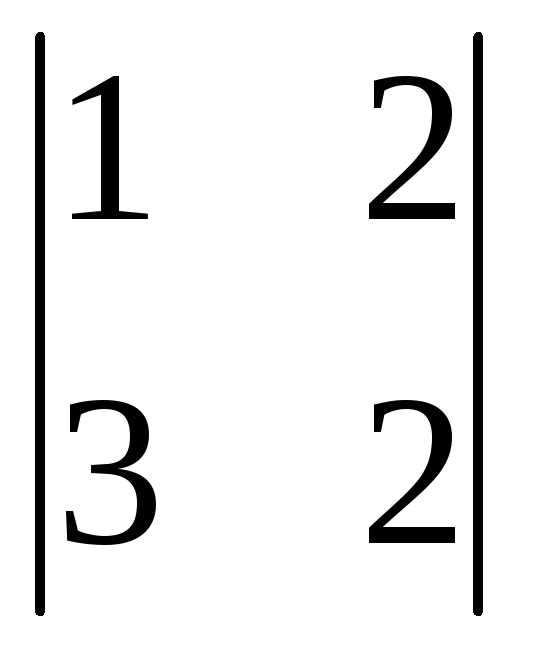 =
2-6= -4
=
2-6= -4
Вычеркиваем третью строку и второй
столбец: =
(-1)3+2
=
(-1)3+2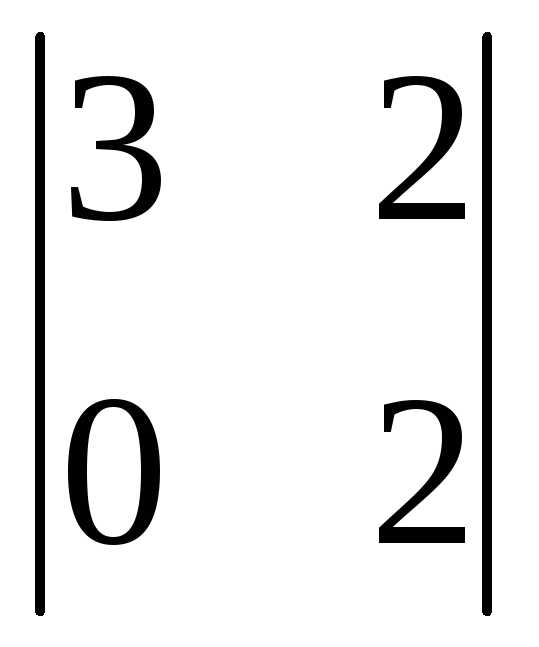 =
-(6-0)= -6
=
-(6-0)= -6
Вычеркиваем третью строку и третий
столбец: =
(-1)3+3
=
(-1)3+3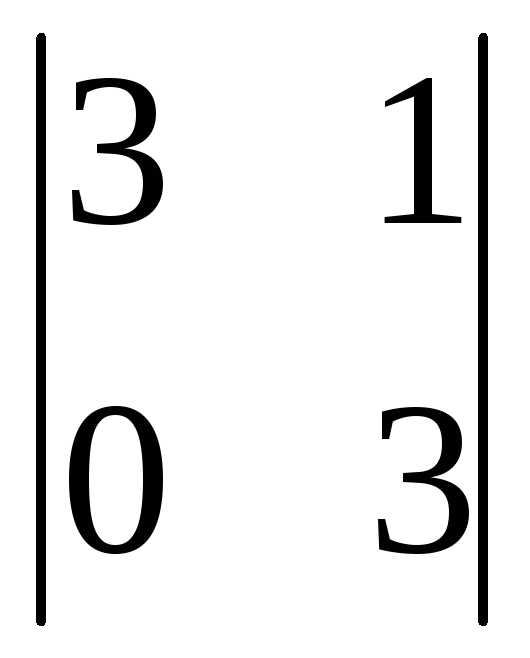 =
9-0=9.
=
9-0=9.
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраическое дополнение:
 =.
=.
Пример 2.4
Дано: А=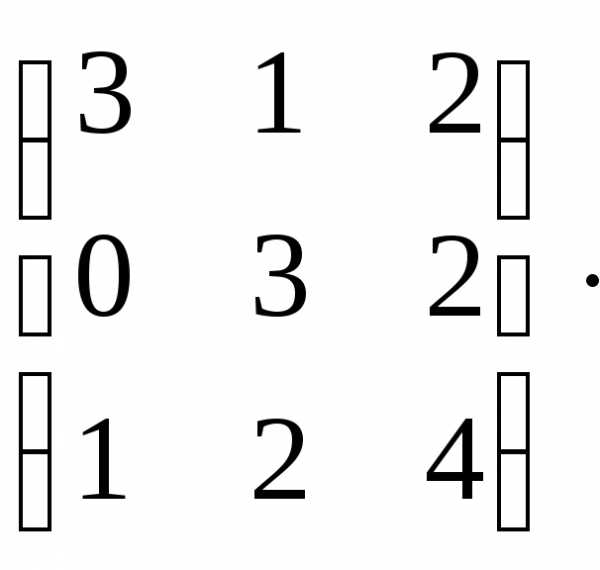 Вычислить определитель третьего порядка.
Вычислить определитель третьего порядка.
Решение.
Вычислим определитель матрицы А, разложив, например, первый столбец:
 =3(-1)1+1
=3(-1)1+1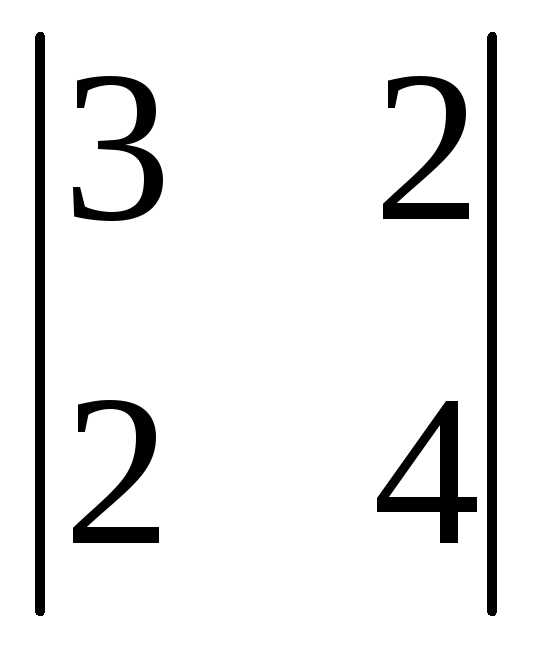 +0(-1)2+1
+0(-1)2+1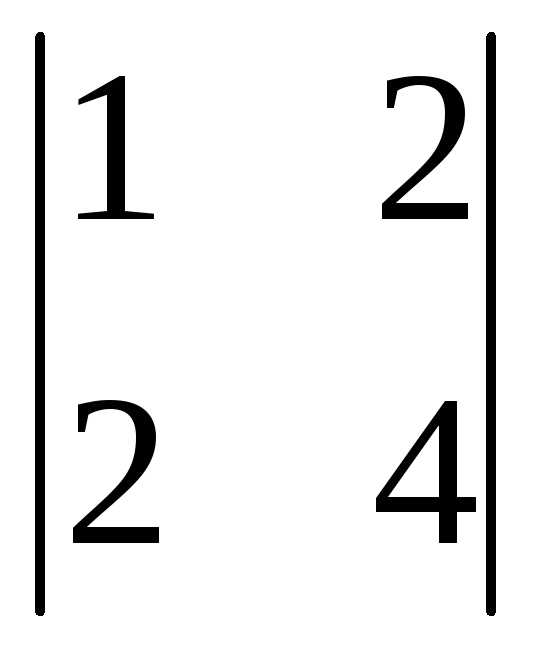 +1(-1)3+1
+1(-1)3+1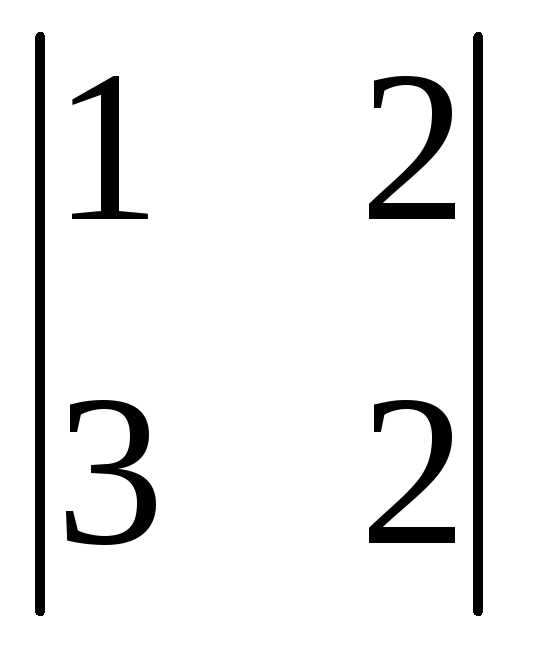 =3(12-4)+0+(2-6)=24-4=20.
=3(12-4)+0+(2-6)=24-4=20.
Основные свойства определителей
определитель не изменится, если его строки заменить столбцами, и наоборот.
при перестановке двух параллельных рядов определитель меняет знак.
определитель, имеющий два одинаковых ряда, равен нулю
общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
определитель с нулевым рядом равен нулю.
если к какому-либо ряду определителя прибавить другой ряд, умноженный на скаляр, то определитель не изменится.
определитель треугольной и диагональной матрицы равен произведению элементов, расположенных на главной диагонали.
Ранг матрицы
Определение. Рангом треугольной матрицы называют число её ненулевых строк.
Чтобы найти ранг матрицы необходимо с помощью элементарных преобразований привести её к треугольному виду.
Элементарные преобразования матрицы, сохраняющие ранг матрицы:
отбрасывание нулевого ряда
умножение всех элементов ряда матрицы на число, неравное нулю.
изменение порядка ряда матрицы
прибавление к каждому элементу одного ряда соответствующих элементов другого ряда, умноженных на число.
транспонирование матрицы.
Рассмотрим пример.
Пример 2.5
Дана матрица А=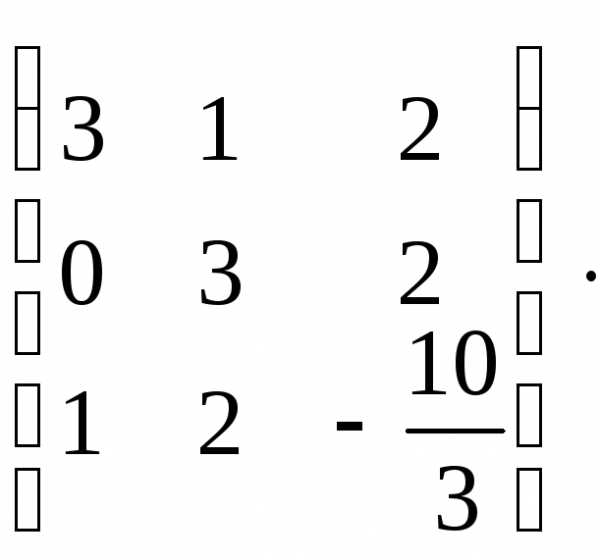 Найти ранг матрицы.
Найти ранг матрицы.
Решение.
Приведём данную матрицу к треугольному виду.
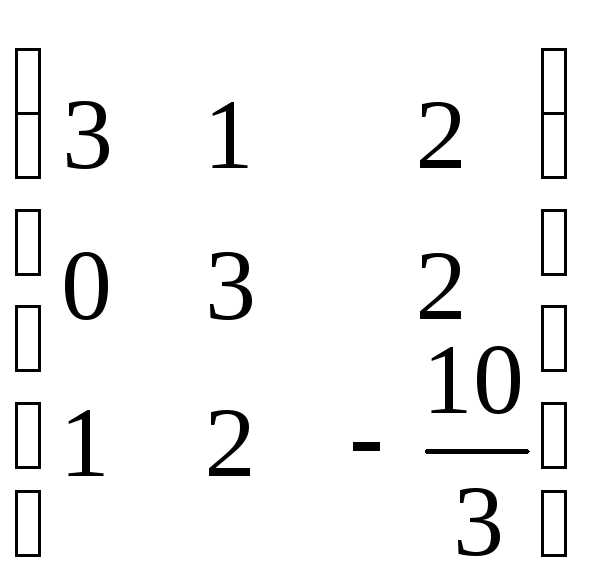
 выбираем
ведущую строку и главный элемент, для
этого поменяем местами первую и третью
строку
выбираем
ведущую строку и главный элемент, для
этого поменяем местами первую и третью
строку
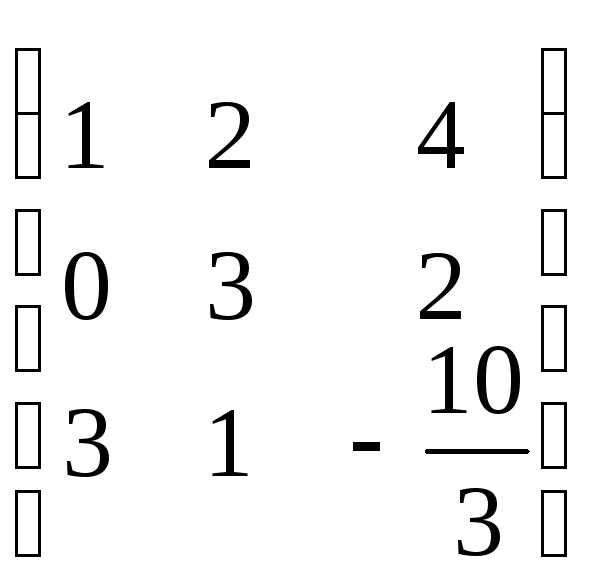
 Теперь должны получить нули под главным
элементом, т.е. под единицей. Первый нуль
во второй строке уже есть, поэтому
переписываем первую строку, как ведущую,
и вторую строку без изменения. Осталось
получить нуль вместо первого элемента
третьей строки, т.е. вместо тройки. Для
этого каждый элемент ведущей строки,
умноженный на минус три, складываем со
соответствующими элементами третьей
строки.
Теперь должны получить нули под главным
элементом, т.е. под единицей. Первый нуль
во второй строке уже есть, поэтому
переписываем первую строку, как ведущую,
и вторую строку без изменения. Осталось
получить нуль вместо первого элемента
третьей строки, т.е. вместо тройки. Для
этого каждый элемент ведущей строки,
умноженный на минус три, складываем со
соответствующими элементами третьей
строки.
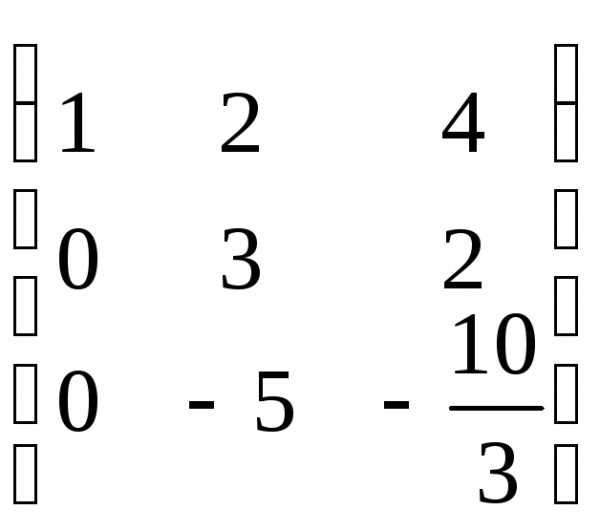
 Выбираем
вторую строку за ведущую, и первый
ненулевой элемент этой строки берем за
главный. Получим нуль под главным
элементом. Для этого к каждому элементу
ведущей строки (второй строки), умноженному
на пять, прибавляем соответствующий
элемент третьей строки, умноженный на
три.
Выбираем
вторую строку за ведущую, и первый
ненулевой элемент этой строки берем за
главный. Получим нуль под главным
элементом. Для этого к каждому элементу
ведущей строки (второй строки), умноженному
на пять, прибавляем соответствующий
элемент третьей строки, умноженный на
три.
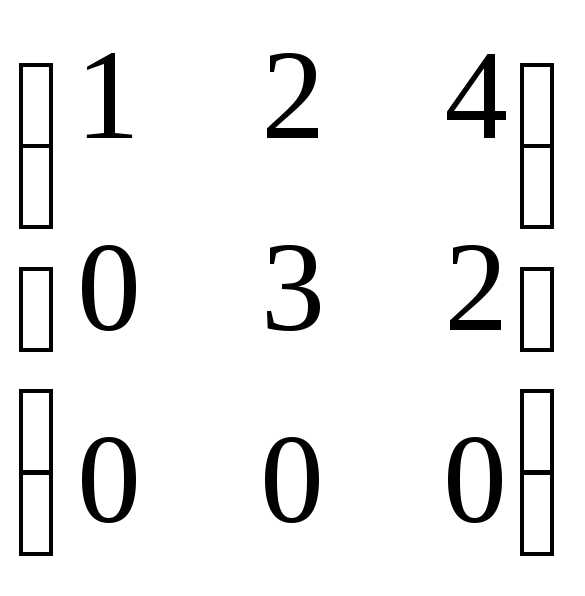 .
В результате получаемr(A)=2.
.
В результате получаемr(A)=2.
studfiles.net

 ,
тогда определитель
,
тогда определитель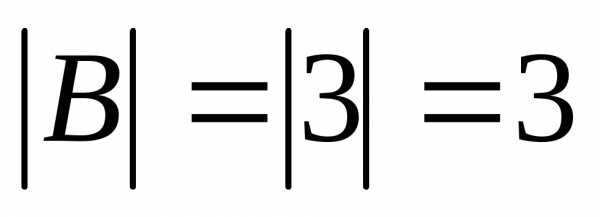
 ,
тогда определитель
,
тогда определитель