Метод Гомори
Метод Гомори решения задач целочисленного программирования является методом отсечения.
Суть метода заключается в построении ограничений, отсекающих нецелочисленные решения задачи линейного программирования, но не отсекающих ни одного целочисленного плана. Для этого сначала решается ослабленная задача линейного программирования без учета условия целочисленности переменных.
Если полученное решение задачи линейного программирования является целочисленным, то задача целочисленного программирования также решена и найденное решение является оптимальным и для нее. Если же в найденном решении задачи линейного программирования одна или большее число переменных не целые, то для отыскания целочисленного решения задачи добавляются новое линейное ограничение, которое отсекает нецелочисленные решения. При продолжении решения расширенной задачи двойственным симплексным методом с учетом этого ограничения получается целочисленный план.
Для нахождения целочисленного решения задачи методом Гомори используется следующий алгоритм.
Решаем ослабленную задачу симплексным методом без учета условия целочисленности. Если все компоненты оптимального плана целые, то он является оптимальным и для задачи целочисленного программирования. Если обнаруживается неразрешимость задачи, то и неразрешима задача целочисленного программирования.
Если в результате решения задачи линейного программирования в полученном оптимальном плане есть нецелая базисная переменная
 ,
то к ограничениям задачи добавляется
новое ограничение, обладающее следующими
свойствами:
,
то к ограничениям задачи добавляется
новое ограничение, обладающее следующими
свойствами:
— оно должно быть линейным;
— должно отсекать найденный оптимальный нецелочисленный план;— не должно отсекать ни одного целочисленного плана.
Если
нецелых базисных переменных несколько,
то для составления ограничения выбираем
компоненту оптимального плана 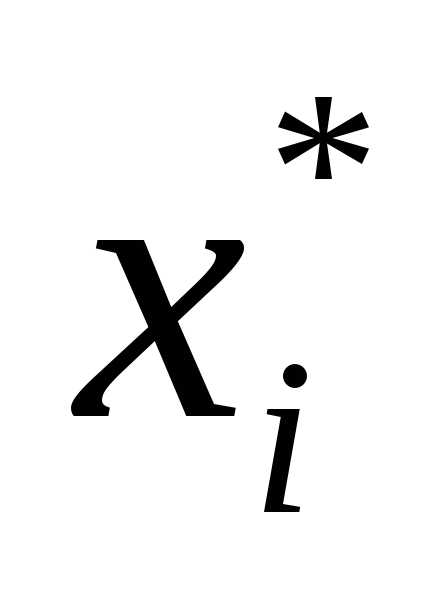 с
наибольшей дробной частью (если таких переменных несколько, то
выбираем любую).
с
наибольшей дробной частью (если таких переменных несколько, то
выбираем любую).
Этой переменной соответствует строка симплексной таблицы, называемая строкой, производящей отсечение (производящей строкой).
Для изложения метода вводим следующие понятия. Пусть a – действительное число.
Под целой частью некоторого числа а понимается максимальное целое число [a], не превосходящее данного.
Под дробной
частью некоторого числа а понимается наименьшее неотрицательное
число 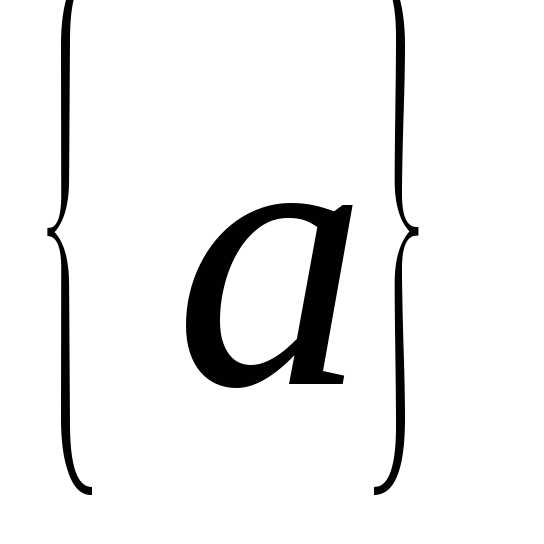
Для
выбранной базисной переменной 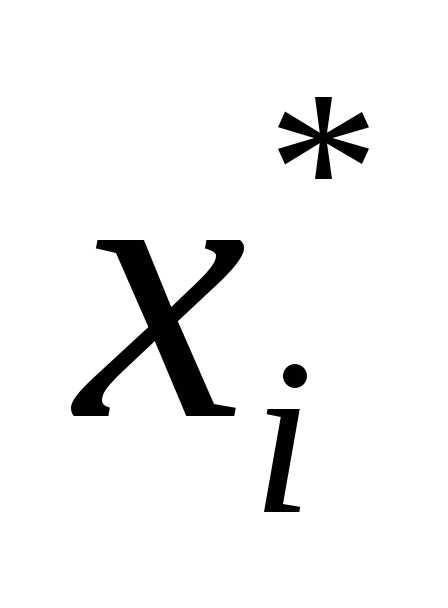 с
наибольшей дробной частью находим дробную часть
с
наибольшей дробной частью находим дробную часть 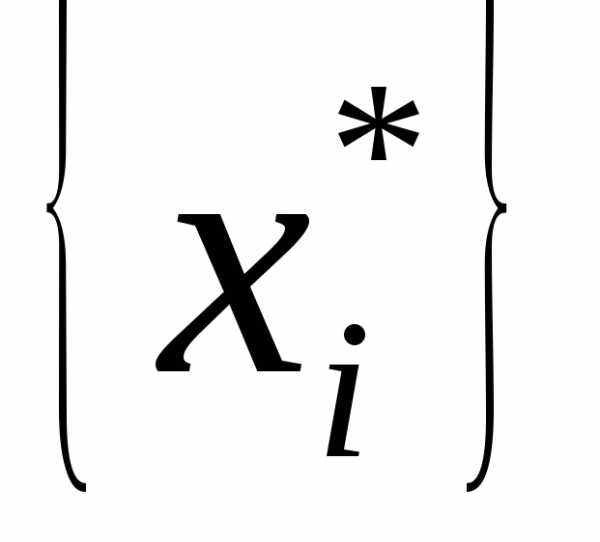 этой переменной и дробные части всех
коэффициентов при переменныхi — й строки системы ограничений
(производящей
строкой).
этой переменной и дробные части всех
коэффициентов при переменныхi — й строки системы ограничений
(производящей
строкой).
Обозначим 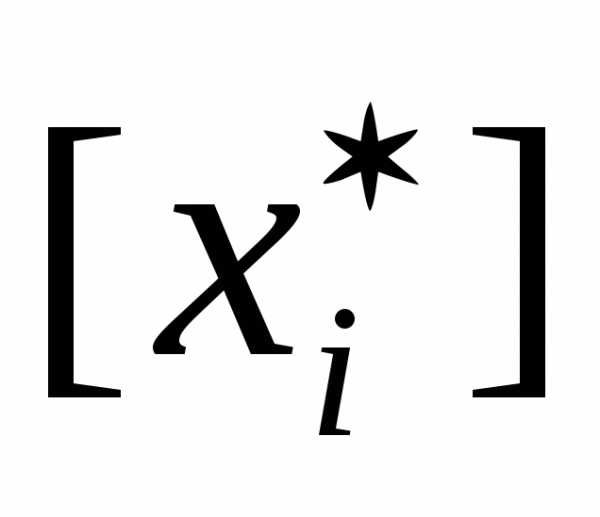 и
и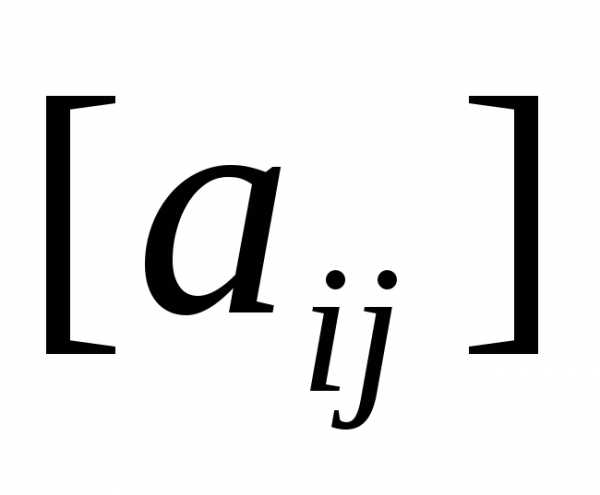 целые
части чисел
целые
части чисел  и
и  .
Величины дробных частей
.
Величины дробных частей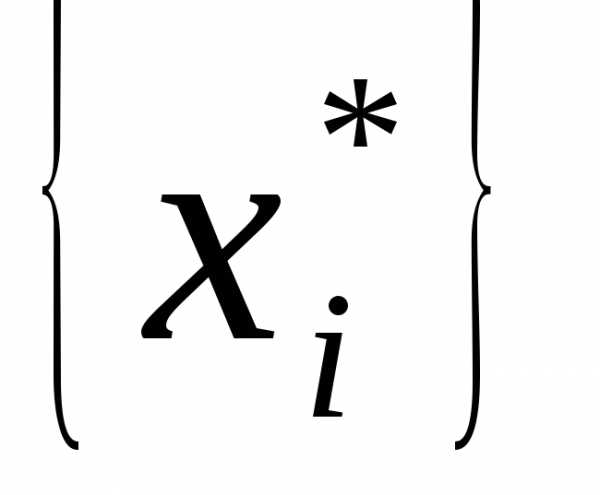 и
и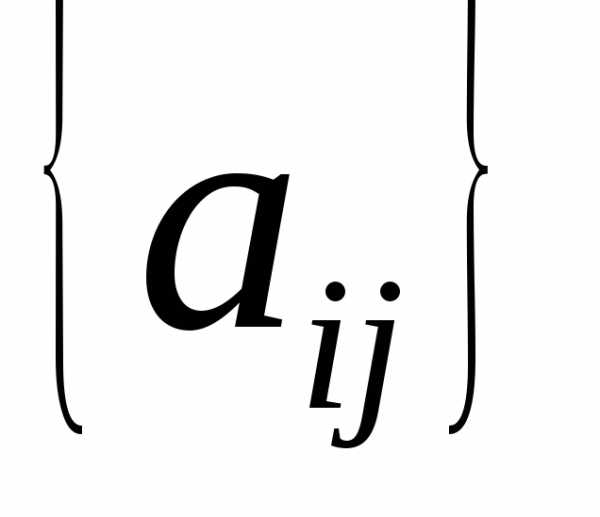 ()
определяются следующим образом
()
определяются следующим образом

Составляем неравенство Гомори и включаем его в систему ограничений исходной задачи.
Для этого по производящей строке симплексной таблицы выписывается уравнение, предполагая, что первые m переменных являются базисными для данного оптимального плана
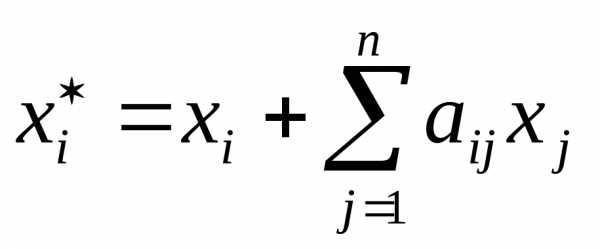 или
или 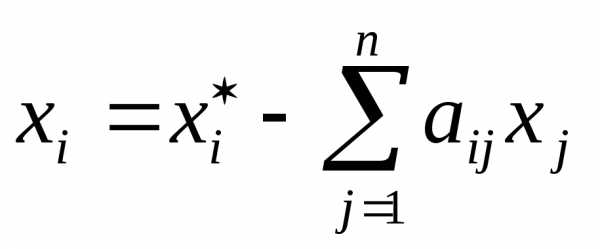
Переносим все целые части коэффициентов в одну сторону, оставляя все дробные в другой:
Так
как  <1,
то заменяя в правой части
<1,
то заменяя в правой части 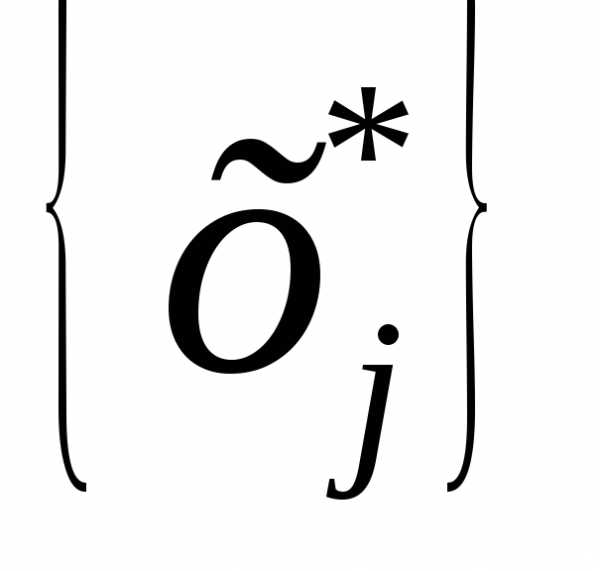 ,
получим строгое неравенство
,
получим строгое неравенство
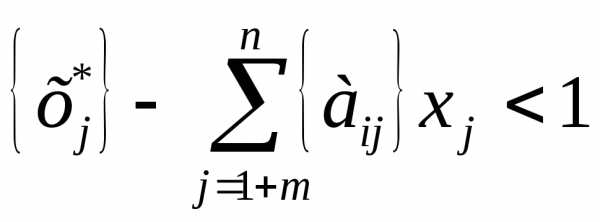
Так как левая часть неравенства должна принимать целые значения, то, следовательно, необходимое условие ее целочисленности можно записать только в следующем виде:

Неравенство преобразуется в уравнение путем введения дополнительной неотрицательной переменной и включается в оптимальную симплексную таблицу.
Решаем задачу, используя двойственный симплексный метод. Если новый оптимальный план расширенной задачи будет целочисленным, то задача решена. Если же решение нецелое, то нужно повторять алгоритм метода Гомори вплоть до получения целочисленного решения.
Пример. Методом Гомори найти решение задачи целочисленного программирования, состоящей в определении максимального значения функции при условии
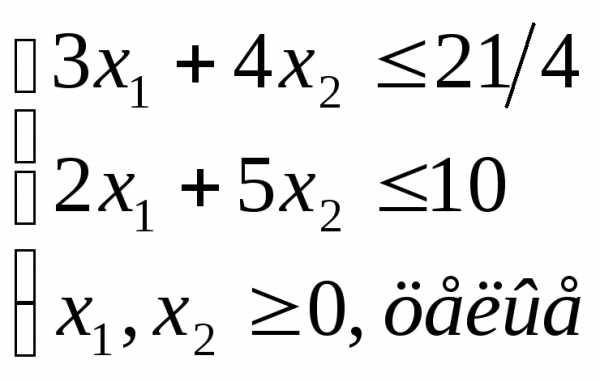
Решение. Выравнивая неравенства с помощью вспомогательных переменных х3, х4, получаем задачу линейного программирования в канонической форме:
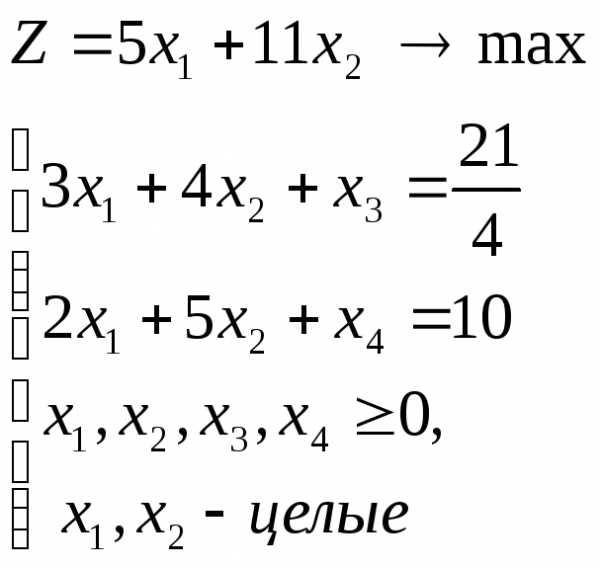
Решаем задачу линейного программирования симплексным методом, используя поэтапный переход от одного базиса к другому. Ход решения задачи и полученное оптимальное решение представлены в таблицах.
Б | СБ | В | С1=5 | С2=11 | С3=0 | С4=0 |
а2 | а3 | а4 | ||||
а3 | 0 | | 3 | 4 | 1 | 0 |
а4 | 0 | 10 | 2 | 5 | 0 | 1 |
∆j =Zj–Сj | 0 | -5 | -11 | 0 | 0 | |
СБ | В | С1=5 | С2=11 | С3=0 | С4=0 | |
а1 | а2 | а3 | а4 | |||
а | 11 |
|
| 1 |
| 0 |
а4 | 0 |
|
| 0 |
| 1 |
∆j =Zj–Сj |
|
| 0 |
| 0 | |
В найденном оптимальном плане значение переменной х2 равно дробному числу. Находим его дробную часть и дробные части всех элементов строки, содержащей переменную х2 , а именно:
Теперь составляем для найденных значений дробных частей неравенство Гомори:
.
Выравниваем неравенство Гомори с помощью новой вспомогательной переменной х5, переносим свободный член уравнения в правую часть и получаем новое ограничение:
.
Добавляем в симплексную таблицу строку, содержащую новое ограничение, и столбец, содержащий новую переменную, и продолжаем решать задачу двойственным симплексным методом, так как теперь в таблице записан псевдоплан.
Б | СБ | В | С1=5 | С2=11 | С3=0 | С4=0 | С5=0 |
а1 | а2 | а3 | а4 | а5 | |||
а2 | 110 |
|
| 1 |
| 0 | 0 |
а4 | 0 |
|
| 0 |
| 1 | 0 |
а5 | 0 |
|
| 0 |
| 0 | 1 |
∆j=Zj–Сj |
|
| 0 |
| 0 | 0 | |
Б | СБ | В | С1=5 | С2=11 | С3=0 | С4=0 | С5=0 |
а1 | а2 | а3 | а4 | а5 | |||
а2 | 11 | 1 | 0 | 1 | 0 | 0 | 1 |
а4 | 0 |
| 0 | 0 |
| 1 |
|
а1 | 0 |
| 1 | 0 |
| 0 |
|
∆j=Zj–Сj |
| 0 | 0 |
| 0 | ||
Полученное оптимальное решение расширенной задачи содержит нецелое значение переменной х1, поэтому находим для этой строки дробные части всех нецелых чисел, а именно:
и новое неравенство Гомори имеет вид:
Выравниваем неравенство Гомори с помощью новой вспомогательной переменной х6, переносим свободный член уравнения в правую часть и получаем новое ограничение: .
Добавляем его к решаемой задаче, выравниваем с помощью вспомогательной переменной и решаем расширенную задачу
Б | СБ | В | С1=5 | С2=11 | С3=0 | С4=0 | С5=0 | С6=0 |
а1 | а2 | а3 | а4 | а5 | а6 | |||
а2 | 110 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
а4 | 0 |
| 0 | 0 |
| 1 |
| 0 |
а1 | 0 |
| 1 | 0 |
| 0 |
| 0 |
а6 | 0 |
| 0 | 0 |
| 0 |
| 1 |
∆j=Zj–Сj |
| 0 | 0 |
| 0 | 0 | ||
Б | СБ | В | С1=5 | С2=11 | С3=0 | С4=0 | С5=0 | С6=0 |
а1 | а2 | а3 | а4 | а5 | а6 | |||
а2 | 110 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
а4 | 0 | 5 | 0 | 0 | 0 | 1 | -1 | -2 |
а1 | 0 | 0 | 1 | 0 | 0 | 0 | -2 | 1 |
а3 | 0 |
| 0 | 0 | 1 | 0 | 2 | -3 |
∆j=Zj–Сj | 11 | 0 | 0 | 0 | 0 | 1 | 5 | |
Таким образом, найдено оптимальное решение задачи целочисленного программирования: Zmax =11 при .
Замечания:
Если
в процессе решения в симплексной таблице
появится уравнение с нецелой компонентой 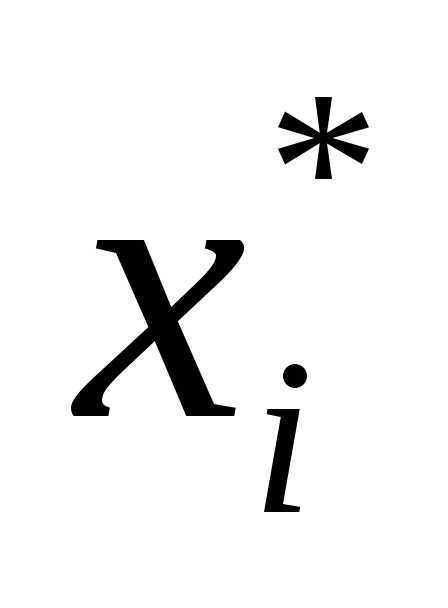 и целыми коэффициентами в соответствующей
строке системы ограничений
и целыми коэффициентами в соответствующей
строке системы ограничений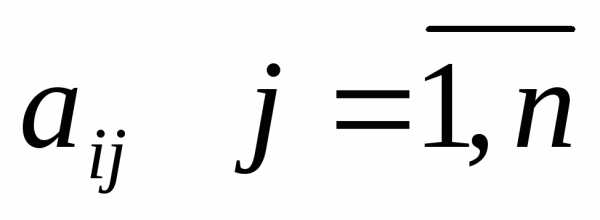 ,
то данная задача не имеет целочисленного
решения.
,
то данная задача не имеет целочисленного
решения.
studfiles.net
Методы отсечения.
Суть метода состоит в том, что сначала решается задача линейного программирования без условия целочисленности. Если полученный ответ удовлетворяет условию целочисленности, то задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:
оно должно быть линейным;
оно должно отсекать найденный оптимальный нецелочисленный план;
оно не должно отсекать ни одного целочисленного плана.
Такие ограничения называются правильными отсечениями.
После введения нового ограничения вновь решается задача линейного программирования. Если вновь полученный план целочисленный то задача решена. Если это не так, то к задаче добавляется новое ограничение. Процесс повторяется до тех пор, пока полученный оптимальный план не будет полностью целочисленным.
Геометрический смысл добавления каждого нового линейного ограничения состоит в проведении дополнительной прямой (гиперплоскости), которая отсекает от многоугольника (многогранника) допустимых решений его часть вместе с оптимальной точкой с нецелыми координатами. В отсекаемую часть не должна попасть ни одна точка с целыми координатами. В результате новый многогранник решений содержит все точки с целыми координатами, содержавшиеся в первоначальном многограннике решений. Следовательно, полученное при этом многограннике оптимальное решение будет целочисленным.
Пример 11.

х1, х2— целые.
Построим область допустимых решений задачи (рис.). Это многоугольник АВСДЕ. Построим вектор градиент целевой функции (1;-3). Ясно, что точкой оптимума будет точка В(3.5;6.5). Полученное решение не удовлетворяет условию целочисленности. Проведем прямую А‘B‘, отсекающую точку В и не отсекающую ни одну целую точку. Получаем новый многоугольник АА‘B‘СДЕ, где А’ и B’ имеют целые координаты. Точка А'(3;6) — новое решение задачи целочисленного программирования.

Метод Гомори.
Пусть задача линейного программирования имеет оптимальное решение. Не нарушая общности задачи предположим х1, х2,…хm-это базисные переменные, полученные на последнем шаге симплекс-метода. Они выражены через небазисные переменные хm+1, хm+2,…хn.
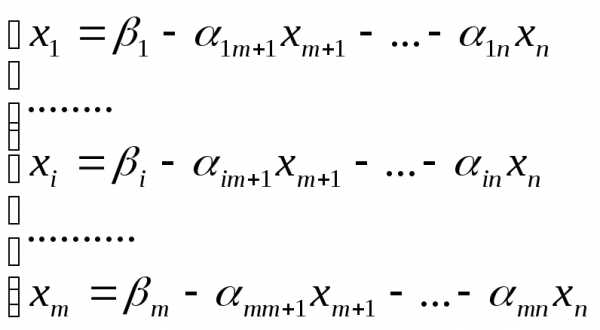
Оптимальное решение задачи Х*(1,2, …,m, 0, 0,…,0).
Пусть в этом оптимальном решении iне целая компонента.
Алгоритм метода Гомори.
Решаем задачу симплекс методом. Если найденное решение целочисленно, то задача решена. Если задача не разрешима, то она не имеет решений и в целых числах.
Если среди компонент оптимального решения есть не целые, то надо выбрать компоненту с оптимальной целой частью и сформулировать правильное отсечение из условия
Вводим дополнительную неотрицательную целую переменную хn+1и получаем новое уравнение

Полученную расширенную задачу решаем симплекс-методом. Если новый найденный план целочисленный, то задача решена, если нет то повторяем процедуру.
Замечание. — дробная часть числа.
— дробная часть числа.
Если задача разрешима в целых числах, то после конечного числа шагов (итераций) оптимальный целочисленный план будет найден. Если в процессе решения появится уравнение, выражающее основную переменную через неосновные, в котором свободный член не целый, а все остальные коэффициенты целые, то задача в целых числах решений не имеет. В симплекс таблице это условие соответствует тому, что в строке с нецелым свободным членом все остальные коэффициенты целые.
Пример 12.
Решить задачу в целых числах.
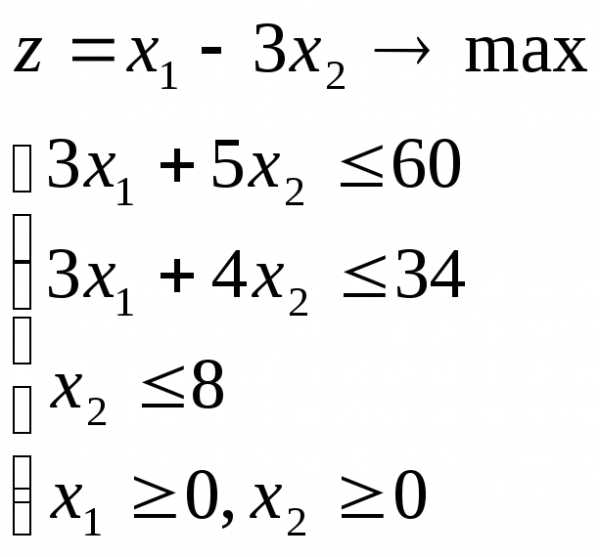
Приведем задачу к каноническому виду:
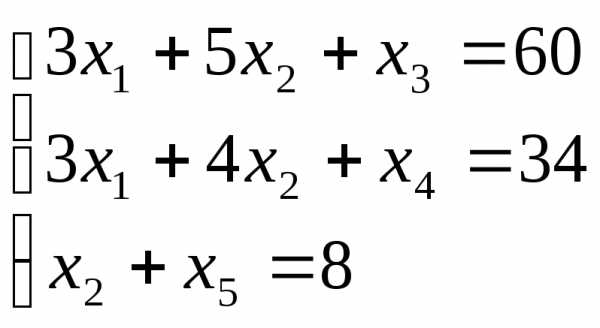
Построим симплекс таблицу
Базис | Свободный член | Переменные | Оценочные отношения | ||||
x1 | x2 | x3 | x4 | x5 | |||
x3 | 60 | 3 | 5 | 1 | 0 | 0 | 12 |
x4 | 34 | 3 | 4 | 0 | 1 | 0 | 17/2 |
x5 | 8 | 0 | 1 | 0 | 0 | 1 | 8 |
z | 0 | -2 | -3 | 0 | 0 | 0 | |
Данный план не оптимален, так как в оценочной строке есть отрицательные элементы. Наибольший по модулю в столбце х2. Следовательно х2переменная вводимая в базис. Построим оценочные отношения. Наименьшее соответствует строке х5. Значит х5вводимая в базис переменная. Переходим к новой симплекс-таблице.
Базис | Свободный член | Переменные | Оценочные отношения | ||||
x1 | x2 | x3 | x4 | x5 | |||
x3 | 20 | 3 | 0 | 1 | 0 | -5 | 20/3 |
x4 | 2 | 3 | 0 | 0 | 1 | -4 | 2/3 |
x2 | 8 | 0 | 1 | 0 | 0 | 1 | |
z | 24 | -2 | 0 | 0 | 0 | 3 | |
Полученное решение не является оптимальным. х1вводимая, х4выводимая переменная. Переходим к новой симплекс-таблице.
Базис | Свободный член | Переменные | Оценочные отношения | ||||
x1 | x2 | x3 | x4 | x5 | |||
x3 | 18 | 0 | 0 | 1 | -1 | -1 | |
x1 | 2/3 | 1 | 0 | 0 | 1/3 | -4/3 | |
x2 | 8 | 0 | 1 | 0 | 0 | 1 | |
z | 76/3 | 0 | 0 | 0 | 2/3 | 1/3 | |
Полученное решение Х(2/3;8;18;0;0) оптимально, но не является целочисленным (х1=2/3).
Построим правильное отсечение из условия:
Найдем дробные части от чисел стоящих в фигурных скобках:
 ;
;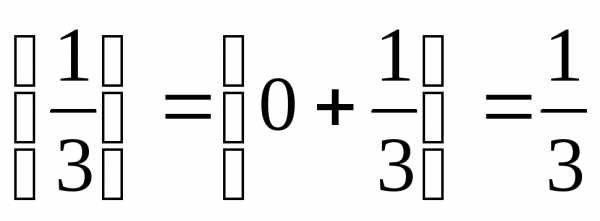 ;
;
Получим неравенство:
Введем дополнительную целую переменную 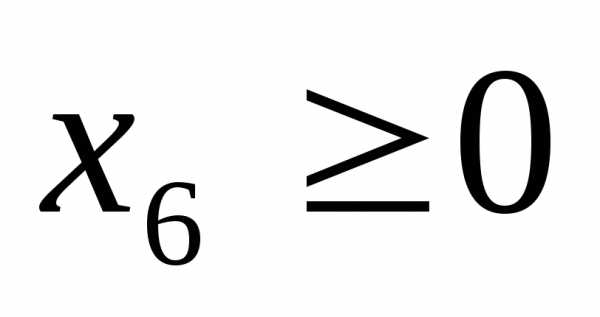
Полученное уравнение надо добавить в систему ограничений и решить симплекс-методом новую задачу.
Для сокращения числа шагов можно вводить новое уравнение в симплекс-таблицу, полученную на последнем шаге.
Базис | Свободный член | Переменные | Оценочные отношения | |||||
x1 | x2 | x3 | x4 | x5 | x6 | |||
x3 | 18 | 0 | 0 | 1 | -1 | -1 | 0 | |
x1 | 2/3 | 1 | 0 | 0 | 1/3 | -4/3 | 0 | |
x2 | 8 | 0 | 1 | 0 | 0 | 1 | 0 | 8 |
x6 | 2/3 | 0 | 0 | 0 | 1/3 | 1/3 | -1 | 1 |
z | 76/3 | 0 | 0 | 0 | 2/3 | 1/3 | 0 | |
Полученное базисное решение не допустимо (х6=-1).
Замечание.Включение в систему ограничений дополнительного ограничения, соответствующего правильному отсечению всегда дает недопустимое базисное решение.
Для получения допустимого базисного решения необходимо перевести в основные переменные переменную, входящую со знаком «+» в уравнение, в котором свободный член отрицательный. В нашем случае это переменная х4или.x5. Введем х5.
Базис | Свободный член | Переменные | Оценочные отношения | |||||
x1 | x2 | x3 | x4 | x5 | x6 | |||
x3 | 19 | 0 | 0 | 1 | -1/2 | 0 | -2/3 | |
x1 | 2 | 1 | 0 | 0 | 1 | 0 | -2 | |
x2 | 7 | 0 | 1 | 0 | -1/2 | 0 | 3/2 | |
x5 | 1 | 0 | 0 | 0 | 1/2 | 1 | 3/2 | |
z | 25 | 0 | 0 | 0 | 1/2 | 0 | 1/2 | |
Полученное решение является оптимальным. Найденный план целочисленен Х(2;7;19;0;1;0).
studfiles.net
Метод Гомори — это… Что такое Метод Гомори?
МЕТОД ГОМОРИ — (Gomoris method) метод окрашивания гистологических образцов, применяемый для выявления в них некоторых ферментов, особенно фосфатазы и липазы … Толковый словарь по медицине
Метод Гомори (Gomori’S Method) — метод окрашивания гистологических образцов, применяемый для выявления в них некоторых ферментов, особенно фосфатазы и липазы. Источник: Медицинский словарь … Медицинские термины
Метод Ньютона — Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном… … Википедия
Метод золотого сечения — метод поиска значений действительно значной функции на заданном отрезке. В основе метода лежит принцип деления в пропорциях золотого сечения. Наиболее широко известен как метод поиска экстремума в решении задач оптимизации Содержание 1 Описание… … Википедия
Метод сопряжённых градиентов — Метод сопряженных градиентов метод нахождения локального минимума функции на основе информации о её значениях и её градиенте. В случае квадратичной функции в минимум находится за шагов. Содержание 1 Основные понятия … Википедия
Метод роя частиц — (МРЧ) метод численной оптимизации, для использования которого не требуется знать точного градиента оптимизируемой функции. МРЧ был доказан Кеннеди, Эберхартом и Ши[1] [2] и изначально предназначался для имитации социального поведения.… … Википедия
Метод потенциалов — является модификацией симплекс метода решения задачи линейного программирования применительно к транспортной задаче. Он позволяет, отправляясь от некоторого допустимого решения, получить оптимальное решение за конечное число итераций. Содержание… … Википедия
Метод Хука — Дживса (англ. Hooke Jeeves), также как и алгоритм Нелдера Мида, служит для поиска безусловного локального экстремума функции и относится к прямым методам, то есть опирается непосредственно на значения функции. Алгоритм делится на две… … Википедия
Метод Гаусса (оптимизация) — У этого термина существуют и другие значения, см. Метод Гаусса. Метод Гаусса[1] прямой метод решения задач многомерной оптимизации. Содержание 1 Описание 2 Примечания … Википедия
Метод Нелдера — … Википедия
dic.academic.ru
Метод Гомори решения задач целочисленного программирования. Примеры решения экономических задач.
Графический метод решения задач целочисленного программирования.
При наличии в задаче линейного программирования двух переменных, а в системе ограничения – неравенств, она может быть решена графическим методом без требований целочисленных переменных.
Если оптимальное решение этой задачи является целочисленным, то оно и является оптимальным для исходной задачи.
Если же полученное оптимальное решение не целочисленное, то строится дополнительное линейное ограничение. Оно обладает следующими свойствами:
1. Оно должно быть линейным;
2. Должно отсекать найденный оптимальный не целочисленный план;
3. Не должно отсекать ни одного целочисленного плана.
Алгоритм графического решения задачи
Целочисленного программирования.
1. Построить систему координат x10х2и выбрать масштаб.
2. Найти область допустимых решений (ОДР) системы ограничений задачи.
3. Построить целевую функцию, являющуюся линией уровня и на ней указать направление нормали.
4. Переместить линию целевой функции по направлению нормали через ОДР, чтобы она из секущей стала касательной к ОДР и проходила через наиболее удаленную от начала координат точку. Эта точка будет являться точкой экстремума, т.е. решением задачи.
Если окажется, что линия целевой функции параллельна одной из сторон ОДР, то в этом случае экстремум достигается во всех точках соответствующей стороны, а задача линейного программирования будет иметь бесчисленное множество решений.
5. Найти координаты, точки экстремума и значение целевой функции в ней. Если полученные значения не целочисленные, то перейти к следующему шагу.
6. Выделить у этих координат область с целочисленными значениями.
7. Определить новые координаты и построить граф.
8. Найти точки с целыми значениями искомых переменных, подставить в уравнение целевой функции и найти её значение. Максимальное из полученных значений целевой функции и будет решением задачи.
Метод Гомори решения задач целочисленного программирования. Примеры решения экономических задач.
Данный метод основан на симплексном методе.
На первом этапе данная задача решается симплекс-методом, если полученное решение не целочисленное, то вводим дополнительное ограничение, которые должны быть:
— линейным;
— отсекать найденный оптимальный не целочисленный план;
— не должно отсекать ни одного целочисленного плана.
Дополнительное ограничение обладающие этими свойствами называются правильным отсечением.
Ограничение накладывается на нецелочисленную переменную или на ту переменную, которая имеет большее дробное значение. Ограничение накладывается на не целочисленную переменную через не основные переменные. Ограничение составляется используя следующее правило: дробная часть свободного члена берётся с тем же знаком, который он имеет и в уравнении, а дробные части неосновных переменных — с противоположным знаком и выделяется положительная дробь. Например, {a}=a, {-a}={-A+a*}, где А — целая часть отрицательное число, а*-положительная дробь.
Получаем новое ограничение, вводим новую основную переменную, приведённое в формуле (1.2.3).
где xn+1 — нововведённая переменная,
xj — переменные не входящие в базис.
Новое ограничение следует вводить в последний этап симплекс метода, когда все переменные, имеющиеся в целевой функции, так же входят в базис.
Полученное базисное решение всегда не допустимое, соответствующее правильному отсечению.
Для получения допустимого базисного решения необходимо перевести в основные переменную, входящую с положительным коэффициентом в уравнение, в котором свободный член отрицательный .
При выборе какую переменные ввести в базис взамен нововведённой, следует выразить эти переменные и следую логическому рассуждения, подставить в базис ту переменную которая даёт целочисленное решение на наложенное ограничение.
Введение новых ограничений следует производить, если не получено целочисленное решение, после решения на первом этапе симплекс-методом и после введения новых ограничений.
Если в процессе решения появится выражение с нецелым свободным членом и целыми остальными коэффициентами, то соответствующее уравнение не имеет решения в целых числах. В этом случае и данная задача не имеет целочисленного оптимального решения.
Задача.Контейнер объемом помещен на контейнеровоз грузоподъемностью 12т. Контейнер требуется заполнить грузом двух наименований. Масса единицы груза, объем единицы груза, стоимости приведены в таблице:
| Вид груза | т | ден.ед. | |
Требуется загрузить контейнеровоз таким образом, чтобы стоимость перевозимого груза была максимальной.
Решим задачу методом Гомори.
Введем обозначения: х1 – количество груза первого вида, х2 – количество груза второго вида. Тогда экономико-математическая модель задачи примет вид:
.
Преобразуем математическую модель ЗЛП без учета целочисленности переменных к допустимому предпочтительному виду канонической формы:
.
По алгоритму основного симплекс-метода заполним симплексную таблицу решения ЗЛП:
Оптимальное решение ЗЛП не удовлетворяет ограничению целочисленности, следовательно, к основным ограничениям необходимо добавить новое линейное ограничение.
Замечание 9.1. Если имеется несколько дробных , то для той у которой дробная часть больше всего составляется ограничение.
Составим сечение Гомори для первого ограничения оптимальной симплекс-таблицы решения ЗЛП (так как ):
,
иначе
.
Преобразуем полученное ограничение к канонической форме с предпочтительной переменной:
.
Продолжим решение задачи двойственным симплекс-методом, включив новое ограничение в оптимальную симплекс-таблицу решения ЗЛП:
Оптимальное решение расширенной ЗЛП удовлетворяет ограничению целочисленности.
Ответ: , .
Таким образом, контейнер надо загрузить 3 ед. груза первого вида и 1 ед. второго вида, при этом стоимость перевозимого груза максимальна и равна 42 ден. ед.
Замечание 9.2. Если в процессе решения получена оптимальная таблица, в которой вспомогательная переменная имеет положительное значение, то соответствующая строка может быть вычеркнута.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Метод Гомори в решении целочисленной задачи оптимизации информационной системы
Библиографическое описание:
Семахин А. М. Метод Гомори в решении целочисленной задачи оптимизации информационной системы // Молодой ученый. 2013. №1. С. 38-43. URL https://moluch.ru/archive/48/5986/ (дата обращения: 13.06.2019).
Целочисленное линейное программирование ориентировано на решение задач линейного программирования, в которых все или некоторые переменные принимают целочисленные значения [1, c. 136].
Для решения целочисленной задачи линейного программирования Р. Гомори предложил метод отсечения плоскостей в 1958 г. [1, c. 143].
Алгоритм Гомори содержит этапы:
Этап 1. Решение непрерывной задачи. Если решение дробное переход на 2 этап.
Этап 2. Решение расширенной задачи [2, c. 410].
Разработаем целочисленную математическую модель информационной системы и определим оптимальное решение методом Гомори.
Математическая модель формулируется следующим образом: из числа фирм, предоставляющих услуги спутникового Internet на территории Российской Федерации, требуется выбрать провайдера спутникового Internet с максимальной величиной чистого приведенного эффекта (NPV) и удовлетворяющих финансовым ограничениям [3, c. 58].
Пусть
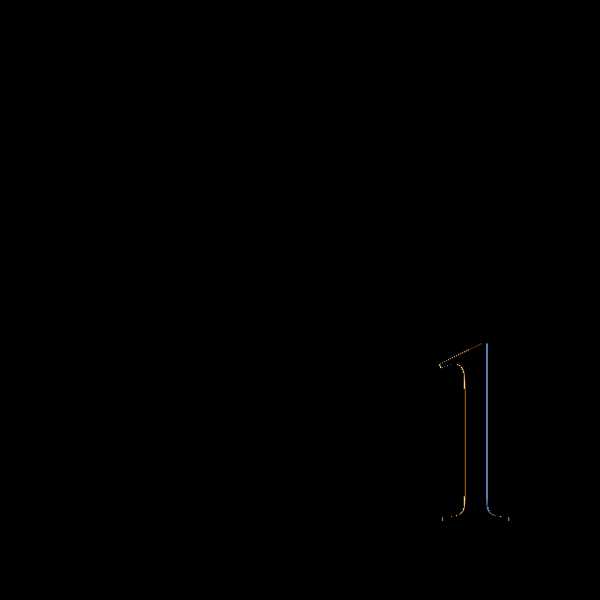 —
доля финансирования проекта “НТВ-Плюс”,
—
доля финансирования проекта “НТВ-Плюс”,
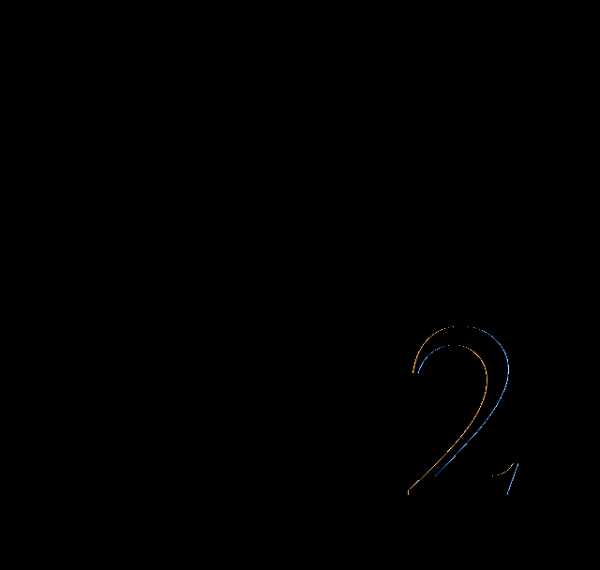 —
доля финансирования проекта Europe
On
Line,
—
доля финансирования проекта Europe
On
Line,
 —
доля финансирования проекта Astra
Network,
—
доля финансирования проекта Astra
Network,
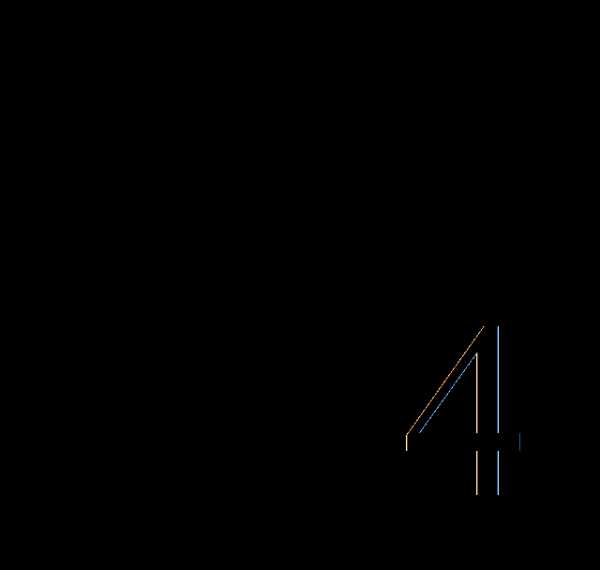 —
доля финансирования проекта Satpro,
—
доля финансирования проекта Satpro,
 —
доля финансирования проекта Network
Service.
—
доля финансирования проекта Network
Service.
Целочисленная математическая модель имеет вид
при ограничениях (1)
Решим непрерывную задачу. Приведем к стандартной форме и составим исходную Жорданову таблицу (табл. 1).
при ограничениях (4)
 (2)
(2)
Таблица 1
Начальная Жорданова таблица
|
БП |
1 |
— |
— |
— |
— |
— |
|
= |
6,5 |
5,4 |
3,2 |
2,931 |
6,286 |
5,9 |
|
= |
3,0 |
2,006437 |
1,5 |
3,000547 |
3,000575 |
3,2 |
|
= |
3,0 |
0,0 |
2,5 |
2,0 |
0,0 |
1,6 |
|
= |
1,5 |
0,0 |
0,881832 |
0,0 |
0,0 |
1,186 |
|
Z= |
0 |
-1,52727 |
-0,741239 |
-1,374394 |
-0,14511 |
-0,530312 |
В табл.2 приведена первая итерация.
Таблица 2
Первая итерация
|
БП |
1 |
— |
— |
— |
— |
— |
|
|
||||||
|
= |
0,58484 |
-0,371563 |
0,311 |
1,911498 |
0,664934 |
1,007782 |
|
= |
3,0 |
0 |
2,5 |
2,0 |
0 |
1,6 |
|
= |
1,5 |
0 |
0,881832 |
0 |
0 |
1,186 |
|
Z= |
1,83838 |
0,282827 |
0,16381 |
-0,545426 |
1,632745 |
1,138371 |
В табл.3 приведено оптимальное решение непрерывной задачи.
Переход ко второму этапу алгоритма Гомори.
Выбирается базисная
переменная
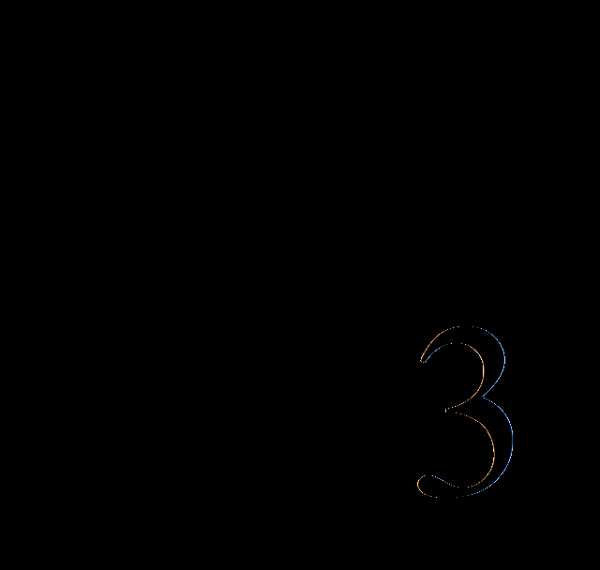 с наибольшей дробной частью:
,
,
.
Для переменной
с наибольшей дробной частью:
,
,
.
Для переменной
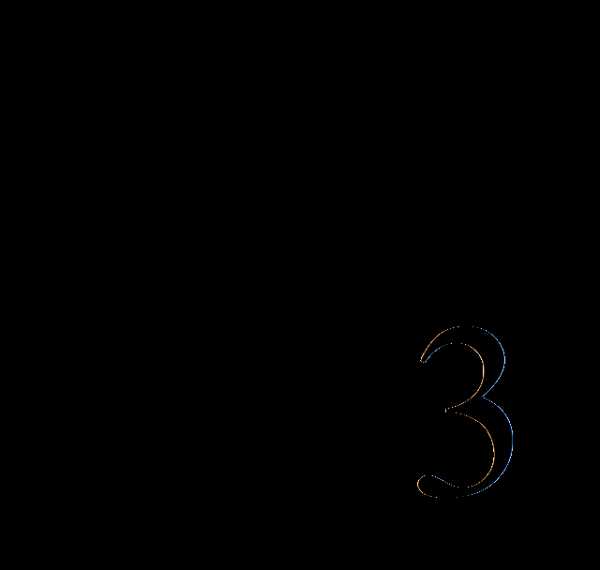 составляется уравнение.
составляется уравнение.
В табл. 4 и табл. 5 представлены расширенная задача и 3 итерация.
Таблица 3
Оптимальное решение непрерывной задачи. Вторая итерация
|
БП |
1 |
— |
— |
— |
— |
— |
|
|
1,037635 |
0,290692 |
0,504283 |
-0,283954 |
0,975263 |
0,806429 |
|
|
0,305961 |
-0,194383 |
0,1627 |
0,52315 |
0,34786 |
0,527221 |
|
= |
2,388078 |
0,388766 |
2,174601 |
-1,0463 |
-0,69572 |
0,545558 |
|
= |
1,5 |
0 |
0,881832 |
0 |
0 |
1,186 |
|
Z= |
2,00526 |
0,176807 |
0,252551 |
0,28534 |
1,822477 |
1,425931 |
Таблица 4
Расширенная задача с первым дополнительным ограничением
|
БП |
1 |
— |
— |
— |
— |
— |
|
|
1,037635 |
0,290692 |
0,504283 |
-0,283954 |
0,975263 |
0,806429 |
|
|
0,305961 |
-0,194383 |
0,1627 |
0,52315 |
0,34786 |
0,527221 |
|
= |
2,388078 |
0,388766 |
2,174601 |
-1,0463 |
-0,69572 |
0,545558 |
|
= |
1,5 |
0 |
0,881832 |
0 |
0 |
1,186 |
|
= |
-0,305961 |
0,194383 |
-0,1627 |
-0,52315 |
-0,34786 |
-0,527221 |
|
Z= |
2,00526 |
0,176807 |
0,252551 |
0,28534 |
1,822477 |
1,425931 |
Таблица 5
Третья итерация
|
БП |
1 |
— |
— |
— |
— |
— |
|
|
0,569642 |
0,588017 |
0,25542 |
-1,084156 |
0,443182 |
1,529584 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
= |
2,071475 |
0,58991 |
2,006242 |
-1,587645 |
-1,055679 |
1,034781 |
|
= |
0,811731 |
0,437271 |
0,515833 |
-1,176842 |
-0,782522 |
2,249531 |
|
= |
0580328 |
-0,368694 |
0,308599 |
0,992278 |
0,659799 |
-1,896738 |
|
Z= |
1,177753 |
0,702539 |
-0,18749 |
-1,129581 |
0,881649 |
2,704617 |
В табл.6 приведено оптимальное нецелочисленное решение.
В табл.7 представлена расширенная задача со вторым дополнительным ограничением.
Таблица 6
Оптимальное нецелочисленное решение
|
БП |
1 |
— |
— |
— |
— |
— |
|
|
1,203704 |
0,185185 |
0,592593 |
1,09259 |
1,164074 |
-0,542779 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
= |
3 |
0 |
2,5 |
1,6 |
0 |
-2 |
|
= |
1,5 |
0 |
0,881832 |
1,186 |
0 |
0 |
|
= |
0,584844 |
-0,371563 |
0,311001 |
1,007782 |
0,664934 |
-1,911499 |
|
Z= |
1,838386 |
0,282829 |
0,16381 |
1,13837 |
1,632745 |
0,545424 |
Таблица 7
Расширенная задача со вторым дополнительным ограничением
|
БП |
1 |
— |
— |
— |
— |
— |
|
|
1,203704 |
0,185185 |
0,592593 |
1,09259 |
1,164074 |
-0,542779 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
= |
3 |
0 |
2,5 |
1,6 |
0 |
-2 |
|
= |
1,5 |
0 |
0,881832 |
1,186 |
0 |
0 |
|
= |
0,584844 |
-0,371563 |
0,311001 |
1,007782 |
0,664934 |
-1,911499 |
|
= |
-0,203704 |
-0,185185 |
-0,592593 |
-0,09259 |
-0,164074 |
0,542779 |
|
Z= |
1,838386 |
0,282829 |
0,16381 |
1,13837 |
1,632745 |
0,545424 |
В табл.8 приведена четвертая итерация. В табл.9 и табл.10 представлены расширенная задача и оптимальное целочисленное решение. Оптимальный целочисленный план = (табл. 10). Значение целевой функции Z=1.52728.
Результаты проведенных исследований позволили сделать следующие выводы.
Разработана целочисленная математическая модель оптимизации информационных систем, позволяющая сократить затраты и сроки проектирования информационных систем и повысить обоснованность принимаемых решений.
Найдено оптимальное решение целочисленной задачи оптимизации информационной системы методом Гомори.
Таблица 8
Четвертая итерация.
Отсечение дробной части переменной

|
БП |
1 |
— |
— |
— |
— |
— |
|
|
1 |
0 |
1 |
1 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
= |
2,14062 |
-0,781249 |
4,21875 |
1,20939 |
-0,692187 |
0,289847 |
|
= |
1,19687 |
-0,275572 |
1,48809 |
1,04822 |
-0,244157 |
0,807704 |
|
= |
0,477937 |
-0,468751 |
0,524814 |
0,959189 |
0,578826 |
-1,62664 |
|
= |
0,34375 |
0,312499 |
-1,6875 |
0,156246 |
0,276875 |
-0,915939 |
|
Z= |
1,78208 |
0,231638 |
0,276429 |
1,11278 |
1,58739 |
0,695464 |
Таблица 9
Расширенная задача с третьим дополнительным ограничением
|
БП |
1 |
— |
— |
— |
— |
— |
|
|
1 |
0 |
1 |
1 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
= |
2,14062 |
-0,781249 |
4,21875 |
1,20939 |
-0,692187 |
0,289847 |
|
= |
1,19687 |
-0,275572 |
1,48809 |
1,04822 |
-0,244157 |
0,807704 |
|
= |
0,477937 |
-0,468751 |
0,524814 |
0,959189 |
0,578826 |
-1,62664 |
|
= |
0,34375 |
0,312499 |
-1,6875 |
0,156246 |
0,276875 |
-0,915939 |
|
= |
-0,34375 |
-0,312499 |
0,68785 |
-0,156246 |
-0,276875 |
0,915939 |
|
Z= |
1,78208 |
0,231638 |
0,276429 |
1,11278 |
1,58739 |
0,695464 |
Таблица 10
Оптимальное целочисленное решение
|
БП |
1 |
— |
— |
— |
— |
— |
|
|
1 |
0 |
1 |
1 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
= |
3 |
-2,5 |
2,5 |
1,60001 |
0 |
-2 |
|
= |
1,5 |
-0,881833 |
0,88183 |
1,186 |
0 |
0 |
|
= |
0,993565 |
-1,50001 |
-0,506442 |
1,19356 |
0,994141 |
-3,00056 |
|
= |
0 |
1 |
-1 |
0 |
0 |
0 |
|
= |
1,1 |
-3,20001 |
-2,20001 |
0,499989 |
0,886003 |
-2,93101 |
|
Z= |
1,52727 |
0,741244 |
0,786034 |
0,996964 |
1,38216 |
1,3744 |
Литература:
Таха Х. А. Введение в исследование операций. 7-е издание.: Пер. с англ. М.: Издательский дом “Вильямс”, 2005–912 c.
Конюховский П. В. Математические методы исследования операций в экономике. — СПб.: Издательство «Питер», 2000. — 208 с.
Семахин А. М. Анализ математической модели информационной системы. В сб. материалов X Всероссийской научно-практической конференции с международным участием (25–26 ноября 2011 г.). — Томск: Изд-во Том.ун-та, 2011. — Ч.2–206 с.
moluch.ru
Методы отсечения. Метод Гомори — МегаЛекции
Лекция № 4 «ЦЕЛОЧИСЛЕННОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ»
Постановка задачи целочисленного программирования
По смыслу значительной части экономических задач, относящихся к задачам линейного программирования, компоненты решения должны выражаться в целых числах, т.е. быть целочисленными. К ним относятся, например, задачи, в которых переменные означают количество единиц неделимой продукции, число станков при загрузке оборудования, число судов при распределениях по линиям, число турбин в энергосистеме, число вычислительных машин в управляющем комплексе и многие другие.
Задача линейного целочисленного программирования формулируется следующим образом: найти такое решение (план) х = (х1, х2,…, хn), при котором линейная функция
(4.1)
принимает максимальное или минимальное значение при ограничениях
(4.2)
(4.3)
(4.4)
Следует отметить, что классическая транспортная задача и некоторые другие задачи транспортного типа «автоматически» обеспечивают решение задачи в целых числах (если, конечно, целочисленны параметры условий). Однако в общем случае условие целочисленности (4.4), добавляемое к обычным задачам линейного программирования, существенно усложняет ее решение.
Для решения задач линейного целочисленного программирования используется ряд методов. Самый простой из них — обычный метод линейного программирования. В случае если компоненты оптимального решения оказываются нецелочисленными, их округляют до ближайших целых чисел. Этот метод применяют тогда, когда отдельная единица совокупности составляет малую часть объема всей совокупности. В противном случае округление может привести к далекому от оптимального целочисленному решению, поэтому используют специально разработанные методы.
Методы целочисленной оптимизации можно разделить на три основные группы:
Þ методы отсечения;
Þ комбинаторные методы;
Þ приближенные методы.
Остановимся подробнее на методах отсечения.
Методы отсечения. Метод Гомори
Сущность методов отсечения состоит в том, что сначала задача решается без условия целочисленности. Если полученный план целочисленный, задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:
Ø оно должно быть линейным;
Ø должно отсекать найденный оптимальный нецелочисленный план;
Ø не должно отсекать ни одного целочисленного плана.
Дополнительное ограничение, обладающее указанными свойствами, называется правильным отсечением.
Далее задача решается с учетом нового ограничения. После этого в случае необходимости добавляется еще одно ограничение и т. д.
Если наложить требование целочисленности, то допустимое множество решений вырождается в систему точек и уже в общем случае не является выпуклым. Если добавить новые ограничения, связывающие внешние целочисленные точки,
а затем в качестве многоугольника (многогранника) решений использовать все выпуклое множество, то получим новую задачу линейного программирования со следующими свойствами:
Рис. 4.1
Ø новый многоугольник решений содержит все целые точки, заключавшиеся в первоначальном многоугольнике (многограннике) решений; любая угловая его точка является целой;
Ø так как линейная функция достигает оптимума в угловой точке многоугольника (многогранника) решений, то построением такого многоугольника и обеспечивается целочисленность оптимального решения.
Решение поставленной задачи ведем симплексным методом без учета требования целочисленности. Если оптимальный план целочисленный, то вычисления заканчивают; если же в оптимальном решении такой задачи хотя бы одна компонента не будет целым числом, то вводятся дополнительные ограничения и процесс решения продолжается.
Предположим, что, максимизируя (4.1) при условиях (4.2) и (4.3) без учета требования целочисленности переменных, мы пришли к оптимальному решению с предпочитаемым эквивалентом системы ограничений (4.2) вида:
(а)
Пусть правые части fj некоторых уравнений оказались дробными. Выберем одну из них, например f1. Каждый коэффициент e1j при неизвестной в соответствующем уравнении системы и свободный член f1 представим в виде суммы целой части и правильной неотрицательной дроби
(4.5)
помня, что целой частью любого числа называется наибольшее целое число, не превосходящее данного числа. Тогда соответствующее уравнение системы можно записать:
или (b)
где k=n+m
Левая часть этого равенства должна быть числом целым, так как мы требуем, чтобы все переменные принимали целые неотрицательные значения. Поэтому и правая часть должна быть целым числом и, очевидно, это число не больше, чем γ1. Но γ1 есть правильная не отрицательная дробь и, следовательно, правая часть не может превышать нуля:
(c)
откуда
(d)
Вычитая из левой части новую неотрицательную неизвестную xn + l заменим неравенство (d) уравнением:
или
(4.6)
где γ1,m+1, γ1,m+2, …, — коэффициенты, стоящие в первой строке оптимальной, но нецелочисленной таблицы, и под неизвестными xm + l, xm + 2,….
Это и есть дополнительное ограничение, которое следует ввести. Новая задача с (m + 1) уравнениями (4.2) и (4.6) является задачей дискретного программирования, так как «-хn + 1» совпадает с правой частью равенства (b). На данном этапе значение хn + 1 равно «- γ1» т. е. отрицательно и дробно. Мы добавляем к последней симплексной таблице еще одну строку, соответствующую уравнению (4.6). При этом относительные оценочные коэффициенты не изменяются, т. е. условие оптимальности сохраняется.
Возобновляя процесс преобразования симплексных таблиц, применим двойственный метод и переведем неизвестную хn + 1 из базисных в свободную. Возможно, что после этого получится базисное неотрицательное решение с целочисленными компонентами и задача решена. Если нет, то составляем следующее дополнительное ограничение, учитывающее целочисленность. Процесс присоединения дополнительных ограничений повторяют до тех пор, пока либо будет найден целочисленный оптимальный план, либо будет доказано, что задача не имеет целочисленных планов.
Если имеются несколько дробных fi то дополнительное ограничение (4.6) составляют для mахγ1. Это ускоряет процесс получения оптимального целочисленного решения.
4.3. Задача определения оптимального плана производства
Пусть предприятие для производства трех размерных наименований изделий использует три вида ресурсов в количестве 10, 11 и 13 ед. Затраты каждого из перечисленных трех видов ресурсов на изготовление одного изделия 1-го, 2-го или 3-го видов и прибыль от реализации одного изделия каждого из видов отражены в табл. 4.1.
Таблица 4.1
| Объем ресурсов | Затраты на одно изделие | ||
| l-го вида | 2- го вида | 3-го вида | |
| Прибыль в усл. ед. |
Предполагая, что предприятие может выпускать изделия разных наименований в любых соотношениях, найти план производства, обеспечивающий максимальную рентабельность.
Если обозначить через хl, х2 и х3 ед. количество изделий, которые должно выпускать предприятие для обеспечения максимальной рентабельности, то имеем задачу целочисленного программирования.
Максимизировать линейную функцию
(e)
при ограничениях
(f)
Соответственно соотношениям (e) и (f) записываем систему уравнений:
(g)
Строим симплексную таблицу 4.2. Произведя три шага симплексных преобразований, получаем табл. 4.3 – 4.5.
Таблица 4.2
| № 1 | cj | c0 | ||||
| ci | СП БП | ai0 | х1 | х2 | х3 | aio/aij* |
| х4 | ||||||
| х5 | ||||||
| х6 | ||||||
| - | z=Δ | -4 | -5 | -1 | - |
Таблица 4.3
Таблица 4.4
Таблица 4.5
Табл. 4.5 дает оптимальное, но нецелочисленное решение
х=( , , , 0, 0, 0) и max z(x)=
Для отыскания целочисленного решения нужно ввести дополнительное ограничение (4.6).
Из соотношений (4.5):
Так как mах γi = mах ( ), тогда дополнительное ограничение (4.6) строим для х1-строки табл. 4.5.
Находим
Тогда γ11=γ14, γ12=γ15, γ13=γ16 и дополнительное ограничение имеет вид:
-γ14 х4 — γ15 х5 — γ16 х6 + х7 = — γ1 или
(h)
Вводя уравнение (h) как новую строку в табл. 4.5, получим табл. 4.6 и, совершая симплексное преобразование с разрешающим элементом « » (освобождаемся от отрицательного элемента в 1-столбце), придем к табл. 4.7.
Таблица 4.6
Таблица 4.7
Из табл. 4.7 получаем оптимальное целочисленное решение хопт=(2; 2; 1; 0; 1; 0; 0) и max z = 19.
Следовательно, максимальная прибыль в 19 усл. ед. будет достигнута при производстве двух ед. изделий l-го вида, двух ед. изделий 2-го вида и одной ед. изделий 3-го вида.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru

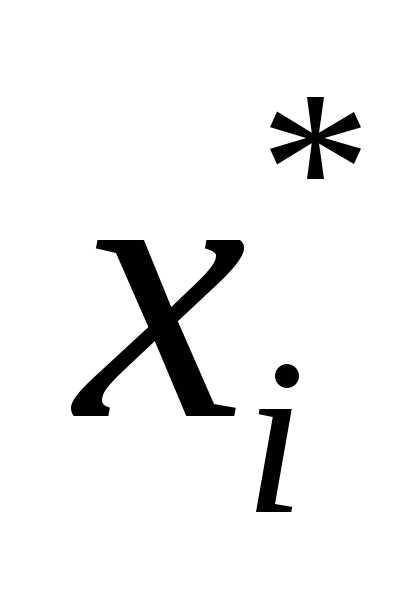 ,
то к ограничениям задачи добавляется
новое ограничение, обладающее следующими
свойствами:
,
то к ограничениям задачи добавляется
новое ограничение, обладающее следующими
свойствами: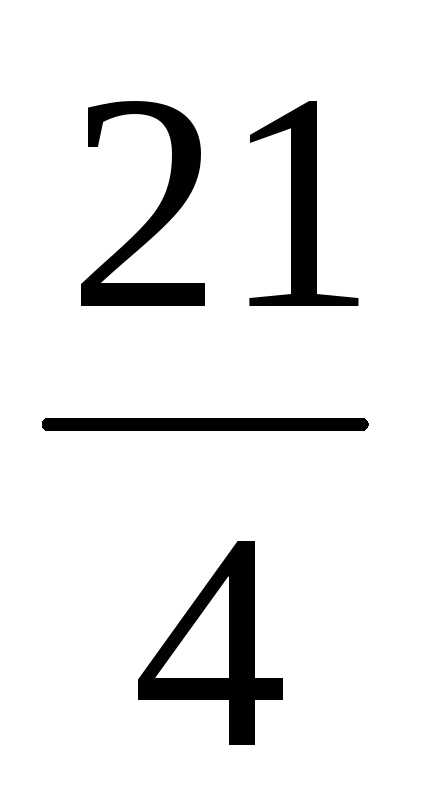
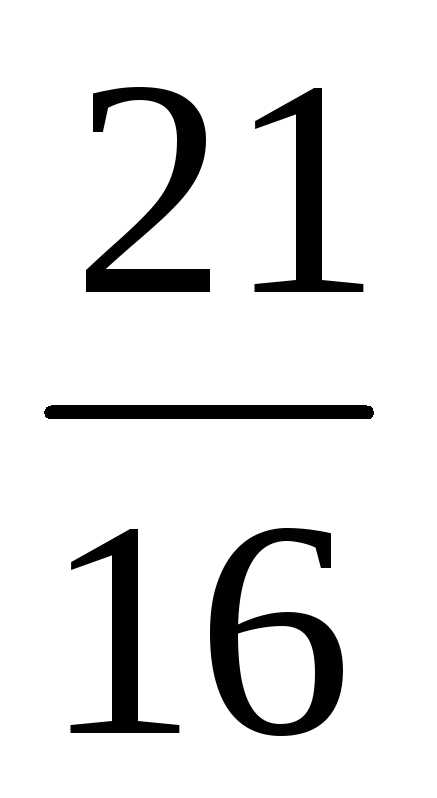
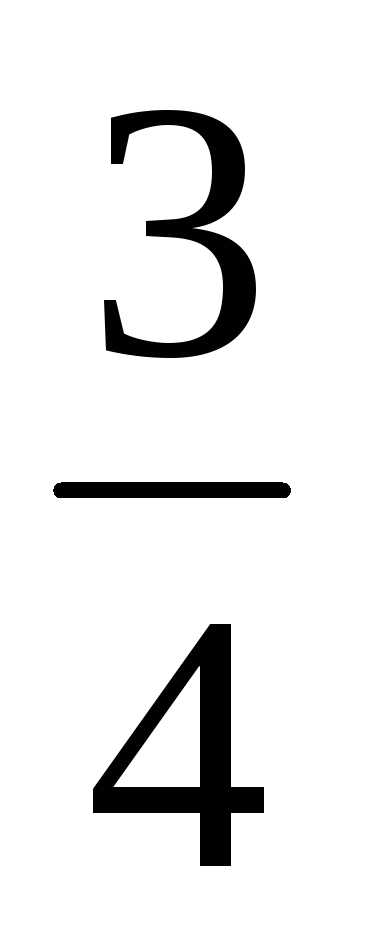

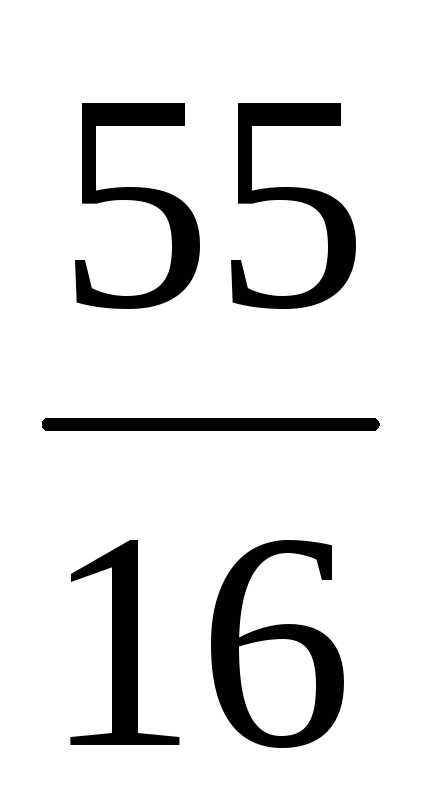
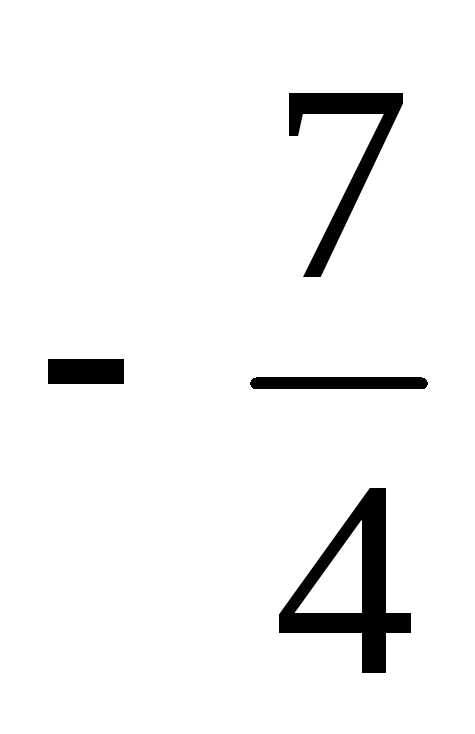
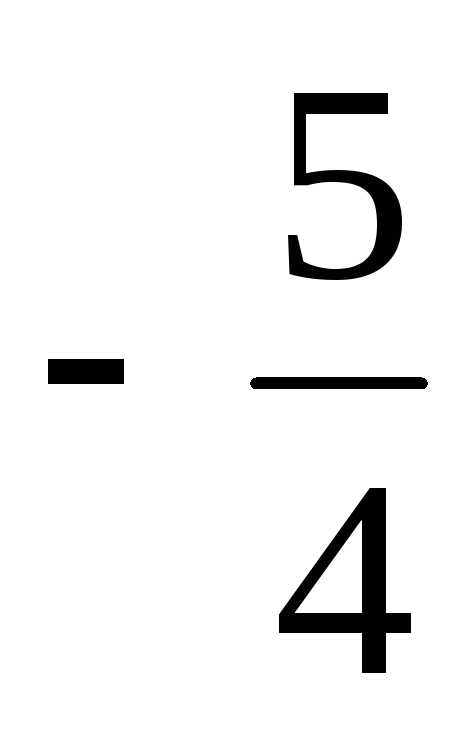

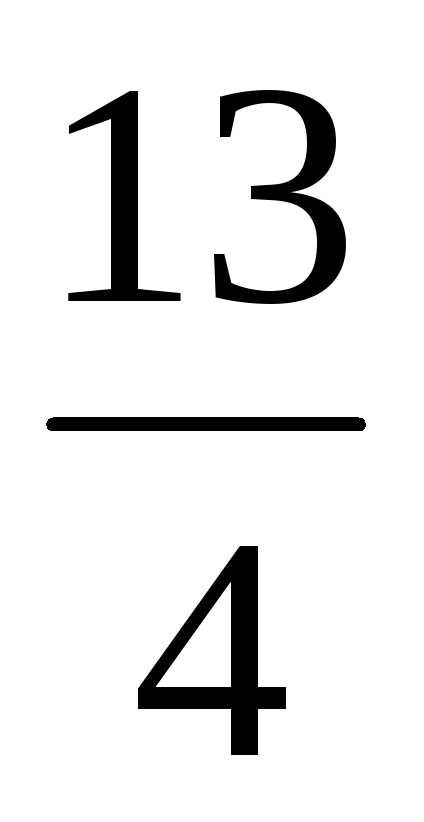
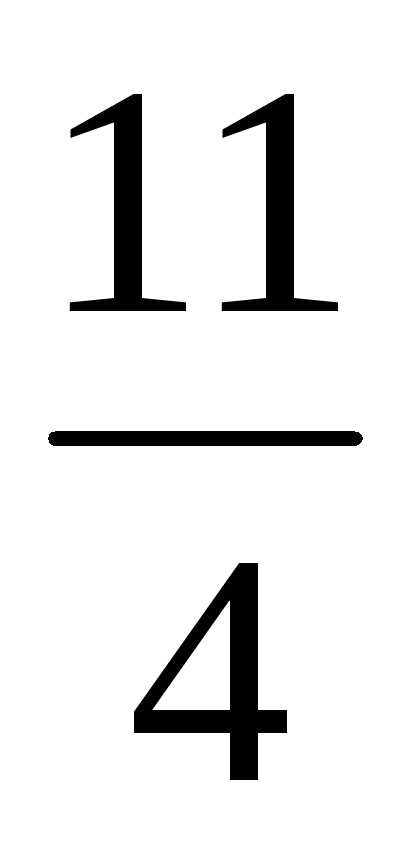
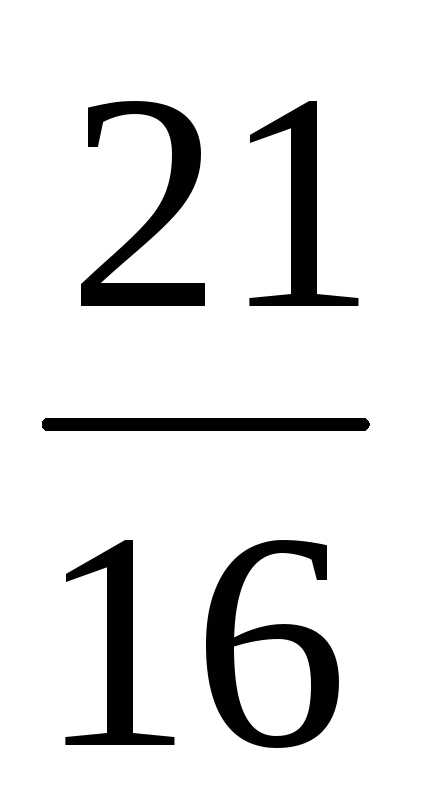
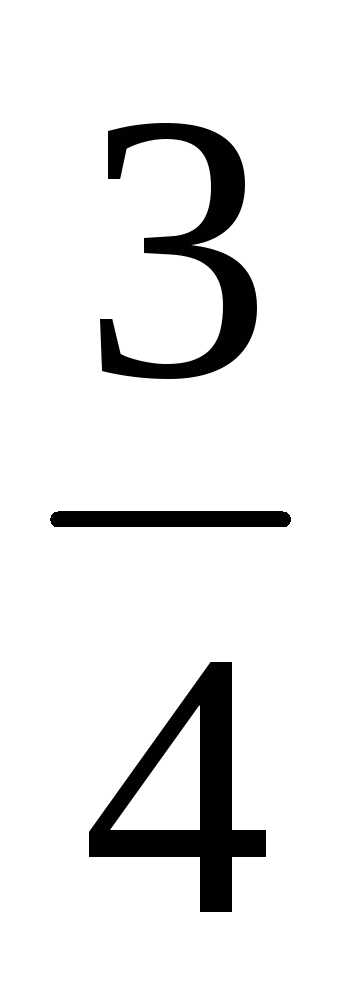
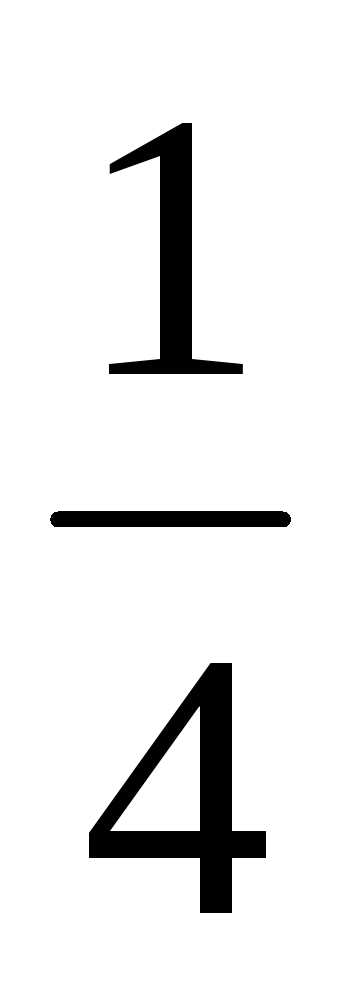

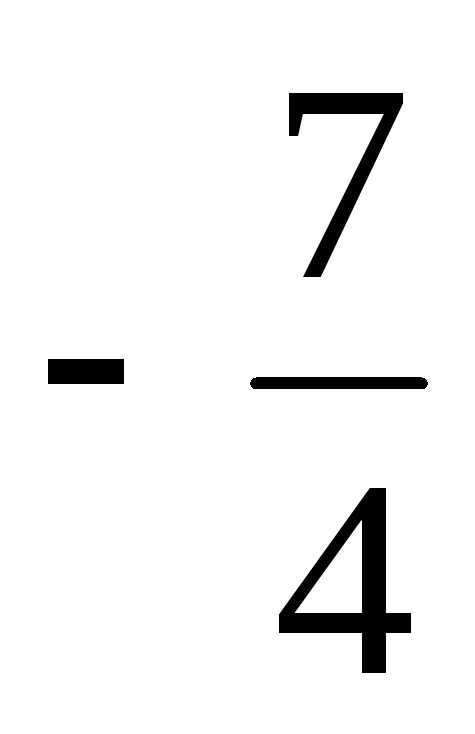
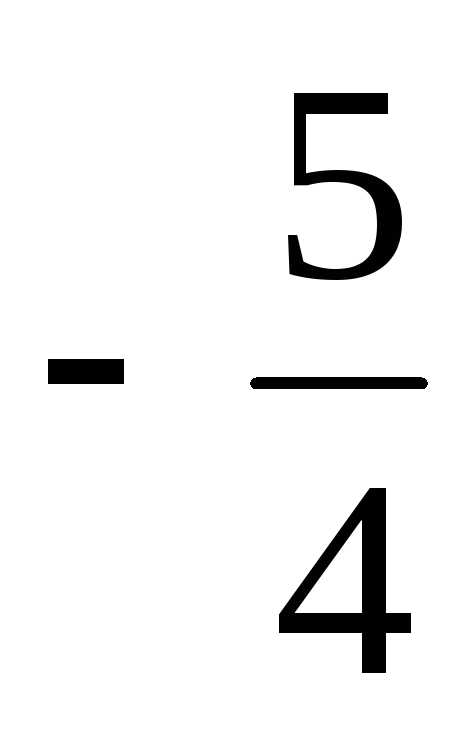
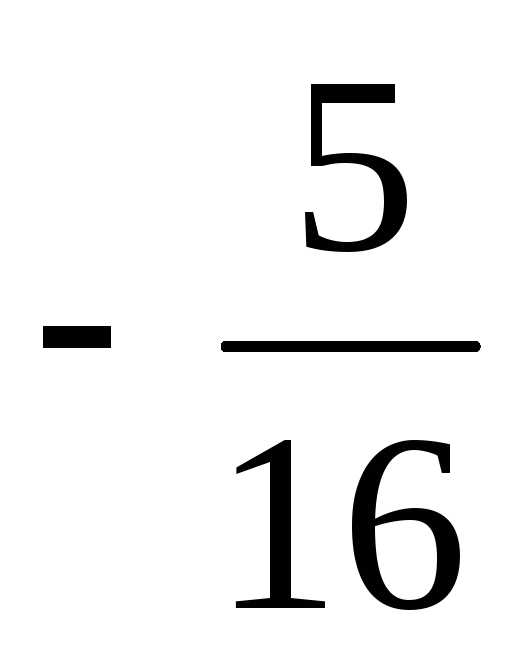
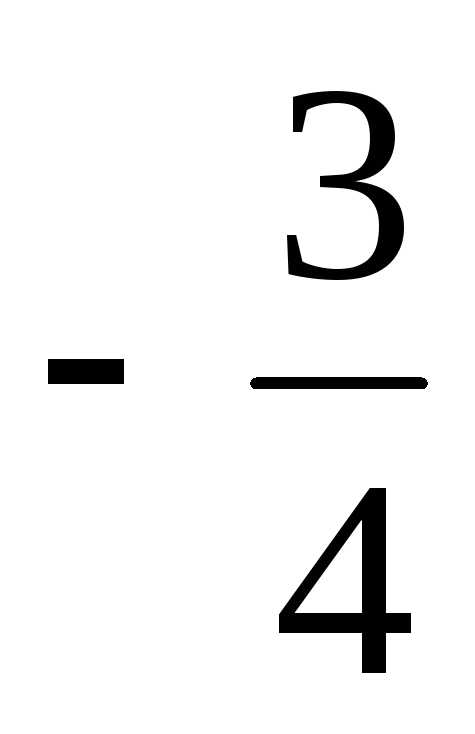
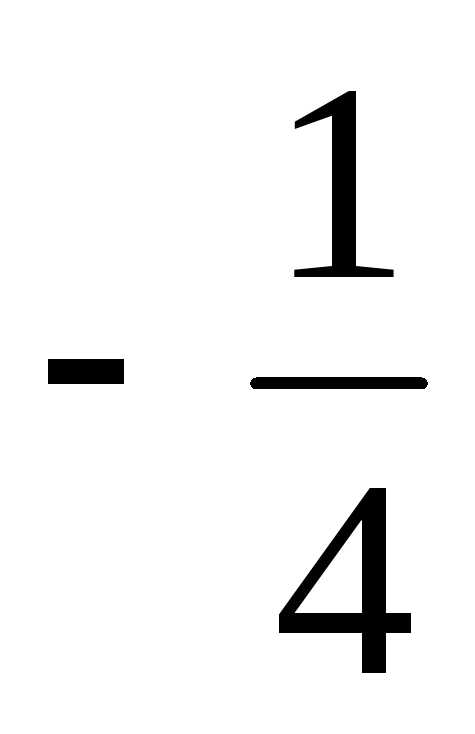

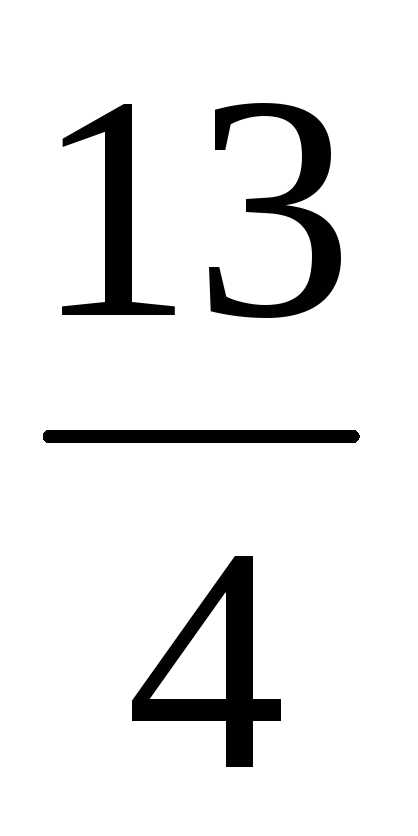
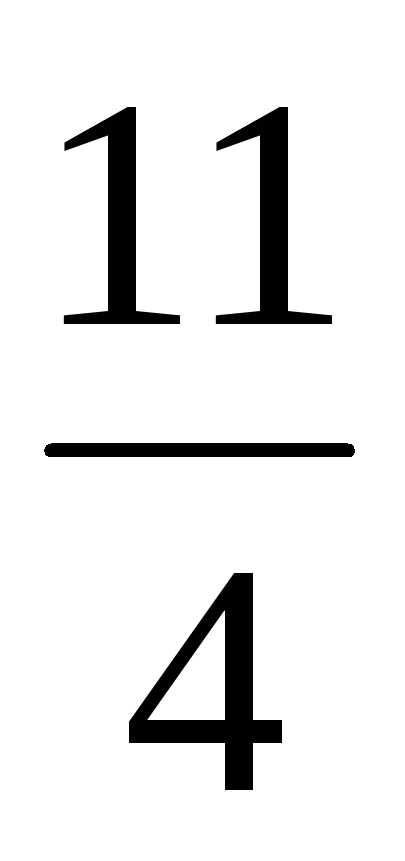

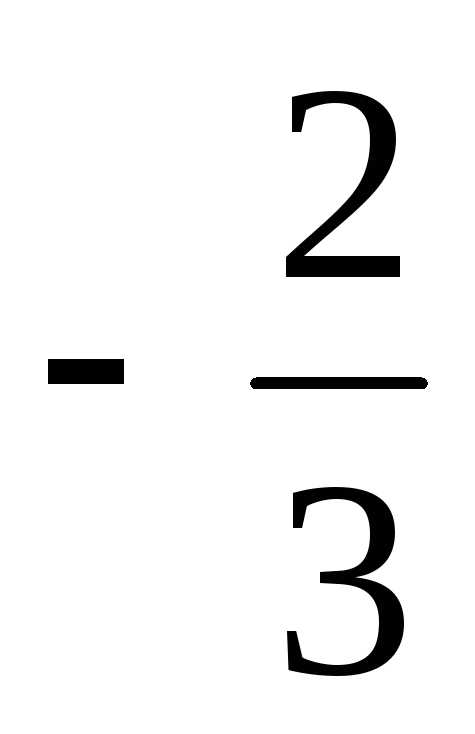
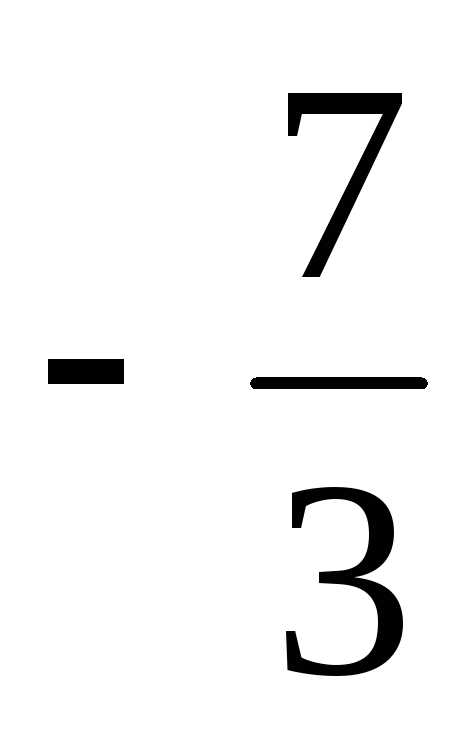
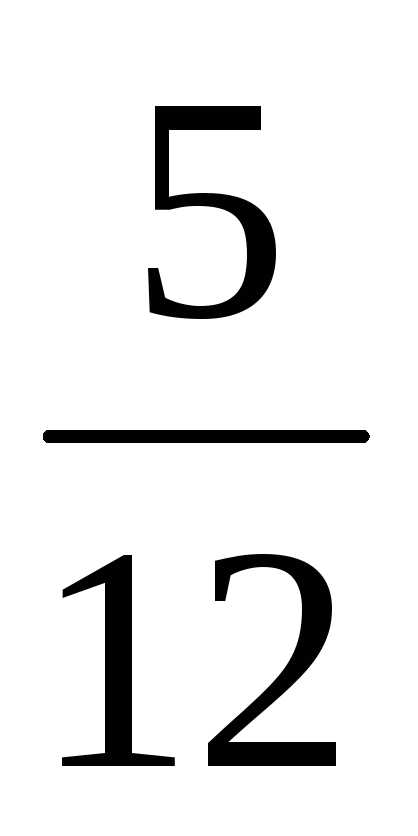
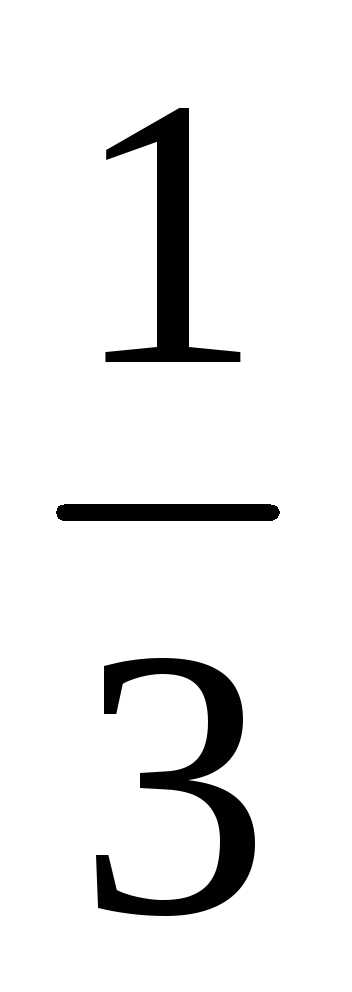
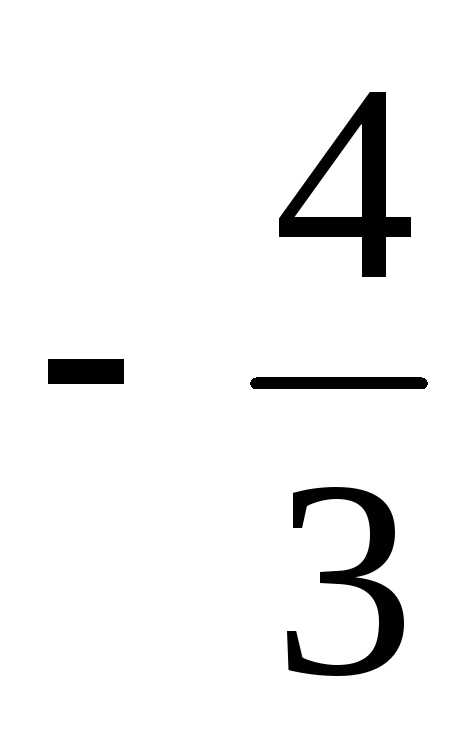
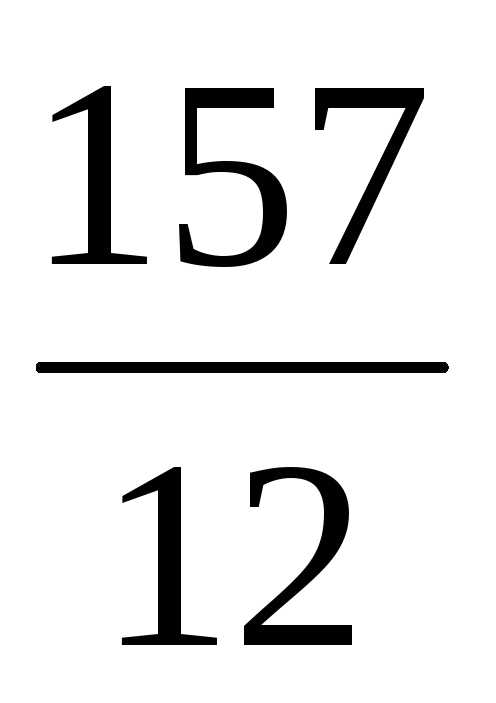

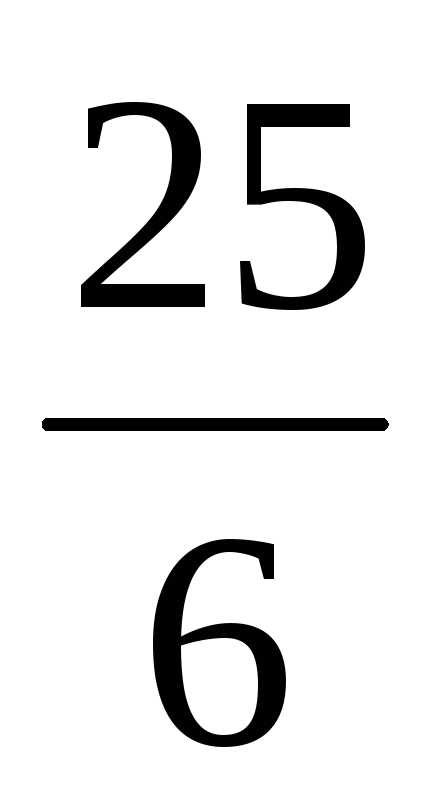
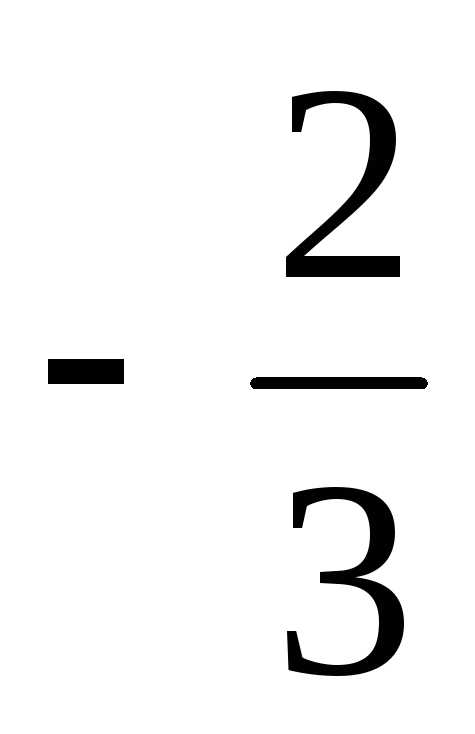

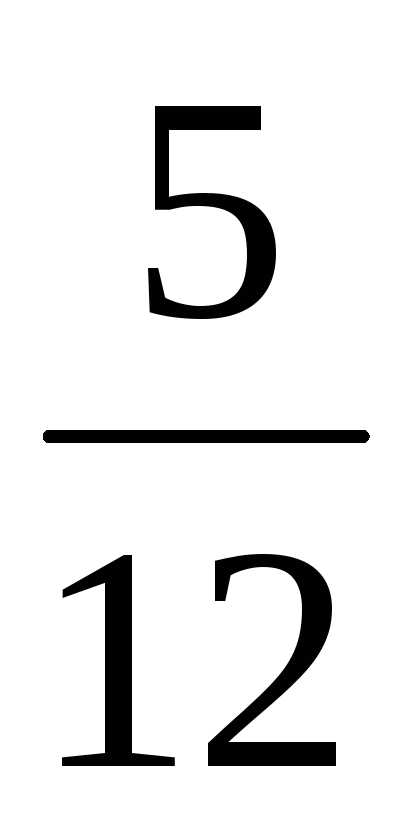

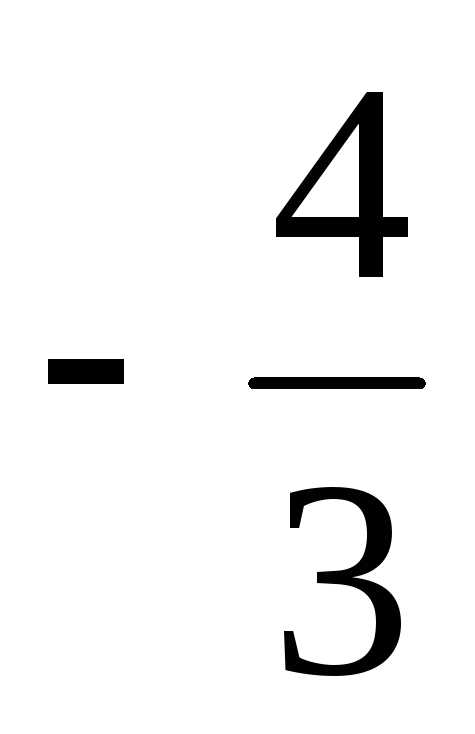
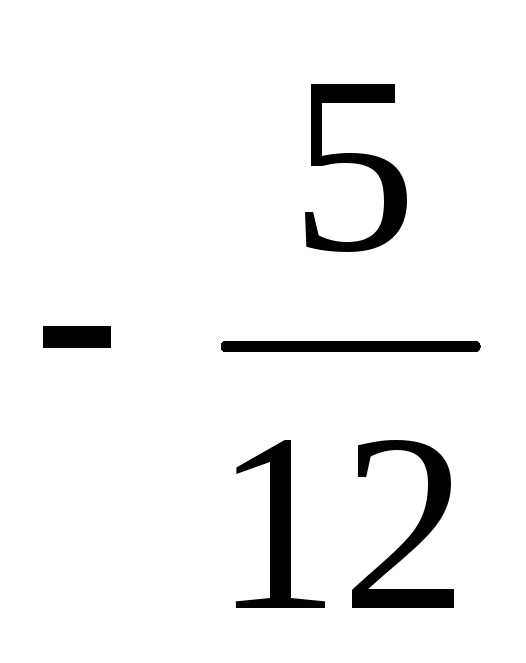
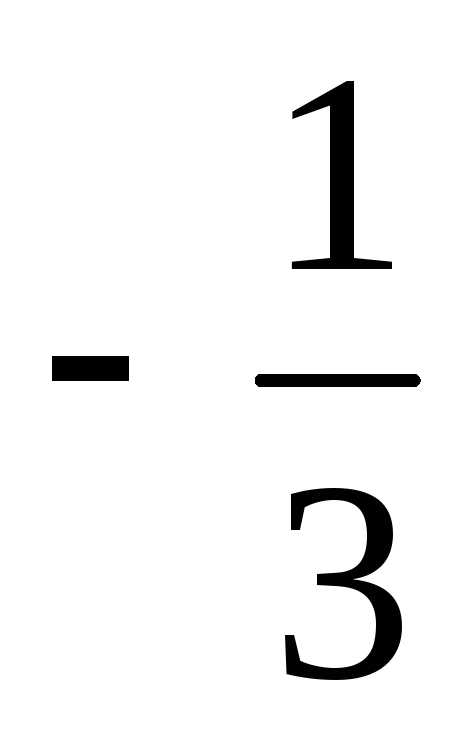

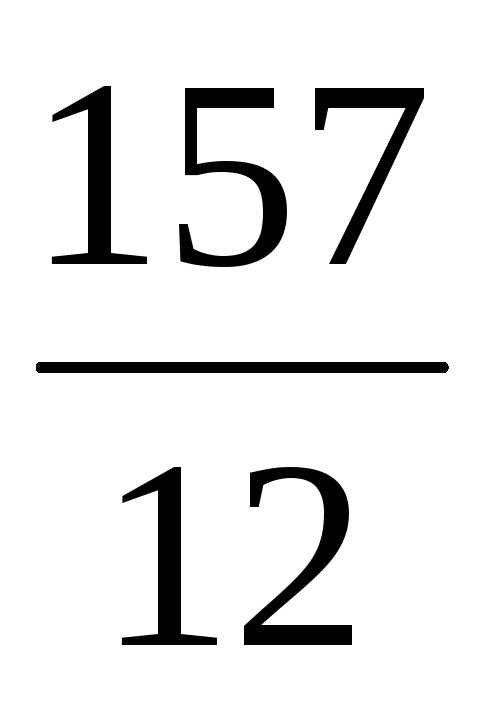
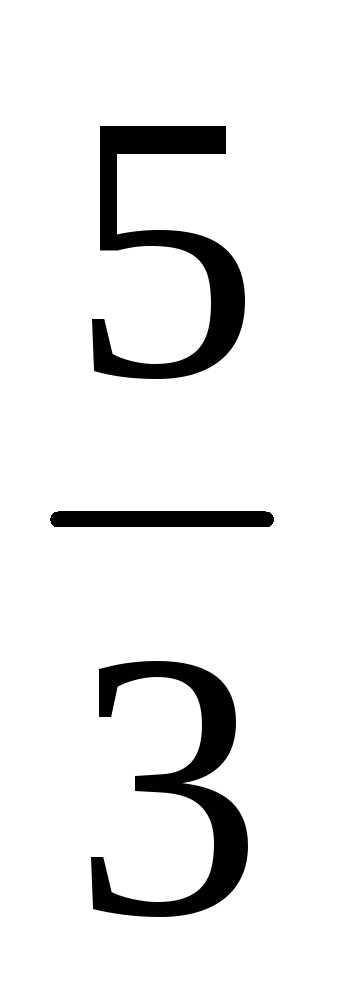
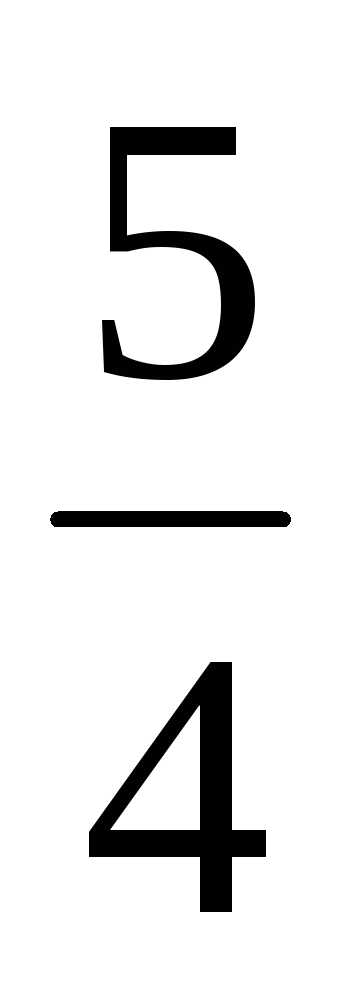

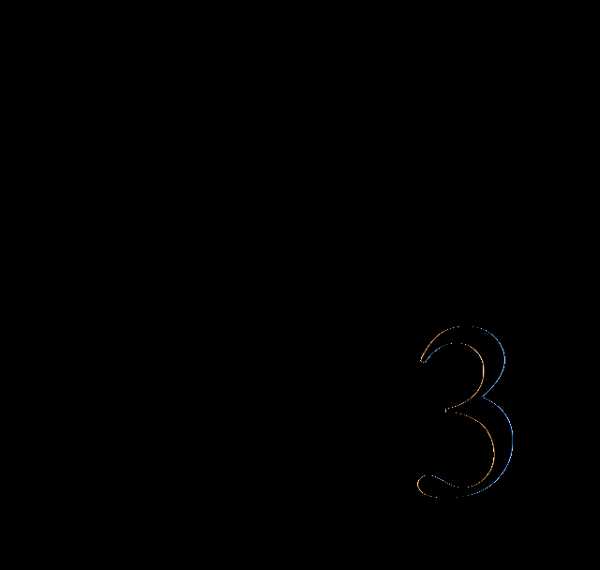
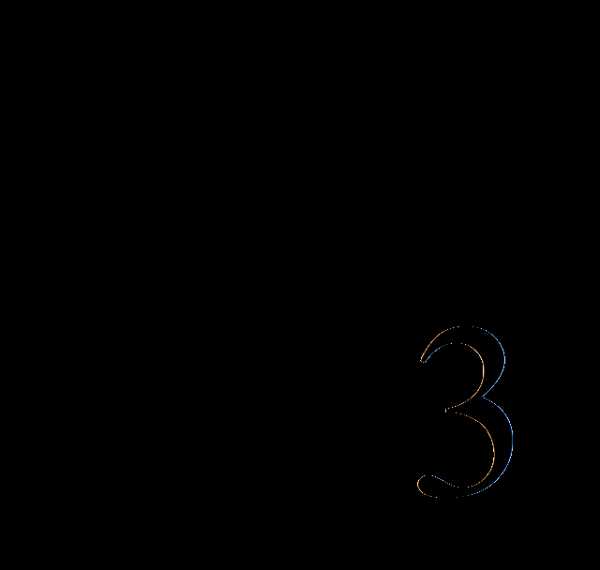
 =
=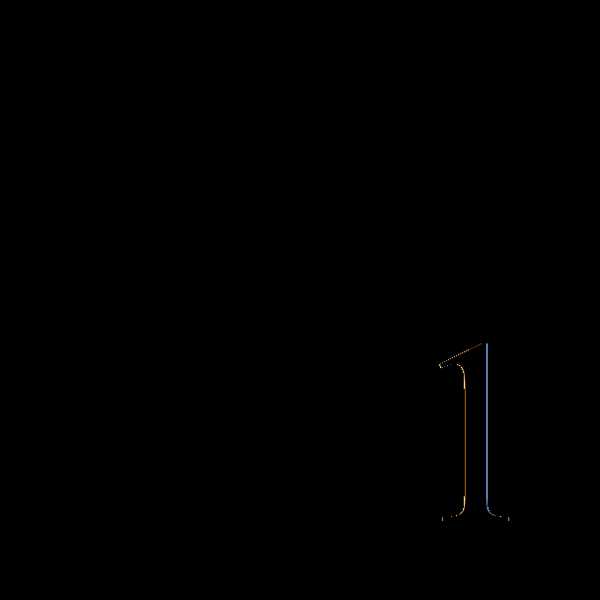 =
= =
= =
=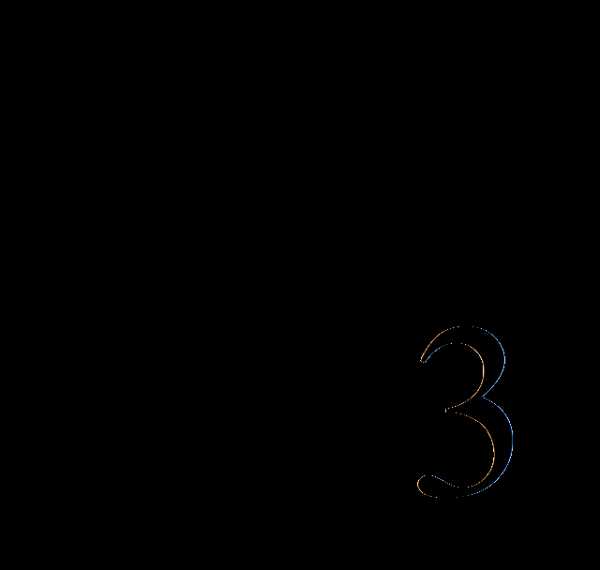 =
=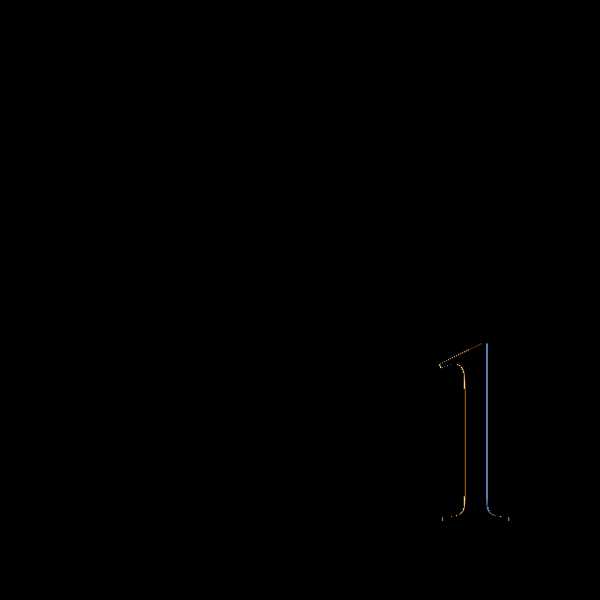 =
=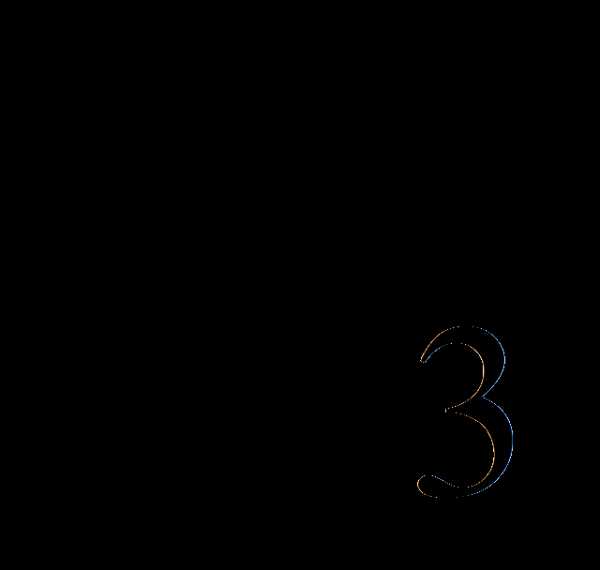 =
=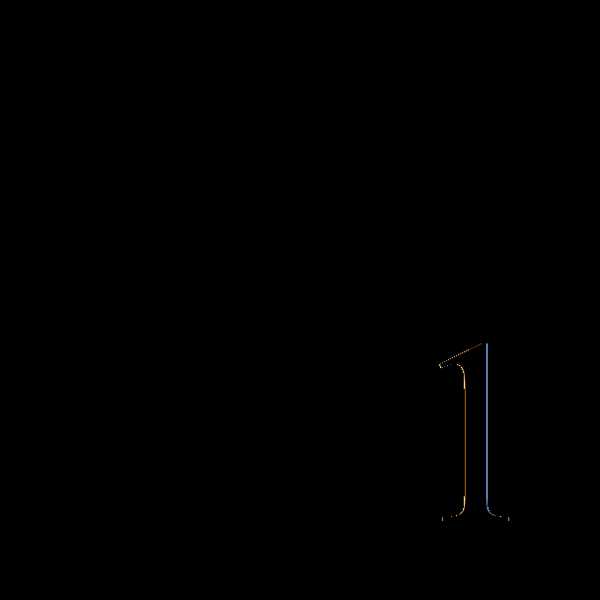 =
= =
=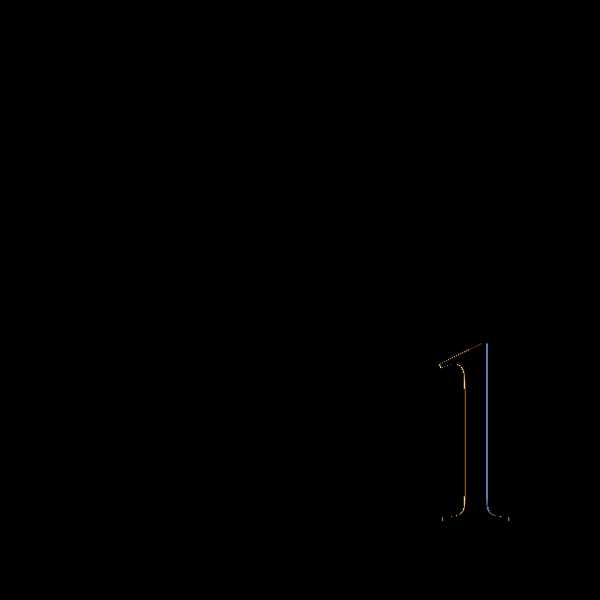 =
= =
= =
=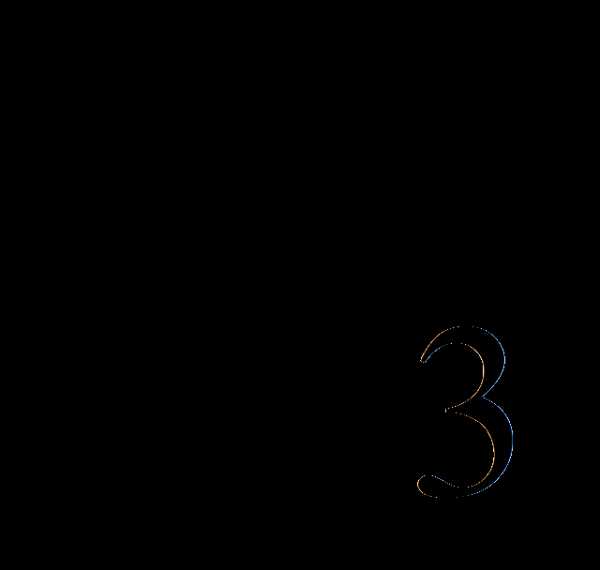 =
= =
=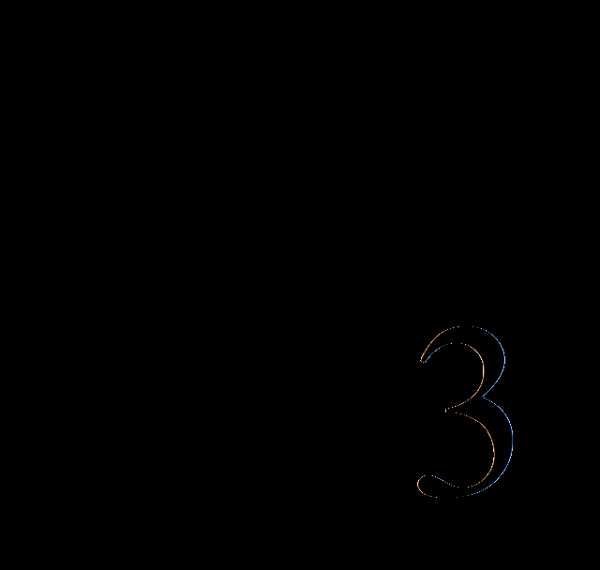 =
=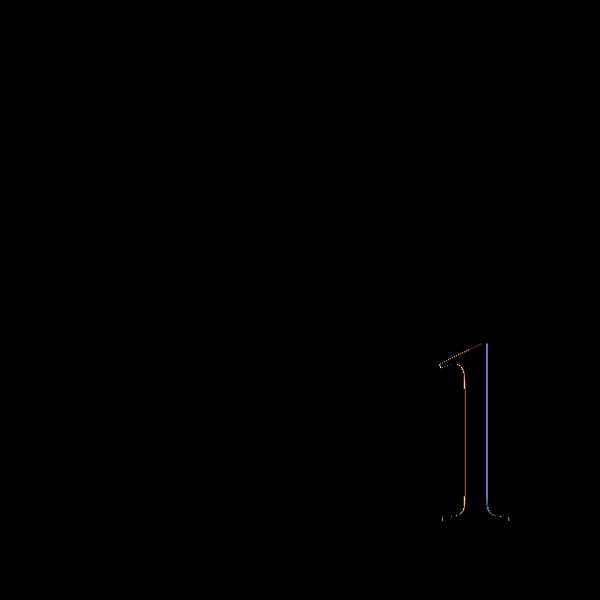 =
=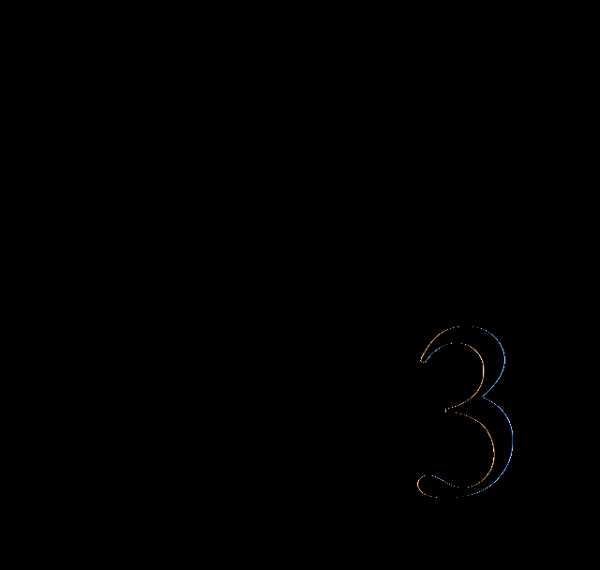 =
=