Метод Крамера
Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.
Теорема 1
Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений: $x_i = \frac{D_i}{D}$
В чем заключается метод Крамера
Суть метода Крамера в следующем:
- Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
- Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
- Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ — номер крайнего справа столбца.
- После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.
Приёмы для вычисления определителя матрицы
Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:
- Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей — со знаком минус.
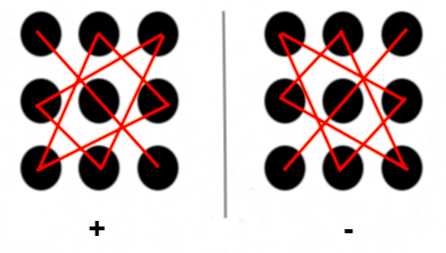
Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера
- С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
- При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.
Решение систем уравнений методом Крамера
Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:
$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$
Отобразим её в расширенной форме для удобства:
$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$
Найдём определитель основной матрицы, также называемый главным определителем системы:
$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$
Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:
$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$
$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$
Теперь найдём неизвестные $x_1$ и $x_2$:
$x_1 = \frac {D_1}{D}$
$x_2 = \frac {D_2}{D}$
Пример 1
Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.
Решите систему уравнений:
$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 — x_3 = 10 \\ \end{cases}$
Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:
$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 3 = — 12 – 8 -12 -32 – 6 + 6 = — 64$
А теперь три других детерминанта:
$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 21 = — 84 – 40 – 36 – 160 – 18 + 42 = — 296$
$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = — 27 + 120 + 84 – 72 + 63 – 60 = 108$
$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 — (-2) \cdot 3 \cdot 10 — (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = — 60$
Найдём искомые величины:
$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$
$x_2 = \frac{D_1} {D} = \frac{108} {-64} = — 1 \frac {11} {16}$
$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$
spravochnick.ru
Как решать систему методом крамера
Автор КакПросто!
Решение системы линейных уравнений второго порядка можно найти методом Крамера. Данный метод основан на вычислении определителей матриц заданной системы. Поочередно вычисляя главный и вспомогательные детерминанты, можно заранее сказать, имеет ли система решение или она является несовместной. При нахождении вспомогательных определителей, элементы матрицы поочередно заменяются ее свободными членами. Решение системы находится простым делением найденных детерминантов.
Статьи по теме:
Инструкция
Запишите заданную систему уравнений. Составьте ее матрицу. При этом первый коэффициент первого уравнения соответствует начальному элементу первой строки матрицы. Коэффициенты из второго уравнения составляют вторую строку матрицы. Свободные члены записываются в отдельный столбец. Заполните таким образом все строки и столбцы матрицы.
Вычислите главный определитель матрицы. Для этого найдите произведения элементов, расположенных по диагоналям матрицы. Сначала умножьте все элементы первой диагонали, расположенной от левого верхнего до нижнего правого элемента матрицы. Потом вычислите так же вторую диагональ. От первого произведения отнимите второе. Результат вычитания и будет главным определителем системы. Если главный детерминант не равен нулю, значит система имеет решение.Затем найдите вспомогательные определители матрицы. Сначала вычислите первый вспомогательный определитель. Для этого замените первый столбец матрицы столбцом свободных членов решаемой системы уравнения. После этого определите детерминант полученной матрицы по аналогичному алгоритму, как описано выше.
Подставьте вместо элементов второго столбца исходной матрицы свободные члены. Вычислите второй вспомогательный определитель. Всего количество данных детерминантов должно быть равно числу неизвестных переменных в системе уравнений. Если все полученные детерминанты системы равны нулю, считается, что система имеет множество неопределяемых решений. Если нулю равен лишь главный определитель – система несовместима и корней у нее нет.
Найдите решение системы линейных уравнений. Первый корень вычисляется, как частное от деления первого вспомогательного определителя на главный детерминант. Запишите выражение и посчитайте его результат. Второе решение системы вычислите так же, поделив второй вспомогательный определитель на главный детерминант. Запишите полученные результаты.
Видео по теме
Совет полезен?
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Метод Крамера — вывод формул — Мегаобучалка
Метод Крамера.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля. В этой статье мы разберем как по методу Крамера находятся неизвестные переменные и получим формулы. После этого перейдем к примерам и подробно опишем решение систем линейных алгебраических уравнений методом Крамера.
При изучении материала Вам может быть полезна статья вычисление определителя матрицы, свойства определителя.
Навигация по странице.
- Метод Крамера — вывод формул.
- Алгоритм решения систем линейных алгебраических уравнений методом Крамера.
- Примеры решения систем линейных алгебраических уравнений методом Крамера.
Метод Крамера — вывод формул.
Пусть нам требуется решить систему линейных уравнений вида
где x1, x2, …, xn – неизвестные переменные, ai j , i = 1, 2, …, n, j = 1, 2, …, n – числовые коэффициенты, b1, b2, …, bn — свободные члены. Решением СЛАУ называется такой набор значений x1, x2, …, xn при которых все уравнения системы обращаются в тождества.
В матричном виде эта система может быть записана как A ⋅ X = B, где — основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных, — матрица – столбец свободных членов, а — матрица – столбец неизвестных переменных. После нахождения неизвестных переменных x1, x2, …, xn, матрица становится решением системы уравнений и равенство A ⋅ X = B обращается в тождество .
Будем считать, что матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера. (Методы решения систем при разобраны в разделе решение систем линейных алгебраических уравнений).
Метод Крамера основывается на двух свойствах определителя матрицы:
1. Определитель квадратной матрицы равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:
2. Сумма произведений элементов какой-либо строки (столбца) квадратной матрицы на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю:
Итак, приступим к нахождению неизвестной переменной x1. Для этого умножим обе части первого уравнения системы на А1 1 , обе части второго уравнения – на А2 1 , и так далее, обе части n-ого уравнения – на Аn 1 (то есть, уравнения системы умножаем на соответствующие алгебраические дополнения первого столбца матрицы А):
Сложим все левые части уравнения системы, сгруппировав слагаемые при неизвестных переменных x1, x2, …, xn, и приравняем эту сумму к сумме всех правых частей уравнений:
Если обратиться к озвученным ранее свойствам определителя, то имеем
и предыдущее равенство примет вид
откуда
Аналогично находим x2. Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А:
Складываем все уравнения системы, группируем слагаемые при неизвестных переменных x1, x2, …, xn и применяем свойства определителя:
Откуда
.
Аналогично находятся оставшиеся неизвестные переменные.
Если обозначить
то получаем формулы для нахождения неизвестных переменных по методу Крамера .
Замечание.
Если система линейных алгебраических уравнений однородная, то есть , то она имеет лишь тривиальное решение (при ). Действительно, при нулевых свободных членах все определители будут равны нулю, так как будут содержать столбец нулевых элементов. Следовательно, формулы дадут .
К началу страницы
megaobuchalka.ru
Решение линейных уравнений методом Крамера: правило и примеры.
Правило крамера.
Среди способов решения линейных уравнений — не только методика Гаусса и метод обратной матрицы, но и правило Крамера. Метод основан на работе с определителями и позволяет легко решить систему уравнений.
Следует отметить, что метод Крамера подходит только для тех ситуаций, когда определитель не равен нулю. В ином случае придется использовать метод Гаусса.
Итак, как же решается система линейных уравнений по методу Крамера?
Решение линейных уравнений по Крамеру.
Пример решения системы линейных уравнений методом Крамера.
Разберем на примере.
Первый этап работы — это вычислить главный определитель системы, в нашем случае:
Как уже было сказано, если определитель системы равен нулю, то метод Крамера не подходит для работы, поскольку выходит, что система или не имеет решений, или имеет бесконечное множество их. В таком случае используется метод Гаусса.
Если же определитель больше или меньше нуля, то методом Крамера мы можем вычислить единственное верное решение. Для этого необходимо найти еще два определителя системы:
Теперь остается лишь найти корни уравнения, а они рассчитываются по следующим формулам:
Рассмотрим еще один пример. Возьмем систему линейных уравнений:
Метод Крамера – наиболее удобный метод как раз для работы со сложными уравнениями, включающими в себя десятичные дроби. Иные методы оказываются сложнее, да и в вычислениях можно просто запутаться. Здесь же все довольно просто. Находим главный определитель:
Определитель не равен нулю, следовательно, система имеет решение, и мы можем найти его методом Крамера.
Таким образом, получаем, что а = — 0,35, в = 37,77. Система линейных уравнений полностью решена, можно записывать ответ.
Похожие статьи
infoogle.ru
Метод Крамера и его применение
Метод Крамера – это один из точных методов решения систем линейных алгебраических уравнений (СЛАУ). Точность его обусловлена использованием определителей матрицы системы, а также некоторыми ограничениями, накладываемыми в ходе доказательства теоремы.
Системой линейных алгебраических уравнений с коэффициентами, принадлежащими, например, множеству R – действительных чисел, от неизвестных x1, x2 ,…, xn называют набор выражений вида
ai2 x1+ai2 x2 +… ain xn =bi при i=1, 2, … ,m, (1)
где aij, bi – действительные числа. Каждое из этих выражений называется линейным уравнением, aij – коэффициентами при неизвестных, bi – свободными коэффициентами уравнений.
Решением системы (1) называют n-мерный вектор x° = (x1°, x2°,…, xn°), при подстановке которого в систему вместо неизвестных x1, x2 ,…, xn каждая из строк в системе становится верным равенством.
Система называется совместной, если у нее есть хотя бы одно решение, и несовместной, если ее множество решений совпадает с пустым множеством.
Необходимо помнить, что для того, чтобы найти решение систем линейных алгебраических уравнений, используя метод Крамера, матрицы систем должны быть квадратными, что по сути означает одинаковое количество неизвестных и уравнений в системе.
Итак, чтобы использовать метод Крамера, необходимо как минимум знать, что такое матрица систем линейных алгебраических уравнений и как она выписывается. А во-вторых, понимать, что называют определителем матрицы и владеть навыками его вычисления.
Предположим, что этими знаниями вы владеете. Замечательно! Тогда вам остается всего лишь запомнить формулы, определяющие метод Крамера. Для упрощения запоминания воспользуемся следующими обозначениями:
Det – главный определитель матрицы системы;
deti – это определитель матрицы, полученной из основной матрицы системы, если заменить i-й столбец матрицы на вектор-столбец, элементами которого являются правые части систем линейных алгебраических уравнений;
n – количество неизвестных и уравнений в системе.
Тогда правило Крамера вычисления i-й компоненты xi (i=1,..n) n-мерного вектора x можно записать в виде
xi = deti/ Det, (2).
При этом Det строго отличен от нуля.
Единственность решения системы при ее совместности обеспечивает условие неравенства нулю главного определителя системы. В противном случае, если сумма (xi), возведенных в квадрат, строго положительна, то СЛАУ с квадратной матрицей будет несовместной. Это может произойти, в частности, когда, по крайней мере, один из deti отличен от нуля.
Пример 1. Решить трехмерную систему ЛАУ, используя формулы Крамера.
x1 + 2 x2 + 4 x3 = 31,
5 x1 + x2 + 2 x3 = 29,
3 x1 – x2 + x3 =10.
Решение. Выпишем матрицу системы построчно, где Ai – это i -я строка матрицы.
A1=(1 2 4), A2=(5 1 2), A3=(3 –1 1).
Столбец свободных коэффициентов b=(31 29 10).
Главный определитель Det системы равен
Det= a11 a22 a33 + a12 a23 a31 + a31 a21 a32 – a13 a22 a31 – a11 a32 a23 – a33 a21 a12 = 1 – 20 + 12 – 12 + 2 – 10 = –27.
Для вычисления det1 используем подстановку a11= b1, a21 = b2, a31 = b3. Тогда
det1= b1 a22 a33 + a12 a23 b3 + a31 b2 a32 – a13 a22 b3 – b1 a32 a23 – a33 b2 a12 =…= –81.
Аналогично, для вычисления det2 используем подстановку a12= b1, a22 = b2, a32 = b3 и, соответственно, для вычисления det3 – a13= b1, a23 = b2, a33 = b3.
Тогда можете проверить, что det2 = –108, а det3 = – 135.
Согласно формулам Крамера находим x1 = -81/(-27) = 3, x2 = -108/(-27) = 4, x3 = -135/(-27) = 5.
Ответ: x°=(3,4,5).
Опираясь на условия применимости данного правила, метод Крамера решения систем линейных уравнений можно использовать опосредованно, например, с целью исследовать систему на возможное число решений в зависимости от величины некоторого параметра k.
Пример 2. Определить, при каких значениях параметра k неравенство |kx – y – 4|+|x + ky + 4|<=0 имеет ровно одно решение.
Решение.
Данное неравенство в силу определения модуля функции может быть выполнено, только если оба выражения одновременно равны нулю. Поэтому эта задача сводится к нахождению решения линейной системы алгебраических уравнений
kx – y = 4,
x + ky = –4.
Решение данной системы единственное, если ее главный определитель
Det = k^{2} + 1 отличен от нуля. Очевидно, что это условие выполняется для всех действительных значений параметра k.
Ответ: для всех действительных значений параметра k.
К задачам данного вида также могут быть сведены многие практические задачи из области математики, физики или химии.
fb.ru
Метод Крамера — Циклопедия
Видеоурок «Метод определителей (Крамера)» // Математика от alwebra.com.ua [4:20]Метод Крамера — это способ решения системы линейных уравнений, при котором неизвестные вычисляются в виде отношений определителей.
[править] Описание метода
Суть метода Крамера состоит в расчёте определителей и применении формул Крамера, по которым решение xi равно отношению i-го вспомогательного определителя Δi к главному Δ.
Для решения методом Крамера системы линейных уравнений вида Ax=b (где A – квадратная матрица nxn коэффициентов системы, а b – вектор свободных членов системы), сначала найдём главный определитель системы Δ. Метод Крамера применим, если главный определитель системы Δ≠0.
[править] Решение системы двух уравнений с двумя неизвестными
[править] Решение системы трёх уравнений с тремя неизвестными
[править] Решение системы четырёх уравнений с четырьмя неизвестными
[править] Методы решения систем уравнений:
[править] Численные методы:
- Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Наука, 1970.
- Участник:Logic-samara
cyclowiki.org
Метод Крамера
Метод Крамера.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля. В этой статье мы разберем как по методу Крамера находятся неизвестные переменные и получим формулы. После этого перейдем к примерам и подробно опишем решение систем линейных алгебраических уравнений методом Крамера.
При изучении материала Вам может быть полезна статья вычисление определителя матрицы, свойства определителя.
Навигация по странице.
Метод Крамера — вывод формул.
Алгоритм решения систем линейных алгебраических уравнений методом Крамера.
Примеры решения систем линейных алгебраических уравнений методом Крамера.
Метод Крамера — вывод формул.
Пусть нам требуется решить систему линейных уравнений вида гдеx1, x2, …, xn – неизвестные переменные, ai j , i = 1, 2, …, n, j = 1, 2, …, n – числовые коэффициенты, b1, b2, …, bn — свободные члены. Решением СЛАУ называется такой набор значений x1, x2, …, xn при которых все уравнения системы обращаются в тождества.
В матричном виде эта система может быть записана как A ⋅ X = B, где — основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных,- матрица – столбец свободных членов, а- матрица – столбец неизвестных переменных. После нахождения неизвестных переменныхx1, x2, …, xn, матрица становится решением системы уравнений и равенствоA ⋅ X = B обращается в тождество .
Будем считать, что матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера. (Методы решения систем при разобраны в разделерешение систем линейных алгебраических уравнений).
Метод Крамера основывается на двух свойствах определителя матрицы:
Определитель квадратной матрицы равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:
Сумма произведений элементов какой-либо строки (столбца) квадратной матрицы на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю:
Итак, приступим к нахождению неизвестной переменной x1. Для этого умножим обе части первого уравнения системы на А1 1 , обе части второго уравнения – на А2 1 , и так далее, обе части n-ого уравнения – на Аn 1 (то есть, уравнения системы умножаем на соответствующие алгебраические дополнения первого столбца матрицы А):
Сложим все левые части уравнения системы, сгруппировав слагаемые при неизвестных переменных x1, x2, …, xn, и приравняем эту сумму к сумме всех правых частей уравнений:
Если
обратиться к озвученным ранее свойствам
определителя, то имеем 
и
предыдущее равенство примет видоткуда
Аналогично находим x2. Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А:
Складываем
все уравнения системы, группируем
слагаемые при неизвестных переменных x1,
x2,
…, xn и
применяем свойства определителя: 
Откуда .
Аналогично находятся оставшиеся неизвестные переменные.
Если
обозначить 
то
получаемформулы
для нахождения неизвестных переменных
по методу Крамера .
Замечание.
Если система линейных алгебраических уравнений однородная, то есть , то она имеет лишь тривиальное решение(при). Действительно, при нулевых свободных членах все определителибудут равны нулю, так как будут содержать столбец нулевых элементов. Следовательно, формулыдадут.
К началу страницы
Алгоритм решения систем линейных алгебраических уравнений методом Крамера.
Запишем алгоритм решения систем линейных алгебраических уравнений методом Крамера.
Вычисляем определитель основной матрицы системы и убеждаемся, что он отличен от нуля.
Находим определители которые являются определителями матриц, полученных из матрицыА заменой k-ого столбца (k = 1, 2, …, n) на столбец свободных членов.
Вычисляем искомые неизвестные переменные x1, x2, …, xn по формулам .
Выполняем проверку результатов, подставляя x1, x2, …, xn в исходную СЛАУ. Все уравнения системы должны обратиться в тождества. Можно также вычислить произведение матриц A ⋅ X, если в результате получилась матрица, равная B, то решение системы найдено верно. В противном случае в ходе решения была допущена ошибка.
К началу страницы
Примеры решения систем линейных алгебраических уравнений методом Крамера.
Разберем решения нескольких примеров.
Пример.
Найдите решение неоднородной системы линейных алгебраических уравнений методом Крамера .
Решение.
Основная матрица системы имеет вид . Вычислим ее определитель по формуле:
Так как определитель основной матрицы системы отличен от нуля, то СЛАУ имеет единственное решение, и оно может быть найдено методом Крамера. Запишем определители и. Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель. Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем.
Вычисляем эти определители:
Находим неизвестные переменные x1 и x2 по формулам :
Выполним проверку. Подставим полученные значения x1 и x2 в исходную систему уравнений:
Оба уравнения системы обращаются в тождества, следовательно, решение найдено верно.
Ответ:
.
Некоторые элементы основной матрицы СЛАУ могут быть равны нулю. В этом случае в уравнениях системы будут отсутствовать соответствующие неизвестные переменные. Разберем пример.
Пример.
Найдите решение системы линейных уравнений методом Крамера .
Решение.
Перепишем систему в виде , чтобы стало видно основную матрицу системы. Найдем ее определитель по формуле
Имеем
Определитель
основной матрицы отличен от нуля,
следовательно, система линейных уравнений
имеет единственное решение. Найдем его
методом Крамера. Вычислим определители :
Таким образом,
Ответ:
.
Обозначения неизвестных переменных в уравнениях системы могут отличаться от x1, x2, …, xn. Это не влияет на процесс решения. А вот порядок следования неизвестных переменных в уравнениях системы очень важен при составлении основной матрицы и необходимых определителей метода Крамера. Поясним этот момент на примере.
Пример.
Используя метод Крамера, найдите решение системы трех линейных алгебраических уравнений с тремя неизвестными .
Решение.
В данном примере неизвестные переменные имеют другое обозначение (x, y и z вместоx1, x2 и x3). Это не влияет на ход решения, но будьте внимательны с обозначениями переменных. В качестве основной матрицы системы НЕЛЬЗЯ брать . Необходимо сначала упорядочить неизвестные переменные во всех уравнениях системы. Для этого перепишем систему уравнений как. Теперь основную матрицу системы хорошо видно. Вычислим ее определитель:
Определитель
основной матрицы отличен от нуля,
следовательно, система уравнений имеет
единственное решение. Найдем его методом
Крамера. Запишем определители (обратите
внимание на обозначения) и вычислим
их:
Осталось найти неизвестные переменные по формулам :
Выполним проверку. Для этого умножим основную матрицу на полученное решение (при необходимости смотрите разделоперации над матрицами):
В результате получили столбец свободных членов исходной системы уравнений, поэтому решение найдено верно.
Ответ:
x = 0, y = -2, z = 3.
Пример.
Решите методом Крамера систему линейных уравнений , гдеa и b – некоторые действительные числа.
Решение.
Вычислим определитель основной матрицы системы:
Определитель отличен от нуля, следовательно, можно применить метод Крамера.
Находим неизвестные переменные
Рекомендуем проверить полученные результаты.
Ответ:
.
Пример.
Найдите решение системы уравнений методом Крамера,- некоторое действительное число.
Решение.
Вычислим определитель основной матрицы системы: .Область значений выражения есть интервал, поэтомупри любых действительных значениях. Следовательно, система уравнений имеет единственное решение, которое может быть найдено методом Крамера. Вычисляеми:
Таким образом, .
Выполним
проверку: 
Уравнения системы обращаются в тождества, следовательно, решение найдено верно.
Ответ:
.
Пример.
Решите систему линейных алгебраических уравнений методом Крамера .
Решение.
Вычислим определитель основной матрицы системы уравнений:
Определитель основной матрицы равен нулю, следовательно, метод Крамера не подходит для решения такой системы уравнений.
Пример.
Методом Крамера найдите решение СЛАУ .
Решение.
Эта система однородная, так как все свободные члены равны нулю. Определитель основной матрицы отличен от нуля , поэтому ее единственным решением являетсяx1 = 0, x2 = 0. О таких СЛАУ мы уже упоминали вышев замечании.
Ответ:
x1 = 0, x2 = 0.
Пример.
Найдите решение системы четырех линейных алгебраических уравнений содержащую четыре неизвестных переменных.
Решение.
Сразу скажем, что не будем подробно описывать вычисление определителей матриц, так как это выходит за рамки данной статьи.
Вычислим
определитель основной матрицы системы,
разложив его по элементам второй
строки: 
Определитель основной матрицы системы отличен от нуля, поэтому можно воспользоваться методом Крамера для решения системы.
Найдем :
аналогично
вычисляются
Таким образом,
Ответ:
.
К началу страницы
Подведем итог.
Метод Крамера позволяет находить решение систем линейных алгебраических уравнений, если определитель основной матрицы отличен от нуля. По сути метод сводится к вычислению определителей матриц порядка n на n и применению соответствующих формул для нахождения неизвестных переменных.
studfiles.net