Вычисление определителей
Пусть требуется вычислить определитель матрицы
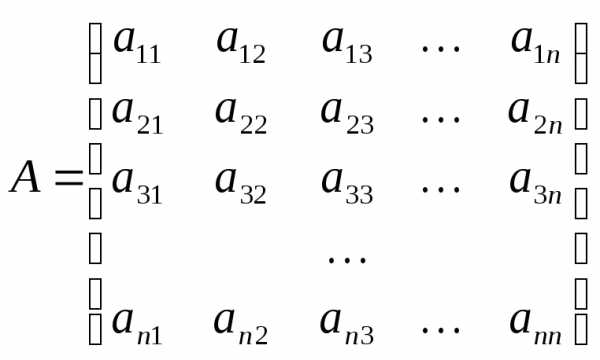
Для вычисления
определителя можно использовать
Жордановые исключения аналогичные
методу Жордана-Гауса, при решении систем
линейно алгебраических уравнений. За
исключением деления каждой строки на 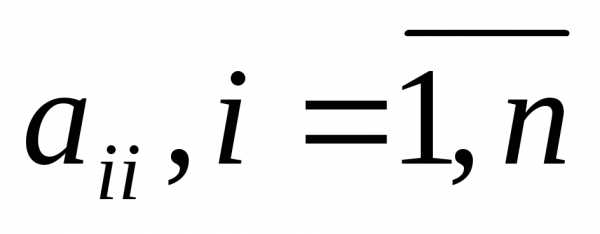

Если перестановка строк и столбцов не производилась, тогда
Если применяется метод исключения с выбором данного элемента, то определитель матрицы
где к — количество перестановок строк или столбцов.
Вычисление обратной матрицы
Пусть дана матрица
А необходимо вычислить 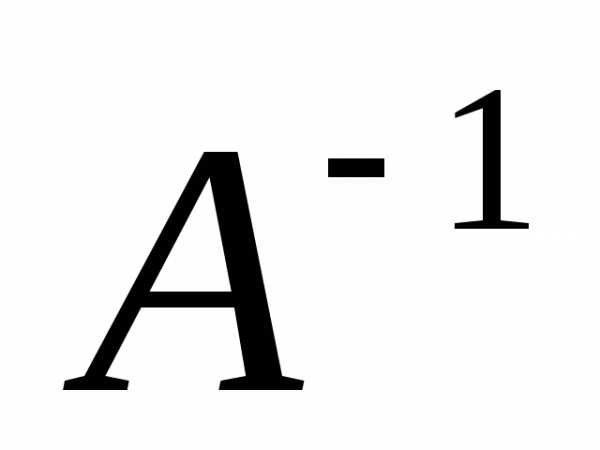
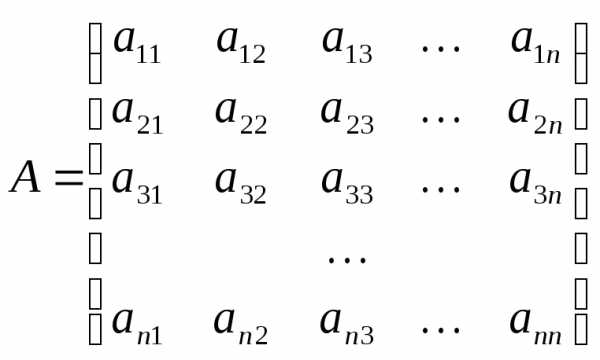 .
.
Можно использовать метод Гауса
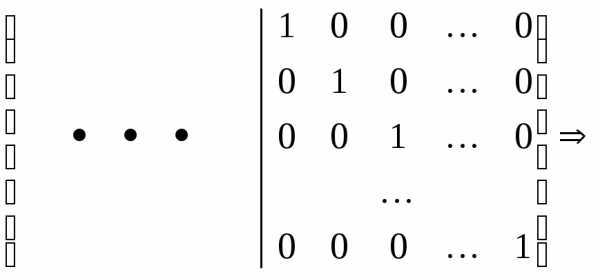
Методом Жорданового исключается с учетом правой части добиваемся, чтобы в левой части матрицы была единичная матрица
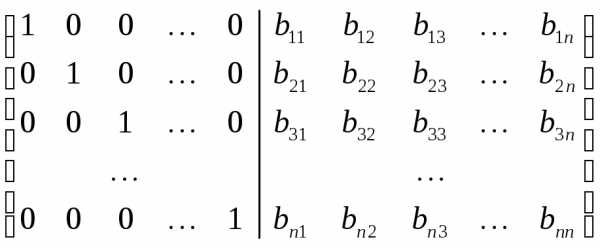
Тогда матрица
образуемая в правой части будет
представлять собой искомую 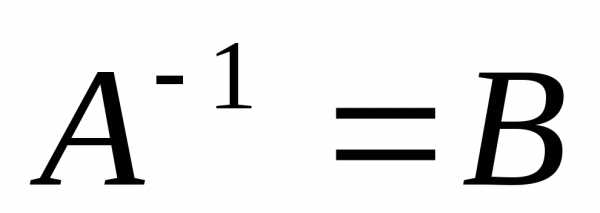 .
.
Приближенные( итерационны ) методы решения систем алгебраических уравнений
Итерационные
методы решения систем уравнения вида
AX=B
основаны на выборе некоторого начального
приближения
с
последующим его уточнением рекуррентным
формамгде к- номер итерации для вычисления
приближенного метода решения, с заданной
точностью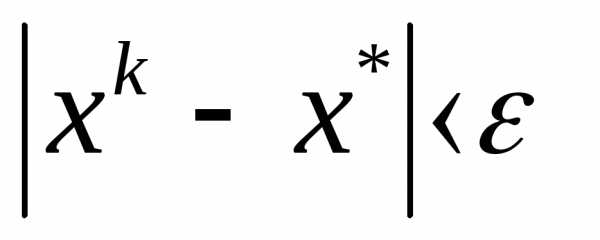
 -точные
решения.
-точные
решения.Процесс итерации легко реализуется на ЭВМ он самоисправляемый т.е.некоторые ошибки в вычислениях устраняются а следующей итерации и они не отражаются на окончательном результате решения. Существует несколько разновидностей метода итерации.
Метод простых итераций(метод Якоби)
Сущность данного метода состоит в том, что исходную систему уравнений AX=B, преобразуем к видуX=CX+D и подставляем в правую часть получаемого уравнения мы вычисляем,, далее, где каждая новая точка приближается к искомому решению.
Итерационный процесс будет сходиться если .
Покажем условные сходимости данного метода. Пусть дана система уравнений
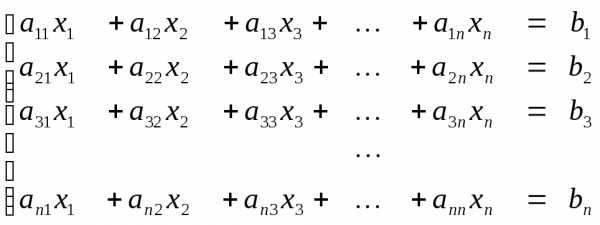
Из теории приближенных вычислений следует, что итерационный процесс будет сходиться если
Диагональный элемент по модулю будет больше суммы всех остальных коэффициентов
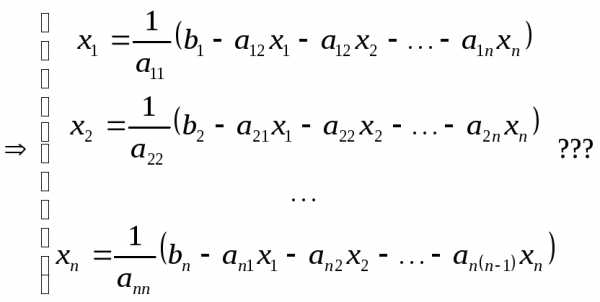
Для того чтобы получить условие сходимости (*) можно выполнять следующие операции над строками исходной системы уравнений. Можно вычитать любые строки системы уравнений, умножать строку на коэффициент, производить операцию сложения, комбинируя этими операциями можно добиться чтобы из исходной системы получить систему удовлетворяющую условию сходимости
Метод Зайделя
При исполнении метода простых итераций используется следующая схема
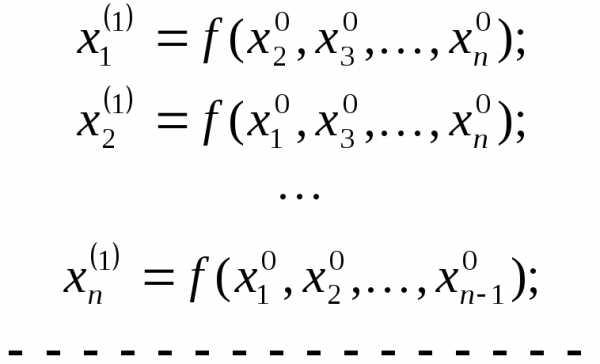
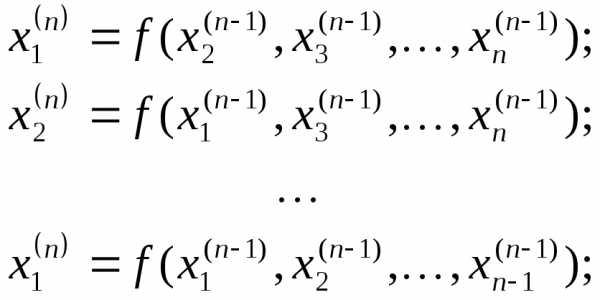
Метод Зайделя
основан на методе простых итераций,
однако для повышения сходимости на
каждой итерации используется ранее
вычисленные значения 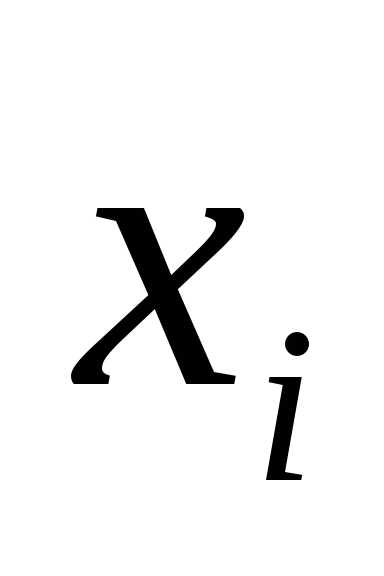 ,
тогда по схеме Зайделя
,
тогда по схеме Зайделя
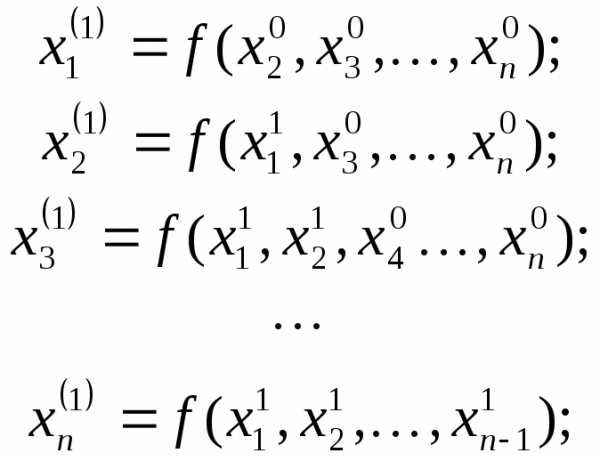
и так далее
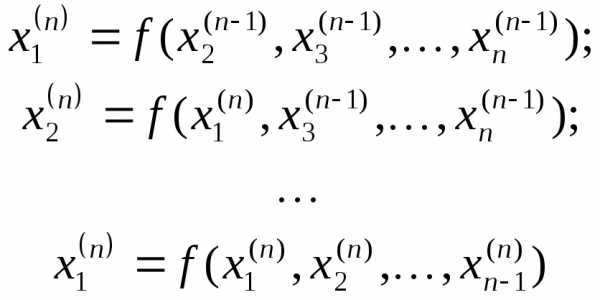
На практике итерационный процесс заканчивается, если выполняется условие

к- номер итерации.
Решение систем не линейных уравнений
Пусть дана система
линейных уравнений F(x)=0
в векторном виде, либо 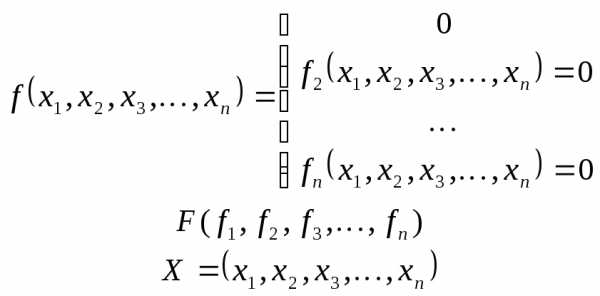
Такие системы решаются только итерационными методами, т.е. численными методами. Сущность которых заключается в том, что начиная с некоторого начального значения в близи искомого решения определяют
через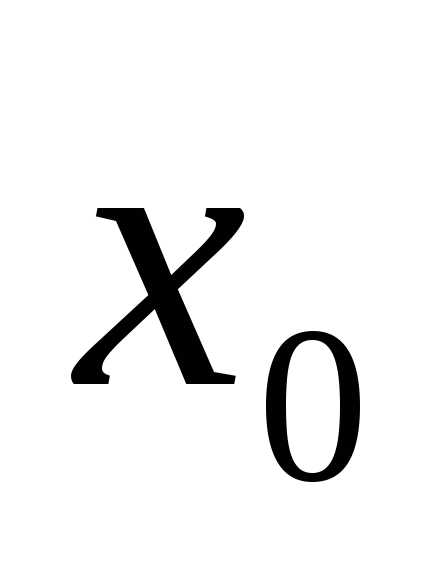
через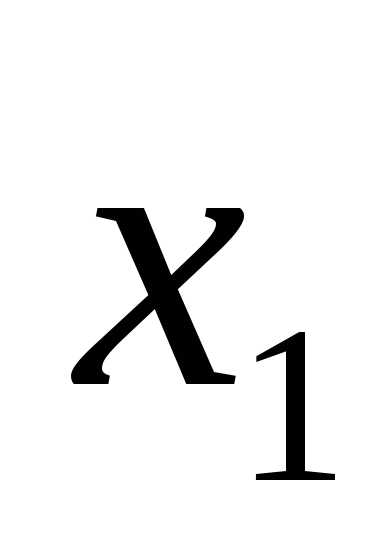
…
так что
;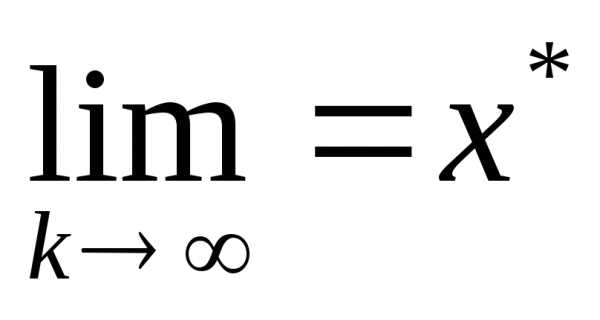
Вычисление заканчивают , если ; ;
;

;
Существует целый ряд методов :
1. метод простых итераций
метод Зайделя
метод Ньютона
метод релаксации
метод Пикара
метод найскорейшего спуска
гибридные методы
studfiles.net
§ 2. Определители, их основные свойства и методы вычисления
8
|
| a | a | 21 | … | a | m1 |
|
|
|
| 11 |
|
|
|
|
| ||
T |
| a12 | a22 | … | am2 |
|
| ||
A | = | … | … | … | … |
| , | ||
|
| a | a | 2n | … | a | mn |
|
|
|
| 1n |
|
|
|
|
| ||
которую называют транспонированной к матрицеA .
6. Элементарные преобразования матриц.
Элементарными называются следующие преобразования матриц:
1)умножение всех элементов какой-либостроки (столбца) матрицы на одно и то же число, отличное от нуля;
2)прибавление к элементам какой-либостроки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на одно и то же число;
3)перемена местами строк (столбцов) матрицы;
4)отбрасывание строк (столбцов) матрицы, все элементы которых равны нулю.
Если матрица B получена из матрицыA с помощью элементарных преобразований, то ее называютэквивалентной матрицеA и пишутA ~B . Заметим, что эквивалентные матрицы, вообще говоря, не равны друг другу.
2.1 Определители второго порядка
Определение. Пусть дана квадратная матрица второго порядка
Определителем (или детерминантом) второго порядка, соответствующим данной матрице, называется число, получаемое по правилу:
det A = | a11 | a12 | = a | a | 22 | − a | a | 21 | . | (1) |
| a21 | a22 | 11 |
| 12 |
|
|
| ||
|
|
|
|
|
|
|
|
|
Числа a11 , a12 , a21 , a22 называют элементами определителя.
Учитывая приведенные выше определения, можно сказать, что определителем второго порядка, соответствующим данной матрице, называется число, равное разности произведений элементов матрицы, стоящих на главной и на побочной диагоналях матрицы.
Пример 1.
4 | − 2 |
| = 4 8− (− 2) 3= 38 . |
| |||
3 | 8 |
|
|
9
Свойства определителей второго порядка
Свойство 1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами, т.е.
a11 | a12 | = | a11 | a21 | . | |||
a | 21 | a | 22 |
| a | a | 22 |
|
|
|
| 12 |
|
| |||
Следствие. Все свойства определителя, имеющие место для его строк, остаются верными и для столбцов определителя.
Свойство 2. При перестановке двух строк (столбцов) определитель меняет свой знак на противоположный, сохраняя абсолютную величину, т.е.
a11 | a12 | = − | a21 | a22 | . | ||
a | 21 | a | 22 |
| a | a |
|
|
|
| 11 | 12 |
| ||
Свойство 3. Определитель с двумя одинаковыми строками (столбцами) равен нулю.
Свойство 4. Общий множитель всех элементовкакой-либостроки (столбца) определителя можно выносить за знак определителя:
a11 | k a12 |
| = k |
| a11 | a12 |
| . |
|
|
| ||||||
a21 | k a22 |
|
|
| a21 | a22 |
|
|
Свойство 5. Если все элементыкакой-либостроки (столбца) определителя равны нулю, то определитель равен нулю.
Свойство 6. Если каждый элементi -йстроки (столбца) определителя равен сумме двух чисел, то его можно представить в виде суммы двух определителей. Вi -йстроке (столбце) первого из них будут стоять первые из вышеуказанных слагаемых, вi -йстроке (столбце) второго – вторые слагаемые. Все остальные элементы этих определителей равны соответствующим элементам исходного определителя:
a11 | a12 |
| = | a11 | a12 | + | a11 | a12 | . | |||
b | + c | b | + c | 2 |
| b | b |
| c | c | 2 |
|
1 | 1 | 2 |
|
| 1 | 2 |
| 1 |
|
| ||
Свойство 7. Если к элементамкакой-либостроки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, то определитель не изменит своей величины:
a11 | + k a12 | a12 |
| = |
| a11 | a12 |
| . |
|
|
| |||||||
a21 | + k a22 | a22 |
|
|
| a21 | a22 |
|
|
studfiles.net
Методы вычисления определителей
Как убедились выше, определители низших порядков (2-го и 3-го) находят, используя определения. Но бывают случаи, когда для вычисления таких определителей сначала лучше использовать свойства.
Пример 2.4. Найти определитель 2-го порядка: .
Решение. Умножим первую строку на (-1) и прибавим ко второй, получим
.
,
Определение определителя n-го порядка, а также свойства легли в основу некоторых методов вычисления определителей 4-го и выше порядков. Рассмотрим эти методы.
1) Используя разложение по строке или столбцу. В результате использования определения определителя n-го порядка мы приходим к вычислению определителей (n-1)-го порядка.
2) Метод эффективного понижения порядка. Используя основные свойства определителей, вычисление всегда можно свести к вычислению одного определителя (n-1)-го порядка, сделав в каком-либо ряду все элементы, кроме одного, равными нулю.
3) Приведение определителя к треугольному виду. Определитель, у которого все элементы, находящиеся выше или ниже главной диагонали, равны нулю, называются
4) Использование программы Excel пакета Microsoft Office. Excel имеет в своем составе большое количество различных функций — предустановленных формул, использующихся для выполнения стандартных вычислений. Для вычисления определителя из математических функций используется МОПРЕД (массив).
Пример 2.5. Найти определитель 4-го порядка используя все три способа:
.
Решение.
1) Воспользуемся разложением определителя по второй строке, поскольку в этой строке один элемент нулевой. Получаем
.
2) Воспользуемся приведением определителя к треугольному виду. Умножим вторую строку на (-2) и прибавим к первой строкой, умножим вторую строку на (-3) и прибавим к третьей, умножим вторую строку на (-4) и прибавим к четвертой. Получаем
[поменяем местами первую и вторую строку]
[складываем вторую и третью строку, вторую строку умножаем на 2
и складываем с четвертой строкой]
[умножаем третью строку на (-11/8) и складываем с четвертой строкой]
.
3) Используем метод эффективного понижения порядка. Умножим первый столбец на (-2) и прибавим к третьему столбцу, умножим первый столбец на (-1) и прибавим к четвертому столбцу.
[к первой строке прибавим вторую; первую строку умножим на 2
и прибавим третью строку]
= .
4) Открываем экран Excel. Последовательно заносим в ячейки элементы определителя в виде массива. Например, ячейки B5:E8 (Рис. 1).
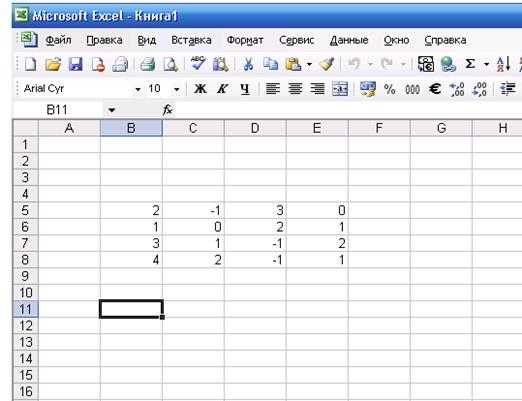
Рис. 1. Внесенные в ячейки элементы определителя
Входим в диалоговое окно — Мастер функций. Выбираем категорию: математические функции. Из предложенных выбираем функцию МОПРЕД (массив). Нажимаем ОК (Рис. 2).
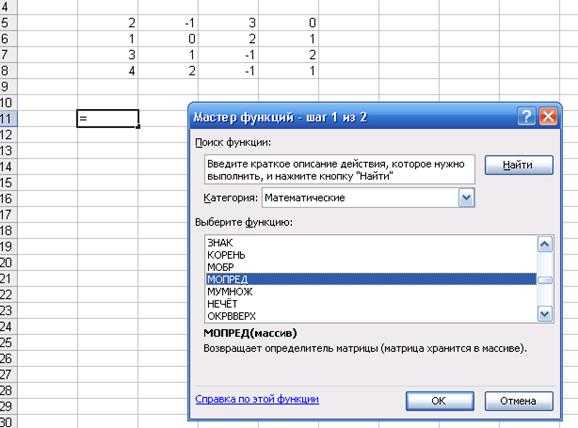
Рис. 2. Диалоговое окно Мастер функций
В результате появляется окно Аргументы функции, где в ячейку Массив вносим выделенный массив элементов определителя: B5:E8 (Рис. 3). Внизу этого окна появляется значение 23.
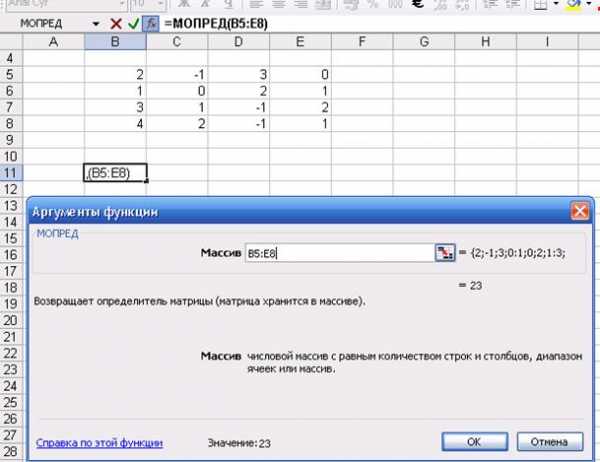
Рис. 3. Диалоговое окно Аргументы функции
Если нажать на ОК, то в выделенной ячейке появится 23.
,
3. ОБРАТНАЯ МАТРИЦА
3.1. Теорема существования обратной матрицы
Определение 3.1. Квадратная матрица A называется невырожденной, если ее определитель . В противном случае матрица A называется вырожденной или особенной.
Определение 3.2. Матрицей, присоединенной к матрице A, называется матрица вида
,
где — алгебраическое дополнение элемента данной матрицы A (оно определяется так же, как и алгебраическое дополнение элемента определителя).
Определение 3.3. Матрица называется обратной матрице A, если выполняется условие
, (3.1)
где E – единичная матрица того же порядка, как и матрица A.
Матрица имеет тот же порядок, что и матрица A.
Пример 3.1. Показать,что матрица A является обратной для матрицы B, если
.
Решение. Найдем произведение матриц A и B.
.
Аналогично . Следовательно, матрица A является обратной для B.
,
Теорема 3.1. Для невырожденной матрицы A существует единственная обратная матрица , определяемая формулой
, (3.2)
где — матрица, присоединенная к матрице A.
Доказательство.
1) Сначала докажем существование единственной обратной матрицы.
Пусть и — матрицы, обратные для матрицы A. Тогда, используя свойство умножения матрицы на единичную матрицу, свойство ассоциативности и равенства (3.1), получаем следующее
.
Таким образом, .
2) Используя равенство (3.1) докажем справедливость формулы (3.2). Покажем, что . В ходе преобразований будем использовать свойство 9 для определителей и разложение определителя n-го порядка по i-ой строке.
.
Аналогично убеждаемся, что .
,
Пример 3.2. Найти , если .
Решение. 1) Находим определитель матрицы A.
.
Матрица A – невырожденная, значит, существует ей обратная.
2) Находим алгебраические дополнения элементов матрицы A.
.
Составляем матрицу, присоединенную к матрице A.
.
3) Находим .
.
Сделаем проверку:
,
infopedia.su
Лекция 2 Определители
6
Лекция 2. определители
Определители второго порядка
Определители третьего порядка
Алгебраические дополнения и миноры
Разложение определителя по строке или столбцу
Свойства определителей
Обратная матрица
Свойства обратной матрицы
1. Определители второго порядка
Понятие определителя вводится только для квадратной матрицы.
Определитель – это число, которое считается по определенным правилам. Порядок определителя – это порядок квадратной матрицы. Если для задания матриц использовались круглые скобки, то в теории определителей используют прямые скобки.
Каждой квадратной матрице поставим в соответствие некоторое число, которое будем называть определителем матрицы, и укажем правило его вычисления. Обозначения:
.
Пример 1. .
2. Определители третьего порядка
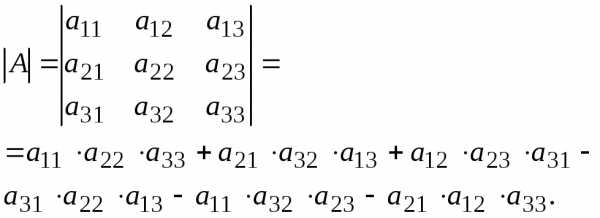
В каждом произведении нет чисел из одного столбца или одной строки.
Приведем схему для запоминания порядка получения слагаемых в определителе.

Произведение чисел на одной диагонали берется со знаком «+» (это главная диагональ матрицы), а на другой – с противоположным знаком.
Пример 2.
3. Алгебраические дополнения и миноры
Для вычисления определителей порядка больше третьего применяют другие способы вычисления.
Пример
3. Минор 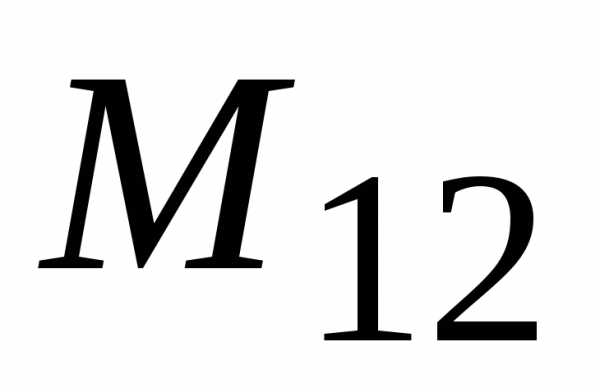 определителя
определителя 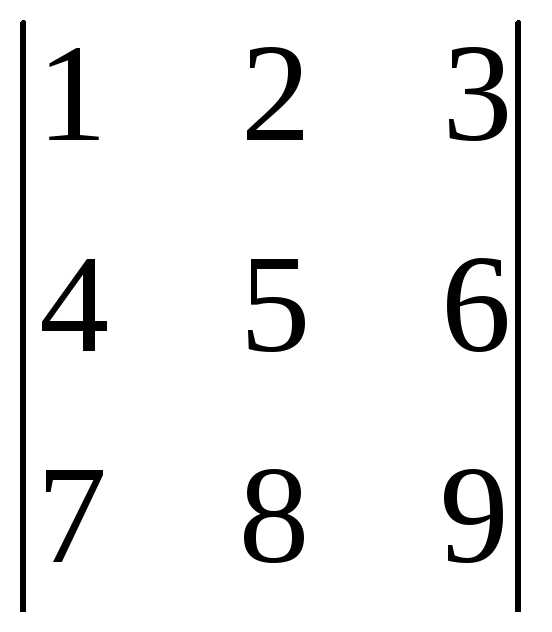 есть.
есть.
.
Полезно
запомнить, что 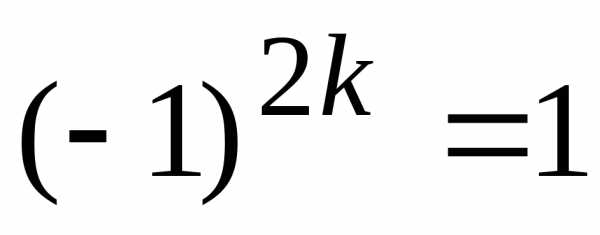 и.
и.
Пример 4. В примере 3 алгебраическое дополнение
.
4. Разложение определителя по строке или столбцу
Вычисление
определителя 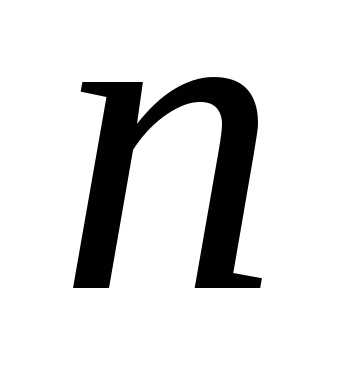 -го
порядка можно свести к вычислению
определителей порядка
-го
порядка можно свести к вычислению
определителей порядка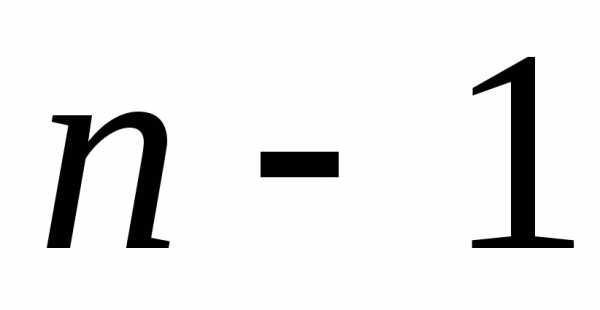 ,
используя следующие формулы.
,
используя следующие формулы.
Разложение определителя по
 -й
строке:
-й
строке:
Это
число равно сумме произведений элементов любой 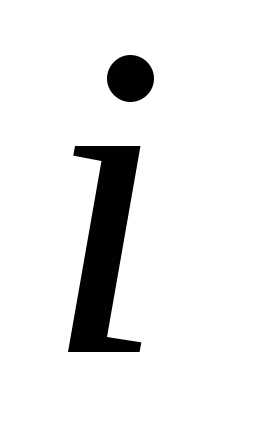 -йстроки на их алгебраические
дополнения.
-йстроки на их алгебраические
дополнения.
Пример
5. Вычислить
определитель третьего порядка  разложением по первой строке.
разложением по первой строке.
Решение
Разложение определителя по
 -му
столбцу:
-му
столбцу:
Это
число равно сумме произведений элементов
любого  -го
столбца на их алгебраические дополнения.
-го
столбца на их алгебраические дополнения.
Независимо от способа разложения всегда получается один и тот же ответ.
5. Свойства определителей
1. При
транспонировании квадратной матрицы ее определитель не меняется: 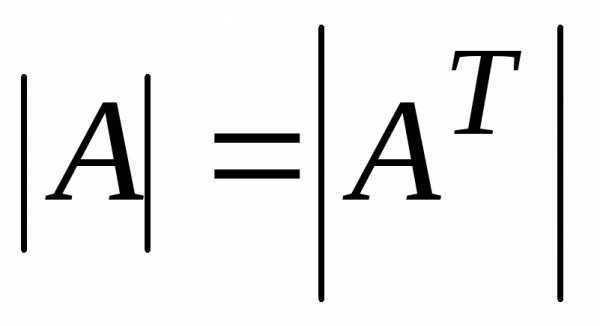 .
.
Вывод. Свойства определителей, сформулированных для строк, справедливы и для столбцов.
2. При перестановке двух строк (столбцов) определитель меняет знак на противоположный. Например, .
3. Определитель равен нулю, если:
а)
он имеет нулевую строку (столбец) 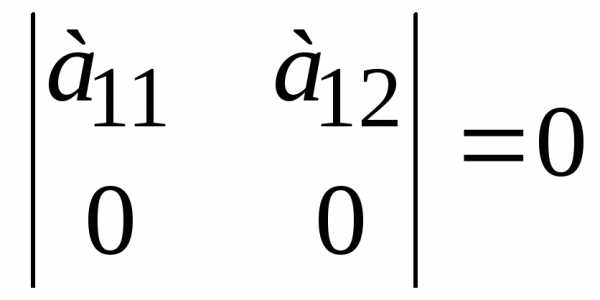 ;
;
б)
он имеет пропорциональные (одинаковые)
строки (столбец) 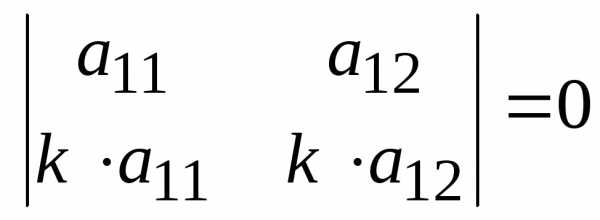 .
.
4. Общий множитель в строке (столбце) можно выносить за знак определителя. Например, .
5. Определитель не изменяется, если к элементам какой-либо строки прибавить (вычесть) соответствующие элементы другой строки, умноженные на любое число.
Например, .
6. Если в определителе каждый элемент строки есть сумма двух слагаемых, то этот определитель равен сумме двух определителей:
.
7. Определитель произведения двух квадратных матриц одного и того же порядка равен произведению определителей этих матриц:
.
8. Определитель квадратной матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали:
.
6. Обратная матрица
Вместо операции деления матриц вводится понятие обратной матрицы.
Обозначается
обратная матрица 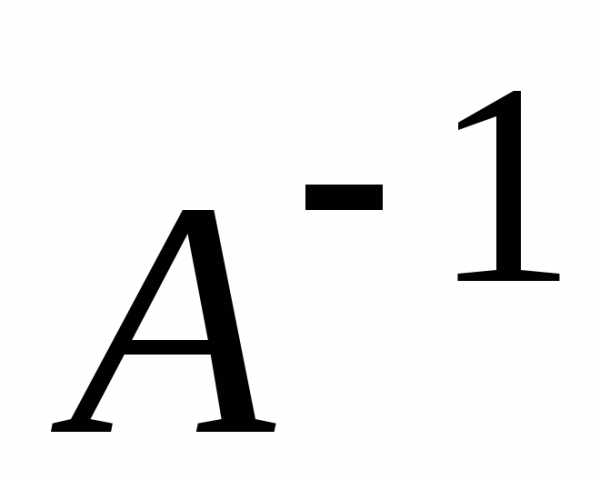 , то
есть .
, то
есть .
Очевидна
аналогия с числами: для числа 2 число ½
есть обратное, так как
.
Именно поэтому матрица, обратная к А,
обозначается 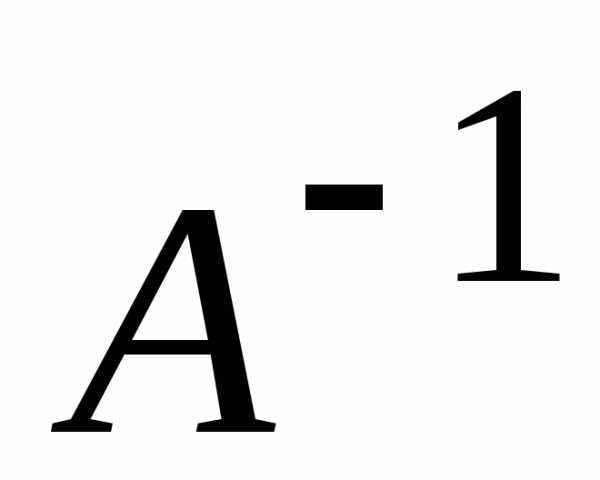 .
.
Теорема
«Необходимое и достаточное условие
существования обратной матрицы». Для
того чтобы квадратная матрица  имела обратную матрицу
имела обратную матрицу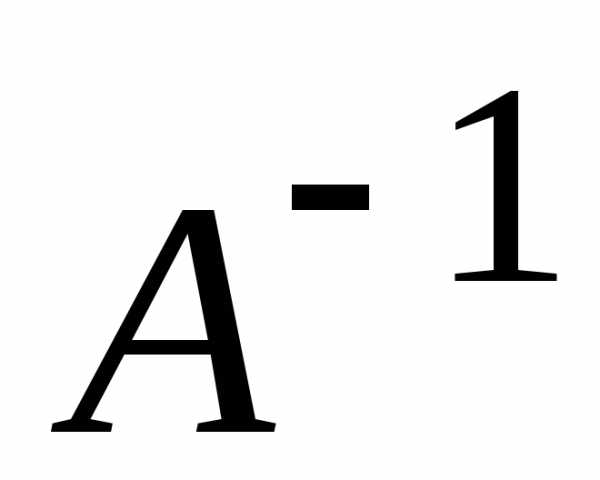 ,
необходимо и достаточно, чтобы определитель
матрицы
,
необходимо и достаточно, чтобы определитель
матрицы был не равен нулю.
был не равен нулю.
Правило
нахождения обратной матрицы 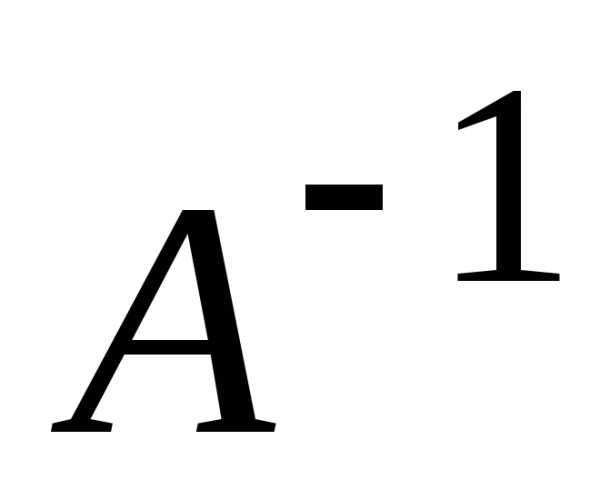
0) Смотрим, является ли матрица квадратной. Если нет, то обратной матрицы не существует; если квадратная, то переходим к пункту 1.
1) Вычисляем определитель матрицы 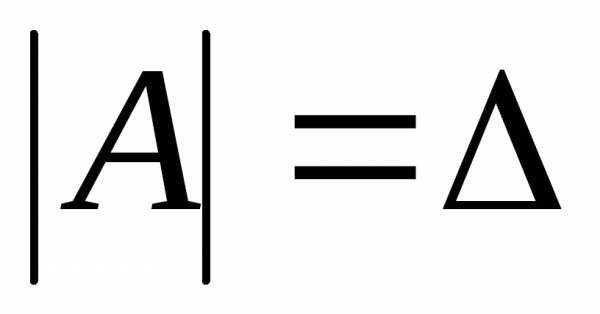 :
если он не равен нулю, то обратная матрица
существует:;
:
если он не равен нулю, то обратная матрица
существует:;  если
равен нулю, то обратной матрицы нет.
если
равен нулю, то обратной матрицы нет.
2) Для каждого элемента матрицы  вычисляем его алгебраическое дополнение
вычисляем его алгебраическое дополнение .
.
3) Составляем матрицу из алгебраических дополнений, которая затем транспонируем: .
4) Каждый элемент матрицы 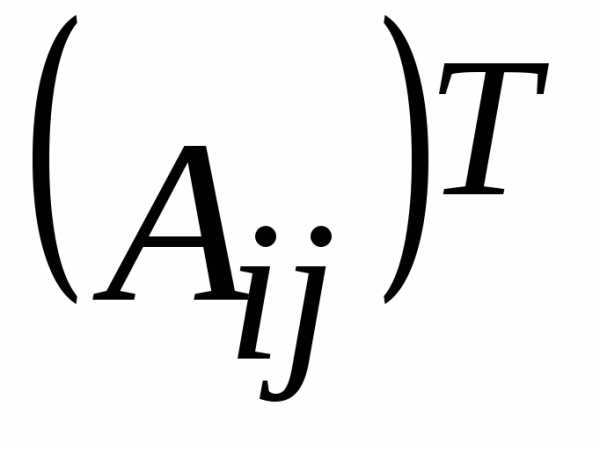 делим на определитель
делим на определитель :
: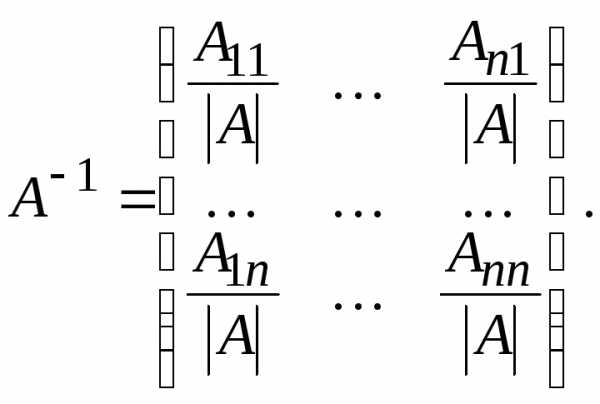 Получаем матрицу, обратную данной.
Получаем матрицу, обратную данной.
7. Нахождение обратной матрицы для матриц второго порядка
Пример
6. Дана матрица 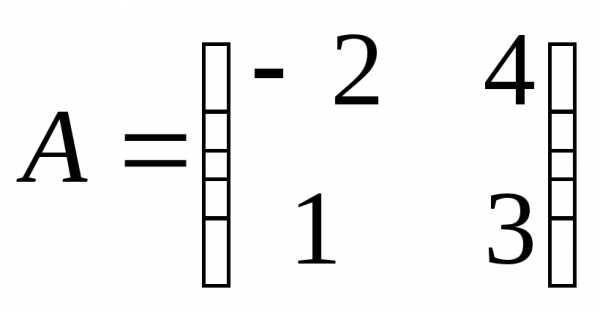 .
Найти обратную матрицу.
.
Найти обратную матрицу.
Решение.
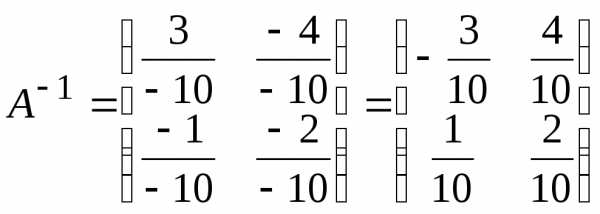
Проверка. Убедимся, что найдена действительно
обратная матрица. Найдем произведение
матриц  и
и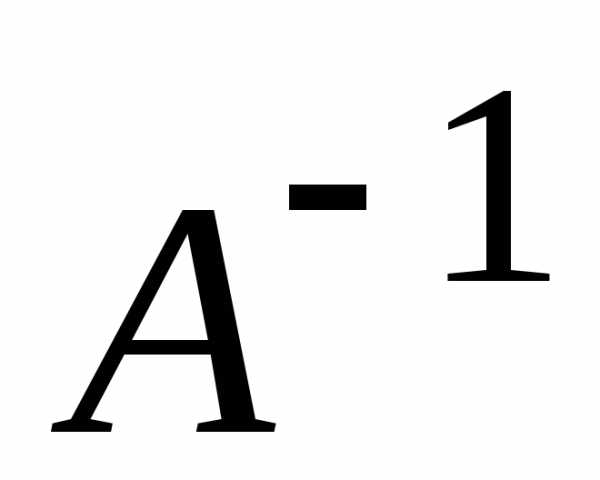 .
.
8. Свойства обратной матрицы
1. ,
где А и В – невырожденные квадратные матрицы одинакового порядка.
2. .
3. .
4. 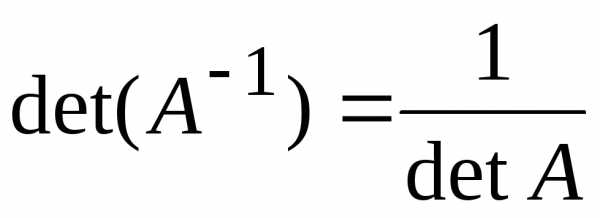 .
.
Контрольные вопросы
Что называется определителем второго порядка?
Как вычислить определитель третьего порядка?
Как вычислить определитель 3 порядка по правилу треугольников?
Что называется алгебраическим дополнением элемента определителя? Приведите примеры для определителей 2 и 3 порядков.
Напишите разложения определителя третьего порядка по элементам произвольной строки и произвольного столбца.
Сформулируйте основные свойства определителей.
В каком случае определители равны нулю? Приведите примеры.
Представьте определитель
 в виде суммы двух определителей.
в виде суммы двух определителей.Заполните пропущенные места так, чтобы значения определителей были одинаковы:
 и
и .
.Запишите определитель третьего порядка треугольного вида. Как его вычислить?
Какая матрица называется обратной для данной матрицы?
Для любой ли квадратной матрицы существует обратная?
Пусть . Будут ли матрицы
 и
и взаимно обратными?
взаимно обратными?При каких значениях параметра существует матрица, обратная матрице
 ?
?Запишите формулу для нахождения обратных матриц 2 и 3 порядков.
Сформулируйте правило нахождения обратной матрицы.
studfiles.net
Методы вычисления определителей — Мегаобучалка
Определитель второго порядка вычисляется по определению – по формуле (1.1) (см. пример 1.2.1).
Определитель третьего порядка также можно вычислять по определению – по формуле (1.3). Для запоминания, какие произведения элементов надо выписать и с каким знаком, обычно используют правило треугольников (рис. 1.1) – произведения элементов, стоящих на главной диагонали и в вершинах двух треугольников, одна из сторон которых параллельна главной диагонали, берутся со знаком (+), а произведения элементов, стоящих на другой диагонали и в вершинах двух треугольников, одна из сторон которых параллельна этой диагонали, берутся со знаком (–) (см. пример 1.2.3).
Для вычисления определителей третьего порядка можно использовать формулы (1.4) и (1.5) разложения определителя по строкам и столбцам (см. пример 1.2.1).
Определители четвертого и большего порядков находить по определению и даже разложением по строкам (столбцам) практически невозможно из-за громоздких вычислений. Более эффективно нахождение определителей методом Гаусса: используя свойства 7) и 2) можно преобразовать матрицу в треугольную, не изменив определителя (см. примеры 1.2.4и 1.2.5). Определитель треугольной матрицы мы вычислять умеем – он равен произведению элементов главной диагонали.
Примеры решения задач
1.2.1.Вычислить определитель второго порядка .
◄ По формуле (1.1) . ►
1.2.2.Вычислить определитель матрицы .
◄ По формуле (1.1) определитель матрицы
. ►
1.2.3.Найти алгебраические дополнения элементов первой строки матрицы
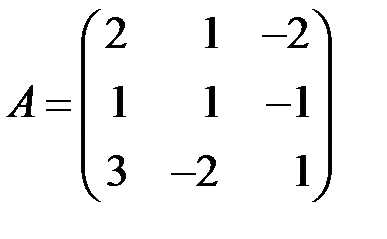 .
.
◄ Алгебраическое дополнение первого элемента первой строки – определитель матрицы, полученной вычеркиванием 1-й строки и 1-го столбца, в которых находится этот элемент, умноженный на : . Алгебраическое дополнение второго элемента первой строки – определитель матрицы, полученной вычеркиванием 1-й строки и 2-го столбца, в которых находится этот элемент, умноженный на : . Алгебраическое дополнение третьего элемента первой строки – определитель матрицы, полученной вычеркиванием 1-й строки и 3-го столбца, в которых находится этот элемент, умноженный на :
. ►
1.2.4.Вычислить определитель матрицы из примера 1.2.3.
Решение 1. (по определению – правило треугольников).
◄
.
Здесь первые три слагаемых – произведение элементов, стоящих на главной диагонали и в вершинах двух треугольников, одна из сторон которых параллельна главной диагонали, последние три слагаемых – произведения элементов, стоящих на другой диагонали и в вершинах двух треугольников, одна из сторон которых параллельна этой диагонали, взятые со знаком (–).
►
Решение 2.(разложение по первой строке). ◄ По формуле (1.4) для вычисления определителя надо каждый элемент строки умножить на его алгебраическое дополнение и сложить полученные числа. Алгебраические дополнения элементов первой строки мы уже нашли в примере 1.2.3. Итак,
.►
Решение 3. (Метод Гаусса – приведение к треугольному виду).
◄
Шаг 1. Поменяли местами 1-ю и 2-ю строки и умножили 2-ю строку на –1. Каждое действие меняет знак определителя (свойства 2-3), в результате определитель не изменится. Цель этих действий – получить в левом верхнем углу единицу (см. замечание 1 в конце решения).
Шаг 2. Ко 2-й строке прибавили 1-ю, умноженную на 2, к 3-й строке прибавили 1-ю, умноженную на (–3). По свойству 7) определитель не изменится. Цель – получить в первом столбце нули ниже первого элемента столбца.
Шаг 3. К 3-й строке прибавили 2-ю, умноженную на 5. Цель – получить во втором столбце нули ниже второго элемента столбца.
В итоге получили определитель треугольной матрицы, равный произведению диагональных элементов. ►
Замечание 1. Если бы мы не сделали 1-й шаг и начали со второго, то пришлось бы ко 2-й строке прибавить 1-ю, умноженную на , к 3-й строке прибавить 1-ю, умноженную на . В итоге пришлось бы работать с десятичными дробями. Если определитель не специально подобран для упражнений, то этого не избежать.
Замечание 2. Для определителя третьего порядка можно опустить шаг 3, разложив определитель, полученный на шаге 2 по первому столбцу:
.
Конечно, алгебраические дополнения, которые умножаются на нули, ни выписывать, ни считать не нужно. ►
1.2.5.Вычислить определитель матрицы 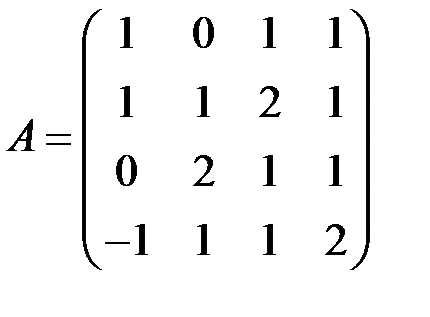 .
.
◄ 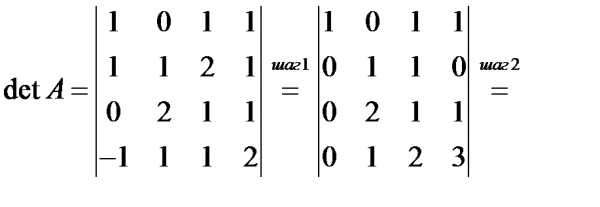
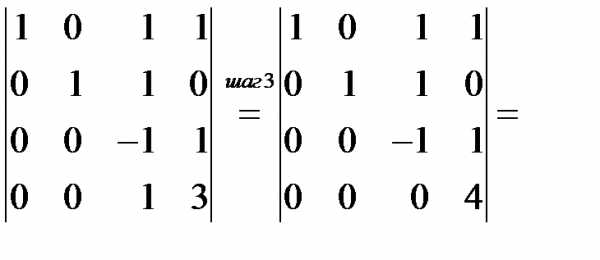
.
Шаг 1. Ко 2-й строке прибавили 1-ю, умноженную на –1, 3-ю строку не меняли, к 4-й строке прибавили 1-ю.
Шаг 2. К 3-й строке прибавили 2-ю, умноженную на –2, к 4-й строке прибавили 2-ю, умноженную на –1.
Шаг 3. К 4-й строке прибавили 3-ю. ►
1.2.6.Проверить, что общее определение (1.2) определителя -го порядка при совпадает с формулой (1.1).
◄ Согласно (1.2) при
,
где и – все возможные произведения по два элемента, взятые из разных строк и разных столбцов, выписанные в порядке возрастания
номеров строк; и – число инверсий – нарушений естественного порядка в последовательностях и из номеров столбцов. ►
megaobuchalka.ru
Вычисление определителей
Вычисление определителей зависит от порядка определителя. Рассмотрим вычисление определителя второгопорядка:
,
т.е. определитель второго порядка равен произведению элементов, находящихся на главной диагонали минус произведение элементов, находящихся на побочной диагонали.
Вычисление определителей третьегопорядка можно произвести различными способами. Рассмотрим их подробнее с наглядными примерами. Подчеркнем, что первые три способа относятся к вычислению определителей толькоIII-го порядка.
1 способ. По определению (по правилу треугольников).
Рассмотрим сначала в общем виде:
Схематическая запись этого правила выглядит следующим образом:
+ –
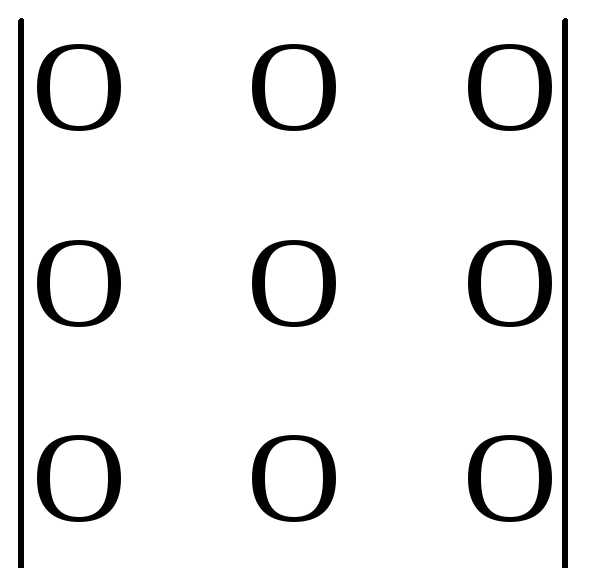
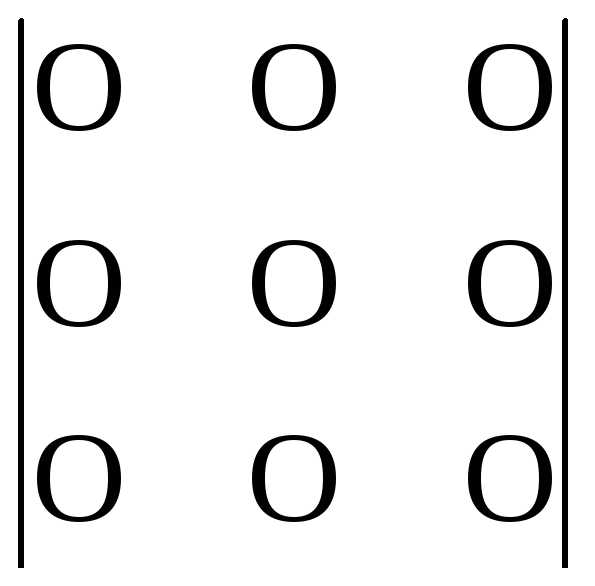
2 способ. По правилу Саррюса.
Схематически:
–
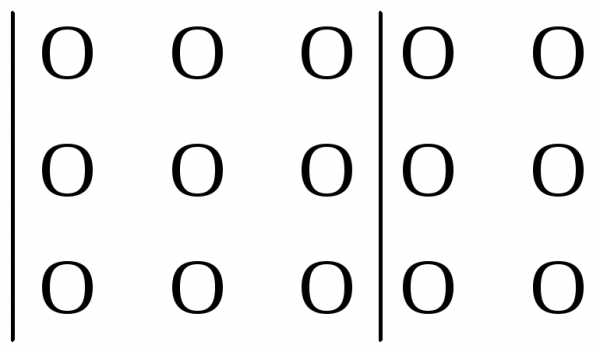
+
В результате этот способ сводиться к подсчету по определению, т.е. к Iспособу.
3 способ. По правилу Фридерищева.
4 способ. Вычисление определителя с помощью разложения по элементам ряда.
Если первые три способа относятся к вычислению определителей только третьего порядка, то этот способ и следующие применимы и к определителям третьего и выше порядков.
Итак, определитель равен сумме произведений элементов любого ряда на их алгебраические дополнения:
Введем новые понятия:
здесь
— это алгебраические дополнения, каждое
из которых соответствует элементу, т.е. соответствует элементу
соответствует элементу ,элементу
,элементу .
.
Алгебраические дополнения определяются по формуле:
где 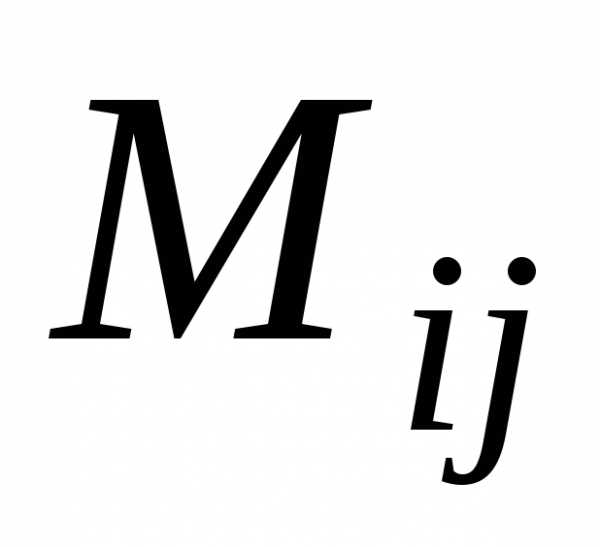 — минор, также соответствующий элементу.
— минор, также соответствующий элементу.
Минором 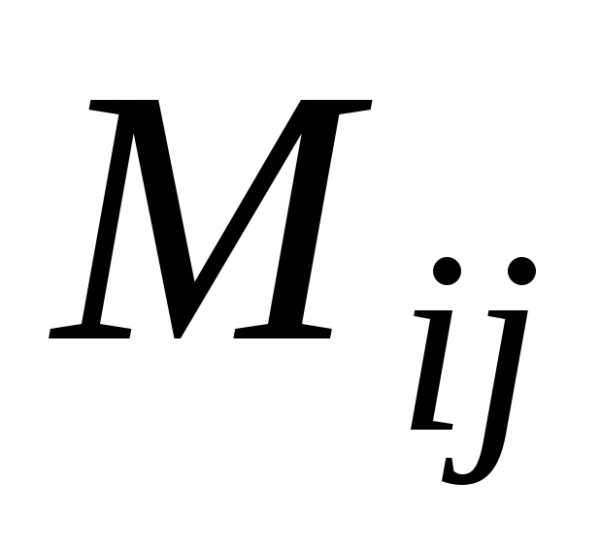 элемента
элемента называется определитель
называется определитель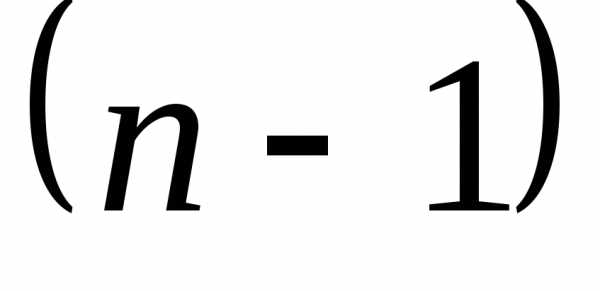 -го
порядка
-го
порядка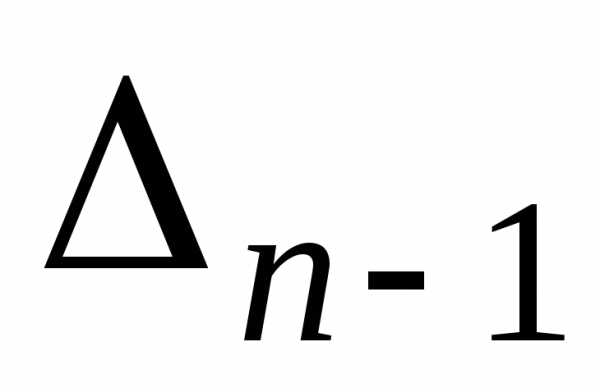 ,
полученный из определителя
,
полученный из определителя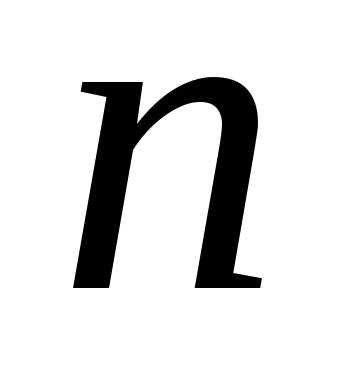 -го
порядка
-го
порядка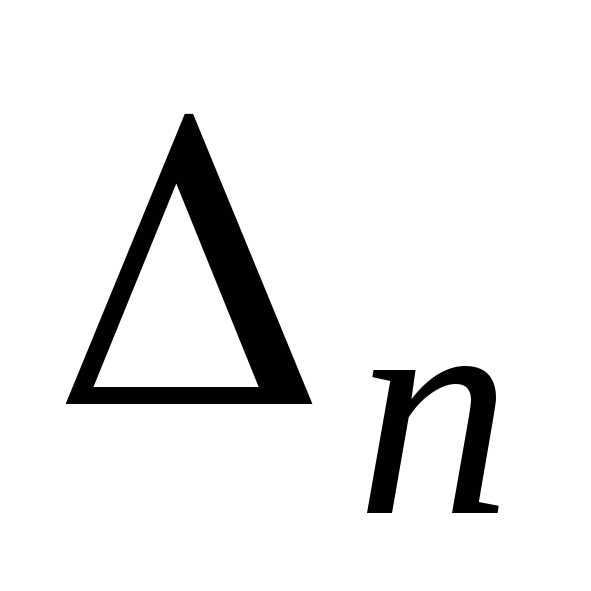 вычеркиванием
вычеркиванием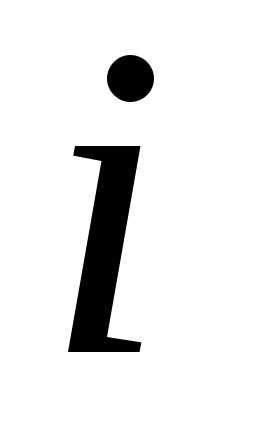 -й
строки и
-й
строки и -го
столбца (на пересечении которых стоит
элемент).
-го
столбца (на пересечении которых стоит
элемент).
5 способ. Вычисление определителя методом обнуления элементов какого-либо ряда.
В этом способе используется 7-е свойство определителей (из раздела 1.1). Способ будем рассматривать на примерах.
6 способ. Приведение определителя к треугольному виду.
В этом способе также используется 7-е свойство определителей (из раздела 1.1). Способ будем рассматривать на примерах.
Пример 1.1.
Вычислить определитель третьего порядка:
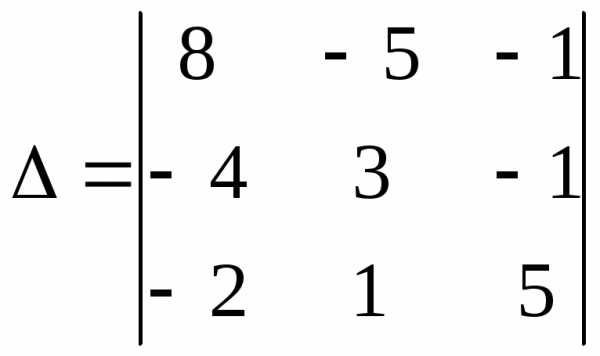
1 способ.По определению:
2 способ.По правилу Саррюса:
3 способ.По правилу Фридерищева:
4 Способ.
а). Разложив по элементам третьей строки:
б). Разложив по элементам второго столбца:
5 Способ.
а). Получив нули в третьем столбце.
Когда получают нули в столбце, то работают со строчками. Схематически будем работать так:
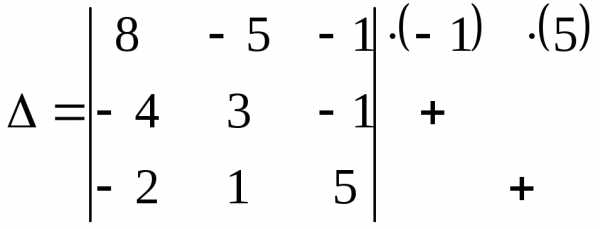
Это
означает, что элементы первой строки
умножим на 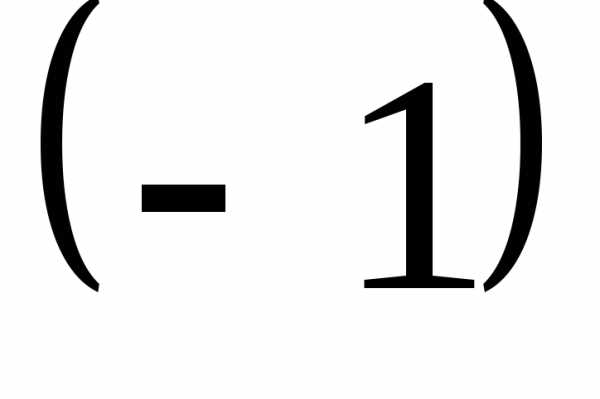 и сложим с соответствующими элементами
второй строки, затем элементы первой
строки умножим на 5 и сложим с
соответствующими элементами третьей
строки.
и сложим с соответствующими элементами
второй строки, затем элементы первой
строки умножим на 5 и сложим с
соответствующими элементами третьей
строки.
Итак: 
Теперь вычислим определитель, разложенный по элементам третьего столбца:
б). Получив нули во второй строке (значит будем работать со столбцами).
+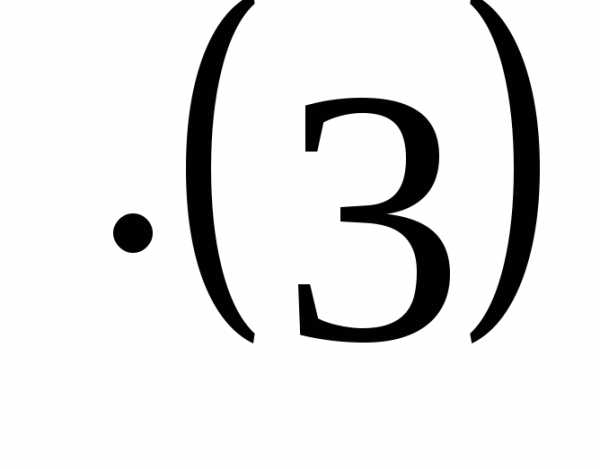
+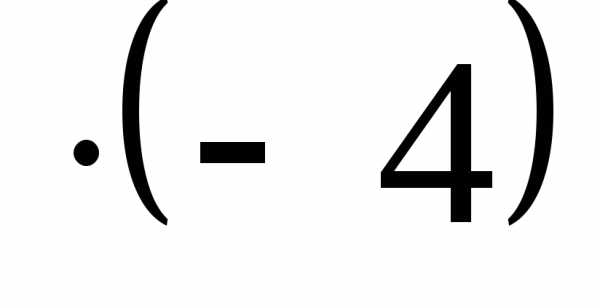
6 Способ.
Преобразовав его к треугольному виду:
Можно
еще раз убедиться в том, что вычисляя
один и тот же определитель любым способом,
мы получили одно и то же число 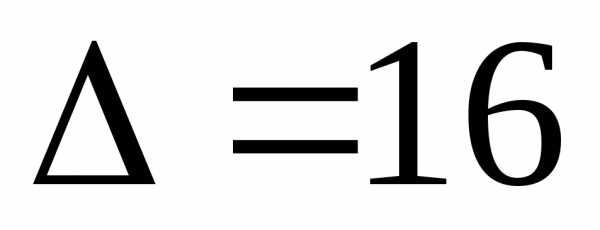 .
.
Пример 1.2.
Вычислить определитель четвертого порядка
Получив нули в 1 строке (значит работать будем со столбцами)
Приведя к треугольному виду
 +
+
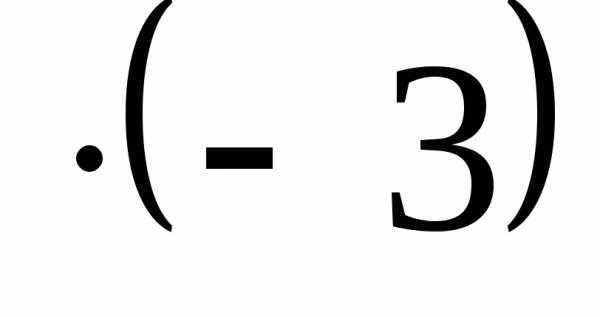 +
+
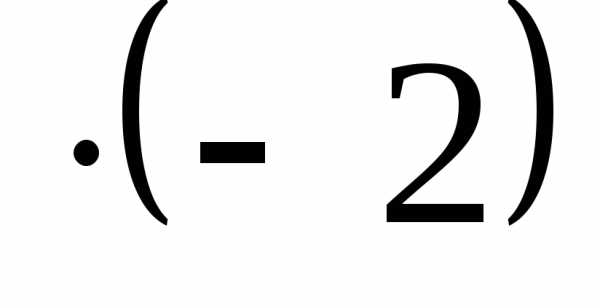 +
+
studfiles.net
3. Вычисление определителя порядка n
Вычисление определителей произвольного порядка можно выполнять, используя их разложение по строке или столбцу, аналогично тому, как это сделано в случае определителя третьего порядка. При этом вычисление определителя порядка n сводится к вычислению определителей порядка n-1. Разложение определителей порядка n-1 сводит его вычисление к вычислению определителей порядка n-2 и т.д. до тех пор, пока не получим определители третьего или второго порядков, которые можно вычислить, используя приведенные выше правила.
Пример. Вычислить определитель:
 .
.
Вычислим определитель разложив его по третьей строке.
 ==
==
=+
+(=
==0.
Обратим внимание на то, что при разложении определителя удобно выбирать ту строку (или столбец), которая содержит много нулей: выпадает необходимость вычислений соответствующих им алгебраических дополнений, так как умножение на нуль любого числа все равно дает нуль.
3.4. Свойства определителей. Методы вычисления, основанные на свойствах
Пусть 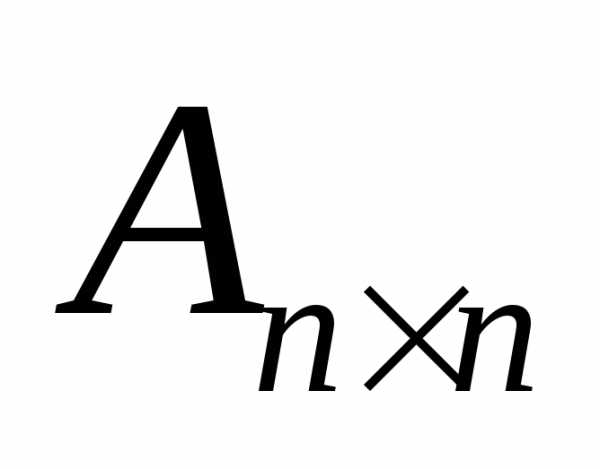 — квадратная матрица порядка n. Представим ее как систему n арифметических
векторов-строк:
— квадратная матрица порядка n. Представим ее как систему n арифметических
векторов-строк:
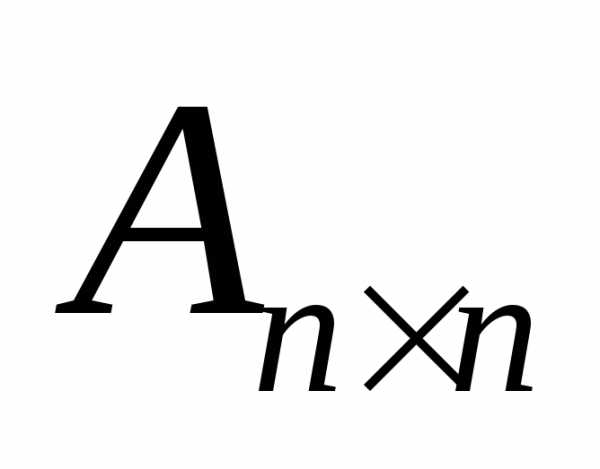 =
= =
=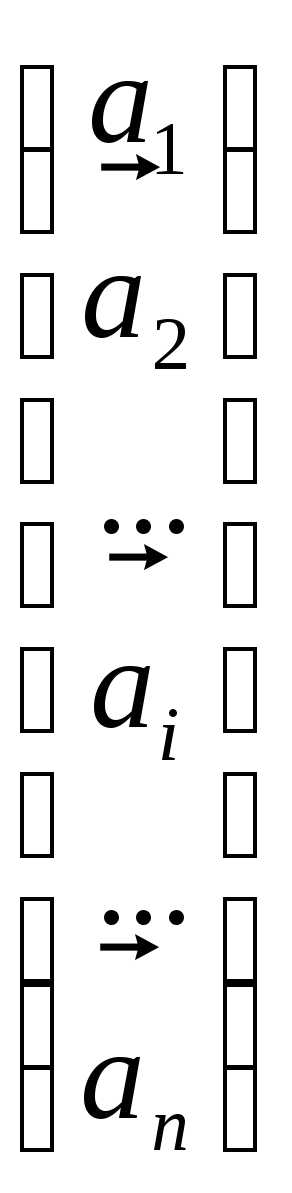 .
.
Основные свойства определителей приведены в таблице на следующей странице. Опираясь на эти свойства, можно свести вычисление определителя к последовательности однотипных действий.
Прежде всего, обратим внимание на то, что при транспонировании столбцы матрицы становятся строками, а строки столбцами. Такая операция, согласно свойству симметричности, не меняет определителя этой матрицы. Поэтому, все остальные свойства (аддитивность, однородность, антикоммутативность), касающиеся строк, в равной мере относятся и к столбцам.
Опираясь на свойства определителей, выведем следующее важное утверждение.
Утверждение. Определитель матрицы равен нулю тогда и только тогда, когда система строк ( столбцов) матрицы линейно зависима.
Напомним, что система векторов является линейно зависимой, если хотя бы один из векторов системы может быть представлен линейной комбинацией других ее векторов. Пусть система векторов строк матрицы A линейно зависима. Одна из ее строк является линейной комбинацией других. Пусть это будет первая строка:
Основные свойства определителей
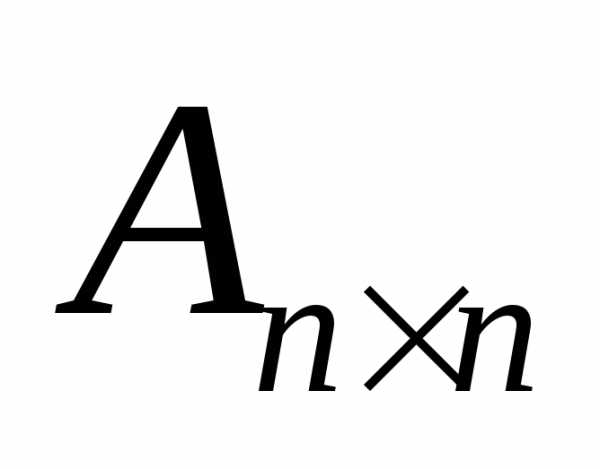 =
=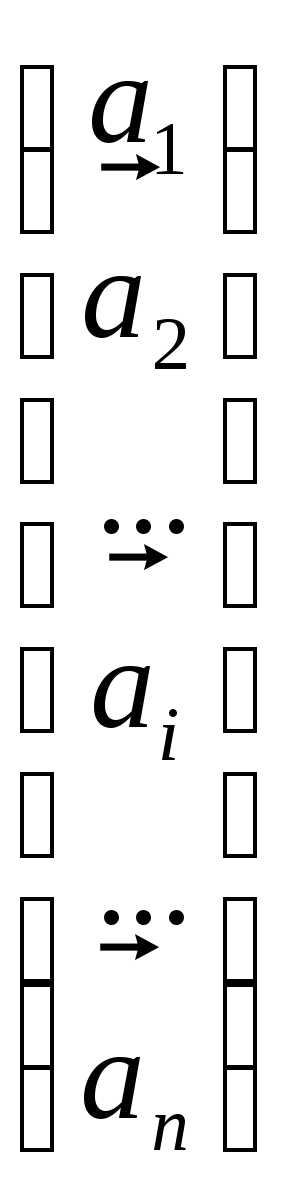 =
=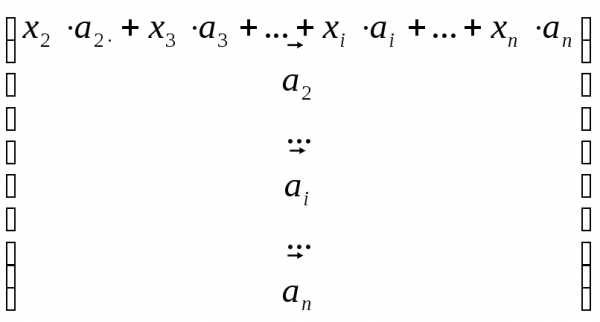
Используя свойства аддитивности и однородности определителей, запишем:
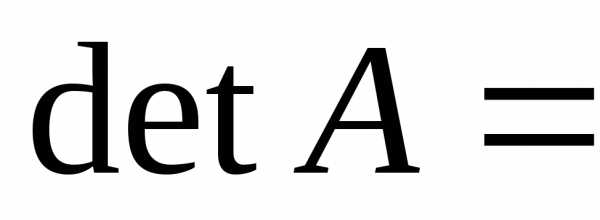
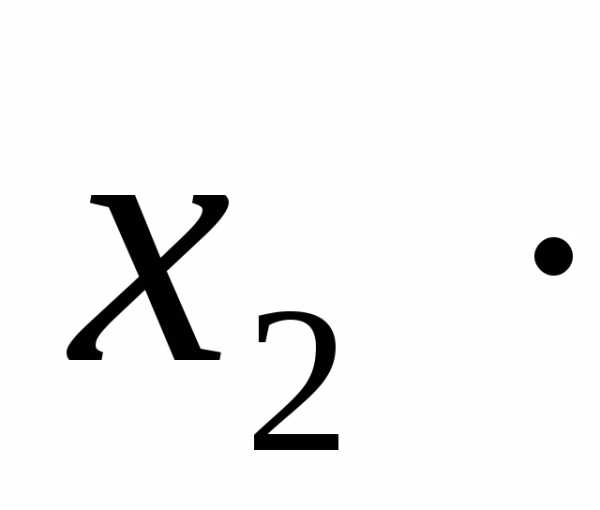

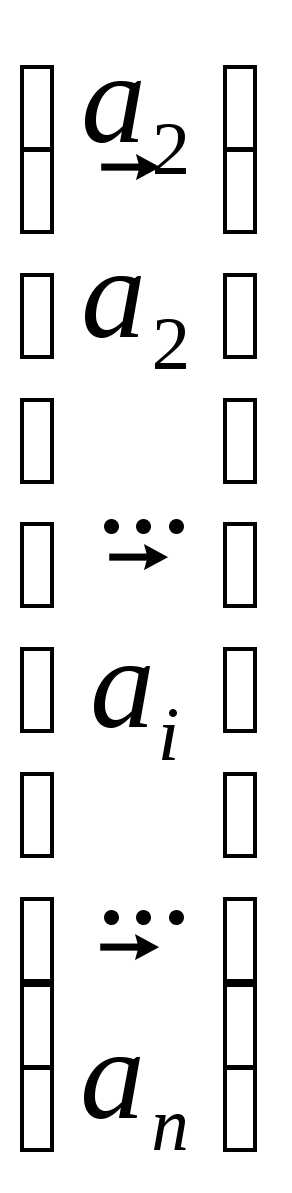 +
+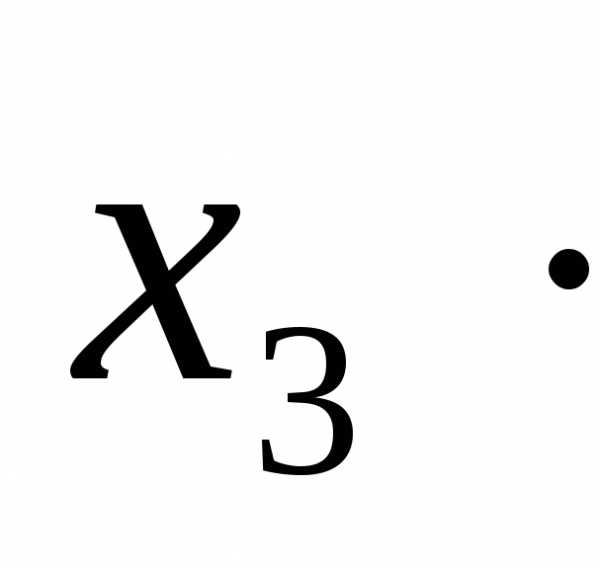

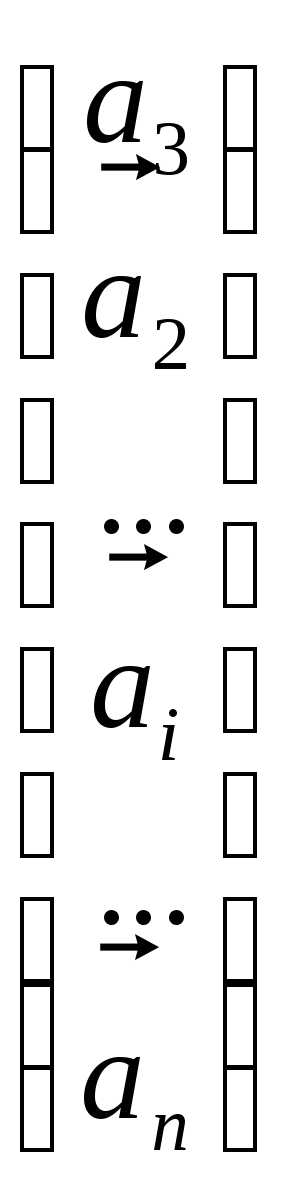 +….+
+….+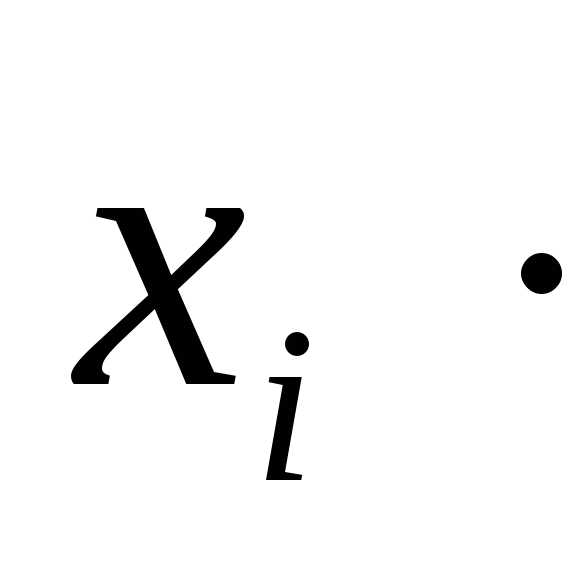

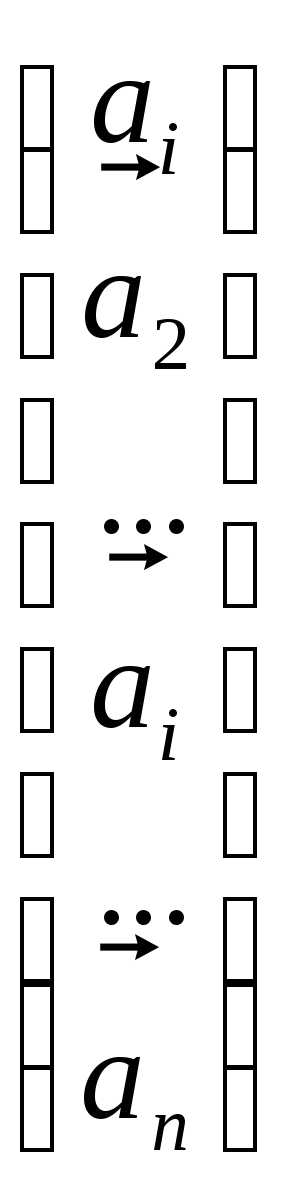 +….+
+….+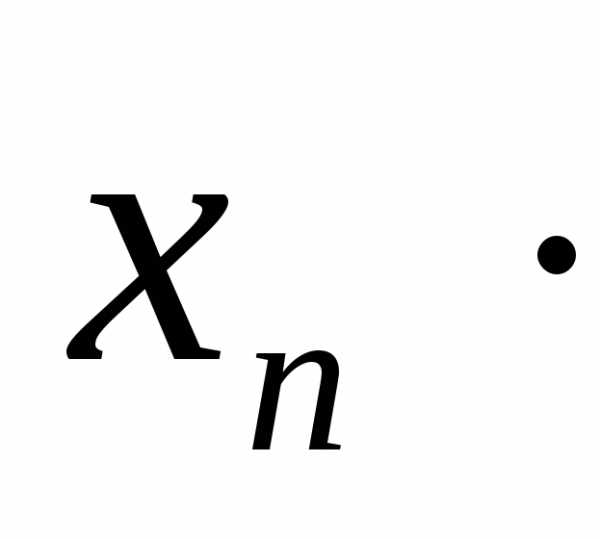

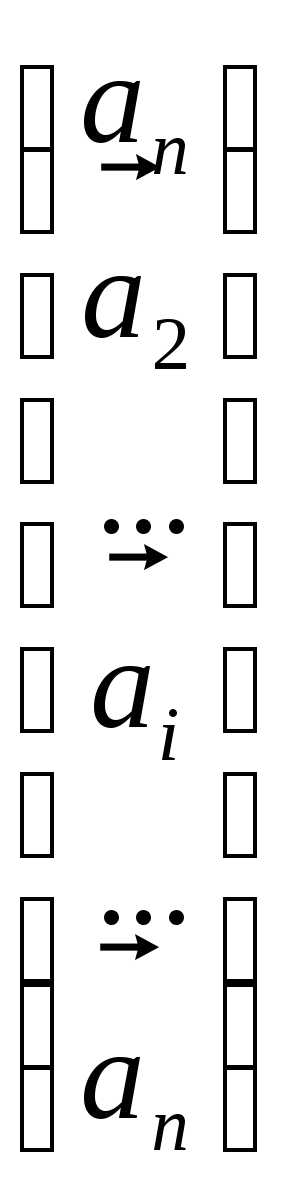 (*)
(*)
Каждый из определителей в правой части равенства (*) содержит 2 одинаковые строки.
Рассмотрим  Ai=
Ai=
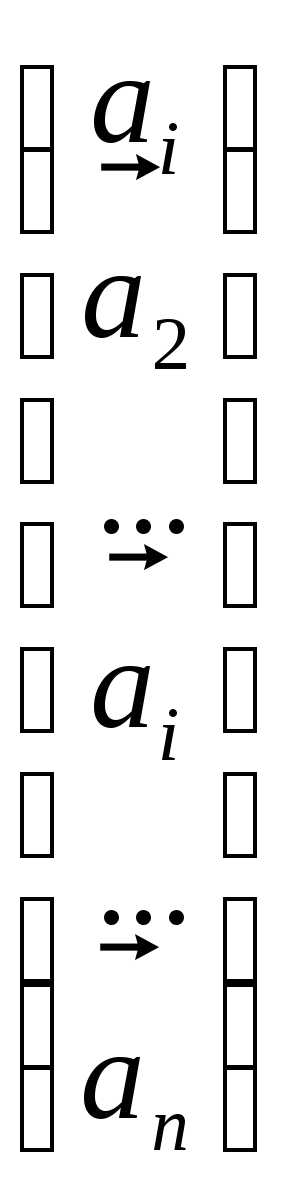 .
Если поменять местами первую иi-тую
строку в этом определителе, то он не
изменится, так как эти строки состоят
из одинаковых чисел. Но согласно свойству
антикоммутативности, определитель при
этом должен сменить знак:
.
Если поменять местами первую иi-тую
строку в этом определителе, то он не
изменится, так как эти строки состоят
из одинаковых чисел. Но согласно свойству
антикоммутативности, определитель при
этом должен сменить знак:
 Ai = —
Ai = —  Ai.
Ai.
Но
существует единственное число, для
которого справедливо подобного рода
равенство – это нуль. Следовательно,  Ai=0.
Но тогда и все остальные определители
в правой части равенства (*) равны нулю.
Из этого вытекает, что
Ai=0.
Но тогда и все остальные определители
в правой части равенства (*) равны нулю.
Из этого вытекает, что 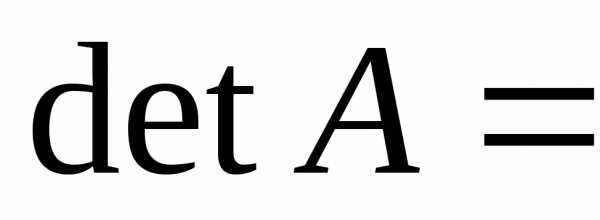 0.
0.
Из рассмотренного утверждения вытекает следствие:
Если к какой-либо строке (столбцу) определителя прибавить любую линейную комбинацию других строк (столбцов) определителя, то определитель не изменится.
Следствие может быть использовано для сведения определителя к треугольному или диагональному виду, после чего вычисление определителя становится очень простым.
Покажем на примере, как вычисляются определители треугольных и диагональных матриц.
Пример.
.
Вычисляя определитель, мы последовательно раскладывали определители 4, 3, 2-го порядков по первому столбцу. Процедура вычисления не изменилась бы, если бы матрица определителя была нижнетреугольной или диагональной.
Вывод. Определители треугольных и диагональных матриц равны произведению элементов, стоящих на главной диагонали.
Любой определитель, не равный нулю, можно свести к вычислению определителя треугольного или диагонального вида, пользуясь элементарными преобразованиями его матрицы.
№ п/п | Элементарные преобразования матрицы определителя | Операции с определителями |
1 | Умножение строки (столбца) на любое, отличное от нуля, число x. | Умножить определитель на число . |
2 | Деление строки на любое, отличное от нуля, число x. | Умножить определитель на число x. |
3 | Сложение любой строки (столбца) с линейной комбинацией других строк (столбцов). | Определитель не меняется. |
4 | Изменение порядка следования строк (столбцов) | Поменяв местами две любые строки (столбца) определителя, поставить перед определителем знак «-». |
Пример.
Вычислить определитель, сведя его к треугольному виду:
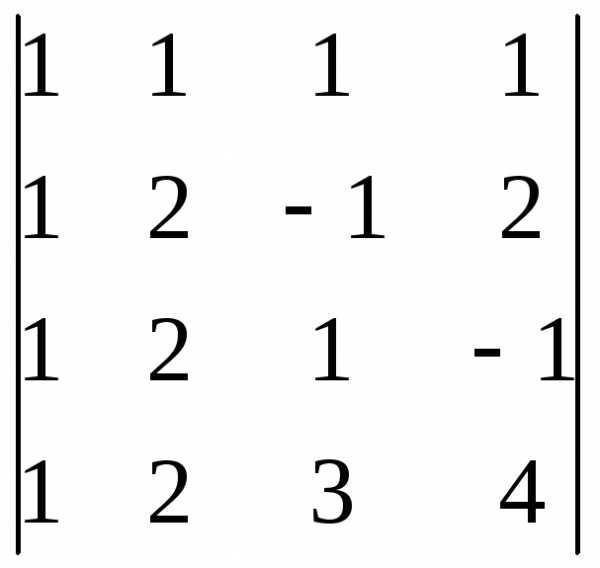 =
=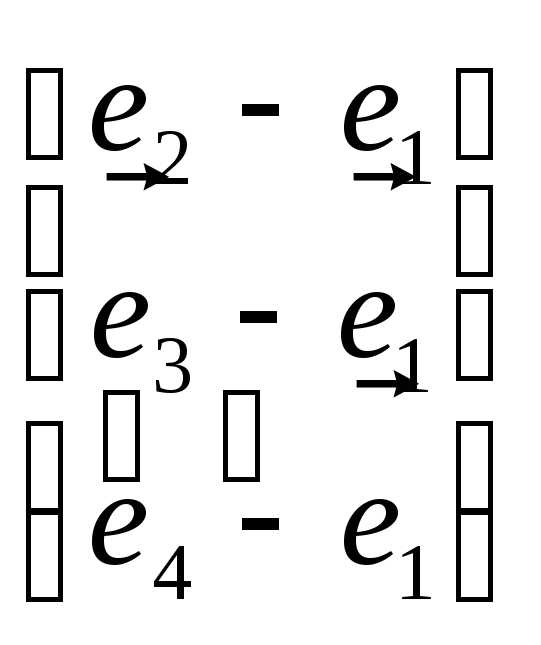 =
= =
=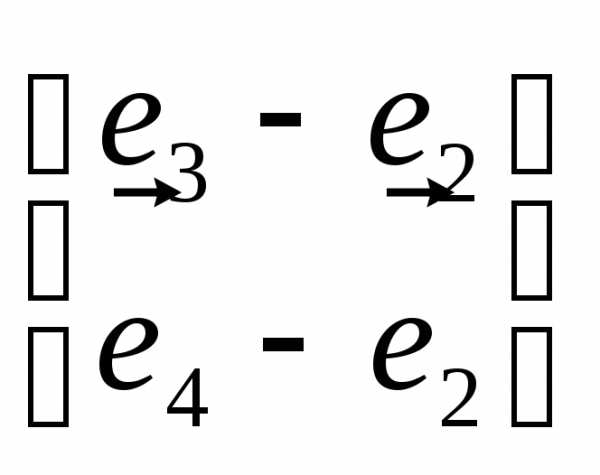 =
= =
=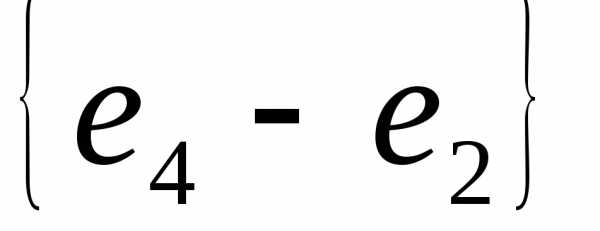 =
=
= =.
=.
В
фигурных скобках указаны выполняемые
действия. Например, 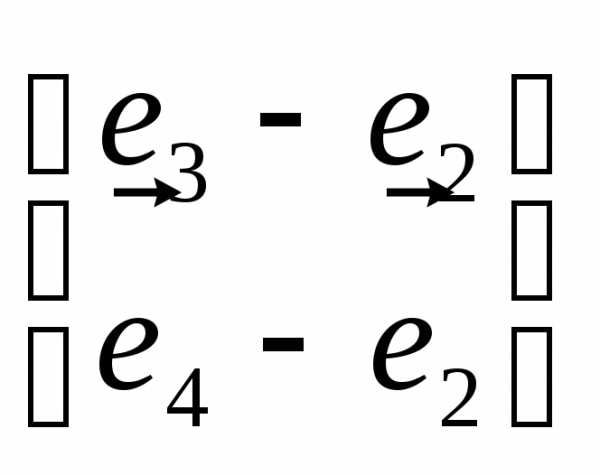 означает: из третьей и четвертой строк
вычли вторую строку.
означает: из третьей и четвертой строк
вычли вторую строку.
Если порядок матрицы велик, то сведение ее к треугольному виду удобно выполнять по следующему алгоритму:
Выделить разрешающий элемент. При вычислении определителя – это элемент, стоящий на главной диагонали
 .
.Переписать строку, в которой стоит разрешающий элемент (разрешающую строку
 ).
).В столбце под разрешающим элементом (разрешающем столбце
 )
записать нули.
)
записать нули.Остальные элементы, стоящие ниже разрешающей строки и правее разрешающего столбца, вычислить по формуле:
 ,
(),
которую легко запомнить какправило
прямоугольника:
,
(),
которую легко запомнить какправило
прямоугольника:
| Натягиваем прямоугольник так, чтобы одна его диагональ соответствовала разрешающему элементу и вычисляемому элементу. На месте вычисляемого элемента записываем разность вычисляемого элемента и дроби, в числителе которой — произведение элементов, стоящих на другой диагонали прямоугольника, а в знаменателе – разрешающий элемент. |
При
вычислении определителя матрицы n-ного
порядка последовательность действий
1- 4 выполняется за n—1
шаг: на первом шаге в качестве разрешающего
элемента выбирают  ,
на втором —
,
на втором —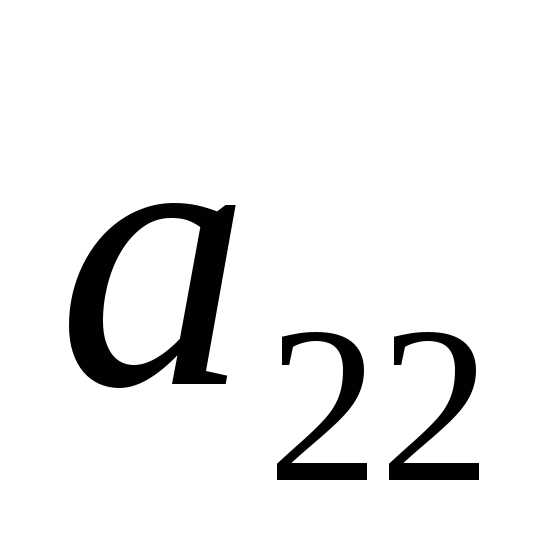 и т.д., на шаге (n—1)
—
и т.д., на шаге (n—1)
— 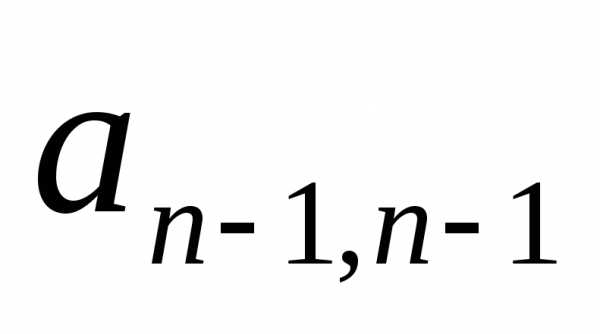 .
.
Применим данный алгоритм к решению следующего примера.
Пример.
Вычислить
определитель матрицы: 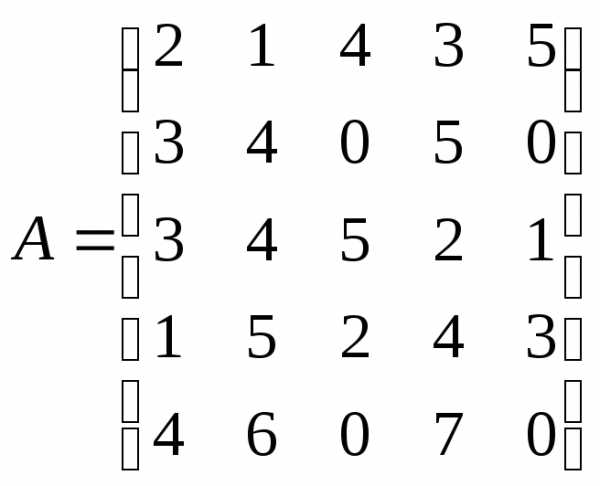
Решение
Шаг
0. Запишем
определитель: 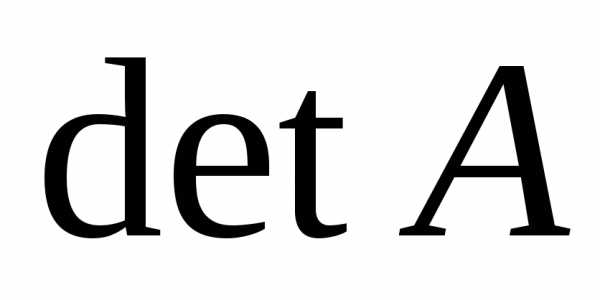 =
=
Шаг
1. Разрешающий
элемент 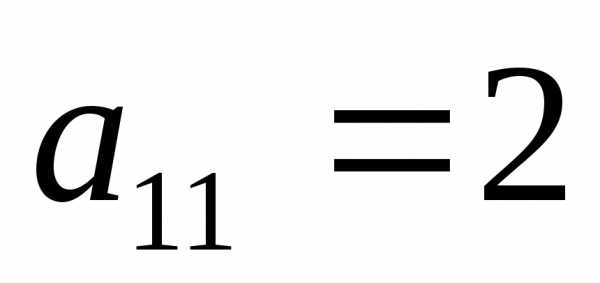 .
Выполняем последовательность действий
1-4:
.
Выполняем последовательность действий
1-4:
 =
= 
Шаг
2. Разрешающий
элемент 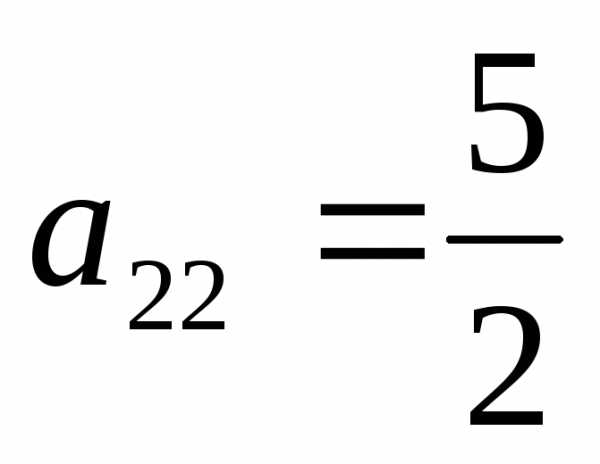 .
Выполняем последовательность действий
1-4:
.
Выполняем последовательность действий
1-4:
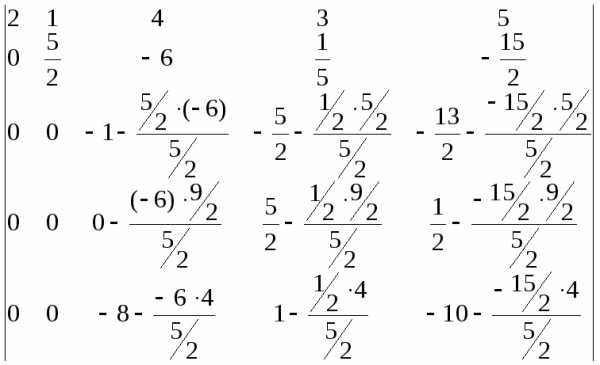 =
= 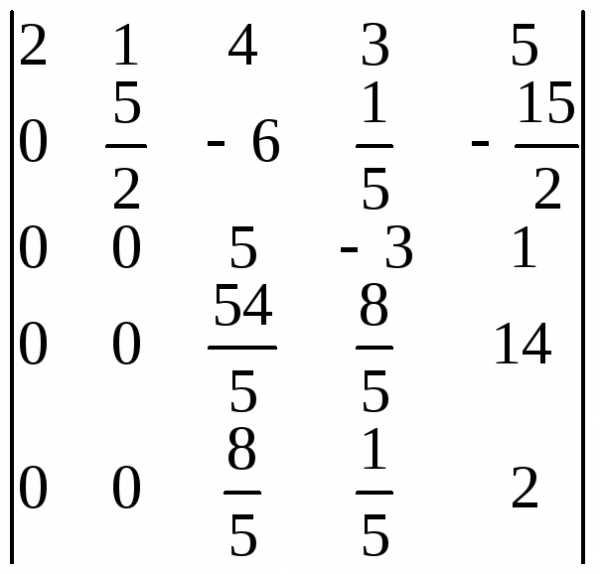
Шаг
3. Разрешающий
элемент 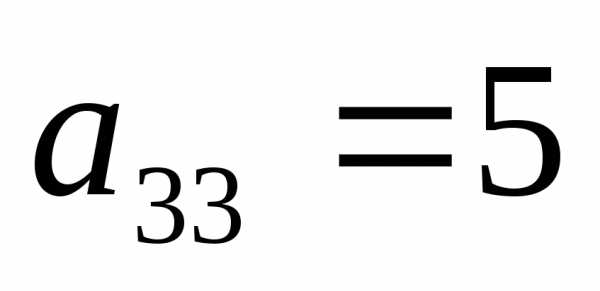 .
Выполняем последовательность действий
1-4:
.
Выполняем последовательность действий
1-4:
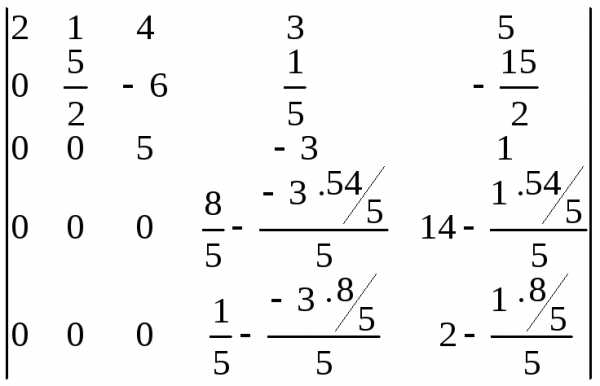 =
= 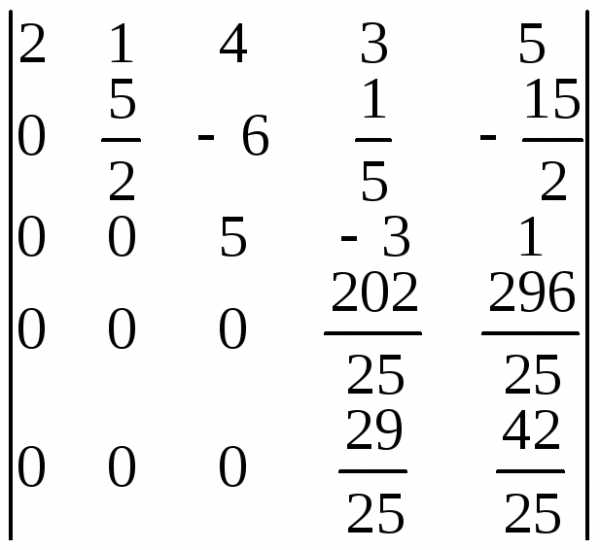
Шаг
4. Разрешающий
элемент 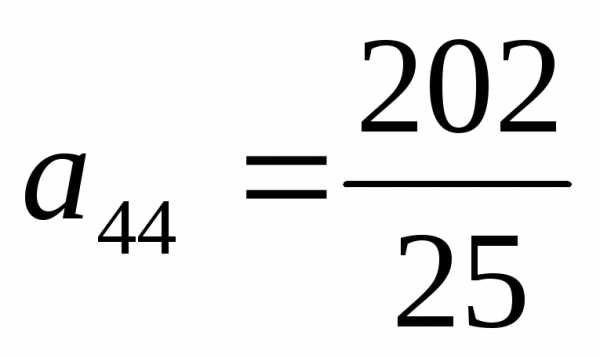 .
Выполняем последовательность действий
1-4:
.
Выполняем последовательность действий
1-4:
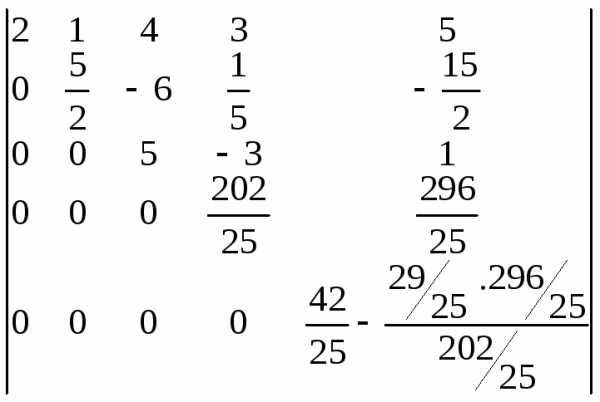 =
=  .
.
Матрица имеет треугольный вид, следовательно, ее определитель равен произведению диагональных элементов:
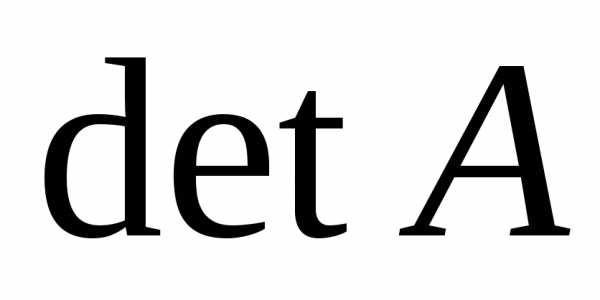 =
=
Замечание. Правило прямоугольника широко применяется в Линейном программировании – специальной дисциплине, которая изучается на старших курсах студентами экономического профиля.
studfiles.net

 -й
строке:
-й
строке: -му
столбцу:
-му
столбцу: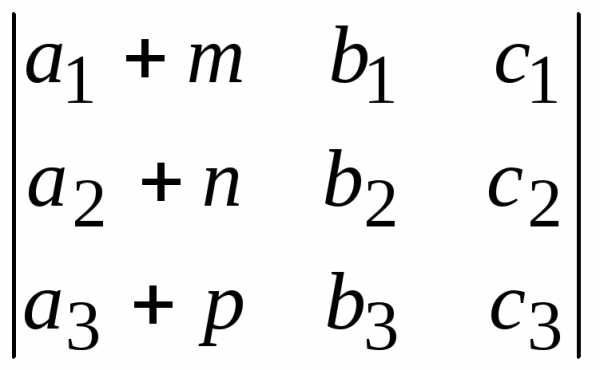 в виде суммы двух определителей.
в виде суммы двух определителей.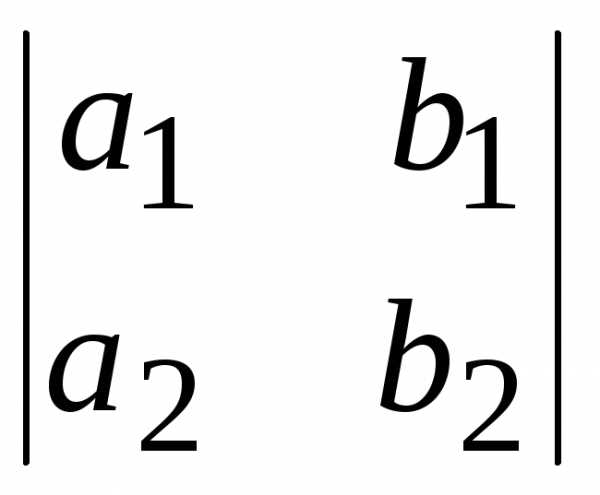 и
и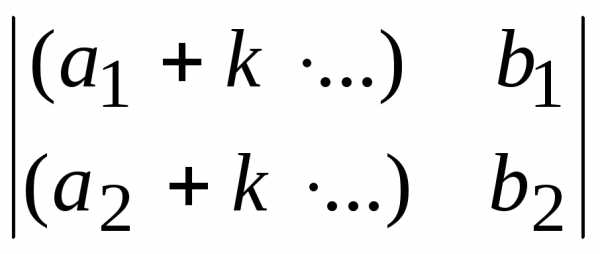 .
. и
и взаимно обратными?
взаимно обратными?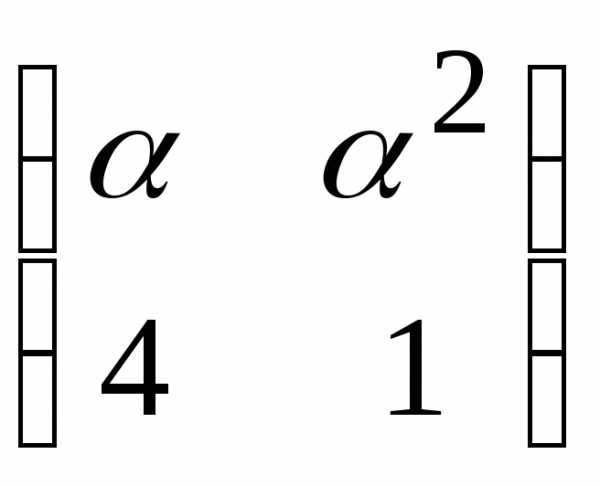 ?
?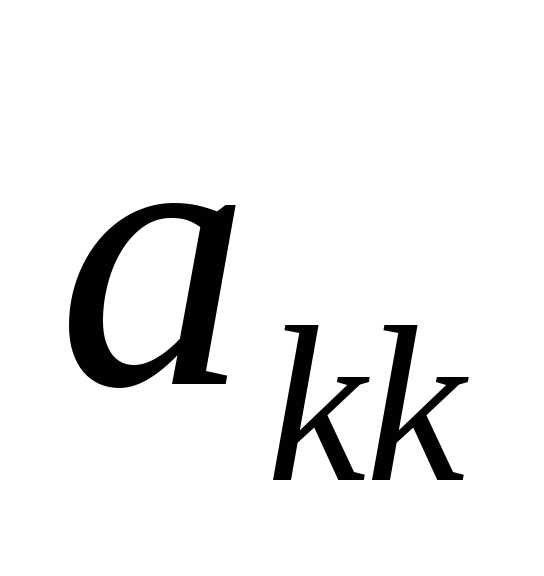 .
.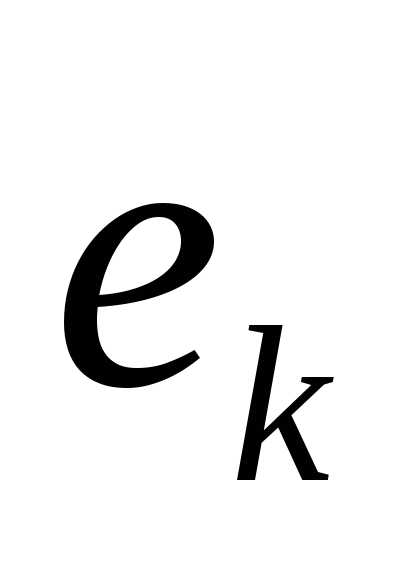 ).
).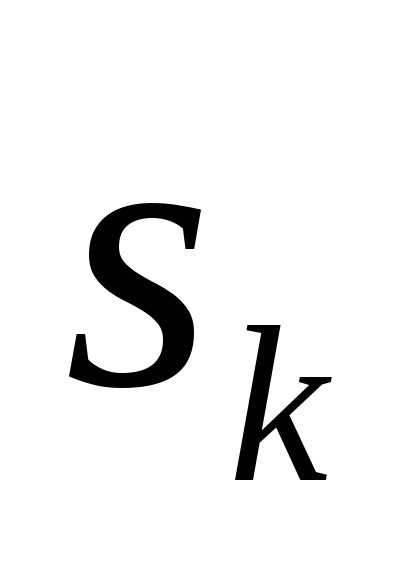 )
записать нули.
)
записать нули.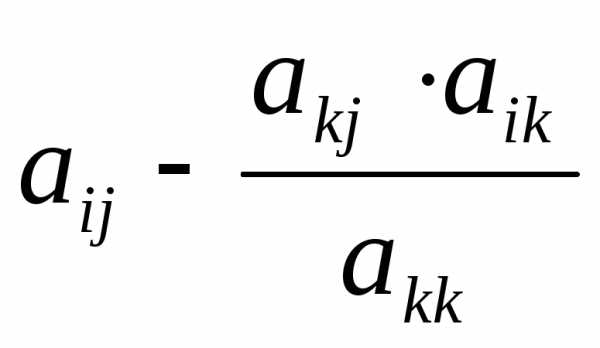 ,
(),
которую легко запомнить какправило
прямоугольника:
,
(),
которую легко запомнить какправило
прямоугольника:
