Найти наименьшее значение функции на отрезке – Как найти наибольшее и наименьшее значение функции, примеры

В15 ЕГЭ по математике. Исследование функции

 
Продолжение (начало здесь).
 
 
В заданиях №12  ЕГЭ по математике Вам предстоит производить элементарное исследование функции. Вы должны уметь находить точки экстремумов, экстремумы, наибольшие и наименьшие значения функций.
 
 

 Задание 1.

Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .

Решение: + показать

Задание 2.

Най­ди­те точку минимума функ­ции .

Решение: + показать

Задание 3.

Най­ди­те наи­мень­шее зна­че­ние функ­ции на

 Решение: + показать

Знаки производной распределяются следующим образом на образовавшихся промежутках:

Вообще говоря, мы работаем на отрезке , поведение функции  на нем следующее:

Наименьшее значение функции в данном случае* совпадает с минимумом функции (в точке ).

Ответ: 60.

Задание 4.

Най­ди­те точку мак­си­му­ма функ­ции

Решение: + показать

В соответствии со знаками производной указываем поведение функции:

Тогда точка – точка максимума функции.

Ответ: 16. 

Задание 5.

Най­ди­те точку ми­ни­му­ма функ­ции

Решение: + показать

Нам предстоит находить производную от произведения:

или

В соответствии со знаками производной указываем поведение функции:

Точка минимума – .

Ответ: 3. 

Задание 6.

Най­ди­те наи­мень­шее зна­че­ние функ­ции на  отрезке .

Решение: + показать

Задание 7.

Най­ди­те наи­боль­шее зна­че­ние функ­ции   на от­рез­ке

Решение: + показать

На отрезке  мы увидим  следующие знаки производной, и, соответственно,  следующее поведение функции:

Наибольшее значение функции на отрезке совпадает с максимумом функции в точке :

Ответ: 27. 

Задание 8.

Най­ди­те наи­боль­шее зна­че­ние функ­ции   на от­рез­ке

Решение: + показать

Задание 9.

Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке

Решение: + показать

Задание 10.

Най­ди­те наи­боль­шее зна­че­ние функ­ции   на от­рез­ке  .

Решение: + показать

Задание 11.

Най­ди­те точку ми­ни­му­ма функ­ции  при­над­ле­жа­щую про­ме­жут­ку .

Решение: + показать

Задание 12.

Най­ди­те наи­мень­шее зна­че­ние функ­ции   на от­рез­ке .

Решение: + показать

* Замечание. Важно!

Не следует считать (могло сложиться такое мнение при разборе примеров выше), что наименьшее (наибольшее) значение функции на отрезке совпадает с минимумом (максимумом) на отрезке!

Например, на рисунке ниже наименьшее значение функции  на отрезке достигается на конце отрезка , а именно, в точке .

То есть, вообще говоря, при нахождении наименьшего значения функции на отрезке следует выбрать наименьшую из величин:

1) (их может быть несколько) из рассматриваемого отрезка 

2) ,  

При нахождении наибольшего значения функции на отрезке следует выбрать большую из величин:

1) (их может быть несколько) из рассматриваемого отрезка 

2) ,  

Но, если, например, на рассматриваемом отрезке функция имеет только один экстремум – минимум и мы ищем наименьшее значение, то отпадает необходимость находить значения функции на концах отрезка.

Аналогично в случае с нахождением наибольшего значения функции на отрезке, на котором содержится только один экстремум – максимум.

В случае же, когда на отрезке рассматриваемом функция не имеет экстремумов, то для нахождения наибольшего/наименьшего значений требуется лишь сравнить эти самые значения функции на концах отрезка и взять наибольшее/наименьшее из них.

 

Переменка! Отдохните… + показать

 

Вы можете пройти тест №2 по Задачам №12.

 

egemaximum.ru

Найдите наибольшее значение функции

В прошлой статье мы рассмотрели задания на определение точек максимума (минимума) степенной функции. Здесь представлено 7 примеров со степенной функцией. Требуется определить наибольшее (или наименьшее) значение функции на интервале. На блоге уже рассматривались подобные примеры функций с числом е, логарифмические, тригонометрические, рациональные.

Стандартный алгоритм решения таких заданий предполагает после нахождения нулей функции, определение знаков производной на интервалах. Затем вычисление значений в найденных точках максимума (или минимума) и на границе интервала, в зависимости от того какой вопрос стоит в условии. 

Советую поступать немного по-другому. Почему? Писал об этом здесь.

Предлагаю решать такие задания следующим образом:

1. Находим производную.
2. Находим нули производной.
3. Определяем какие из них принадлежат данному интервалу.
4. Вычисляем значения функции на границах интервала и точках п.3.
5. Делаем вывод (отвечаем на поставленный вопрос).

В ходе решения представленных примеров подробно не рассмотрено решение квадратных уравнений, это вы должны уметь делать. Так же должны знать производные элементарных функций.

Рассмотрим примеры:

77422. Найдите наибольшее значение функции у=х³–3х+4 на отрезке [–2;0].

Найдём производную заданной функции:

Найдем нули производной:

Указанному в условии интервалу принадлежит точка х = –1.

Вычисляем значения функции в точках   –2, –1 и 0:

Наибольшее значение функции равно 6.

Ответ: 6

77425. Найдите наименьшее значение функции у = х³ – 3х² + 2 на отрезке [1;4].

Найдём производную заданной функции:

Найдем нули производной:

Указанному в условии интервалу принадлежит точка х = 2.

Вычисляем значения функции в точках  1, 2 и 4:

Наименьшее значение функции равно –2.

Ответ: –2

77426. Найдите наибольшее значение функции у = х³ – 6х² на отрезке [–3;3].  

Найдём производную заданной функции:

Найдем нули производной:

Указанному в условии интервалу принадлежит точка х = 0.

Вычисляем значения функции в точках  –3, 0 и 3:

Наименьшее значение функции равно 0.

Ответ: 0

77429. Найдите наименьшее значение функции у = х³ – 2х² + х +3 на отрезке [1;4] .

Найдём производную заданной функции:

Найдем нули производной, решаем квадратное уравнение:

3х² – 4х + 1 = 0

Получим корни:  х₁ = 1    х₁ = 1/3.   

Указанному в условии интервалу принадлежит  только х = 1.

Найдём значения функции в точках  1 и 4:

Получили, что наименьшее значение функции равно 3.

Ответ: 3

77430. Найдите наибольшее значение функции у = х³ + 2х² + х + 3 на отрезке [– 4; –1].

Найдём производную заданной функции:

Найдем нули производной, решаем квадратное уравнение:

3х² + 4х + 1 = 0

Получим корни:

Указанному в условии интервалу принадлежит  корень х = –1.

Находим значения функции в точках  –4, –1, –1/3 и 1:

Получили, что наибольшее значение функции равно 3.

Ответ: 3

77433. Найдите наименьшее значение функции у = х³ – х² – 40х +3 на отрезке [0;4].

Найдём производную заданной функции:

Найдем нули производной, решаем квадратное уравнение:

 3х² – 2х – 40 = 0

Получим корни:

Указанному в условии интервалу принадлежит  корень х = 4.

Находим значения функции в точках  0 и 4:

Получили, что наименьшее значение функции равно   –109.

Ответ: –109

Рассмотрим способ определения наибольшего и наименьшего значения функций без производной. Этот подход можно использовать, если с определением производной у вас большие проблемы. Принцип простой – в функцию подставляем все целые значения из интервала (дело в том, что во всех подобных прототипах ответом является целое число).

77437. Найдите наименьшее значение функции у=7+12х–х³ на отрезке [–2;2].

Подставляем точки от  –2  до  2:

у(–2)=7+12 (–2) – (–2)³ = – 9

у(–1)=7+12 (–1) – (–1)³ = – 6

у(0)=7+12∙0 – 0³ = 7

у(1)=7+12∙1 – 1³ = 18

у(2)=7+12∙2 – 2³ = 23

Наименьшее значение равно –9.

Ответ: –9

77441. Найдите наименьшее значение функции у=9х²–х³ на отрезке [–2;2].

Подставляем точки от  –2  до  2:

у(–2)=9 (–2)² – (–2)³ = 44

у(–1)=9 (–1)² – (–1)³ = 10

у(0)=9∙0² – 0³ = 0

у(1)=9∙1² – 1³ = 8

у(2)=9∙2² – 2³ = 28

Наименьшее значение равно 0.

Ответ: 0

77442. Найдите наибольшее значение функции у=9х²–х³ на отрезке [2;10].

Подставляем точки от 2  до 10. В данном примере интервал большой и вычислений будет больше, но способ вполне применим.

Ответ: 108

*Чем меньше интервал, тем быстрее решите задачу.

 

77421. Найдите наименьшее значение функции у=х³ –27х на отрезке [0;4].

Посмотреть решение

77434. Найдите наибольшее значение функции у=х³ + 2х² – 4х + 4 на отрезке  [–2;0].

Посмотреть решение

На этом всё. Успеха вам!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Наибольшее и наименьшее значение функции.

В этой статье я расскажу о том, как применять умение находить производную сложной функции к исследованию функции: к нахождению ее наибольшего или наименьшего значения. А затем мы решим несколько задач из Задания В15 из  Открытого банка заданий для подготовки к ЕГЭ  по математике.

Как обычно,  сначала вспомним теорию.

В начале любого исследования функции находим ее область определения.

Чтобы найти наибольшее или наименьшее значение функции , нужно исследовать, на каких промежутках функция возрастает, и на каких убывает.

Для этого надо найти производную функции  и исследовать ее промежутки знакопостоянства, то есть промежутки, на которых производная сохраняет знак.

Промежутки, на которых производная функции положительна, являются промежутками возрастания функции.

Промежутки, на которых производная функции отрицательна, являются промежутками убывания функции.

1. Решим задание В15 (№ 245184)

Найдите наибольшее значение функции 

Для его решения будем следовать такому алгоритму:

а) Найдем область определения  функции 

б) Найдем производную функции .

в) Приравняем ее к нулю.

г) Найдем промежутки знакопостоянства функции.

д) Найдем точку, в которой функция принимает наибольшее значение.

е) Найдем значение функции в этой точке.

Подробное решение этого задания я рассказываю в ВИДЕОУРОКЕ:

Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачать
Firefox

2. Решим задание В15 (№282862)

Найдите наибольшее значение функции  на отрезке [1;3]

а) Найдем область определения функции  . Эта функция определена при любом действительном значении  

б) Найдем производную функции  . Для этого удобно  правую часть уравнения функции преобразовать в многочлен. Можно, конечно, использовать формулу для нахождения производной произведения, но в этом случае, мне кажется, что это нецелесообразно.

в) Приравняем производную к нулю:

,  

г) Исследуем знаки производной:

Мы исследуем поведение функции на отрезке [1;3]:

Очевидно, что наибольшее значение на отрезке  [1,3] функция принимает в точке максимума, при х=2. Найдем значение функции в этой точке:

Ответ: 5

3. Решим задание В15 (№245180):

Найдите наибольшее значение функции 

a) Найдем область определения функции . Выражение, стоящее под знаком логарифма должно быть больше нуля: . Пока на этом остановимся, решим  неравенство, если  в этом возникнет необходимость в процессе решения.

а) Найдем производную функции :

В таблице производных найдем производную логарифмической функции:

Для   производной сложной функции эта формула выглядит так:

Выясним  промежутки знакопостоянства выражения 

Воспользуемся методом интервалов.

1. , , т.к.  , поэтому это число не влияет на знак неравенства.

2. Т.к по область определения исходной функции  , следовательно знаменатель дроби всегда больще нуля и дробь меняет знак только в нуле числителя.

3. Числитель равен нулю при . Проверим, принадлежит ли   ОДЗ функции. Для этого проверим, выполняется ли условие    при .

,  

значит, точка   принадлежит ОДЗ функции

Исследуем знак производной справа и слева от точки :

Мы видим, что наибольшее значение функция принимает в точке . Теперь найдем значение функции при :

Ответ: 4

Замечание 1. Заметим, что в этой задаче мы не находили область определения функции: мы только зафиксировали ограничения и проверили, принадлежит ли точка, в которой производная равна нулю области определения  функции. В данной задаче этого оказалось достаточно. Однако, так бывает не всегда. Это зависит от задачи.

Замечание 2. При исследовании поведения сложной функции можно пользоваться таким правилом:

• если внешняя функция сложной функции возрастающая, то функция принимает наибольшее значение в той же точке, в которой внутренняя функция принимает наибольшее значение. Это следует из определения возрастающей функции: функция возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.
• если внешняя функция сложной функции убывающая, то функция принимает наибольшее значение в той же точке, в которой внутренняя функция принимает наименьшее значение. Это следует из определения убывающей функции: функция убывает на промежутке I, если большему значению аргумента из этого промежутка соответствует меньшее значение функции

 В нашем примере внешняя функция — возрастает на всей области определения.  Под знаком логарифма стоит выражение  — квадратный трехчлен, который при отрицательном старшем коэффициенте принимает наибольшее значение в точке . Далее подставляем это значение х в уравнение функции  и находим ее наибольшее значение.

И.В. Фельдман, репетитор по математике.

 

ege-ok.ru

Найдите наименьшее значение функции

В недавней статье мы рассмотрели нахождение точек максимума (минимума) для иррациональной функции. Здесь представлено решение нескольких примеров на нахождение наибольшего (наименьшего) значения таких функции на данном отрезке.

Алгоритм решения уже описывался не раз, посмотрите его в статье, где мы рассматривали задания с логарифсами. Если у вас есть общие вопросы по теории, то советую изучить эту статью. Данный тип заданий включает в себя все действия, которые производятся при вычислении точек максимума (минимума). После этого необходимо определить какие из этих точек принадлежат указанному интервалу, затем вычислить значения функции в этих точках и на границах интервала, а далее выбрать наибольшее или наименьшее. Рассмотрим примеры:

77454. Най­ди­те наи­мень­шее зна­че­ние функ­ции y=(2/3) x^3/2 −3x+1 на отрезке [1;9].

Найдём производную заданной функции:

Найдем нули производной:

Решаем уравнение:

Полученное значение х входит в данный интервал.

Вычисляем значения функции в точках 1 и 9:

Наименьшее значение функции равно –8.

Ответ: −8

77456. Найдите наибольшее значение функции

на отрезке [0;4].

Найдём производную заданной функции:

Найдем нули производной:

Решаем уравнение:

Данное значение х входит в интервал.

Вычисляем значения функции в точках  0, 1 и 4:

Большее значение функции равно 1.

Ответ: 1

77466. Найдите наибольшее значение функции

на отрезке [1;9].

Найдём производную заданной функции:

Найдем нули производной:

Решаем уравнение:

Данное значение х входит в интервал (лежит на его границе).

Вычисляем значения функции в точках   1 и 9:

Наибольшее значение функции равно 10.

*На данном интервале производная положительна, поэтому наибольшее значение будет в крайней правой точке.

Ответ: 10

 

77452. Найдите наименьшее значение функции y = x^3/2– 3x+1 на отрезке [1;9].

Посмотреть решение

На этом всё. Учитесь с удовольствием!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Найдите наименьшее значение функции y = 5cosx – 6x + 4

   Здравствуйте! В этой статье мы с вами рассмотрим задачи на нахождение наибольшего (наименьшего) значения тригонометрической функции на заданном отрезке. Рассмотрим несколько примеров. Но сначала советую повторить теорию, всё необходимое есть в статье «Исследование функций, это нужно знать!».

На блоге уже рассмотрены подобные задачи с логарифмической функцией, функции с числом е, а также функции в составе которых имеется квадратичная функция (решаются без нахождения производной). Можете ознакомиться со статьёй, в которой мы рассматривали нахождение точек максимума (минимума) тригонометрических функций.

Алгоритм процесса решения прост, кратко напомню:

1. Находим производную.

2. Приравниваем её к нулю и решаем уравнение (находим вероятные точки экстремумов).

3. Далее вычисляем значения данной функции на границах отрезка, также в найденных точках п.2.

4. Определяем наибольшее (наименьшее), в зависимости от поставленного вопроса.

Здесь стоит отметить, что если уравнение п.2 не имеет решения, то это означает, что функция на всём отрезке возрастает (рис.1) или убывает (рис.2):

 

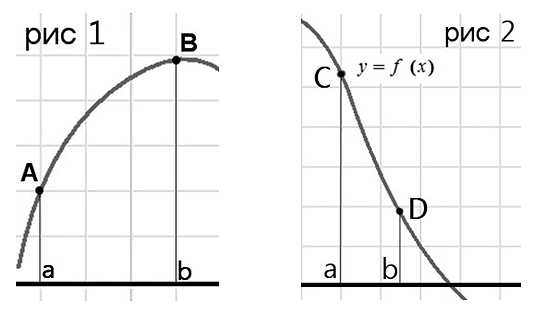
Что это означает? 

Это значит то, что точек минимума (максимума) нет и нам необходимо определить знак производной.

— Если производная имеет отрицательное значение, то функция убывает.

— Если производная имеет положительное значение, то функция возрастает.

Далее мы уже без труда сможем выявить в какой (пограничной) точке отрезка значение функции наибольшее, а в какой наименьшее.

Подробнее:

— если функция возрастает и стоит вопрос о нахождении наибольшего значения на отрезке, то оно будет в крайней правой точке отрезка;

— если функция возрастает и стоит вопрос о нахождении наименьшего значения на отрезке, то оно будет в крайней левой точке отрезка;

— если функция убывает и стоит вопрос о нахождении наибольшего значения на отрезке, то оно будет в крайней левой точке отрезка;

— если функция убывает и стоит вопрос о нахождении наименьшего значения на отрезке, то оно будет в крайней правой точке отрезка.

В представленных ниже задачах нахождение производной подробно не расписано, производные элементарных функций вы должны знать на отлично.

Что ещё следует помнить?

1. Когда речь идёт о синусе и косинусе имеются ограничения:

– 1 ≤ sin x ≤  1      и     – 1 ≤ cos x ≤  1

2. В ответе должно получится целое число, либо конечная десятичная дробь. Если  получили числовое выражение с неизвлекаемым корнем, то оно ответом являться не будет.

25594. Найдите наименьшее значение функции y = 5cosx – 6x + 4

на отрезке [–3П/2; 0].

Найдём производную заданной функции:

Найдем нули производной на заданном отрезке:

Известно, что  – 1 ≤ sin x ≤  1, то есть уравнение не имеет решения.

Это означает, что в пределах заданного интервала нет точек минимума и максимума. Производная будет отрицательна при всех значениях переменной. Почему?

Если учесть, что  – 1≤sinx≤ 1,  то получаем

– 1≤sinx≤1   =>  5 ≥ –5sinx≥ –5   =>   –1 ≥ –5sinx–6 ≥ –11

то есть значение выражения (производной) «–5cosx – 6» лежит в пределах от  – 11 до  – 1 включительно.

Следовательно на указанном интервале функция убывает, и наименьшее значение будет в крайней правой  точке, то есть при х = 0. Таким образом,

Ответ: 9

26697. Найдите наименьшее значение функции y = 7sin x – 8x + 9

на отрезке [–3П/2; 0].

Найдём производную заданной функции:

Найдем нули производной на заданном отрезке:

Известно, что  – 1 ≤ cos x ≤  1, то есть уравнение не имеет решения.

Это означает, что в пределах заданного интервала нет точек минимума и максимума. Производная отрицательна при всех значениях переменной, значение производной лежит в пределах от   – 15 до  – 1 включительно.

Значит на указанном интервале функция убывает. 

Следовательно наименьшее значение функции на заданном отрезке будет в правой крайней точке, то есть при х = 0.

Ответ: 9

77498. Найдите наибольшее значение функции

Найдём производную заданной функции:

Найдем нули производной на заданном отрезке:

Точка x = П/6, принадлежит заданному интервалу.

Вычислим значение функции в точках: 0, П/6, П/2.

Если учесть, что число Пи равно 3,14 а корень из трёх  ≈ 1,73  то значения  вычислить будет не трудно:

Значит наибольшим значением функции на отрезке  будет 12. Данные приближённые значения можно и не вычислять. Достаточно  помнить то, что ответом в задачах части В является целое число, а там где присутствует неизвлекаемый в целых числах корень, целое число мы никак не получим.

Ответ: 12

*Примечание. Корень уравнения мы записали сразу с учётом данного в условии отрезка, поэтому период косинуса в результате не записан.

26699. Найдите наибольшее значение функции

Найдем производную заданной функции:

Найдем нули производной на заданном отрезке:

Значит уравнение не имеет решения, так  как  – 1 ≤ cos x ≤  1.

Учитывая данное ограничение, производная  на данном отрезке имеет отрицательное значение:

Следовательно она убывает. 

Таким образом, наибольшее значение функции на заданном отрезке будет в левой  крайней точке, то есть при х = – 5П/6.

Ответ: 32

26692. Найдите наибольшее значение функции

Посмотреть решение

26693. Найдите наименьшее значение функции

Посмотреть решение

26695. Найдите наибольшее значение функции

Посмотреть решение

26696. Найдите наименьшее значение функции

Посмотреть решение

77499. Найдите наименьшее значение функции

Посмотреть решение

*Примечание. Безусловно, можно после вычисления нулей функции, определить точки максимума (минимума) и далее исходя из этого вычислять наибольшее (наименьшее) значение. Но можно обойтись без этого, так как при подстановке нулей и границ отрезка мы однозначно, и наверняка, искомое значение найдём. В любом случае, используйте тот путь (способ), к которому вы привыкли.

В будущем рассмотрим ещё несколько заданий с тригонометрическими функциями, не пропустите!

На этом всё! Успехов Вам!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

§ 15. Наибольшее и наименьшее значения функции на отрезке

Пусть функция y

= f(x),x[a; b], непрерывна на отрезке [а; b], дифференцируема во всех точках этого отрезка и имеет на нем конечное число критических точек первого рода.

Очевидно, что если данная функция монотонна на отрезке [а; b], то наибольшее и наименьшие значения достигаются на концах этого отрезка, а именно:

1) если функция f(x) возрастающая, то f(а)-наименьшее значение и f(b)—наибольшее значение;

2) если функция f(x) убывающая, то f(a)—наиболь­шее значение и f(b)— наименьшее значение. Если функция f(x) не является монотонной, то свое наибольшее значение на отрезке [а;b] она дости­гает либо в одной из то­чек максимума, либо на одном из концов этого отрезка. Точно так же наименьшее значение на отрезке [а; b] функция f(

x) достигает либо в одной из точек минимума, либо на одном из концов отрезка [а; b] (см., например, рис.18)

Рис 18

Таким образом, чтобы найти наибольшее и наимень­шее значения функции f(x) на отрезке [а; b] нужно:

1) найти критические точки первого рода данной функции;

2) вычислить значения функции во всех критических точках, принадлежащих интервалу ]а;b[ и на концах отрезка [a; b];

3) из полученных значений выбрать наибольшее и наименьшее.

Пример 1. Найти наибольшее и наименьшее значе­ния функции у = f(x) = х⁴ —2х² + 5 на отрезке [-2; 3]

Решение. 1) Находим критические точки данной функции: у’ = 4x³ — 4х, 4х³ — 4х = 0, откуда

= -1,

=0 и

2) Находим: f(-2)= 12, f(-1) = 4, f(0)=5, f(1) = 4 и f(3)= 68.

Итак, = 68, = 4.

Нахождение наибольшего и наименьшего значений функции широко применяется при решении многих практических задач.

20

studfiles.net

Как найти наименьшее значение функции на отрезке: правила, примеры и особенности

Исследование функций и их графиков – это тема, которой уделяется особое внимание в рамках школьной программы старших классов. Некоторые основы математического анализа – дифференцирования – включены в профильный уровень экзамена по математике. У некоторых школьников возникают проблемы с этой темой, так как они путают графики функции и производной, а также забывают алгоритмы. В этой статье будут рассмотрены основные типы заданий и способы их решения.

Что такое значение функции?

Математическая функция представляет собой особое уравнение. Оно устанавливает взаимосвязь между числами. Функция зависит от значения аргумента.

Значение функции рассчитывается по заданной формуле. Для этого следует подставить любой аргумент, который соответствует области допустимых значений, в эту формулу на место х и выполнить необходимые математические операции. Какие?

Как можно найти наименьшее значение функции, используя график функции?

Графическое изображение зависимости функции от аргумента называется графиком функции. Он строится на плоскости с определенным единичным отрезком, где по горизонтальной оси абсцисс откладывается значение переменной, или аргумента, а по вертикальной оси ординат – соответствующее ему значение функции.

Чем больше значение аргумента, тем правее он лежит на графике. И чем больше значение самой функции, тем выше находится точка.

О чем это говорит? Самым маленьким значением функции будет являться точка, которая лежит ниже всего на графике. Для того чтобы найти его на отрезке графика, нужно:

1) Найти и отметить концы этого отрезка.

2) Визуально определить, какая точка на этом отрезке лежит ниже всего.

3) В ответ записать ее числовое значение, которое можно определить, спроецировав точку на ось ординат.

Точки экстремума на графике производной. Где искать?

Однако при решении задач иногда дан график не функции, а ее производной. Для того чтобы случайно не допустить глупую ошибку, лучше внимательно читать условия, так как от этого зависит, где нужно искать точки экстремума.

Итак, производная — это мгновенная скорость возрастания функции. Согласно геометрическому определению производная соответствует угловому коэффициенту касательной, которая непосредственно проведена к данной точке.

Известно, что в точках экстремума касательная параллельна оси Ox. Это значит, что ее угловой коэффициент — 0.

Из этого можно сделать вывод, что в точках экстремума производная лежит на оси абсцисс или обращается в ноль. Но кроме того, в этих точках функция меняет свое направление. То есть после периода возрастания начинает убывать, а производная, соответственно, сменяется с положительной на отрицательную. Или наоборот.

Если производная из положительной становится отрицательной — это точка максимума. Если из отрицательной становится положительной — точка минимума.

Важно: если в задании требуется указать точку минимума или максимума, то в ответ следует записать соответствующее значение по оси абсцисс. Но в случае, если требуется найти значение функции, то предварительно нужно подставить соответствующее значение аргумента в функцию и рассчитать его.

Как находить точки экстремума с помощью производной?

Рассмотренные примеры в основном относятся к заданию под номером 7 экзамена, которое подразумевает работу с графиком производной или первообразной. А вот задание 12 ЕГЭ – найти наименьшее значение функции на отрезке (иногда – наибольшее) – выполняется без каких-либо чертежей и требует базовых навыков математического анализа.

Для его выполнения нужно уметь находить точки экстремума с помощью производной. Алгоритм их нахождения таков:

• Найти производную от функции.
• Приравнять ее к нулю.
• Найти корни уравнения.
• Проверить, являются ли полученные точки точками экстремума или перегиба.

Для этого нужно начертить схему и на получившихся промежутках определить знаки производной, подставляя числа, принадлежащие отрезкам, в производную. Если при решении уравнения вы получили корни двойной кратности – это точки перегиба.

• Применив теоремы, определить какие точки являются точками минимума, а какие – максимума.

Вычисление наименьшего значения функции с применением производной

Однако, выполнив все эти действия, мы найдем значения точек минимума и максимума по оси абсцисс. Но как найти наименьшее значение функции на отрезке?

Что необходимо сделать для того, чтобы найти число, которому соответствует функция в конкретной точке? Нужно подставить в данную формулу значение аргумента.

Точки минимума и максимума соответствуют наименьшему и наибольшему значению функции на отрезке. Значит, чтобы найти значение функции, нужно рассчитать функцию, используя полученные значения х.

Важно! Если в задании требуется указать точку минимума или максимума, то в ответ следует записать соответствующее значение по оси абсцисс. Но в случае, если нужно найти значение функции, то предварительно следует подставить соответствующее значение аргумента в функцию и выполнить необходимые математические операции.

Что делать, если на данном отрезке отсутствуют точки минимума?

Но как найти наименьшее значение функции на отрезке, на котором отсутствуют точки экстремума?

Это значит, что на нем функция монотонно убывает или возрастает. Тогда в функцию нужно подставить значение крайних точек этого отрезка. Есть два пути.

1) Рассчитав производную и промежутки, на которых она положительна или отрицательна, сделать вывод о том, убывает функция на данном отрезке или возрастает.

В соответствии с ними подставить в функцию большее или меньшее значение аргумента.

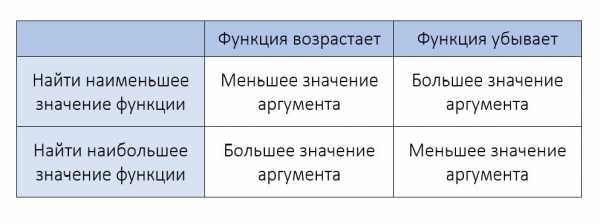
2) Просто подставить в функцию обе точки и сравнить полученные значения функции.

В каких заданиях нахождение производной необязательно

Как правило, в заданиях ЕГЭ все же нужно находить производную. Есть только пара исключений.

1) Парабола.

Вершина параболы находится по формуле.

Если a < 0, то ветви параболы направлены вниз. И ее вершина является точкой максимума.

Если a > 0, то ветви параболы направлены вверх, вершина – точка минимума.

Рассчитав точку вершины параболы, следует подставить ее значение в функцию и вычислить соответствующее значение функции.

2) Функция y = tg x. Или y = ctg x.

Эти функции являются монотонно возрастающими. Поэтому, чем больше значение аргумента, тем больше значение самой функции. Далее мы рассмотрим, как найти наибольшее и наименьшее значение функции на отрезке с примерами.

Основные типы заданий

Задание: наибольшее или наименьшее значение функции. Пример на графике.

На рисунке вы видите график производной функции f (x) на интервале [-6; 6]. В какой точке отрезка [-3; 3] f (x) принимает наименьшее значение?

Итак, для начала следует выделить указанный отрезок. На нем функция один раз принимает нулевое значение и меняет свой знак – это точка экстремума. Так как производная из отрицательной становится положительной, значит, это точка минимума функции. Этой точке соответствует значение аргумента 2.

Ответ: 2.

Продолжаем рассматривать примеры. Задание: найти наибольшее и наименьшее значение функции на отрезке.

Найдите наименьшее значение функции y = (x — 8) e^x-7 на отрезке [6; 8].

1. Взять производную от сложной функции.

y’ (x) = (x — 8) e^x-7 = (x — 8)’ (e^x-7) + (x — 8) (e^x-7)’ = 1 * (e^x-7) + (x — 8) (e^x-7) = (1 + x — 8) (e^x-7) = (x — 7) (e^x-7)

2. Приравнять полученную производную к нулю и решить уравнение.

y’ (x) = 0

(x — 7) (e^x-7) = 0

x — 7 = 0, или e^x-7 = 0

x = 7; e^x-7 ≠ 0, нет корней

3. Подставить в функцию значение крайних точек, а также полученные корни уравнения.

y (6) = (6 — 8) e^6-7 = -2e^-1

y (7) = (7 — 8) e^7-7 = -1 * e⁰ = -1 * 1 = -1

y (8) = (8 — 8) e^8-7 = 0 * e¹ = 0

Ответ: -1.

Итак, в этой статье была рассмотрена основная теория о том, как найти наименьшее значение функции на отрезке, необходимая для успешного решения заданий ЕГЭ по профильной математике. Также элементы математического анализа применяются при решении заданий из части С экзамена, но очевидно, они представляют иной уровень сложности, и алгоритмы их решений сложно уместить в рамки одного материала.

fb.ru

No related posts.