Как округлить число до тысячных
Рассмотрим, как округлить число до тысячных, применяя правило округления.
Правило округления числа до тысячных
Чтобы округлить десятичную дробь до тысячных, надо оставить после запятой только три цифры, а остальные следующие за ней цифры отбросить.
Если первая из отброшенных цифр 0,1,2,3 или 4, то предыдущую цифру оставляем без изменений.
Если первая из отброшенных цифр 5,6,7,8 или 9, то предыдущую цифру увеличиваем на единицу.
Примеры.
Округлить число до тысячных:
Чтобы округлить число до тысячных, после запятой нужно оставить лишь три цифры, а четвертую — отбросить. Поскольку отброшенная цифра — 4, предыдущую цифру оставляем без изменений. Читают: «Три целых, семь тысяч восемьсот пятьдесят четыре десятитысячных приближенно равно три целых, семьсот восемьдесят пять тысячных».
Чтобы округлить это число до тысячных, после запятой оставляем три цифры, а четвертую — отбрасываем. Отброшенная цифра — 6, значит предыдущую цифру увеличиваем на единицу. Читают: «Тридцать семь целых две тысячи семьдесят шесть десятитысячных приближенно равно тридцать семь целых двести восемь тысячных».
Округляя число до тысячных, оставляем после запятой три цифры, а все остальные — отбрасываем. Так как первая из отброшенных цифр — 8, к предыдущей прибавляем единицу. Читают: «Шестьдесят девять целых девяносто девять тысяч девятьсот восемьдесят одна стотысячная приближенно равно семьдесят целых нуль тысячных».
Округляем число до тысячных, поэтому после запятой оставляем первые три цифры, а следующие за ними — отбрасываем. Так как первая из отброшенных цифр — 2, то предыдущую цифру не меняем. Читают: «Восемьсот шестьдесят три целых двенадцать тысяч четыреста двадцать три стотысячных приближенно равно восемьсот шестьдесят три целых сто двадцать четыре тысячных».
Чтобы округлить данное число до тысячных, первые три цифры, стоящие после запятой, оставляем, а все остальные — отбрасываем. Первая из отброшенных цифр равна 5, а это означает, что предыдущую цифру следует увеличить на единицу. Читают: «Нуль целых триста пятьдесят девять стотысячных приближенно равно нуль целых четыре тысячных».
И еще пара примеров на округление числа до тысячных:
www.for6cl.uznateshe.ru
Округление числа до необходимого десятичного разряда
Если отображение ненужных разрядов вызывает появление знаков ######, или если микроскопическая точность не нужна, измените формат ячеек таким образом, чтобы отображались только необходимые десятичные разряды.
Или если вы хотите округлить число до ближайшего крупного разряда, например, тысячной, сотой, десятой или единицы, используйте функцию в формуле.
С помощью кнопки
-
Выделите ячейки, которые нужно отформатировать.
-
На вкладке Главная выберите команду Увеличить разрядность или Уменьшить разрядность, чтобы отобразить больше или меньше цифр после запятой.
С помощью встроенного числового формата
-
На вкладке Главная в группе Число щелкните стрелку рядом со списком числовых форматов и выберите пункт Другие числовые форматы.
-
В списке Категория выберите значение Денежный, Финансовый, Процентный или Экспоненциальный в зависимости от типа ваших данных.
-
В поле Число десятичных знаков введите число знаков после запятой, которые вы хотите отображать.
С помощью функции в формуле
-
Первый аргумент — это число, которое необходимо округлить. Он может быть ссылкой на ячейку или числом.
-
Второй аргумент — это количество цифр, до которого необходимо округлить число.
Предположим, что ячейка A1 содержит число 823,7825. Вот как можно округлить его.
-
Чтобы округлить до ближайшей тысяч и
-
Введите =ОКРУГЛ(A1;-3), что равно 1000
-
Число 823,7825 ближе к 1000, чем к 0 (0 кратно 1000 )
-
В этом случае используется отрицательное число, поскольку округление должно состоятся влево от запятой. Такое же число применяется в следующих двух формулах, которые округляют до сотен и десятков.
-
-
Чтобы округлить до ближайших сотен
-
Введите =ОКРУГЛ(A1;-2), что равно 800
-
Число 800 ближе к 823,7825, чем к 900. Наверное, теперь вам все понятно.
-
-
Чтобы округлить до ближайших десятков
-
Чтобы округлить до ближайших единиц
-
Введите =ОКРУГЛ(A1;0), что равно 824
-
Используйте ноль для округления числа до ближайшей единицы.
-
-
Чтобы округлить до ближайших десятых
-
Введите =ОКРУГЛ(A1;1), что равно 823,8
-
В этом случает для округления числа до необходимого количества разрядов используйте положительное число. То же самое касается двух следующих формул, которые округляют до сотых и тысячных.
-
-
Чтобы округлить до ближайших сотых
-
Чтобы округлить до ближайших тысячных
Округлите число в большую сторону с помощью функции ОКРУГЛВВЕРХ. Она работает точно так же, как функция ОКРУГЛ, за исключением того, что она всегда округляет число в большую сторону. Например, если необходимо округлить число 3,2 до ноля разрядов:
Округлите число вниз с помощью функции ОКРУГЛВНИЗ. Она работает точно так же, как функция ОКРУГЛ, за исключением того, что она всегда округляет число в меньшую сторону. Например, необходимо округлить число 3,14159 до трех разрядов:
-
=ОКРУГЛВНИЗ(3,14159;3), что равно 3,141
Стандартный десятичный разделитель для чисел можно настроить в параметрах Excel.
-
Щелкните Параметры (в Excel 2010–2016) или нажмите кнопку Microsoft Office и выберите Параметры Excel (в Excel 2007).
-
В категории Расширенные параметры нужно выбрать пункт Параметры правки, а затем установить флажок Автоматическая вставка десятичной запятой.
-
В поле Число знаков после запятой введите положительное число для количества цифр справа от запятой или отрицательное число для количества цифр слева от запятой.
Примечание: Например, если ввести 3 в поле Число знаков после запятой, а затем — 2834 в ячейке, то значение будет равно 2,834. Если ввести –3 в поле Число знаков после запятой, а затем — 283 в ячейке, то значение будет равно 283000.
-
Нажмите кнопку ОК.
В строке состояния будет отображаться индикатор Фиксированный десятичный формат.
-
Выберите ячейку на листе и введите нужное число.
Примечание: Установка флажка Фиксированный десятичный формат не влияет на уже введенные данные.
-
-
Чтобы удалить десятичные запятые из чисел, введенных с использованием фиксированного десятичного формата, сделайте следующее:
-
Щелкните Параметры (в Excel 2010–2016) или нажмите кнопку Microsoft Office и выберите Параметры Excel (в Excel 2007).
-
В категории Расширенные параметры в разделе Параметры правки снимите флажок Автоматическая вставка десятичной запятой.
-
В пустой ячейке введите число, соответствующее числу десятичных знаков, которое вы хотите удалить, например 10, 100 или 1000.
Например, введите 100 в ячейке, если числа содержат два десятичных знака и вы хотите преобразовать их в целые числа.
-
На вкладке Главная в группе Буфер обмена нажмите кнопку Копировать (или нажмите клавиши CTRL+C).
-
Выделите на листе ячейки, содержащие числа с десятичными разрядами, которые вы хотите изменить.
-
На вкладке Главная в группе Буфер обмена щелкните стрелку под кнопкой Вставить и выберите команду Специальная вставка.
-
В диалоговом окне Специальная вставка в разделе «Операция» выберите Умножить.
-
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community, попросить помощи в сообществе Answers community, а также предложить новую функцию или улучшение на веб-сайте Excel User Voice.
См. также
Округление числа
Почему число округляется?
support.office.com
Округление чисел
Сегодня мы рассмотрим довольно скучную тему, без понимания которой двигаться дальше не представляется возможным. Эта тема называется «округление чисел» или по-другому «приближённые значения чисел».
Приближённые значения
Приближённые (или приблизительные) значения применяются тогда, когда точное значение чего-либо найти невозможно, или же это значение не важно для исследуемого предмета.
Например, на словах можно сказать, что в городе проживает полмиллиона человек, но это высказывание не будет истинным, поскольку количество человек в городе меняется — люди приезжают и уезжают, рождаются и умирают. Поэтому правильнее будет сказать, что в городе проживает приблизительно полмиллиона человек.
Ещё пример. В девять утра начинаются занятия. Мы вышли из дома в 8:30. Через некоторое время по дороге мы встретили своего товарища, который спросил у нас сколько сейчас времени. Когда мы выходили из дома было 8:30, на дорогу мы потратили какое-то неизвестное время. Мы не знаем сколько сейчас времени, поэтому отвечаем товарищу: «сейчас приблизительно около девяти часов».
В математике приближенные значения указываются с помощью специального знака. Выглядит он следующим образом:
Читается как «приблизительно равно».
Чтобы указать приблизительное значение чего-либо, прибегают к такой операции, как округление чисел.
Округление чисел
Для нахождения приближенного значения применяется такая операция, как округление чисел.
Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулем. Например, следующие числа являются круглыми,
10, 20, 30, 100, 300, 700, 1000
Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числа.
Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак. По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.
На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.
Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.
Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, от нас требуют найти ближайшее круглое число для числа 17. При этом, в ходе этого поиска возможно изменения коснутся и цифры, которая находится в разряде десятков в числе 17 (т.е единицы).
Представим, что все числа от 10 до 20 лежат на прямой линии:
На рисунке видно, что для числа 17 ближайшее круглое число это 20. Значит ответ к задаче таким и будет: 17 приблизительно равно 20
17 ≈ 20
Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.
Попробуем найти приближённое число для числа 12. Для этого снова представим, что все числа от 10 до 20 лежат на прямой линии:
На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приблизительно равно 10
12 ≈ 10
Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так случилось мы рассмотрим позже.
Попробуем найти ближайшее число для числа 15. Снова представим, что все числа от 10 до 20 лежат на прямой линии:
На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать большее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20
15 ≈ 20
Округлять можно и большие числа. Естественно, для них рисовать прямую линию и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.
Мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:
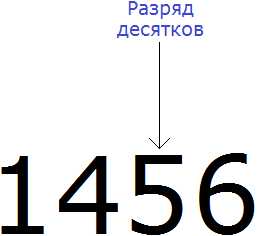
Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56
Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60
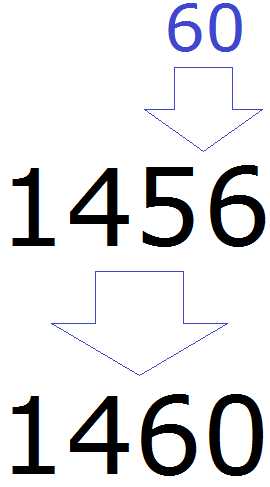
Значит при округлении числа 1456 до разряда десятков получим 1460
1456 ≈ 1460
Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самого разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.
Округлять числа можно не только до разряда десятков. Округлять можно также до разряда сотен, тысяч, десятков тысяч.
После того, как становится понятно, что округление это ни что иное, как поиск ближайшего числа, можно применять готовые правила, которые значительно облегчают округление чисел.
Первое правило округления
Из предыдущих примеров стало ясно, что округляя число до определенного разряда, младшие разряды заменяются нулями. Цифры, которые заменяются нулями, называют отбрасываемыми цифрами.
Первое правило округления выглядит следующим образом:
Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Например, округлим число 123 до разряда десятков.
В первую очередь находим сохраняемую цифру. Для этого надо прочитать само задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 123 до разряда десятков.
Видим, что в разряде десятков находится двойка. Значит сохраняемой цифрой является цифра 2

Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после двойки это цифра 3. Значит цифра 3 является первой отбрасываемой цифрой.

Теперь применяем правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Так и делаем. Оставляем без изменения сохраняемую цифру, а все младшие разряды заменяем нулями. Другими словами, всё что следует после цифры 2 заменяем нулями (точнее нулём):
123 ≈ 120
Значит при округлении числа 123 до разряда десятков, получаем приближённое ему число 120.
Теперь попробуем округлить то же самое число 123, но уже до разряда сотен.
Нам требуется округлить число 123 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 1, поскольку мы округляем число до разряда сотен.

Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после единицы это цифра 2. Значит цифра 2 является первой отбрасываемой цифрой:

Теперь применим правило. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Так и делаем. Оставляем без изменения сохраняемую цифру, а все младшие разряды заменяем нулями. Другими словами, всё что следует после цифры 1 заменяем нулями:
123 ≈ 100
Значит при округлении числа 123 до разряда сотен, получаем приближённое ему число 100.
Пример 3. Округлить число 1234 до разряда десятков.
Здесь сохраняемая цифра это 3. А первая отбрасываемая цифра это 4. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит оставляем сохраняемую цифру 3 без изменений, а всё что располагается после неё заменяем нулём:
1234 ≈ 1230
Пример 4. Округлить число 1234 до разряда сотен.
Здесь сохраняемая цифра это 2. А первая отбрасываемая цифра это 3. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит оставляем сохраняемую цифру 2 без изменений, а всё что располагается после неё заменяем нулями:
1234 ≈ 1200
Пример 3. Округлить число 1234 до разряда тысяч.
Здесь сохраняемая цифра это 1. А первая отбрасываемая цифра это 2. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит оставляем сохраняемую цифру 1 без изменений, а всё что располагается после неё заменяем нулями:
1234 ≈ 1000
Второе правило округления
Второе правило округления выглядит следующим образом:
Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Например, округлим число 675 до разряда десятков.
В первую очередь находим сохраняемую цифру. Для этого надо прочитать само задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 675 до разряда десятков.
Видим, что в разряде десятков находится семёрка. Значит сохраняемой цифрой является цифра 7

Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после семёрки это цифра 5. Значит цифра 5 является первой отбрасываемой цифрой.
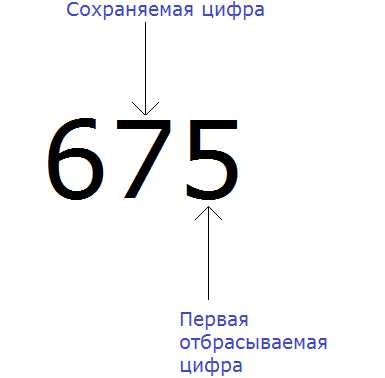
Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
У нас первая из отбрасываемых цифр это 5. Значит мы должны увеличить на единицу сохраняемую цифру 7, а всё что следует после неё заменить нулём:
675 ≈ 680
Значит при округлении числа 675 до разряда десятков, получаем приближённое ему число 680.
Теперь попробуем округлить то же самое число 675, но уже до разряда сотен.
Нам требуется округлить число 675 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 6, поскольку мы округляем число до разряда сотен:

Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после шестёрки это цифра 7. Значит цифра 7 является первой отбрасываемой цифрой:
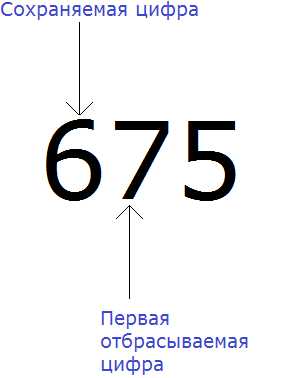
Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
У нас первая из отбрасываемых цифр это 7. Значит мы должны увеличить на единицу сохраняемую цифру 6, а всё что следует после неё заменить нулями:
675 ≈ 700
Значит при округлении числа 675 до разряда сотен, получаем приближённое ему число 700.
Пример 3. Округлить число 9876 до разряда десятков.
Здесь сохраняемая цифра это 7. А первая отбрасываемая цифра это 6. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 7, а всё что располагается после неё заменяем нулём:
9876 ≈ 9880
Пример 4. Округлить число 9876 до разряда сотен.
Здесь сохраняемая цифра это 8. А первая отбрасываемая цифра это 7. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 8, а всё что располагается после неё заменяем нулями:
9876 ≈ 9900
Пример 5. Округлить число 9876 до разряда тысяч.
Здесь сохраняемая цифра это 9. А первая отбрасываемая цифра это 8. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 9, а всё что располагается после неё заменяем нулями:
9876 ≈ 10000
Пример 6. Округлить число 2971 до сотен.
При округлении этого числа до сотен следует быть внимательным, поскольку сохраняемая цифра здесь 9, а первая отбрасываемая цифра это 7. Значит цифра 9 должна увеличиться на единицу. Но дело в том, что после увеличения девятки на единицу получится 10, а это цифра не вместится в разряд сотен нового числа.
В этом случае, в разряде сотен нового числа надо записать 0, а единицу перенести на следующий разряд и сложить с цифрой, которая там находится. Далее заменить все цифры после сохраняемой нулями:
2971 ≈ 3000
Округление десятичных дробей
При округлении десятичных дробей следует быть особенно внимательным, поскольку десятичная дробь состоит из целой и дробной части. И каждая из этих двух частей имеет свои разряды:
Разряды целой части:
- разряд единиц
- разряд десятков
- разряд сотен
- разряд тысяч
Разряды дробной части:
- разряд десятых
- разряд сотых
- разряд тысячных
Рассмотрим десятичную дробь 123,456 — сто двадцать три целых четыреста пятьдесят шесть тысячных. Здесь целая часть это 123, а дробная часть 456. При этом у каждой из этих частей есть свои разряды. Очень важно не путать их:
Для целой части применяются те же правила округления, что и для обычных чисел. Отличие в том, что после округления целой части и замены нулями всех цифр после сохраняемой цифры, дробная часть полностью отбрасывается.
Например, округлим дробь 123,456 до разряда десятков. Именно до разряда десятков, а не разряда десятых. Очень важно не перепутать эти разряды. Разряд десятков располагается в целой части, а разряд десятых в дробной.
Мы должны округлить 123,456 до разряда десятков. Сохраняемая цифра здесь это 2, а первая из отбрасываемых цифр это 3

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. А что делать с дробной частью? Её просто отбрасывают (убирают):
123,456 ≈ 120
Теперь попробуем округлить ту же самую дробь 123,456 до разряда единиц. Сохраняемая цифра здесь будет 3, а первая из отбрасываемых цифр это 4, которая находится в дробной части:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. Оставшаяся дробная часть будет отброшена:
123,456 ≈ 123,0
Ноль, который остался после запятой тоже можно отбросить. Значит окончательный ответ будет выглядеть следующим образом:
123,456 ≈ 123,0 ≈ 123
Теперь займёмся округлением дробных частей. Для округления дробных частей справедливы те же правила, что и для округления целых частей. Попробуем округлить дробь 123,456 до разряда десятых. В разряде десятых располагается цифра 4, значит она является сохраняемой цифрой, а первая отбрасываемая цифра это 5, которая находится в разряде сотых:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит сохраняемая цифра 4 увеличится на единицу, а остальная часть заменится нулями
123,456 ≈ 123,500
Попробуем округлить ту же самую дробь 123,456 до разряда сотых. Сохраняемая цифра здесь это 5, а первая из отбрасываемых цифр это 6, которая находится в разряде тысячных:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит сохраняемая цифра 5 увеличится на единицу, а остальная часть заменится нулями
123,456 ≈ 123,460
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Навигация по записям
spacemath.xyz
Округление чисел
Чтобы округлить число до какого-либо разряда – подчеркнем цифру этого разряда, а затем все цифры, стоящие за подчеркнутой, заменяем нулями, а если они стоят после запятой – отбрасываем. Если первая замененная нулем или отброшенная цифра равна 0, 1, 2, 3 или 4, то подчеркнутую цифру оставляем без изменения. Если первая замененная нулем или отброшенная цифра равна 5, 6, 7, 8 или 9, то подчеркнутую цифру увеличиваем на 1.
Примеры.
Округлить до целых:
1) 12,5; 2) 28,49; 3) 0,672; 4) 547,96; 5) 3,71.
Решение. Подчеркиваем цифру, стоящую в разряде единиц (целых) и смотрим на цифру, стоящую за ней. Если это цифра 0, 1, 2, 3 или 4, то подчеркнутую цифру оставляем без изменения, а все цифры после нее отбрасываем. Если же за подчеркнутой цифрой стоит цифра 5 или 6 или 7 или 8 или 9, то подчеркнутую цифру увеличим на единицу.
1) 12,5≈13;
2) 28,49≈28;
3) 0,672≈1;
4) 547,96≈548;
5) 3,71≈4.
Округлить до десятых:
6) 0, 246; 7) 41,253; 8 ) 3,81; 9) 123,4567; 10) 18,962.
Решение. Подчеркиваем цифру, стоящую в разряде десятых, а затем поступаем согласно правилу: все стоящие после подчеркнутой цифры отбросим. Если за подчеркнутой цифрой была цифра 0 или 1 или 2 или 3 или 4, то подчеркнутую цифру не изменяем. Если за подчеркнутой цифрой шла цифра 5 или 6 или 7 или 8 или 9, то подчеркнутую цифру увеличим на 1.
6) 0, 246≈0,2;
7) 41,253≈41,3;
8 ) 3,81≈3,8;
9) 123,4567≈123,5;
10) 18,962≈19,0. За девяткой стоит шестерка, поэтому, девятку увеличиваем на 1. (9+1=10) нуль пишем, 1 переходит в следующий разряд и будет 19. Просто 19 мы в ответе записать не можем, так как должно быть понятно, что мы округляли до десятых — цифра в разряде десятых должна быть. Поэтому, ответ: 19,0.
Округлить до сотых:
11) 2, 045; 12) 32,093; 13) 0, 7689; 14) 543, 008; 15) 67, 382.
Решение. Подчеркиваем цифру в разряде сотых и, в зависимости от того, какая цифра стоит после подчеркнутой, оставляем подчеркнутую цифру без изменения (если за ней 0, 1, 2, 3 или 4) или увеличиваем подчеркнутую цифру на 1 (если за ней стоит 5, 6, 7, 8 или 9).
11) 2, 045≈2,05;
12) 32,093≈32,09;
13) 0, 7689≈0,77;
14) 543, 008≈543,01;
15) 67, 382≈67,38.
Важно: в ответе последней должна стоять цифра в том разряде, до которого вы округляли.
www.mathematics-repetition.com
Округлить до десятитысячных
Автор Сергей Валерьевич
Четверг, Февраль 18, 2016
| Что значит округлить число до десятитысячных? Зачем иногда нужно это делать? Для этого существует несколько причин:
|
Как же округлить число до десятитысячных (то есть до четвертой цифры после запятой)? Для этого нужно воспользоваться следующим алгоритмом:
|
На самом деле, представленный алгоритм справедлив не только для округления до десятитысячных. Вы легко сможете сами адаптировать его на случай любого другого округления.
Теория и практика округления чисел до десятитысячных
Чтобы понять, как округлить число до десятитысячных, познакомимся подробнее с представленным алгоритмом и закрепим его на конкретных примерах.
- Первый пример. Выполним округление числа 34,48342 до десятитысячных, руководствуясь представленным алгоритмом. Получается число, равное 34,4834, которое ближе к исходному, чем 34,4835.
- Второй пример. Согласно третьему пункту алгоритма при округлении числа 54,72549 до десятитысячных у нас должно получиться 54,7255. Мы увеличиваем четвёртую цифру после запятой до пяти, так как пятая цифра после запятой (девять) превосходит пятёрку. В результате полученное число 54,7255 ближе к исходному, чем, если бы мы округлили его до 54,7254.
- Третий пример. Процесс округления числа 31,365451 до десятитысячных даёт 31,3655. Четыре десятитысячных возросло до пяти, поскольку цифра, которую мы отбрасываем, является пятёркой, а после неё стоит одна значащая цифра. В результате полученное число 31,3655 ближе к исходному, чем если бы мы округлили его до 31,3656.
Нестандартные приёмы округления до десятитысячных
Выше описаны стандартные приёмы округления дробных чисел до десятитысячных. Существует, впрочем, еще одно правило при округлении, которое не изучается в курсе средней школы. Но тем не менее, вам может быть полезно о нём знать. Вот это правило.
| Когда удаляется пятёрка, за которой не стоят значащие цифры, то округление до десятитысячных долей связано с ближайшим числом: последняя остающаяся цифра не меняется при её чётности, и увеличивается на один при нечётности. |
- Четвёртый пример. Округляя число 12,36565 до десятитысячного разряда, получаем 12,3656. Увеличение не делается, т. к. последней остающейся цифрой является чётная шестёрка. Не увеличенное (12,3656) и увеличенное (12,3657) числа равноудалены от исходного числа (12,36565).
- Пятый пример. Округление 23,41635 до десятитысячных даст результат 23,4164, что диктуется нечётностью последней из сохраняемых цифр, которая должна быть усилена.
В чём смысл третьего правила? Ведь такое округление, применённое в отношении одного числа, не способствует увеличению точности. Но когда округляется множество чисел, количество увеличенных чисел примерно совпадёт с количеством уменьшенных. В результате погрешности взаимно компенсируются, что повышает истинность суммы этих чисел.
Материал представлен репетитором по математике и физике в Москве, Сергеем Валерьевичем
yourtutor.info
Округление чисел. Приближенные значения чисел
Числа, с которыми нам приходится иметь дело в реальной жизни, бывают двух типов. Одни в точности передают истинную величину, другие – только приблизительную. Первые называют точными, вторые – приближёнными.
В реальной жизни чаще всего пользуются приближёнными числами вместо точных, так как последние обычно не требуются. Например, приближённые значения используются при указании таких величин как длина или вес. Во многих же случаях точное число найти невозможно.
Правила округления
Для получения приближённого значения, полученное в результате каких-либо действий число нужно округлить, то есть заменить его ближайшим круглым
числом.
Числа всегда округляют до определённого разряда. Натуральные числа округляются до десятков, сотен, тысяч и т. д. При округлении чисел до десятков, их заменяют круглыми
числами, состоящими только из целых десятков, у таких чисел в разряде единиц стоят нули. При округлении до сотен, числа заменяются на более круглые
, состоящие только из целых сотен, то есть нули стоят уже и в разряде единиц, и в разряде десятков. И так далее.
Десятичные дроби можно округлять так же как и натуральные числа, то есть до десятков, сотен и т. д. Но также их можно округлять и до десятых, сотых, тысячных частей и т. д. При округлении десятичных знаков разряды не заполняются нулями, а просто отбрасываются. В обоих случаях округление производится по определённому правилу:
Если отбрасываемая цифра больше или равна 5, то предыдущую нужно увеличить на единицу, а если меньше 5, то предыдущая цифра не меняется.
Рассмотрим несколько примеров округления чисел:
- Округлить 43152 до тысяч. Здесь надо отбросить 152 единицы, так как справа от разряда тысяч стоит цифра 1, то предыдущую цифру отставляем без изменений. Приближённое значение числа 43152, округлённое до тысяч будет равно 43000.
- Округлить 43152 до сотен. Первая из отбрасываемых чисел 5, значит предыдущую цифру увеличиваем на единицу: 43152 ≈ 43200.
- Округлить 43152 до десятков: 43152 ≈ 43150.
- Округлить 17,7438 до единиц: 17,7438 ≈ 18.
- Округлить 17,7438 до десятых: 17,7438 ≈ 17,7.
- Округлить 17,7438 до сотых: 17,7438 ≈ 17,74.
- Округлить 17,7438 до тысячных: 17,7438 ≈ 17,744.
Знак ≈ называют знаком приближённого равенства, он читается – «приближённо равно».
Если при округлении числа результат получился больше начального значения, то полученное значение называется приближённым значением с избытком, если меньше – приближённым значением с недостатком:
7928 ≈ 8000, число 8000 – приближённое значением с избытком
5102 ≈ 5000, число 5000 – приближённое значением с недостатком
naobumium.info
Округлить до тысяч онлайн калькулятор — ОКРУГЛЕНИЕ ЧИСЕЛ — 22 ответа
В разделе Образование на вопрос ОКРУГЛЕНИЕ ЧИСЕЛ заданный автором Black star лучший ответ это десятки — 79310; 951040
сотни — 79300; 951000
тыщи — 79000; 951000
десятки тыщ — 80000; 100000
единицы — 11; 7
деятые — 10,5; 7,0
сотые — 10,50; 7,02
тысячные — 10,530; 7,025
Привет! Вот подборка тем с ответами на Ваш вопрос: ОКРУГЛЕНИЕ ЧИСЕЛ
Ответ от Катерина[гуру]
ничего не поняла, что вы хотели!
Ответ от Anna koroleva[активный]
идите вы
Ответ от Ёергей Златоустов[гуру]
Не понял!
Ответ от Легенда[гуру]
Что там округлять, если следующая за нужной цифрой 5 и больше, к предыдущей прибавляем единицу, если нет, то нет. Н-р: 10,5296 ~10,5 или 10,5296 ~10,53 Ну и т.п.
Держите: 10,5296 ~10,5; 10,5296 ~10,53; 7,02546 ~ 7,0; 7,02546 ~ 7,03; 7,02546 ~ 7,025; 7,02546 ~ 7,0255
Ответ от Коротеев Александр[гуру]
Что бы округлить до некоторого знака, надо посмотреть на предыдущий знак.
Если он от 0 до 4, то отбрасывается и всё, а если от 5 до 9 — отбрасывается, а к знаку до которого производится округление прибавляется 1.
Например 79306.
До десятков: 79310 (ибо 6 от 5 до 9),
до сотен: 79300 (ибо 0 от 0 до 4)
до тысяч: 79000
до десятков тысяч: 80000
10,5296
до единиц: 11 (ибо 5 от 5 до 9)
до десятых: 10,5 (ибо 2 от 0 до 4)
до сотых: 10,53
до тысячных: 10,530 (6 от 5 до 9 — поэтому к 9 прибавляется 1. 9+1=10, поэтому 1 переносится в следующий разряд. А 0 в конце я оставил — чтобы показать. Можно его и не писать на самом деле) .
Остальные аналогично, хорошо?
Ответ от Вероника[гуру]
А что вы хотели и поконкретнее пожалуйста,
Ответ от Пользователь удален[активный]
10,5296 ~10,5; 10,5296 ~10,53; 7,02546 ~ 7,0; 7,02546 ~ 7,03; 7,02546 ~ 7,025; 7,02546 ~ 7,0255 вроде так
Ответ от 2 ответа[гуру]
Привет! Вот еще темы с нужными ответами:
Ответить на вопрос:
22oa.ru
