Методы построения графиков функций содержащих модуль
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (200,7 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель урока:
- повторить построение графиков функций содержащих знак модуля;
- познакомиться с новым методом построения графика линейно-кусочной функции;
- закрепить новый метод при решении задач.
Оборудование:
- мультимедиа проектор,
- плакаты.
Ход урока
Актуализация знаний
На экране слайд 1 из презентации.
Что является графиком функции y=|x| ? (слайд 2).
(совокупность биссектрис 1 и 2 координатных углов)
Найдите соответствие между функциями и графиками, объясните ваш выбор (слайд 3).
Рисунок 1
y=| x+3|
y=| x| +3
y=-2| x| -2
y=6-| x-5|
y=1/3| x-6| -3
Расскажите алгоритм построения графиков функций вида y=|f(x)| на примере функции y=|x2-2x-3| (слайд 4)
Ученик: чтобы построить график данной функции нужно
— построить параболу y=x2-2x-3
— часть графика над ОХ сохранить, а часть графика расположенную ниже ОХ отобразить симметрично относительно оси ОХ (слайд 5)
Рисунок 2
Рисунок 3
Расскажите алгоритм построения графиков функций вида y=f(|x|) на примере функции y=x2-2|x|-3 (слайд 6).
Ученик: Чтобы построить график данной функции нужно:
— построить параболу.
— часть графика при х 0 сохраняется и отображается симметрии относительно оси ОУ (слайд 7)
Рисунок 4
Расскажите алгоритм построения графиков функций вида y=|f(|x|)| на примере функции y=|x2-2|x|-3| (слайд 8).
Ученик: Чтобы построить график данной функции нужно:
— нужно построить параболу у=x2-2x-3
— строим у= x2-2|x|-3, часть графика сохраняем и симметрично отображаем относительно ОУ
— часть над ОХ сохраняем, а нижнюю часть симметрично отображаем относительно ОХ (слайд 9)
Рисунок 5
Следующее задание выполняем письменно в тетрадях.
1. Построить график линейно-кусочной функции у=|х+2|+|х-1|-|х-3|
Ученик на доске с комментарием:
— находим нули подмодульных выражений х1=-2, х2=1, х3=3
— разбиваем ось на промежутки
— для каждого промежутка запишем функцию
при х < -2, у=-х-4
при -2 х<1, у=х
при 1 х<3, у = 3х-2
при х 3, у = х+4
— строим график линейно-кусочной функции.
Мы с вами построили график функции используя определение модуля (слайд 10).
Рисунок 6
Предлагаю вашему вниманию “метод вершин”, который позволяет строить график линейно-кусочной функции (слайд 11). Алгоритм построения дети записывают в тетрадь.
Метод вершин
Алгоритм:
- Найдем нули каждого подмодульного выражения
- Составим таблицу, в которой кроме нулей запишем по одному значению аргумента слева и справа
- Нанесем точки на координатную плоскость и соединим последовательно
2. Разберем этот метод на той же функции у=|х+2|+|х-1|-|х-3|
Учитель на доске, дети в тетрадях.
Метод вершин:
— найдем нули каждого подмодульного выражения;
— составим таблицу, в которой кроме нулей запишем по одному значению аргумента слева и справа
х -3 -2 1 3 4
у -1 -2 1 7 8
— нанесем точки на координатную плоскость и соединим последовательно.
Графиком линейно-кусочной функции является ломанная с бесконечными крайними звеньями (слайд 12) .
Рисунок 7
Каким же методом график получается быстрее и легче?
3. Чтобы закрепить данный метод предлагаю выполнить следующее задание:
При каких значения х функция у=|х-2|-|х+1| принимает наибольшее значение.
Следуем алгоритму; ученик на доске.
у=|х-2|-|х+1|
х1=2, х2=-1
у(-2)=4-1=3
у(-1)=3
у(2)=-3
у(3)=1-4=3, соединяем последовательно точки.
унаиб = 3
4. Дополнительное заданиеПри каких значениях а уравнение ||4+x|-|x-2||=a имеет два корня.
5. Домашняя работа
а) При каких значениях Х функция у =|2x+3|+3|x-1|-|x+2| принимает наименьшее значение.
б) Построить график функции y=||x-1|-2|-3| .
16.02.2013
Поделиться страницей:urok.1sept.ru
Построение графиков функций, содержащих модуль
Разделы: Математика
Тип урока: изучение и закрепление новых знаний.
Цели урока:
Образовательная: освоить метод линейного сплайна для построения графиков, содержащих модуль; научить применять его в простых ситуациях;
Развивающая: развивать логическое и творческое мышление; формирование навыков самостоятельной деятельности, выработка внимания.
Воспитательная: привитие интереса к изучаемому предмету.
Ход урока
Непрерывная кусочно-линейная функция называется линейным сплайном. Её график есть ломаная с двумя бесконечными крайними звеньями. Подобный график вы видите на рис.1
Эта функция задается тремя формулами
Но нетрудно заметить, что эту же функцию можно задать одной формулой, используя модули: у= ¦х¦ -¦х-1¦
Оказывается, что и любую кусочно–линейную функцию можно задать формулой вида
График любой такой функции – ломаная с бесконечными крайними звеньями. Чтобы построить такую ломаную. Достаточно знать все её вершины и по одной точке на левом и правом бесконечных звеньях. Эти соображения позволяют легко строить графики функций такого вида без раскрытия модулей, не переходя к их кусочному заданию.
Достаточно составить таблицу
Х Х0 Х1 Х2 … Хn X n+1 Y Y0 Y1 Y2 … Yn Y n+1
Где х
Пример 1. Построить график функции у=3х+1 -¦х+1¦+2¦х¦
Точки смены формул: х+1=0, х=-1 и х=0.
Составим таблицу:
график изображен на рисунке 2.
Пример 2. задайте функцию у=х+¦х-2¦-¦х¦в виде кусочно-линейной и постройте график двумя способами.
I способ.
Подготовим таблицу для построения графика с учетом линейного сплайна:
Получим график (см.рис 3)
II способ.
Значение х, при которых выражения, стоящее под знаком модуля, меняют знак, х=2 их=0. значит они точки смены формул. Найдем эти формулы.
Если х<0, то у= х-х+2+х, у=х+2.
если 0x, то у=х-х+2-х, у= -х+2.
Если х>2, то у=х+х-2-х, у=х-2.
Очевидно, что график остается неизменным.
Закрепление изученного
Для закрепления изученного материала проводится самостоятельная работа
Учитель должен заранее подготовить чистые листочки форматом в половину листа (примерно 6 штук на каждого ученика). Непосредственно перед уроком, на перемене учитель записывает на доске два варианта работы. Причем каждый вариант он пишет особым цветным мелом. Степень трудности вариантов различна. Оценка “4” примерно соответствует тексту, написанному синим цветом, оценка “5” — красному. Для того, чтобы работа проходила быстро и организованно, учителю нужно помнить наизусть
ответы всех заданий, тогда его проверка будет мгновенной. Кроме того, необходимо подготовить специальный лист для учета каждого выполненного задания ручки трёх цветов. На листе слева помещается колонка с фамилиями учащихся, а справа колонки, соответствующие количеству заданий в работе. Какой бы вариант ни выбрал ученик, соответствующую клеточку закрашивают выбранным цветом. Ученики на своих листочках выполняют первый пример выбранного варианта. Как только пример решен. Ученик с листочком подходит к учителю, который мгновенно видит, правильное решение или нет. Если ответ ученика неправильный, то учитель не берет у него листочек, а отправляет искать ошибку или выполнять задание более лёгкого варианта. Если ответ правильный, то учитель забирает листочек и закрашивает соответствующую клеточку.
Задания для самостоятельной работы.
| на “4” | на “5” |
| Постройте графики функции: | Постройте графики функций: |
| а) у = ¦х+1¦+ ¦х¦-¦х-2¦ | а) у = ¦х+2¦- ¦2х -4¦+¦х-3¦- ¦х+1¦ |
| б) у = ¦х+2¦+¦х¦- 2¦х-2¦ | б) у = 1- ¦2-х¦+¦3+х¦- ¦х¦ +¦х-1¦ |
| в) у = 2- ¦2х +5¦ | в) у = ¦х-5¦+¦х¦- 2¦1- х¦-¦х+3¦ |
| ответы смотри в Приложении 1, приложении 2 | |
| а) рис. 4 | а) рис.7 |
| б) рис. 5 | б) рис.8 |
| в) рис. 6 | в) рис.9 |
1.03.2007
Поделиться страницей:urok.1sept.ru
График квадратичной функции, содержащей модуль.
XIII республиканский научный конкурс молодых исследователей «Шаг в будущее Осетии».
Секция – математика.
«График квадратичной функции, содержащей переменную под знаком абсолютной величины.»
Автор:
Асламурзаева Белла Артуровна
СОШ №46, 9 «А» класс.
Научный руководитель:
Преподаватель математики СОШ №46 им. И.М.Дзусова
Дряева М.Г.
город Владикавказ, СОШ №46.
Аннотация
Цель работы: рассмотреть построение графика квадратичной функции, содержащей переменную под знаком модуля.
Методы и приемы: рассмотрение, анализ и построение графиков функций, содержащих переменную под знаком модуля, обзор информации в сети Интернет.
Выводы:
1)Для построения графика функции y = |f(x)| , надо сохранить ту часть графика функции y = f(x), точки которой находятся на оси Ох или выше оси Ох, и симметрично отразить относительно оси Ох ту часть графика функции y = f(x), которая расположена ниже оси Ох.
2) Для построения графика y = f(|x|) надо сохранить ту часть графика функции y = f(|x|), точки которой на оси Оу или справа от неё и симметрично отразить эту часть графика относительно оси Оу.
3) Чтобы построить график функции |y|= x 2 – 6х +5 нужно:
Отбросить ту часть графика , которая лежит ниже оси
Ох, а оставшуюся часть симметрично отобразить
относительно оси Ох
Задачи:
1) Изучить литературу о свойствах абсолютной величины и квадратичной функции.
2) Исследовать изменения графика квадратичной функции в зависимости от расположения знака абсолютной величины.
1.Введение.
Функция, определяемая формулой у=ах²+вх+с, где х и у переменные, а параметры а, в и с – любые действительные числа, причём а≠0, называется квадратичной.
График функции у=ах²+вх+с есть парабола; осью симметрии параболы является прямая . При а>0 «ветви» параболы направлены вверх, при а<0 – вниз.
Чтобы построить график квадратичной функции, нужно:
1) найти координаты вершины параболы и отметить её в координатной плоскости;
2) построить ещё несколько точек, принадлежащих параболе;
3) соединить отмеченные точки плавной линией.
Определение: абсолютной величиной неотрицательного числа называется само это число, абсолютной величиной отрицательного числа называется противоположное ему положительное число.
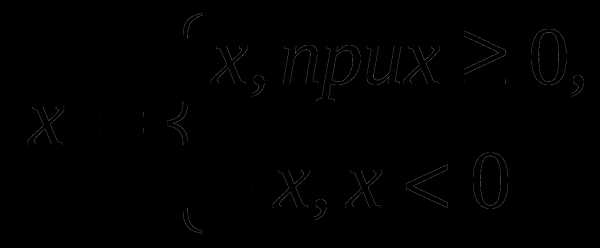
Свойства: 1 .|a| ≥0, 3 .|a∙b|=|a|∙|b|,
2. |a|²= a², 4. |a/b|=|a|/|b|, b≠0
2. Построение графика квадратичной функции, содержащей переменную под знаком модуля.
На примере функции у= x 2– 6х +5 я рассмотрела всевозможные случаи расположения модуля.
у = |x 2 – 6х +5|
у = | х | 2 – 6х +5
у = х² – 6|х| +5
у = |х|² — 6|х|+5
у = |х² – 6х| +5
у = |х² – 6|х| +5|
у = x 2 -|6х + 5|
|y|= x 2 – 6х +5
Пример 1:Построим график функции у = |x 2 – 6х +5|.
Пользуясь определением модуля, рассмотрим два случая:
1) x 2– 6х +5≥ 0, тогда у= x 2– 6х +5.
Построим данную параболу. Выделим все точки параболы с неотрицательной ординатой.
2) x 2– 6х +5<0, тогда у= -(x 2– 6х +5) или -x 2+ 6х -5>0, y= -x 2+ 6х -5.
Построим график данной функции, и выделим все точки параболы с положительной ординатой. Все выделенные в обоих случаях точки образуют график функции у = |x 2 – 6х +5|.
. 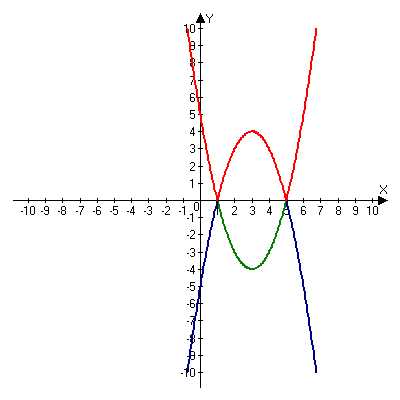
Итак ,можно сделать вывод: чтобы получить график функции у = |x 2 -6х + 5|, нужно часть параболы, расположенной ниже оси Ох, зеркально отобразить относительно оси Ох .
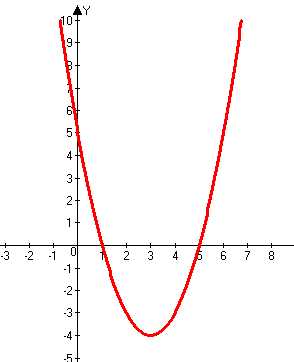
Пример 2:Рассмотрим график функции у = |х|²– 6х +5.
Т. к. |х|²= х², то график функции у =|х|² — 6х +5 совпадет с графиком функции у = х² — 6х +5, не содержащей знак абсолютной величины.
.
Пример 3: Рассмотрим график функции у = х² – 6|х| +5.
Воспользуемся определением модуля числа.
Пусть x≥0, тогда y= х² — 6х +5.
Построим параболу у = х² — 6х +5 и обведём ту её часть, которая соответствует неотрицательным значениям х , т.е. часть, расположенную правее оси Оу.
2)Пусть x<0, тогда y= x² + 6х +5.
В той же координатной плоскости построим параболу у = х² +6х +5 и обведём ту её часть, которая соответствует отрицательным значениям х, т.е. часть, расположенную левее оси Оу. Обведённые части парабол вместе образуют график функции у = х² — 6|х| +5
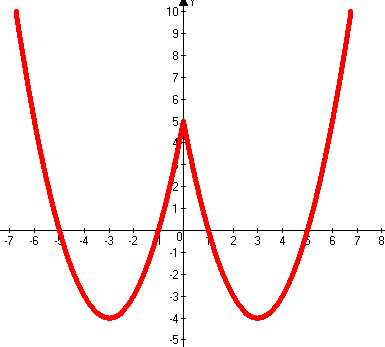
Итак, можно сделать вывод: для построения графика функции у = х² – 6|х| +5. надо сохранить ту часть графика , точки которой находятся на оси Oy или справа от нее
infourok.ru
