Построить график распределения функции – Найти функцию распределения и построить ее график. |

Свойства функции распределения:

Свойство 1: Значения функции распределения принадлежат отрезку [0, 1]: .

Свойство 2: F(x) – неубывающая функция, т. е. F(x₂) ≥F(x₁), если х₂>x₁.

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале: Р(аХ<b)=F(b)– F(a).

Следствие 2. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение равна нулю.

Свойство 3.

Если возможные значения случайной величины принадлежат интервалу (a,b), то F(x)=0 при хa; F(x)=1 при хb.

Следствие. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения:

График функции распределения

График функции распределения расположен в полосе, ограниченной прямыми у=0, у=1 . При возрастании х в интервале (а, b), в котором за­ключены все возможные значения случайной величины, график «поднимается вверх». При х а ординаты графика равны нулю; при х b ординаты графика равны единице.

Следует отметить, что график дискретной функции распределения имеет ступенчатый вид.

Плотность распределения вероятностей. Дифференциальная функция распределения

Плотностью распределения вероятностей непрерывной случайной величины Х называется функцию f(x) – первую производную от функции распределения: .

Для описания дискретной случайной величины плотность распределения неприменима. Иногда функцию плотности распределения называют дифференциальной функцией распределения. Линию y=f(x) называют кривой распределения.

Свойства плотности распределения

Свойство 1. Вероятность того, что непрерывная случайная величина в результате испытания примет какое-нибудь значение из интервала (a, b), равна определенному интегралу от плотности вероятности в пределах от a до b:

.

Свойство 2. Если значения случайной величины принадлежат всей числовой оси, то имеет место утверждение .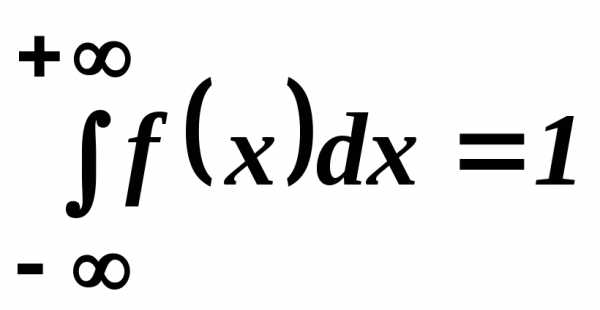

Свойство 3. Плотность вероятности функция неотрицательная f(x)0.

Решение задач

1). Дискретная случайная величина Х задана таблицей распределения

Найти функцию распределения и построить ее график.

2). Случайная величина Х задана функцией распределения:

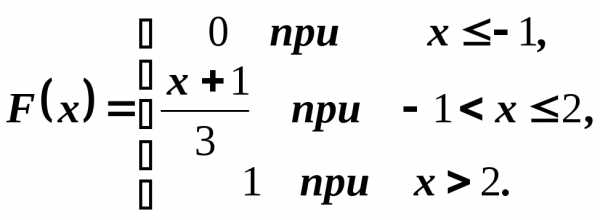
Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (0, 1).

2) Задана плотность вероятности случайной величины Х

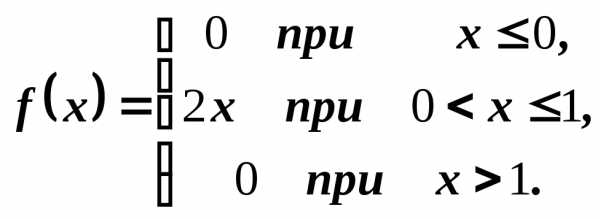
Найти вероятность того, что в результате испытания Х примет значение, принадлежащие интервалу (0,5; 1).

5. Самостоятельная работа студентов на занятии

5.1. Случайная величина Х задана функцией распределения:

Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (2, 3).

5.2. Задана плотность вероятности случайной величины Х

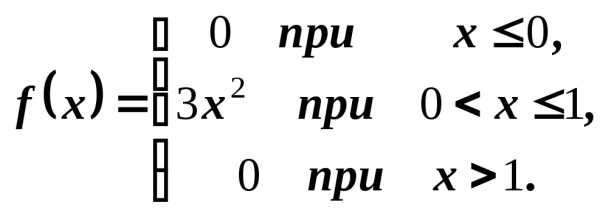
Найти вероятность того, что в результате испытания Х примет значение, принадлежащие интервалу (; 1).

5.3. Дискретная случайная величина задана законом распределения:

Х	1	4	5	8
Р	0,2	0,3	0,4	0,1

Найти функцию распределения и построить ее график.

studfiles.net

04_Функция распределения

§4. Функция распределения

Функция распределения (интегральная)

Х

Х

Функцией распределения F(X) называется функция, которая для каждого значения аргумента равна вероятности того, с.в. Х примет значение меньшее, чем аргумент (попадает в область, лежащую слева от аргумента).

F(x)=P(X<x) (3)

Например: Дискретная с.в. задана рядом распределения

ХI	2	4	7	9
PI	0.2	0.4	0.3	0.1

-3 0 2 П 4 6 7 9 12 X

F(П)=P(X<П)=P(X=2)=0,2

F(12)=P(X<12)=P(V)=1

F(6)=P(X<6)=0,2+0,4=0,6

Свойства функции распределения:

1 область определения: Х Є R

2 область значений: 0<=F(x)<=1

3 F(-∞)=0 [P(X<= -∞)=0]

4 F(+∞)=1 [P(X<=+∞)=P(V)=1]

F(x) неубывающая функция:

X₁<X₂ F(X₁)<=F(X₂)

X₁ X₂ X

(X<x₂)=(X<x₁)+(x₁ <X<x₂)

несовместные

P(X<x₂)=P(X<x₁)+P(x₁<X<x₂)

F(x₂) >= F(x₁) >0

Неубывание доказано.

Следствие: Р(Х₁<=X<Х₂) = F(X₂) – F(X₁) (4)

Замечание: функция распределения F(x) – универсальный способ задания закона распределения. Он пригоден и для дискретных и для непрерывных с.в.. С ростом аргумента Х идет накопление вероятности, т.е. функция F(X) увеличивается. Для дискретных с.в. рост происходит скачком при переходе через очередное возможное значение X

IДля непрерывной с.в. F(X) накапливается непрерывно.

Качественный график функции распределения:

Непрерывная с.в. дискретная с.в.

Замечание к формуле (4)

Пусть с.в. непрерывна и функция F(X) непрерывна.

Найдем вероятность попадания в точку:

P(X=x₁)=

Для непрерывной с.в. вероятность попадания в точку равна нулю P(X=a)=0

Для непрерывной с.в. Р(α<X<β)=F(β)-F(α) (5)

Например: Дискретная с.в. задана рядом распределения

ХI	2	4	5	7
PI	0,1	0,3	0,2	0,4

Найти значения функции распределения в указанных точках. Построить функцию распределения для всех значений аргумента.

F(-3)=P(X<-3)=0

F(П)=Р(Х<П)=0,1

F(2L)=P(X<2L)=0.1+0.3+0.2=0.6

F(8)=P(X<8)=P(U)=1

F(50)=P(X<50)=P(U)=1

-∞<x<+∞

2<x<=2 F(x)=0 F(2)=P(X<2)=0

2<x<=4 F(x)=P(X<x)=P(x=2)=0,1

4<x<=5 F(x)=P(4<X<2)=0,4

5<x<=7 F(x)=0,6

7<x< +∞ F(x)=1

0 при -∞<x<=2

0,1 2<=x<=4

F(X) 0,4 4<x<=5 В точках разрыва

0,6 5<x<=7 значение функции равно

1 7<x<+∞ пределу слева

С.в. задана функцией распределения. Составить ряд распределения.

ХI	1	2	4	6	7	10
PI	0,1	0,2	0,2	0,2	0.1	0.2

Непрерывная с.в. задана функцией распределения

0 -∞<X <=0

F(X) CX² 0< X<=3

1 3< X < + ∞

1 С-?

Найти С из условия непрерывности функции F(X).

2 Найти вероятности попадания в указанные интервалы.

3Найти плотность распределенияf(X).

1 Проверяя непрерывность в т. Х=0 и в т. Х=3:

(Х=0)

F(0)=0

В т. Х=0 функция непрерывна при любом С.

(Х=3)

9c=1

c=1/9

F(3)=c*9

2Р(-2<X<1)=F(1) – F(2) = (CX²)_X=1 – 0_X=-2 = C = 1/9

Р(0<X<2)=F(2) – F(0) = (CX²)_X=1 – 0 = 4C = 4/9

Р(1<X<5)=F(5) – F(1) =1- (CX²)_X=1 = 1-1/9= 8/9

Р(0.5<X<2.5)=F(2.5) – F(0.5) = (CX²)_X=5/2 – (CX²)_X=1/2 = C(25/4 – 1/4) = 6C =

= 6/9=2/3

Р(2<X<9)=F(9) – F(2) = 1 – (CX²)_X=2 = 1- 4C = 1 – 4/9 = 5/9

Р(X>2.5)=P(2,5<X<+∞) = F(+∞) – F(2.5) = 1 — (CX²)_X=5/2= 1 – 25/4 * 1/9 = 1 – 25/36 = 11/36

3f(X) — ? f(X) = F¹(X) = 0 -∞<X<=0

2CX = 2X/9 0<X<3

0 3<X<+∞

Для непрерывной случайной величины X задана функция распределения F(x).

Необходимо:

1. Найти значение параметра С из условия непрерывности F(x),

Построить график F(x).

2. Подсчитать вероятности попаданий в указанные интервалы.

3. Найти плотность распределения F(x) и построить ее график.

Рассматриваемая случайная величина непрерывна. При такой функции распределения все ее возможные значения находятся только на интервале (1<x4). Вне этого интервала возможных значений нет.

1. Находим значение параметра С. Используем условие непрерывности

функции распределения F(x).

Чтобы функция была непрерывна, нужно, чтобы предел слева, предел справа и значение функции в точке совпадали.

В точке x=1 : F(1-0)= 0; F(1+0)= 0; F(1)= 0;  функция непрерывна.

В точке x=4 : F(4-0)= С(4-1)³ =27С; F(4+0)= 1; F(4)= 27С;  функция непрерывна, если 27С =1, откуда получаем С=1/27.

График F(x):

2. Находим вероятности попаданий в указанные интервалы :

Если задана функция распределения, то вероятность попадания случайной величины в заданный интервал подсчитывается по известной формуле:

P(-7<X<2) = F(2) — F(-7) = C(2-1)³ — 0 = 1/27.

P(1<X<3) = F(3) — F(1) = C(3-1)³ — 0 = 8/27.

P(2<X<7) = F(7) — F(2) = 1 — C(2-1)³ = 1 — 1/27 = 26/27.

P(X<2,5) = P(-<X<2,5) = F(2,5) — F(-) = C(2,5-1)³ — 0 = 0,125.

P(X>1,5) = P(1,5<X<+) = F(+) — F(1,5) = 1 — C(1,5-1)³ = 0,9954.

P(-4<X<40) = F(40) — F(-4) = 1 — 0 = 1.

В последнем случае все возможные значения случайной величины лежат внутри интересующего нас интервала, поэтому попадание в этот интервал — достоверное событие и вероятность его равна 1.

3. Находим плотность распределения случайной величины X . По определению, это первая производная функции распределения.

f(x) = F^(x).

На разных участках функция распределения задана различными выражениями. Поэтому и производная будет на разных участках различной:

при x  1 f(x) = (0)^ = 0.

при 1<x <4 f(x) = [C(x-1)³]^ = 3C(x-1)² = (x-1)² /9.

при 4<x f(x) = (1)^ = 0.

График плотности распределения:

Когда мы проводим наблюдения над случайной величиной, мы можем обнаружить, что одни возможные значения появляются чаще, другие реже. Т.е., у одних значений вероятность появления больше, у других меньше.

П римеры:

1. Опыт – бросание кубика.

Случайная величина Х – выпавшее число очков.

Возможные значения{1, 2, 3, 4, 5, 6 }.

2. Опыт – трехкратное бросание монеты.

Случайная величина Х –число выпавших гербов .

Возможные значения { 0, 1, 2, 3 }.

3. Опыт – лекция по теории вероятностей.

Случайная величина Х – число присутствующих студентов.

Возможные значения { 0, 1, 2, …, N }.

4. Опыт – работа банковского служащего в течение часа.

Случайная величина Х – число обслуженных клиентов.

Возможные значения { 0, 1, 2, …, N }.

О3 :Законом распределения вероятностей случайной величины Х (дальше везде будем говорить кратко – Законом распределения) называется всякое правило, устанавливающее соответствие между возможными значениями случайной величины и вероятностями того, что она примет эти значения.

Это соответствие можно устанавливать по-разному, в зависимости от того, с какой случайной величиной мы работаем, с дискретнойили снепрерывной. Существуют три способа задания закона распределения, которые мы далее по очереди подробно рассмотрим.

Сейчас мы только перечислим их и отметим главное: если закон распределения задан (любым из этих способов) то мы можем прогнозировать поведение случайной величины. Точно предсказать до опыта, какое именно значение примет случайная величина, мы не можем в принципе, но зато мы сможемподсчитывать вероятностьтого, что она примет то или иное значение, попадет в интересующий нас интервал.

Способы задания закона распределения:

1. Ряд распределения;

2. Функция распределения F(x)

( иногда ее еще называют интегральная Функция распределения)

3. Плотность распределения f(x)

(ее еще называют также дифференциальная Функция распределения )

Следующая схема показывает, когда применяется каждый из этих способов:

Изменить примеры

studfiles.net

Теперь рисуем график функции распределения f(X):

2. Выполняем интервальную оценку параметров распределения .

Точное значение математического ожидания, дисперсии и среднеквадратического отклонения мы найти по опытным данным в принципе не можем, так как в опытах мы получаем только часть информации о случайной величине.

Когда вместо математического ожидания мы берем из опыта выборочную среднюю, мы допускаем погрешность. Оценить ее можно с помощью доверительного интервала . Выбирается интервал и находитсядоверительная вероятность  — вероятность того, что истинное значение математического ожидания лежит в этом интервале. Имеются формулы, по которым для заданного  находят величину и положение доверительного интервала:

s (1-q_)   _x  s (1+q_)

Д 12ля того, чтобы ими воспользоваться, находим числовые характеристики выборки:

.

выборочная средняя

средняя квадратов

Дисперсия

Исправленная дисперсия

Исправленное выборочное среднеквадратическое отклонение

Коэффициенты t _ (,n) и q _ (,n) находим по соответствующим таблицам :

t _ (0,95; 76) = 1,994 ; q _ (0,95; 76) = 0,168 .

Подставляем в формулы для доверительных интервалов :

;

5,7608(1-0,168)   _x  5,7608 (1+0,168) .

Окончательно получаем:

;

4,7930   _x  6,7286 .

С вероятностью 0,95 истинные значения математического ожидания и среднеквадратического отклонения лежат в полученных интервалах.

из конспекта

Статистическая оценка параметров распределения.

Задача: по опытным данным восстановить числовые характеристики распределения или параметры предполагаемого распределения:

1. Нормального (а, σ)

2. Показательного (λ)

3. Равномерного (a,b)

4. Пуассоновского (а)

Понятие статистической оценки как с.в.

Пусть необходимо оценить по выборке некоторый параметр распределения а. Для оценки имеются только данные вошедшие в выборку (х₁,х₂…х_n). По этим числа мы должны подсчитать (≈) значение а. Точное значение а мы получить не можем, т.к. в выборке содержится только часть информации с.в. и данные, вошедшие в выборку случайные. В другой серии опытов это будут другие числа. То число, которое мы подсчитаем по выборке, назовем оценкой параметра а .

(1) – это функция данных, попавших в выборку.

Подсчитав по выборке это число, получим 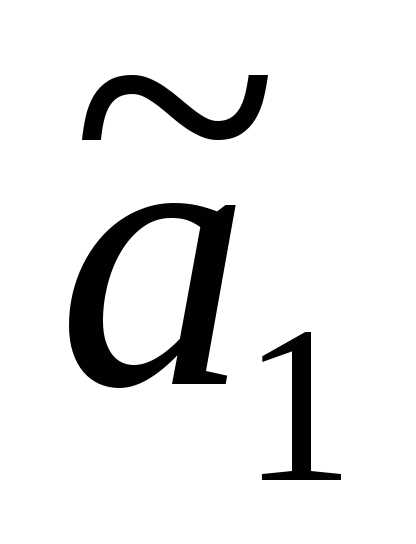. Проведя другую серию опытов, по этой же формуле, получим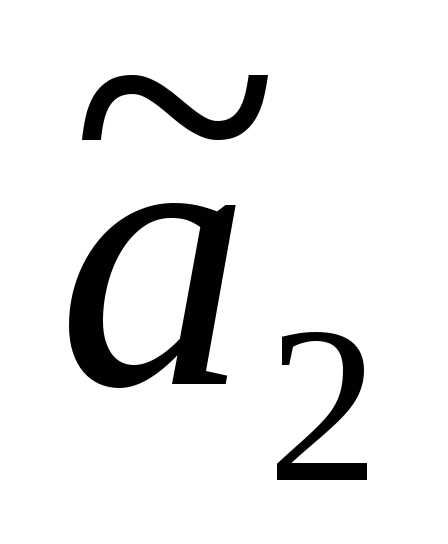и тд.

Статистическая оценка 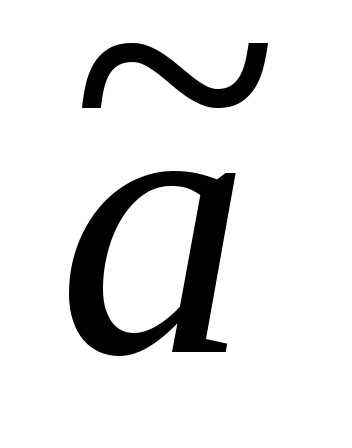для параметра а сама есть с.в. с каким-то законом распределения. Как найти ее закон распределения?

Каждая из вариант, попадающих в выборку, одновременно является с.в. (в разных сериях опытов получим для нее разные значения) и закон распределения этой варианты совпадает с законом распределения с.в. Х, над которым ставятся опыты. Таким образом статистическая оценка 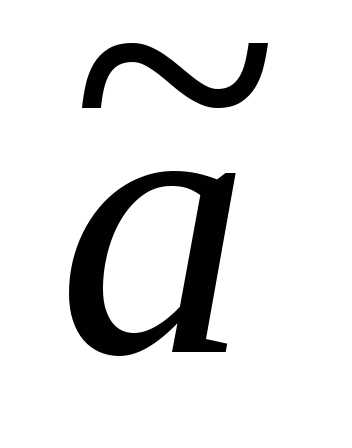является функцией одинакового распределения с.в.x_i.

(2)

Если закон распределения х является известным, то можно построить закон распределения для .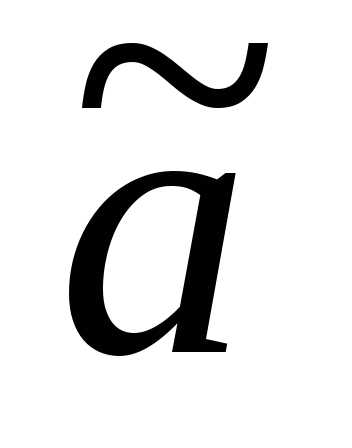

studfiles.net

Методика построения гистограммы и графика интегральной функции распределения

Для определения вида закона распределения случайной величины удобно представить данные наблюдений в графическом виде. Для графического представления данных наблюдения используется специальный график – гистограмма (рисунок 1).

Гистограмма является важным вспомогательным средством при принятии гипотезы о виде функции распределения. Поэтому необходимо извлечь из нее максимум информации. Дело в том, что форма гистограммы зависит от числа и величины интервалов разбиения. При слишком малом числе интервалов разбиения (интервал велик), плохо выявляются характерные особенности распределения. С ростом числа интервалов характерные особенности выявляются все лучше, но лишь до определенного предела.

Рис. 1 – Гистограмма и полигон распределения

При большом числе интервалов (интервал слишком мал) гистограмма снова теряет характерные особенности распределения, превращаясь в пределе (когда в каждом интервале не более одного значения) в чередование «пустых» интервалов и одинаковых по высоте прямоугольников.

Наиболее простой способ разбиения вариационного ряда — это использование равновеликих интервалов, количество которых определяется по специальным формулам, например, по формуле (2.6).

Согласно этому правилу при объеме выборки до тысячи полных реализаций рекомендуемое число интервалов разбиения не превышает одиннадцати. Для объемов выборки n < 50, с которыми в основном приходится иметь дело при обработке результатов испытаний на надежность, вид гистограмм слишком чувствителен к способу разбиения, поэтому правило (2.6) можно использовать лишь как ориентировочное. В этих случаях рекомендуется построить несколько вариантов гистограмм для различных способов разбиения вариационного ряда – для k = 6,7,8 и т.д.

При построении гистограммы по оси абсцисс откладывают в выбранном масштабе интервалы, и, взяв их как основания, строят прямоугольники, высота которых равна статистической плотности распределения на интервале.

Построенная таким образом ступенчатая функция f_j называется гистограммой выборки. Эта функция служит статистическим аналогом плотности распределения вероятности случайной величины u=f(x) на j-ом интервале. Определяется по формуле 2.12

(2.12)

Площадь гистограммы равна единице.

Если соединить прямыми линиями середины верхних (горизонтальных) сторон прямоугольников гистограммы, то получится полигон распределения в виде ломаной линии (рисунок 1).

При построении нескольких гистограмм с разным количеством интервалов лучшей нужно считать гистограмму, имеющую меньшее число инверсий. Признаком инверсии считается изменение знака приращения высоты прямоугольника. Если число инверсий одинаково, лучшей следует считать ту, которая имеет большее число интервалов.

По данным статистического ряда можно вычислить еще одну характеристику случайной величины — эмпирическую интегральную функцию распределения. Значение эмпирической интегральной функции распределения для j-ого интервала F_j определяется по формуле:

(2.13)

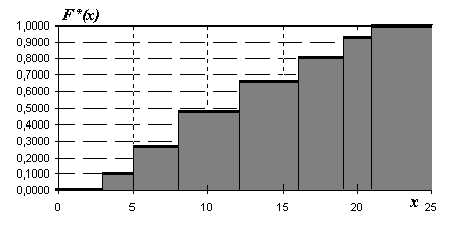
Функция распределения F(x) может быть представлена в виде графика, который строится подобно гистограмме, только высоты прямоугольников равны значениям функции распределения соответствующих интервалов.

Пример графика приведен на рисунке 2.

Рис.2 График эмпирической интегральной функции распределения

Интегральная функция распределения является более универсальной характеристикой распределения по сравнению с гистограммой, которая определяет вероятность того события, что случайная величина X будет меньше или равна заданному значению u. Эмпирическая интегральная функция распределения определяет вероятность события X ≤ u.

Задача 5

Построить гистограмму и график интегральной функции распределения для данных из примера 2. В качестве первого приближения принять число интервалов рассчитанное по формуле (2.6) Стенжерса.

Пример решения

Построим гистограмму и график интегральной функции распределения для данных из примера 2.

Значения наработок разжимных кулаков тормоза на отказ в порядке возрастания в тыс. км:

70,0 102,1 118,7 125,0 133,5 139,9 144,3 145,6 160,0 163,6 165,1 165,6 167,6 173,2 174,3 175,2 177,7 177,9 197,6 198,9 199,2 201,4 205,2 209,6 217,1 218,3 218,5 219,5 220,3 221,0 221,4 223,8 234,0 236,1 243,5 244,8 246,0 246,6 250,8 251,7 287,3 290,6 300,0 308,0 329,9

В качестве первого приближения принять число интервалов, рассчитанное по формуле Стенжерса.

Принимаем число интервалов k =6, ширину интервала

Определить границы интервалов

,

Середину интервала X_j, вычислить по формуле (2.5):

Подсчитать число попаданий m_j наблюденийвходящих в середину первого интервала. Полученные параметры свести в таблицу 4.

Гистограмма выборки на полученных интервалах (2.12)

=1/(45·43,3)=0,0005

=3/(45·43,3)=0,0015

Аналогично определить: f₃=0,0051; f₄=0,0051; f₅=0,0031; f₆=0,0020.

Таблица 4

Номер интервала	Границы интервалов	Середина интервала,	Число попаданий,
	70 — 113,3	91,7
	113,3 — 156,6
	156,6 — 200	178,3
	200 — 243,3	221,7
	243,3 — 286,6
	286,6 — 329,9	308,3

Тогда гистограмма распределения случайной величины пробега автомобиля при исправных кулаках тормозной системы примет вид (рис. 3).

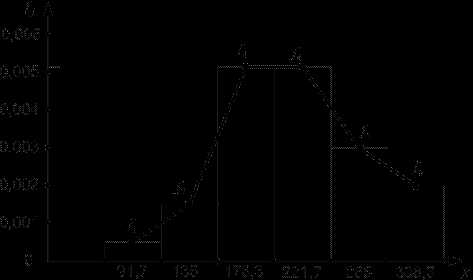
Рис. 3

В этом случае распределение имеем одну инверсию (при переходе с 4 на 5 интервал).

Принять число интервалов k = 7, ширина интервала ∆x = 37,1. Расчеты свести в таблицу 5.

Подсчет частот

Таблица 5

Номер интервала	Границы интервалов	Середина интервала,	Число попаданий,
	70 — 107,1	88,6
	107,1 — 144,3	125,7
	144,3 — 181,4	162,8
	181,4 — 218,5	200,0
	218,5 — 255,6	237,1
	255,6 — 292,8	274,2
	292,8 — 329,9	311,3

 

Гистограмма выборки на полученных интервалах: f₁=0,0006; f₂=0,0012; f₃=0,0018; f₄=0,0018; f₅=0,0048; f₆=0; f₇=0,0012

Тогда гистограмма распределения случайной величины пробега автомобиля при исправных кулаках тормозной системы примет вид (рис. 4).

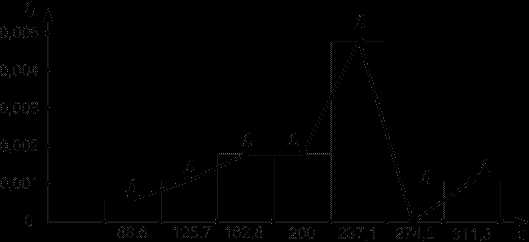
Рис. 4

В этом случае опять получаем две инверсии (при переходе с 5 на 6 интервал и с 6 на 7).

Принимаем число интервалов k = 8, ширина интервала ∆x = 32,5. Расчеты свести в таблицу 6.

Подсчет частот

Таблица 6

Номер интервала	Границы интервалов	Середина интервала	Число попаданий, mj
	70 — 102,5	86,24
	102,5 — 135	118,7
	135 — 167,5	151,2
	167,5 — 200	183,7
	200 — 232,4	216,2
	232,4 — 264,9	248,7
	264,9 — 297,4	281,2
	297,4 – 329,9	313,7

 

Гистограмма выборки на полученных интервалах: f₁=0,0007; f₂=0,0007; f₃=0,002; f₄=0,004; f₅=0,002; f₆=0,004; f₇=0, f₈=0,0014

Тогда гистограмма распределения случайной величины пробега автомобиля при исправных кулаках тормозной системы примет вид (рис. 5).

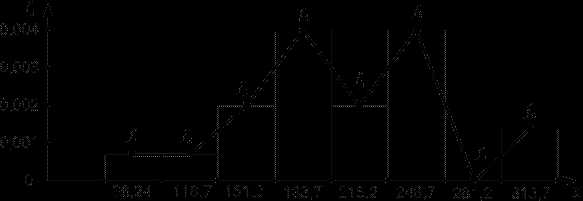
Рис. 5

 

И в этом случае получаем четыре инверсии (при переходе с 4 на 5, с 5 на 6, с 6 на7 и с 7 на 8 интервалы).

Примем число интервалов k = 9, ширина интервала ∆x = 28,9. Расчеты сведём в таблицу 7.

Подсчет частот

Таблица 7

 

Номер интервала	Границы интервалов	Середина интервала,	Число попаданий,
	70 — 98,88	84,4
	98,88 — 127,8	113,2
	127,8 — 156,6	142,2
	156,6 — 185,5	171,1
	185,5 — 214,4
	214,4 — 243,3	228,8
	243,3 — 272,1	257,7
	272,1 — 301	286,5
	301 — 329,9	315,4

 

Гистограмма выборки на полученных интервалах при k=9: f₁=0; f₂=0,0008; f₃=0,002; f₄=0,004; f₅=0,0023; f₆=0,006; f₇=0,0046; f₈=0; f₉=0,0008

Тогда гистограмма распределения случайной величины пробега автомобиля при исправных кулаках тормозной системы примет вид (рис.6).

В данном случае имеем четыре инверсии (при переходе с 4 на 5, с 5 на 6, с 6 на 7 и с 8 на 9 интервал).

Таким образом для нормального закона распределения правомерно принять количество интервалов равное 7, т.к. количество инверсий минимально, а количество интервалов наибольшее.

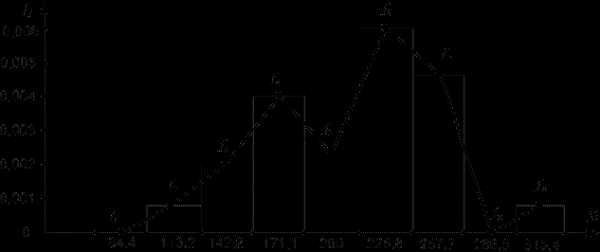
Рис.6

Определить функцию распределения случайной величины F(x_j) (2,13) при семи интервалах группирования:

Для первого интервала ; для второго интервала ; и т.д.

Опытные значения функция распределения F(x_j) представить в виде графика (рис.7)

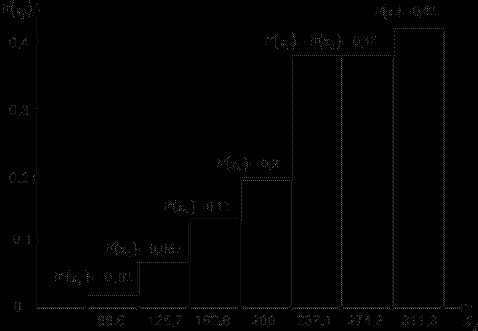
Рис. 7

megaobuchalka.ru

Свойства функции распределения, график

Свойства функции распределения

Вначале напомним определение функции распределения вероятностей.

Определение 1

Функцией распределения называется функция $F(x)$ удовлетворяющая условию $F\left(x\right)=P(X

Введем свойства функции распределения:

1. Функция распределения является неубывающей функцией.

Доказательство: очевидно, что для любых событий $x_1 \[F\left(x_1\right)=P\left(Xч. т. д.

2. Существуют пределы ${\mathop{lim}_{x\to -\infty } F(x)\ }$ и ${\mathop{lim}_{x\to +\infty } F(x)\ }$, причем выполняются равенства:

Доказательство: Существование данных пределов следует из непрерывности и ограниченности функции $F(x)$. Докажем сначала, что:

Рисунок 1.

Рассмотрим убывающую последовательность событий $A_n=(X

Лемма 1: Дана убывающая последовательность вложенных друг друга множеств ${\dots \subseteq A_n\subseteq A_{n-1}\subseteq \dots \subseteq A}_3\subseteq A_2\subseteq A_1$ удовлетворяющая условиям $A={\cap A}_n$ и $\mu \left(A_n\right)

Используя лемму 1, получим

Докажем теперь, что:

Рисунок 2.

Рассмотрим убывающую последовательность событий $B_n=(X\ge n)$, такую что$B_{n+1}=(X\ge (n+1))\subseteq B_n=(X\ge n)$ для всех $n\ge 1$. Очевидно, что пересечение всех событий $B_n$ $B={\cap B}_n=\emptyset $. Поэтому, по лемме 1, получим

ч. т. д.

3. $F(x)$ непрерывна слева любой точке, то есть:

Рисунок 3.

Доказательство. Существование предела следует из непрерывности и ограниченности функции $F(x)$. Рассмотрим следующую разность $F\left(x_0\right)-F\left(x_0-\frac{1}{n}\right)$. Очевидно, что

Следовательно, $F\left(x_0\right)-F\left(x_0-\frac{1}{n}\right)\to 0$. То есть:

Рисунок 4.

ч. т. д.

4. Для любых $x_0$ выполняется равенство: $F\left(x_0+0\right)-F\left(x_0\right)=P({X=x}_0)$.

Это свойство очевидно.

5. Для любых $X$ выполняется равенство: $P\left(a\le X

Доказательство. Очевидно, что $\left(X \[F\left(a\right)+P\left(a\le Xч. т. д.

Примечание 1

Если функция непрерывна во всех точках справа, то$P\left(a\le X\le b\right)=P\left(a

График функции распределения вероятностей

1. Пусть случайная величина $X$ является дискретной. Тогда график функции распределения такой случайной величины всегда представляет собой ступенчатую функцию, скачки которой происходят в точках возможных значений случайной величины (рис. 1).

1. Пусть случайная величина $X$ теперь является непрерывной. График функции распределения такой случайной величины всегда представляет собой неубывающую непрерывную функцию (рис. 2).

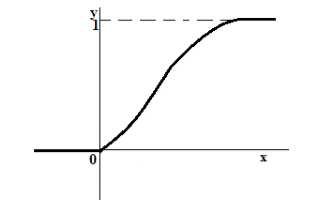
1. Пусть случайная величина $X$ является смешанной. График функции распределения такой случайной величины всегда представляет собой неубывающую функцию, которая имеет минимальное значение в 0, максимальное значение в 1, но которая не на всей области определения является непрерывной функцией (имеет скачки в отдельных точках) (рис. 3).

Рисунок 7. Функция распределения смешанной случайной величины

Примеры задач с использованием понятия функции распределения

Пример 1

Приведен ряд распределений появления события $A$ в трех опытах

Рисунок 8.

Найти функцию распределения вероятностей и построить её график.

Решение.

При $x\le 1$, $F\left(x\right)=0$;

При $1

При $2

При $x>3$, $F\left(x\right)=0,2+0,1+0,3+0,4=1$;

Отсюда получаем следующую функцию распределения вероятностей:

Рисунок 9.

Пример 2

Случайная величина задана следующей функцией распределения:

Рисунок 10.

Найти вероятность, что величина $X$ будет принадлежать интервалу $\left(\frac{7}{6};;1,2\right)$.

Решение. Нам необходимо найти значение $P\left(\frac{7}{6} \[P\left(\frac{7}{6}\le XОтвет: 0,1.

spravochnick.ru

Как построить функцию распределения 🚩 Математика

11 февраля 2012

Автор КакПросто!

Закон распределения случайной величины — это соотношение, устанавливающее связь между возможными значениями случайной величины и вероятностями появления их в испытании. Известно три основных закона распределения случайных величин: ряд распределения вероятностей (только для дискретных случайных величин), функция распределения, плотность вероятности.

Статьи по теме:

Инструкция

Функция распределения (иногда – интегральный закон распределения) – это универсальный закон распределения, пригодный для вероятностного описания как дискретных, так и непрерывных СВ Х (случайных величин Х). Определяется как функция аргумента х (может быть и своего возможного значения Х=х), равная F(x)=P(X

Рассмотрим задачу построения F(x) дискретной случайной величины Х, заданной рядом вероятностей и представленной многоугольником распределения на рисунке 1. Для простоты ограничимся 4-мя возможными значениями.

При Х≤x1 F(x)=0, т.к. событие {Xпоявилась одна возможность выполнения неравенства {Xпроисходит с вероятностью p1. Таким образом, в (х1+0) произошел скачек F(x) от 0 до р. При x2

При X>x4 F(x)=p1+p2+p3+p4=1 (по условию нормировки). Иное объяснение — в данном случае событие {х<X} достоверно, так как все возможные значения данной случайной величины меньше такого х (одно из них должно быть принято СВ в опыте обязательно). График построенной F(x) приведен на рисунке 2.

Для дискретных СВ, имеющих n значений, число «ступенек » на графике функции распределения, очевидно, будет равно n. При n, стремящемся к бесконечности, в предположении, что дискретные точки «сплошь» заполняют всю числовую прямую (или ее участок), получаем, что на графике функции распределения появляется все больше и больше ступенек, все меньшего размера («ползущих», кстати, вверх), которые в пределе переходят в сплошную линию, которая и образует график функции распределения непрерывной случайной величины.

Стоит отметить, что основное свойство функции распределения: P(x1≤X<x2)=F(x2)-F(x1). Так что, если требуется построить статистическую функцию F*(x) распределения (на основе опытных данных), то за эти вероятности следует принять частоты интервалов pi*=ni/n (n – общее число наблюдений, ni – число наблюдений в i-м интервале). Далее используйте изложенную методику построения F(x) дискретной случайной величины. Отличие лишь в том, что «ступеньки» не стройте, а соединяйте (последовательно) точки прямыми линиями. Должна получиться неубывающая ломаная. Ориентировочный график F*(x) приведен на рисунке 3.

www.kakprosto.ru

Построить график распределения в Excel

Использование

Excel при изученииоснов теории вероятности и математической статистики

Тампишева С.Б.,

старший преподаватель Казахского финансово-экономического института, г.Семипалатинск, Республика Казахстан

Высшее образование и наукастановятся глобальным фактором общественного развития, выдвигаются в числонаиболее важныхнациональных и общемировых приоритетов, выступаютв качестве важнейших компонентовкультурного, социального и экономическиустойчивого развития людей, сообществ, наций[1].

В докладе ЮНЕСКО«Высшее образование в XXI веке: подходы и практические меры» (1998г.) отмечалось, что «в сфере высшего образования наблюдается теснейшее сближение, если не общность проблем, тенденций, задач и целей, заставляющихзабыватьо национальных и региональныхразличиях и специфике«[2]. Сложившиеся в настоящее время социально-экономическиеи социально-культурные условиятребуют подготовки специалиста, конкурентоспособного на рынке труда.

Для успешного функционированияспециалиста в высокотехнологическом обществе необходимо постоянное пополнениебагажа знаний, умений и навыков.Непрерывное образование- необходимость и требование современнойнаучно-технической цивилизации.

Главная задача высшейшколы- поднять профессиональную и социальнуюкомпетентность выпускников вузов, научить их ориентироваться в потоке постоянно меняющейся информации, мыслитьсамостоятельно, критически и творчески. Сегодня этоневозможно без овладения студентами знаниями, умениями, навыками использования информационных технологий в сферебудущей профессиональной деятельности.

К настоящему времени исследователи пришлик единому мнению, что информационные технологии должны разрабатываться с учетом классических дидактических требований: принципа научности, доступности и посильной трудности, систематичности и последовательности, прочности усвоения, наглядности, связи теории с практикой, сознательности и активности (самостоятельности), принципа коллективного характера обучения и учета индивидуальных особенностейобучающихся, однако применительно к новым информационным технологиямониимеют свою специфику [3].

ПЭВМ наиболее полно удовлетворяет дидактическим требованиям и позволяет управлять процессом обучения, максимально адаптировать его киндивидуальнымособенностям обучаемого. Знания, полученные при компьютерном обучении, выступают в познавательной деятельностив качестве средстварешения профессиональных задачдеятельности специалиста.

Также исследователи выделяют возможные направлениявключениякомпьютера в процесс учебно-познавательной деятельности обучаемых: диагностика, обучающий режим, отработка умений и навыковпри решении задачпосле изучения темы, моделирование сложных процессов, графическая иллюстрация изучаемого материала, работа с базами данных [4].

Остановимся наприменениитабличного процессора MicrosoftExcel при изучении элементов теории вероятностей и математической статистики вкурсематематики для экономистов. Курс математики в системе подготовки экономистовявляется основой дляизучения таких дисциплин какэконометрика, статистика, микроэкономика, макроэкономика, а математические методы исследуютсяво всех областях знаний. В процессе обучения математике у студентов вырабатываютсянавыки исследовательской работы, формируются приемы умственной деятельности, развивается интеллект, т. е.формируетсяличностьбудущего специалиста с необходимымипрофессионально значимымикачествами.

Применение математического аппарата теории вероятностей и математической статистики позволяетполучать наиболее вероятныеколичественныезначенияэкономических показателей, устанавливать связьмежду различнымислучайными параметрами и приниматьобоснованные решения в экономике.

В настоящее время математико-статистические методы широко внедрилисьв жизнь, благодаряперсональным электронно-вычислительным машинам. Статистическиепрограммные пакеты сделали эти методы более доступными и наглядными, так как трудоемкуюпо расчету различныхстатистик, параметров, характеристик, построению таблиц и графиков в основном стал выполнять компьютер, а исследователюостаетсяглавным образом творческая работа: постановка задачи, выбор методов ее решения и интерпретация результатов.

Существует множество различных пакетов программ по работе со статистическими данными, но наибольшее распространение в деловой сфере получил табличный процессор MicrosoftExcel. Он включает в себя программную надстройку «Пакет анализа» и библиотеку из83 (в среде MicrosoftExcel2000) статистических функций, 50 математических функций,которые позволяют автоматизироватьрасчеты, а такжена их основеполучить графическую интерпретацию.

При изучении основных понятий и теорем теории вероятностей можно использовать, например,такие функции Excel как: экспонента, степень, факториал, перестановки, число комбинаций, вероятность. Изучаяслучайные величины и их характеристики, можно использовать, например, такие статистические функции как дисперсия, доверительный интервал, медиана, мода , различные виды распределений случайных величин и др. Кроме того,в дальнейшем, при изучении эконометрикии статистики,предоставляется широкийвыбор другихстатистических функций.

Рассмотрим использование Excelпри изученииразличных видовраспределений дискретных инепрерывных случайных величин.

При работе со случайными величинамина лекционных занятиях студентовзнакомят с понятиемслучайной величины, законами ее распределения, математическим ожиданием, дисперсией. Формируются вероятностные модели биномиального распределения, распределения Пуассона, геометрического и гипергеометрического и других распределений, во время практических занятий эти понятия закрепляются и отрабатываются. Задания, выполненные на компьютере, помогут вывести обучающихсяна более высокий уровень усвоения знаний и умений,и сопровождаться значительной экономией времени.

При рассмотрениизаконов распределения, например, нужно обратить внимание насферы ихиспользования. При построении графиков функцийсравнивать их кривые, анализировать, делать выводы.

Рассмотрим задание набиномиальное распределение:

Задание 1. Построить с помощью программы Excel, многоугольникбиномиального распределения для следующих параметров:

a)n=10; p=0,5; q=0,5;

b)n=10; p=0,1; q=0,9;

c)n=20; p=0,3; q=0,7;

d)n=20; p=0,7; q=0,3;

Используетсястатистическая функция БИНОМРАСПР:

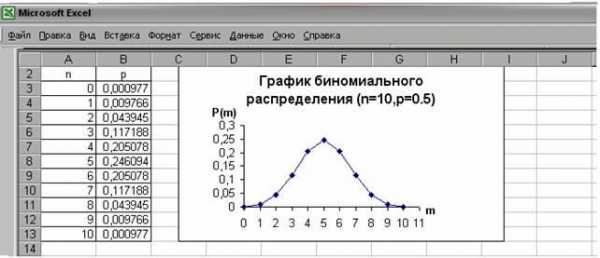
Рис.1Многоугольникбиномиального распределения( n=10, p=0,5)

Изменяя параметры распределения, проследить как изменяетсяконтур многоугольника распределения.

Задание 2. Работа уличного агента по приглашению потенциальных покупателей тайм-шер считаетсяудовлетворительной, если по его приглашению за день на презентацию придет более 10 покупателей. Считая, что вероятность того, что лицо, к которому агент обратится с предложением, с вероятностью 0,1 придет на презентацию, вычислить вероятность того, что работаагента будет признана удовлетворительной, если агент обратится с предложением к 40 прохожим.

Для задачи необходимо составление компьютерной модели, выполнение громоздкихрасчетовс помощью функции БИНОМРАСПР.

Для закрепленияраспределения Пуассона можно предложить задание 3.

Задание 3. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени Т равно 0,002. Найти вероятность того, что за время Т откажут ровно k элементов. Построить график распределения вероятности k=0;1;2;3;4;5;6;7.

Используется функция ПУАССОН:

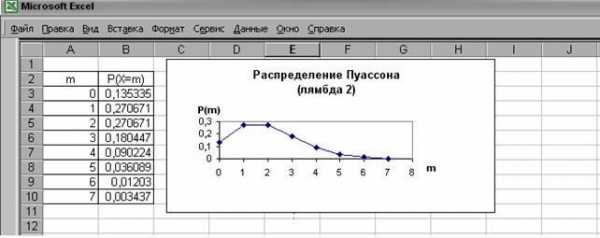
Рис.2Многоугольник распределения Пуассона (l=2)

После построения графика целесообразно поставить вопрос: от какого параметра зависит распределение Пуассона?

Задание 4 и 5 на гипергеометрическое распределение, выполнение расчетов и построение графика.

Задание 4. В лотерее «Спортлото 6 из 45 «денежные призы получают участники, угадавшие 3, 4, 5 и 6 видов спорта из отобранныхслучайно 6 видов из 45. Найти закон распределения случайной величины Х- числа угаданных видов спорта среди случайно отобранных шести. Какова вероятность получения денежного приза? Найти математическое ожидание и дисперсию случайной величины Х.

В задании 4строитсямодель, через функцию ГИПЕРГЕОМЕТвыполняются громоздкие вычисления длярядаэтого распределения.

Задание 5. Построить графики гипергеометрического распределения для следующих значений параметров:

a)N=200;M=25; n=7;

b)N=200;M=50; n=10

Нормальный закон распределенияприменяется взаданиях 6 и 7.

Задание 6.Построить кривую Гаусса для:

а) а=2; s=2; б)а=2; s=1; в)а=2; s=0,5. Сделать выводы по графикам. Найти площадь под каждой кривой Гаусса.

Эта задача подразумевает несколько этапов решения, процесс построениякривой , анализ полученных результатов, их геометрическую интерпретацию.

Задание 7. Полагая, что рост мужчин определенной возрастнойгруппы есть нормально распределеннаяслучайная величина Х с параметрамиа=173, _{, найти:}

а) выражение плотности вероятности и функции распределения случайной величины Х;

b) доли костюмов 4-го роста (176-) и 3-го роста (170-176см), которыенужно предусмотреть в общем объеме производства для данной возрастной группы;

с) квантиль _{и 10 % -ную точку случайной величины Х.}

В задании 7 необходимо построитьмодель нормального распределения, вероятность попадания в интервал,применить правиланахождения квантиля .

Задание 8. Непрерывная случайная величина Храспределенапо показательному закону, заданному при _{плотностьюраспределения ; при x<0f(x)=0. Найти вероятность того, что в результате испытания Х попадает в интервал (0,13; 0,7 ). Построить кривую распределения играфик функциираспределения.}

Используетсяфункция ЭКСПРАСП :

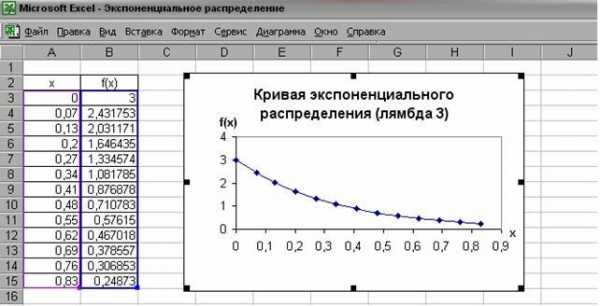
Рис. 3График плотности экспоненциального распределения (l=3)

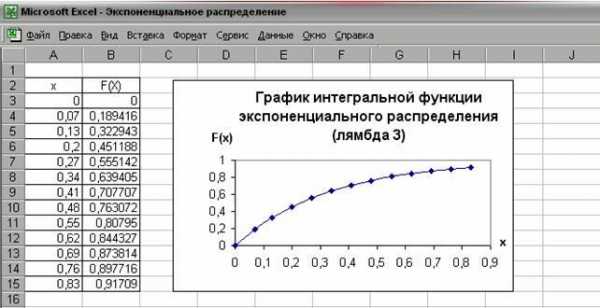
Рис.4График интегральной функции экспоненциального распределения (l=3)

Для решения задач на компьютере преподаватель выполняет отборзаданий для закрепления новых понятий и навыков поэтапно,различнойстепени сложности, а такжепозволяющиеизучить их в динамике. Содержание заданийтребует включения не только фундаментальных положений науки, но и вопросы,связанные с перспективами ее развития,также должно способствоватьсистематизации знаний. Необходимо использовать богатые иллюстрационныеграфические возможности компьютера для представления в наглядной форменекоторого процесса иего изучения. В процессе решения задачформируется их графическое представление,анализируютсяразличные ситуации, строятсякомпьютерные модели,автоматизируются непростые расчеты. Таким образом, компьютер служит инструментом для решениязадач, в том числе профессионально направленных .

Исследователи считают, что применение информационных технологийсущественным образомпреобразует мыслительную деятельность человека [6]. Формируется не только логическое, но икритическое мышление — качества, необходимыедля выработкинового стилямышления, приэтом повышаетсяобщий уровень интеллектуальной деятельности..

Современный специалистбез знания компьютера и компьютерных технологийне готов к реальной жизни не только профессионально, но и психологически. Студент-первокурсник с помощью Excel делает первые статистические расчеты при изучениитеории вероятностей и математической статистике,в дальнейшем он продолжит эту практику при освоении другихбазовых и специальных дисциплин. Информационная культураспециалиста является одной из составляющих профессионализма, помочь овладеть ее — важнейшая задача высшей школы. Таким образом, педагогически обоснованноеиспользованиеинформационных технологийв учебном процессе вузовобеспечиваетзаинтересованное повышениеконкурентоспособности молодых специалистов на рынке труда.

Литература:

1. Закон РеспубликиКазахстан «Об образовании» от 7 июня 1999 года, № 389-1 //Казахстанская правда. 11 июня.1999, № 147-148.

2. Heyn Michael,Katrina Lythoe andCharles Meyers,1999. «Education and Economic Development: Sustainability. Threshold and Equity. Proceedings of the Third UNESCO-ACEID International Conference on Educational Innovation for Sustainable Development». UNESCO: .

3. Сережкина А.Е., Садыкова В.А. Обучение в новой информационной среде: психолого-педагогические особенности//Высшее образование сегодня. — 2004. -.№ 1. — с.54-59.

4. Бекбаева З. Роль и функции средств информационной технологии в активизации самостоятельной учебно-познавательной деятельности учащихся.// Поиск, серия ест. наук. −2001. -№ 6, — с.113-119.

5. Кремер Н.Ш. Теория вероятностейи математическая статистика: Учебник для вузов. — М.: ЮНИТИ-ДАНА, 2006.-573 с.

6. Тихомиров О.К. Бабанин Л.Н. ЭВМи новые проблемы психологии. М.: Изд-во Моск.ун-та, 1986.

officeassist.ru