Правила формулы сокращенного умножения – Формулы сокращенного умножения. Подробная теория с примерами.

Применение формул сокращённого умножения

Урок обобщающего повторения «Формулы сокращенного умножения». 7-й класс

Цели урока:

Образовательные: проверить уровень усвоения учащимися темы, знание ими соответствующих формул и правил.
Развивающие: углубить знания учащихся, развить умения применять приемы сокращенного умножения при решении уравнений, при обнаружении и исправлении ошибок, объяснении своих действий, развитие творческой деятельности учащихся.
Воспитательные: создание условий для включения каждого ученика в активную учебно-познавательную деятельность,  где каждый может проявить себя,   воспитание интереса к математике,   расширение кругозора, включение в урок исторического материала.

Тип урока: урок проверки, оценки и коррекции знаний, умений и навыков в форме путешествия « По стране формул». Задания подобраны по нарастающей степени сложности.

План путешествия:

1. Проверка готовности к дороге

2. «Поляна соответствий» (верно установив соответствия ученик получает имя великого математика «Диофант», портрет, историческая справка).

3. «Озеро ошибок»

4. «Болото заданий» (игра «Математическое поле чудес».  Решив правильно уравнения, ученик
выбирает ответы и переворачивает их. В результате получает имя великого математика «Эйлер»,
портрет, историческая справка).

5. «Остров формул» (творческое задание).

Каждый ученик получает маршрутный лист путешествия, на доске также написан план путешествия и формулы:

1.(a-b)²=a²-2ab+b²
2.(a+b)²=a²+2ab+b²
3.(a-b)(a+b)= a²-b²
4. a²-b²=(a-b)(a+b)
5.a³+b³=(a+b)(a²-ab+b²)
6. a³-b³=( a-b)(a²+ab+b²)
7. a²-2ab+b²=(a-b)²
8. a²+2ab+b²= (a+b)²

На доске эпиграф:

«Единственный путь, ведущий к знаниям – это деятельность»
Бернард Шоу

 

Ход урока:

Мотивационная часть.
Ребята, посмотрите в окно, на улице уже чувствуется приход весны, а мы с вами сидим и решаем, а вам хочется путешествовать? Ну что собираемся в поход! А для этого проверим ваш багаж знаний, ведь поход будет связан с математикой, где вам потребуется знание, как вы думаете чего? (формул сокращенного умножения), конечно ведь именно они имеют широкое применение в математике, особенно в старших классах. Их используют при решении уравнений, раскрытии скобок, разложении многочленов на множители, нахождении значений выражений. Поэтому надо хорошо знать эти формулы и уметь применять их в преобразованиях выражений.
А сейчас мы проверим, как вы подготовились к походу.

1.« Проверка готовности к дороге»

1. Проверка знания правил

Вопрос.       Старт.
Квадрат суммы двух выражений равен

Вопрос.
Разность квадратов двух выражений равна

Вопрос.
Квадрат разности двух выражений равен

Вопрос.
Произведение разности двух выражений и их суммы равно

Вопрос.
Сумма кубов двух выражений равна

2. Работа усно.

Ну что, в путь! Ребята, смотрите что впереди, ведь мы попали на «Поляну соответствий», что же от нас требуется, как вы думаете?

 

2. «Поляна соответствий»

Мы справились с этим заданием, а на поляне появились какие то буквы, как вы думаете, что это за слово.

Молодцы ребята, вы получили имя великого математика.  Показываю его портрет.
Историческая справка: Очень давно, в Древней Греции жили и работали замечательные ученые-математики, которые всю свою жизнь отдали служению науке. В то время все алгебраические утверждения выражали в геометрической форме, вместо сложения чисел говорили о сложении отрезков, а произведение двух чисел сравнивали с площадью, трех чисел-с объемом и т.д. первым ученым, который отказался от геометрических способов выражения и перешел к алгебраическим уравнениям был древнегреческий ученый-математик, живший в 3 веке до нашей эры Диофант. Появились формулы, которые стали называться формулами сокращенного умножения.

А какого ещё знаменитого ученого математика вы уже знаете?

Некоторые правила сокращенного умножения были известны еще около 4 тыс. лет назад. Их знали вавилоняне и другие народы древности. Знаменитый ученый Евклид дал полный свод математических знаний своих предшественников, системно изложив все достижения греческой математики, что дало возможность дальнейшему развитию данной науки.

3. «Озеро ошибок»

Ученику нужно найти ошибку в каждой формуле и исправить ее на своих листах.

1.(4у-3х)(4у+3х)=8у²-9у²   (вместо 8у² должно быть16у²)
2.100х²-4у²=(50х-2у)(50х+2у)  (вместо50х должно быть10х)
3.(3х+у)²=9х²-6ху+у²           (вместо-6ху должно быть+6ху)

4.(6a-9c)²=36a²-54ac+81c²    (вместо-54ac должно быть-108ac)
5.х³+8=(х+2)(х²-4х+4)        (вместо-4х должно быть-2х)

Затем вызываю учеников к доске исправить ошибки в примерах, они еще раз проговаривают формулы и правила. Ребята, мы преодолели «Озеро ошибок» и подошли к «Болоту заданий».

4. «Болото заданий»

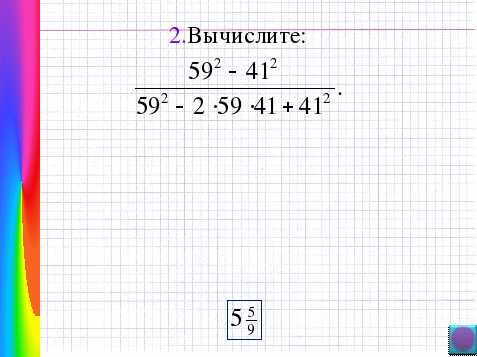
Да справились на славу со всеми трудностями, а вон смотрите и наша школа и снова мы на уроке.

И раз уж сегодня мы с вами говорили о ученых математиках, мне хотелось бы рассказать ещё об одном из них. Это Блез Паскаль Французский философ, писатель, физик, математик, изобрел первую счетную машину и сделал многое в области математики, которая называется комбинаторикой.

В 1654 г. Паскаль опубликовал одну из самых популярных своих работ «Трактат об арифметическом треугольнике». Теперь его называют треугольником Паскаля.

Итог урока

infourok.ru

Формулы сокращенного умножения

Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть.

Пусть а, b   R. Тогда:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a + b)² = a² + 2ab + b²

2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a — b)² = a² — 2ab + b²

3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.

a² — b² = (a -b) (a+b)

4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(a + b)³ = a³ + 3a²b + 3ab² + b³

5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a — b)³ = a³ — 3a²b + 3ab² — b³

6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.

a³ + b³ = (a + b) (a² — ab + b²)

7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.

a³ — b³ = (a — b) (a² + ab + b²)

8. Разность чисел в четвертой степени

(a — b)⁴ = a⁴ — 4a³b + 6a²b² — 4ab³ + b⁴

9. Сумма чисел в четвертой степени

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

10. Разность чисел в пятой степени

(a — b)⁵ = a⁵ — 5a⁴b + 10a³b² — 10a²b³ + 5ab⁴ — b⁵

11. Сумма чисел в пятой степени

(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

12. Квадрат трехчлена

(a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc

13. Квадрат линейной формы

(a + b + c + … + u + v)² = a² + b² + c² + … + u² + v² + 2(ab + ac + … + au + av + bc + … + bu + bv + … + uv)

14. Куб трехчлена

(a + b + c)³ = a³ + b³ + c³ + 3a²b + 3ab² + 3a²c + 3ac² + 3b²c + 3bc² + 6abc

formuly-sokrashhennogo-umnozheniya.ru

Алгоритм преобразования выражений с помощью формул сокращенного умножения

Алгоритм преобразования выражений

с помощью формул сокращенного умножения

Каждому из нас, наверняка, приходилось сталкиваться с умножением многочлена на многочлен, возведением его в степень, и для решения таких задач приходилось выполнять множество различных действий в длинных выражениях. Однако в некоторых случаях данное действие можно заменить и выполнить короче с помощью формул сокращенного умножения.

Квадрат суммы

1. Рассмотрим формулу — квадрат суммы.

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражения плюс квадрат второго выражения.

Некоторые правила сокращенного умножения были известны еще 4 тысячи лет тому назад. Их знали вавилоняне и другие народы древности. Но в то время они формулировались словесно или геометрически. У древних греков величины обозначались не числами или буквами, а отрезками прямых. Они говорили не а

2, а “квадрат на отрезке а”, не “ab”, а “прямоугольник, заключенный между отрезками a и b”. Правило, сформулированное во второй книге “Начал” Евклида в III веке до нашей эры, звучало так: “Если прямая линия как-либо рассечена, то квадрат на всей прямой равен квадратам на отрезках вместе с дважды взятым прямоугольником, заключенным между отрезками”.

Также в началах Евклида справедливость данного равенства при положительных значениях a и b доказана геометрическим способом с помощью вышеприведенного чертежа.

Алгоритм решения:

1. Возведем в квадрат выражение .

2. Воспользуемся формулой и выполним первое действие – возведем в квадрат первое выражение. Получим

3. Следующим шагом является нахождение удвоенного произведения первого и второго выражения. Так как первое выражения – a, второе — b

4. Следующим шагом по данной формуле будет возвести в квадрат второе выражение, и так как второе выражение в нашем примере —

5. Чтобы получить окончательный результат нам следует сложить все три выражения —

Примеры:

1)

2)

Квадрат разности

Формула квадрата разности очень похожа на формулу квадрата суммы и содержит различия лишь в знаках.

Рассмотрим формулу — квадрат разности.

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения.

Геометрическое объяснение квадрата разности ничем не отличается от объяснения первой формулы.

Алгоритм решения:

1. Возведем в квадрат выражение .

2. Воспользуемся формулой и выполним первое действие – возведем в квадрат первое выражение. Получим

3. Следующим шагом является нахождение удвоенного произведения первого и второго выражения. Так как первое выражения – a, второе — b

4. Следующим шагом по данной формуле будет возвести в квадрат второе выражение, и так как второе выражение в нашем примере —

5. Чтобы получить окончательный результат нам следует вычесть из квадрата первого выражения удвоенное произведение первого и второго выражений, а затем прибавить квадрат второго выражения —

Примеры:

1)

2)

Разность квадратов

Рассмотрим формулу — разность квадратов.

Или

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Разность квадратов выражений равна произведению разности выражений и их суммы.

Для данной формулы также существует графическое объяснение.

Алгоритм решения:

1. Выполним действия в выражении .

2. Найдем разность первого и второго выражений .

3. Найдем сумму первого и второго выражений.

4. Перемножим результат сумму и разность первого и второго выражения

Примеры:

1)

2)

Куб суммы

Рассмотрим формулу — куб суммы.

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

Алгоритм решения:

1. Возведем в куб выражение .

2. Воспользуемся формулой и выполним первое действие – возведем в куб первое выражение. Получим .

3. Найдем утроенное произведение квадрата первого выражения на второе.

4. Найдем утроенное произведение первого выражения на квадрат второго.

5. Найдем куб второго выражения.

6. Найдем сумму куба первого выражения, утроенного произведения квадрата первого выражения на второе, утроенного произведения первого выражения на квадрат второго и куба второго выражения. Получим — .

Пример:

1)

2)

Куб разности

Рассмотрим формулу — куб разности.

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

Алгоритм решения:

1. Возведем в куб выражение .

2. Воспользуемся формулой и выполним первое действие – возведем в куб первое выражение. Получим .

3. Найдем утроенное произведение квадрата первого выражения на второе.

4. Найдем утроенное произведение первого выражения на квадрат второго.

5. Найдем куб второго выражения.

6. Из куба первого выражения вычтем утроенное произведение квадрата первого выражения на второе, затем прибавим утроенное произведения первого выражения на квадрат второго и вычтем куб второго выражения. Получим —

7. Примеры:

Сумма кубов

Рассмотрим формулу — сумма кубов.

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

Алгоритм решения:

1. Выполним действия в выражении .

2. Найдем сумму первого и второго выражений .

3. Найдем неполный квадрат разности первого и второго выражений

4. Перемножим сумму первого и второго выражений и неполный квадрат первого и второго выражения

Примеры:

1)

2)

Разность кубов

Рассмотрим формулу — разность кубов.

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

Алгоритм решения:

1. Выполним действия в выражении .

2. Найдем сумму первого и второго выражений .

3. Найдем неполный квадрат разности первого и второго выражений

4. Перемножим сумму первого и второго выражений и неполный квадрат первого и второго выражения

Примеры:

1)

2)

Треугольник Паскаля

Этот треугольник позволит найти коэффициенты членов многочлена при возведении двучлена в любую степень. На третьей строке видим коэффициенты, получаемые при возведении в квадрат, на четвёртой – в куб.

Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух, расположенных над ним чисел. Продолжать треугольник можно бесконечно. Строки треугольника симметричны относительно вертикальной оси.

Первое упоминание треугольной последовательности биномиальных коэффициентов под названием «meru-prastaara» встречается в комментарии индийского математика X века Халаюдхи к трудам другого математика, Пингалы. Треугольник исследуется также Омаром Хайямом около 1100 года, поэтому в Иране эту схему называют треугольником Хайяма. В 1303 году была выпущена книга «Яшмовое зеркало четырёх элементов» китайского математика Чжу Шицзе, в которой был изображен треугольник Паскаля на одной из иллюстраций; считается, что изобрёл его другой китайский математик, Ян Хуэй (поэтому китайцы называют его треугольником Яна Хуэя). На титульном листе учебника арифметики, написанном в 1529 году Петром Апианом, астрономом из Ингольтштадского университета, также изображён треугольник Паскаля. А в 1653 году (в других источниках в 1655 году) вышла книга Блеза Паскаля «Трактат об арифметическом треугольнике».

Составитель Кашина Маргарита,

ученица 7 класса школы при Посольстве РФ в Великобритании

Учитель математики Щербакова В.Б.

Кашина Маргарита, 7 класс

gigabaza.ru

правила применения формул сокращенного умножения

Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.

Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).

Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.

Квадрат суммы

Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².

Квадрат разности

Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².

Разность квадратов

Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a – с).

Куб суммы

Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого. В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.

Сумма кубов

Согласно формуле, сумма кубов приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·( а² — ас + с²).

Пример. Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.

Если значения сторон небольшие, то выполнить вычисления просто.

Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.

Куб разности

Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.

Разность кубов

Формула разности кубов отличается от суммы кубов лишь одним знаком. Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде математического выражения разность кубов выглядит следующим образом: а³ – с³ = (а – с)(а² + ас + с²).

Пример. Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. Известна лишь величина стороны маленького и большого куба.

Если значения сторон небольшие, то вычисления довольно просты. А если длины сторон выражаются в значительных числах, то стоит применить формулу, озаглавленную «Разность кубов» (или «Куб разности»), которае значительно упростит вычисления.

fb.ru

Формулы сокращенного умножения

1) каждой группе раздаются карточки с заданием, нужно раскрыть скобки, умножив многочлен на многочлен, определить закономерность и вывести ФСУ: 1) а) (a—b)(a+b)=

б) (m+n)(m—n)=

в)(x—y)(x+y)=

2) а) (a-b)(a-b)=

б) (m—n)(m—n)=

в) (x—y)(x—y)=

3) а) (a+b)(a+b)=

б) (m+n)(m+n)=

в) (x+y)(x+y)=

критерий	дескриптор
Умножает многочлен на многочлен	— правильно раскрыли скобки — нашли закономерность — могут раскрыть скобки применяя закономерность

Даем название каждой формуле, проговариваем определения (5 минуты)

2) учитель задает проблемные вопросы «Как можно определить, какой знак будет стоят перед удвоенным произведением?», ставит учащимся наводящие вопросы, помогающие в сборе идей. (светофор) (3 минут)

3) При записи формул были допущены ошибки . Найдите и исправьте их.

          1)  (а+в)² =а²+ав+в²

     Ответ : (а+в)²=а²+2ав+в²

2)  (а-с)²=а²-2ав+в²

     Ответ : (а-в)²=а²-2ав+в²

3)  (а+в)³=а³+а²в+ав²-в³

     Ответ : (а-в)³=а³-3а²в+3ав²-в³

4)  (а-в)³=а³-3ав+3ав-в³

     Ответ : (а-в)³=а³-3а²в+3ав²-в³

5)  а²-в²=(а-в)(а-в)

     Ответ : а²-в²=(а-в)(а+в)

(3 минут), группы обмениваются конвертами и оценивают задания, используя правильные ответы

4) физ. минутка «Разминка для шеи и головы». Учитель задает наводящие вопросы, учащиеся должны соответственно кивнуть: согласны, не знают или не согласны (2 минуты)

5) В таблицах представлены выражения. Выберите   правильный ответ.

                                                              Ответы:

Задание	1	2	3
(с+3)2=	с2 — 6с + 9	с2 + 2с + 9	с2 + 6с + 9
(4-2у)2=	16 + 16у + у2	16 — 16у + у2	8 — 8у + у2
(9+5х)2=	25х2+90х+81	25х2+81	25х2-90х- 81

(5 минут) работа в парах и тройках, взаимопроверка внутри группы с правильными ответами на доске.

1. Теоретическая разминка с карточками (формулы).

• учитель показывает – дети говорят

• учитель говорит – дети показывают

• учитель показывает – дети говорят правило

(3 минут)

videouroki.net