Таблица эквивалентности пределов — энциклопедический справочник и словарь для студента от А до Я
ОПРЕДЕЛЕНИЕ Таблица эквивалентных функций используется для вычисления пределов и изучения числовых рядов для сходимости. Пусть функция — бесконечно малая функция в точке а, т. Е. то имеют место следующие соотношения: Примеры решения проблем ПРИМЕР Используя таблицу эквивалентных бесконечно малых, вычислите предел Этот предел имеет неопределенность. Перейдем под знаком предела к эквивалентной бесконечно малой (это можно сделать, поскольку аргументы арксина и синуса стремятся к нулю): ПРИМЕР Найти предел То есть, мы имеем неопределенность типа . Поскольку касательный аргумент стремится к нулю, когда х стремится к единице, можно заменить касательную на ее эквивалентное значение: Для знаменателя фракции применяйте сокращенную формулу умножения «разность квадратов»: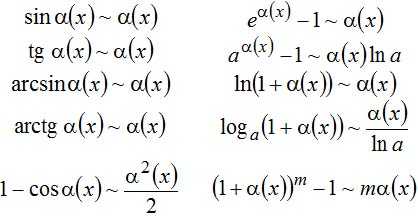
sciterm.ru
51. Эквивалентные бесконечно малые функции. Таблица эквивалентных бесконечно малых функций.
Функции и называют бесконечно малыми при , если и
Функции и называют эквивалентными бесконечно малыми при , если
Очень удобно пользоваться заменой эквивалентных бесконечно малых при нахождении пределов. Замена производится на основе таблицы.
Таблица эквивалентных бесконечно малых.
Пусть — бесконечно малая при .

Эквивалентность всех величин таблицы можно доказать, основываясь на равенстве .
52. Теорема о применении эквивалентных бесконечно малых к вычислению пределов.
При вычислении пределов часто применяется следующая Теорема. Предел отношения двух бесконечно малых (неопределенность ) равен пределу отношения двух других бесконечно малых, эквивалентных данным, т.е.
Отметим также: если , то.
3.2. Основные формулы эквивалентности бесконечно малых.
Известна формула первого замечательного предела:
Используя это равенство, получим
Отсюда получаем первую группу формул эквивалентности бесконечно малых.
При
. (1)
Вторая группа формул связана с логарифмической функцией.
Имеем:
Если при , то
Получаем вторую группу формул:
(2)
Третья группа формул связана с показательной функцией. Имеем:
Отсюда
Тогда
Итак, третья группа формул эквивалентности бесконечно малых
,
, (3)
Четвертая группа формул связана со степенной функцией.
Имеем:
Итак, четвертая группа формул эквивалентности бесконечно малых
,
,
(4)
53. Односторонние пределы функции в точке. Односторонняя непрерывность функции в точке.
Определение. Предела слева (справа)
Число А(В) по определению называется пределом функции f(x) в точке х0 слева (справа), если
>0 >0 : x из x0-<x<x0 (x0<x<x0+)
f(x)-A< (f(x)-B<),
при этом пишут:
Пример.
Справедлив критерий 2 существования предела функции в точке.
Теорема.
Для того, чтобы у функции f(x) существовал предел при хх0 необходимо и достаточно, чтобы существовал левосторонний предел в т. х0, существовал правосторонний предел в т. х0 и они были бы равны между собой.
Определение. Н
Функция f(x) определенная в левосторонней окрестности т. х0 (или в правосторонней окрестности т.х0) и в самой точке х0 называется непрерывной в т. х0 слева (справа), если
>0 >0 : x из x0-<xx0 (x0x<x0+)
f(x)-f(x0-0)< (f(x)-f(x0+0)<)
При этом значения f(x0-0) (f(x0+0)) называют значениями функции в точке х0 слева (справа).
Пример .
f(-0)=0.
Теорема. Критерий непрерывности функции в точке.
Для того чтобы функция f(x) была непрерывной в т. х0 необходимо и достаточно, чтобы она была непрерывна слева в т. х 0, справа в т. х0 и при этом выполнялось соотношение :
f(x0-0)=f(x0+0)=f(x0)
54. Точки разрыва функции и их классификация.
Определение. Разрывной функции в т. x0.
Функция f(x) не являющаяся непрерывной в т. x0 называется разрывной в т. x0.
При этом точки разрыва функции подразделяются на точки разрыва I рода и II рода.
Определение. Точка разрыва I рода.
Если у функции f(x) и они конечны, то говорят, что точка x0— точка разрыва первого рода.
При этом, если , то говорят, что точкаx0— точка устранимого разрыва.
-разрывная функция.
Если положить — то произойдет устранение разрыва и функция станет непрерывной.
У функции так как
— имеется конечный скачок.
Определение. Точка разрыва II рода.
Если у функции f(x) хотя бы один из односторонних пределов не существует или равен , то говорят, что т. х0— точка разрыва II рода.
Пример
Если устремить х к 0 разными способами, то получим различные значения пределов:
, kN, x0 , а ;
kN, x0 , а ,
значит функция f(x) не имеет предела â т. х0=0, то есть т. х0 точка разрыва II рода.studfiles.net
Таблица эквивалентных — ПриМат
Таблица эквивалентных
Отношения бесконечно малых можно упрощать, отбрасывая бесконечно малые слагаемые большего порядка и заменяя множители в числителе и знаменателе на эквивалентные им бесконечно малые. Чтобы этот способ вычисления пределов (точнее, раскрытия неопределённостей вида ) можно было применять к большему числу примеров, мы должны иметь достаточно большой запас известных пар эквивалентных величин. Создадим такой запас для базы в виде таблицы «стандартных» эквивалентных бесконечно малых.
Поскольку в этой таблице мы всегда будем рассматривать базу , для простоты записи будем писать знак вместо .
Докажем некоторые утверждения:
1)
2)
3)
4)
Источники:
- Лысенко З.М. Конспект лекций по курсу математического анализа. (Тема «Сравнение функций»).
Лимит времени: 0
Информация
Тест по теме «Эквивалентные функции»
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 6
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
- С ответом
- С отметкой о просмотре
Поделиться ссылкой:
Похожее
ib.mazurok.com
Применение теорем об эквивалентных бесконечно малых при вычислении пределов и таблицы эквивалентностей
Замена переменных при вычислении пределов, использование непрерывности функции при вычислении пределов.
а) Правило замены переменной для непрерывной функции.
По определению непрерывности функции в точке ,
Если дана сложная функция , функция имеет предел в точке и функция непрерывна в точке , то
.
То есть при вычислении предела непрерывной функции можно перейти к пределу под знаком функции. Например, в силу непрерывности основных элементарных функций справедливы равенства:
если – непрерывные функции и т. д.
Пример 5. Вычислить
б) Правило замены переменной для пределов функций в общем виде.
Пусть существуют пределы и и при . Тогда при существует предел сложной функции и .
Это правило полезно при вычислении предела в том случае, когда вычислить трудно. Полагают и находят предел при условии, что этот предел вычисляется проще первоначального.
Пример 6. Вычислить .
Решение. Сделаем замену переменной , тогда
.
Применение замечательных пределов при вычислении пределов функций
Предел называется первым замечательным пределом (раскрывает неопределенность ).
Если функция такова, что , то .Этот предел имеет важное значение при раскрытии неопределенности .
Пример 7. Вычислить
а) ; б) .
Решение. а) Имеем неопределенность .
б) .
Так как стремится не к 0, а к , то сделаем замену переменной . При при , а .
Имеем
Второй замечательный предел имеет вид
или
, где е=2,71826…– иррациональное и трансцендентное число. Если , то . Если , то .
С помощью второго замечательного предела раскрывается неопределенность , то есть ищутся пределы показательно- степенных функций , где .
Предположим, что в окрестности точки , за исключением, быть может, самой точки . Применяя формулу второго замечательного предела и возможность перехода к пределу отдельно в основании и показателе степени, получаем:
Пример 8. Вычислить .
Решение.
в окрестности за исключением точки .
Применяя вышеуказанные преобразования, получим
В процессе вычисления предела получили
Вычисляем
Следовательно, и .
Ответ:
Пример 9.Вычислить
Решение. Имеем
При вычислении этого предела аналогично используем второй замечательный предел
Применение теорем об эквивалентных бесконечно малых при вычислении пределов и таблицы эквивалентностей.
Пусть и . Если , то и называются эквивалентными бесконечно малыми в точке . Это обозначается как при .
Теорема 1. Если , при , то при .
Теорема 2. Если , при , то
Теорема 3. Алгебраическая сумма конечного числа бесконечно малых эквивалентна бесконечно малой низшего порядка. Иначе: пусть – бесконечно малая низшего порядка по сравнению с , , тогда .
Теорема 4. Если , при , причем существует и отличен от –1, то при .
Таблица эквивалентностей.
Пусть – бесконечно малая при , то есть . Тогда
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11. .
Все приведенные выше формулы справедливы при . Рассмотрим примеры на вычисление пределов с помощью теорем об эквивалентных бесконечно малых и таблицы эквивалентностей.
Пример 10. Вычислить
а) б) в)
Решение.
При вычислении этого предела применили теоремы 2 и 5 и табличные эквивалентности 1) и 7).
б) Имеем неопределенность .
Применим эквивалентность , так как . Но нельзя считать, что , поскольку при . Поэтому сделаем замену переменной при . Тогда имеем:
Использовали формулы приведения , табличные эквивалентности 1) и 11) и теорему 1: , так как .
в) В данном случае также имеем неопределенность .
Сделаем замену при .
Получаем
Применили эквивалентности 1) и 6).
Ответ: а) б) в)
Пример 11. Вычислить .
Решение. Так как при , то
Ответ:
megaobuchalka.ru
Эквивалентные бесконечно малые функции при вычислении пределов
Быстрым способом нахождения пределов функций имеющих особенности выда ноль на ноль является применение эквивалентных бесконечно малых функций. Они крайне необходимы если нужно находить границы без применения правила Лопиталя. Эквивалентности заключаются в замене функции ее разложением в ряд Маклорена. Как правило при вычислении предела используют не более двух членов разложения. Для удобства приведем небольшую таблицу эквивалентностей основных функций при движении переменной к нулю
есть еще несколько формул однако они встречаются редко.
Рассмотрим некоторые примеры из сборника задач Дубовика В.П., Юрика И.И. «Высшая математика» для закрепления практических знаний.
————————————
Пример 1. Найти пределы.
1) (5. 492. 1)
2) (5. 492. 7)
3) (5. 492. 8)
4) (5. 492. 9)
5) (5. 492. 11)
6) (5. 492. 13)
7) (5. 492. 15)
8) (5. 492. 17)
9) (5. 492. 19)
Решение.
1) Согласно правилам разложения в окрестности нуля поведение заданных функций будет следующим
На основе этого предел примет значение
2) Использую правила эквивалентностей преобразим функцию
граница примет значение
3) Преобразуем числитель и знаменатель по правилам
и найдем предел
4) Если Вам встречаются подобные примеры то нужно выполнить следующее: на основе формул разложения упростить числитель
Подстановкой в предел получим
неопределенность вида ноль на ноль . Для ее раскрытия нужно знаменатель разложить на простые множители.
Чтобы не решать квадратное или другие уравнения, которые могут быть, можете смело делить знаменатель на числитель
Подставляем в предел и вычисляем
Такого рода примеры задуманы таким образом что знаменатель или числитель имеют особенности, избавившись от которых без проблем вычисляем пределы.
5) Согласно правилам эквивалентности поведение числителя и знаменателя подменяем функциями
В результате находим предел
6) Производим замену функций эквивалентными
На основе этого получим
7) Для применения правил эквивалентности добавим и вычтем в числителе единицу.
Далее делаем замену
После подстановки в предел получим
8) Преобразуем числитель
Подставим и сведем к первому замечательному пределу
9) Согласно разложению в окрестности нуля получим
Граница примет вид
Применение эквивалентных функций позволяет быстро находить границы функций. Используйте их в тех случаях, когда это необходимо, изучайте и обогащайте знания самостоятельным решением подобных примеров. Это позволит Вам быть спокойными и уверенными при написании контрольных работ и домашних заданий.
————————————
Посмотреть материалы:
yukhym.com
25. Эквивалентные бесконечно малые функции (таблица). Теорема об эквивалентных бесконечно малых функциях.
Определение: функция  называется бесконечно
малой при
называется бесконечно
малой при 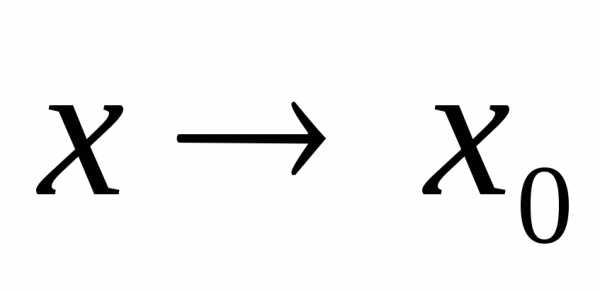 ,
если
,
если 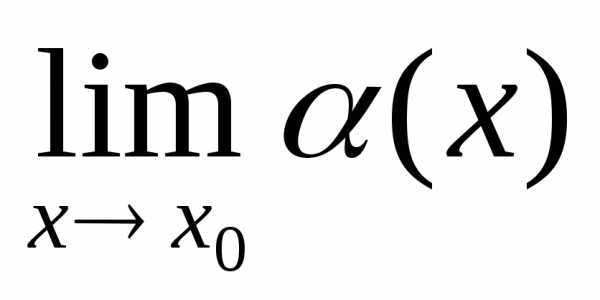 =0. Теорема
(критерий эквивалентности):
=0. Теорема
(критерий эквивалентности):
Пусть 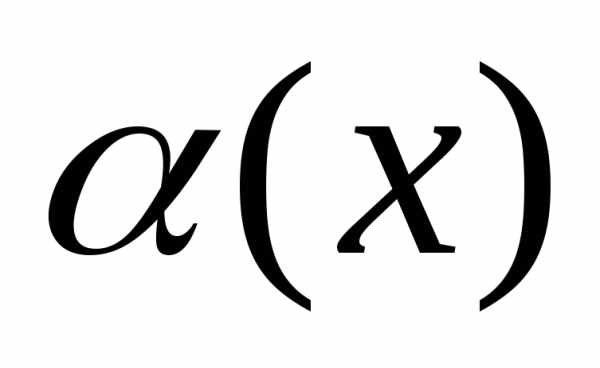 ,
, -бесконечно
малые функции при
-бесконечно
малые функции при 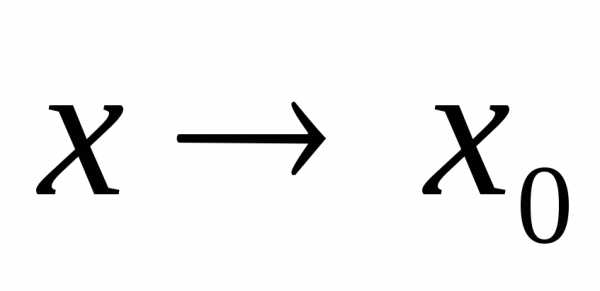 .
.

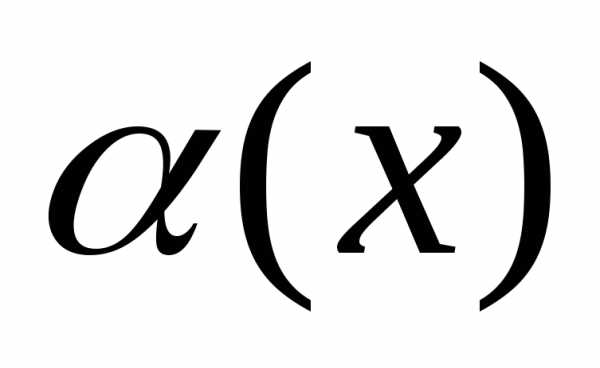 —
— .
Тогда
.
Тогда 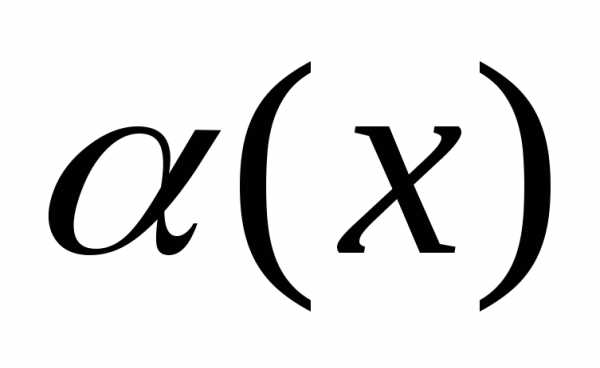 ~
~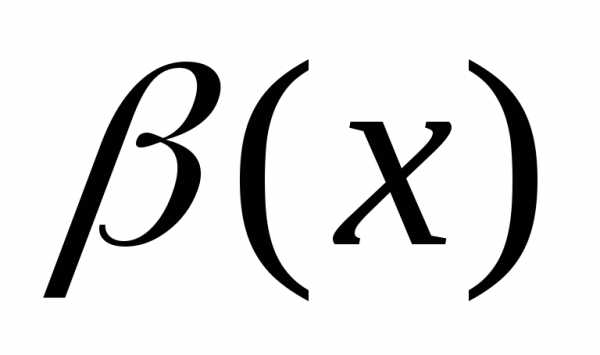 при
при 
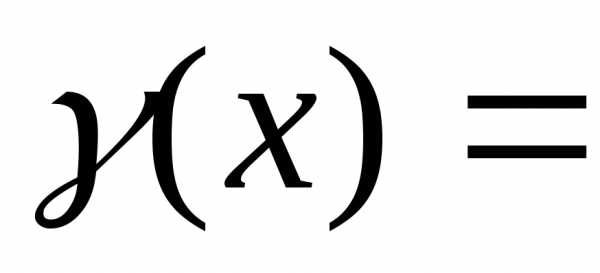 .
.
Доказательства:
( ). Пусть
). Пусть 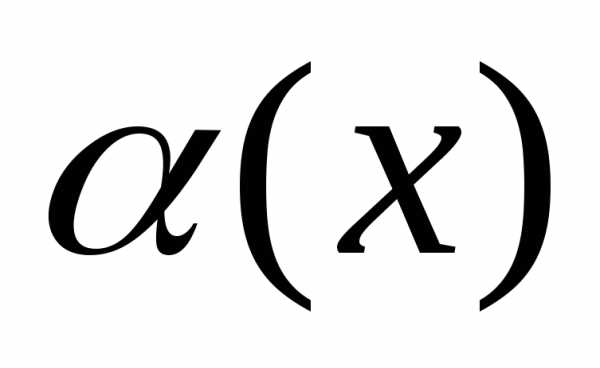 ~
~ ,
, 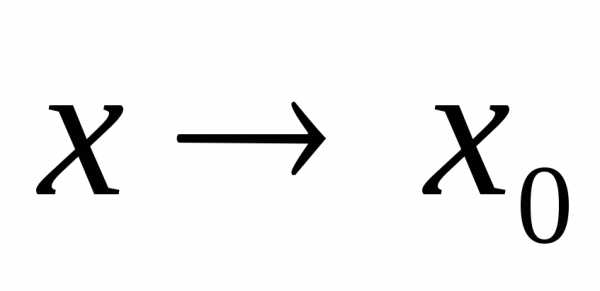 ,
то есть
,
то есть 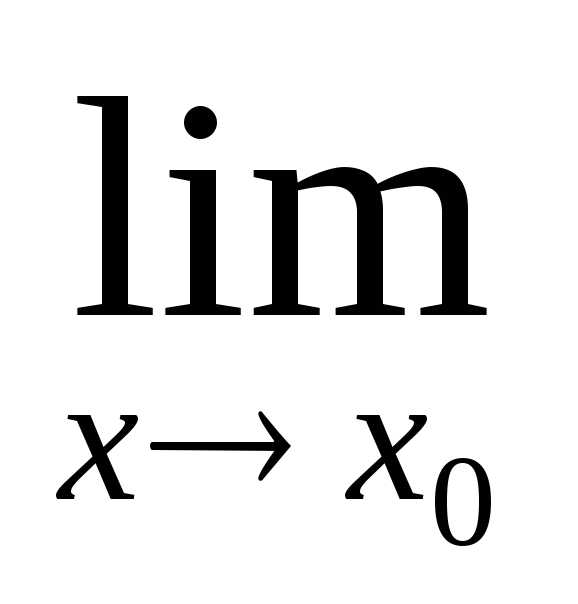
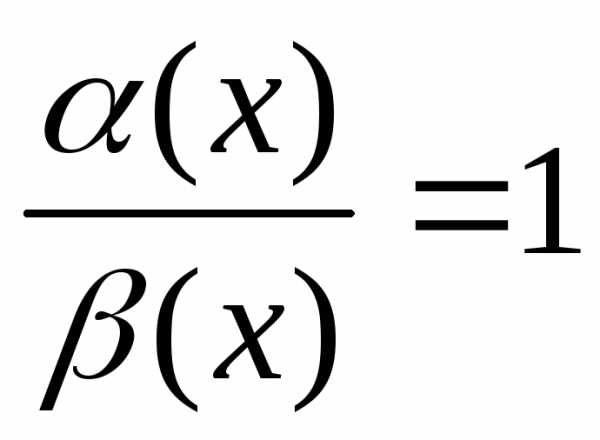 .
.

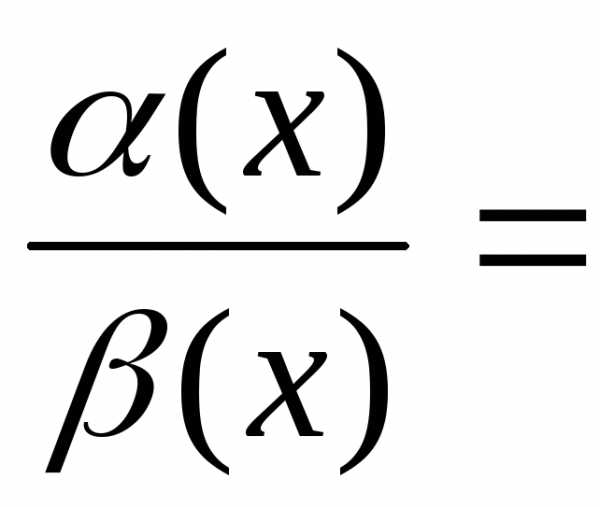
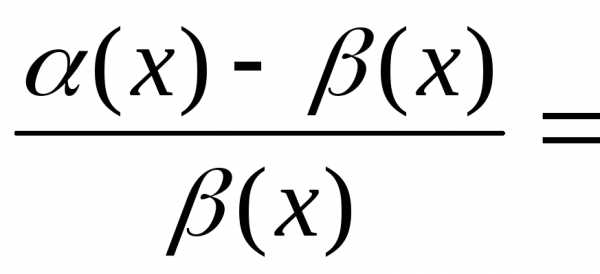

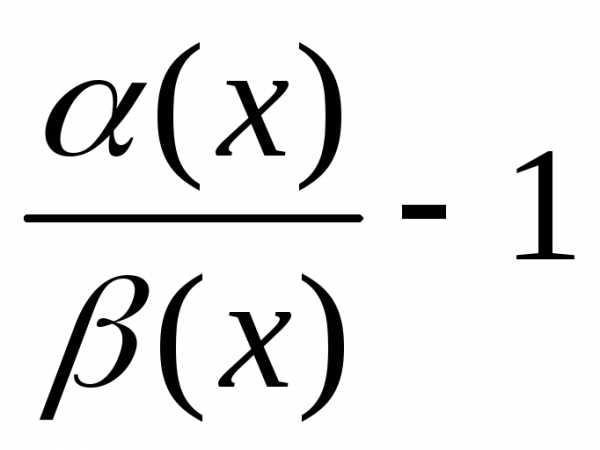 =0,
=0,
то
есть 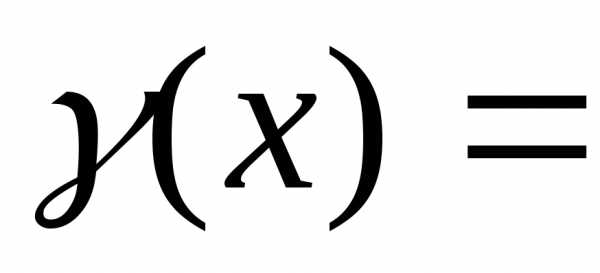 .
.
( ).
).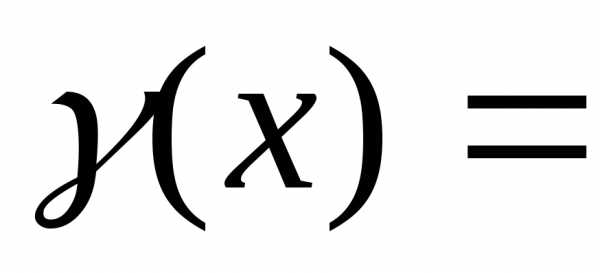 .,
.,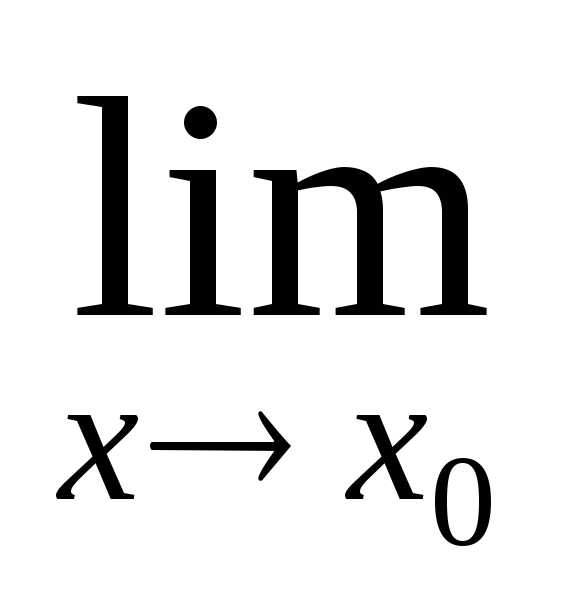
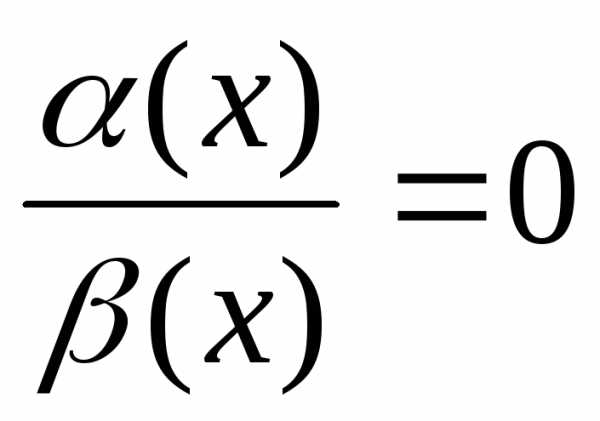 .
.
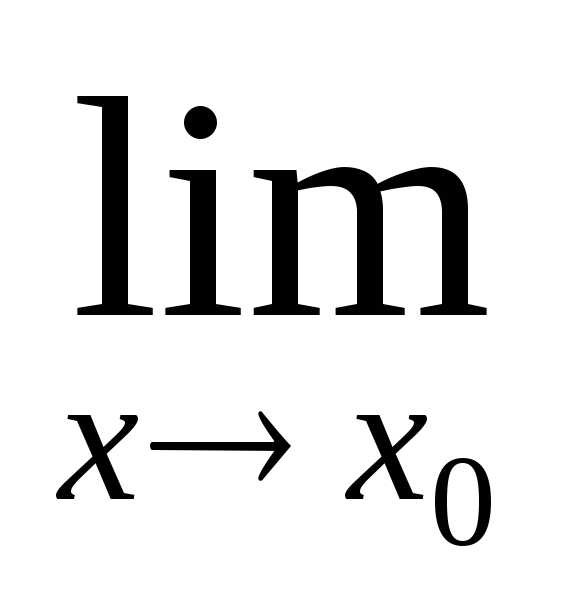

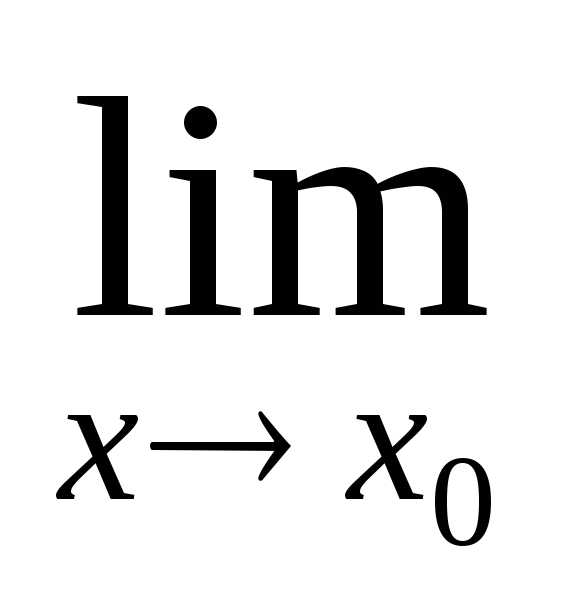
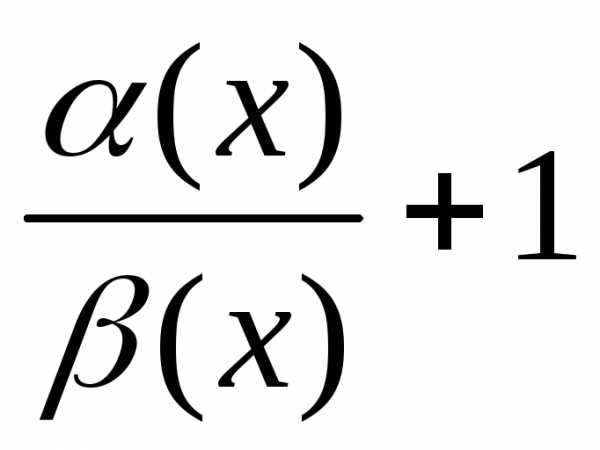 =1.
=1.
Эквивалентные бесконечно малые функции. Теорема о замене на эквивалентные.
Определение: функция 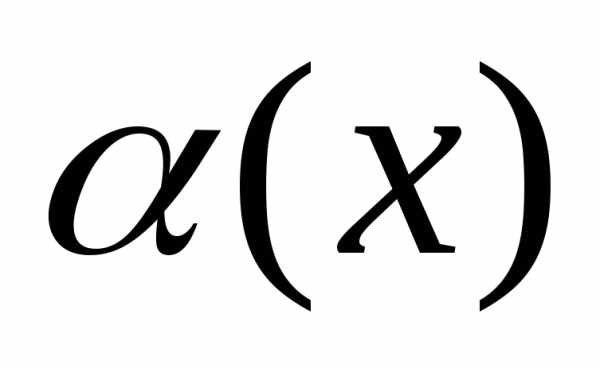 называется бесконечно
малой при
называется бесконечно
малой при  ,
если
,
если  =0.
=0.
Теорема (о замене на эквивалентные):
Пусть
функция 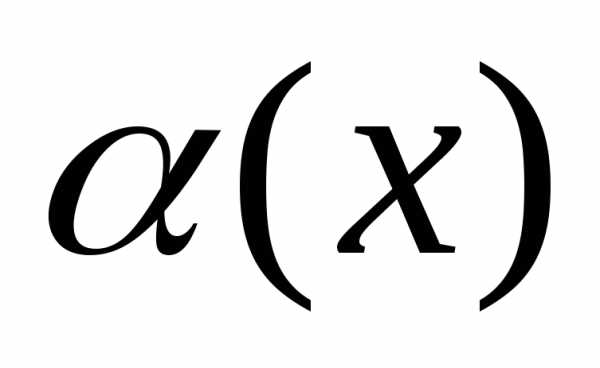 ~
~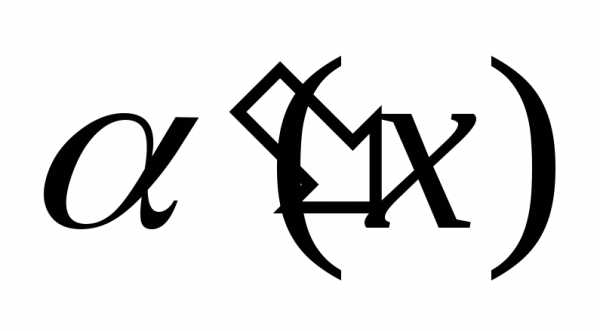 ,
,  ~
~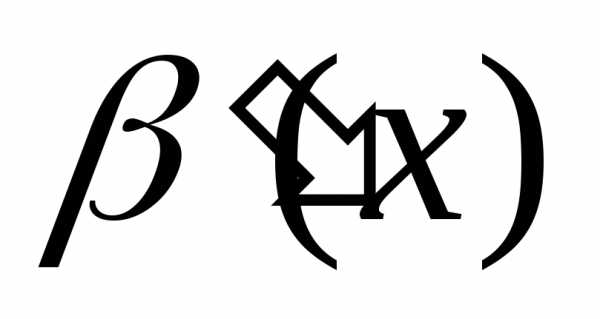 при
при 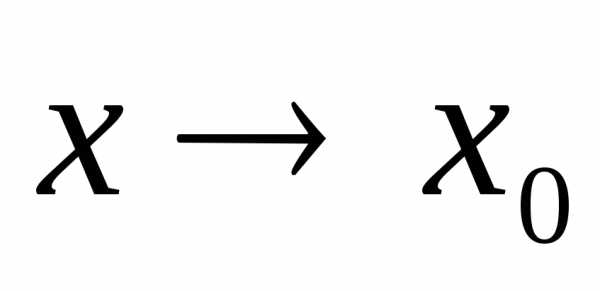 и существует
и существует 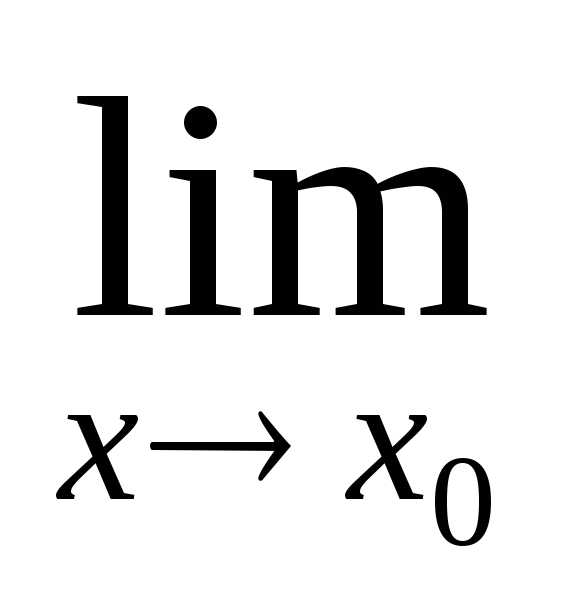
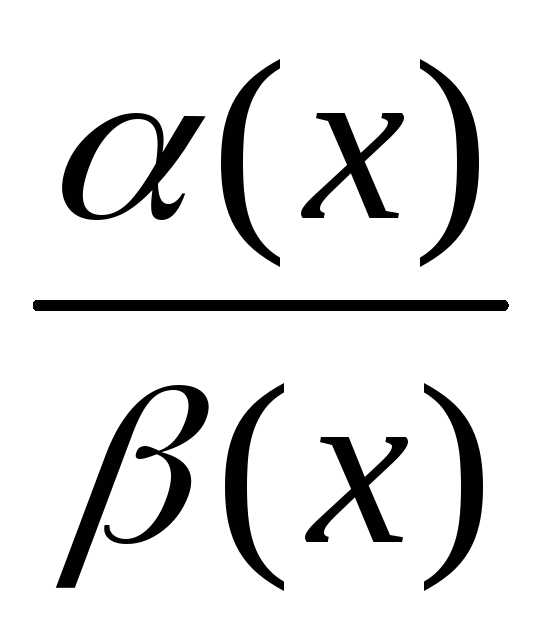 ,
тогда существует и
,
тогда существует и 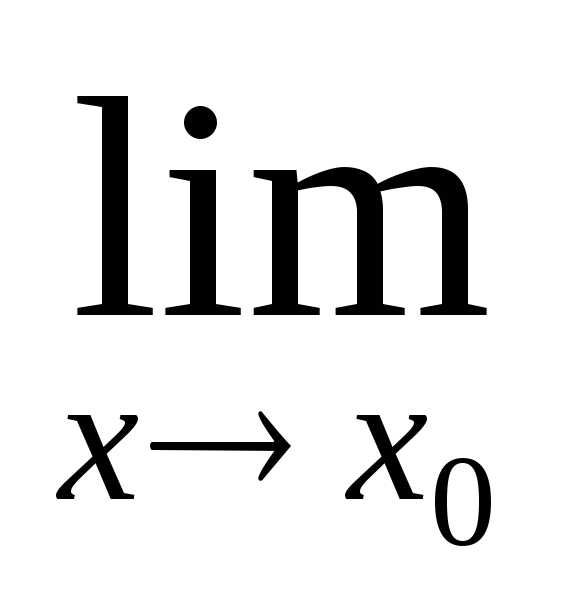
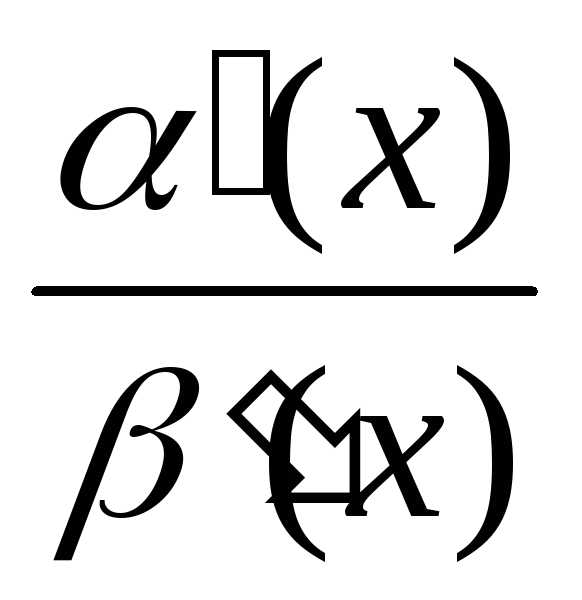 =
=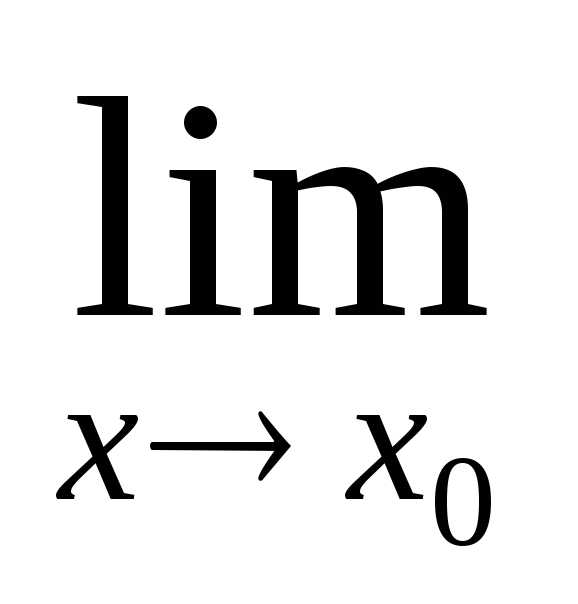
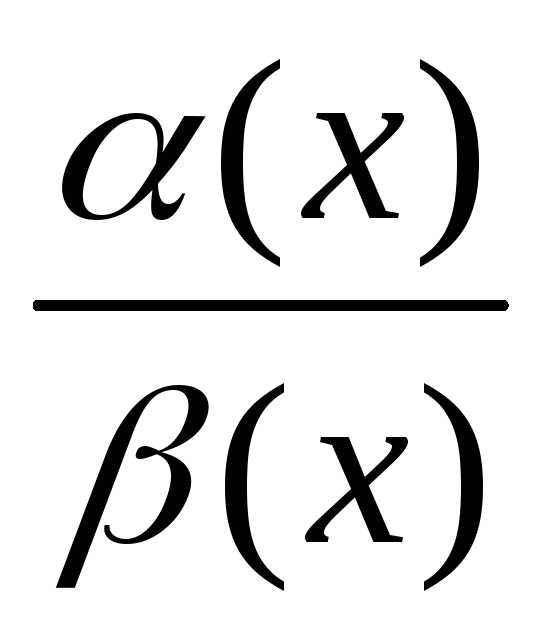 .
То есть выражение или функцию можно
заменять на эквивалентное.
.
То есть выражение или функцию можно
заменять на эквивалентное.
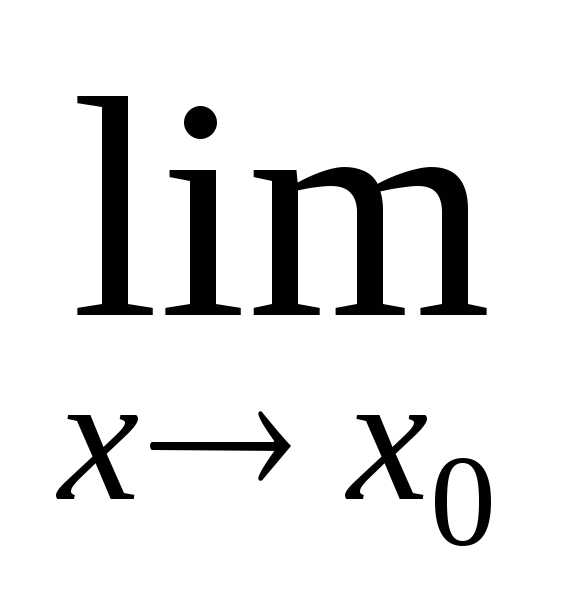
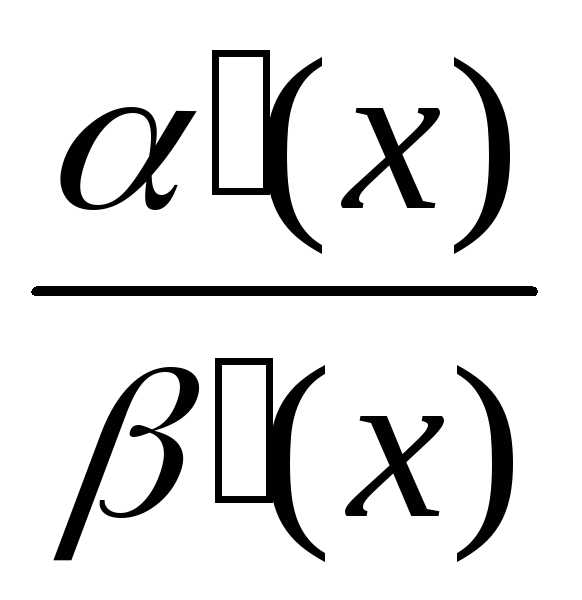 =
=
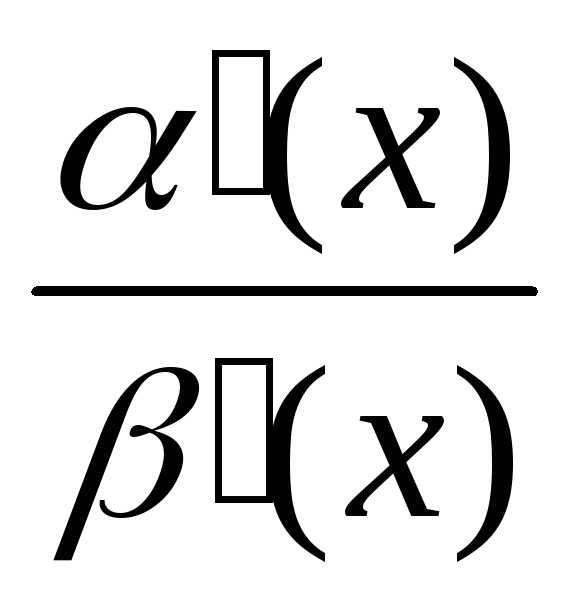 *
*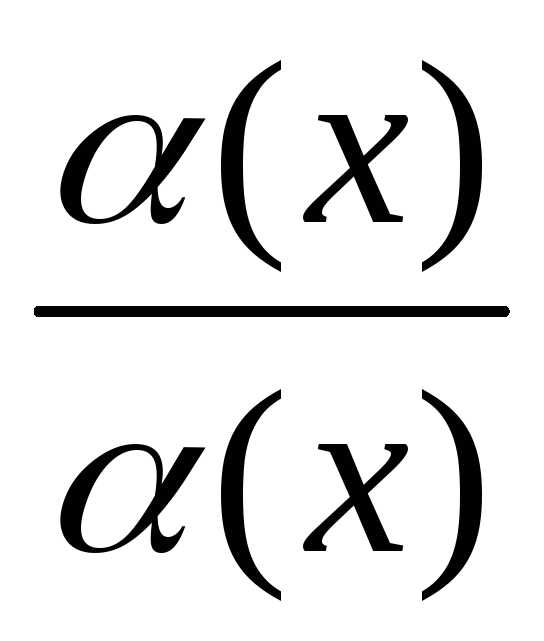 *
* =
=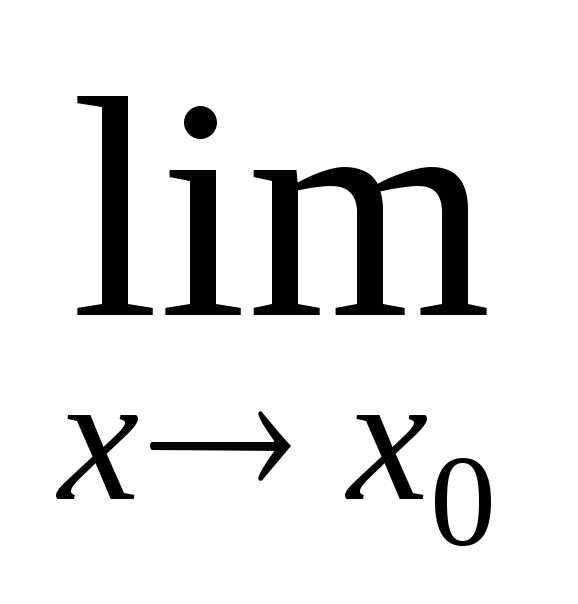
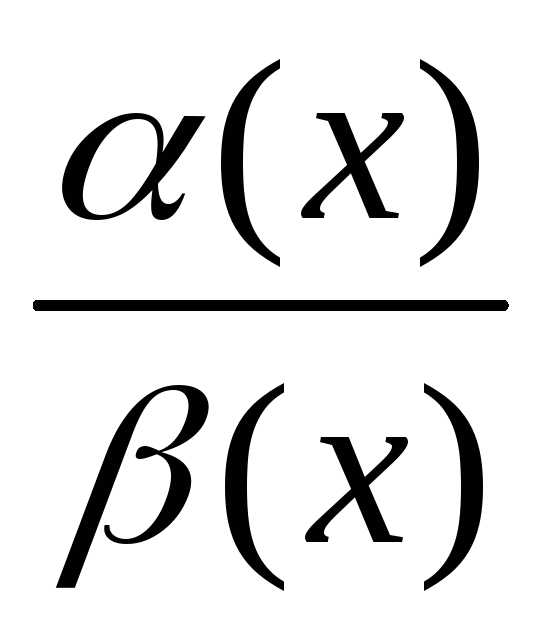 .
.
1 1
26. Сравнение бесконечно больших функций. Примеры.
27. Непрерывность функции в точке (3 определения). Свойства функций, непрерывных в точке.
Определение 1: Функция 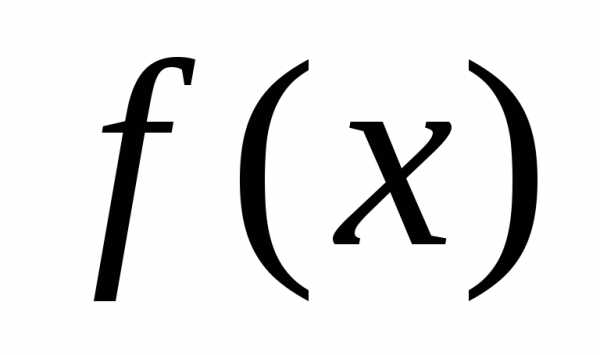 непрерывна
в точке
непрерывна
в точке 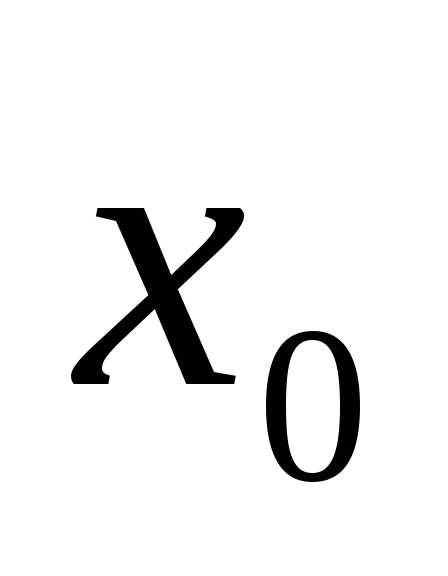 ,
если
.
,
если
.
Определение 2: Функция 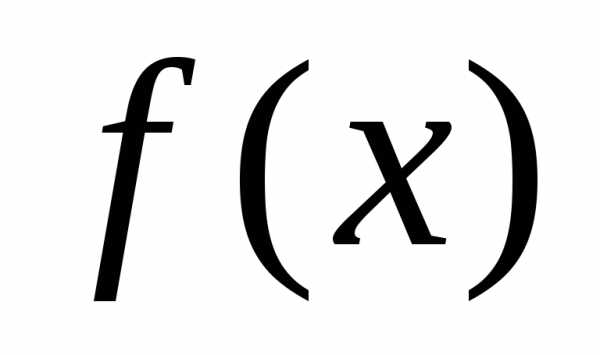 непрерывна
в точке
непрерывна
в точке 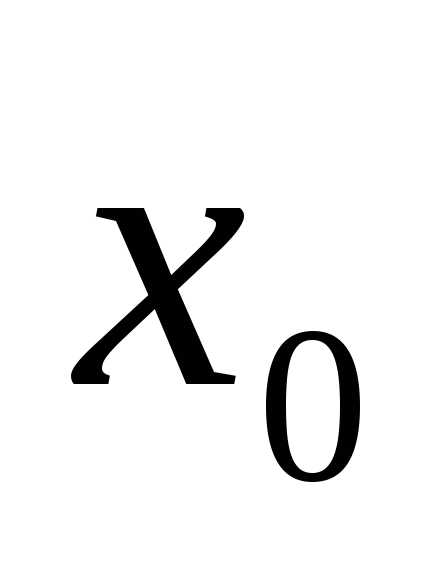 ,
если
,
если 
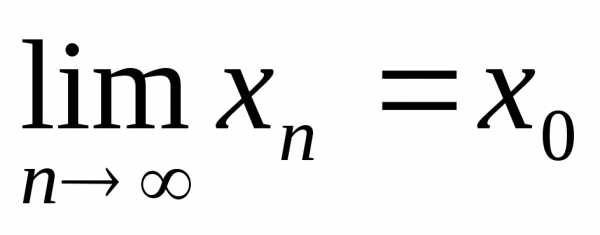 , .
, .
Определение 3: Функция  непрерывна
в точке
непрерывна
в точке  ,
если
,
если 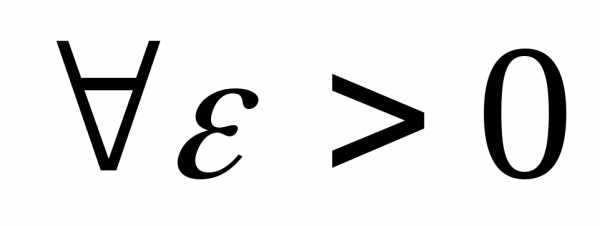


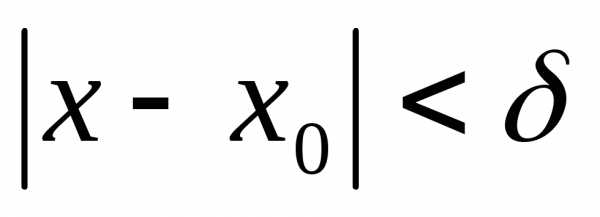
.
Свойства непрерывных функций:
Теорема 1 (локальная
огр.): Пусть
функция 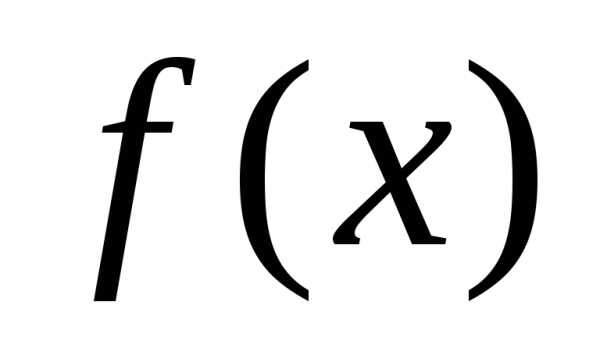 непрерывна
в точке
непрерывна
в точке  ,
тогда
,
тогда 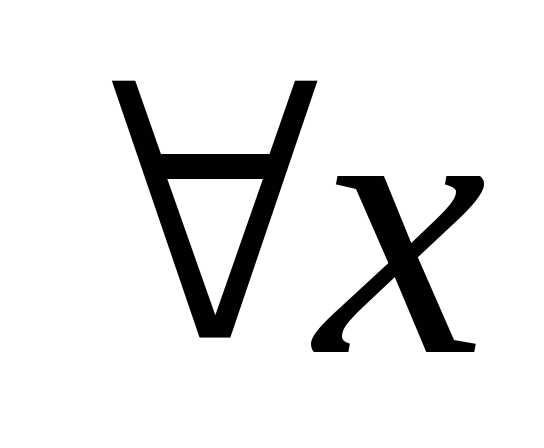
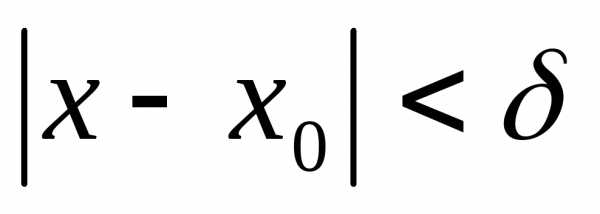
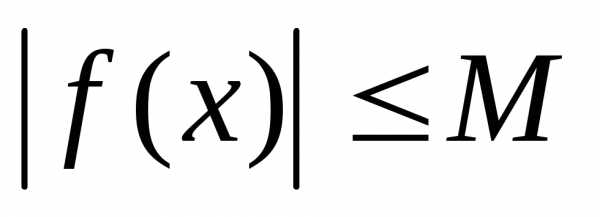 .
.
Теорема 2
(отделимость от 0): Пусть
функция  непрерывна
в точке
непрерывна
в точке 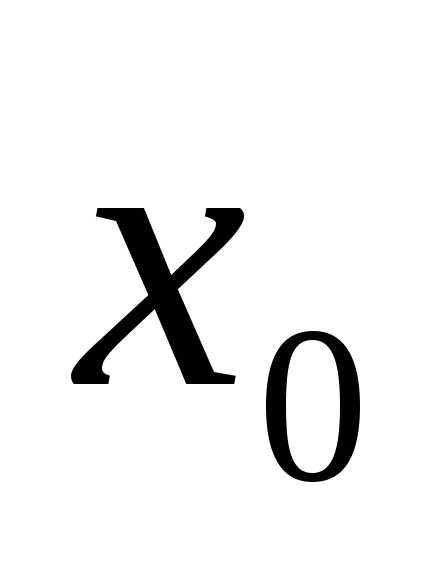 и
и 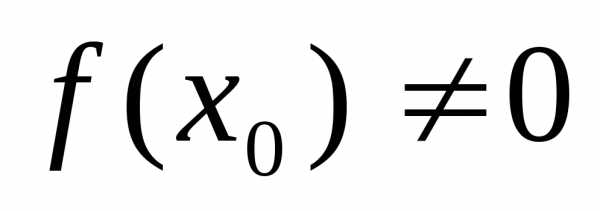 ,
тогда
,
тогда

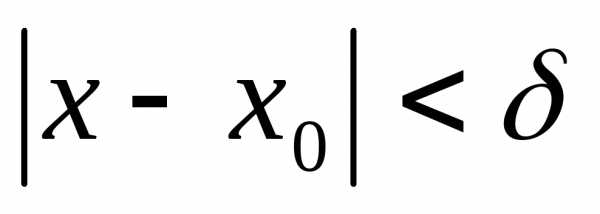
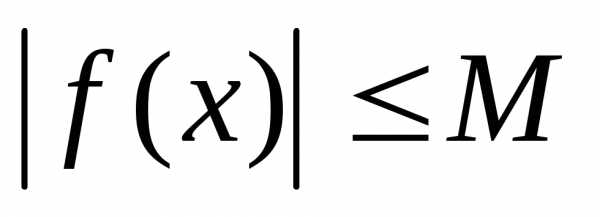 . .
. .
Теорема 3
(арифметика непрерывных функций): Пусть 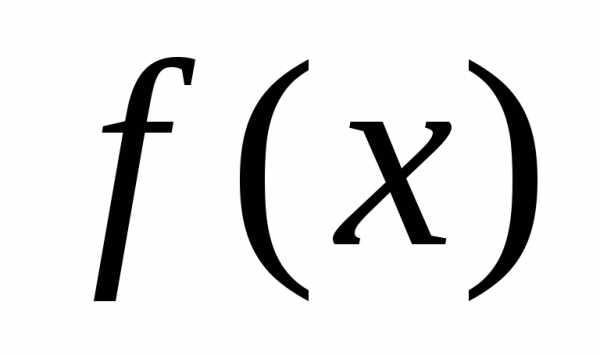 ,
,  непрерывны
в точке
непрерывны
в точке 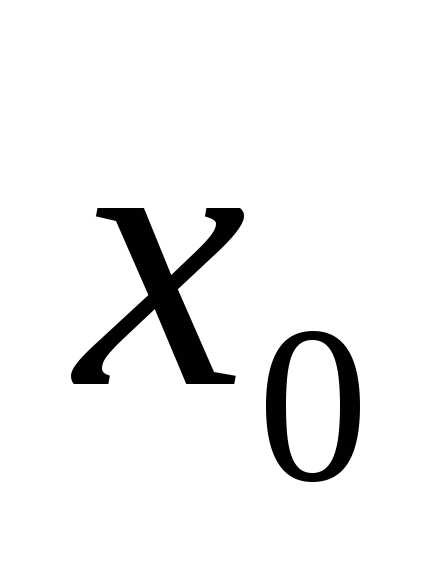 ,
тогда:
,
тогда:
1). непрерывна в точке  .
.
2). непрерывно в точке 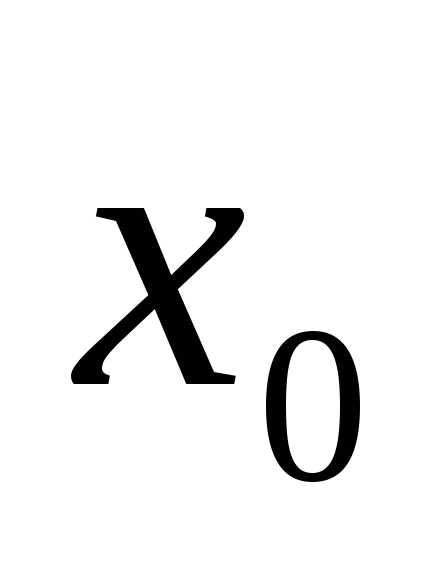 .
.
3). Если 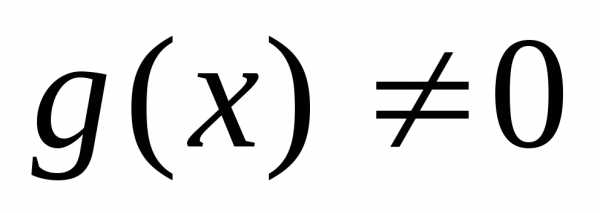 ,
то
,
то  непрерывно
в точке
непрерывно
в точке  .
.
28. Непрерывность сложной функции.
Теорема: если функция 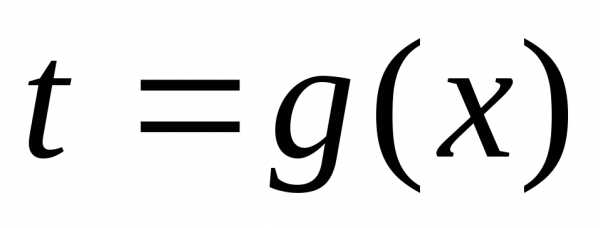 непрерывна
в точке
непрерывна
в точке 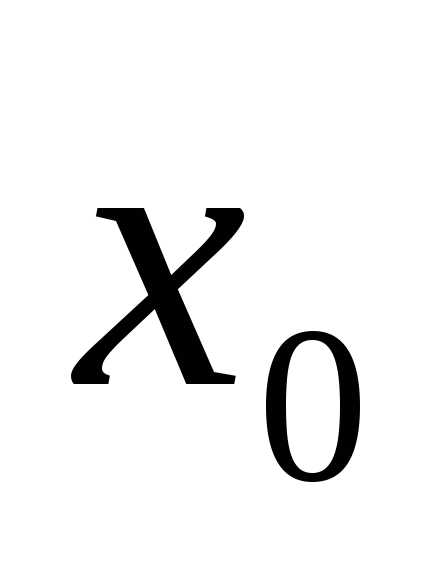 ,
а функция
,
а функция 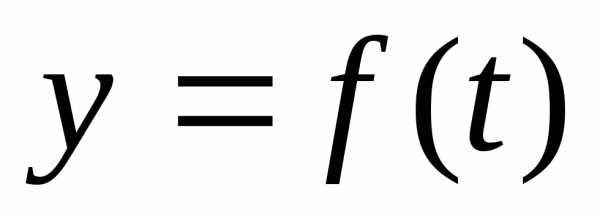 непрерывна
в точке то сложная функция
непрерывна
в точке то сложная функция 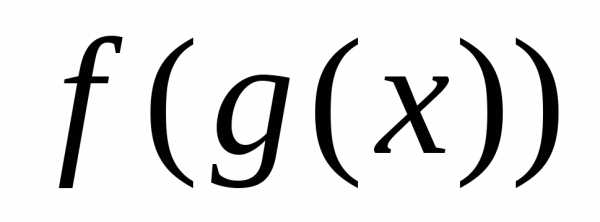 непрерывна в точке
непрерывна в точке 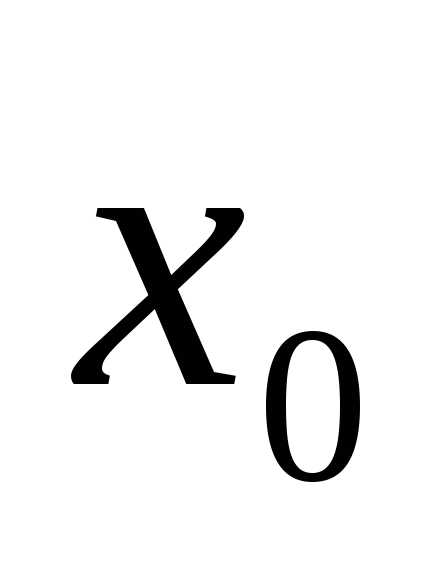 .
.
Доказательство:
Возьмем
число  >0.
Так как функция
>0.
Так как функция 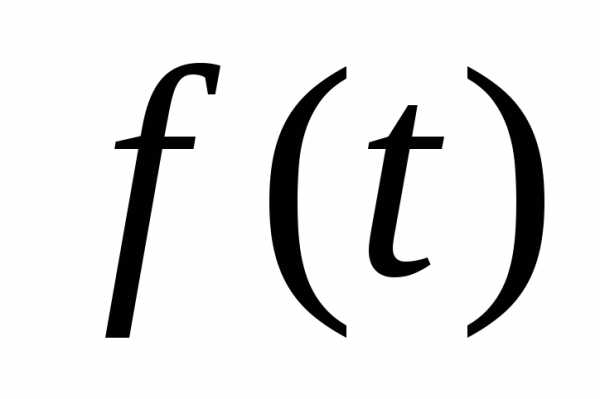 непрерывна
в точке
то
можно подобрать такое число
непрерывна
в точке
то
можно подобрать такое число 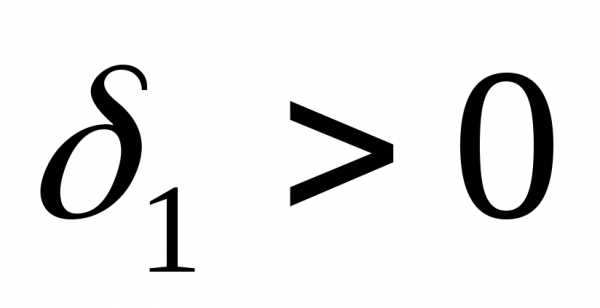 ,
что
,
что
для
любого 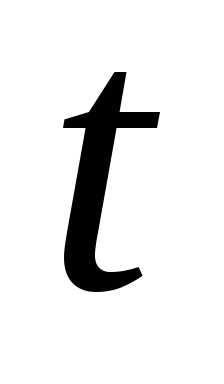 ,
такого, что
,
такого, что 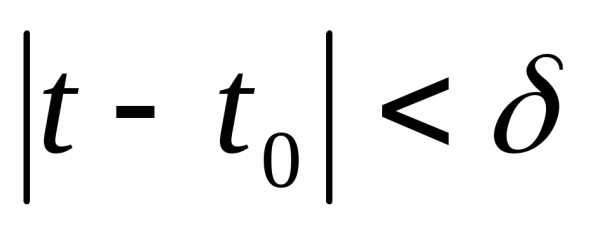 . (1)
. (1)
А
так как функция 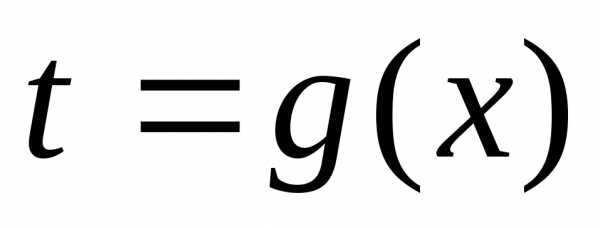 непрерывна в точке
непрерывна в точке 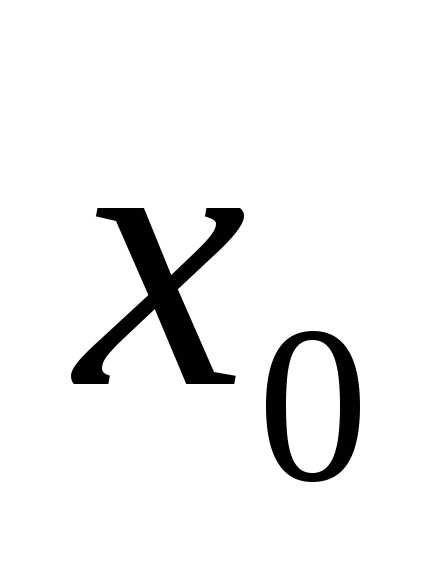 ,
то для положительного числа
,
то для положительного числа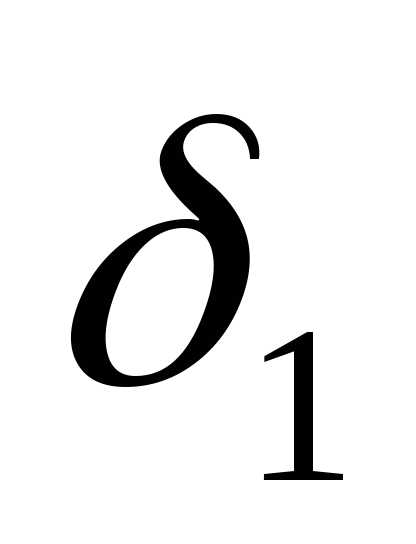 можно подобрать такое число
можно подобрать такое число 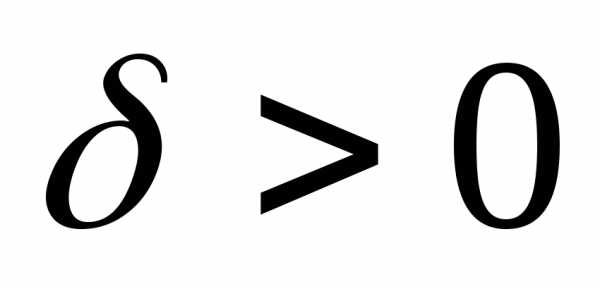 ,
что
,
что
для любого 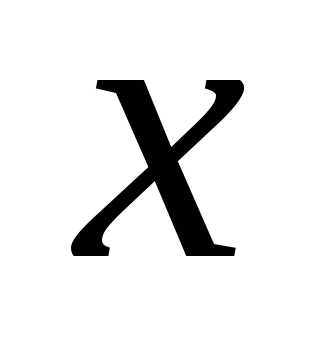 ,
такого, что
,
такого, что 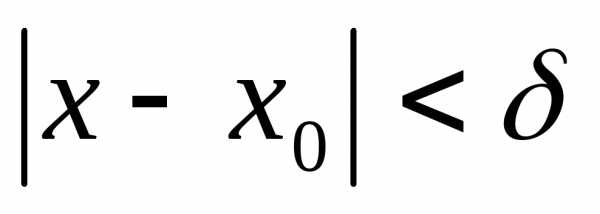 . (2)
. (2)
Возьмем
любое число 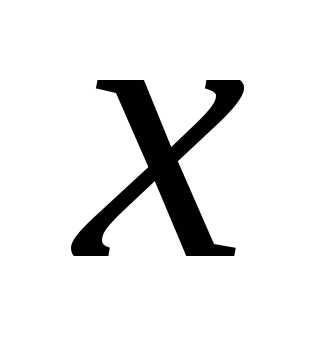 такое, что
такое, что 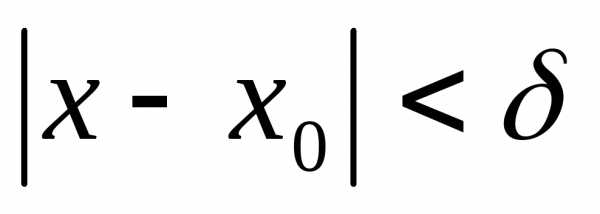 .
Тогда в силу (2) число
.
Тогда в силу (2) число 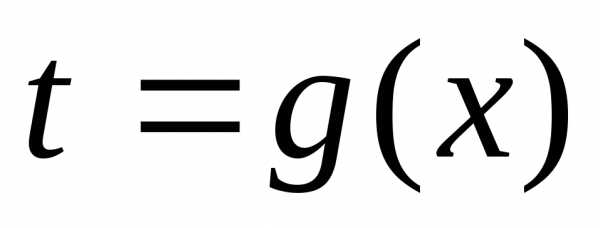 удовлетворяет неравенству
,
и поэтому в силу (1) .
Так как все эти вычисления проведены
для любого
удовлетворяет неравенству
,
и поэтому в силу (1) .
Так как все эти вычисления проведены
для любого  >0,
то непрерывность функции
>0,
то непрерывность функции 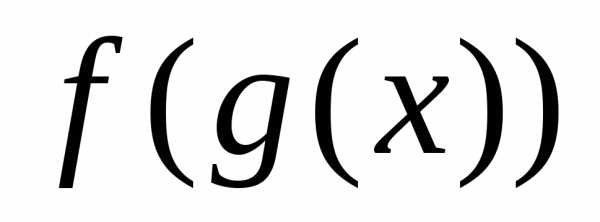 в точке
в точке 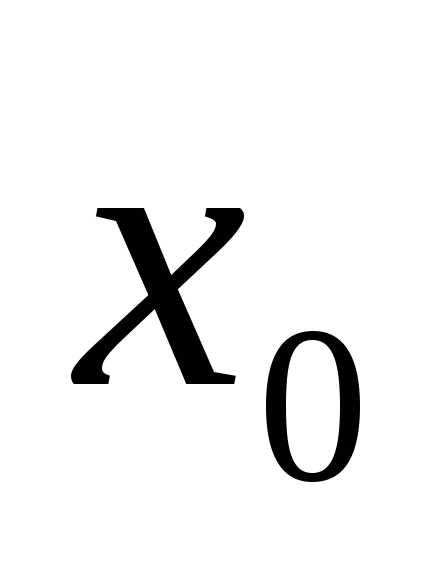 доказана
доказана
29. Классификация точек разрыва функции.
Определение:  -точка
разрыва функции
-точка
разрыва функции 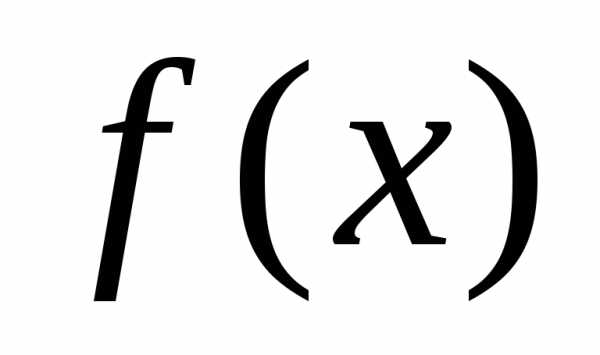 ,
если в точке
,
если в точке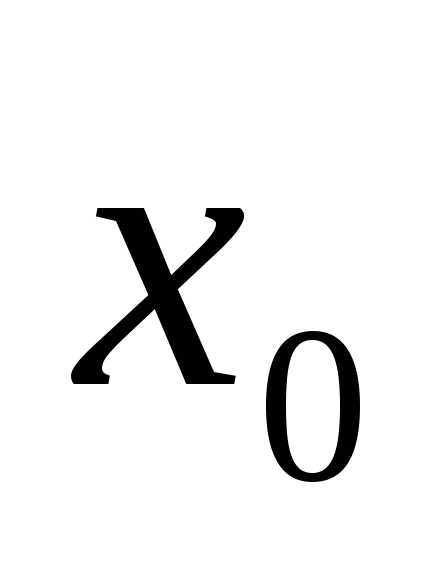 функция
функция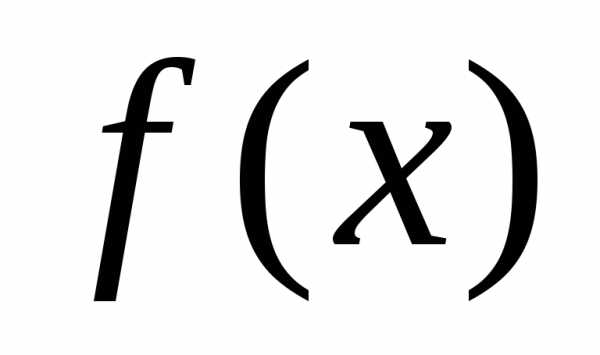 не
является непрерывной.
не
является непрерывной.
Определение: точка -точка
устранимого разрыва функции
-точка
устранимого разрыва функции 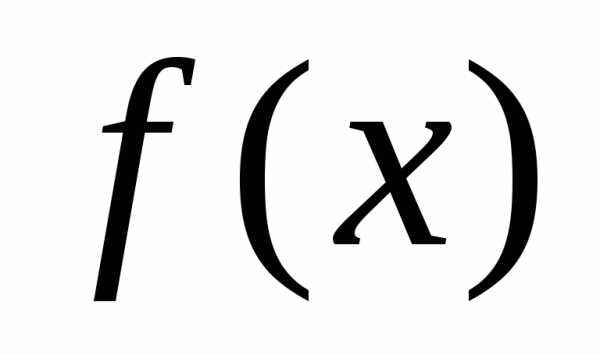 ,
если существует
,
если существует  ,
но
,
но 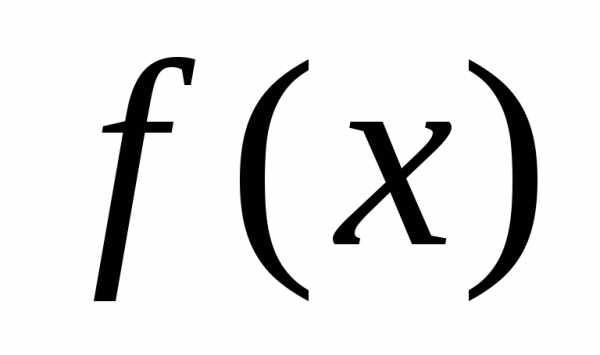 неопределена
в точке
неопределена
в точке 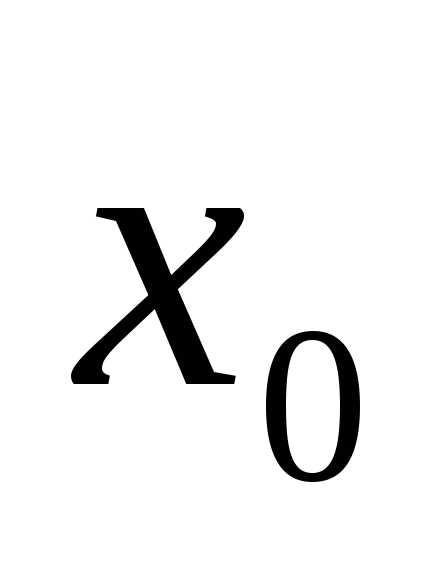 ,
либо
.
,
либо
.
Замечание: Если в точке устранимого разрыва доопределить (переопределить) функцию:
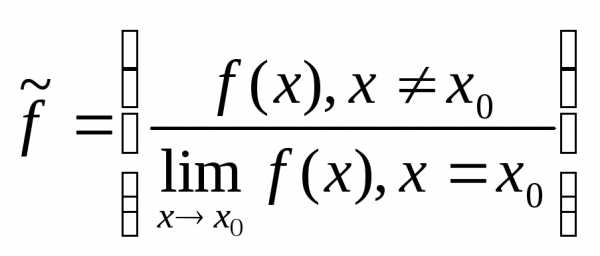 —
непрерывна в точке
—
непрерывна в точке  .
.
Пример:  .
.
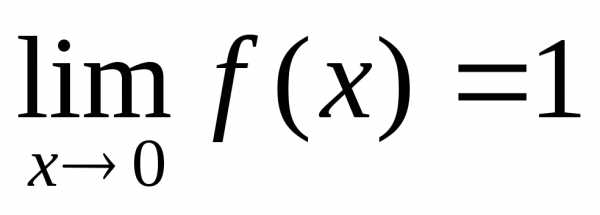 ,
, 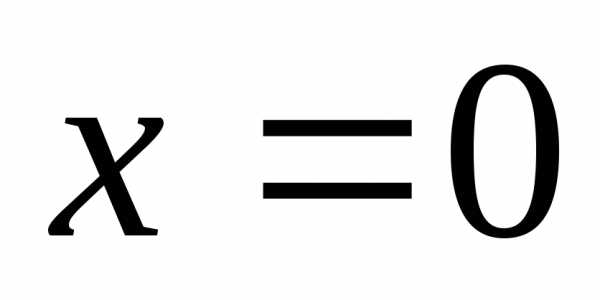 —
точка устранимого разрыва
—
точка устранимого разрыва  .
.
Если 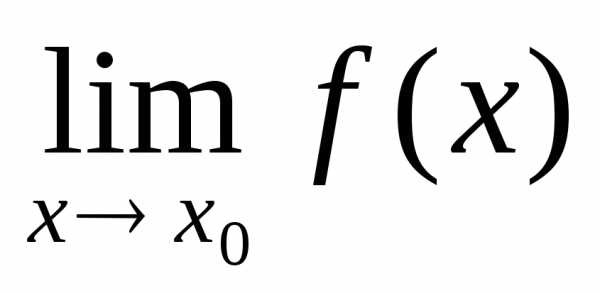 не
существует, то
не
существует, то  -точка
неустранимого
-точка
неустранимого
разрыва 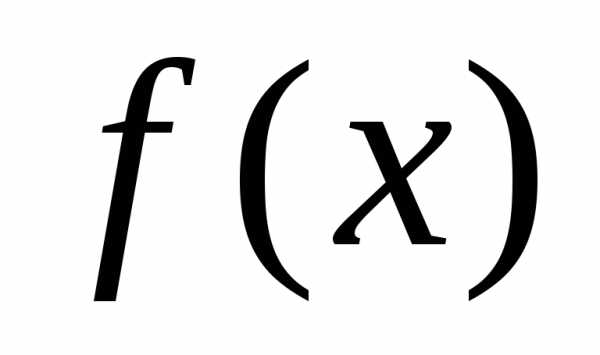 .
.
Определение: Пусть точка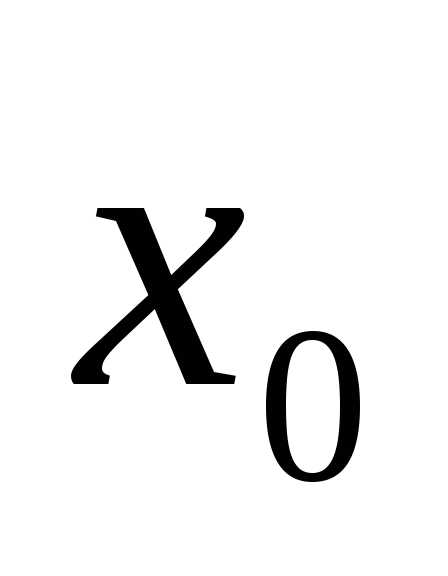 -точка
неустранимого разрыва функции
-точка
неустранимого разрыва функции 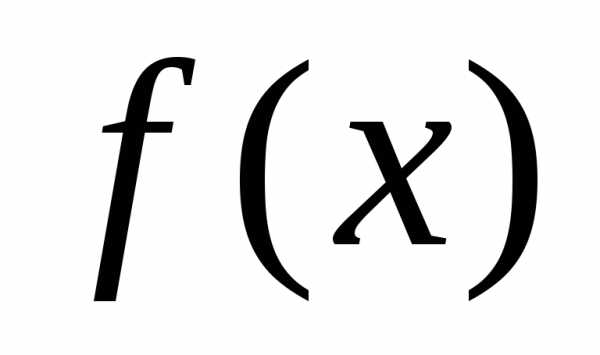 ,
тогда:
,
тогда:
если существует , то .
если
 ,
то
,
то  -точка
разрыва функции
-точка
разрыва функции  1-го рода.
1-го рода.если
 ,
то
,
то  -точка
разрыва функции
-точка
разрыва функции  2-го рода.
2-го рода.
Примеры:
1). .
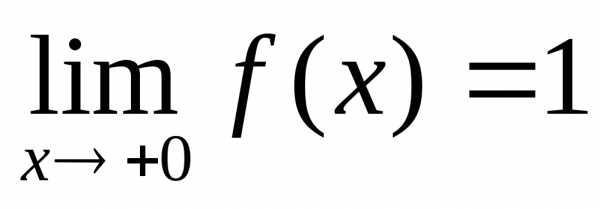 ,
,
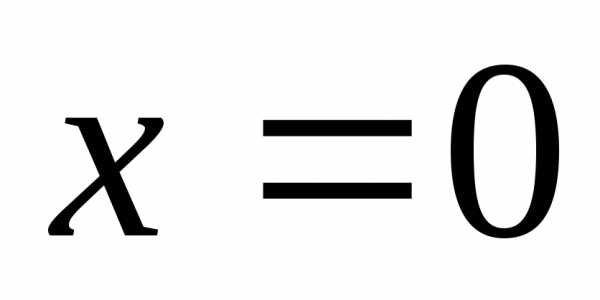 —
точка разрыва
—
точка разрыва 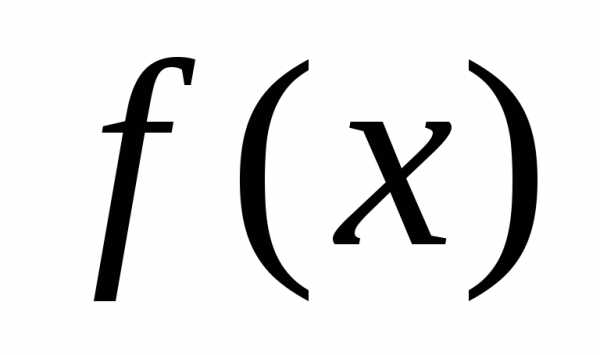 1-го рода.
1-го рода.
2).  .
.
,
 —
точка разрыва
—
точка разрыва  2-го рода.
2-го рода.
3). 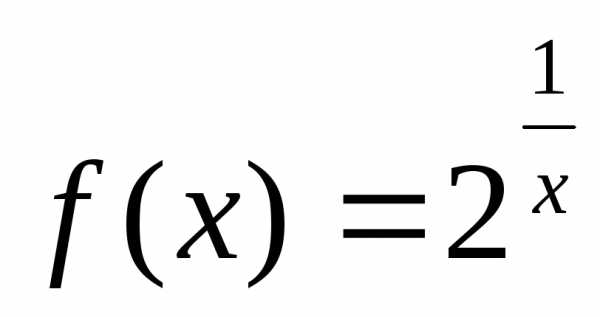
, 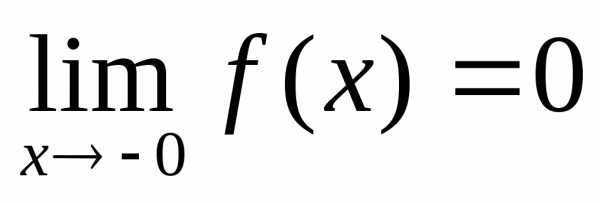
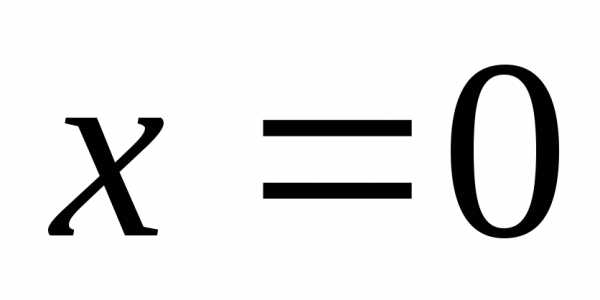 —
точка разрыва
—
точка разрыва 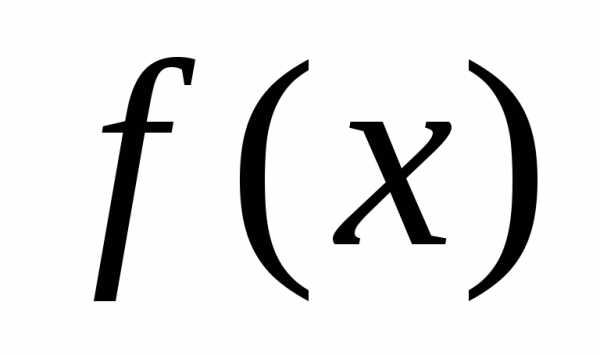 2-го рода.
2-го рода.
4). 

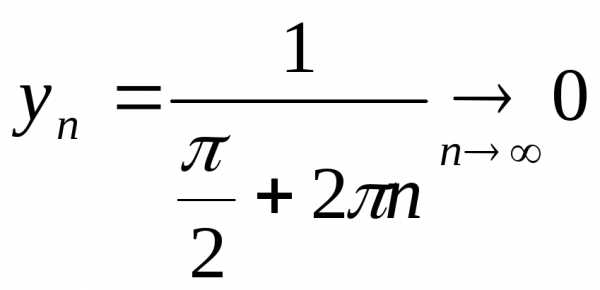
 не существует
не существует  точка
точка 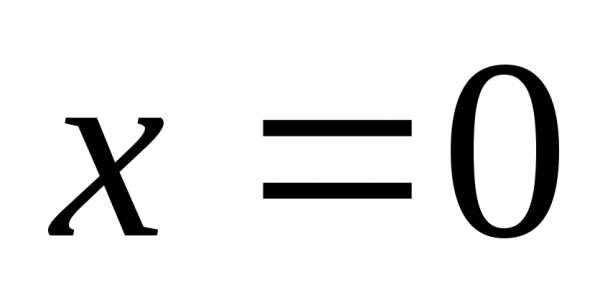 —
точка разрыва
—
точка разрыва 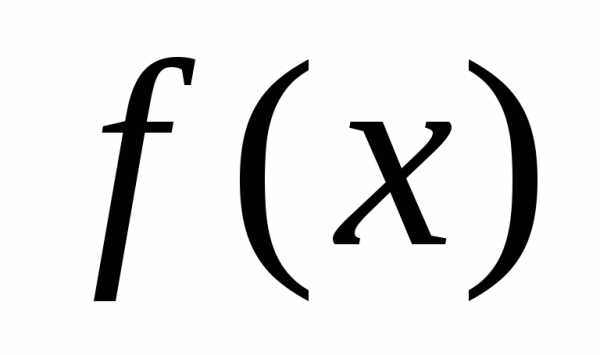 2-го рода.
2-го рода.
, .
Точка  —
точка разрыва
—
точка разрыва 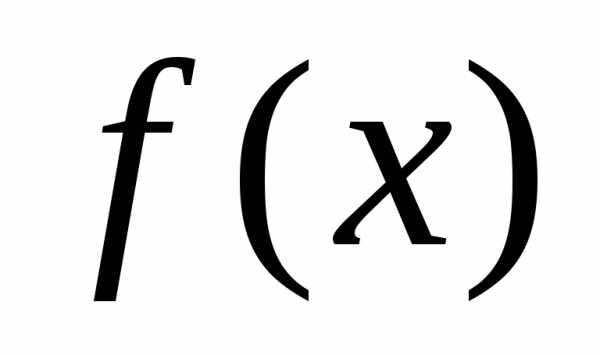 2-го рода
2-го рода
30. Точки разрыва монотонной функции.
31. Первая теорема Вейерштрасса.
Пусть
.
Тогда  ограничена
на
ограничена
на .
.
Доказательство:
Докажем, что .
Предположим
противное, то есть
.
Возьмем 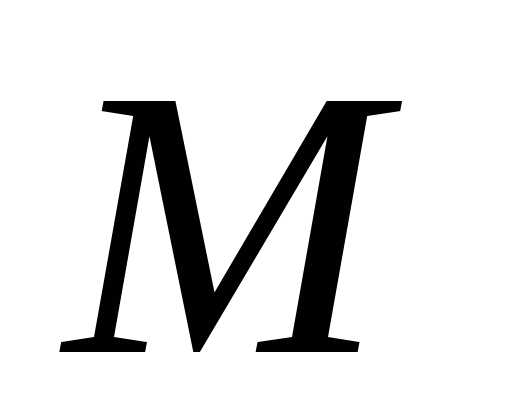 =1,2,3…
=1,2,3…
Получим 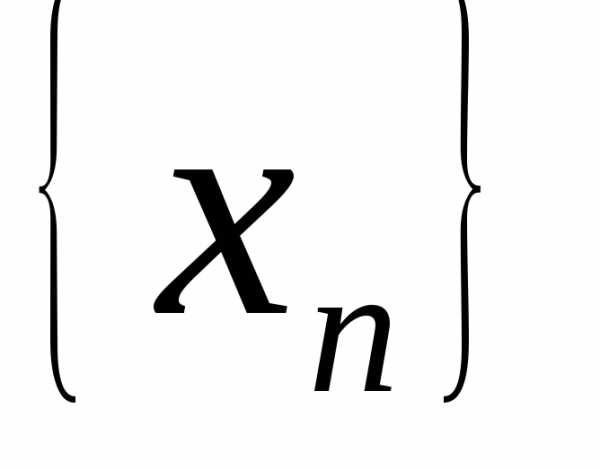 :
:
1) 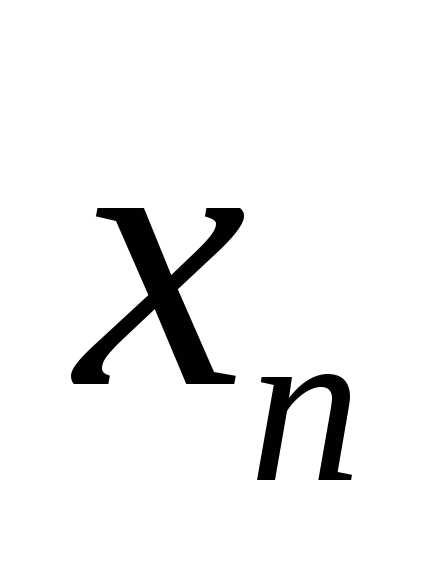

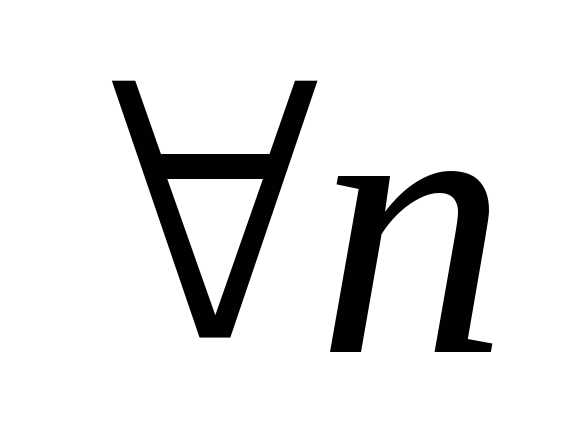
2) 
Из этих определений
получаем  .
.

 =>
=> 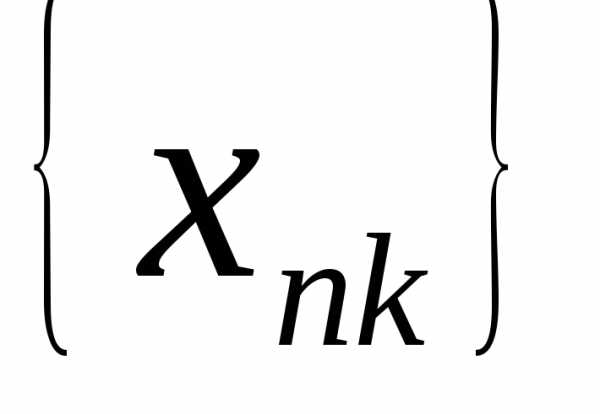 -подпоследовательность
последовательности
-подпоследовательность
последовательности  :
:
 .
.
-непрерывна
в точке 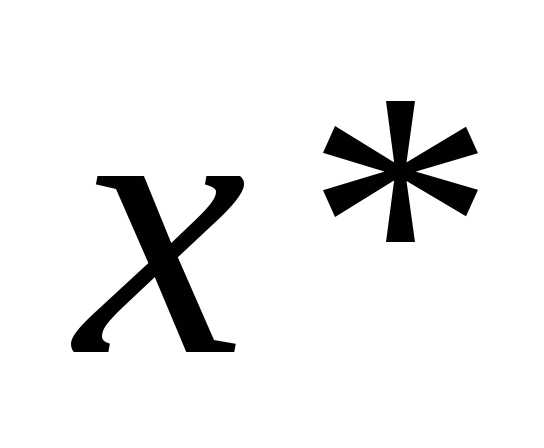 => .
=> .
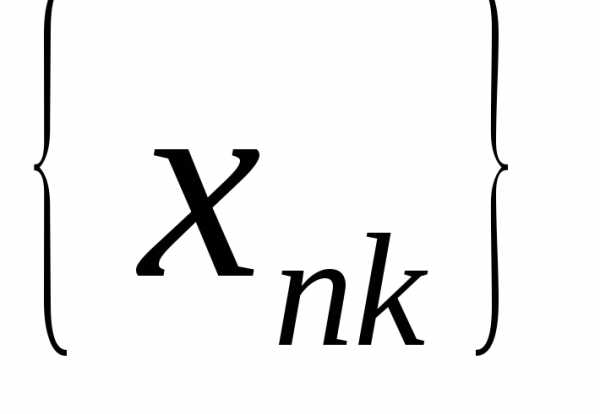 -подпоследовательность
последовательности
-подпоследовательность
последовательности 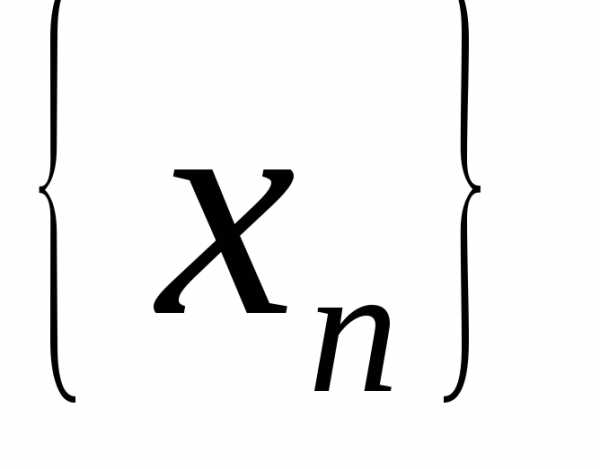 : => .
Противоречие.
: => .
Противоречие.
Замечание: Замкнутость  по
существу.
по
существу. 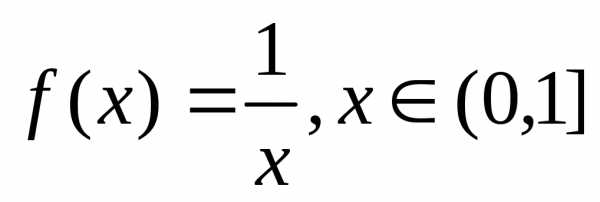 , ,
но
, ,
но 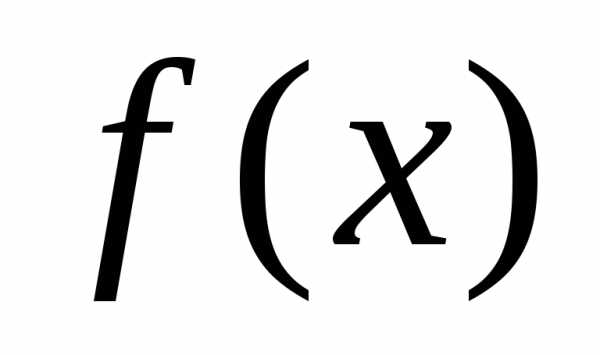
Не является
ограниченной на 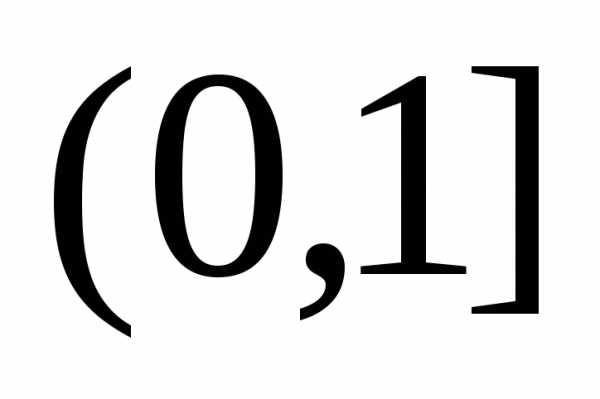 .
.
32. Вторая теорема Вейерштрасса.
Пусть . Тогда
Замечание: Непрерывная на отрезке  функция на этом отрезке достигает своего
наибольшего и наименьшего значения,
причем в условиях теоремы отрезок по
существу.
функция на этом отрезке достигает своего
наибольшего и наименьшего значения,
причем в условиях теоремы отрезок по
существу.
Доказательство:
По условию теоремы => 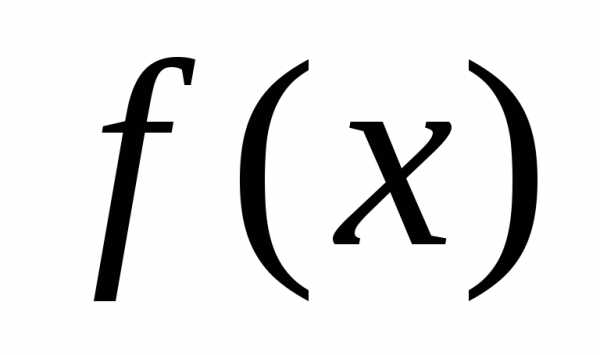 ограничена
на
ограничена
на 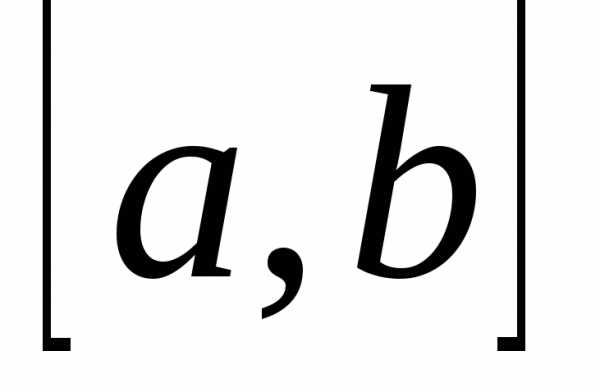 => Докажем, что
.
Предположим противное, то есть
=> Докажем, что
.
Предположим противное, то есть 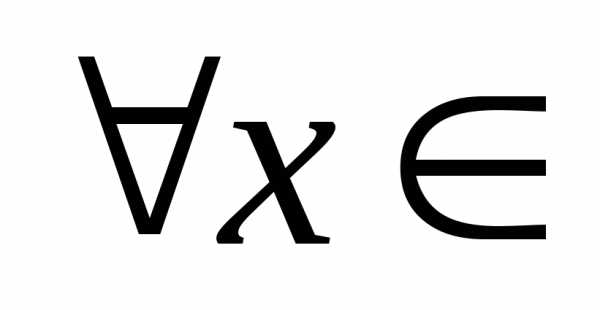
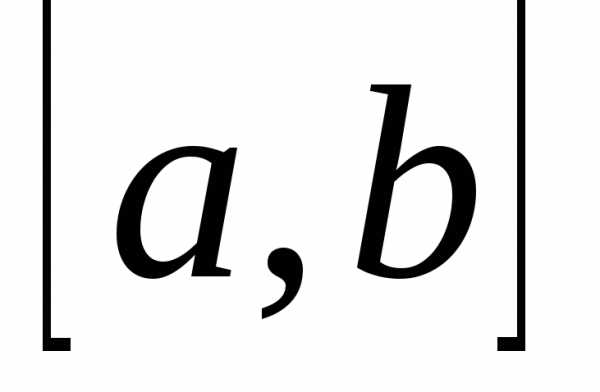 .
Рассмотрим вспомогательную функцию на
.
Рассмотрим вспомогательную функцию на 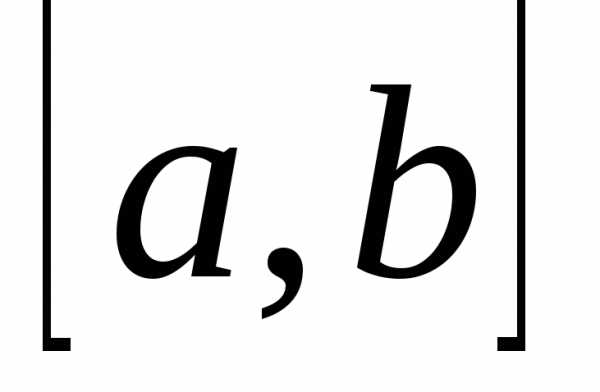 .
По 1 теореме Вейерштрасса
ограничена
на
.
По 1 теореме Вейерштрасса
ограничена
на  ,
то есть
,
то есть 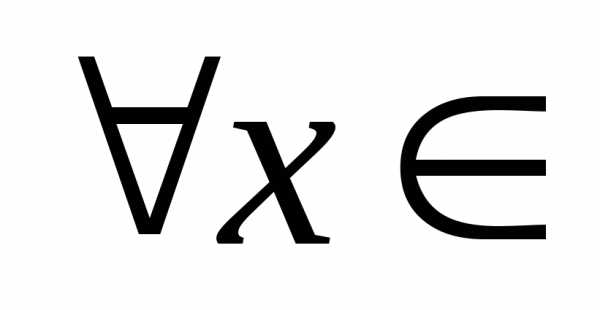
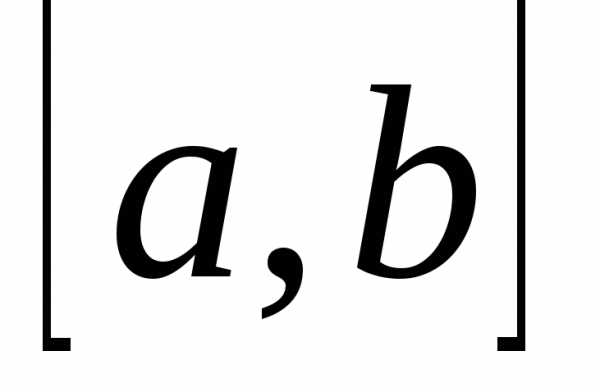 .
.


 (<
(<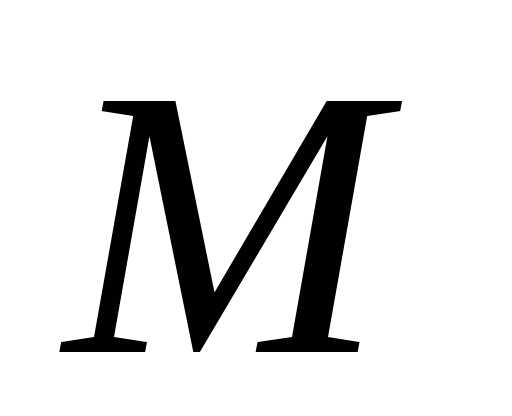 )-
верхняя граница.
)-
верхняя граница.  ,
то есть
,
то есть 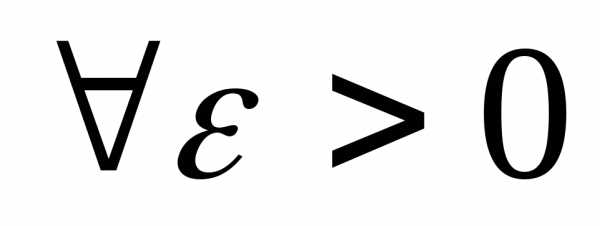 .
.
Противоречие.
Следствие: если , то .
33 и 34. Теорема о нуле непрерывной функции. Теорема Больцано-Коши о промежуточных значениях непрерывной функции. Следствие теоремы Больцано-Коши.
Определение: 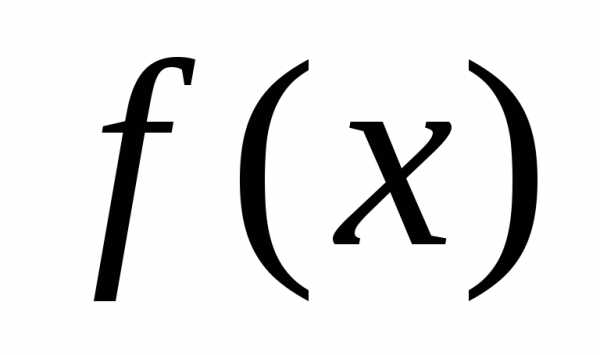 непрерывна на
непрерывна на 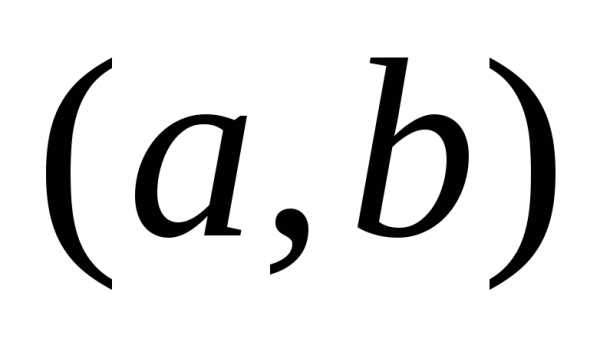 ,
если
,
если 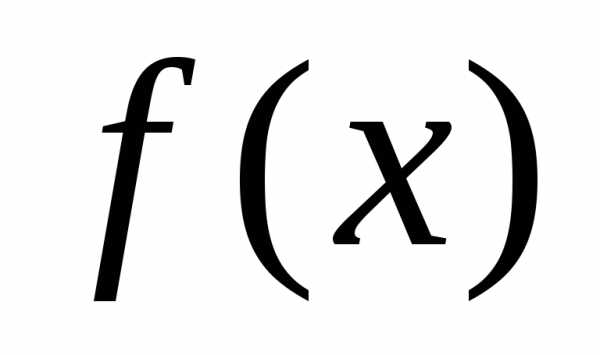 непрерывна в точке
непрерывна в точке 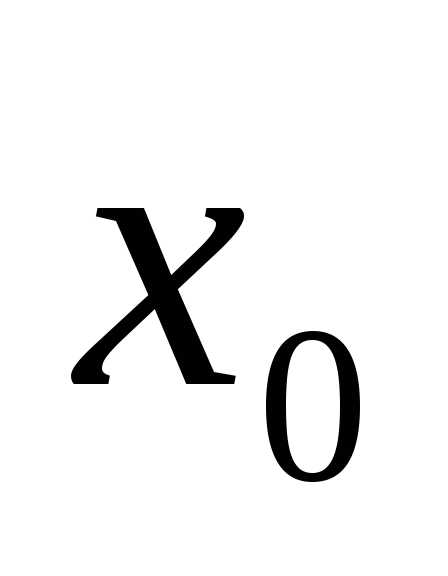 ,
,
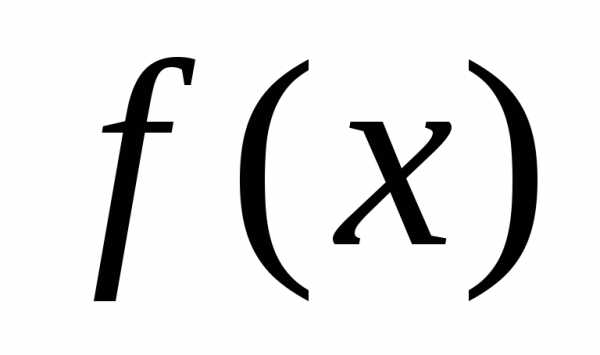 непрерывна на
непрерывна на 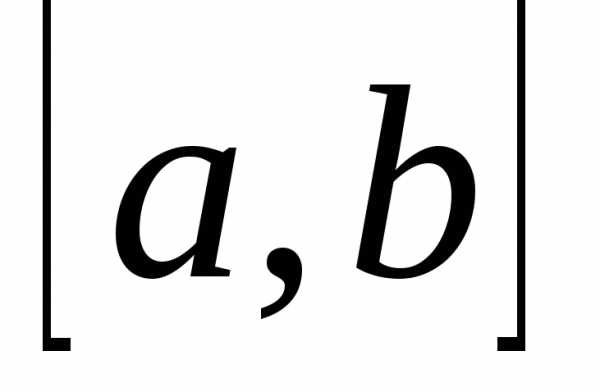 ,
если
,
если 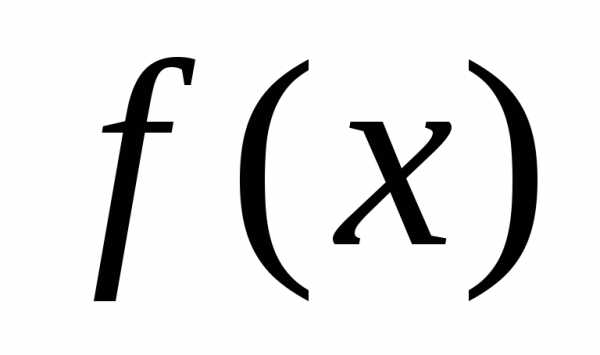 непрерывна в точке
непрерывна в точке 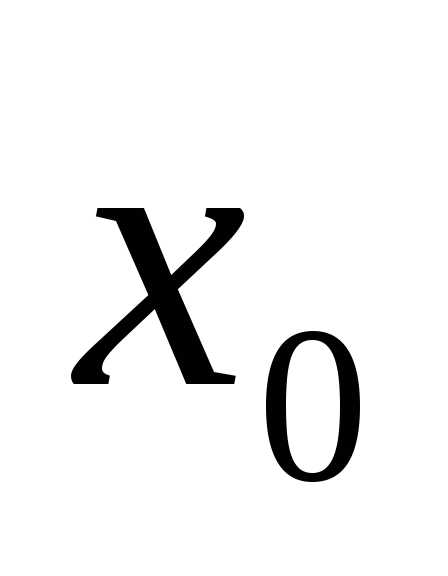 , и
, и
Существует , .
Теорема: Пусть  определена на
определена на 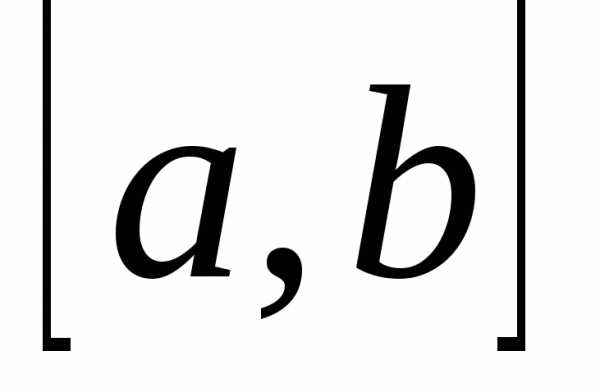 и
,
причем
.
Тогда
и
,
причем
.
Тогда
.
Пусть  ,
, 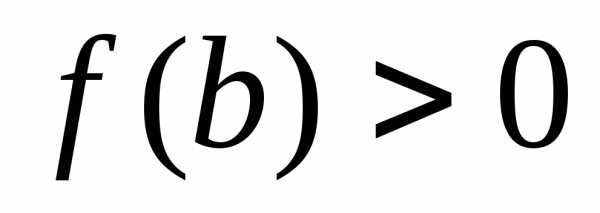 .
Используем метод деления отрезка
пополам.
.
Используем метод деления отрезка
пополам.
Обозначим: 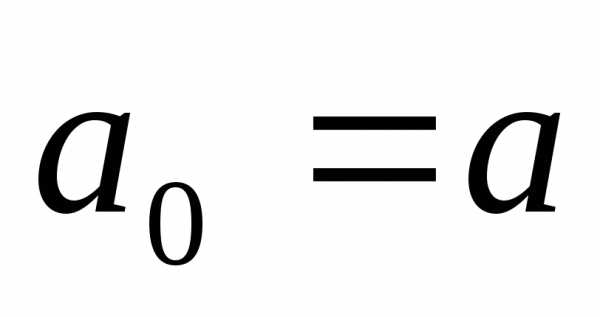 ,
, 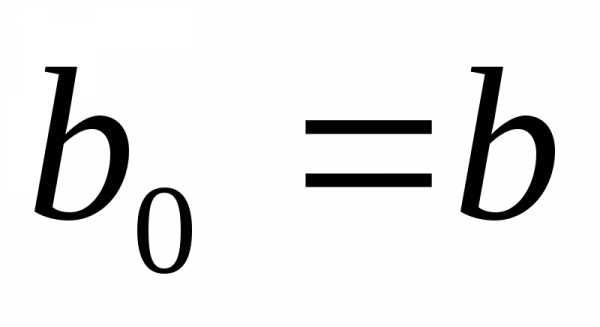 .
.
Определим 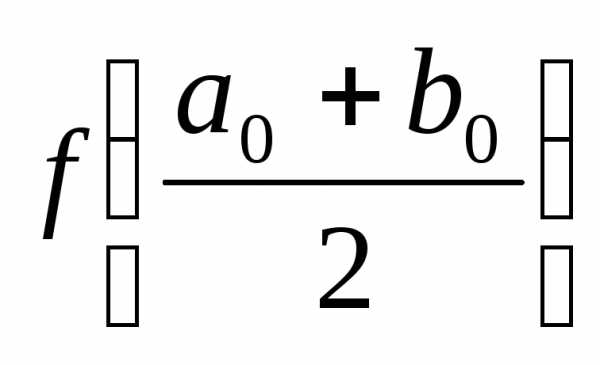
1) 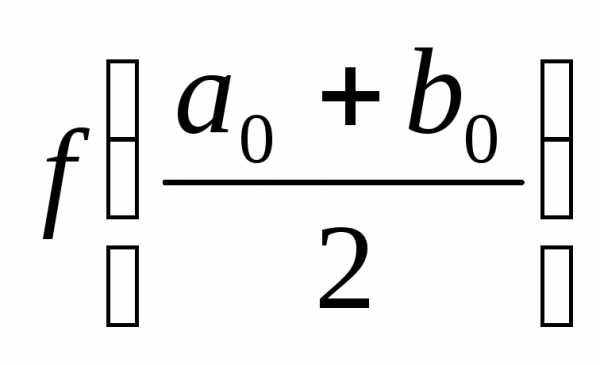 =0
=0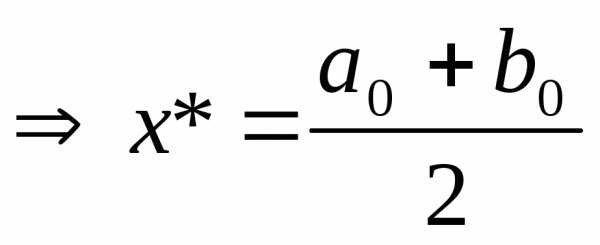 .
.
2) 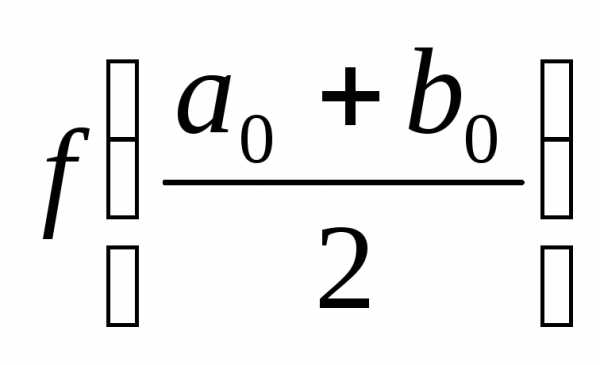 <
0
<
0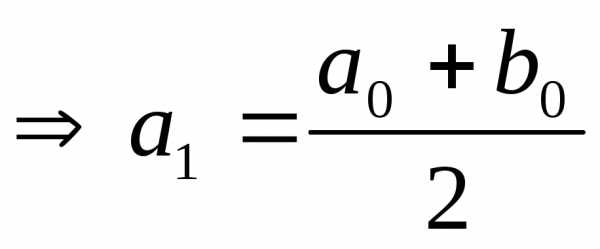 ,
, 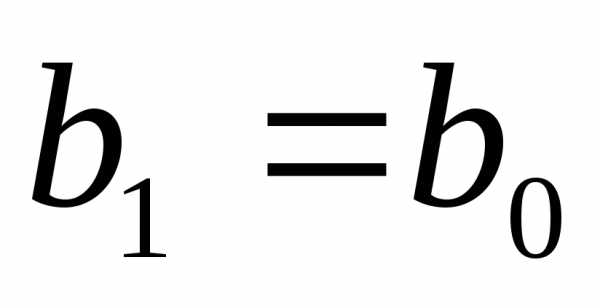 .
.
3) 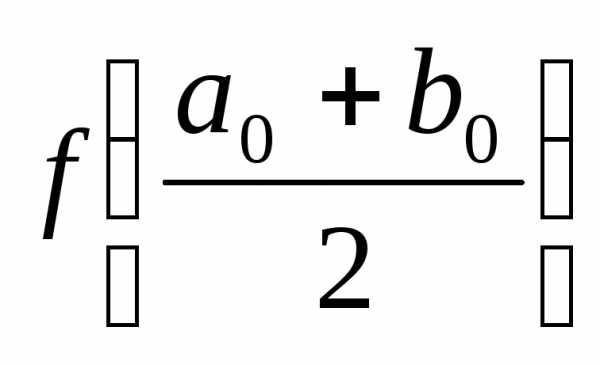 >
0
>
0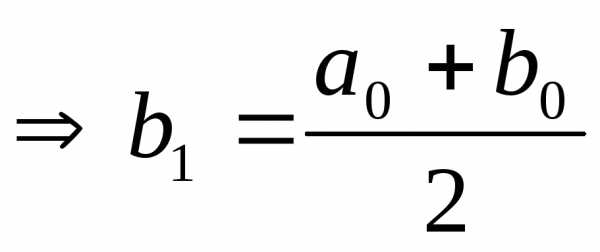 ,
, 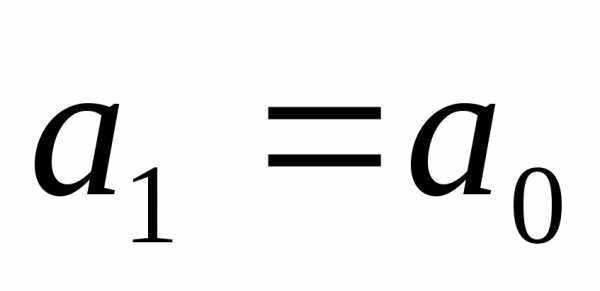 и так далее.
и так далее.
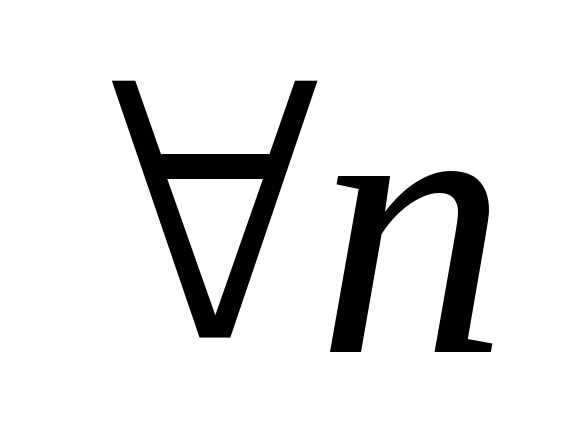 .
.
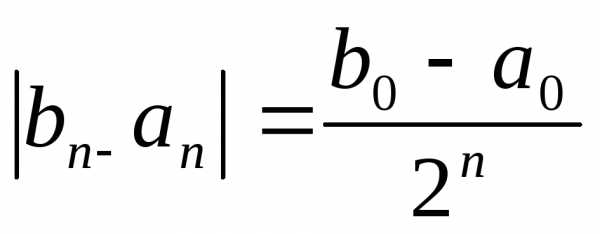 .
.
По лемме о вложенных
отрезках: 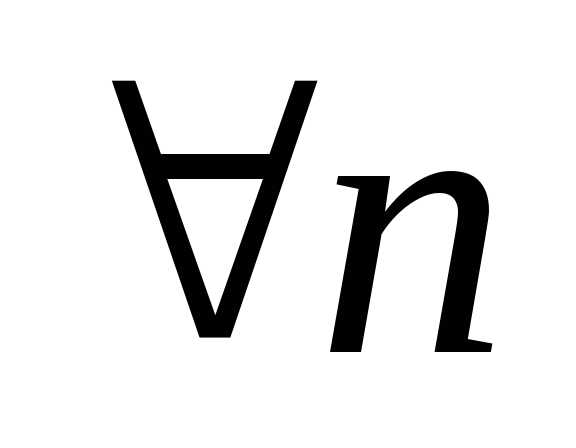 ,
то есть
,
то есть  .
.
непрерывна в точке
.
.
0 ()
.
Рассмотрим
произвольн. непрерывна на Из этих двух утверждений следует: , то есть Последнее!!! |
0 ()
Следствие (т. о промежуточном значении непрерывной функции):
Пусть 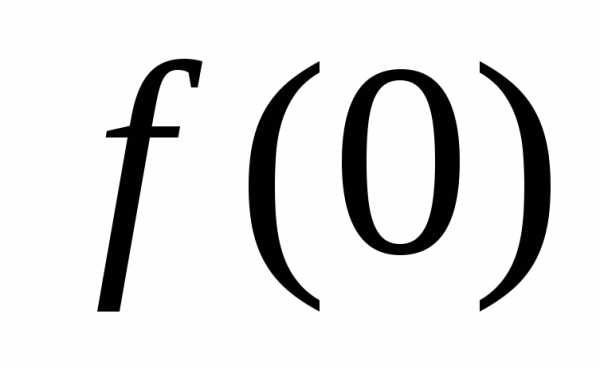 определена на
определена на 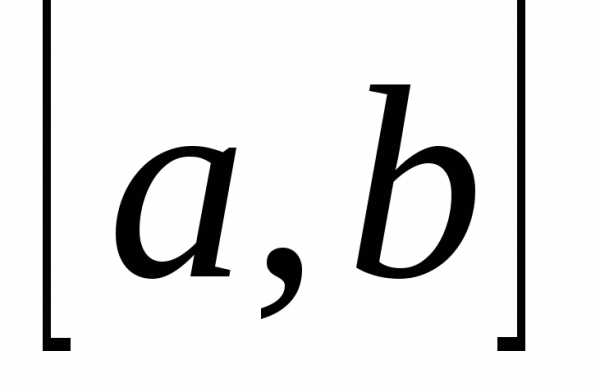 и
, ,
и
, ,  ,
, 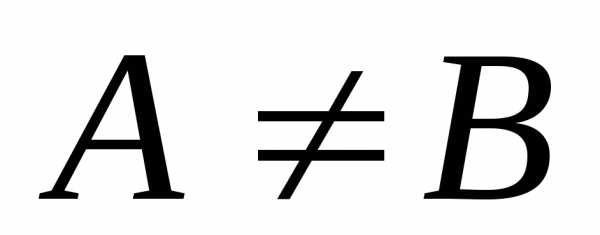
Тогда  : .
: .
Пусть для ограничения  .
.
35. Критерий непрерывности монотонной функции.
36. Непрерывность обратной функции.
studfiles.net
2.2. Эквивалентные бесконечно малые.
Функции и называют бесконечно малыми при , если и
Функции и называют эквивалентными бесконечно малыми при , если
Очень удобно пользоваться заменой эквивалентных бесконечно малых при нахождении пределов. Замена производится на основе таблицы.
Таблица эквивалентных бесконечно малых.
Пусть — бесконечно малая при .

Эквивалентность всех величин таблицы можно доказать, основываясь на равенстве .
2.3. Бесконечно большие функции.
Последовательность называется бесконечно большой, если .
Функция называется бесконечно большой в окрестности точки , если .
Функция называется бесконечно большой на бесконечности, если либо
2.4. Асимптоты графика функции.
Определение. Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
По способам их отыскания выделяют три вида асимптот: вертикальные , горизонтальные , наклонные .
Очевидно, горизонтальные являются частными случаями наклонных (при ).
| |
|
|
Нахождение асимптот графика функции основано на следующих утверждениях.
Теорема 1. Пусть функция определена хотя бы в некоторой полуокрестности точкии хотя бы один из ее односторонних пределов в этой точке бесконечен, т.е. равенили. Тогда прямаяявляется вертикальной асимптотой графика функции.
Таким образом, вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа).
Теорема 2. Пусть функция определена при значениях аргумента, достаточно больших по абсолютной величине, и существует конечный предел функции . Тогда прямая есть горизонтальная асимптота графика функции .
Может случиться, что , а , причем и конечные числа, тогда график имеет две различные горизонтальные асимптоты: левостороннюю и правостороннюю. Если же существует лишь один из конечных пределов или , то график имеет либо одну левостороннюю, либо одну правостороннюю горизонтальную асимптоту.
Теорема 3. Пусть функция определена при значениях аргумента, достаточно больших по абсолютной величине, и существуют конечные пределы и . Тогда прямая является наклонной асимптотой графика функции .
Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет.
Наклонная асимптота так же, как и горизонтальная, может быть односторонней.
3 Вопрос: Арифметические действия с пределами. Теоремы о переходе к пределу в неравенствах. Теорема о пределе промежуточной функции.
3.1. Арифметические действия с пределами.



3.2. Теоремы о переходе к пределу в неравенствах.
Теорема о переходе к пределу в равенстве
Если на и существует , то существует и .
ПРИМЕР. Поскольку для и , то .
ТЕОРЕМА (о переходе к пределу в неравенстве)
Если или на и существуют – к.ч. и – к.ч., то .
Доказательство можно провести методом от противного. Рекомендуем провести самостоятельно.
ТЕОРЕМА (о перенесении неравенства между пределами на функции)
Если существуют пределы и и выполняется неравенство , то существует окрестность , на которой .
Доказательство. Имеем
,
в частности, при : , т.е. . Аналогично
,
в частности, при , т.е. или .
Поскольку при , то на пересечении окрестностей имеем , т.е. указали окрестность , на которой характер неравенства между пределами переносится на функции.
Следствие. Если – конечное число и , то можно указать окрестность , на которой .
studfiles.net

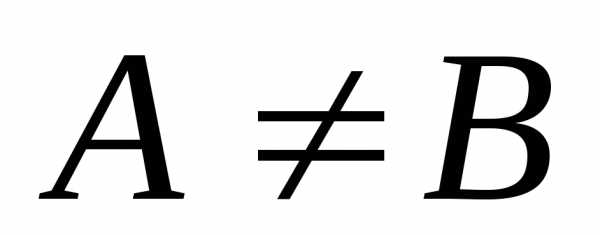 ,
то
,
то  -точка
разрыва функции
-точка
разрыва функции  1-го рода.
1-го рода.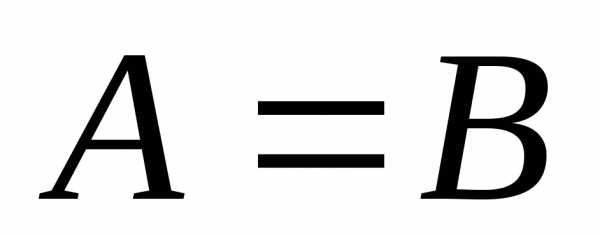 ,
то
,
то 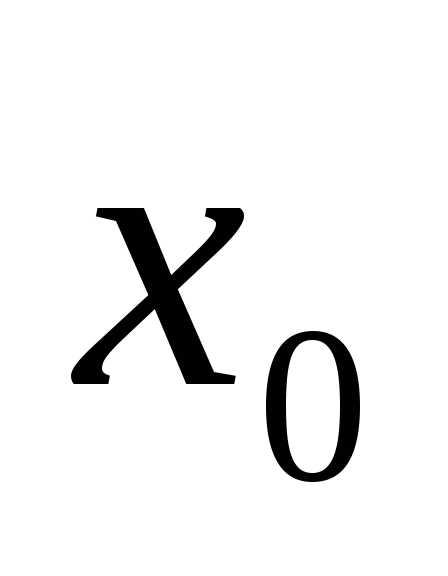 -точка
разрыва функции
-точка
разрыва функции 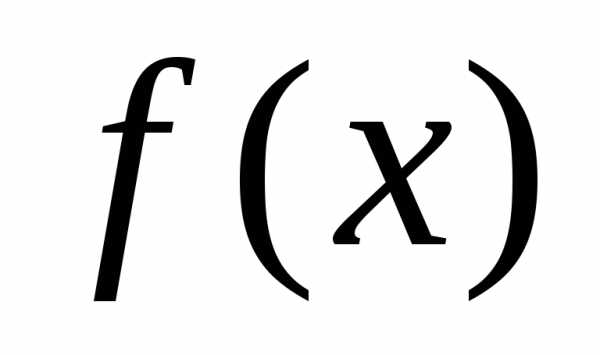 2-го рода.
2-го рода. :
: .
.
