?.4 Независимость событий, примеры независимых и зависимых событий.
Вероятность появления события А при условии, что событие В произошло, называется условной вероятностью события А и вычисляется по формуле:
где A, B E, P(B) 0.
События A, B E называются независимыми, если .
В противном случае события А и В называются зависимыми.
Пример независимого события:
Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (событие A) равна 0,8, а вторым (событие В) — 0,7.
Решение. События А и В независимые, поэтому, по теореме умножения, искомая вероятность
Р(АВ) = Р(А)Р(В) = 0,7 * 0,8 = 0,56.
Пример зависимого события:
В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.
Решение. Обозначим A извлечение изношенного резца в первом случае, а — извлечение нового. Тогда . Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим.
Обозначим B событие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:
Следовательно, вероятность события B зависит от того, произошло или нет событие A.
??.1 Неравенство Чебышева, закон больших чисел.Неравенства Чебышёва
Все неравенства в этой теме принято относить к одному классу, называемому «неравенствами Чебышёва». Следующее неравенство часто называют неравенством Чебышёва, хотя в такой форме оно появилось впервые, видимо, в работах Маркова.
Теорема (неравенство Маркова). Если , то для любого
Доказательство: Нам потребуется следующее понятие:
Определение: Пусть A — некоторое событие. Назовём индикатором события A случайную величину I(A), равную единице, если событие A произошло, и нулю, если A не произошло.
По определению, величина I(A) имеет распределение Бернулли с параметром
,
и её математическое
ожидание равно вероятности успеха ).
Индикаторы прямого и противоположного
событий связаны равенством
Тогда
Осталось разделить обе части неравенства на положительное x.
Следующее неравенство мы будем называть обобщённым неравенством Чебышёва.
Следствие (обобщённое неравенство Чебышёва). Пусть функция g не убывает и неотрицательна на R. Если , то для любого
Доказательство: Заметим, что , поскольку функция g не убывает. Оценим последнюю вероятность согласно неравенству Маркова, которое можно применять в силу неотрицательности g:
??.2 Эргодическая теорема для цепей Маркова.
??.3 Свойства характеристических функций.
Характеристическая функция случайной величины х – это есть мат.ожидание eitx
f(t)=Eeitx=E(cos tx)+iE(sin tx) – функция вещественных переменных, но с комплексными значениями. В частном случае – преобразование Лапласа.
Свойства характеристической функции:
Существует плотность распределения
f(t)=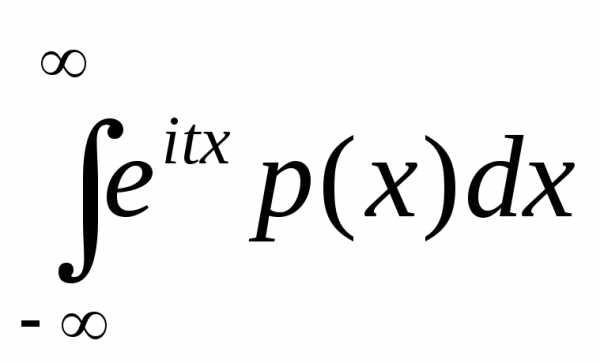
f(t)=
когда есть плотность, то dF(x)=p(x)dx, когда дискретные: dF(x)=F(x+)-F(x)=P(X=x)
Для дискретных x: f(t)=nj=1eitxj p(X=xj)
f(0)=1
|f(t)|<1, т.к. |eitx|<1
|EX|<E|x|
Пусть y=ax+b, где a,b – const, тогда f
Если случайные величины x,y – независимы, то fx+y(t)=fx(t)fy(t), т.к. fx+y(t)=E(eit(x+y))= =E(eitxeity)=EeitxEeity= fx(t)fy(t)
Вполняется для любого количества независимых случайных величин.
Существует x1,…,xn – независимых случайных величин
Sn= x1+…+xn, тогда fSn(t)=Пni=1fXi(t)
a) Пусть E|x| — конечна и f(t) — это характеристическая функция, тогда f(t) дифференцируема и производная =
f `(t)|t=0=iEx
b) Если E|x|2 – конечна, то функция f(t) – дважды дифференцируема:
f `(t)|t=0=iEx,
f «(t)|t=0=-Ex2
c) Если E|x|n – конечна, функция f(t) – n раз дифференцируема:
f(n)(t)|t=0=(i)nExn
В случае a существует разложение f(t)=1+iExt+0(t)
В случае b существует разложение f(t)=1+iExt-Ex2t2/2+0(t)
В случае c существует разложение f(t)=1+iExt-Ex2t2/2+…+(i)nExntn/n!+0(t)
Доказательство:
f `(t)|t=0=iEx
E – это интеграл, поэтому, когда мы берем производную по интегралу, по параметру – когда интеграл равномерно и абсолютно сходится, то дифференцирование под знаком интеграла.
Надо проверить:
Продифференцировать, будет ли такой интеграл равномерно сходится.
E|ixeitx|=E|x| — пусть плоское распределение.
E|x|=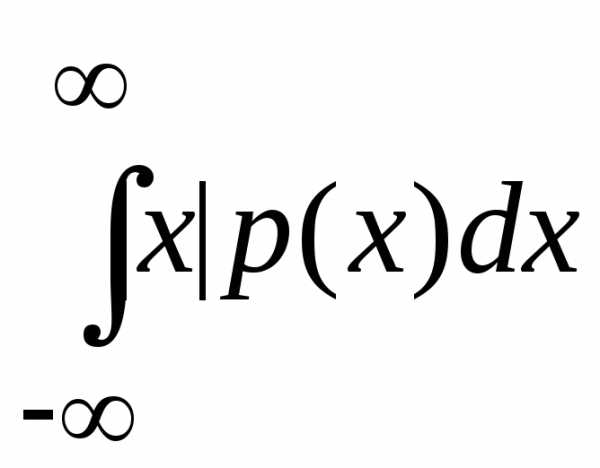
,
сходится равномерно, если интеграл по
множеству, гдеx>A
или x<-A
стремится к 0, когда A.
Это выполняется, т.к. это свойство любого интеграла.
Следовательно f `(t)=E(ixeitx)=iEx, если t=0
b,c) точно также доказывается, что можно дифференцировать под знаком интеграла.
f «(t)=E(-x2eitx)=-Ex2 при t=0
f(n)(t)=E((ix)neitx)=(i)nExn при t=0
a,b,c) Вторая часть это разложение по формуле Тейлора с остаточным членом в форме Пиано.
Между функциями распределения и характеристическими функциями существует взаимнооднозначное соответствие: каждой характеристической функции соответствует 1 функция распределения и наоборот.
F(x)f(t)
Свойство непрерывности.
2 свойства равносильны
Fn(x)F(x) в каждой точке, сходимость слабая равносильна
fn(t)f(t), сходимости характеристических функций в каждой точке.
8) Обозначим через tхарактеристическую функцию стандартного нормального закона.
Это значит,
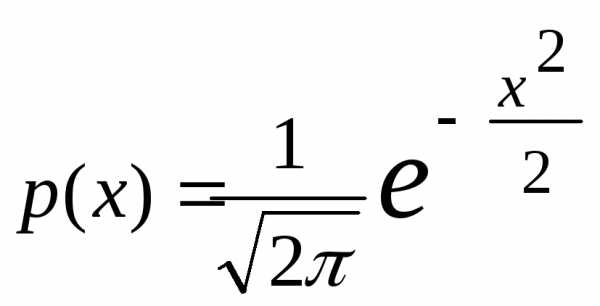, тогда характеристическая функция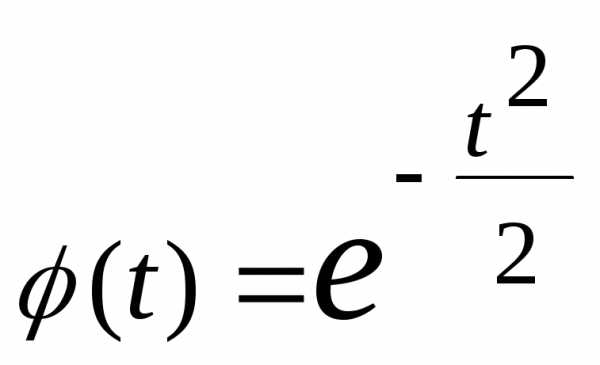
Доказательство:
Обозначим
= 
=
=
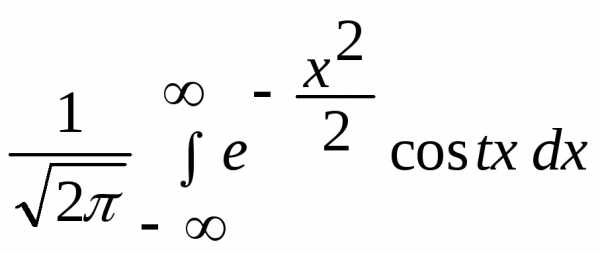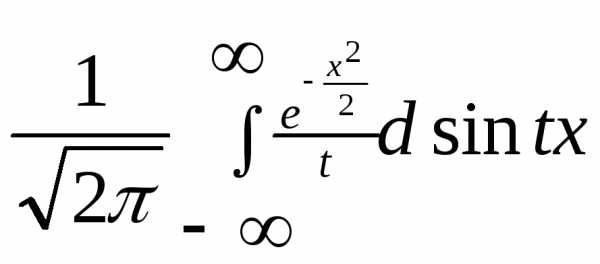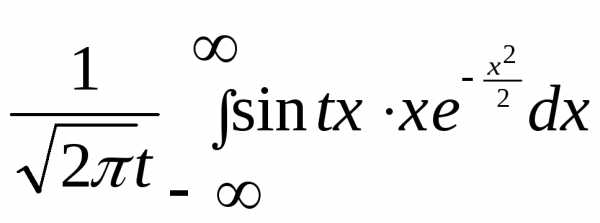
С другой стороны
`(t)=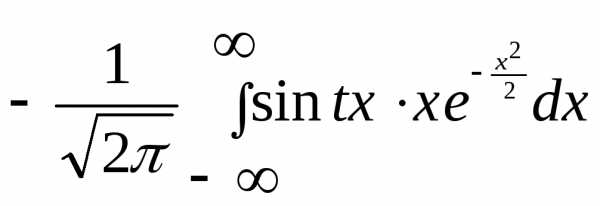 
Получим дифференциальное уравнение.
`(t)=-t(t) — оно имеет следующее решение.
=-t
Проинтегрируем
ln (t)=-t2/2+C
(t)=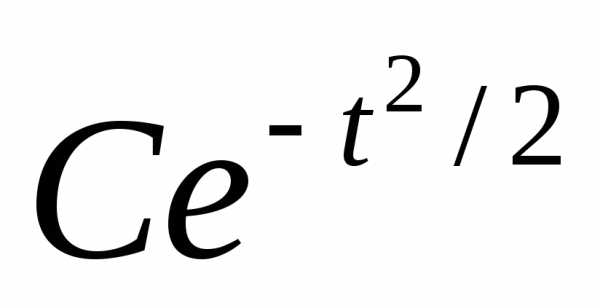 
C-
какая-то постоянная
Пусть t=0 (t)=1 1 – это постоянная =>
(t)=C,
т.е. (t)=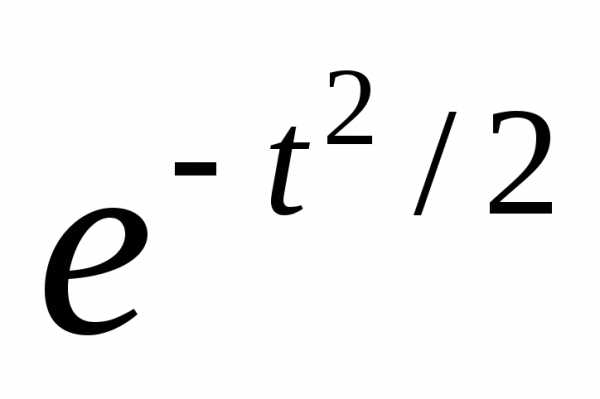
, ч.т.д.
??.4 Коэффициент корреляции и его свойства.
Как мы знаем, если и — независимые случайные величины, то по свойству математического ожидания
Если же и не являются независимыми случайными величинами, то, вообще говоря,
Условились за меру связи (зависимости) двух случайных величин и принять безразмерную величину , определяемую соотношением.
и называемую коэффициентом корреляции.
Рассмотрим некоторые свойства коэффициента корреляции.
Если и — независимые случайные величины, то коэффициент корреляции равен нулю.
Заметим, что обратное утверждение, вообще говоря, неверно, т. е. если , то отсюда еще не следует, что и независимы.
Заметим без доказательства, что . При этом если , то между случайными величинами и имеет место функциональная, а именно линейная зависимость.
Замечание. Двумерная случайная величина распределена нормально, если плотность распределения системы величин и имеет вид
Можно показать, что постоянная R равна коэффициенту корреляции величин и , т.е. . Следует заметить, что в случае, когда система величин и распределена нормально и коэффициент корреляции , то величины и независимы.
studfiles.net
Тема 2
11
ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ СОБЫТИЯ.
ОСНОВНЫЕ ФОРМУЛЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
Понятия зависимости и независимости случайных событий. Условная вероятность. Формулы сложения и умножения вероятностей для зависимых и независимых случайных событий. Формула полной вероятности и формулы Бейеса.
Теоремы сложения вероятностей.
Найдем вероятность суммы событий и(в предположении их совместности либо несовместности).
Теорема 2.1. Вероятность суммы конечного числа несовместных событий равна сумме их вероятностей:
.
Пример 1. Пусть вероятность того, что в магазине очередной будет продана пара мужской обуви -го размера, равна,-го -,-го или большего -. Найти вероятность того, что очередной будет продана пара мужской обуви не менее-го размера.
Решение . Искомое событие произойдет, если будет продана пара обуви-го размера (событие), или-го (событие) или не менее-го (событие), т. е. событиеесть сумма событий,,. События,инесовместны. Поэтому, применяя теорему сложения вероятностей, получим:
.
Пример 2. В условиях примера 1 найти вероятность того, что очередной будет продана пара обуви меньше -го размера.
Решение. События “очередной будет продана пара обуви меньше -го размера” и “будет продана пара обуви размера не меньше-го” — противоположные. Поэтому по формуле (1.2) вероятность искомого события равна
,
поскольку , как это было найдено в примере 1.
Теорема 2.1 сложения вероятностей справедлива только для несовместных событий. Использование ее для нахождения вероятности совместных событий может привести к неправильным, а иногда и абсурдным выводам, что хорошо видно на следующем примере. Пусть всхожесть семян оценивается вероятностью . Какова вероятность того, что из трех посеянных семян взойдет какое-либо одно (безразлично какое)? Через,,обозначим события, состоящие в том, что взойдут соответственно первое, второе, третье семена. Если для отыскания искомой вероятности мы применим теорему 2.1 сложения вероятностей, то получим. Вероятность события оказалась больше единицы. Абсурдность ответа объясняется тем, что события,,являются совместными. Действительно, если произошло, например, событие(взошло первое семя), то это не исключает того, что произойдет и событие(взойдет второе семя).
Сформулируем теорему сложения вероятностей в случае двух совместных событий (будет учитываться вероятность их совместного появления).
Теорема 2.2. Вероятность суммы двух совместных событий равна сумме вероятностей этих двух событий без вероятности их совместного появления:
.
2. Зависимые и независимые события. Условная вероятность.
Различают зависимые и независимые события. Два события называется независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не связанные между собой, то остановки этих линий являются независимыми событиями.
Пример 3. Монета брошена два раза. Вероятность появления “герба” в первом испытании (событие ) не зависит от появления или непоявления “герба” во втором испытании (событие). В свою очередь, вероятность появления герба во втором испытании не зависит от результата первого испытания. Таким образом, событияи- независимые.
Несколько событий называются независимыми в совокупности, если любое из них не зависит от любой комбинации остальных. События называются зависимыми, если одно из них изменяет вероятность появления другого. Например, две производственные установки связаны единым технологическим циклом. Тогда вероятность выхода из строя одной из них зависит от того, в каком состоянии находится другая. Вероятность одного события , вычисленная в предположении осуществления другого события, называетсяусловной вероятностью события и обозначается через.
Условие независимости события от событиязаписывают в виде, а условие зависимости — в виде. Рассмотрим пример вычисления условной вероятности события.
Пример 4. В ящике находятся резцов — два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.
Решение. Обозначим через извлечение изношенного резца в первом случае, а через- извлечение нового. Тогда,. Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим. Обозначим черезсобытие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:
, .
Следовательно, вероятность события зависит от того, произошло или нет событие.
3. Формулы умножения вероятностей.
Пусть события инезависимые, причем вероятности этих событий известны. Найдем вероятность совмещения событийи.
Теорема 2.3. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
.
Следствие 2.1. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий.:
.
Пример 5. Имеется три ящика, содержащих по деталей. В первом ящике -, во втором -, в третьем -стандартных деталей. Из каждого ящика наудачу вынимается по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.
Решение. Вероятность того, что из первого ящика вынута стандартная деталь (событие ) равна. Вероятность того, что из второго ящика вынута стандартная деталь (событие) равна. Вероятность того, что из третьего ящика вынута стандартная деталь (событие) равна. Так как события,инезависимые в совокупности, то искомая вероятность (по теореме умножения) равна.
Пусть события изависимые, причем вероятностииизвестны. Найдем вероятности совмещения этих событий, т. е. вероятность того, что появится и событие, и событие.
Теорема 2.4. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
,
.
Следствие 2.2. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
Пример 6. В урне находится белых,черных исиних шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну. Найти вероятность того, что при первом испытании появится белый шар (событие), при втором — черный (событие) и при третьем — синий (событие).
Решение. Вероятность появления белого шара при первом испытании равна
.
Вероятность появления черного шара при втором испытании, вычисленная в предположении, что при первом испытании появился белый шар, т. е. условная вероятность равна
.
Вероятность появления синего шара при третьем испытании, вычисленная в предположении, что при первом испытании появился белый шар, а при втором — черный, равна
.
Искомая вероятность равна
.
4. Формула полной вероятности.
Теорема 2.5. Если событие может наступить только при условии появления одного из событий, образующих полную группу несовместных событий, то вероятность событияравна сумме произведений вероятностей каждого из событийна соответствующую условную вероятность события:
. (2.1)
Эта формула носит название формулы полной вероятности.
Пример 7. На сборочный конвейер поступают детали с трех станков. Производительность станков неодинакова. Первый дает % программы, второй -%, а третий -%. Если в сборку попадает деталь, сделанная на первом станке, то вероятность получения годного узла равна. Для продукции второго и третьего станков соответствующие вероятности равныи. Определить вероятность того, что узел, сходящий с конвейера, годный.
Решение. Обозначим через событие, означающее годность собранного узла; через,исобытия, означающие, что детали сделаны соответственно на первом, втором, третьем станках. Тогда имеем:
; ;
; ;.
Искомая вероятность равна:
.
5. Формулы Бейеса.
Формулы Бейеса применяются при решении практических задач, когда событие , появляющееся совместно с каким-либо из событий,, … ,, которые образуют полную группу несовместимых событий, произошло и требуется произвести количественную переоценку вероятностей событий,, … ,. Априорные (до опыта) вероятности,, … ,известны. Требуется вычислить апостериорные (после опыта) вероятности, т. е. по существу нужно найти условные вероятности,, … ,. Для событияформула Бейеса выглядит так:
.
Раскрывая в этом равенстве по формуле полной вероятности (2.1), имеем:
.
Пример 8. Пользуясь данными примера 7, рассчитать вероятности того, что в сборку попала деталь, изготовленная на первом, втором и третьем станках соответственно, если узел сходящий с конвейера, годный.
Решение. Расчет условных вероятностей произведем по формуле Бейеса. Имеем:
для первого станка
;
для второго станка
;
для третьего станка
.
ЗАДАЧИ
1. Бросили монету и игральную кость. Определить, зависимы или независимы события: — выпал “герб”;- выпало четное число очков.
Ответ: независимы.
2. Брошены последовательно три монеты. Определить, зависимы или независимы события: — выпадение “герба” на первой монете;- выпадение хотя бы одной “решетки”.
Ответ: зависимы.
3. Бросили игральную кость. Какова вероятность того, что выпало простое число очков, если известно, что число выпавших очков нечетно ?
Ответ: 2/3.
4. В ящике лежат красных,зеленых исиних шаров. Наудачу вынимается два шара. Какова вероятность, что извлечены шары разного цвета, если известно, что не извлечен синий шар ?
Ответ: 48/95.
5. В одном ящике белых икрасных шаров, в другом ящикебелых икрасных шаров. Найти вероятность того, что хотя бы из одного ящика будет извлечен один белый шар, если из каждого ящика извлечено по одному шару.
Ответ: 7/9.
6. Вероятность того, что в течение одной смены возникнет неполадка станка, равна . Какова вероятность того, что не произойдет ни одной неполадки за три смены ?
Ответ: (0,95)3=0,857375.
7. В ящике красных исиних пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность того, что пуговицы будут одноцветными ?
Ответ: 0,5.
8. Найти вероятность того, что наудачу взятое двузначное число окажется кратным , либо, либо тому и другому одновременно.
Ответ: 0,6.
9. Студент пришел на зачет, зная из вопросов только. Какова вероятность сдать зачет, если после отказа отвечать на вопрос преподаватель задает еще один вопрос ?
Ответ: 28/29.
10. Имеется два одинаковых ящика с шарами. В первом ящике белых ичерный шар, во втором -белый ичерных шара. Наудачу выбирают один ящик и извлекают из него шар. Какова вероятность, что извлеченный шар окажется белым ?
Ответ: 13/30.
11. В цехе работают станков. Из нихмарки,маркиимарки. Вероятность того, что качество деталей окажется отличным, для этих станков соответственно равна:,и. Какой процент отличных деталей выпускает цех в целом ?
Ответ: 83%.
12. Студент знает не все экзаменационные билеты. В каком случае вероятность вытащить неизвестный билет будет для него наименьшей, когда он тащит билет первым или последним ?
Ответ: безразлично.
13. На фабрике, изготовляющей болты, первая машина производит %, вторая — %, третья — % всех изделий. В их продукции брак составляет соответственно %, % и %.
а) Какова вероятность того, что случайно выбранный болт дефектный ?
б) Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен первой, второй, третьей машиной ?
Ответ: а) 0,0345; б) 125/345, 140/345, 80/345.
studfiles.net
8. Независимость событий, примеры независимых и зависимых событий.
Вероятность появления события Апри условии, что событиеВпроизошло, называетсяусловной вероятностьюсобытияАи вычисляется по формуле:
где A, B E, P(B) 0.
События A, B Eназываютсянезависимыми, если.
В противном случае события АиВназываютсязависимыми.
Пример независимого события:
Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (событие A) равна 0,8, а вторым (событие В) — 0,7.
Решение.События А и В независимые, поэтому, по теореме умножения, искомая вероятность
Р(АВ) = Р(А)Р(В) = 0,7 * 0,8 = 0,56.
Пример зависимого события:
В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.
Решение.ОбозначимAизвлечение изношенного резца в первом случае, а— извлечение нового. Тогда. Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим.
Обозначим Bсобытие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:
Следовательно, вероятность события Bзависит от того, произошло или нет событиеA.
9. Формула полной вероятности, примеры.
Предположим, что в результате опыта может произойти одно из n несовместных событий (гипотез) Н1,H2,…,Hn. Пусть также имеется некоторое событие А и известны
Р(Hi) — вероятность гипотезы, P(A/Hi) — условная вероятность события А при этой гипотезе.
Тогда вероятность события А вычисляется по формуле полной вероятности:
Доказательство. Заметим, что
и событияпопарно несовместны. Поэтому
Во втором равенстве мы использовали -аддитивность вероятностной меры, а в третьем — теорему умножения вероятностей.
Пример. Из 40 деталей 10 изготовлены в первом цехе, 25 — во втором, а остальные — в третьем. Первый и третий цехи дают продукцию отличного качества с вероятностью 0,9, второй цех — с вероятностью 0,7. Какова вероятность того, что взятая наудачу деталь будет отличного качества?
Решение: обозначим событие А = {выбрана деталь отличного качества},
Hi= {выбранная деталь изготовлена в i цехе}, i=1, 2, 3. Тогда
; ; .
По условию задачи
По формуле полной вероятности находим искомую вероятность:
10. Формула Байеса, примеры.
Формула Байеса
Пусть H1,H2,… — полная группа событий, и A — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие Hk, если в результате эксперимента наблюдалось событие A, может быть вычислена по формуле:
Доказательство. По определению условной вероятности,
Пример
Два стрелка подбрасывают монетку и выбирают, кто из них стреляет по мишени (одной пулей). Первый стрелок попадает по мишени с вероятностью 1, второй стрелок — с вероятностью 0,00001. Можно сделать два предположения об эксперименте:
H1 = {стреляет 1-ый стрелок} и H2 = {стреляет 2-ый стрелок}.
Априорные (a’priori — «до опыта») вероятности этих гипотез одинаковы:
Рассмотрим событие A = {пуля попала в мишень}. Известно, что
Поэтому вероятность пуле попасть в мишень
Предположим, что событие A произошло. Какова теперь апостериорная (a’posteriori — «после опыта») вероятность каждой из гипотез?
Очевидно, что первая из этих гипотез много вероятнее второй (а именно, в раз).
Действительно,
studfiles.net
Зависимые и независимые условия — Теория вероятностей
Введём понятие зависимых и независимых событий.
Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.
Пример 1.
Монета брошена два раза. Вероятность появления «герба» в первом испытании (событие A) не зависит от появления или не появления «герба» во втором испытании (событие B). В свою очередь, вероятность появления «герба» во втором испытании не зависит от результата первого испытания. Таким образом, события A и B независимые.
Пример 2.
При бросании кубика вероятность появления числа 2 при втором бросании не зависит от результатов первого бросания.
Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.
Причём, если А1, А2, …, Аn— независимые события, то и противоположные им события Ᾱ1, Ᾱ2, …, Ᾱn— независимы.
Замечание:
Если события независимы в совокупности, то из определения следует их попарная независимость, то есть любые два из них независимы. Обратное, вообще говоря, неверно, то есть из попарной независимости не следует их независимость в совокупности.
Пример.
Пусть имеется тетраэдр (объемная фигура, сторонами которой являются правильные треугольники, всего — четыре стороны). Пусть три стороны раскрашены в красный, зеленый и синий цвета (по одному на каждую сторону), а четвертая содержит все три цвета. Будем бросать тетраэдр наудачу, и цвет, оказавшийся на нижней грани, назовем выпавшим. Очевидно, что вероятность выпадения красного цвета (а также вероятность выпадения зеленого и вероятность выпадения синего цветов) равны Р(К)=Р(С)=Р(К) (каждый цвет содержится на двух гранях из четырех). Вероятность одновременного выпадения двух цветов, например, красного и зеленого, равна Р(КЗ)=0,25 . Таким образом, имеем Р(КЗ)=Р(К)Р(З) (Правая часть находится по теореме об умножении вероятностей, которую мы подробно рассмотрим в следующей теме). Аналогично для других комбинаций из двух цветов, то есть события выпадение цвета — попарно независимы. Вероятность же выпадения всех трех цветов одновременно (Р(КЗС)) равна 0,25 и не равна произведению вероятностей выпадения каждого из трёх цветов (Р(В)Р(К)Р(С)) , то есть события не независимы в совокупности.
События называются зависимыми, если одно из них влияет на вероятность появления другого.
Пример 1.
При вытягивании экзаменационных билетов вероятность вытащить самый простой билет (№ 13) восьмым студентом зависит от результатов всех предыдущих.
Пример 2.
Две производственные установки связаны единым технологическим циклом. Тогда вероятность выхода из строя одной из них зависит от того, в каком состоянии находится другая.
teoria-veroyatnostei.jimdo.com