Примеры сложение и вычитание дробей с одинаковыми знаменателями – Сложение и вычитание дробей

Вычитание дробей. Вычитание дробей с разными знаменателями

Следующее действие, которое можно выполнять с обычными дробями это вычитание. Вычитание дробей выполняется по нескольким правилам. Рассмотрим эти правила подробнее. Вычитание смешанных дробей с разными знаменателями можно посмотреть нажав на ссылку.

Вычитание дробей с одинаковым знаменателем.

Рассмотрим, пока примеры в которых уменьшаемое больше вычитаемого.

\(\frac{7}{13}-\frac{3}{13} = \frac{7-3}{13} = \frac{4}{13}\)

Чтобы выполнить вычитание дробей с одинаковыми знаменателями, нужно посчитать разность числителя уменьшаемого и вычитаемого, а знаменатель оставить без изменения.

\(\frac{a}{b}-\frac{c}{b} = \frac{a-c}{b}\)

Вычитание дробей с разными знаменателями.

Чтобы выполнить вычитание дробей с разными знаменателями, нужно привести дроби к общему знаменателю, а потом применить правило вычитания дробей с одинаковыми знаменателями.

Рассмотрим пример:

Выполните вычитание дробей \(\frac{5}{6}\) и \(\frac{1}{2}\).

Общий знаменатель этих двух дробей latex]\frac{5}{6}[/latex] и \(\frac{1}{2}\) равен 6. Умножим вторую дробь \(\frac{1}{2}\) на дополнительный множитель 3.

\(\frac{5}{6}-\frac{1}{2} = \frac{5}{6}-\frac{1 \times \color{red} {3}}{2 \times \color{red} {3}} = \frac{5}{6}-\frac{3}{6} = \frac{2}{6} = \frac{1}{3}\)

Дробь \(\frac{2}{6}\) сократили и получили \(\frac{1}{3}\).

Буквенная формула вычитания дробей с разными знаменателями.

\(\bf \frac{a}{b}-\frac{c}{d} = \frac{a \times d-c \times b}{b \times d}\)

Вопросы по теме:
Как вычитать дроби с разными знаменателями?
Ответе: нужно найти общий знаменатель и далее по правилу выполнить вычитание дробей с одинаковыми знаменателями.

Как выполнить вычитание дробей с одинаковыми знаменателями?
Ответ: у числителей посчитать разность, а знаменатель оставить тот же.

Как правильно сделать проверку вычитания двух дробей?
Ответ: для проверки правильности вычитания  дробей, нужно выполнить сложение вычитаемого и разности, результат их суммы будет равен вычитаемому.

\(\frac{7}{8}-\frac{3}{8} = \frac{7-3}{8} = \frac{4}{8}\)

Проверка:

\(\frac{4}{8} + \frac{3}{8} = \frac{4 + 3}{8} = \frac{7}{8}\)

Пример №1:
Выполните вычитание дробей: а) \(\frac{1}{2}-\frac{1}{2}\) б) \(\frac{10}{19}-\frac{7}{19}\)

Решение:
а) \(\frac{1}{2}-\frac{1}{2} = \frac{1-1}{2} = \frac{0}{2} = 0\)

При вычитание двух одинаковых дробей получаем нуль.

б) \(\frac{10}{19}-\frac{7}{19} = \frac{10-7}{19} = \frac{3}{19}\)

Пример №2:
Выполните вычитание и проверьте сложением: а) \(\frac{13}{21}-\frac{3}{7}\) б) \(\frac{2}{3}-\frac{1}{5}\)
Решение:

а)Найдем общий знаменатель дробей \(\frac{13}{21}\) и \(\frac{3}{7}\), он будет равен 21. Умножим вторую дробь \(\frac{3}{7}\) на 3.

\(\frac{13}{21}-\frac{3}{7} = \frac{13}{21}-\frac{3 \times \color{red} {3}}{7 \times \color{red} {3}} = \frac{13}{21}-\frac{9}{21} = \frac{13-9}{21} = \frac{4}{21}\)

Выполним проверку вычитания:

\(\frac{4}{21} + \frac{3}{7} = \frac{4}{21} + \frac{3 \times \color{red} {3}}{7 \times \color{red} {3}} = \frac{4}{21} + \frac{9}{21} = \frac{4 + 9}{21} = \frac{13}{21}\)

б) Найдем общий знаменатель дробей \(\frac{2}{3}\) и \(\frac{1}{5}\), он будет равен 15. Умножим первую дробь \(\frac{2}{3}\) на дополнительный множитель 5, вторую дробь \(\frac{1}{5}\) на 3.

\(\frac{2}{3}-\frac{1}{5} = \frac{2 \times \color{red} {5}}{3 \times \color{red} {5}}-\frac{1 \times \color{red} {3}}{5 \times \color{red} {3}} = \frac{10}{15}-\frac{3}{15} = \frac{10-3}{15} = \frac{7}{15}\)

Выполним проверку вычитания:

\(\frac{7}{15} + \frac{1}{5} = \frac{7}{15} + \frac{1 \times \color{red} {3}}{5 \times \color{red} {3}} = \frac{7}{15} + \frac{3}{15} = \frac{7 + 3}{15} = \frac{10}{15} = \frac{2}{3}\)

tutomath.ru

Сложение и вычитание дробей с одинаковыми знаменателями

Следующие правила применяются для правильных и неправильных дробей (смешанную дробь всегда можно перевести в неправильную дробь) с одинаковыми знаменателями.

Правило. Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители и оставить тот же знаменатель.

Например:

Правило. Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби и оставить тот же знаменатель.

Например:

Следующие правила применяются для смешанных дробей с одинаковыми знаменателями.

Правило. Чтобы сложить смешанные дроби, необходимо отдельно сложить их целые и дробные части и записать сумму целых частей и сумму дробных частей смешанной дробью.

Если суммарная дробная часть окажется неправильной дробью, то те следует перевести в смешанную дробь, а выделенную из неправильной дроби целую часть добавить к сумме целых частей. Окончательную сумму целой и дробной частей записать смешанной дробью.

Например, сложить дроби:

Правило, Чтобы вычесть смешанные дроби, необходимо отдельно вычесть их целые и отдельно их дробные части и записать сумму полученных разностей смешанной дробью.

Если дробная часть уменьшаемого меньше дробной части вычитаемого, то от целой части уменьшаемого «одалживаем» 1, которую представляем как дробь с тем же знаменателем, что и у дробной части смешанных дробей, и с равным этому знаменателю числителем. Одолженную 1, выраженную неправильной дробью с одинаковыми числителем и знаменателем, суммируем с дробной частью уменьшаемого. После этого производим вычисления согласно правилу вычитания смешанных дробей.

Например, вычесть дроби:

shkolo.ru

Сложение и вычитание дробей с одинаковыми знаменателями

Вы уже хорошо умеете складывать и вычитать обыкновенные дроби с одинаковыми знаменателями. Давайте вспомним правила, по которым складывают и вычитают обыкновенные дроби.

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же.

Чтобы из одной дроби вычесть другую дробь с таким же знаменателем, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тем же.

В буквенном виде эти правила можно записать так:   

Например

Эти равенства являются тождествами, т.к. они верны при любых значениях переменных a, b и c, кроме цэ равного нулю.

Доказательство:

Таким образом, складывают любые

рациональные дроби с одинаковыми знаменателями.

Правило сложения рациональных дробей с одинаковыми знаменателями:

Чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же.

В буквенном виде это правило можно записать так:

Это правило справедливо при сложении любого числа дробей.

Пример 1. Найти сумму дробей.

Решение:

Пример 2. Найти сумму дробей.

Решение:

Пример 3. Найти сумму дробей.

Решение:

Вычитание рациональных дробей с одинаковыми знаменателями выполняется аналогично сложению.

Правило вычитания рациональных дробей с одинаковыми знаменателями

Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.

В буквенном виде это правило можно записать так:

Пример 4. Найти разность дробей.

Решение:

Пример 5. Найти разность дробей.

Решение:

Пример 6. Выполнить действия.

Решение:

Итоги:

Чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же.

Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.

videouroki.net

Сложение и вычитание дробей с одинаковыми знаменателями

Дробные числа, как и натуральные числа, можно складывать и вычитать.

На рисунке 201 прямоугольника разделен на 9 равных частей. Сначала закрасили 2 части, а потом еще 5 частей. Таким образом, закрашенными оказались 

$\frac{7}{9}$

прямоугольника. Тогда можно сделать вывод, что:

$\frac{2}{9}$

+ 

$\frac{5}{9}$

= 

$\frac{2 + 5}{9}$

  = 

$\frac{7}{9}$

.

Этот пример иллюстрирует следующее правило.

Чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.

В буквенном виде это правило записывают так:

$\frac{a}{c}$

+ 

$\frac{b}{c}$

= 

$\frac{a + b}{c}$

 

Рассмотрим разность 

$\frac{7}{9}$

 − 

$\frac{2}{9}$

. Вычесть из дроби 

$\frac{7}{9}$

дробь 

$\frac{2}{9}$

− значит найти такое число, которое в сумме с числом 

$\frac{2}{9}$

дает число 

$\frac{7}{9}$

. Поскольку 

$\frac{2}{9}$

+ 

$\frac{5}{9}$

= 

$\frac{7}{9}$

, то 

$\frac{7}{9}$

− 

$\frac{2}{9}$

= 

$\frac{5}{9}$

.

Чтобы вычесть дроби с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.

 

В буквенном виде это правило записывают так:

$\frac{a}{c}$

−

$\frac{b}{c}$

=

$\frac{a — b}{c}$

Пример. На выполнение домашнего задания по математике Вася потратил 32 мин. Решение задачи заняло у него 

$\frac{3}{8}$

потраченного времени, а решение уравнения − 

$\frac{2}{8}$

потраченного времени. Сколько минут потратил Вася на решение задачи и уравнения?

Решение.

1) 

$\frac{3}{8}$

+ 

$\frac{2}{8}$

  = 

$\frac{5}{8}$

(времени) − Вася потратил на решение задачи и уравнения.

2) 32 : 8 = 4 (мин) − составляют 

$\frac{1}{8}$

времени выполнения домашнего задания по математике.

3) 4 * 5 = 20 (мин) − Вася потратил на решение задачи и уравнения.

Ответ: 20 мин.

 

reshalka.com

3. Сложение и вычитание смешанных чисел (одинаковые знаменатели)

Рассмотрим примеры сложения и вычитания смешанных чисел.

Задача 1. На столе лежали 238 плитки шоколада.

Сколько плиток шоколада будет лежать на столе, если на стол положить ещё 128 плитки?

 

Решение. Чтобы решить задачу, надо сложить числа 238 и 128.
Так как 238=2+38;128=1+28,  то

238+128=2+38+1+28=2+1+38+28=3+3+28=3+58=358.

Обычно записывают коротко: 238+128=358.

Ответ: 358 плитки шоколада.

Задача 2. На тарелке лежали 238 плитки шоколада. Сколько останется плиток шоколада на тарелке, если 128 плитки съедят?

Решение. Чтобы решить задачу, надо из 238 вычесть 128.

 

Тогда:

238−128=2+38−1+28=2+38−1−28=2−1+38−28==1+3−28=1+18=118.

 

Пишут короче: 238−128=118.

Ответ: 118 плитки шоколада.

 

Обрати внимание!

При сложении (и вычитании) чисел в смешанной записи целые части складывают (вычитают) отдельно, а дробные — отдельно.

В случае, когда при сложении смешанных чисел в их дробной части получается неправильная дробь, из неё выделяют целую часть и добавляют её к уже имеющейся целой части.

 

Пример 1.
15711+3611=181311=18+1311=18+1211=19211.

 

Рассмотрим пример, в котором при вычитании смешанных чисел дробная часть уменьшаемого меньше дробной части вычитаемого.

 

Пример 2.

713−523=7+13−523=6+1+13−523=6+113−523==6+43−523=643−523=123.

 

Обычно пишут короче: 713−523=643−523=123.

Таким же образом поступают и при вычитании дроби из натурального числа, и при вычитании смешанного числа из натурального числа.

25−713=241313−713=2413−713=24613.

 

Пример 4.

12−857=1177−857=37−57=327.

www.yaklass.ru

Сложение и вычитание дробей с одинаковыми знаменателями 5 класс

Технологическая карта урока

Шемилина Анна Викторовна

учитель математики

МБОУ «Ара-Илинская основная общеобразовательная школа»

Тема: «Сложение и вычитание дробей с одинаковыми знаменателями»

Класс: 5

Тип урока: урок открытия новых знаний

Цели: а) вывести правила сложения и вычитания дробей с одинаковыми знаменателями;

б) развивать умения анализировать, сравнивать, обобщать, делать выводы, развивать внимание;

в) развивать познавательный интерес через игровые моменты взаимоконтроля, взаимопроверки, способствовать пониманию необходимости интеллектуальных усилий для успешного обучения, положительного эффекта настойчивости для достижения цели, аргументировать свою точку зрения.

Планируемые результаты:

Предметные результаты: знать правила сложения и вычитания дробей с одинаковыми знаменателями, уметь применять их при решении примеров, уравнений, задач.

Метапредметные результаты: уметь воспроизводить сложение и вычитание дробей с одинаковыми знаменателями; уметь обрабатывать информацию; формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; контролировать и оценивать процесс и результаты своей деятельности; уметь приводить свои примеры.

Личностные результаты: умение работать в коллективе, слушать собеседника и вести диалог, аргументировать свою точку зрения.

Метод обучения: частично-поисковый метод и метод проблемного обучения

Технология обучения: технология сотрудничества

Оборудование: интерактивная и меловая доска, проектор

Материалы: учебник «Математика 5» Виленкин Н. Я. и др., 2014 «Мнемозина», план-конспект урока, презентация, раздаточный материал

Этапы урока

Цель этапа

Деятельность учителя

Деятельность учащихся

Формы обучения

Результативность

1. Организационный момент

Создать благоприятный психологический настрой на работу

— Здравствуйте ребята! Повернитесь к ним поприветствуйте, посмотрите друг на друга, улыбнитесь, желаю вам успешной работы! Садитесь.

Чем мы занимались на прошлом уроке?

Вспомните определения правильных и неправильных дробей, числителя и знаменателя.

Включаются в деловой ритм урока.

Мы сравнивали дроби, узнавали о неправильных дробях, сравнивали их с правильными дробями, с единицей, расставляли различные виды дробей на координатном луче.

Дают определения правильных и неправильных дробей, числителя и знаменателя.

Фронтальный опрос

Личностные: самоопределение.

Регулятивные: целеполагание.

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.

2. Актуализация и фиксирование индивидуального затруднения в пробном учебном действии, целеполагание

Актуализация опорных знаний и способов действий, принятие цели урока учащимися и определение темы урока

1. Что изображено на доске? (слайд 1 на интерактивной доске) 

Среди данных дробей найдите правильные, обоснуйте свой выбор.

Среди данных дробей найдите неправильные и обоснуйте свой выбор.

(слайд)

2. Задача на нахождение суммы дробей с одинаковыми знаменателями (слайды2,3). Как узнать?

— Что для этого нужно сделать?

— Что мы должны научиться делать?

— Значит какая задача, цель стоит перед нами?

– Хорошо! Чтобы продолжить работу, надо записать тему урока. Т.О. Какая же тема сегодняшнего урока?

Попробуйте сформулировать правило сложения дробей с одинаковыми знаменателями?

Прочитаем это правило по учебнику.

Как вы думаете как можно записать правило в буквенной форме?

Запись на доске

Дроби.

Называют номер дроби и доказывают свой выбор: числитель меньше знаменателя,

Называю по очереди неправильные дроби и обосновывают свой выбор: числитель больше или равен знаменателю.

Надо узнать сколько всего кусков съели.

Для этого надо сложить куски торта.

Складывать дроби с одинаковыми знаменателями

научиться складывать и вычитать дроби с одинаковыми знаменателями и применять эти знания при решении задач.

Тема урока «Сложение и вычитание дробей с одинаковыми знаменателями.»

Чтобы сложить дроби с одинаковыми знаменателями нужно сложить их числители, а знаменатель оставить тем же.

Выходит к доске ученик, который знает эту запись

Проговаривают вполголоса правила в парах.

Разрешение проблемы, пробные действия, индивидуальная работа с учебным материалом, диалог с учителем

Коммуникативные: планирование учебного сотрудничества с учителем и сверстником.

Познавательные: логические — анализ объектов с целью выделения признаков.

3. Мотивация

Обеспечение мотивации учения детьми.

4. Задача на нахождение разности дробей с одинаковыми знаменателями.

Проблема: как вычесть из одной дроби другую?

-Что заметили?

-Как вы думаете, это правило без исключений?

По аналогии с суммой вычисляют разность дробей с разными знаменателями.

Делают вывод:

Знаменатель оставляем тот же.

Правило без исключений, только числитель уменьшаемого должен быть больше числителя вычитаемого.

(a>c)

Частично-поисковая работа учащихся

Регулятивные: целеполагание.

Коммуникативные: постановка вопросов.

Познавательные: самостоятельное выделение-формулирование познавательной цели; логические — формулирование проблемы.

4. Усвоение новых знаний и способов усвоения

Обеспечение восприятия, осмысления и первичного запоминания детьми изученной темы: сложение и вычитание дробей с разными знаменателями

-Повторим, как найти сумму дробей с одинаковыми знаменателями?

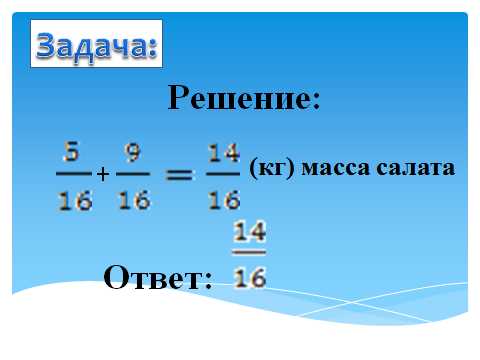
Задача:

Из помидоров массой  кг и огурцов массой  кг сделали салат. Какова масса салата?. Решают самостоятельно, сверяем с доской.

Слайд:

Проблема:

-если в ответе получаем числитель равный знаменателю, как записываем ответ?

Для подтверждения предположений работаем в группах: учитель предлагает 2 задачи

Придумайте аналогичную задачу.

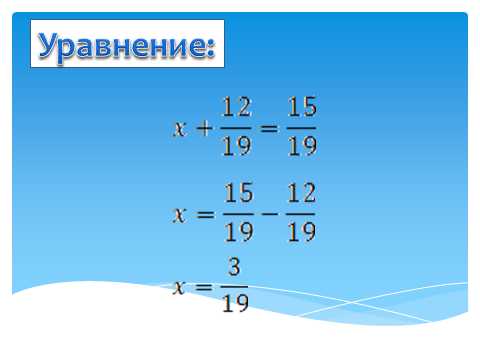
-если у нас будет дано уравнение с дробями, как мы будем решать?

Слайд для самопроверки:

-Чтобы сложить 2 дроби с одинаковыми знаменателями необходимо сложить числители, а знаменатель оставить тем же.

Решение:

1. +(кг) масса салата

Ответ: кг

Самопроверка по слайду

Предположения:

— если в ответе получается дробь, в которой числитель и знаменатель равны, то получаем единицу. На примере разрезанного торта)

Две группы учащихся решают предложенные учителем задачи. Делают выводы: действительно: если в ответе получается дробь, в которой числитель и знаменатель равны, то эта дробь равна 1

В первый день засеяли 4/11 поля, а во второй день – 7/11 поля. Какую часть поля засеяли за два дня?

получаем единицу.

Уравнение решают самостоятельно, проверяем ответ:

Говорят, что здесь неизвестное слагаемое. Проговаривают правило нахождения неизвестного слагаемого и решают уравнение самостоятельно.

Самопроверка через слайд

Индивидуальная работа, самопроверка, работа в группах, самостоятельная работа

Коммуникативные: постановка вопросов, инициативное сотрудничество.

Познавательные: самостоятельное выделение-формулирование познавательной цели; логические- формулирование проблемы, решение проблемы, построение логической цепи рассуждений; доказательство.

Регулятивные: планирование, прогнозирование.

5.Первичное закрепление

Установление правильности и осознанности изучения темы.

Выявление пробелов первичного осмысления изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы по новому материалу.

Задача №1006

Масса станка равна  т., а масса его упаковки  т. Найдите массу станка вместе с упаковкой?

Слайд для самопроверки

Задача № 1009 (реши самостоятельно). (слайд )

За два дня засеяли  поля. В первый день засеяли  поля. Какую часть поля засеяли во второй день?

Взаимопроверка в парах

Проблема.

Как найти какую часть засеяли во второй день, если известно какую часть засеяли за два дня вместе и за первый?

Выполните действие: на доске

А) 

Б) 

В) 

Г) 

Д) 

Е) 

Ж) 

З) 

Ребята делают предположения и обосновывают свои ответы.

(т) масса станка вместе с упаковкой.

Ответ: 

Самопроверка по слайду

 (ч) поля засеяли во второй день.

Ответ: 

взаимопроверка

Делают вывод: если известно какую часть проделали за два дня и за один день, то чтобы узнать какую часть выполнили во второй день, выполняют вычитание

Взаимопроверка по записи на обратной стороне доски:

А) 

Б) 

В) 

Г) 

Д) 

Е) 

Ж) 

З) 

Первичное закрепление, само-, взаимопроверка, решение проблемной ситуации, самостоятельная работа с последующей проверкой

Регулятивные: контроль, оценка, коррекция.

Познавательные: умение структуризировать знания, выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия.

Коммуникативные: управление поведением партнера, контроль, коррекция, оценка действий партнера.

6. Организация первичного контроля

Выявление качества и уровня усвоения знаний и способов действий, а также выявление недостатков в знаниях и способах действий, установление причин выявленных недостатков.

Вариант I.

Задача 1008.

Одна бригада получила  т гвоздей, а вторая – на т меньше. Сколько гвоздей получила вторая бригада?

Задача 1012(а, в) Найдите значение выражения:

А) , если а=

В)  если с=

Вариант II

Задача 1010.

Цистерна на  наполнена бензином,  цистерны перелили в бочку. Какая часть цистерны осталась заполненной бензином?

Задача 1012 (б, г) Найдите значение выражения:

Б) если с=, ,

Г) , если с=, 

Самопроверка.

Самостоятельное решение в тетради.

Взамопроверка:

№1008

 (т) гвоздей получила вторая бригада

Ответ: 

№1012

А) 

В) 

№1010

(ч) цистерны заполнена бензином

Ответ:

№1012

Б) , 

Г) 

Контроль и коррекция первичного освоения материала через самостоятельную работу с последующей проверкой

Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения;

Личностные: самоопределение.

7. Подведение итогов урока.

Дать качественную оценку работы класса и отдельных обучаемых

-Что изучили сегодня на уроке?

-Кто желает сформулировать правило сложения дробей с одинаковыми знаменателями?

Кто желает сформулировать правило вычитание дробей с одинаковыми знаменателями

-Что еще узнали сегодня нового?

Оценить отдельных учащихся

Подведение итога урока через фронтальный опрос

Регулятивные: оценка-осознание уровня и качества усвоения; контроль

8. Информация о домашнем задании

Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания.

№ 1039, 1041(а, в, д, ж), 1042

Инструктаж домашнего задания

9. Рефлексия

Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе.

Если вы считаете, что поняли тему урока, то поднимите красную окружность (окружности раздает учитель на листочках вначале урока)

Если вы считаете, что не достаточно усвоили материал, то поднимите зеленую окружность.

Если вы считаете, что не поняли тему урока, то поднимите желтую окружность.

Рефлексия через индивидуальное общение с учащимися

Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли;

Познавательные: рефлексия.

infourok.ru

Сложение и вычитание дробей с одинаковыми знаменателями

На этом уроке мы продолжим изучение дробей. Научимся складывать дроби с одинаковыми знаменателями. А также научимся отнимать дроби с одинаковыми знаменателями.

Задача

Аня и Таня заказали пиццу. Пиццу разрезали на 8 равных частей. Аня съела 3 кусочка пиццы, а Таня – 2 кусочка. Сколько кусочков пиццы съели девочки?

Решение

Запомним правило:

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же.

В буквенном виде правило сложения дробей с одинаковыми знаменателями можно записать так:

где a, b, c – любые натуральные числа.

Пример

Найдите сумму дробей: .

Задача

Маша разделила яблоко на 10 равных частей. 2 дольки она съела сама, а 8 долек Маша решила дать своим братикам Ване и Диме. Мальчишки вместе съели 5 долек. Сколько долек яблока осталось?

Решение

Запомним правило:

Чтобы из одной дроби вычесть другую дробь с таким же знаменателем, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тем же.

В буквенной записи правило вычитания дробей с одинаковыми знаменателями записывают так:

где a, b, c – любые натуральные числа.

Пример

Найдите разность дробей: .

Правилами сложения и вычитания дробей с одинаковыми знаменателями пользуются и при решении уравнений.

Решить уравнения

Итоги

Итак, сегодня на уроке мы узнали, какими правилами пользуются при сложении и вычитании дробей с одинаковыми знаменателями. И применили знания данных правил при решении примеров, уравнений и задач.

videouroki.net