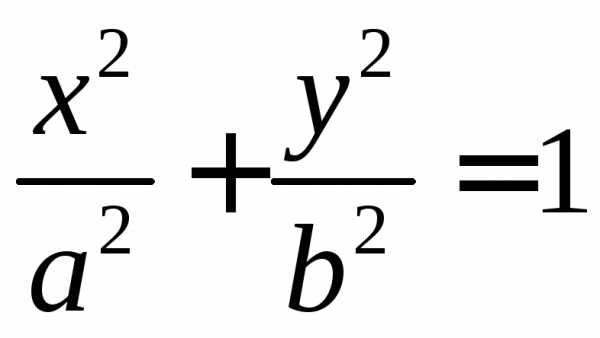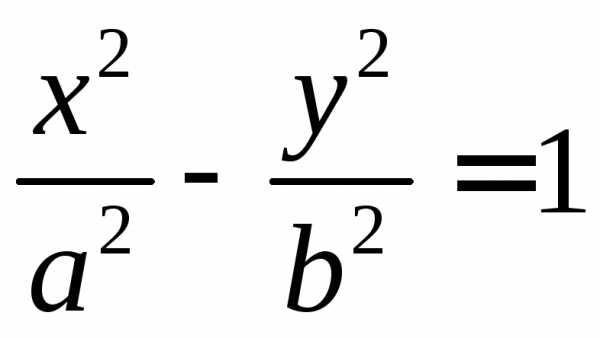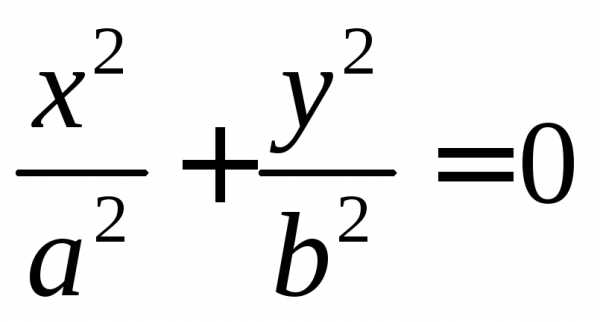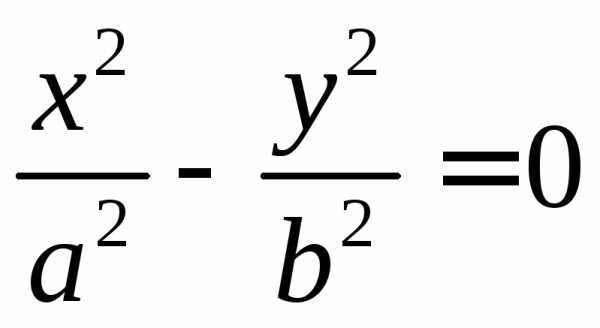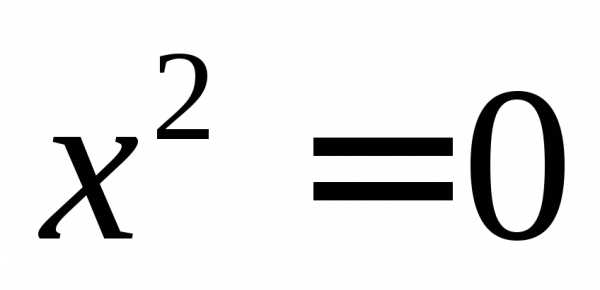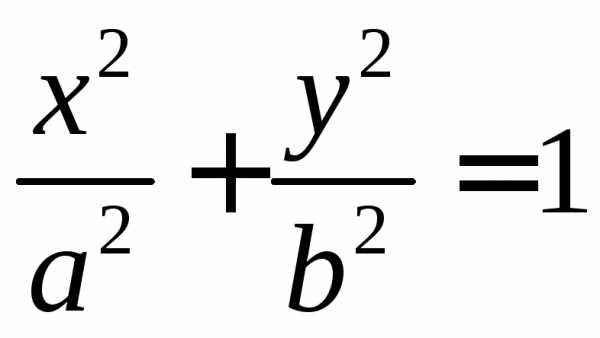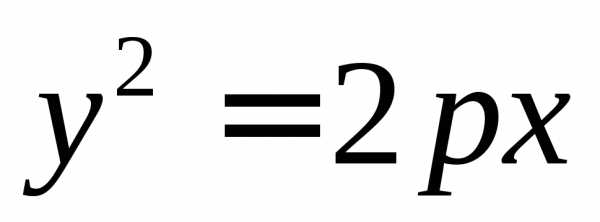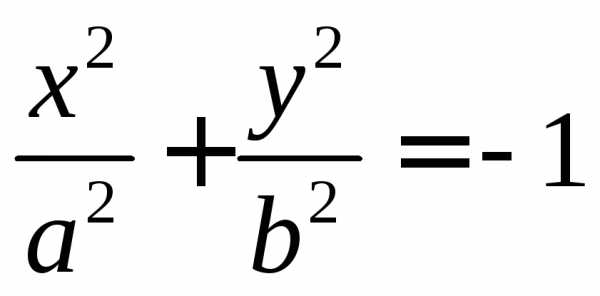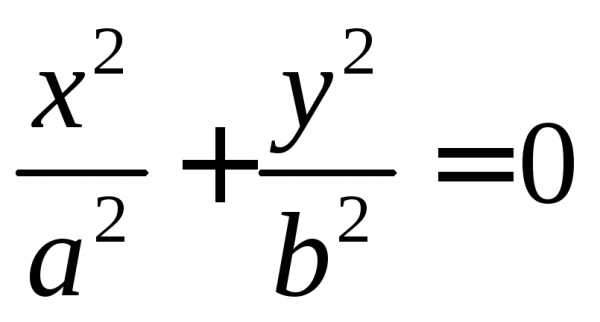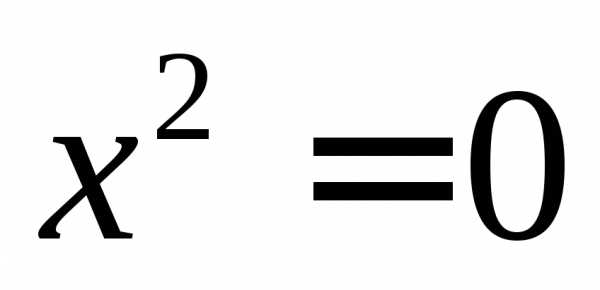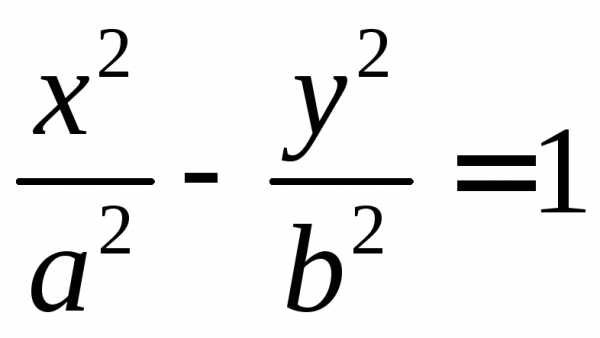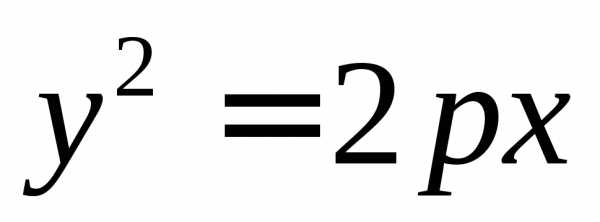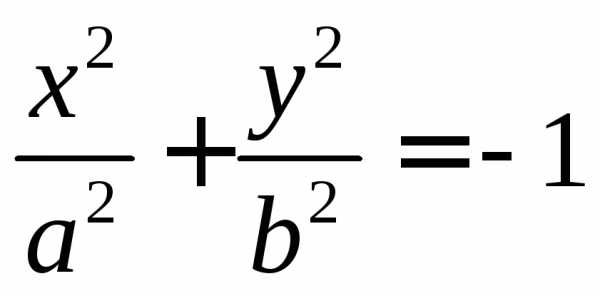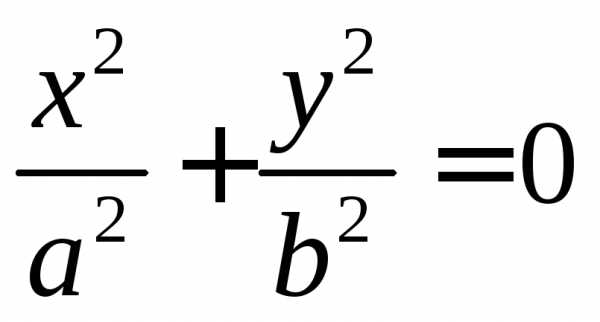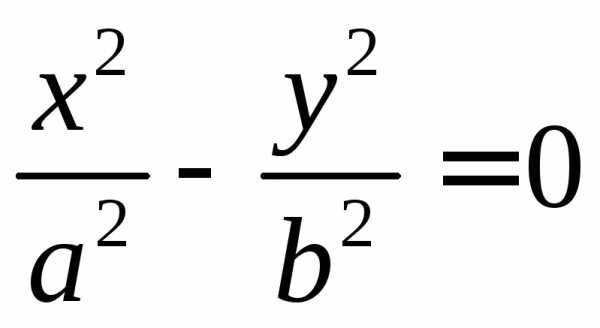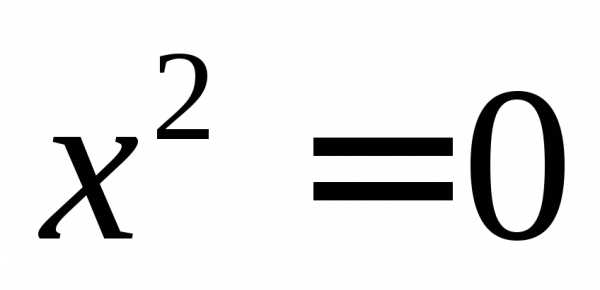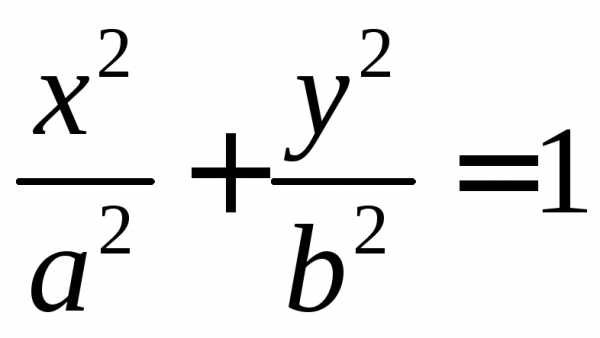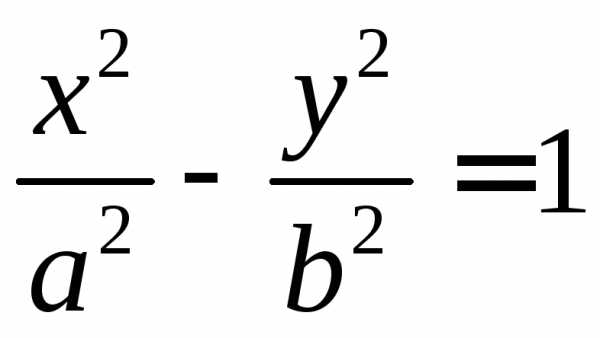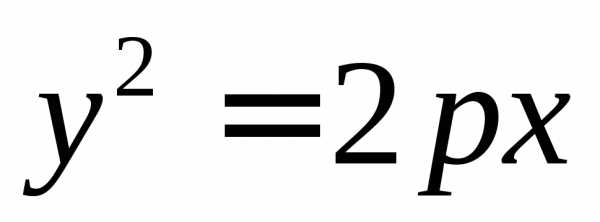4.3.7 Приведение кривой второго порядка к каноническому виду
Уравнение второго порядка вида
определяет на плоскости кривую. Группа членов называется квадратичной формой, – линейной формой. Если в квадратичной форме содержатся только квадраты переменных, то такой ее вид называется каноническим, а векторы ортонормированного базиса, в котором квадратичная форма имеет канонический вид, называются главными осями квадратичной формы.
Матрица называется матрицей квадратичной формы. Здесь . Чтобы матрицу привести к диагональному виду, необходимо за базис взять собственные векторы этой матрицы, тогда , где и – собственные числа матрицы .
В базисе из собственных векторов матрицы квадратичная форма будет иметь канонический вид: .
Эта операция соответствует повороту осей координат. Затем производится сдвиг начала координат, избавляясь тем самым от линейной формы.
Канонический вид кривой второго порядка: , причем:
А) если – эллипс, в частности, при это окружность;
Б) если имеем гиперболу;
В) если либо , то кривая является параболой и после поворота осей координат имеет вид (здесь ). Дополняя до полного квадрата, будем иметь: .
Пример 14. Дано уравнение кривой
в системе координат , где и .
1. Определить тип кривой.
2. Привести уравнение к каноническому виду и построить кривую в исходной системе координат.
3. Найти соответствующие преобразования координат.
Решение. Приводим квадратичную форму к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы . Находим собственные числа и собственные векторы этой матрицы:
Характеристическое уравнение:
; . Вид квадратичной формы: .
Исходное уравнение определяет гиперболу.
Заметим, что вид квадратичной формы неоднозначен. Можно записать , однако тип кривой остался тот же – гипербола.
Находим главные оси квадратичной формы, то есть собственные векторы матрицы . .
Собственный вектор, отвечающий числу при : .
В качестве единичного собственного вектора принимаем вектор , где – длина вектора .
Координаты второго собственного вектора, соответствующего второму собственному числу , находим из системы
.
; .
Итак, имеем новый ортонормированный базис .
По формулам (5) пункта 4.3.3. переходим к новому базису:
или
; . (*)
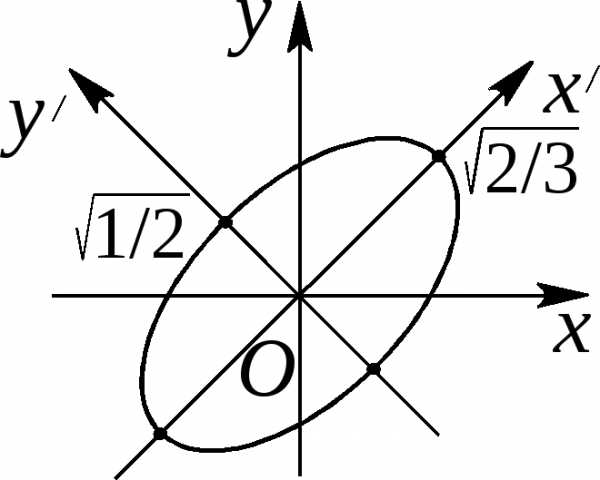
Вносим выражения и в исходное уравнение и, после преобразований, получаем: .
Выделяем полные квадраты: .
Проводим параллельный перенос осей координат в новое начало: , .
Если внести эти соотношения в (*) и разрешить эти равенства относительно и , то получим: , . В системе координат данное уравнение имеет вид: .
Для построения кривой строим в старой системе координат новую: ось задается в старой системе координат уравнением , а ось уравнением . Начало новой системы координат является точкой пересечения этих прямых.
Для упрощения восприятия разобьем процесс построения графика на 2 этапа:
1. Переход к системе координат с осями , заданными в старой системе координат уравнениями и Соответственно.
2. Построение в полученной системе координат графика функции.
 |
Окончательный вариант графика выглядит следующим образом
Аналогично можно упростить, то есть привести к каноническому виду, поверхность второго порядка.
Для самостоятельной работы.
1. Оператор в пространстве действует по закону .
А) Доказать, что вектор является собственным вектором оператора . Найти его собственное число.
Б) Привести матрицу оператора к диагональному виду путем перехода к новому базису. Найти этот базис и соответствующую ему матрицу.
Ответ: ; ; .
2. Доказать, что матрица к диагональному виду не приводится.
3. Даны уравнения кривых:
А) ;
Б) ;
В) .
Определить тип кривых; кривую а) построить.
Ответ: а) эллипс; б) парабола; в) гипербола.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
§ 2. Приведение к каноническому виду уравнения кривой второго порядка
Общее уравнение кривой второго порядка имеет вид
причем предполагается, что среди чисел есть хотя бы одно ненулевое.
Существует система координат (называемая канонической), в которой уравнение кривой второго порядка имеет вид, приведенный в таблице (канонический вид).
| эллипс |
| гипербола |
| парабола |
| мнимый эллипс (эта “кривая” не имеет действительных точек) |
| на действительной плоскости “кривая” имеет лишь одну точку |
| две пересекающиеся прямые |
две параллельные прямые | |
| две совпадающие прямые |
две мнимые параллельные прямые (“кривая” не имеет ни одной действительной точки) |
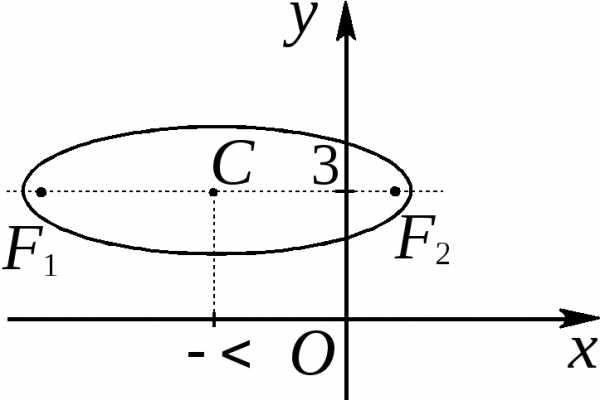
Задача 1. Изобразить кривую, найти ее характеристики:
Р
 и по
и по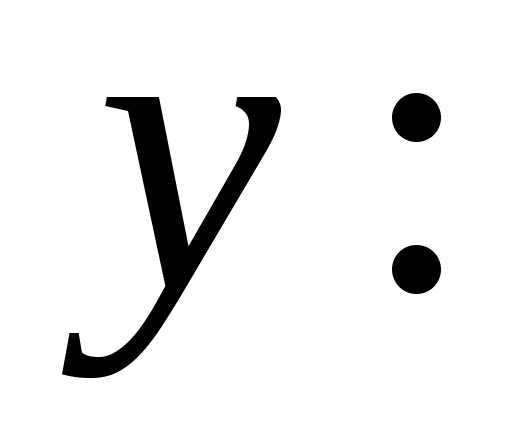 Следовательно, данная кривая является
эллипсом. Его центр:Полуоси:
Следовательно, данная кривая является
эллипсом. Его центр:Полуоси: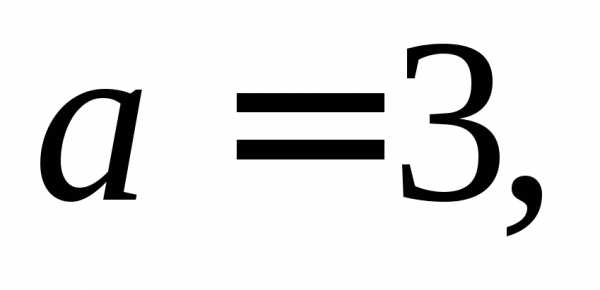
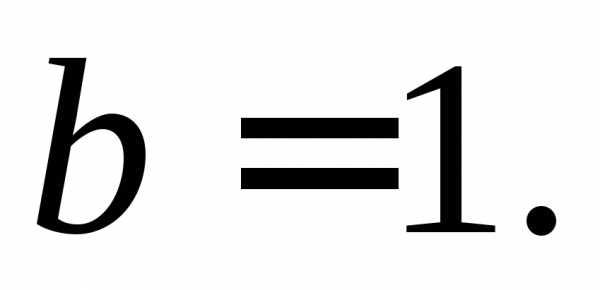 Для нахождения координат фокусов находим
параметр
Для нахождения координат фокусов находим
параметр (половину расстояния между фокусами):Отсюда получаем фокусы:Эксцентриситет:
(половину расстояния между фокусами):Отсюда получаем фокусы:Эксцентриситет: Задача 2.
Составить
уравнение гиперболы с асимптотами
касающейся оси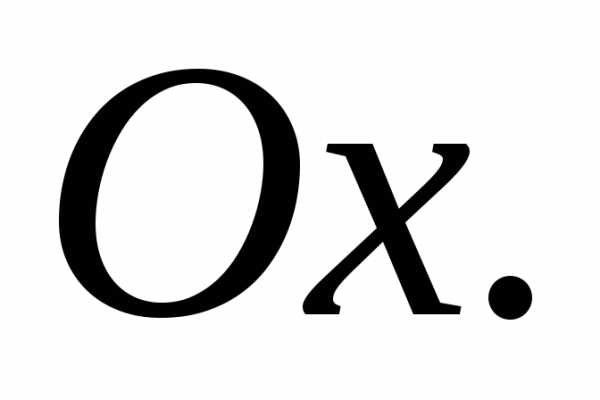
Р

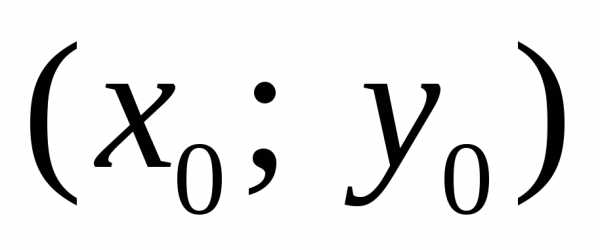 имеют видСледовательно, центр гиперболы имеет
координаты
имеют видСледовательно, центр гиперболы имеет
координаты  и
Нарисуем гиперболу, учитывая, что она
касается оси абсцисс.
и
Нарисуем гиперболу, учитывая, что она
касается оси абсцисс.
Из
рисунка видно, что  Так както
Так както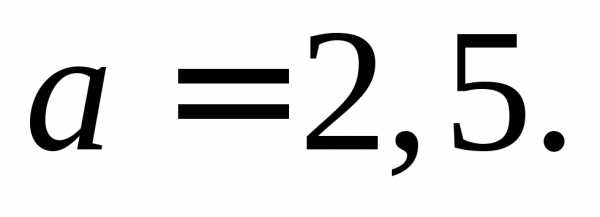 Так как действительная ось гиперболы
параллельна оси
Так как действительная ось гиперболы
параллельна оси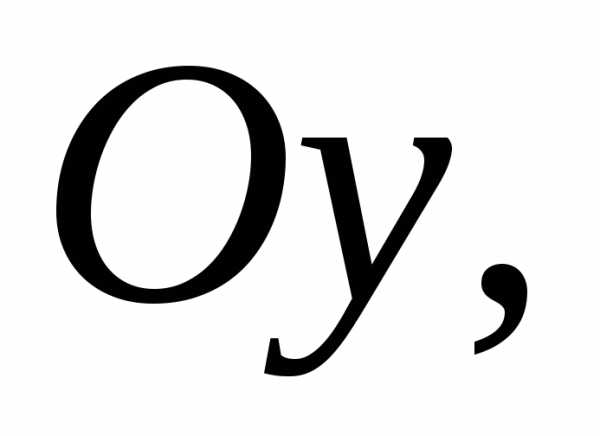 то в правой части уравнения будет
то в правой части уравнения будет вместо
вместо Отсюда получаем уравнение:
Отсюда получаем уравнение:
Задача 3. Найти площадь области, ограниченной кривой
Решение. В случае, когда коэффициенты при 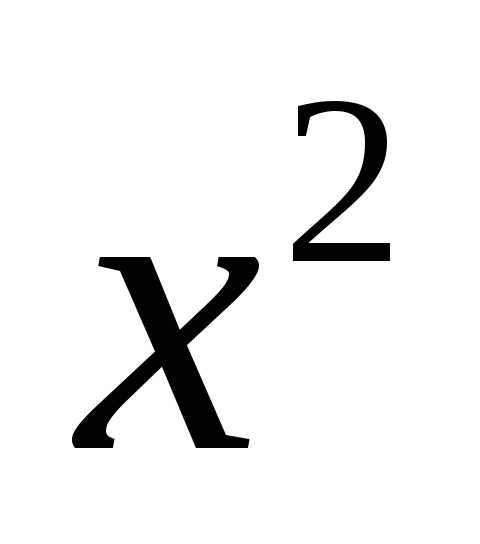 и
и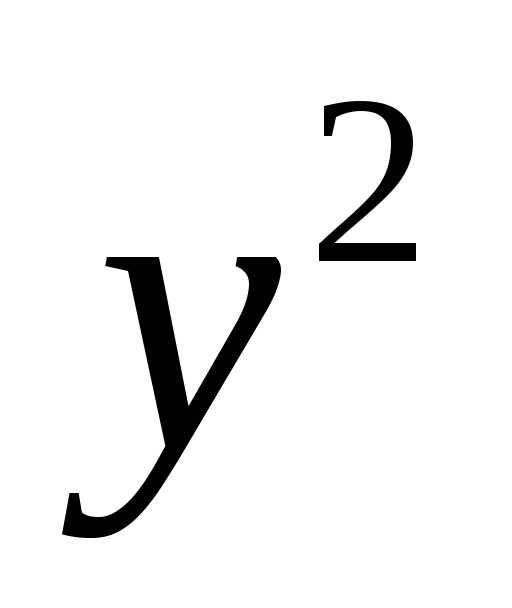
 можно избавиться от произведения
можно избавиться от произведения в уравнении кривой. Напишем формулы
поворота на угол
в уравнении кривой. Напишем формулы
поворота на угол
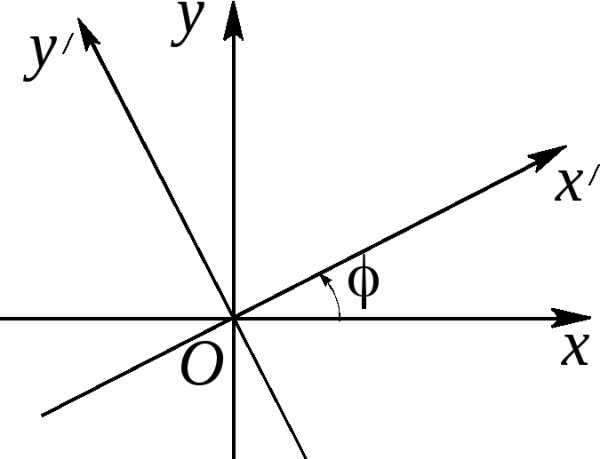
(здесь 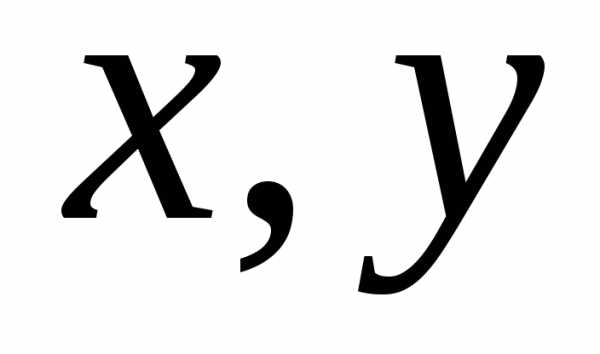 – координаты точки в исходной системе
координат, а
– координаты точки в исходной системе
координат, а – координаты той же точки в системе
координат, повернутой на угол
– координаты той же точки в системе
координат, повернутой на угол
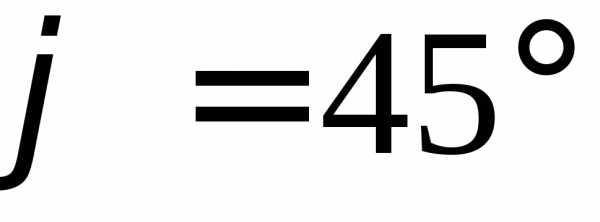 получаем прямые и обратные формулы:
получаем прямые и обратные формулы: 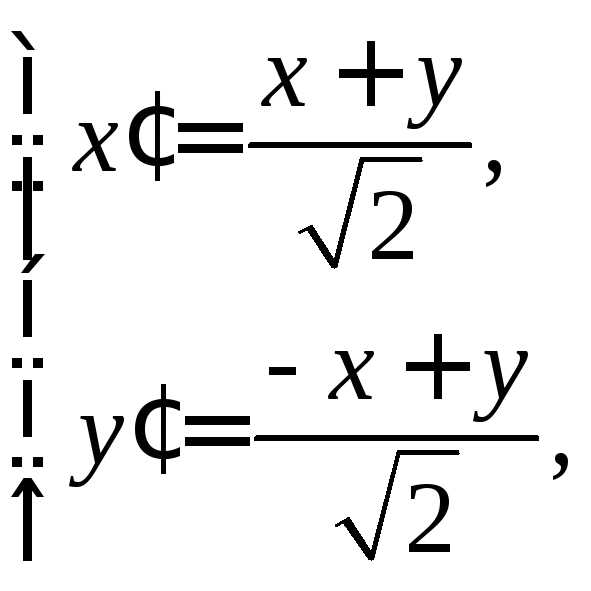
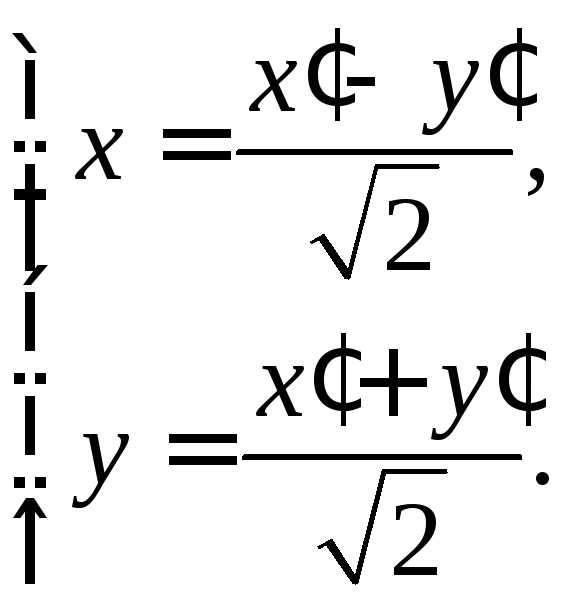
Подставим обратные формулы в уравнение кривой:
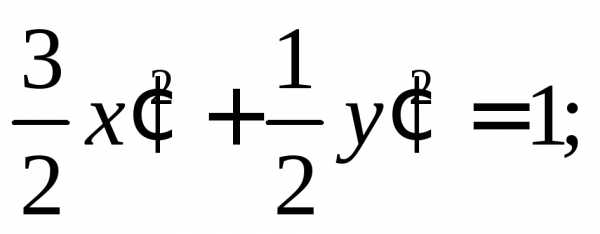
Следовательно, 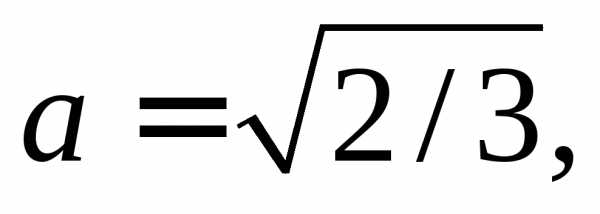
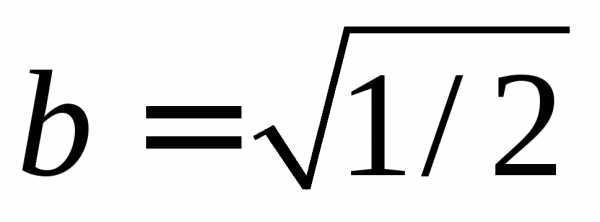 .
Отсюда
.
Отсюда
)
Рис. 5.30
. Рисуем оси эллипса, находим отрезки и
и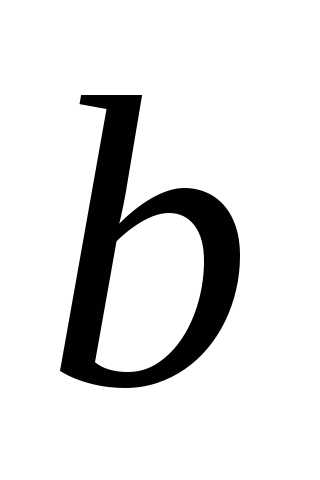 (его полуоси). Далее строим отрезок(рис. 5.34) и фокусы
(его полуоси). Далее строим отрезок(рис. 5.34) и фокусы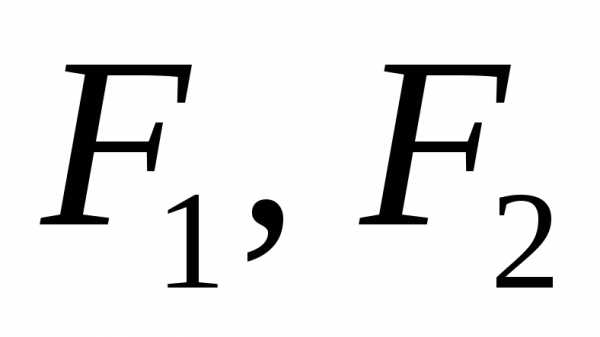 эллипса.
эллипса.Задача 4. Установить, что уравнение
определяет эллипс, найти его центр и полуоси.
Решение. Преобразуем это уравнение:
, или
, или
 .
.
Положим 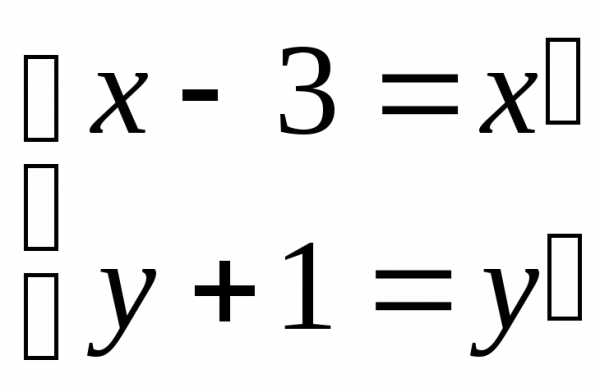 и уравнение примет вид
и уравнение примет вид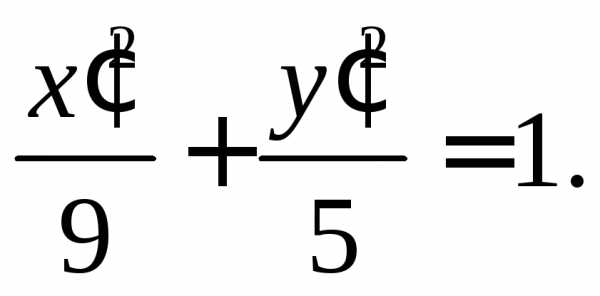 Это уравнение эллипса с полуосями
Это уравнение эллипса с полуосями и
и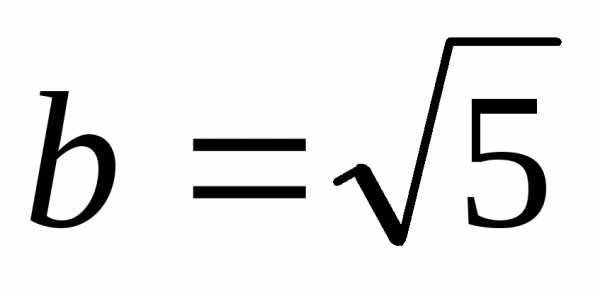 .
.
Задача
5. Установить, что уравнение 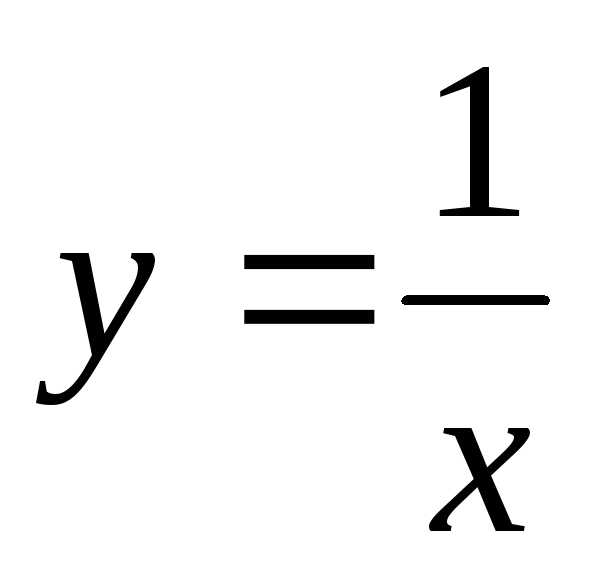 определяет гиперболу, найти ее центр и
полуоси.
определяет гиперболу, найти ее центр и
полуоси.
Подберём
угол  ,
после поворота на который уравнение
кривой не будет содержать произведения
переменных
,
после поворота на который уравнение
кривой не будет содержать произведения
переменных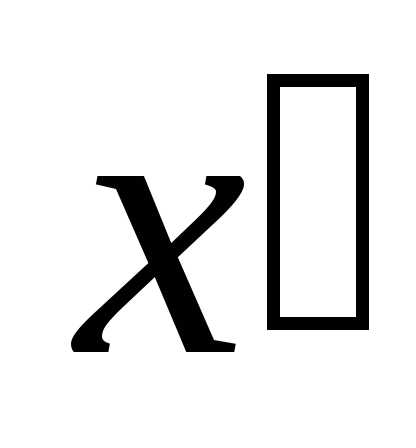 и
и .
Подставим формулы поворота в заданное
уравнение,
которое лучше переписать в виде
.
Подставим формулы поворота в заданное
уравнение,
которое лучше переписать в виде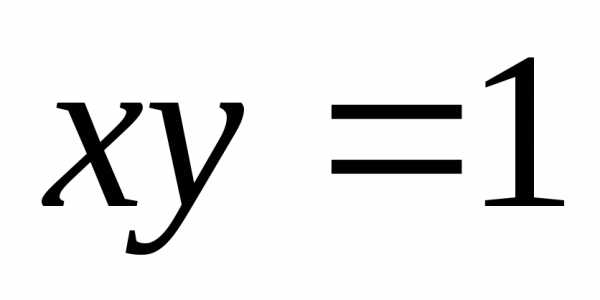 :
:
,
,
.
Найдём
такой угол  ,
чтобы в последнем уравнении не содержалось
слагаемое
,
чтобы в последнем уравнении не содержалось
слагаемое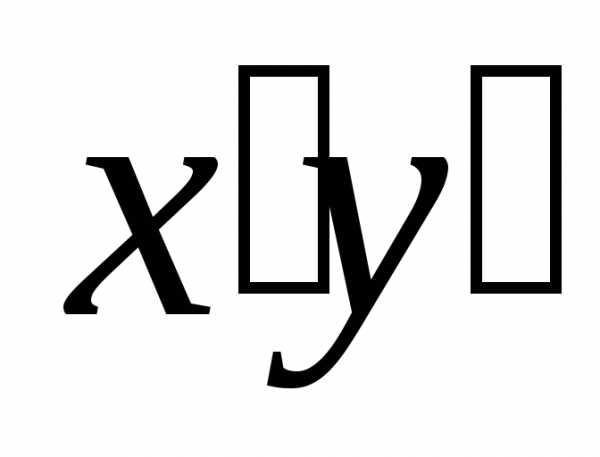 .
Достаточно положить,,
то есть
.
Достаточно положить,,
то есть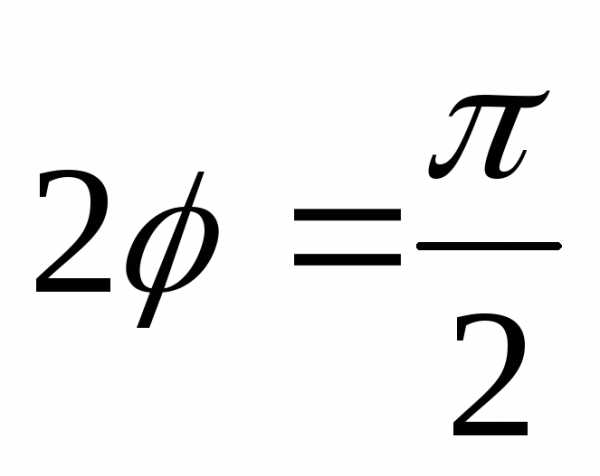 ,
,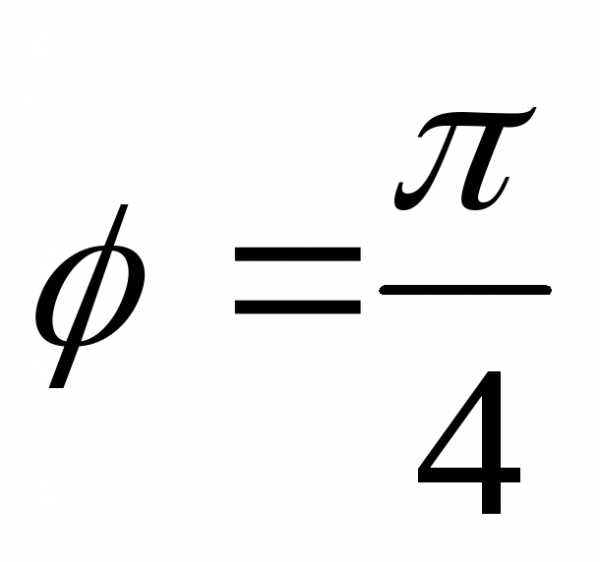 .
.
Тогда преобразование примет вид
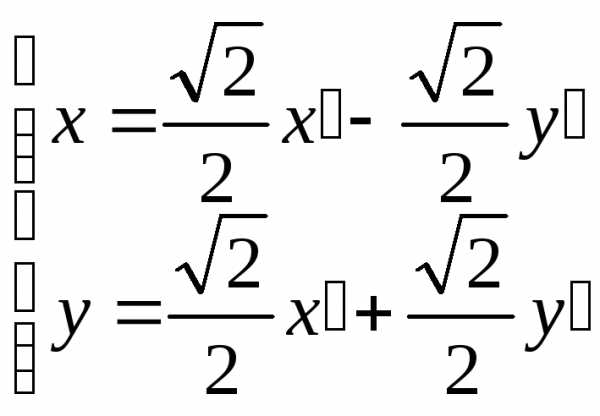
—
поворот против часовой стрелки вокруг
точки  ,
а уравнение кривой (5.28) в новой системе
координат:
,
а уравнение кривой (5.28) в новой системе
координат:
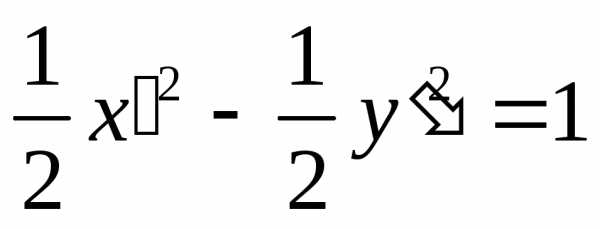
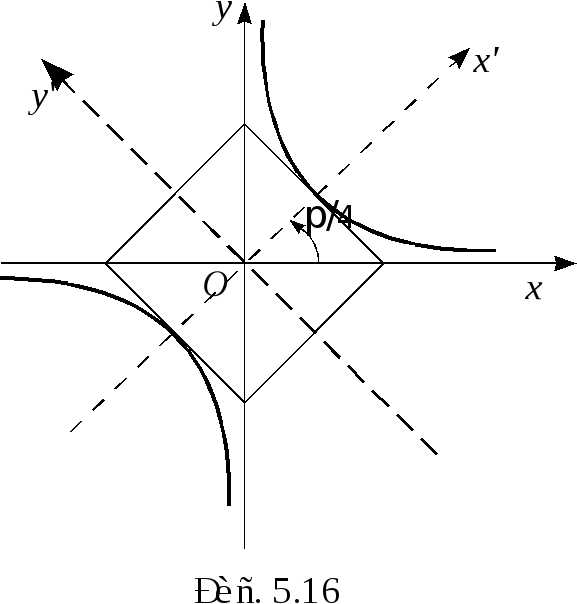
—
это уравнение гиперболы с полуосями и
центром в точке 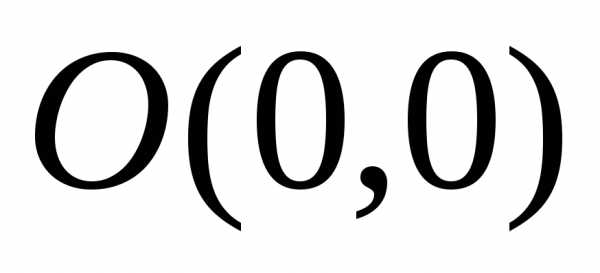 (рис. 5.16).
(рис. 5.16).
studfiles.net
§ 2. Приведение к каноническому виду уравнения кривой второго порядка
Общее уравнение кривой второго порядка имеет вид
причем предполагается, что среди чисел есть хотя бы одно ненулевое.
Существует система координат (называемая канонической), в которой уравнение кривой второго порядка имеет вид, приведенный в таблице (канонический вид).
| эллипс |
| гипербола |
| парабола |
| мнимый эллипс (эта “кривая” не имеет действительных точек) |
| на действительной плоскости “кривая” имеет лишь одну точку |
| две пересекающиеся прямые |
две параллельные прямые | |
| две совпадающие прямые |
две мнимые параллельные прямые (“кривая” не имеет ни одной действительной точки) |
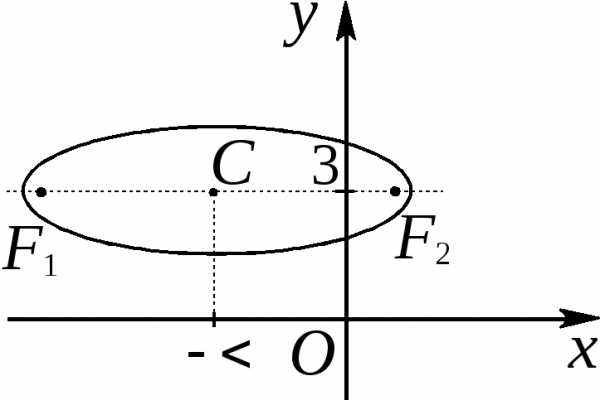
Задача 1. Изобразить кривую, найти ее характеристики:
Р
 и по
и по Следовательно, данная кривая является
эллипсом. Его центр:Полуоси:
Следовательно, данная кривая является
эллипсом. Его центр:Полуоси:
 Для нахождения координат фокусов находим
параметр
Для нахождения координат фокусов находим
параметр (половину расстояния между фокусами):Отсюда получаем фокусы:Эксцентриситет:
(половину расстояния между фокусами):Отсюда получаем фокусы:Эксцентриситет: Задача 2.
Составить
уравнение гиперболы с асимптотами
касающейся оси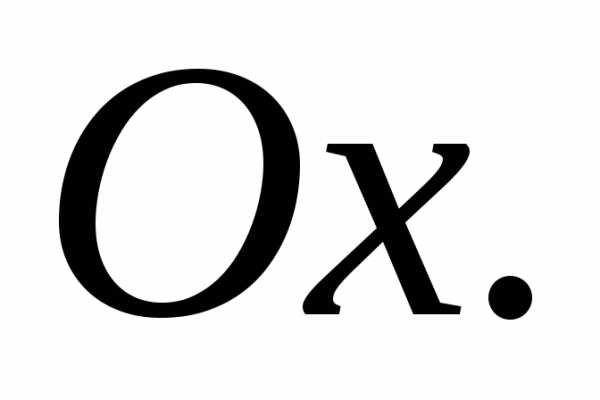
Р

 имеют видСледовательно, центр гиперболы имеет
координаты
имеют видСледовательно, центр гиперболы имеет
координаты  и
Нарисуем гиперболу, учитывая, что она
касается оси абсцисс.
и
Нарисуем гиперболу, учитывая, что она
касается оси абсцисс.
Из
рисунка видно, что  Так както
Так както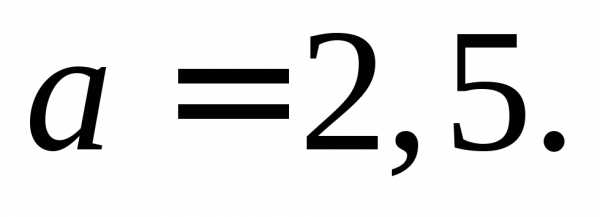 Так как действительная ось гиперболы
параллельна оси
Так как действительная ось гиперболы
параллельна оси то в правой части уравнения будет
то в правой части уравнения будет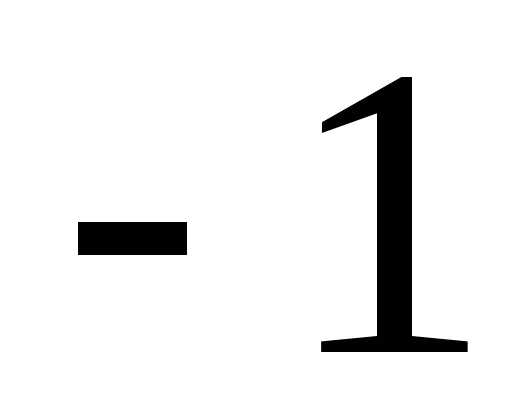 вместо
вместо Отсюда получаем уравнение:
Отсюда получаем уравнение:
Задача 3. Найти площадь области, ограниченной кривой
Решение. В случае, когда коэффициенты при 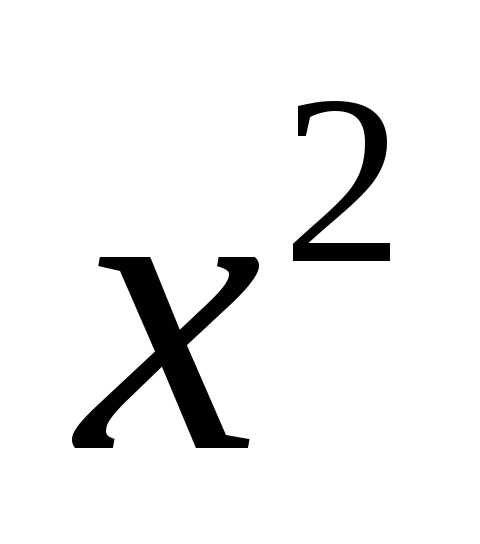 и
и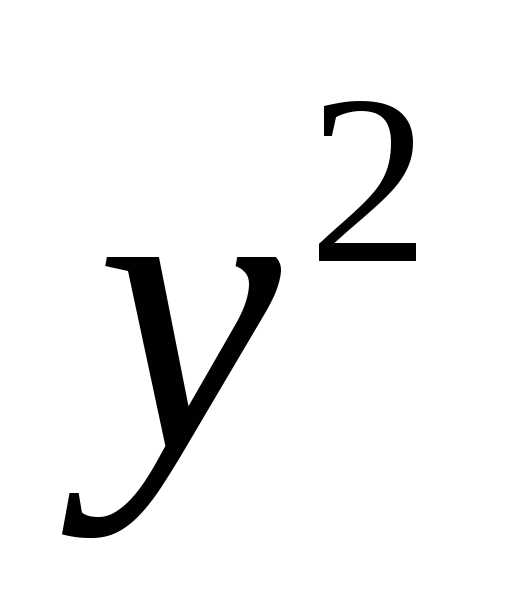 равны друг другу, то поворотом системы
координат на угол в
равны друг другу, то поворотом системы
координат на угол в можно избавиться от произведения
можно избавиться от произведения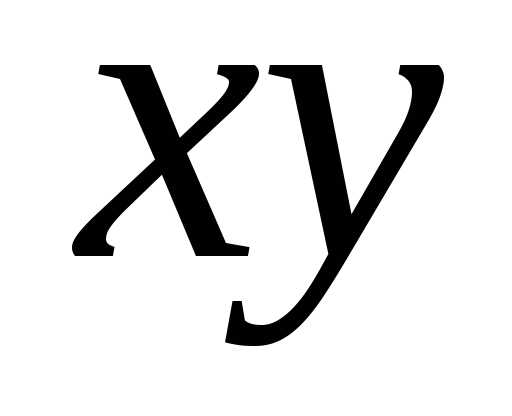 в уравнении кривой. Напишем формулы
поворота на угол
в уравнении кривой. Напишем формулы
поворота на угол
(здесь 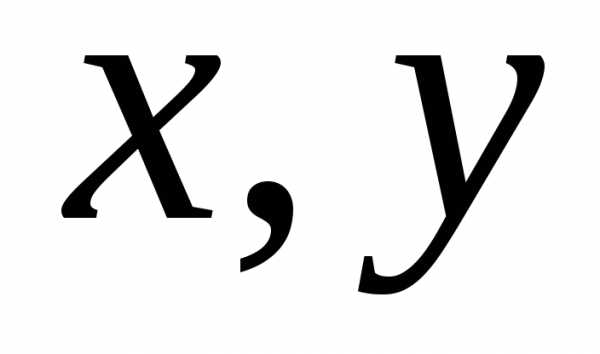 – координаты точки в исходной системе
координат, а
– координаты точки в исходной системе
координат, а – координаты той же точки в системе
координат, повернутой на угол
– координаты той же точки в системе
координат, повернутой на угол .
При
.
При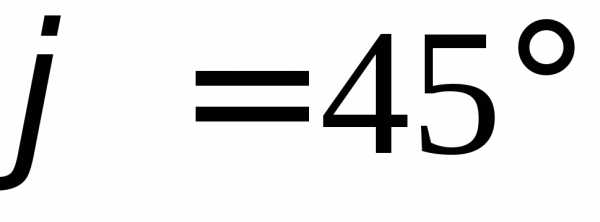 получаем прямые и обратные формулы:
получаем прямые и обратные формулы:
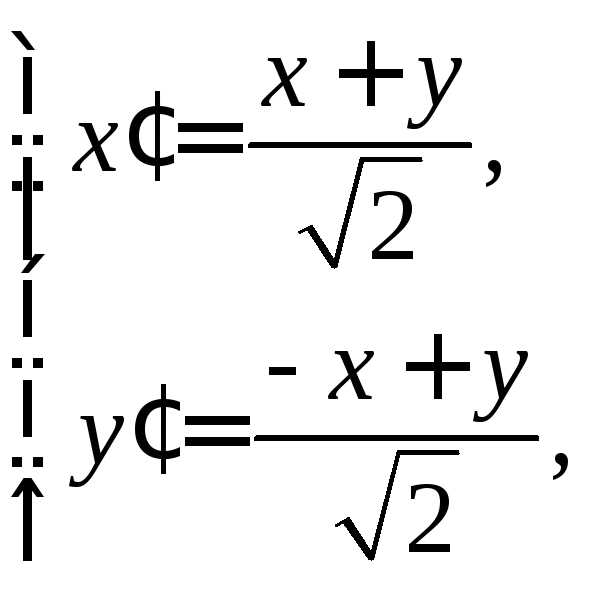
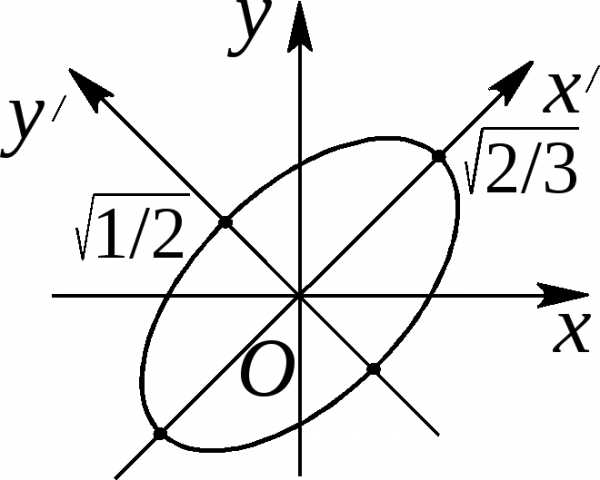

Подставим обратные формулы в уравнение кривой:

Следовательно, 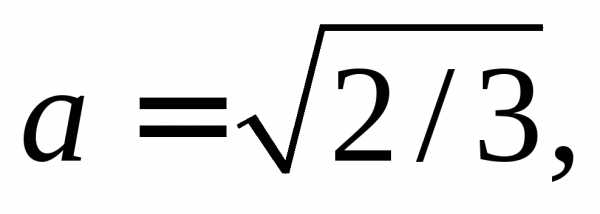
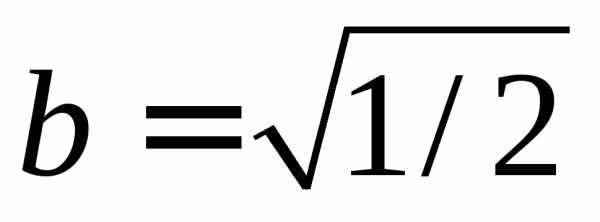 .
Отсюда
.
Отсюда
)
Рис. 5.30
. Рисуем оси эллипса, находим отрезки и
и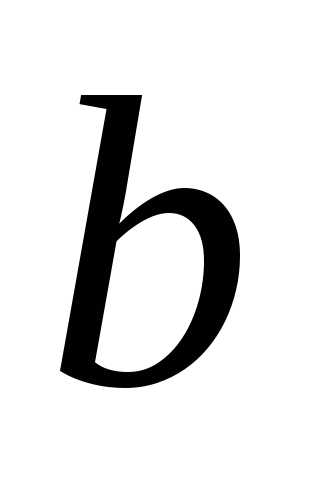 (его полуоси). Далее строим отрезок(рис. 5.34) и фокусы
(его полуоси). Далее строим отрезок(рис. 5.34) и фокусы эллипса.
эллипса.Задача 4. Установить, что уравнение
определяет эллипс, найти его центр и полуоси.
Решение. Преобразуем это уравнение:
, или
, или
 .
.
Положим  и уравнение примет вид
и уравнение примет вид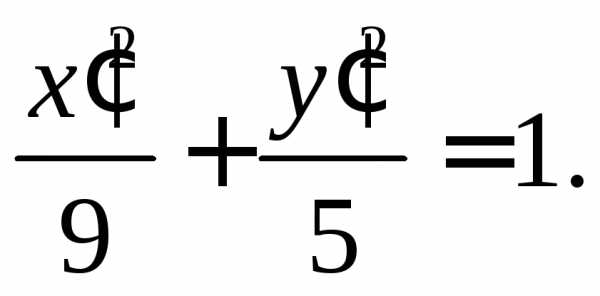 Это уравнение эллипса с полуосями
Это уравнение эллипса с полуосями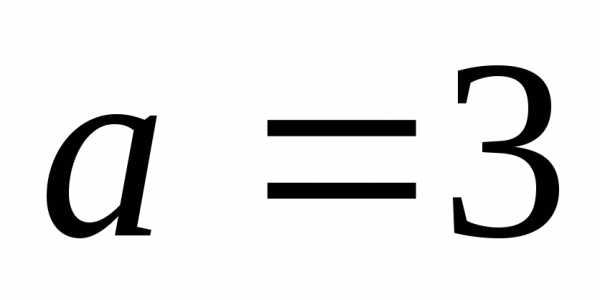 и
и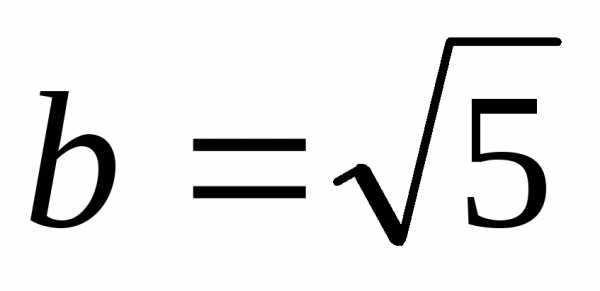 .
.
Задача
5. Установить, что уравнение 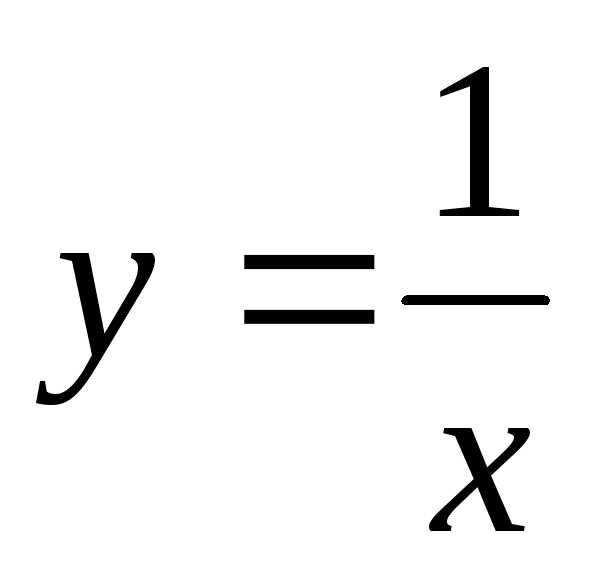 определяет гиперболу, найти ее центр и
полуоси.
определяет гиперболу, найти ее центр и
полуоси.
Подберём
угол  ,
после поворота на который уравнение
кривой не будет содержать произведения
переменных
,
после поворота на который уравнение
кривой не будет содержать произведения
переменных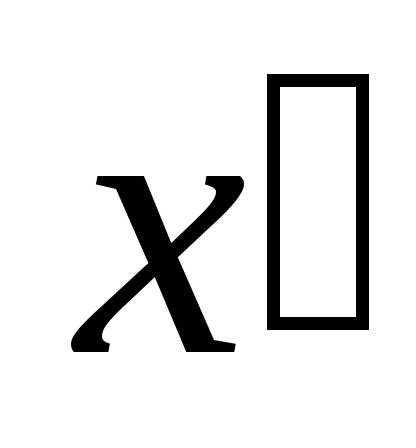 и
и .
Подставим формулы поворота в заданное
уравнение
.
Подставим формулы поворота в заданное
уравнение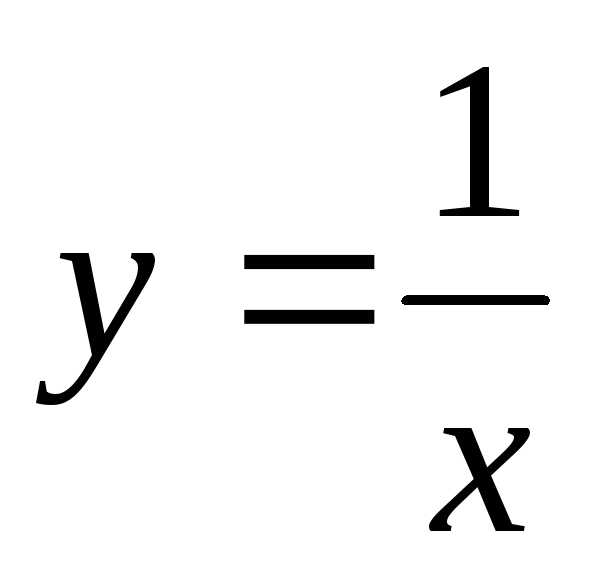 ,
которое лучше переписать в виде
,
которое лучше переписать в виде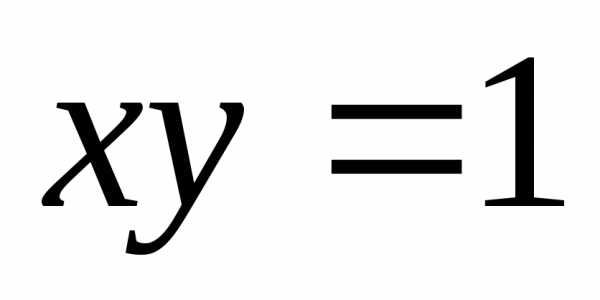 :
:
,
,
.
Найдём
такой угол  ,
чтобы в последнем уравнении не содержалось
слагаемое
,
чтобы в последнем уравнении не содержалось
слагаемое .
Достаточно положить,,
то есть
.
Достаточно положить,,
то есть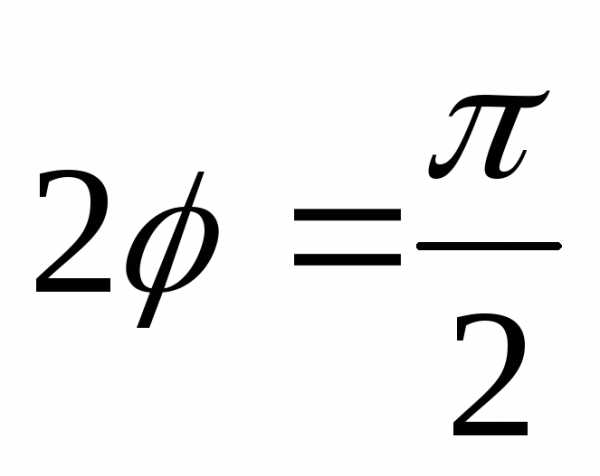 ,
,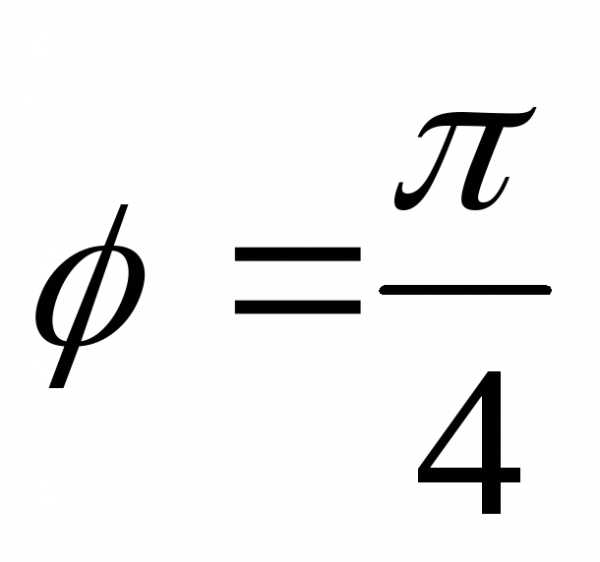 .
.
Тогда преобразование примет вид
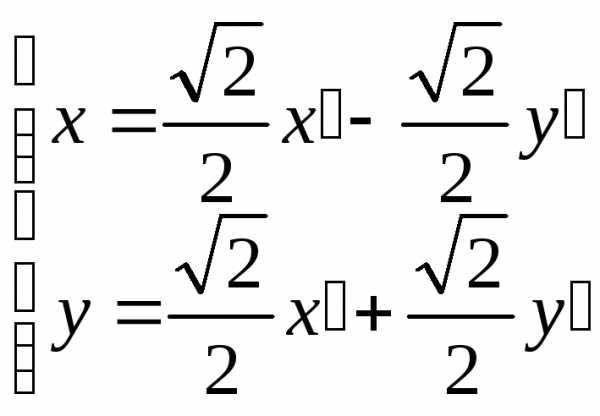
—
поворот против часовой стрелки вокруг
точки  ,
а уравнение кривой (5.28) в новой системе
координат:
,
а уравнение кривой (5.28) в новой системе
координат:
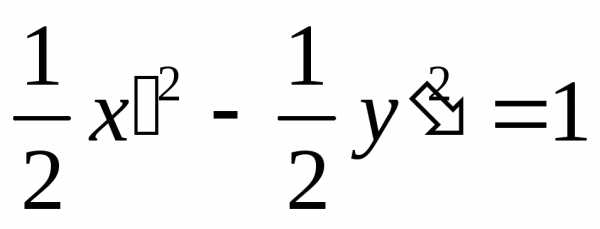
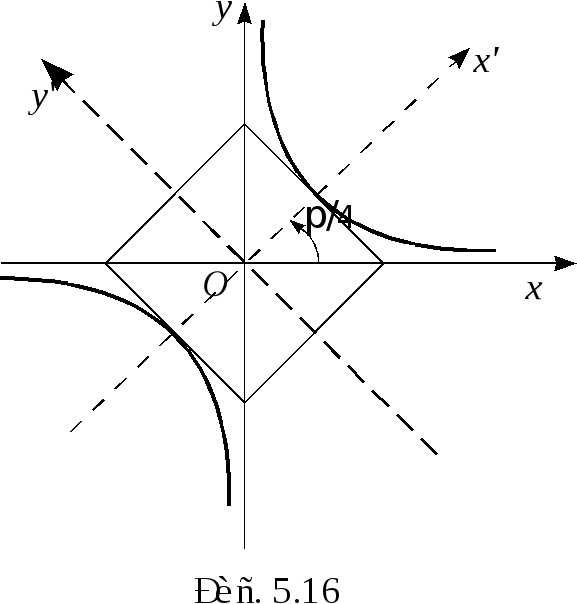
—
это уравнение гиперболы с полуосями и
центром в точке  (рис. 5.16).
(рис. 5.16).
studfiles.net
§ 2. Приведение к каноническому виду уравнения кривой второго порядка
Общее уравнение кривой второго порядка имеет вид
причем предполагается, что среди чисел есть хотя бы одно ненулевое.
Существует система координат (называемая канонической), в которой уравнение кривой второго порядка имеет вид, приведенный в таблице (канонический вид).
| эллипс |
| гипербола |
| парабола |
| мнимый эллипс (эта “кривая” не имеет действительных точек) |
| на действительной плоскости “кривая” имеет лишь одну точку |
| две пересекающиеся прямые |
две параллельные прямые | |
| две совпадающие прямые |
две мнимые параллельные прямые (“кривая” не имеет ни одной действительной точки) |
Задача 1. Изобразить кривую, найти ее характеристики:
Р
 и по
и по Следовательно, данная кривая является
эллипсом. Его центр:Полуоси:
Следовательно, данная кривая является
эллипсом. Его центр:Полуоси:
 Для нахождения координат фокусов находим
параметр
Для нахождения координат фокусов находим
параметр (половину расстояния между фокусами):Отсюда получаем фокусы:Эксцентриситет:
(половину расстояния между фокусами):Отсюда получаем фокусы:Эксцентриситет: Задача 2.
Составить
уравнение гиперболы с асимптотами
касающейся оси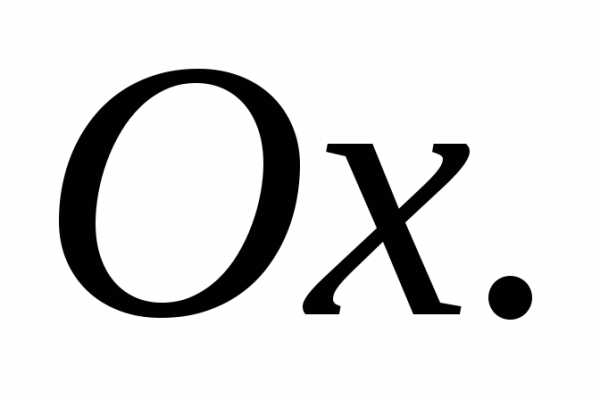
Р
 имеют видСледовательно, центр гиперболы имеет
координаты
имеют видСледовательно, центр гиперболы имеет
координаты  и
Нарисуем гиперболу, учитывая, что она
касается оси абсцисс.
и
Нарисуем гиперболу, учитывая, что она
касается оси абсцисс.
Из
рисунка видно, что  Так както
Так както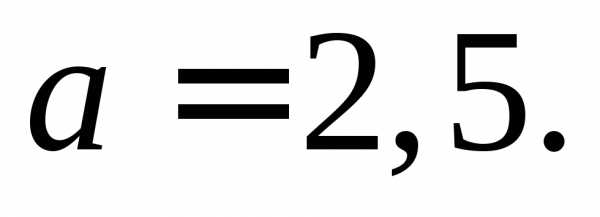 Так как действительная ось гиперболы
параллельна оси
Так как действительная ось гиперболы
параллельна оси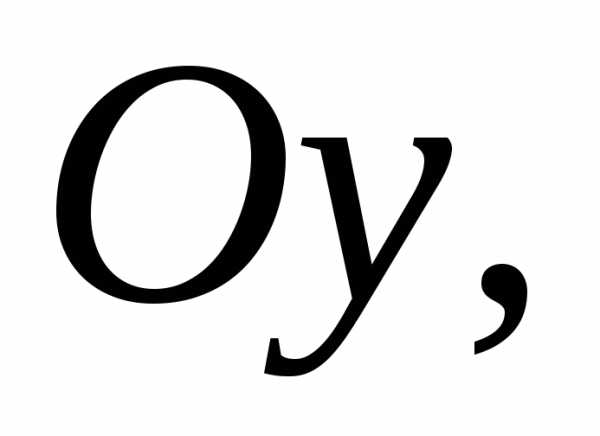 то в правой части уравнения будет
то в правой части уравнения будет вместо
вместо Отсюда получаем уравнение:
Отсюда получаем уравнение:
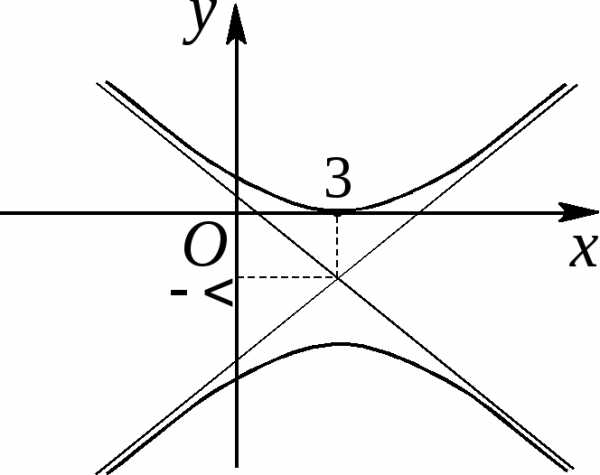
Задача 3. Найти площадь области, ограниченной кривой
Решение. В случае, когда коэффициенты при 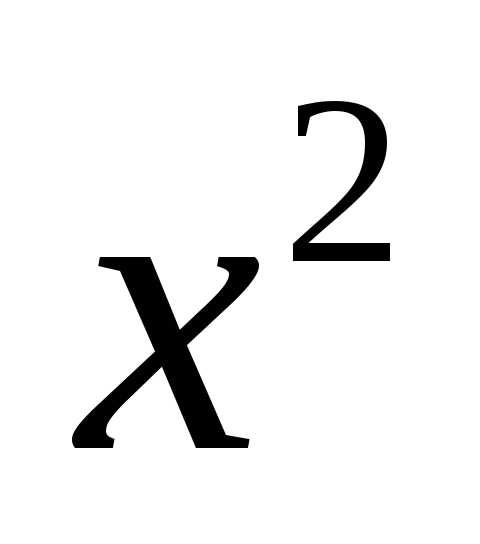 и
и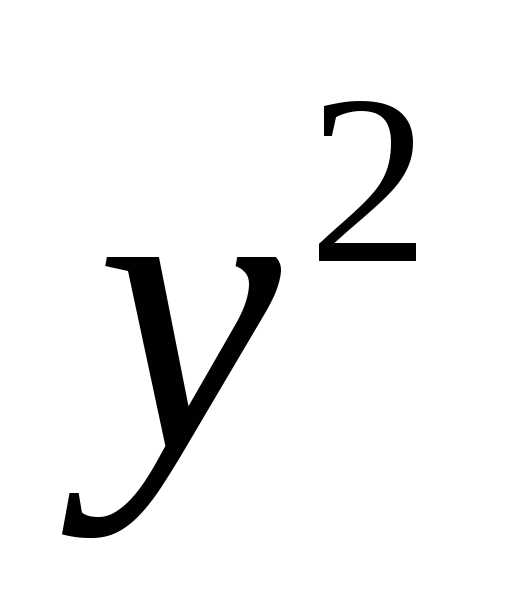 равны друг другу, то поворотом системы
координат на угол в
равны друг другу, то поворотом системы
координат на угол в можно избавиться от произведения
можно избавиться от произведения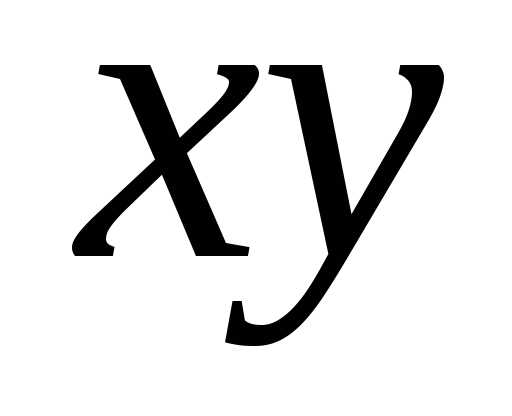 в уравнении кривой. Напишем формулы
поворота на угол
в уравнении кривой. Напишем формулы
поворота на угол
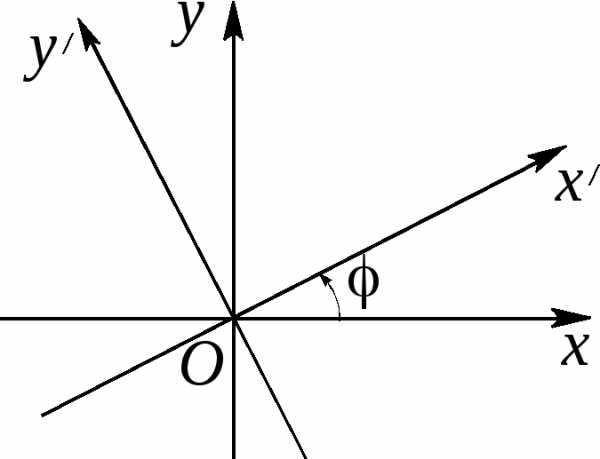
(здесь 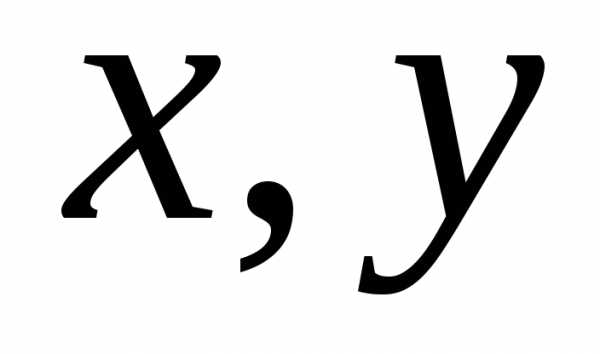 – координаты точки в исходной системе
координат, а
– координаты точки в исходной системе
координат, а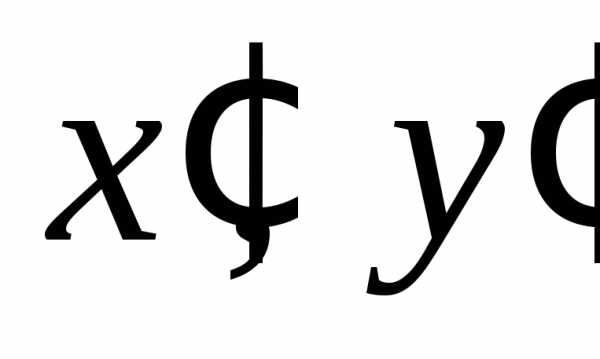 – координаты той же точки в системе
координат, повернутой на угол
– координаты той же точки в системе
координат, повернутой на угол .
При
.
При получаем прямые и обратные формулы:
получаем прямые и обратные формулы:
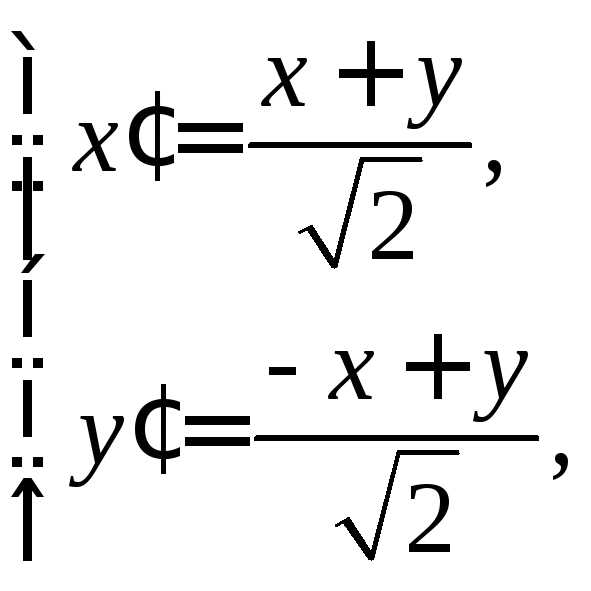
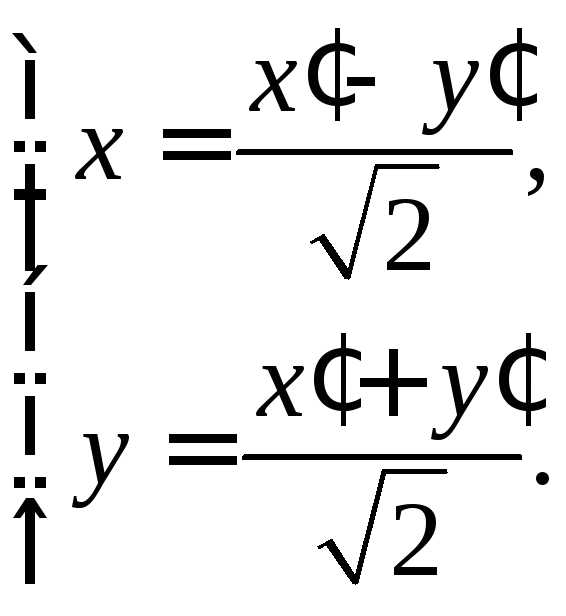
Подставим обратные формулы в уравнение кривой:

Следовательно, 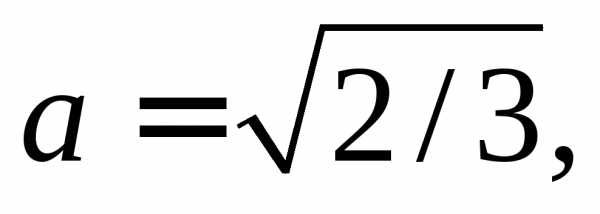
 .
Отсюда
.
Отсюда
)
Рис. 5.30
. Рисуем оси эллипса, находим отрезки и
и (его полуоси). Далее строим отрезок(рис. 5.34) и фокусы
(его полуоси). Далее строим отрезок(рис. 5.34) и фокусы эллипса.
эллипса.Задача 4. Установить, что уравнение
определяет эллипс, найти его центр и полуоси.
Решение. Преобразуем это уравнение:
, или
, или
 .
.
Положим 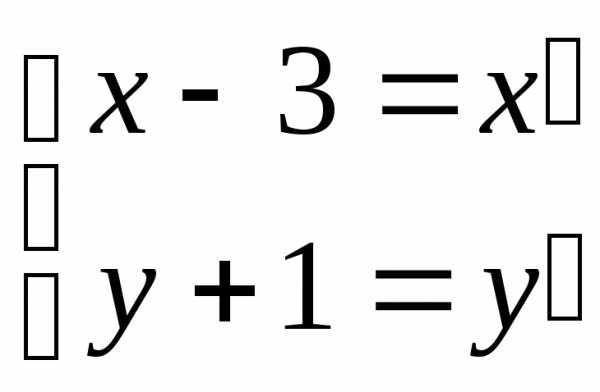 и уравнение примет вид
и уравнение примет вид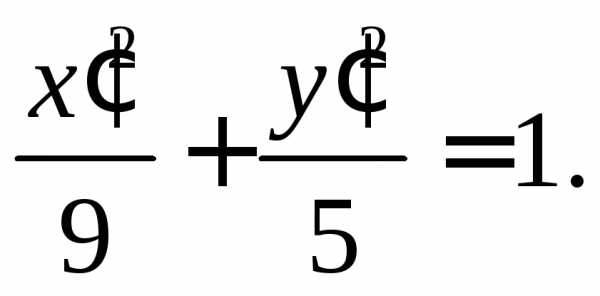 Это уравнение эллипса с полуосями
Это уравнение эллипса с полуосями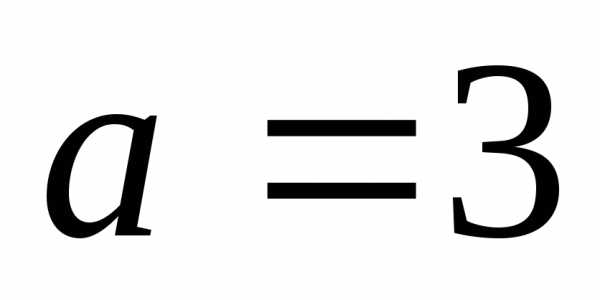 и
и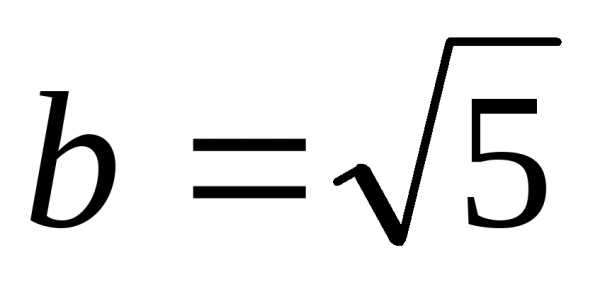 .
.
Задача
5. Установить, что уравнение 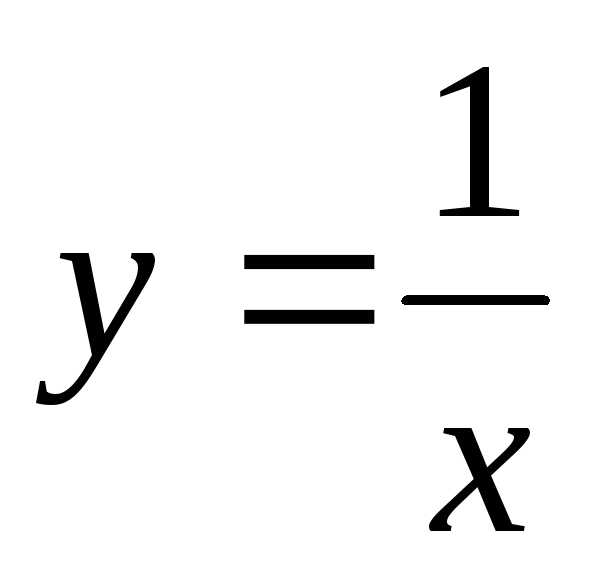 определяет гиперболу, найти ее центр и
полуоси.
определяет гиперболу, найти ее центр и
полуоси.
Подберём
угол  ,
после поворота на который уравнение
кривой не будет содержать произведения
переменных
,
после поворота на который уравнение
кривой не будет содержать произведения
переменных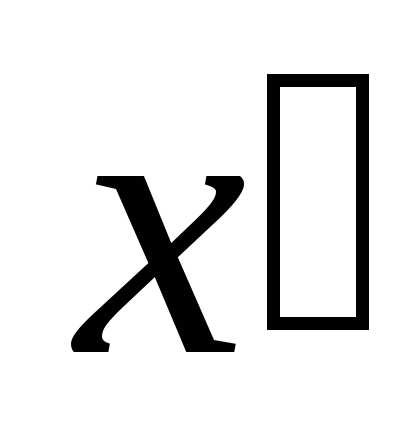 и
и .
Подставим формулы поворота в заданное
уравнение
.
Подставим формулы поворота в заданное
уравнение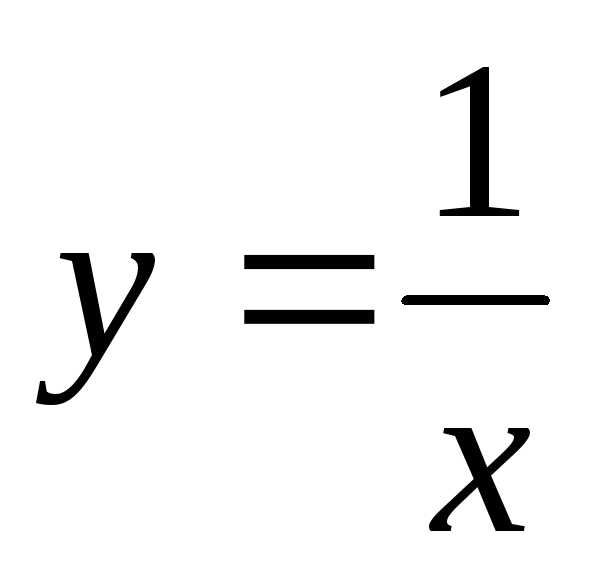 ,
которое лучше переписать в виде
,
которое лучше переписать в виде :
:
,
,
.
Найдём
такой угол  ,
чтобы в последнем уравнении не содержалось
слагаемое
,
чтобы в последнем уравнении не содержалось
слагаемое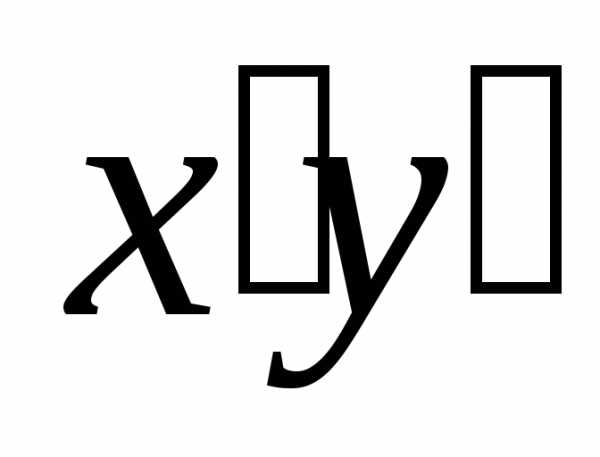 .
Достаточно положить,,
то есть
.
Достаточно положить,,
то есть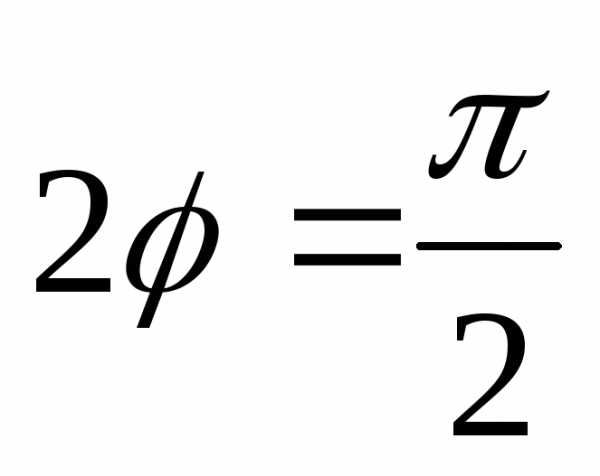 ,
,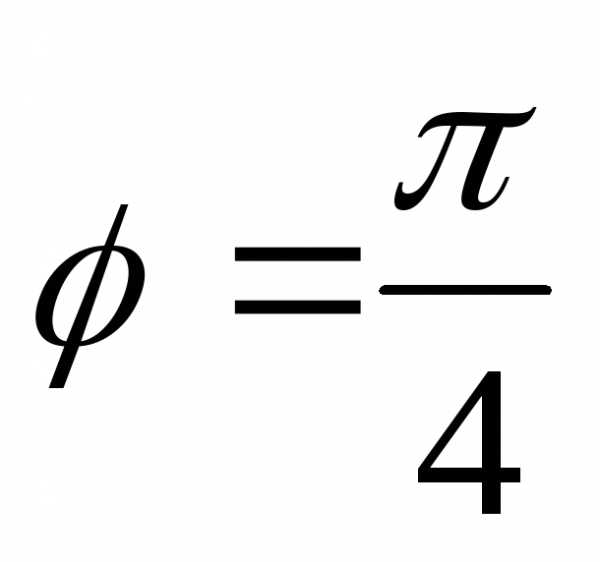 .
.
Тогда преобразование примет вид
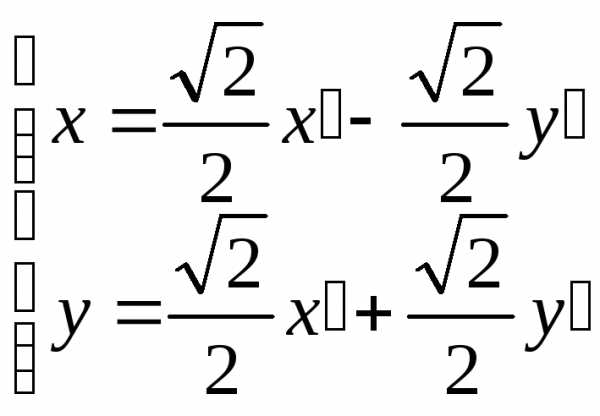
—
поворот против часовой стрелки вокруг
точки  ,
а уравнение кривой (5.28) в новой системе
координат:
,
а уравнение кривой (5.28) в новой системе
координат:
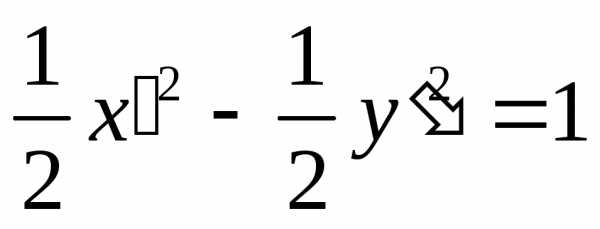
—
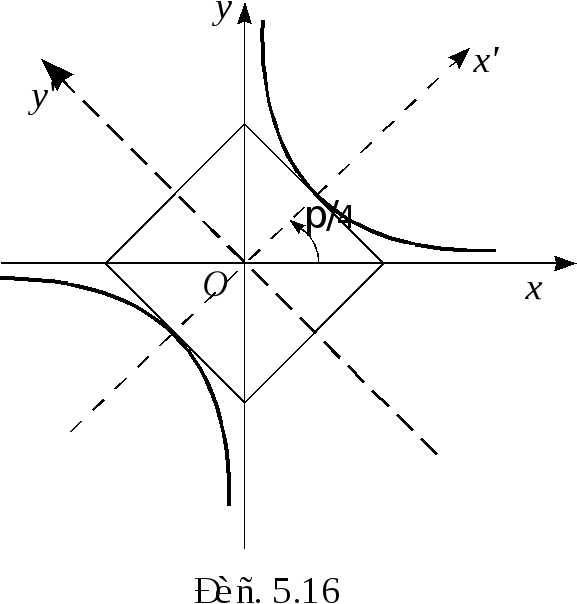
это уравнение гиперболы с полуосями и
центром в точке 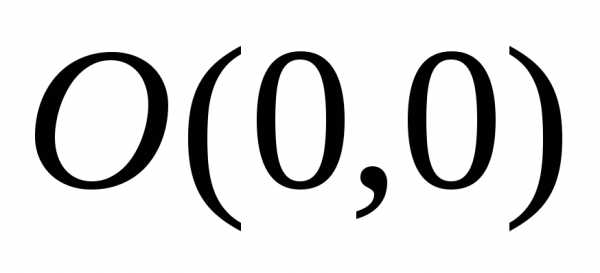 (рис. 5.16).
(рис. 5.16).
studfiles.net
§ 2. Приведение к каноническому виду уравнения кривой второго порядка
Общее уравнение кривой второго порядка имеет вид
причем предполагается, что среди чисел есть хотя бы одно ненулевое.
Существует система координат (называемая канонической), в которой уравнение кривой второго порядка имеет вид, приведенный в таблице (канонический вид).
| эллипс |
| гипербола |
| парабола |
| мнимый эллипс (эта “кривая” не имеет действительных точек) |
| на действительной плоскости “кривая” имеет лишь одну точку |
| две пересекающиеся прямые |
две параллельные прямые | |
| две совпадающие прямые |
две мнимые параллельные прямые (“кривая” не имеет ни одной действительной точки) |
Задача 1. Изобразить кривую, найти ее характеристики:
Р

 и по
и по Следовательно, данная кривая является
эллипсом. Его центр:Полуоси:
Следовательно, данная кривая является
эллипсом. Его центр:Полуоси: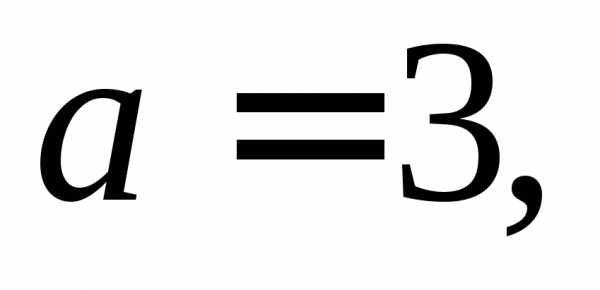
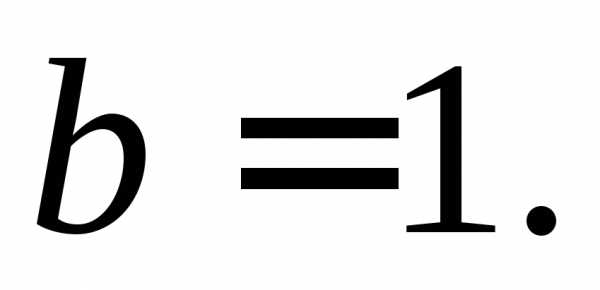 Для нахождения координат фокусов находим
параметр
Для нахождения координат фокусов находим
параметр (половину расстояния между фокусами):Отсюда получаем фокусы:Эксцентриситет:
(половину расстояния между фокусами):Отсюда получаем фокусы:Эксцентриситет: Задача 2.
Составить
уравнение гиперболы с асимптотами
касающейся оси
Р

 имеют видСледовательно, центр гиперболы имеет
координаты
имеют видСледовательно, центр гиперболы имеет
координаты  и
Нарисуем гиперболу, учитывая, что она
касается оси абсцисс.
и
Нарисуем гиперболу, учитывая, что она
касается оси абсцисс.
Из
рисунка видно, что
Так както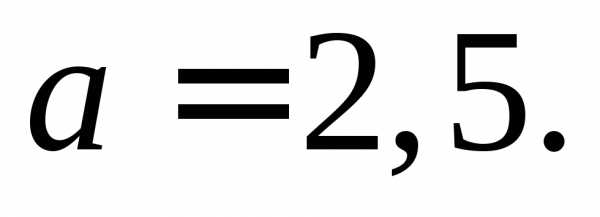 Так как действительная ось гиперболы
параллельна оси
Так как действительная ось гиперболы
параллельна оси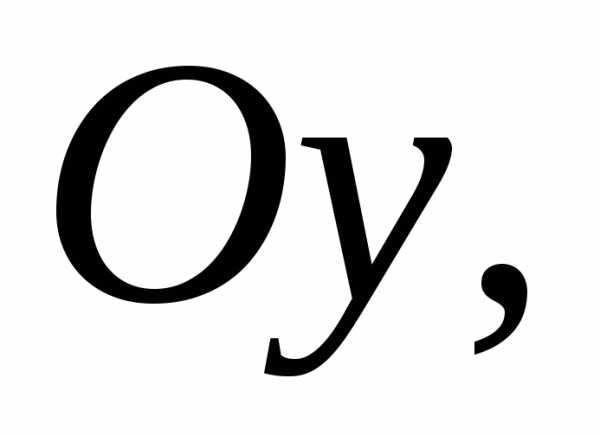 то в правой части уравнения будет
то в правой части уравнения будет вместо
вместо Отсюда получаем уравнение:
Отсюда получаем уравнение:
Задача 3. Найти площадь области, ограниченной кривой
Решение. В случае, когда коэффициенты при 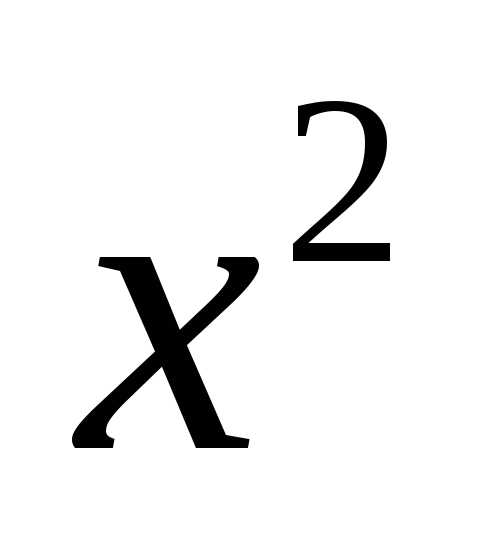 и
и равны друг другу, то поворотом системы
координат на угол в
равны друг другу, то поворотом системы
координат на угол в можно избавиться от произведения
можно избавиться от произведения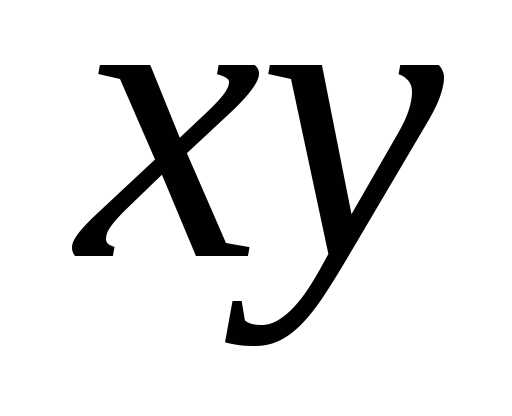 в уравнении кривой. Напишем формулы
поворота на угол
в уравнении кривой. Напишем формулы
поворота на угол
(здесь 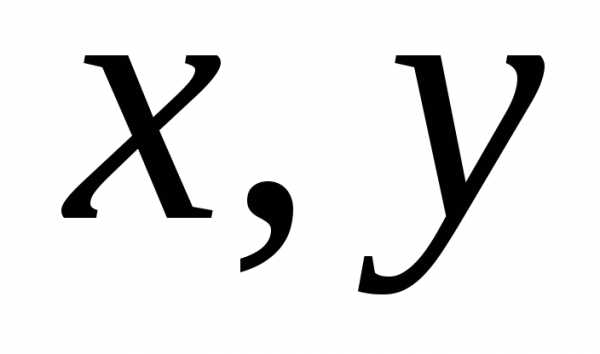 – координаты точки в исходной системе
координат, а
– координаты точки в исходной системе
координат, а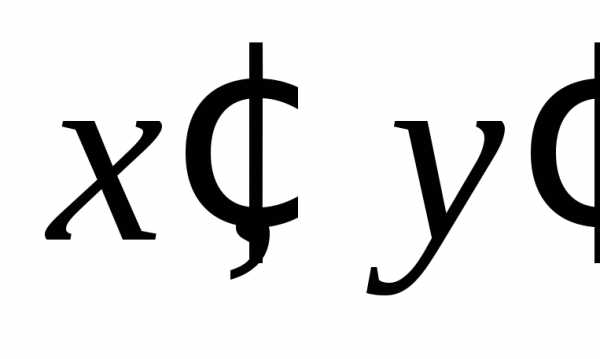 – координаты той же точки в системе
координат, повернутой на угол
– координаты той же точки в системе
координат, повернутой на угол .
При
.
При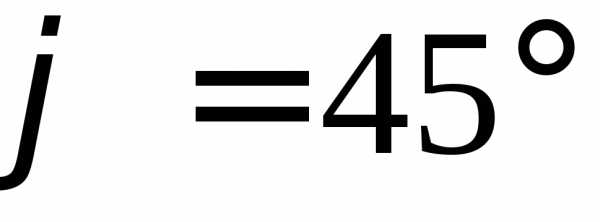 получаем прямые и обратные формулы:
получаем прямые и обратные формулы:
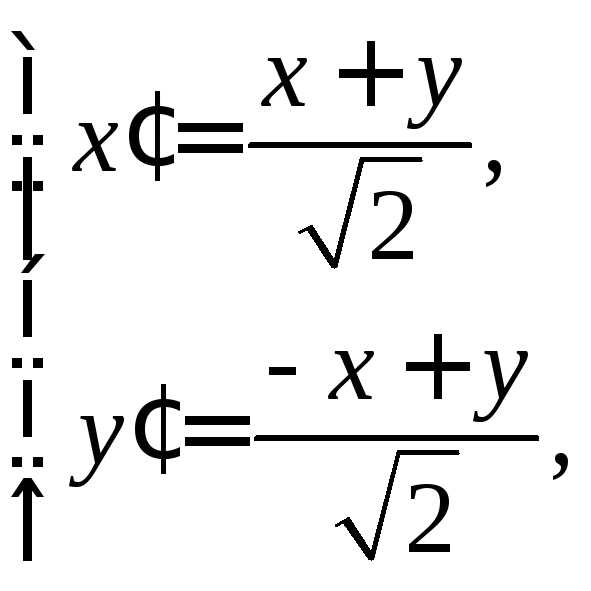

Подставим обратные формулы в уравнение кривой:
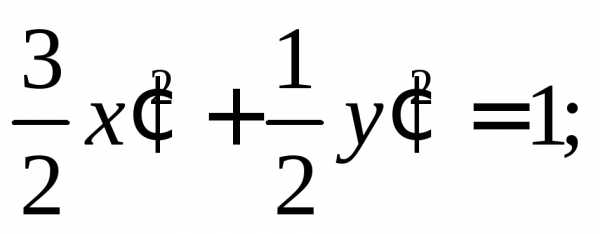
Следовательно, 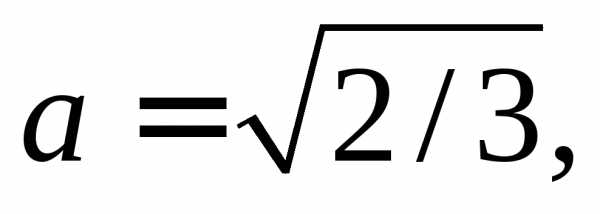
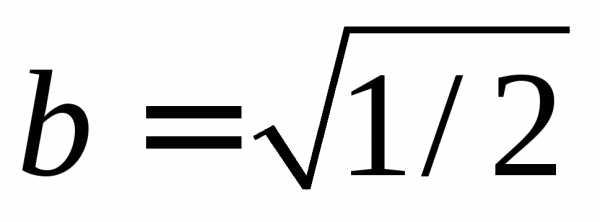 .
Отсюда
.
Отсюда
)
Рис. 5.30
. Рисуем оси эллипса, находим отрезки и
и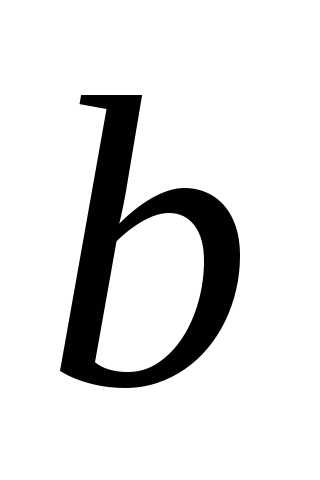 (его полуоси). Далее строим отрезок(рис. 5.34) и фокусы
(его полуоси). Далее строим отрезок(рис. 5.34) и фокусы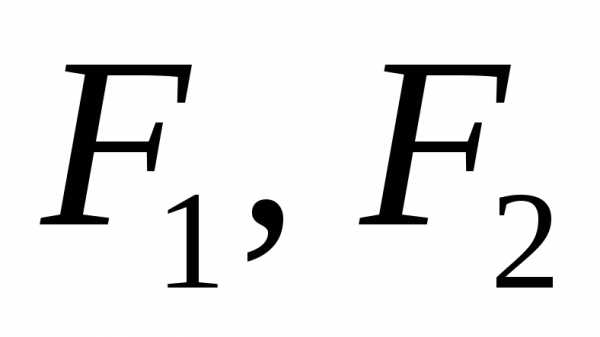 эллипса.
эллипса.Задача 4. Установить, что уравнение
определяет эллипс, найти его центр и полуоси.
Решение. Преобразуем это уравнение:
, или
, или
 .
.
Положим 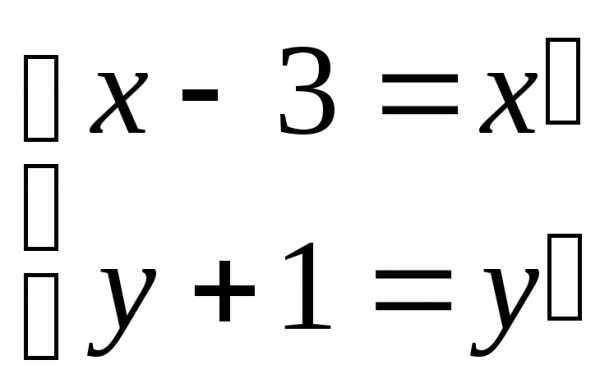 и уравнение примет вид
и уравнение примет вид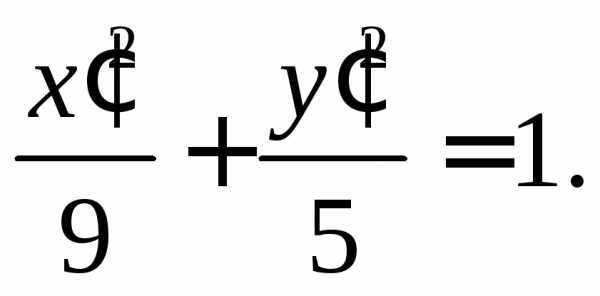 Это уравнение эллипса с полуосями
Это уравнение эллипса с полуосями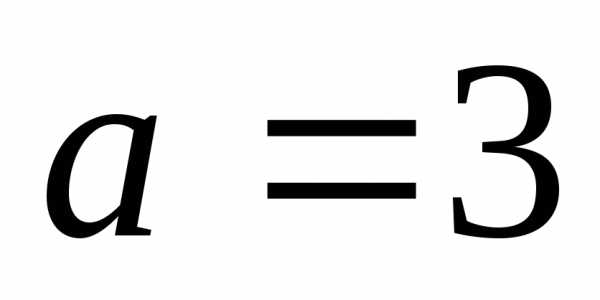 и
и .
.
Задача
5. Установить, что уравнение 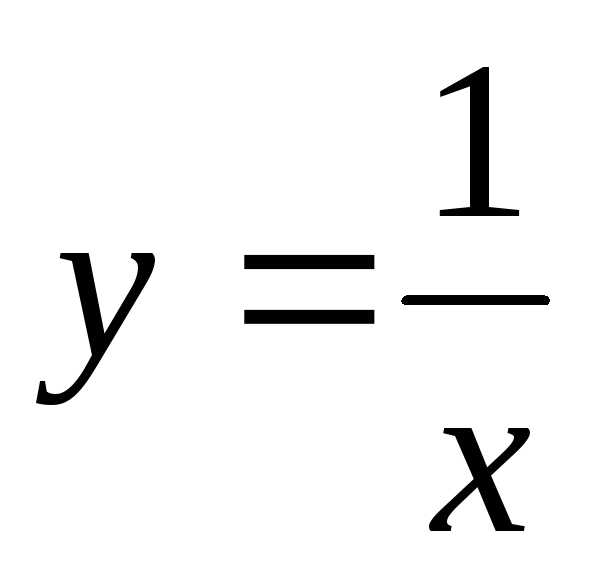 определяет гиперболу, найти ее центр и
полуоси.
определяет гиперболу, найти ее центр и
полуоси.
Подберём
угол  ,
после поворота на который уравнение
кривой не будет содержать произведения
переменных
,
после поворота на который уравнение
кривой не будет содержать произведения
переменных и
и .
Подставим формулы поворота в заданное
уравнение,
которое лучше переписать в виде
.
Подставим формулы поворота в заданное
уравнение,
которое лучше переписать в виде :
:
,
,
.
Найдём
такой угол  ,
чтобы в последнем уравнении не содержалось
слагаемое
,
чтобы в последнем уравнении не содержалось
слагаемое .
Достаточно положить,,
то есть
.
Достаточно положить,,
то есть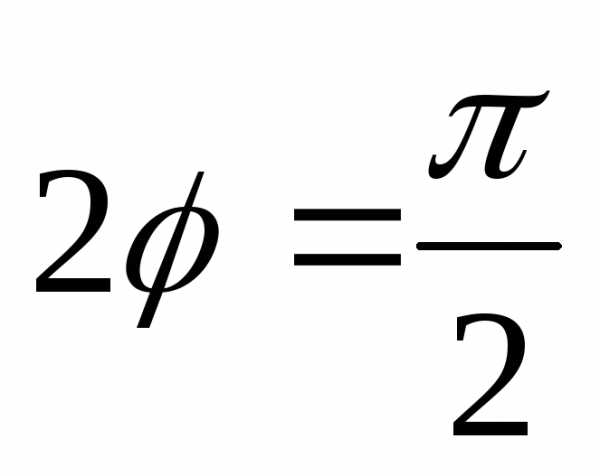 ,
, .
.
Тогда преобразование примет вид
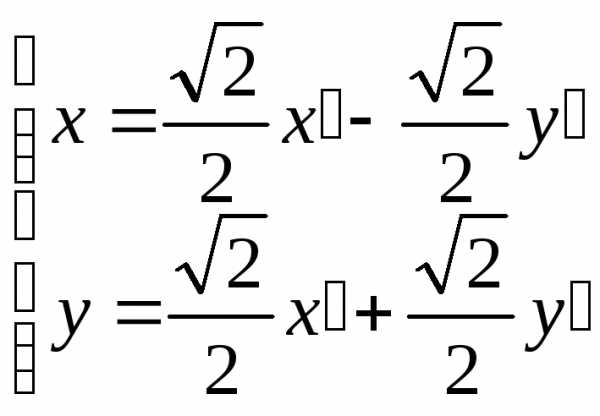
—
поворот против часовой стрелки вокруг
точки  ,
а уравнение кривой (5.28) в новой системе
координат:
,
а уравнение кривой (5.28) в новой системе
координат:
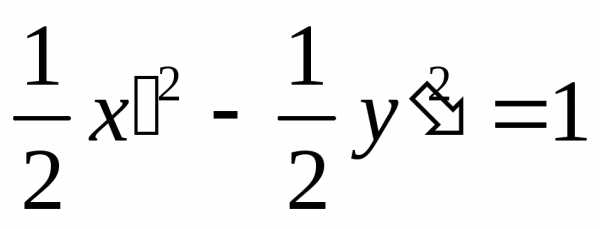
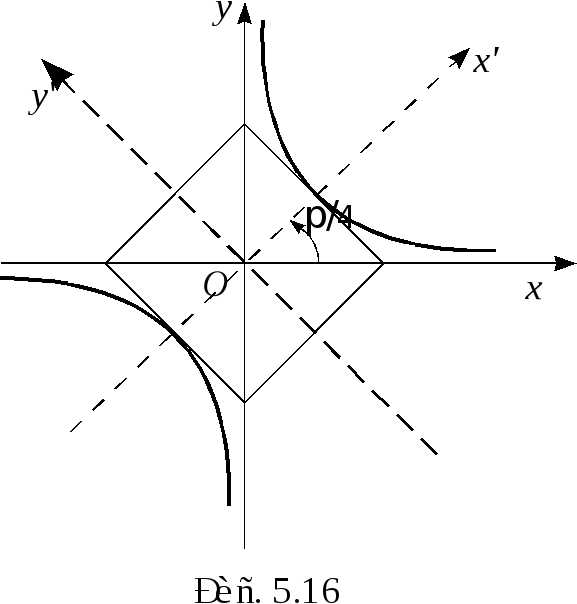
—
это уравнение гиперболы с полуосями и
центром в точке  (рис. 5.16).
(рис. 5.16).
studfiles.net
Приведение уравнения второго порядка к каноническому виду
Приведение уравнения второго порядка к каноническому виду
В главе «Поверхности второго порядка», где рассматривались поверхности второго порядка, было выписано их общее уравнение (13.1), а дальше для каждой поверхности использовалась своя прямоугольная декартова система координат, в которой уравнение поверхности имело канонический вид. В этом разделе мы выясним, как по общему уравнению найти такую систему координат. Результаты этого раздела используются и для приведения общего уравнения кривой второго порядка к каноническому виду. Достаточно будет во всех рассуждениях отбросить третью координату.
Пусть в пространстве задана прямоугольная декартова система координат . Рассмотрим общее уравнение поверхности второго порядка, коэффициенты в котором обозначены специальным образом
(19.7) |
где — числа, причем хотя бы одно из чиселотлично от нуля.
Выделим квадратичную часть выражения, стоящего в уравнении слева,
Такое выражение называется квадратичной формой от трех переменных. Составим матрицу
Эта матрица называется матрицей квадратичной формы . Она является симметричной, то есть, или, другими словами,. Следует обратить внимание на то, как эта матрица составлена. На диагонали у нее стоят коэффициенты при квадратах переменных, а в остальных местах — половины коэффициентов при произведениях переменных.
Исходная система координат является прямоугольной, поэтому скалярное произведение векторов с координатными столбцами ,задается формулой. Сформулируем две теоремы, позволяющие пользоваться приведенным ниже алгоритмом.
Теорема 19.4Если матрица — симметричная, то ее собственные числа являются вещественными числами и существует ортонормированный базис из собственных векторов.
Пусть — матрица квадратичной формы. По сформулированной теореме у нее существует ортонормированный базис из собственных векторов. Обозначим их,,, и пусть эти векторы имеют координаты
Базис i,j,kназовем старым, а базис— новым. Тогда матрица перехода 19.1.4.а будет иметь вид
Выберем новую систему координат так, что начало координат не изменяется, а новые базисные векторы,,задают направления новых координатных осей,,(рис. 19.8).

Рис.19.8.Система координат
Тогда координаты точкиявляются координатами ее радиус-вектораи, следовательно, при замене базиса меняются по формуле (18.1)
(19.8) |
Теорема 19.5Пусть собственные векторы ,,матрицы квадратичной формы, образующие ортонормированный базис, соответствуют собственным числам,,. Тогда в системе координатквадратичная форма принимает вид
Если мы из равенства (19.8) выпишем выражение,,через новые переменные,,и подставим в уравнение (19.7), то обнаружим, что квадратичная его часть и линейная часть преобразуются независимо друг от друга. В результате уравнение в системе координатимеет вид
(19.9) |
Хотя бы одно из чисел ,,отлично от нуля, иначе матрицабыла бы нулевой.
Рассмотрим три случая.
Пусть все собственные числа ,,отличны от нуля. В уравнении (19.9) выделим полные квадраты
Выполним параллельный перенос системы координат , взяв за новое начало системы координат точку(см. формулы (13.21)). Тогда в новой системе координатуравнение запишется в виде
Здесь возможны следующие варианты.
Пусть . Перенесемв правую часть и поделим обе части на, получим
Если числа ,,отрицательны, то ни одна точка пространства не удовлетворяет этому уравнению. Говорят, что оно определяет мнимый эллипсоид.
Если числа ,,положительны, то уравнение является каноническим уравнением эллипсоида.
Если одно из чисел ,,отрицательно, а остальные положительны, то (после переименования осей) получим каноническое уравнение однополостного гиперболоида.
Если одно из чисел ,,положительно, остальные отрицательны, то (после переименования осей) получим каноническое уравнение двуполостного гиперболоида.
Пусть .
Если все числа,,положительны, то только начало координат удовлетворяет этому уравнению. Поверхность выродилась в точку.
Если одно из чисел,,отрицательно, а два положительны, то (после переименования осей) получим каноническое уравнение конуса.
Если же два числа отрицательны или все три отрицательны, то, умножив обе части уравнения на , получим случай2или случай1.
Пусть одно из чисел ,,равно нулю, а два других отличны от нуля. Допустим, что. Тогда в уравнении (19.9) выделим полные квадраты по переменным,
Пусть . Преобразуем уравнение к виду
Поделим обе части уравнения на и выполним параллельный перенос осей координат, взяв за новое начало координат точку. Получим уравнение
Если числаиположительны, то это — каноническое уравнение эллиптического параболоида.
Если,, получим каноническое уравнение гиперболического параболоида.
Если числа иотрицательны или,, то сменим направление у осина противоположное и получим либо случай1, либо случай2.
Пусть . Тогда поверхность является цилиндрической, образующие которой параллельны оси, а направляющей служит кривая на плоскостис уравнением
Анализ поверхностей с таким уравнением предоставляем читателю.
Пусть только одно из чисел ,,отлично от нуля. Допустим, что. Тогда в уравнении (19.9) выделим полный квадрат по переменному
Пусть хотя бы одно из чисел ,отлично от нуля. Тогда на плоскостивозьмем две перпендикулярные прямыеи. Возьмем новую систему координат, у которой начало будет в точке, осьнаправлена по оси, осьнаправлена вдоль второй прямой, а осьнаправлена вдоль первой прямой. Тогда уравнение примет вид
Это — уравнение цилиндрической поверхности, образующие которой параллельны оси , а направляющей служит кривая на плоскостис уравнением
Анализ возможных поверхностей оставляем читателю.
Пусть . Тогда уравнение принимает вид
Если число справа положительно, то уравнение определяет две плоскости
Если число справа равно нулю, то уравнение определяет одну плоскость
Если число справа отрицательно, то ни одна точка пространства уравнению не удовлетворяет.
Итак, получен алгоритм, позволяющий установить, какая поверхность задается уравнением второго порядка и каково ее положение в пространстве.
Пример 19.11Приведите уравнение поверхности
к каноническому виду.
Решение.Квадратичная форма имеет вид
Выписываем ее матрицу
Находим ее собственные числа. Для этого запишем характеристическое уравнение
После вычисления определителя получим
Подбором находим один корень . Преобразуем уравнение, выделяя множитель
или
откуда
Находим два других корня характеристического уравнения и.
Находим собственные векторы. Для собственного числа для координат собственного вектораполучим систему уравнений
Решая ее находим, что фундаментальная система решений содержит только одно решение, и в качестве собственного вектора можно взять . Для собственного числадля координат собственного вектораполучим систему уравнений
Отсюда находим собственный вектор . Для собственного числадля координат собственного вектораполучим систему уравнений
Отсюда находим собственный вектор .
Легко проверить, что , то есть собственные векторы попарно ортогональны. Их длины равны соответственно,,. Поэтому векторы нового ортонормированного базиса будут иметь координаты
Матрица перехода имеет вид
Старые координаты связаны с новыми уравнением , то есть
(19.10) |
Подставим эти выражения в исходное уравнение. Квадратичная форма примет вид, в котором произведения переменных будут отсутствовать, а коэффициентами при квадратах будут служить собственные числа
Приводим подобные члены
Выделим полные квадраты
или
Выполняем параллельный перенос осей координат
Новое начало системы координат имеет координаты
В исходной системе координат точка в соответствии с формулами (19.10) имеет координаты

Рис.19.9.Система координат
В новой системе координат (рис. 19.9) уравнение принимает канонический вид
Это уравнение является каноническим уравнением однополостного гиперболоида. Его центр находится в точке , две вещественные оси параллельны векторам,, вещественные полуоси равны,. Мнимая ось параллельна вектору, мнимая полуось равна. Изображение гиперболоида приведено на рисунке 19.10.
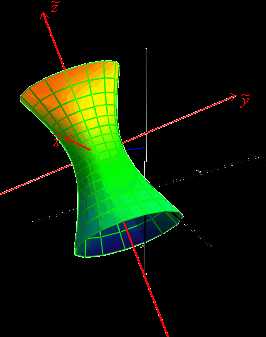
Рис.19.10.Изображение гиперболоида
studfiles.net
как привести уравнение кривой к каноническому виду — 16 Августа 2013 — Примеры решений задач
Приведение уравнений кривых второго порядка к каноническому видуУкажем, как можно с помощью преобразований координат, рассмотренных в предыдущем параграфе, привести общее уравнение кривой второго порядка
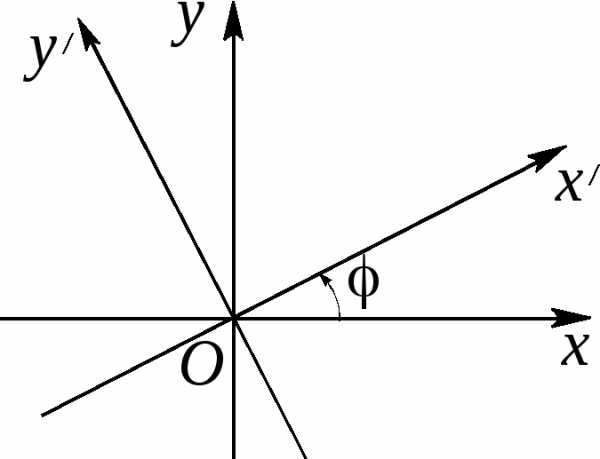
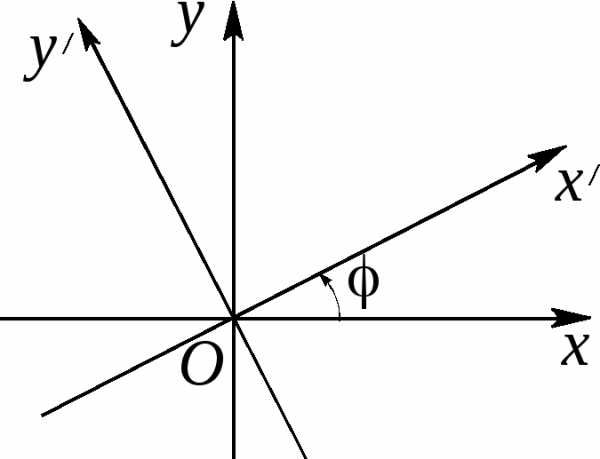
к каноническим уравнениям эллипса, гиперболы или параболы, или к случаям их выражения.С помощью поворота осей координат на некоторый угол α всегда можно избавиться от члена с произведением координат. Действительно, подставляя в (47) вместо x и y их выражения по формуле (43), получим новое уравнение
коэффициент которого a’12 будет равенПриравнивая коэффициент a’12 к нулю, получим тригонометрическое уравнение
Отсюда получаем
Далее, по формулам тригонометрии, получаем нужные нам значения для sin α и cos α :
Следовательно, уравнение кривой в новых координатах O’x’y’ примет вид:
Если в уравнении (50) , то говорят, что это уравнение определяет линию эллиптического типа;
если же , то говорят, что уравнение определяет линию гиперболического типа и, если один из коэффициентов a’11 или a’22 равен нулю, то уравнение (50) определяет линию параболического типа.
Далее с помощью параллельного переноса системы координат O’x’y’ уравнение (50) всегда можно привести к виду:
т.е. фактически к каноническому виду.Из уравнения (51) следует, что мы имеем либо эллипс (если a’11 и a’22 одного знака, а a»0 противоположного),
либо мнимое место точек (если a’11, a’22, a»0 имеют один знак),
либо одну точку (если a’11 и a’22 имеют один знак, а a»0 = 0),
либо гиперболу (если a’11 и a’22 разных знаков и a»0 ≠ 0),
либо две пересекающие прямые (если a’11 и a’22 разных знаков и a»0 = 0).
Если же в уравнении (50) один из коэффициентов a’11 и a’22 , например, a’22 обращается в нуль, то это уравнение с помощью переноса осей приведется к каноническому уравнению параболы при a’22 ≠ 0 или к виду при a’22 = 0, что дает или две параллельные прямые, или мнимое место точек.
Отсюда следует, что всякая кривая 2-го порядка есть либо эллипс, либо гипербола, либо парабола, либо представляет собой их «вырождение».
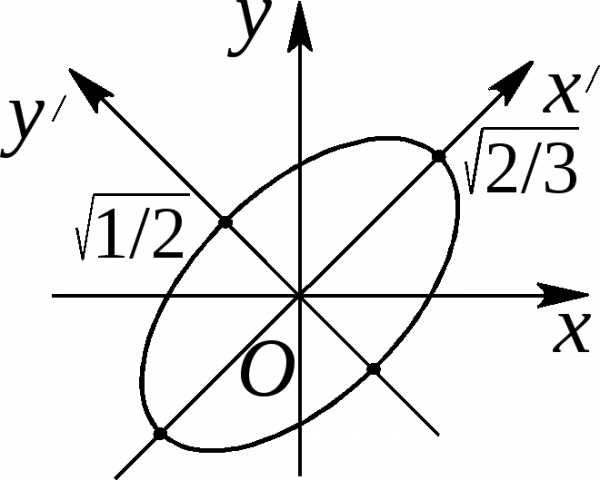
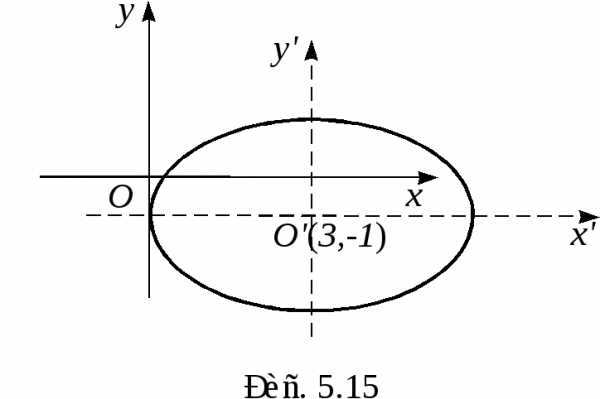
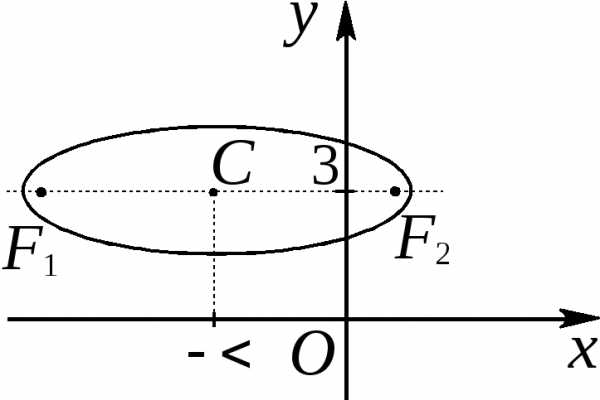
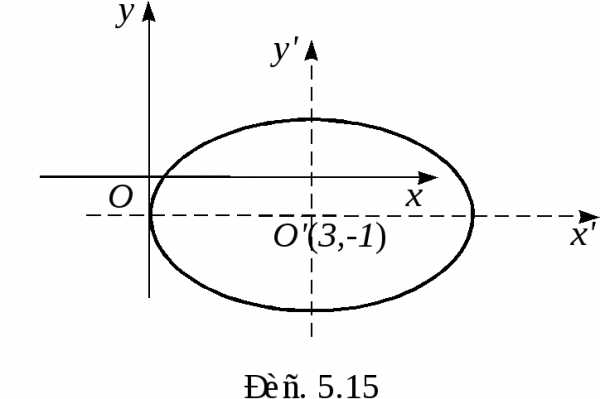
Пример. Привести к каноническому виду уравнение кривой второго порядка 29x2 — 24xy + 36y2 + 82x — 96y — 91 = 0 и сделать чертеж.
Решение. Здесь a11 = 29, a12 =-12, a22 = 36.
Поэтому
решая последнее уравнение, получимИ формулы преобразования координат запишутся в виде:
Подставляем выражения «старых» координат через «новые» в исходное уравнение кривой и, проделав достаточно громоздкие, но простые преобразования, получаем:
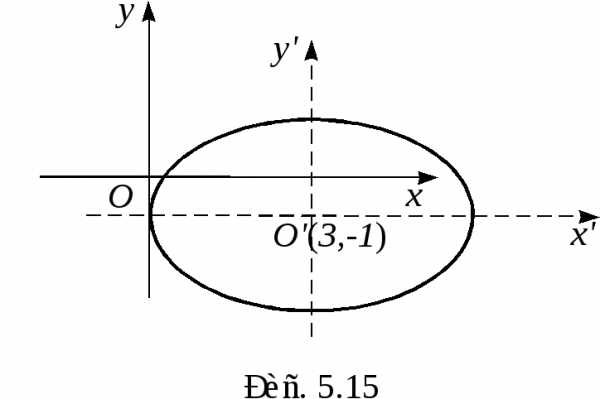
или, выделяя полный квадрат по x’ и y’ можем записать: отсюда:Введем новые координаты и в этих координатах уравнение примет вид
т.е. данная кривая есть эллипс с полуосями a = 3 и b = 2. Сделаем чертеж (рис. 14).www.reshim.su