Онлайн урок: Признаки делимости на 9 и на 3 по предмету Математика 6 класс
Пусть у нас есть 153 конфеты. Нужно раздать их троим детям поровну, используя только признак делимости.
Число 153 можно разложить на 1 сотню, 5 десятков и 3 единицы.
Разделим сначала нашу сотню конфет. Каждый ребенок получит по 33 конфеты и в остатке одна.
Теперь разделим один десяток конфет на троих. Имеем по 3 конфеты у каждого и одна в остатке. Значит, для наших пяти десятков каждому ребёнку по 15 (3•5) конфет и в остатке 5 (1•5) конфет.
По аналогии поступим с количеством конфет в единицах- тут всем достанется 1 конфета.
Мы не смогли разделить 1 конфету из сотен, 5 конфет из десятков. То есть в сумме получим
В итоге каждому ребёнку получится по 33 + 15 + 1 + 2 = 51 конфете.
Значит, число 153 делится без остатка на 3, а 1 + 5 — это сумма цифр этого числа.
Мы на примере посмотрели, как используется признак делимости на 3
Если сумма цифр числа делится на 3, то и число делится на 3
Если сумма цифр числа не делится на 3, то и число не делится на 3
Пример 1
Выберите среди чисел 75432, 2772825, 5402070 те, которые делятся на 3
Решение:
По признаку делимости на 3, нужно найти сумму цифр каждого числа и дальше работать с нею.
Для первого: 7 + 5+ 4+ 3+ 2 = 21,а 21 : 3 = 7, то есть сумма цифр делится на 3, значит и наше число делится на 3
Для второго: 2 + 7 + 7 + 2 + 8 + 2 + 5 = 33, а 33 : 3 = 11, то есть сумма цифр делится на 3, значит и наше число делится на 3
Для третьего: 5 + 4 + 0 + 2 + 0 + 7 + 0 = 18, а 18 : 3 = 6, то есть сумма цифр делится на 3, значит и наше число делится на 3
Пример 2
Замените звёздочки в числах 2*5, 31*, *15, на необходимые цифры, чтобы эти числа стали делиться на 3
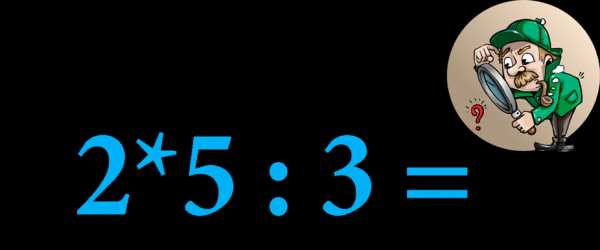
Возьмем первое число 2*5. Из признака делимости мы знаем, что нужно, чтобы сумма цифр числа делилась на 3. Значит, 2 + 5 + * должно делиться на 3.
Сумма известных цифр равна 8, значит, вместо звездочки можно взять, например, 1
Тогда сумма станет 9 и она делится на 3, значит и получившееся число 215 будет делиться на 3
Кроме единицы подходят цифры: 4, 7, так как они отличаются от 1 на 3 и 6 каждая.
Возьмем второе число 31*. Сумма первых цифр равна 4, значит, вместо звездочки минимум надо брать 2, чтоб в сумме было 6
Тогда сумма цифр будет делиться на 3
и само число, 312, будет делиться тоже.Кроме двойки брать можно и другие цифры, прибавляя по 3: 5 или 8
Получившиеся числа 315 или 318 будут делиться на 3
Берём последнее число *15. Сумма последних двух цифр 6, уже делится на 3. Значит нужно брать вместо первой цифры такие, которые делятся на 3. Это 3, 6 или 9
Получившиеся числа 315, 615, 915 будут делиться на 3 без остатка.
У меня есть дополнительная информация к этой части урока!
ЗакрытьИз признака делимости на 3
Чтобы ваше число делилось на 6, нужно чтоб оно делилось на 2 и на 3 одновременно.
Пример
Делится ли 216 на 6?
Решение:
216— это чётное число, значит, оно делится на 2
Сумма цифр числа 216 равна 2 + 1+ 6 = 9, значит, оно делится на 3
Отсюда, делаем вывод, что 216 делится на 6

ladle.ru
рассмотрим на примере и выведем правило
Рассмотрим простенькую задачу.
В одном хозяйстве было собрано утром 846 куриных яиц. Хозяйство это было общим, его содержит 9 семей. Надо разделить между ними поровну все яйца. Как проверить, не выполняя деление, делится ли число 846 на 9 без остатка.Сначала разложим данное число по разрядам. Число 846 состоит из 8 сотен, 4 десятков и 6 единиц.
Начнем разбираться с сотнями. Если в 100 яиц раскладывать по девяти корзинам, то у нас останется одной яйцо лишнее. То есть с каждой сотни яиц будет 1 яйцо. Так как у нас 8 сотен целых, то следовательно останется 8 яиц.
Теперь разберемся с десятками. Если десять яиц раскладывать по девяти корзинам, то тоже останется одно лишнее яйцо, с каждого десятка. Так как в нашем числе десятков 4, то следовательно останется 4 яйца.
6 яиц которые были в разряде единиц, мы никак не сможем разложить по девяти корзинам, следовательно они тоже останутся.
Теперь сложим все яйца, которые у нас остались. 8 от сотен, 4 от десятков и 6 от единиц, в сумме 8+4+6=18 яиц. 18 яиц можно разложить по девяти корзинам, и не останется ни одного лишнего яйца. Следовательно 846 яиц можно разложить поровну по девяти корзинам. Это значит, что число 846 делится без остатка на 9.
Признак делимости на 9
Теперь, можем сформулировать признак делимости числа на 9.
- Если сумма цифр числа делится без остатка на 9, то и само число делится на 9. Если сумма цифр числа не делится без остатка на 9, то и само число не будет делиться на 9 без остатка.
Приведем несколько примеров:
Число 76 005 будет делиться без остатка на 9, так как сумма составляющих его цифр: 7+6+0+0+5=18 делится на 9 без остатка.
Число 51 734 не делится без остатка на 9, так как сумма составляющих его цифр: 5+1+7+3+4=20 не делится на 9 без остатка.
Признак делимости на 3
Аналогичным образом получим признак делимости числа на 3.
От деления сотни на 3, будет оставаться единица. От деления десятки на 3, тоже будет оставаться единица. Получаем копию ситуации с девяткой.
- Если сумма цифр числа делится без остатка на 3, то и само число делится на 3. Если сумма цифр числа не делится без остатка на 3, то и само число не будет делиться на 3 без остатка.
Число 76 005 будет делиться без остатка на 3, так как сумма составляющих его цифр: 7+6+0+0+5=18 делится на 3 без остатка.
Число 51 734 не делится без остатка на 3, так как сумма составляющих его цифр: 5+1+7+3+4=20 не делится на 3 без остатка.
Нужна помощь в учебе?
Предыдущая тема: Признаки делимости на 2, на 5 и на 10: рассуждаем логически и даем ответ!
Следующая тема:   Простые и составные числа: разложение чисел на простые множители
Все неприличные комментарии будут удаляться.
www.nado5.ru
«Признаки делимости на 9 и на 3»
Конспект открытого урока по математике в 6 классе.
Тема: «Признаки делимости на 9 и на 3»
Тип: урок постановки учебной задачи.
Формы организации учебной деятельности: работа в парах; работа в группах; индивидуальная работа; фронтальная работа.
Цели:
Предметные: создать условия для освоения учащимися признаков делимости на 9 и на 3 и формулирования ими данных признаков.
Метапредметные: создать условия для формирования следующих УУД:
личностных: самоопределение, смыслообразование;
познавательных: формулирование познавательной цели, поиск и выделение информации, анализ с целью выделения признаков, формулирование проблемы, самостоятельное создание способов решения проблем творческого и поискового характера;
коммуникативных: планирование, постановка вопросов;
регулятивных: целеполагание (постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что ещё неизвестно), планирование (определение последовательности промежуточных целей с учётом конечного результата; составление плана и последовательности действий).
Задачи. Предметные:
1) актуализировать знания, необходимые для открытия и освоения учащимися признаков делимости на 9 и на 3.
2) с помощью практических заданий обеспечить понимание учащимися признаков, позволяющих без непосредственного деления определять делимость на 9 и на 3.
3) формировать у учащихся навыки определения чисел, делящихся на 9 и на 3 без непосредственного деления, а на основании признаков делимости.
Метапредметные:
1) предложить сформулировать проблему;
2) предложить сформулировать познавательную цель после формулирования проблемы;
4) организовать обсуждение результатов с доведением неверных версий до логического противоречия.
План урока:
Организационный момент (приветствие учащихся).
Устная работа. Актуализация опорных знаний.
Постановка учебной задачи
«Открытие» детьми нового.
Первичное закрепление
Самоонализ и самоконтроль
Применение новых знаний
Итоги урока. Рефлексия.
Ход урока:
1. Организационный момент (приветствие учащихся).
2. Актуализация опорных знаний.
Ребята скажите с какими понятиями мы познакомились на прошлых уроках./ делитель, кратное, признаки делимости на 10, на 5 и на 2.
1. Какое число называют делителем данного натурального числа?
2. Назовите все делители числа 16.
3. Какое число называют кратным натуральному числу a?
4. Выберите из чисел 14, 21, 75,42, 51, 63, 68, 74, 95, 90, 70 те которые:
а) кратны 7;
б) кратны 2;
в) кратны 5;
г) кратны 10.
Работа в парах.
Перед вами записан ряд чисел, попробуйте распределить их по уже известным признакам делимости. (Приложение 1)
240, 242, 244, 414, 40, 120, 246, 95, 54, 235,250,12, 252, 340, 102,
Какие колонки вам не составило трудности заполнить? / Первые три.А как вы определили, что число делится на 2? на 5? на 10? / Использовали признаки делимости на 10, на 5 и на 2.
А как вы определили, что число делится на 9 и на 3?/ Делили
Сформулируйте, в чем возникли затруднения.
Возникает проблема: учащиеся умеют делить числа нацело, не выполняя, деление, используют признаки делимости на 2, на 5, на 10, как по записи натурального числа узнать делится число на 9, или делится оно на 3, вызывает у них затруднение. А можно ли, не выполняя, деление определить, делится ли число на 9 или на 3?
3. Постановка учебной задачи.
Значит, что нового мы должны узнать на этом уроке? Так давайте совместно попробуем вывести новые правила, научимся применять их при решении задач. Предлагается ребятам разделиться на группы для решения проблемы.
Первой группе необходимо найти простой и короткий способ быстрого определения делимости числа на 9 без выполнения деления. Второй группе необходимо найти простой и короткий способ быстрого определения делимости числа на 3 без выполнения деления. — Сформулировать правила.
4. «Открытие» детьми нового.
Задание на 2 — 3 мин. У каждой группы на столе лежит карточка с числами, кратными 3 и 9. Внимательно посмотрите и попробуйте найти то общее, по которому можно определить, что число делится на 3, на 9. Учитель может помогать учащимся наводящими вопросами. А теперь посмотрите, подумайте в группах: что общего у чисел, делящихся на 3? что общего у чисел, делящихся на 9? Карточки (Приложение 2)
Карточка 1. Внимательно посмотрите и попробуйте, не выполняя деление, найти то общее, по которому можно определить, что число делится на 3? 159, 297, 264, 171, 222, 4623?
Карточка 2. Внимательно посмотрите и попробуйте, не выполняя деление, найти то общее, по которому можно определить, что число делится на 9? 297, 171, 468, 117, 396, 7587?
С помощью каких примет можно определить делимость чисел на 3, 9?
Заслушиваются представители каждой группы. Обсуждаются все предложенные способы. Выбираются наиболее рациональный и удобный в применении. Формулируются правила.
Ребята, какая у нас сегодня цель урока? Найти способы быстрого определения делителей числа без выполнения деления. Какая тема урока?
Признаки делимости на 9 и на 3.
Если сумма цифр делится на 3, то само число тоже делится на 3.
Если сумма цифр делится на 9, то само число тоже делится на 9.
5. Первичное закрепление
Выполнение заданий с проговариванием в громкой речи в парах:
1. Из представленных чисел, выбери те числа, которые делятся на 3? Которые делятся на 9? 75 432; 2 772 825; 5 402 070.
2. Из представленных чисел, выбери те числа, которые делятся на 3:
24 600; 67 085; 67 899.
3. Из представленных чисел, выбери те числа, которые делятся на 9:
12 350; 347 958; 67 500.
6. Самоанализ и самоконтроль
Самостоятельная работа по вариантам с последующей самопроверкой.
(Приложение 3)
1. Какие из чисел 23478, 2355, 106200, 3453, 6660, 83400, 45819 делятся:
а) на 3; б) на 9.
2. В числе 2*2 замените * цифрой так, чтобы полученное число:
а) делилось на 3, но не делилось на 9;
б) делилось на 9.
Вариант 2
1. Какие из чисел 45741, 2355, 78000, 3456, 664650, 7545, 65457 делятся:
а) на 3; б) на 9.
2. В числе 112* замените * цифрой так, чтобы полученное число:
а) делилось на 3, но не делилось на 9;
б) делилось на 9.
Прежде чем проверим работу, проведем физкультминутку.
Если число делится на 3, делаем наклоны вперед, если на 9, то делаем наклоны вправо и влево (часики), а если не делится — остаемся неподвижны.
А теперь мы проверим, на сколько вы правильно справились с заданием?
Как вы определили, что делятся на 3 и на 9, по каким признакам?
7. Применение новых знаний. Задания из учебника № 62, 63, 64 (с. 14)
8. Итоги урока. Рефлексия.
1) Ученикам предлагается в листах с фразами поставить знак у тех слов, которые им больше подходят к окончанию урока.
Урок полезен, всё понятно.
Ещё придётся потрудиться.
Да, трудно всё-таки учиться!
2) Учащиеся по кругу высказываются одним предложением.
Я научился…
Мне было трудно…
Сегодня я узнал…
У меня получилось…
Теперь я могу…
Спасибо вам за урок.
Домашнее задание 86, 87
Для желающих дома вывести признак деления на 6.
infourok.ru
Признаки делимости чисел. Признаки делимости на 9, на 3
Разделы: Математика
Цель урока:
Сформулировать признаки делимости натуральных чисел на 9 и на 3.
Развивать коммуникативные умения при работе в парах.
Формировать общеучебные навыки.
Учебник: Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков, С.И.Шварцбурд. Математика. 6 класс. – М.: Мнемозина, 2008.
Ход урока
1. Мотивация на изучение новой темы.
Повторение признаков делимости натуральных чисел на 2, на 5, на 10. Фронтальная работа.
Задание. Любое ли число, делящееся на 5, делится на 10? Всегда ли запись числа, делящегося на 5, оканчивается цифрой 5? Какие цифры можно поставить вместо звёздочки, чтобы полученное число делилось на 5?
а) 378*; б) 25*5; в) 4*13?
2. Изучение и закрепление темы “Признаки делимости на 9, на 3”.
Сформировать группы по 4 человека. Каждому участнику в группе даётся по одному числу 486, 485, 648, 865.
Задание 1. Не выполняя деления, можно ли данное количество яиц разложить в 9 корзин поровну. (Выполняют задание индивидуально, используя текст учебника на с. 13 – 14.)
Формируют в группе пары и рассказывают друг другу деление яиц по корзинам. Перед каждым заданием пары меняют.
Рассказывают деление яиц у доски 4 человека.(486, 485, 648, 865).
Пример. 486 яиц. Если раскладывать поровну в 9 корзин одну сотню яиц, то одно яйцо останется. От четырёх сотен останется 4 яйца. Если раскладывать поровну в 9 корзин один десяток, то останется одно яйцо. От восьми десятков останется 8 яиц. Не разложенными останутся 4 яйца от сотен, 8 яиц от десятков и ещё 6 яиц. 4 + 8 + 6 = 18. 18 яиц можно разложить поровну в 9 корзин. Значит, 486 яиц можно разложить поровну в 9 корзин. Это значит, что число 486 делится без остатка на 9.
Аналогично рассказывают о числах 485; 648; 865.
На доске учитель делает запись:
Задание: Сформулируйте признак делимости числа на 9.
Ответ: Если сумма цифр числа делится на 9, то и число делится на 9.
Задание 2. составьте схему для логического квадрата по признаку делимости чисел на 9. (Учащиеся работают в парах. Изображают схему в тетради. Учитель изображает схему на доске.)
Задание 3. Сформулируйте по логической схеме высказывания и составьте совмещённое правило. (Работают в парах.)
- Если сумма цифр числа делится на 9, то число делится на 9.
- Если сумма цифр числа не делится на 9, то число не делится на 9.
- Если число делится на 9, то сумма цифр числа делится на 9.
- Если число не делится на 9, то сумма цифр числа не делится на 9.
При фронтальной работе правило озвучивают.
Совмещённое правило записывают в тетради и на доске.
Задание 4. Сформулируйте к правилам вопросы-суждения и постройте ответы.
(Работа ведётся в парах.)
Вопрос 1. Чем объяснить, что число 5402070 делится на 9?
Ответ: Сумма цифр данного числа 18 делится на 9.
Если сумма цифр числа делится на 9, то число делится на9.
Число 5402070 делится на 9.
Вопрос 2. Каким образом в числах, делящихся на 9, поставить цифры вместо звёздочек: 2*5, 46*, *14?
Ответ: Суммы цифр 225, 468, 414 делятся на 9.
Если числа делятся на 9, то сумма цифр делится на 9.
Вместо звёздочек поставим цифры 2, 8, 4.
Вопрос 3. Как доказать, что число 75432 не делится на 9?
Ответ: Сумма цифр числа 21 не делится на 9.
Если сумма цифр числа не делится на 9, то число не делится на 9.
Число 75432 не делится на 9.
Задание 5. Запишите какие-нибудь три четырёхзначных числа, которые делятся на 9. (Задание самостоятельно выполняют на карточке, сдают на проверку учителю.)
3.
Рефлексия.Задание 1. Прочитайте тему урока и сформулируйте задачу, которую ещё надо решить.
Ответ: Надо сформулировать признак делимости чисел на 3.
Задание 2. Составьте план решения данной задачи.
Ответ. Идёт фронтальная работа по составлению плана:
- Проанализировать четыре числа.
- Сформулировать признак делимости числа на 3.
- Составить логическую схему по признаку делимости чисел на 3.
- Сформулировать по схеме 4 высказывания.
- К высказываниям сформулировать вопросы-суждения и построить ответы.
- Придумать четыре числа, которые делятся на3.
- Придумать четыре числа, которые не делятся на 3.
Карточки с вопросами раздаются каждому ученику.
(Работают в парах. Запись ведут на отдельных листах.)
Фронтальная работа по вопросам.
На доске логическая схема.
По схеме формулируют четыре высказывания.
4. Домашнее задание.
Подготовить рассказ по карточке.
13.05.2011
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Признаки делимости на 9 и 3
Урок 4
Тема: Признаки делимости на 9 и 3
Оборудование: доска, мел
Повторение:
«Крестики-нолики»
1 – делитель любого числа.
0 – делитель любого числа.
Число 1 имеет только 1 делитель.
Число 5 имеет 3 делителя.
Число 100 кратно 20
Числа 15, 30, 45 кратны 15
Самое маленькое кратное любого числа – 1.
Самое большое кратное числа – само это число
Самый большой делитель числа – само это число.
Новый материал:
Давайте сразу запишем:
Признак делимости на 9: Если сумма цифр числа делится на 9, то и число делится на 9; если сумма цифр числа не делится на 9, то и число не делится на 9.
Прочитаем несколько раз эту запись и постараемся запомнить.
Давайте проверим. так ли это на самом деле:
Возьмём число: 76 455
Найдём сумму его цифр: 7+6+4+5+5=27 – делится на 9
Проверим, действительно ли число 76 455 делится на 9 (76 455 : 9 = 8495)
Проверьте теперь сами число: 33309. (Сумма цифр 18, 33309:9=3701)
Запишем теперь признак делимости на 3. На самом деле он точно такой же попробуйте сформулировать мне его, глядя на предыдущий
Признак делимости на 3: Если сумма цифр числа делится на 3, то и число делится на 3; если сумма цифр числа не делится на 3, то и число не делится на 3.
Упражнение 1: Учебник: №58.
Упражнение 2: Учебник: №60
Упражнение 3: Учебник №62
Задания на урок:
Устно: 72, 73, 74, 75
№ 59
№61
№64
№68
№69
№77
№79
№84
№86(а, в)
Домашнее задание:
Учебник: (стр.13-14) – прочитать.
№ 81, 82, 85, 86(б, г)
globuss24.ru
