Рацио число – . .

Рациональные числа — Циклопедия

Рациональные числа // Доступная математика

Рациональные числа — это всевозможные числа, которые представляются как частное целого и натурального числа, то есть в виде дроби (отношения) p/q, где p — целое число, q — натуральное число. Две такие дроби p₁/q₁ и p₂/q₂ считаются равными, если p₁q₂ − p₂q₁ = 0 (иными словами, дроби можно «сокращать», то есть mp/mq = p/q для ненулевого m).

[править] Основные свойства

Сложение рациональных чисел дробей осуществляется путем «приведения к общему знаменателю»:

p₁/q₁ + p₂/q₂ = (p₁q₂ + p₂q₁)/q₁q₂

Аналогичным образом определяется вычитание рациональных чисел: p₁/q₁ − p₂/q₂ = (p₁q₂ − p₂q₁)/q₁q₂

Противоположным числом к дроби p/q является дробь −p/q:

p/q + (−p/q) = 0.

Произведение рациональных чисел p₁/q₁ и p₂/q₂ — это число p₁p₂/q₁q₂.

Целые числа вкладываются в рациональные, так как любое целое число n можно представить как дробь n/1. Таким образом, рациональные числа являются расширением целых чисел (которые, в свою очередь — расширение натуральных чисел). Если при расширении натуральных чисел до целых становится возможным вычитать любые числа, то при расширении целых чисел до рациональных становится возможным делить на любое число, не равное нулю.

Для рациональных чисел p₁/q₁ и p₂/q₂, второе из которых не равно 0 (то есть p₂ ≠ 0), определено частное этих чисел:

p₁/q₁ : p₂/q₂ = p₁q₂ / q₁p₂.

Для любого ненулевого рационального числа p/q существует обратное к нему по умножению — число q/p. Действительно, p/q · q/p = pq/pq = 1.

Для сложения и умножения рациональных чисел, как и для целых, выполняются свойства коммутативности, ассоциативности и дистрибутивности, а существование обратного элемента по умножению у всех ненулевых рациональных чисел доказывает, что это коммутативное и ассоциативное кольцо является полем.

В математической и учебной литературе поле рациональных чисел обозначается [math]\mathbb Q[/math]. Поле рациональных чисел вкладывается в поле действительных (вещественных) чисел [math]\mathbb R[/math], которое можно представлять, например, как множество бесконечных десятичных дробей (так оно часто определяется в школьном курсе математики). При этом рациональным числам соответствуют периодические десятичные дроби (то есть такие, в которых есть бесконечное повторение одной и той же последовательности, начиная с некоторой позиции). Например, 1,0333333… = 31/30 — рациональное число.

Любое рациональное число с помощью алгоритма Евклида может быть единственным образом представлено в виде (конечной) цепной дроби:
[math]\frac{m}{n} = a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{ \ddots + \cfrac{1}{a_k} }}}[/math]
(a₀ — целое число, a_i — натуральные при 1 ≤ i ≤ k, и обычно полагается, что последний элемент a_k > 1, если рациональное число m/n — не целое).

В алгебре определяется операция расширения коммутативного ассоциативного целостного (в котором произведение ненулевых элементов не равно нулю) кольца до поля, которое называется полем частных, и это вложение аналогично вложению кольца целых чисел в поле рациональных чисел. Например, кольцо многочленов от одной переменной над полем K, обозначаемое K[x], вкладывается в поле рациональных функций одной переменной, обозначаемое K(x).

Уже в Древней Греции стало известно, что [math]\sqrt{2}[/math] (длина диагонали квадрата со стороной 1, равная «квадратному корню из 2») не выражается рациональным числом. Такие числа называются иррациональными. Позднее стало известно что число Пи иррационально (длина окружности с диаметром 1), аналогично и многие другие фундаментальные математические константы иррациональны. Иррациональным числам соответствуют непериодические бесконечные десятичные дроби, также любое иррациональное число раскладывается в бесконечную цепную дробь.

Пример, показывающий возможность нумерации положительных рациональных чисел

Рациональных чисел бесконечно много. При этом это множество счетно, то есть существует взаимно однозначное соответствие между множеством рациональных чисел и множеством натуральных чисел. В то же время, множество всех действительных чисел не является счетным.

• Ван дер Варден Б. Л. Современная алгебра. т.т.1-2, М-Л: ОНТИ НКТП, 1937.

cyclowiki.org

Рациональные числа

От латинского слова ratio — отношение, деление, дробь происходит математический термин рациональное число или рациональная дробь.

---

Суммирование дробей

Рациональное число есть число, представляемое обыкновенной дробью m/n, где m — целое число, а n — натуральное. В рациональной дроби число m называется числителем, а число n — знаменателем. Таким образом, рациональная дробь представляет собой результат деления m на n. В действительности дроби часто используются при подсчете частей целого, но неделимого объекта, а также для приблизительной оценки пространственно-временных отношений протяженных объектов.

Множество рациональных чисел принято обозначать Q. Наиболее точная графическая запись рациональных чисел такова: .

---

Нумерация рациональных чисел

Кстати сказать, что дроби типа 3/4 и 9/12 и входят в множество рациональных чисел как одна дробь. Из этого можно сделать вывод, что множество рациональных чисел — это множество несократимых дробей с целым числителем и натуральным знаменателем: , где GCD (m, n)— наибольший общий делитель чисел m и n. Если он равен единице, то это гарантирует взаимную простоту«числителя и знаменателя, что в свою очередь обуславливает несократимость дроби m/n.

Дробь, у которой модуль числителя меньше модуля знаменателя называется правильной

. Дробь, не являющаяся правильной относится к неправильным.

Приведем пример, дроби 3/5, 7/8, и 1/2 — правильные дроби, а дроби 8/3, 9/5 и 2/1 — неправильные дроби.

Кстати сказать, что всякое целое число можно записать в виде неправильной обыкновенной дроби со знаменателем 1.

Целое число и правильная дробь называется смешанной дробью, представляющая собой сумму числа и дроби. К примеру, 2 3/7 = 2 + 3/7 = 14/7 + 3/7 = 17/7.

Интересно узнать, что в математической литературе такая запись практически не используется в связи с тем, что вид такой дроби очень схож с обозначением произведения целого числа на дробь.

---

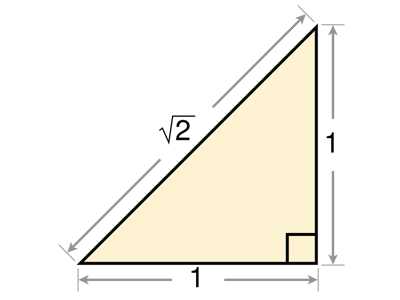
Гипотенуза такого треугольника не выражается никаким рациональным числом

К основным свойствам рациональных чисел относятся следующие:

• Упорядоченность. Для любых рациональных чисел a и b существует
  правило упорядочения, дающее возможность однозначно идентифицировать между ними одно из трёх отношений:» < », « > «или» = «. Точная формулировка этого правила такова: два неотрицательных числа a = m_a/n_aи b = m_b/n_bсвязаны тем же отношением, что и два целых числа m_an_b и m_bn_a; два неположительных числа a и b связаны тем же отношением, что и два неотрицательных числа |b|и |a|; если же вдруг a неотрицательно, а b — отрицательно, то a > b.
• Операция сложения. Любые рациональные числа a и b подчиняются правилу суммирования, которое ставит им в соответствие некоторое рациональное число c, которое называется суммой чисел a и b и обозначается (a + b). Процесс поиска числа с называется суммированием.
  Правило суммирования выглядит следующим образом: m_a/n_am_b/n_b = (m_an_b + m _bn_a) / n_an_b.
• Операция умножения. Для любых рациональных чисел a и b существует справедливо правило умножения, которое ставит им в соответствие некоторое рациональное число c. Здесь число c называется произведением чисел a и b и обозначается (ab). Процесс отыскания числа с называется умножением. Правило умножения имеет следующий вид: m_a/n_am_b/n_b = (m_am_b)/(n_an_b).
• Транзитивность отношения порядка. Для любой тройки рациональных чисел a, b и c в случае, если a меньше b, а b меньше c, то a меньше c. Когда a равно b, а b равно c, то a равно c. Т.е. (a < b & b < c => a < c) & (a = b & b = c => a = c)
• Коммутативность сложения. Всем известное правило: от перемены мест рациональных слагаемых сумма не меняется. Т.е. a + b = b + a.
• Ассоциативность сложения. На результат сложения не влияет порядок сложения трех рациональных чисел. Т.е. (a + b) + c = a + (b + c).
• Наличие нуля. При суммировании любых рациональных чисел рациональное число 0 сохраняет их. a + 0 = a.
• Наличие противоположных чисел. Любое рациональное число имеет противоположное рациональное число, при суммировании с которым даёт 0. a + (-a) = 0.
• Коммутативность умножения. Произведение рациональных чисел от перемены мест рациональных множителей не меняется. ab = ba.
• Ассоциативность умножения. На результат перемножения трех рациональных чисел порядок не влияет. (ab)c = a(bc).
• Наличие единицы. Наличие рационального числа 1 при умножении сохраняет любое другое рациональное число. a1 = a.
• Наличие обратных чисел. Любое рациональное число имеет обратное рациональное число, при умножении на которое даёт 1. aa ^-1 = 1.
• Дистрибутивность умножения относительно сложения. Операция умножения согласуется с операцией сложения на основе распределительного закона: (a + b)c = ac + bc.
• Связь отношения порядка с операцией сложения. Одно и то же рациональное число можно прибавить и к левой и правой частям рационального неравенства. a < b => a + c < b + c.
• Связь отношения порядка с операцией умножения. Одно и то же положительное рациональное число можно умножать на левую и правую части рационального неравенства. c > 0 & a < b => ac < bc.
• Аксиома Архимеда гласит, что каково бы ни было рациональное число a, можно взять столько единиц, что их сумма превзойдёт a.

Кроме основных шестнадцати свойств, присущих рациональным числам существуют и другие, которые могут быть выведены из приведенных свойств. Дополнительных свойств рациональных чисел очень много.

Поделиться ссылкой

sitekid.ru

Рациональное число Википедия

Рациональное число (лат. ratio — отношение, деление, дробь) — число, которое можно представить обыкновенной дробью mn{\displaystyle {\frac {m}{n}}}, числитель m{\displaystyle m} — целое число, а знаменатель n{\displaystyle n} — натуральное число, к примеру 2/3. Понятие дроби возникло несколько тысяч лет назад, когда, сталкиваясь с необходимостью измерять некоторые вещи (длину, вес, площадь и т. п.), люди поняли, что не удаётся обойтись целыми числами и необходимо ввести понятие доли: половины, трети и т. п. Дробями и операциями над ними пользовались, например, шумеры, древние египтяне и греки.

Множество рациональных чисел[ | ]

Множество рациональных чисел обозначается Q{\displaystyle \mathbb {Q} } (от лат. quotient, «частное») и может быть записано в таком виде:

Q={mn∣m∈Z, n∈N}.{\displaystyle \mathbb {Q} =\left\{{\frac {m}{n}}\mid m\in \mathbb {Z} ,\ n\in \mathbb {N} \right\}.}

Другими словами, числитель (m) может иметь знак, а знаменатель (n) должен быть положительным целым числом.

При этом оказывается, что разные записи могут представлять одну и ту же дробь, например, 34{\displaystyle {\frac {3}{4}}} и 912{\displaystyle {\frac {9}{12}}}, (все дроби, которые можно получить друг из друга умножением или делением числителя и знаменателя на одно и то же натуральное число, представляют одно и то же рациональное число). Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно пол

ru-wiki.ru

Число рациональных мыслей и способ мышления человека

Число рациональных мыслей наилучшим образом опишет ваш способ мышления. Как вы мыслите? Вы руководствуетесь здоровой логикой, практичны или же полностью доверяете голосу интуиции? Оригинальны или предпочитаете стандартные решения? Число рациональных мыслей расскажет об этом.

Но стоит помнить, что число рациональных мыслей ярче проявляется, когда перед человеком стоит интеллектуальная задача. Но если решаемый вопрос эмоционально окрашен — это число не оказывает на человека практически никакого влияния.

Как рассчитать число рациональных мыслей

Для расчета числа рациональных мыслей необходимо знать полное имя человека и число его рождения. Первое, что мы сделаем — это переведем имя в числовой код и суммируем все цифры.

Складываем все числа имени: 2+1+2+3+6+6+1 = 21 и сводим ее к однозначному числу 21=3.

Теперь суммируем полученное число с числом рождения. Я родилась 31 числа — оно сокращается до 4. Складываем:

3 (имя) + 4 (число) = 7 (число рациональных мыслей).

При вычислении числа рациональных мыслей управляющие числа (11 и 22) до однозначных не сокращаются.

Теперь вкратце рассмотрим значение каждого из чисел:

Число 1

Вы независимы, упрямы, смелы и решительны.Без колебаний вступаете в дискуссию и умело отстаиваете свою точку зрения.Ваши мысли ярки и оригинальны.

Число 2

Вы открыты для идей окружающих. Мягки и ненавязчивы. Мыслите, по большей части, опираясь на интуицию.

Число 3

Вы, однозначно, натура творческая. Но ваши мысли несколько рассеянны. Для вас свойственно перескакивать с одной мысли на другую. В стремлении охватить все — можете упустить из виду значимые детали. Пусть и не всегда действуете логично, но, практически всегда, принимаете верные решения.

Число 4

Вы практичны и рациональны. Привыкли четко планировать свои действия, шаг за шагом. Однако, новые идеи вас несколько озадачивают и выводят из привычной колеи.

Число 5

Вы гибкий, адаптивный человек и довольно хитрый человек. Способны выиграть спор, даже если и не правы.

Число 6

Справедливость является основой ваших решений. Замечаете то, что многие не способны разглядеть. Концентрируясь на деталях, вы забываете о глобальных задачах.

Число 7

Вы — один из тех, кто всегда докапываются до истины. Никогда не удовлетворяетесь простым ответом. Стремитесь рассмотреть вопрос со всех сторон, пока проблема не станет полностью ясна. И только тогда, без замедлений и колебаний, приступите к решению текущей проблемы.

Число 8

Вы находите баланс между рациональным и иррациональным. Обладаете масштабным зрением. Обожаете интеллектуальные «войны».

Число 9

Вас не тревожит точка зрения окружающих. Не смотря на это, вы не спешите высказывать свое мнение, пока другие не выскажутся. Лишь после этого вы укажете на недостатки, которые ускользали от чужих взглядов. Решаете проблемы скорее посредством озарений, чем путем выстраивания логических цепочек.

Число 11

Данное число является наиболее магическим среди остальных. Вы можете быть духовным учителем или изобретателем. Ваши ответы и озарения просто невероятны!

Число 22

Вы — человек с высокими идеалами. Число 22 создает фундамент, помогает фантазии воплощать в реальность. В целом, вибрация этого числа способствует достижению успеха. Человек способен объективно оценивать ситуацию, но и в то же время, не упускать из виду деталей.

---

Возможно, вас заинтересует:

Уровень развития души по дате рождения

Число моста или как связать основные числа в нумерологической карте

Число зрелости — золотая цель человека

Опубликовано 27 Июл 2017 16:14

Чтобы сообщить об ошибке — выделите фрагмент текста с ошибкой и воспользуйтесь комбинацией клавиш Ctrl+Enter

Оцените, пожалуйста, запись! Я старалась)

Загрузка…

tvkoh.com

Что такое рациональные числа 🚩 что значит рациональное число 🚩 Наука 🚩 Популярное

По определению рациональным числом называется такое число, которое можно представить в виде обыкновенной дроби. Числителем такой дроби должно быть целое число, а знаменателем — натуральное. В свою очередь натуральные числа — это те, которые используются при счете предметов, а целые — это все натуральные, противоположные им и ноль.Множеством рациональных чисел называют множество представлений этих дробей. Дробь следует понимать как результат деления, например, дроби 1/2 и 2/4 следует понимать как аналогичное рациональное число. Поэтому дроби, которые можно сократить, несут один математический смысл с этой точки зрения. Множество всех целых чисел является подмножеством рациональных. Рассмотрим основные свойства. Рациональные числа обладают четырьмя основными свойствами арифметики, а именно — умножением, сложением, вычитанием и делением (кроме ноля), а также возможностью упорядочить эти числа. Для каждого элемента из множества рациональных чисел доказано наличие обратного и противоположного элемента, наличие нуля и единицы. Множество этих чисел ассоциативно и коммутативно как по сложению, так и по умножению. Среди свойств есть известная теорема Архимеда, которая гласит, что какое бы ни взяли рациональное число, можно взять столько единиц, что сумма этих единиц превзойдет данное рациональное число. Заметим, что множество рациональных чисел является полем. Область применения рациональных чисел очень широка. Это те числа, которые применяются в физике, экономике, химии и других науках. Большое значение рациональные числа играют в финансовых и банковских системах. При всей мощности множества рациональных чисел, ее не хватает для решения задач планиметрии. Если взять небезизвестную теорему Пифагора, там возникает пример нерационального числа. Поэтому возникла необходимость расширить это множество до множества так называемых вещественных чисел. Изначально понятия «рациональный», «иррациональный» относились не к числам, а к соизмеримым и несоизмеримым величинам, которые иногда называли выразимыми и невыразимыми.

www.kakprosto.ru

Рациональные числа — это периодические дроби — Науколандия

Как известно, множество рациональных чисел (Q) включает в себя множества целых чисел (Z), которое в свою очередь включает множество натуральных чисел (N). Помимо целых чисел в рациональные числа входят дроби.

Почему же тогда все множество рациональных чисел рассматривают иногда как бесконечные десятичные периодические дроби? Ведь кроме дробей, они включают и целые числа, а также непериодические дроби.

Дело в том, что все целые числа, а также любую дробь можно представить в виде бесконечной периодической десятичной дроби. То есть для всех рациональных чисел можно использовать одинаковый способ записи.

Как представляется бесконечная периодическая десятичная дробь? В ней повторяющуюся группу цифр после запятой берут в скобки. Например, 1,56(12) — это дробь, у которой повторяется группа цифр 12, т. е. дробь имеет значение 1,561212121212… и так без конца. Повторяющаяся группа цифр называется периодом.

Однако в подобном виде мы можем представить любое число, если будем считать его периодом цифру 0, которая также повторяется без конца. Например, число 2 — это то же самое, что 2,00000…. Следовательно, его можно записать в виде бесконечной периодической дроби, т. е. 2,(0).

То же самое можно сделать и с любой конечной дробью. Например:

0,125 = 0,1250000… = 0,125(0)

Однако на практике не используют преобразование конечной дроби в бесконечную периодическую. Поэтому разделяют конечные дроби и бесконечные периодические. Таким образом, правильнее говорить, что к рациональным числам принадлежат

• все целые числа,
• конечные дроби,
• бесконечные периодические дроби.

При этом просто помнят, что целые числа и конечные дроби представимы в теории в виде бесконечных периодических дробей.

С другой стороны, понятия конечной и бесконечной дроби употребимы к десятичным дробям. Если говорить об обыкновенных дробях, то как конечную, так и бесконечную десятичную дробь можно однозначно представить в виде обыкновенной дроби. Значит, с точки зрения обыкновенных дробей, периодические и конечные дроби — это одно и то же. Кроме того, целые числа также могут быть представлены в виде обыкновенной дроби, если представить, что мы делим это число на 1.

Как представить десятичную бесконечную периодическую дробь в виде обыкновенной? Чаще используют примерно такой алгоритм:

1. Приводят дробь к виду, чтобы после запятой оказался только период.
2. Умножают бесконечную периодическую дробь на 10 или 100 или … так, чтобы запятая передвинулась вправо на один период (т. е. один период оказался в целой части).
3. Приравнивают исходную дробь (a) переменной x, а полученную путем умножения на число N дробь (b) — к Nx.
4. Из Nx вычитают x. Из b вычитаю a. Т. е. составляют уравнение Nx – x = b – a.
5. При решении уравнения получается обыкновенная дробь.

Пример перевода бесконечной периодической десятичной дроби в обыкновенную дробь:
x = 1,13333…
10x = 11,3333…
10x * 10 = 11,33333… * 10
100x = 113,3333…
100x – 10x = 113,3333… – 11,3333…
90x = 102
x =

scienceland.info

Определение рациональных чисел. Примеры.

Определение рациональных чисел:

рациональным числом называют число, которое может быть представлено в виде дроби. Числитель такой дроби принадлежит множеству целых чисел, а знаменатель принадлежит множеству натуральных чисел.

Почему числа называют рациональными?

По латински «рацио» (ratio) означает отношение. Рациональные числа могут быть представлены в виде отношения, т.е. другими словами в виде дроби.

Пример рационального числа

Число 2/3 есть рациональное число. Почему? Это число представлено в виде дроби, числитель которой принадлежит множеству целых чисел, а знаменатель – множеству натуральных чисел.

Больше примеров рациональных чисел см. в статье Рациональные числа примеры.

Равные рациональные числа

Разные дроби могут представлять одно рациональное число.

Рассмотрим рациональное число 3/5. Этому рациональному числу равны

3	=	6	=	9	=	12
5		10		15		20

и ещё бесконечное количество дробей.

Таким образом имеем, что каждое рациональное число может быть представлено в виде бесонечного количества других рациональных чисел.

А почему, например, число 6/10 равно числу 3/5?

Вынесем общий множитель в числителе и знаменателе дроби:

Сократим числитель и знаменатель на общий множитель 2:

6	=	2 * 3	=	3
10		2 * 5		5

Мы получили дробь 3/5, а это значит, что

Отсюда видно, как рациональное число представить в виде других рациональных чисел.

Нужно числитель и знаменатель рационального числа умножить на одно и то же число.

Пример:

3	=	3 * 100	=	300
5		5 * 100		500

www.sbp-program.ru