Разложение на множители – онлайн-калькулятор
Онлайн-разложение на множители
Введите число:
Все натуральные числа делятся на простые и составные. Первые отличаются тем, что их можно разделить только на самих себя и на единицу. Простых чисел достаточно много. Представляем вам только первые из них: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107 и т.д.
А вот составное число может быть записано в виде нескольких простых чисел, перемноженных между собой.
Теорема гласит, что если обозначить некое составное число как n, а его потенциальный простой делитель как р, то последний (хотя бы один из множества) может обладать следующей характеристикой: р2≤ n.
При этом 1 считается не простым и не составным числом. Она словно сама по себе.
Процесс разложения составного числа на множители называется факторизацией.
- Для разложения небольших чисел можете прибегнуть к помощи таблицы умножения.
- Для разложения на множители больших чисел используйте таблицу простых чисел.
Работает это так: предположим, у вас есть некое четырехзначное число. Найдите в таблице его наименьший делитель. Разделите свое число на этот делитель – получилось некое трехзначное число. Теперь переберите числа в таблице и найдите делитель для этого трехзначного числа. И так далее о тех пор, пока в конце у вас не останется простое число, которое, по определению, нельзя разложить на простые множители. Произведение всех найденных вами чисел и есть простые множители исходного числа.
Записать это можно так:
Делимое Делитель четырехзначное число х Х1 трехзначное число у У1 простое число р Р1 - Вы также можете воспользоваться нашим калькулятором для разложения числа на простые множители онлайн
Задайте программе составное число любой сложности – она легко и быстро разложит его на простые множители и представит вам результат. Вы можете пользоваться программой, чтобы проверить себя. Или чтобы ускорить выполнение домашней работы.
Это гораздо быстрее, чем перебирать числа в таблице простых чисел. И удобнее, чем вычислять в уме.
Не забудьте порекомендовать этот онлайн калькулятор своим одноклассникам!
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Разложить число на простые множители онлайн калькулятор
Примеры разложения числа на простые множители
Разложим число 120 на простые множители120 = 2 ∙ 2 ∙ 2 ∙ 3 ∙ 5
Решение
Разложим число 120 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
120 : 2 = 60 — делится на простое число 2
60 : 2 = 30 — делится на простое число 2
30 : 2 = 15 — делится на простое число 2
15 : 3 = 5 — делится на простое число 3.
Завершаем деление, так как 5 простое число
Ответ: 120 = 2 ∙ 2 ∙ 2 ∙ 3 ∙ 5
Перейти в калькулятор Разложим число 246 на простые множители246 = 2 ∙ 3 ∙ 41
Решение
Разложим число 246 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
246 : 2 = 123 — делится на простое число 2
123 : 3 = 41 — делится на простое число 3.
Завершаем деление, так как 41 простое число
Ответ: 246 = 2 ∙ 3 ∙ 41
Перейти в калькулятор Разложим число 1463 на простые множители1463 = 7 ∙ 11 ∙ 19
Решение
Разложим число 1463 на простые
множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех
пор, пока частное не окажется простым числом
1463 : 7 = 209 — делится на простое число 7
209 : 11 = 19 — делится на простое число 11.
Завершаем деление, так как 19 простое число
Ответ: 1463 = 7 ∙ 11 ∙ 19
Перейти в калькулятор Разложим число 1268 на простые множители1268 = 2 ∙ 2 ∙ 317
Решение
Разложим число 1268 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с
самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
1268 : 2 = 634 — делится на простое число 2
Завершаем деление, так как 317 простое число
Ответ: 1268 = 2 ∙ 2 ∙ 317
Перейти в калькулятор Разложим число 442464 на простые множители442464 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 11 ∙ 419
Решение
Разложим число 442464 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
442464 : 2 = 221232 — делится на простое число 2
221232 : 2 = 110616 — делится на простое число 2
110616 : 2 = 55308 — делится на простое число 2
55308 : 2 = 27654 — делится на простое число 2
27654 : 2 = 13827 — делится на простое число 2
13827 : 3 = 4609 — делится на простое число 3
4609 : 11 = 419 — делится на простое число 11.
Завершаем деление, так как 419 простое число
Ответ: 442464 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 11 ∙ 419
Перейти в калькуляторmatematika-club.ru
Разложение числа на простые множители
- Главная
- Математические калькуляторы
- Разложение числа на простые множители
Любое натуральное число n > 1 можно представить в виде произведения простых чисел. Это представление называется разложением числа n на простые множители.
Калькулятор разложения числа на простые множители разложит число на множители и выдаст подробное решение задачи.
В школе на уроках математики разложение числа на множители обычно записывают столбиком (в две колонки). Делается это так: в левую колонку выписываем исходное число, затем
Повторяем эти шаги, при этом работаем уже с последним числом в левой колонке и с текущим простым числом. Разложение заканчивается, когда в левой колонке будет записано число 1.
Чтобы лучше понять алгоритм, на примере разложим на множители число 84.
Записываем число 84 в левую колонку:
Берём первое простое число — два и проверяем, делится ли 84 на 2. Так как 84 оканчивается на 4, а 4 делится на 2, то и 84 делится на 2 по признаку делимости. Записываем 2 в правую колонку. 84:2 = 42, число 42 записываем в левую колонку. Получили вот что:
Теперь работаем уже с числом 42. Число 42 делится на 2, поэтому записываем 2 в правую колонку, 42:2 = 21, число 21 записываем в левую колонку.
Число 21 на 2 не делится, поэтому проверяем его делимость на следующее простое число — 3. Число 21 делится на 3, 21:3 = 7. Записали 3 в правую колонку, 7 — в левую. Получили
Число 7 — простое число, поэтому в правой колонке записываем 7, в левую пишем 1. В итоге получили:
Всё, число разложено!
В результате в правой колонке оказались записаны все простые множители числа 84. То есть 84=2∙2∙3∙7.
calculatorium.ru
Разложение числа на простые множители онлайн
Данный онлайн калькулятор производит разложение чисел на простые множители методом перебора простых делителей. Если число большое, то для удобства представления пользуйтесь разделителем разрядов.
Разложение числа на простые множители − теория, алгоритм, примеры и решения
Один из простейших способов разложить число на простые множители − это проверить, делится ли данное число на 2, 3, 5 ,… и т.д., т.е. проверить, делится ли число на ряд простых чисел. Если число n не делится ни на какое простое число до , то даннаое число является простым, т.к. если число составное, то имеет по крайней мере два множителя и оба они не могут быть больше .
Представим алгоритм разложения числа n на простые множители. Подготовим заранее таблицу простых чисел до s=. Обозначим ряд простых чисел через p1, p2, p3, …
Алгоритм разложения числа на простые делители:
- Исходный данные n, i=0, s=.
- Увеличить i: i=i+1.
- Если pi>s, то сохранить значение n и перейти к шагу 8.
- n делить на pi.
- Если n делится на pi, то сохранить значение pi. Вычислить k=n/pi. Брать в качестве n число k: n=k.
- Если n не делится на pi, то перейти к шагу 2.
- Если n≠1, перейти к шагу 4.
- Остановить процедуру.
Пример 1. Разложить число 153 на простые множители.
Решение. Нам достаточно иметь таблицу простых чисел до , т.е. 2, 3, 5, 7, 11.
Делим 153 на 2. 153 не делится на 2 без остатка. Далее делим 153 на следующий элемент таблицы простых чисел, т.е. на 3. 153:3=51. Заполняем таблицу:
Теперь проверяем, делится ли число 51 на 3. 51:3=17. Заполняем таблицу:
Далее проверяем, делится ли число 17 на 3. Число 17 не делится на 3. Оно не делится и на числа 5, 7, 11. Следующий делитель больше . Следовательно 17 простое число, которое делится только на себя: 17:17=1. Процедура остановлена. заполняем таблицу:
Выбираем те делители, на которых числа 153, 51, 17 делились без остатка, т.е. все числа с правой стороны таблицы. Это делители 3, 3, 17. Теперь число 153 можно представить в виде произведения простых чисел: 153=3·3·17.
Пример 2. Разложить число 137 на простые множители.
Решение. Вычисляем . Значит нам нужно проверить делимость числа 137 на простые числа до 11: 2,3,5,7,11. Поочередно делив число 137 на эти числа выясняем, что число 137 не делится ни на одно из чисел 2,3,5,7,11. Следовательно 137 простое число.
matworld.ru
Разложить на простые множители, калькулятор
Разложение чисел на простые множители
Это представление натурального числа a ? 1 в виде произведения простых чисел.
Калькулятор разложения чисел на простые множители
Пример
|
30 = 6 • 5;
12 = 2 • 2 • 3; 84 = 2 • 2 • 3 • 7. |
Основная теорема арифметики: каждое натуральное число, отличное от 1, может быть разложено на простые множители, при этом единственным образом.
Каноническое разложение числа a — разложение a на простые множители, в котором одинаковые сомножители объединены в степени.
Пример|
20 = 22 • 5;
84 = 22 • 3 • 7; 800 = 25 • 52. |
Схема разложения на простые множители
1. Найти наименьший простой делитель p1 числа a.
Разделить a на p1 — a : p1 = a1.
2. Найти наименьший простой делитель p2 числа a1.
Разделить a1 на p2 — a1 : p2 = a2.
3. Повторить эту же операцию для a2 и т.д.
4. Процесс закончен, когда частное an само является простым числом.
5. Записать разложение: a = p1 • p2 • … • pn • an .
Пример
 |
formula-xyz.ru
как записать сумму в виде произведения
Разложение числа на простые множители
Как раскладывать числа на множители?
Любое составное число можно представить в виде произведения его простых делителей:
15 = 3 · 5
28 = 2 · 2 · 7
Правые части полученных равенств называют разложением на простые множители чисел 15 и 28.
Разложить данное составное число на простые множители – значит представить это число в виде произведения его простых делителей.
Разложение данного числа на простые множители выполняется следующим образом:
- Сначала нужно подобрать самое маленькое простое число из таблицы простых чисел, на которое данное составное число делится без остатка, и выполнить деление.
- Далее, нужно опять подобрать самое маленькое простое число, на которое уже полученное частное будет делиться без остатка.
- Выполнение второго действия повторяют до тех пор, пока в частном не получится единица.
В качестве примера, разложим на простые множители число 940. Находим наименьшее простое число, на которое делится 940. Таким числом является 2:
940 : 2 = 470
Теперь подбираем наименьшее простое число, на которое делится 470. Таким числом является опять 2:
470 : 2 = 235
Наименьшее простое число, на которое делится 235 – это 5:
235 : 5 = 47
Число 47 простое, значит наименьшим простым числом, на которое делится 47, будет само это число:
47 : 47 = 1
Таким образом, мы получаем число 940, разложенное на простые множители:
940 = 2 · 470 = 2 · 2 · 235 = 2 · 2 · 5 · 47
Если в разложении числа на простые множители получилось несколько одинаковых сомножителей, то для краткости, их можно записать в виде степени:
940 = 22 · 5 · 47
Разложение на простые множители удобнее всего записывать следующим образом: сначала записываем данное составное число и справа от него проводим вертикальную черту:
Справа от черты записываем самый маленький простой делитель, на который делится данное составное число:
Выполняем деление и получившееся в результате деления частное записываем под делимым:
С частным поступаем так же, как и с данным составным числом, т. е. подбираем самое маленькое простое число, на которое оно делится без остатка и выполняем деление. И так повторяем до тех пор, пока в частном не получится единица:
Обратите внимание, что иногда бывает достаточно трудно выполнить разложение числа на простые множители, так как при разложении мы можем столкнуться с большим числом, которое сложно с ходу определить, простое оно или составное. А если оно составное, то не всегда легко найти его наименьший простой делитель.
Попробуем к примеру разложить на простые множители число 5106:
Дойдя до частного 851, трудно с ходу определить его наименьший делитель. Обращаемся к таблице простых чисел. Если в ней найдётся число, поставившее нас в затруднение, значит оно делится только на себя и на единицу. Числа 851 нет в таблице простых чисел, значит, оно является составным. Остаётся только методом последовательного перебора делить его на простые числа: 3, 7, 11, 13, …, и так до тех пор, пока не найдём подходящего простого делителя. Методом перебора находим, что 851 делится на число 23:
Таким образом, получаем число 5106, разложенное на простые множители:
5106 = 2 · 3 · 23 · 37
Калькулятор разложения на множители
Данный калькулятор поможет вам выполнить разложение числа на простые множители. Просто введите число и нажмите кнопку .
Вопрос к ученому: Я слышал, что сумма всех натуральных чисел равна -1/12. Это какой-то трюк или это правда?
Отвечать Пресс-служба МФТИ — Да, такой результат может быть получен с помощью расширения, называемого расширением функции в строке.
Вопрос, заданный читателем, довольно сложный, поскольку мы отреагировали на это, это не обычная категория «учебный вопрос» с текстом в нескольких точках, а также очень упрощенный способ математических статей.
В научных статьях по математике, где необходимо доказать некоторую сложную теорему, рассказ делится на несколько частей, и в них также могут быть показаны различные вспомогательные утверждения.
Мы предполагаем, что читатели знакомы с курсом математики в девяти классах, поэтому я заранее извиняюсь за тех, кто кажется слишком простым рассказом — выпускники могут перейти непосредственно к http://en.wikipedia.org/wiki/Ramanujan_summation.
Общая сумма
Давайте начнем говорить о том, как вы можете добавить все натуральные числа. Естественные числа — это числа, используемые для подсчета всех объектов — все они целые и отрицательные.
Это естественное число, которое дети впервые изучают: 1, 2, 3 и так далее. Сумма всех натуральных чисел есть выражение вида 1 + 2 + 3 + … = и т. Д. До бесконечности.
Серия натуральных чисел бесконечна, ее легко доказать: потому что вы всегда можете добавить ее к любому большому числу. Или даже умножить это число на себя или даже вычислить его коэффициент — ясно, что будет еще большее значение, которое также будет естественным числом.
Точнее, все операции с бесконечно большими величинами классифицируются в математическом анализе, но теперь, чтобы понять тех, кто еще не завершил этот курс, мы немного упростим суть.
Будем говорить, что бесконечность, к которой была добавлена единица, бесконечность, которая была квадратной или фактор бесконечности, также бесконечна.
Онлайн калькулятор. Число разделено.
Предположим, что бесконечность является таким специальным математическим объектом.
И согласно всем правилам математического анализа в первом семестре сумма бесконечности 1 + 2 + 3 + … + бесконечна.
Это легко понять из предыдущего параграфа: если вы добавите что-то в бесконечность, оно все равно будет бесконечным.
Однако в 1913 году блестящий индийский независимый математик Шриниваса Рамануджан Айенгор придумал способ добавить немного другое число к натуральному числу.
Несмотря на то, что Рамануджан не получал специального образования, его знания не ограничивались нынешней школьной учебной программой — математик знал о существовании формулы Эйлера-Маклорена.
Поскольку он играет важную роль в будущем повествовании, его необходимо будет объяснить более подробно.
Формула Эйлера-Маклорена
Сначала напишите эту формулу:
Как вы можете видеть, это довольно сложно.
Некоторые читатели могут вообще пропустить этот раздел, некоторые могут прочитать соответствующие учебники или, по крайней мере, статью в Википедии, а в остальном мы дадим короткий комментарий.
Ключевую функцию в формуле играет произвольная функция f (x), которая может быть почти любой, если имеет достаточное число производных.
Для тех, кто не знаком с этой математической концепцией (и решил прочитать ее здесь!), Скажем еще проще — график функций не должен быть линией, которая останавливалась бы на каждом шаге.
Производная функции, если ее значение упрощается, является значением, которое показывает, как быстро функция увеличивается или уменьшается. С геометрической точки зрения получается касательный угол наклона касательной к графу.
Слева от формулы сумма формы представляет собой значение f (x) в точке m + значение f (x) в точке m + 1 + значение f (x) в точке m + 2 и так далее до точки m + n «.
В этом случае m и n естественны, это следует подчеркнуть.
Справа мы видим несколько компонентов, которые кажутся довольно смущающими.
Первый (конец с dx) является интегралом функции от точки m до точки n. Учитывая опасность того, что гнев всего математического факультета приведет к примитивному подходу к интегралам, предположим, что эта область находится под кривой f (x) на графике от m до n; Интегралы очень часто используются в различных науках.
На графике «по горизонтальной оси — время, по интегралу от вертикальной скорости», т. Е. Площадь под кривой, будет равным пройденному расстоянию.
График «ежемесячные платежи в вертикальном, горизонтальном времени» является неотъемлемой суммой, которая всегда находилась в счете за все время.
Второй член, обозначенный B1 (f (n) + f (m)), является так называемым числом Бернулли.
Третий член — сумма Бернулли (B2K), деленная на удвоение способности числа k, умноженная на разность между производными функции f (x) в точках, n и m.
Более того, делая проблему еще более сложной, это не просто производная производная, а производная от порядка 2k-1. Это означает, что весь третий термин выглядит следующим образом:
Числа Бернулли B2 («2», как в формуле 2k и времена начала sk = 1), деленные на коэффициент 2 (это все еще только Deuce) и умножаются на разницу первого порядка (2k-1, где k = 1) функционала f (x) в точках n и m
+
Число Бернулли B4 («4», так как формула 2k и k теперь равна 2), деленная на коэффициент 4 (1 x 2×3 x 4 = 24) и умноженная на разницу между функцией третьего порядка (2k-1, sk = 2) f (x) в точках n и m
+
Число Бернулли B6 (см. Выше), деленное на 6 факторов (2×3 1 xxx 6 4×5 = 720), умноженное на разность между производными пятого порядка (2k-1, где k = 3) функции f (x) в n точках и m
+
Сбор продолжается до k = p.
Числа k и p получаются с произвольными произвольными значениями, которые вместе с m и n могут быть выбраны иначе, являются натуральными числами, которые рассматриваемый отрезок ограничивает функцию f (x).
Это означает, что в формуле есть четыре параметра, которые вместе с произволом функции f (x) открывают много возможностей для исследования.
Оставшаяся скромная R, к сожалению, не является постоянной, но также довольно громоздкой конструкцией, выраженной уже упомянутыми числами Бернулли.
Настало время объяснить, что это такое, откуда оно исходит и почему математики начали думать о таких сложных терминах.
Числа и числа Бернулли
Таким образом, математический анализ является ключевым понятием и расширением серии.
Это означает, что он может принимать все функции и не писать напрямую (например, y = sin (x ^ 2) + 1 / ln (x) + 3x), а также бесконечная сумма нескольких подобных выражений. Например, многие функции могут быть представлены как сумма степенных функций, умноженных на некоторые коэффициенты — это означает, что сложная форма графика сводится к комбинации линейных, квадратных, кубических …
и т. д. — кривые.
В теории обработки электрических сигналов так называемая серия Фурье имеет исключительную роль — каждая кривая может расширяться в ряд синусов и косинусов разных периодов; такое разложение необходимо для преобразования сигнала от микрофона в последовательность нуль и внутри, скажем, в электронную схему мобильного телефона. Расширения в серии позволяют учесть неэлементарные функции, и многие из наиболее важных физических уравнений в решении дают точные выражения в виде ряда, а не в виде определенной конечной комбинации функций.
В XVII веке математики начали тесно сотрудничать в теории серии.
Несколько позже он позволил физикам эффективно рассчитать процессы нагрева различных объектов и решить многие другие проблемы, которые мы здесь не будем учитывать. Подчеркнем, что хотя бы один семестр предназначен для уравнений с решениями в виде определенной серии в программе МФТИ и математических курсов всех ведущих физических университетов.
Яков Бернулли изучал задачу объединения натуральных чисел в равной мере (1 ^ 6 + 2 ^ 6 + 3 ^ 6 + …
например) и числа, полученные, с помощью которых можно распространить другие функции, например tg (x), на вышеупомянутые степенные ряды. Хотя кажется, что тангенс по крайней мере не очень похож на параболу, даже с любой мощной функцией!
Полиномы Бернулли позже нашли свое применение не только в уравнениях математики, но и в теории вероятности.
Это, как правило, предсказуемо (ведь число физических процессов, таких как броуновское движение или сбой ядер, является результатом всех видов случайности), но все же заслуживает особого упоминания.
-1/12
Сложная формула Эйлера-Маклорена использовалась математиками для различных целей.
Поскольку, с одной стороны, сумма значения функции находится в некоторых точках, а с другой — они являются интегралами и расширением ряда, используя эту формулу, которая (в зависимости от того, что мы знаем), как комплекс будет интегральным и определить сумму лота.
Шриниваса Рамануджан сформулировал еще одну формулу для этой формулы.
Он немного изменил его и получил следующее выражение:
В функции f (x) изучалось просто x — пусть f (x) = x, это вполне законное предположение. Но для этой функции первая производная равна единице, а другая все равно нулю: если все точно заменено вышеуказанным термином и определяются соответствующие числа Бернулли, мы получаем только -1/12.
Конечно, это видел индийский математик как нечто обычное.
Поскольку он был не только самонаучным человеком и одаренным человеком-самоучкой, он не рассказывал всем о трепете основополагающего открытия математики и вместо того, чтобы писать письмо Годфри Харди, известного специалиста по нумерологии и математическому анализу. Кстати, кстати, в письме содержалось добавление, что Харди, вероятно, хотел подчеркнуть автора в ближайшей психиатрической больнице: конечно, результат был не клинике, а совместной работой.
парадокс
Суммируя все вышесказанное, получаем следующее: сумма всех натуральных чисел получается равной -1/12 при использовании специальной формулы, которая позволяет распространить любую функцию на строку с коэффициентами, называемыми номерами Бернулли.
Но это не означает, что 1 + 2 + 3 + 4 больше 1 + 2 + 3 + … и так далее до бесконечности. В этом случае мы имеем дело с парадоксом, который является следствием того факта, что расширение является своего рода приближением и упрощением.
Можно привести пример гораздо более простого и более очевидного математического парадокса, связанного с выражением чего-то другого через что-то другое.
Вставьте лист бумаги в коробку и нарисуйте линию шириной и высотой ступени в одной клетке. Длина такой линии, очевидно, равна удвоению числа ячеек, но длина прямой «диаграммы» равна числу клеток, умноженному на корень обоих. Если вы сделаете лестницу очень мелкой, она все равно будет иметь одинаковую длину, а ломаная линия, которая практически не отличается от диагонали, будет в корне двукратной большей диагонали!
Как вы можете видеть, нет необходимости писать сложные сложные формулы для парадоксальных случаев.
Формула Эйлера-Маклаурина, если она не входит в беспорядок математического анализа, такая же, как и шероховатая линия, а не плоскость. С этим приближением вы можете получить очень -1/12, но это не всегда уместно и оправдано.
Число теоретических физических проблем такие расчеты используются для расчетов, но это передовая наука, которая слишком рано говорить о правильном представлении математической абстракции реальности и отклонении разных расчетов друг с другом — очень распространенная вещь.
Таким образом, оценки энергетического вакуума, основанные на квантовой теории поля и астрофизических наблюдениях, различаются более чем на 120 порядков.
Это для 10 ^ 120 градусов. Это одна из нерешенных проблем современной физики; Очевидно, есть пробел в наших знаниях о Вселенной. Или проблема заключается в отсутствии соответствующих математических методов для описания окружающего мира. Теоретическая физика в сотрудничестве с математиками пыталась найти способы описания физических процессов, которые будут возникать дивергентно (до бесконечности) серии, но это непростая задача.
Темы: фундаментальная наука, вопрос ученого,
Разложить на простые множители, калькулятор
Виленкин домашняя по математике 5 класс ответы гдз | |||
| |||
| Контент опубликованный на сайте vcevce.ru защищен законом об авторском праве. Любое частичное или полное копирование опубликованной информации запрещено. © |
Численная последовательность — это особый пример числовой функции, поэтому для последовательности также учитывается множество последовательностей функций.
1. Определение.Последовательность {уп} увеличивается, если каждый из его членов (кроме первого) больше предыдущего:
Y1 < Y2 < Y3 < …< уп < уп+1 < ….
2. Определение. Последовательность {уп} называется сокращением, если каждый его член (кроме первого) меньше предыдущего:
Y1 > Y2 > Y3 > … > уп > уп+1 > ….
третий
Возрастающие и уменьшающиеся последовательности объединяют общий термин — монотонные последовательности.
Например: Y1 = 1; уп = N2 … является восходящей последовательностью. Y1 = 1; Уменьшение последовательности.
Калькулятор факторной факторизации
Y1 = 1; — эта последовательность не всегда больше, если она не уменьшается.
4. Определение. Последовательность считается периодической, если существует натуральное число T, так что оно начинается с n, yn = yn + T.
T-номер называется длительностью периода.
5. Последовательность должна быть ограничена ниже, если все ее термины не меньше определенного числа.
6. Приказ должен быть ограничен выше, если все его термины не превышают определенного числа.
7. Последовательность ограничена, если она ограничена сверху и снизу, т.е. существует положительное число, так что все выражения определенной последовательности не превышают этого числового модуля. (Но его граница с обеих сторон не обязательно означает, что она конечна).
восьмых
Последовательность может иметь только одно ограничение.
9. Любые нескорректированные и ограниченные по последовательности имеют предел (lim).
10. Любые неустойчивые и ограниченные в последовательности ограничения.
Границей последовательности является такая точка (число), в окрестности которой расположена большая часть последовательностей, и лучи приближаются к этой границе, но не достигают ее.
Геометрические и арифметические прогрессии являются особыми примерами последовательности.
Методы определения последовательности:
Последовательности могут быть определены различными способами, из которых три имеют особое значение: аналитические, описательные и повторяющиеся.
первый
Последовательность задается аналитически, если дана формула n-го члена:
yn = f (n).
Пример. yn = 2n — 1 — последовательность нечетных чисел: 1, 3, 5, 7, 9, …
2. Описательный метод определения числовой последовательности состоит в том, чтобы объяснить элементы, из которых построена последовательность.
Пример 1. «Все члены последовательности равны 1».
Это означает, что речь идет о стационарной последовательности 1, 1, 1, …, 1, ….
Пример 2. «Последовательность состоит из всех элементов в порядке возрастания».
Таким образом, задана последовательность 2, 3, 5, 7, 11, … Этот метод определения последовательности в этом случае трудно ответить, а именно, например, 1000-й элемент в последовательности.
3. Повторяющимся методом определения последовательности является определение правила, которое позволяет вам вычислить n-й член последовательности, если известны его предыдущие термины.
Имя повторения происходит от латинского слова recurrere — для возврата. Чаще всего в таких случаях вы можете определить формулу, которая позволяет вам выразить n-й член последовательности по сравнению с предыдущими и определить 1-2 последовательности последовательных последовательностей.
Пример 1.
y1 = 3; yn = yn-1 + 4, если n = 2, 3, 4, ….
Здесь y1 = 3; y2 = 3 + 4 = 7; y3 = 7 + 4 = 11; ….
Мы можем видеть, что полученная в этом случае последовательность может быть аналитически задана: yn = 4n — 1.
Пример 2.
Y1 = 1; Y2 = 1; уп = уп-2 + уп-1 если N = 3, 4, ….
здесь: Y1 = 1; Y2 = 1; Y3 = 1 + 1 = 2; Y4 = 1 + 2 = 3; Y5 = 2 + 3 = 5; Y6 = 3 + 5 = 8;
Последовательность, скомпилированная в этом случае, исследуется, в частности, в математике, поскольку она имеет много интересных свойств и приложений.
Это называется последовательностью Фибоначчи, названной в честь итальянской математики XIII века. Последовательность фибоначчи очень легко повторить, но аналитически это очень сложно. N-Число Фибоначчи выражается в соответствии со следующей формулой .
На первый взгляд существует формула для N-го числа Фибоначчи представляется маловероятным, так как в формуле, определяющей последовательность натуральных чисел, содержатся квадратные корни, но вы можете проверить «ручную» справедливость этой формулы для первых нескольких N.
История Фибоначчи:
Фибоначчи (Леонардо из Пизы), ок.
Итальянский математик. Он родился в Пизе, он стал первым великим математиком Европы в позднем средневековье. В математике он руководствовался практической необходимостью установления деловых контактов.
Он опубликовал свои книги по арифметике, алгебре и другим математическим дисциплинам. Мусульманские математики узнали о количестве изобретенной в Индии системы и уже приняли ее в арабском мире и убедились в ее превосходстве (эти цифры являются предшественниками современных арабских цифр).
Леонардо в Пизе, известный как Фибоначчи, был первым из великих математиков Европы в позднем средневековье.
Когда он родился в Пизе в богатой торговой семье, он внес свой вклад в математику благодаря чисто практической необходимости налаживания деловых контактов. В молодости Леонардо много путешествовал и сопровождал отца в командировках. Например, мы знаем о его долгом пребывании в Бизанке и Сицилии. Во время таких поездок он много говорил с местными учеными.
Численный ряд с его именем сегодня вырос из трудностей кроликов, которые Фибоначчи цитирует в своей книге «Liber abacci», пишет в 1202 году:
Человек посадил некоторых кроликов в кораллы, которые окружали стену вдоль стороны.
Сколько пар кроликов может произвести эту пару за год, если известно, что каждая пара, друг от друга, производит пару кроликов каждый месяц?
Он может обеспечить, чтобы количество пар находилось в каждом из двенадцати последовательных месяцев месяцев или 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Другими словами, количество пар кроликов создает серию, каждый член которой имеет сумму двух предыдущих. Он известен как ряд Фибоначчи, а числа — числа Фибоначчи.
Оказалось, что эта последовательность имеет много интересных свойств с точки зрения математики. Вот пример: раздел можно разделить на два сегмента, чтобы соотношение между большим и меньшим сегментами было пропорционально отношению между всей линией и большим сегментом. Этот пропорциональный коэффициент, приблизительно равный 1,618, известен как золотой коэффициент. В эпоху Возрождения вполне вероятно, что эта пропорция, которая заметна в архитектурных сооружениях, наиболее приятна для глаз.
Если вы возьмете последовательные пары из серии Фибоначчи и разделите большее число от каждой пары до меньшей, ваш счет будет постепенно приближаться к золотой части.
Поскольку Фибоначчи обнаружил свою последовательность, были обнаружены даже природные явления, в которых эта последовательность играет важную роль. Один из них — fillotaxis (регулирование листьев) является правилом, например, семян подсолнечника. Семена подсолнечника подсолнечника расположены по двум спиральным путям.
Цифры, указывающие количество семян в каждой спирали, являются членами невероятной математической последовательности. Семена расположены в двух видах спирали, один из которых движется по часовой стрелке, а другой против. И каково количество семян в любом случае? 34 и 55.
Задача № 1:
Напишите первые пять членов последовательности.
1. an = 2n + 1 / 2n
решение:
an = 2n + 1 / 2n
Ответ:
Задача № 2:
Напишите формулу для общего выражения последовательности натуральных чисел с более чем 3.
Ответ: 0,3,6,9,12,15, ….
3n, an = 3n
Задача 3:
Напишите формулу для общего выражения последовательности натуральных чисел, которая, если она разделена на 4, задана в вычете 1.
Ответ: 5,9,13,17,21 ……. 4n +1, an = 4n + 1
№19. Функция.
Функция (отображение, оператор, преобразование) является математическим понятием, которое отражает взаимосвязь между элементами масс. Можно сказать, что функция является «законом», с которой каждый элемент одного набора (называемый областью определения) связан с элементом второго множества (называемым диапазоном значений).
Функция — это зависимость одной переменной от другой.
Другими словами, соотношение между величинами.
Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение второй величины. Следовательно, значение переменной x однозначно определяет значение выражения , и значение месяца однозначно определяет стоимость следующего месяца, и любой человек может связаться с другим человеком — отцом.
Аналогичным образом, определенный предопределенный алгоритм с различными входными данными создает определенные выходные данные.
Часто термин «функция» является числовой функцией; это функция, которая устанавливает одно число в соответствии с другим. Эти функции показаны на графике на рисунке.
Мы можем дать другое определение. Определенная функция вверх над переменной.
Это означает, что мы берем значение , выполнить с ним определенное действие (например, квадрат или вычислить его логарифм) — и получить значение .
Давайте добавим еще одно определение функции — то, что обычно встречается в учебниках.
Функция представляет собой соответствие между двумя массивами, каждый элемент первого набора, соответствующий одному и только одному элементу второго массива.
Например, функция каждому действительному числу число в два раза выше .
Множество элементов некоторого Ф, которое заменяется на х, называется областью его определения и множеством элементов некоторого Ф
называемый диапазоном его значений.
Срок выражения:
Термин «функция» (в его узком смысле) был впервые использован Лейбницем (1692). В письме к тому же Лейбнице Иоганн Бернулли приблизил этот термин к современнику. Первоначально концепция функции не отличалась от концепции аналитического представления. Затем пришло определение функции, заданной Эйлером (1751), а затем — в Лакруа (1806) — почти в современном виде.
Наконец, это было общее определение функции (в современном виде, но для численных функций) относительно Лобачевского (1834) и Дирихле (1837). К концу XIX. На протяжении столетий понятие функции превышало рамки численных систем. Первые сделали векторные функции, Фреге вскоре ввели логические функции (1879), а после теории масс Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение.
№20.
Методы определения функции.
Существует 4 способа определения функции:
1. Табличный Частенько настраивать персональную таблицу
значение аргумента и соответствующее значение функции. Этот метод определения функции используется, если область определения функции является дискретной конечной строкой.
| х | x1 | x2 | x3 | x4 |
| Y | Y1 | y2 | y3 | y4 |
Уместно, что если f — конечная строка, когда f бесконечна, указываются только выбранные пары (x, y).
С помощью табличного метода определения функции мы можем грубо рассчитать значения функции, которые не содержатся в таблице, которые соответствуют промежуточным значениям аргумента.
Для этой цели используется метод интерполяции.
льготы: точность, скорость, таблица значений, легко найти требуемое значение функции. Преимущества табличного метода определения функции — это те, которые позволяют определять эти или другие конкретные значения одновременно без дополнительных измерений или расчетов.
слабые стороны: несовершенство, отсутствие видимости.
В некоторых случаях таблица определяет функцию не полностью, но только для некоторого значения аргумента и не обеспечивает визуального представления о характере изменения функции в зависимости от изменения аргумента.
второй
аналитически (Формулы). Наиболее распространенным является закон, устанавливающий связь между
аргумент и функция задаются с помощью формул. Этот метод определения функции называется аналитическим. Это наиболее важно для MA (математический анализ), потому что метод MA (дифференциальный, интегральный учет) принимает этот метод распределения.
Такую же функцию можно получить с помощью разных формул: Y= | Сын (х) |Y= √1-cos2 (х) Иногда в разных частях их доменов можно определить функцию с разными формулами е(х) = {е1 (х)х∈D1 сноска(х)х∈включенные в другие группировки ∪пк= 1Dk=D(е).
Часто с помощью этого метода определения функции области определения он не определен, тогда область определений области естественного определения, например. группа всех значений х, для которых функция действительно есть.
Этот метод позволяет каждому числовому значению аргумента x точно или точно определять соответствующее числовое значение y.
Особый пример аналитического метода определения функции состоит в том, чтобы дать функцию уравнения вида F (x, y) = 0 (1) Если это уравнение обладает тем свойством, что ∀ходнозначно Y, так, да F(х,Y) = 0, то мы говорим, что уравнение (1) на D неявно определяет функцию.
Другой частный случай определения функции является параметрическим, причем каждая пара (х,Y) ∈е определяется с помощью пары функций х= φ (T)Y= ψ (T), где T∈M.
⇐ previous3456789101112Следующий ⇒
Дата выпуска: 2015-02-03; Читать: 1376 | Нарушение авторских прав
studopedia.org — Studopedia.Org — 2014-2018 лето (0,006 сек) …
Разложение чисел с первичными множителями
Это представление натурального числа стоит? 1 в виде простого числа.
Калькулятор факторного коэффициента в простых коэффициентах
пример:
| 30 = 6 • 5; 12 = 2 • 2 • 3; 84 = 2 • 2 • 3 • 7. |
Основная теорема арифметики: любое натуральное число, отличное от 1, может быть распространено на основные факторы, в данном случае уникальным образом.
Каноническое разложение числа — дезинтеграция к основным факторам, в которых одни и те же факторы объединены в юрисдикции.
пример:
| 20 = 2 • 5; 84 = 2 • 3 • 7; 800 = 2 • 5. |
Схема факторинга
первый Найти наименьший простой делитель р? номер .
Калькулятор факторной факторизации
делить на р — a: p = a.
второй Найти наименьший простой делитель р номер .
делить на р — a: p = a.
третий Повторите для той же операции и так далее.
четвёртая Процесс заканчивается, когда он закрыт это главное число.
пятые Напишите разбивку: a = p • p • … • p • a .
пример:
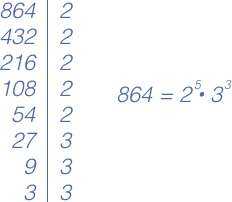 |
{jcomments on}
vipstylelife.ru
Факторизация целых чисел. Перебор делителей
Понадобилось тут научиться раскладывать целые числа на множители. Посколько числа предполагаются не сильно большие, то написал калькулятор разложения числа на множители методом перебора делителей. Описание метода — под калькулятором.
Факторизация
Сохранить share extension
Факторизация целых чисел
Факторизацией натурального числа называется его разложение в произведение простых множителей.
Не будет далеко уходить от Википедии, и скажем, что метод перебора возможных делителей, или метод пробного деления — наиболее тривиальный алгоритм факторизации, с вычислительной сложностью , где N — число, подлежащее факторизации.
Далее описание, которое можно прочитать по ссылке на Википедию выше:
Обычно перебор делителей заключается в переборе всех целых (как вариант: простых) чисел от 2 до квадратного корня из факторизуемого числа n и в вычислении остатка от деления n на каждое из этих чисел. Если остаток от деления на некоторое число m равен нулю, то m является делителем n. В этом случае либо n объявляется составным, и алгоритм заканчивает работу (если тестируется простота n), либо n сокращается на m и процедура повторяется (если осуществляется факторизация n). По достижении квадратного корня из n и невозможности сократить n ни на одно из меньших чисел, n объявляется простым.
Для ускорения перебора часто не проверяются чётные делители, кроме числа 2, а также делители кратные трём, кроме числа 3. При этом тест ускоряется в три раза, так как из каждых шести последовательных потенциальных делителей необходимо проверить только два, а именно вида 6·k±1, где k — натуральное число.
Почему квадратный корень из n?
Опять же, из Википедии: Легко заметить, что если у n есть некоторый делитель p, то n/p также будет делителем, причём один из этих делителей не превосходит .
По-моему, достаточно исчерпывающе.
planetcalc.ru
