Разложение функции в ряд Тейлора, Маклорена, Лорана
Разложение функции в ряд Тейлора, Маклорена и Лорана на Math34.biz для тренировки практических навыков. Это разложение функции в ряд дает представление математикам оценить приближенное значение функции в некоторой точки области ее определения. Намного проще вычислить такое значение функции, по сравнению с применением таблицы Бредиса, так неактуальной в век вычислительной техники. В ряд Тейлора разложить функцию означает вычислить коэффициенты перед линейными функциями этого ряда и записать это в правильном виде. Путают студенты эти два ряда, не понимая, что является общим случаем, а что частным случаем второго. Напоминаем раз и навсегда, ряд Маклорена — частный случай Тейлоровского ряда, то есть это и есть ряд Тейлора, но в точке x = 0. Все краткие записи разложения известных функций, таких как e^x, Sin(x), Cos(x) и другие, это и есть разложения в ряд Тейлора, но в точке 0 для аргумента. Для функций комплексного аргумента ряд Лорана является наиболее частой задачей в ТФКП, так как представляет двусторонний бесконечный ряд. Он и является суммой двух рядов. Мы предлагаем вам посмотреть пример разложения прямо на сайте Math34.biz, это сделать очень просто, нажав на «Пример» с любым номером, а затем кнопку «Решение». Именно такому разложению функции в ряд сопоставлен мажорирующий ряд, ограничивающий функцию исходную в некоторой области по оси ординат, если переменная принадлежит области абсцисс. Векторному анализу поставляется в сравнение другая интересная дисциплина в математике. Поскольку исследовать нужно каждое слагаемое, то необходимо достаточно много времени на процесс. Всякому ряду Тейлора можно сопоставить ряд Маклорена, заменив x0 на нуль, а вот по ряду Маклорена порой не очевидно представление ряда Тейлора обратно. Как бы это и не требуется делать в чистом виде, но интересно для общего саморазвития. Всякому ряду Лорана соответствует двусторонний бесконечный степенной ряд по целым степеням z-a, другими словами ряд вида того же Тейлора, но немного отличающегося вычислением коэффициентов. Про область сходимости ряда Лорана расскажем чуть позже, после нескольких теоретических выкладок. Как и в прошлом веке, поэтапного разложения функции в ряд вряд ли можно достичь только лишь приведением слагаемых к общему знаменателю, так как функции в знаменателях нелинейные. Приближенное вычисление функционального значения требует постановка задач. Задумайтесь над тем, что когда аргумент ряда Тейлора есть линейная переменная, то разложение происходит в несколько действий, но совсем другая картина, когда в качестве аргумента раскладываемой функции выступает сложная или нелинейная функция, тогда очевиден процесс представления такой функции в степенной ряд, поскольку, таким образом, легко вычислить, пусть и приближенное, но значение в любой точке области определения, с минимальной погрешностью, мало влияющей на дальнейшие расчеты. Это касается и ряда Маклорена. когда необходимо вычислить функция в нулевой точке. Однако сам ряд Лорана здесь представлен разложением на плоскости с мнимыми единицами. Также не без успеха будет правильное решение задачи в ходе общего процесса. В математике такого подхода не знают, но он объективно существует. В результате вы можете прийти к выводу так называемых поточечных подмножеств, и в разложении функции в ряд нужно применять известные для этого процесса методы, таких как применение теории производных. Лишний раз убеждаемся в правоте учителя, который сделал свои предположения на счет итогов пост вычислительных выкладок. Давайте отметим, что ряд Тейлора, полученный по всем канонам математики, существует и определен на всей числовой оси, однако, уважаемые пользователи сервиса Math34.biz, не забывайте вид исходной функции, ведь может получиться так, что изначально необходимо установит область определения функции, то есть выписать и исключить из дальнейших рассмотрений те точки, при которых функция не определена в области действительных чисел. Так сказать это покажет вашу расторопность при решении задачи. Не исключением высказанного будет и построение ряда Маклорена с нулевым значением аргумента. Процесс нахождения области определения функции никто при этом не отменял, и вы обязаны подойти со всей серьезностью к этому математическому действию. В случае содержания рядом Лорана главной части, параметр «a» будет называться изолированной особой точкой, и ряд Лорана будет разложен в кольце — это пересечение областей сходимости его частей, отсюда будет следовать соответствующая теорема. Но не все так сложно как может показаться на первый взгляд неопытному студенту. Изучив как раз ряд Тейлора, можно с легкостью понять ряд Лорана — обобщенный случай на расширение пространства чисел. Любое разложение функции в ряд можно производить только в точке области определения функции. Следует учитывать свойства таких функций, например, как периодичность или бесконечная дифференцируемость. Также предлагаем вам воспользоваться таблицей готовых разложений в ряд Тейлора элементарных функций, поскольку одна функция может быть представлена до десятков отличных от друг друга степенных рядов, что можно видеть из применения нашего калькулятора онлайн. Онлайн ряд Маклорена проще простого определить, если воспользоваться уникальным сервисом Math34.biz, вам достаточно только ввести правильную записанную функцию и представленный ответ получите в считанные секунды, он будет гарантированно точным и в стандартно записанном виде. Можете переписать результат сразу в чистовик на сдачу преподавателю. Правильно бы сначала определить аналитичность рассматриваемой функции в кольцах, а затем однозначно утверждать, что она разложима в ряд Лорана во всех таких кольцах. Важен момент чтобы не упустить из вида содержащие отрицательных степеней членов ряда Лорана. На этом сосредоточьтесь как можно сильнее. Применяйте с пользой теорему Лорана о разложении функции в ряд по целым степеням.
math24.biz
Разложение в ряд Тейлора основных элементарных функций — ПриМат
Перед тем прочтением данной статьи следует просмотреть следующий материал определение многочлена Тейлора, Остатки формулы Тейлора, Коэффициенты Тейлора, ряд Тейлора.
Запишем разложения основных элементарных функций в ряд Тейлора в окрестности точки $x_{0}=0$, т.е. в ряд вида $f(x)=$$\sum\limits _{ n=0 }^{ \infty }{ \frac { { f }^{ (n) }(0) }{ n! } } { x }^{ n }$ (1), который называется рядом Маклорена.
Показательная и гиперболические функции
Пусть $f(x)=e^{x}$. Найдем производные функции: ${f}'(x)= e^{x}$, $f^{\prime\prime}( x )=e^{x}$,$\ldots$,$f^{(n)}(x)=e^{x}$. Тогда $0 < f(x) < e^{\rho }$, $0 < f^{(n)}(x) < e^{\rho }$ для любого $x\in(-\rho ,\rho )$, где $\rho > 0$ и для любого $n\in \mathbb{N}$.
Из теоремы о представлении функции в виде ее ряда Тейлора (Курс математического анализа, ст.437) следует, что ряд (1) для $f(x)=e^{x}$ сходится к этой функции на интервале $(-\rho ,\rho )$ при любом $\rho > 0$. Так как для функции $f(x)=e^{x}$ выполняются $f(0)=1$, $f^{(n)}(0)=1$ для всех $n\in \mathbb{N}$, то, по формуле (1), получаем разложение в ряд Маклорена показательной функции:
$$e^{x}=1+x+\frac{x^{2}}{2!}+ \ldots +\frac{x^{n}}{n!}+ \ldots = \sum_{n=0}^{\infty }\frac{x^{n}}{n!}, x\in \mathbb{R} (2)$$
Используя разложение (2), синус и косинус $\text{sh} \, x=\frac{e ^{x}-e ^{-x}}{2}$, $\text{ch} \, x=\frac{e ^{x}+e ^{-x}}{2}$, находим:
$$\text{sh} \, x=x+\frac{x^{3}}{3!}+ \ldots +\frac{x^{2n+1}}{(2n+1)!}+ \ldots =$$ $$=\sum_{n=0}^{\infty }\frac{x^{2n+1}}{(2n+1)!}, x\in \mathbb{R} (3)$$
$$\text{ch} \, x=1+\frac{x^{2}}{2!}+ \ldots +\frac{x^{2n}}{(2n)!}+ \ldots =$$ $$=\sum_{n=0}^{\infty }\frac{x^{2n}}{(2n)!}, x\in \mathbb{R} (4)$$
Радиус сходимости $R=+\infty $.
Тригонометрические функции
Пусть $f(x)=\sin x$. Найдем производные функции: ${f}'(x)= \cos x$, $f^{\prime\prime}(x)= -\sin x$,$\ldots$,$f^{(n)}(x)=\sin x$ при $n$ — четное. Тогда $\left | f^{(n)}(x) \right | \leq 1$, для любого $n\in \mathbb{N}$ и для любого $x\in \mathbb{R}$.
Из теоремы о представлении функции в виде ее ряда Тейлора (Курс математического анализа, ст.437) ряд (1) для $f(x)=\sin x$ сходится для любого $x\in (-\infty , \infty )$. Радиус сходимости $R=+\infty$.
Если $f(x)=\sin x$, то $f(0)=0$, $f^{(2n)}(0)=0$, ${f}'(0)=1$, $f^{(2n+1)}(0)=(-1)^{n}$ для любого $n\in \mathbb{N}$, и, по формуле (1), получаем разложение в ряд Маклорена:
$$\sin x =x-\frac{x^{3}}{3!}+ \ldots +(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}+ \ldots =$$ $$=\sum_{n=0}^{\infty }(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}, x\in \mathbb{R} (5)$$
Пусть $f(x)=\cos x$. Найдем производные функции: ${f}'(x)= -\sin x$, $f^{\prime\prime}(x)= -\cos x$,$\ldots$,$f^{(n)}(x)=\cos x$ при $n$ — четное. Тогда $\left | f^{(n)}(x) \right | \leq 1$, для всех $x\in \mathbb{R}$, $n\in \mathbb{N}$, $f(0)=1$, ${f}'(0)=0$, $f^{(2n)}(0)=(-1)$, $f^{(2n+1)}(0)=0$ для всех $n\in \mathbb{N}$. По формуле (1):
$$\cos x =1-\frac{x^{2}}{2!}+ \ldots +(-1)^{n}\frac{x^{2n}}{(2n)!}+ \ldots =$$ $$=\sum_{n=0}^{\infty }(-1)^{n}\frac{x^{2n}}{(2n)!}, x\in \mathbb{R} (6)$$
Радиус сходимости $R=+\infty$.
Логарифмическая функция
Пусть $f(x)=\ln(1+x)$. Тогда $$f^{(n)}(x)=\frac{(-1)^{(n-1)}(n-1)!}{(1+x)^{n}} (7),$$ откуда находим $$\frac{f^{(n)}(0)}{n!}=\frac{(-1)^{(n-1)}}{n}.$$
Оценим остаток по формуле остаточного члена в интегральной форме: $$r_{n}=\frac{1}{n!}\int\limits_{0}^{x}(x-t)^{n}f^{(n+1)}(t)dt=\frac{x^{(n+1)}}{n!}\int\limits_{0}^{1}(1-\tau )^{n}f^{(n+1)}(\tau x)d\tau.$$ Используя равенство (7), получаем $$r_{n}=(-1)^{n}x^{n+1}\int\limits_{0}^{1}\frac{(1-\tau )^{n}}{(1+\tau x)^{n+1}}d\tau.$$ Пусть $\left | x \right |
Пусть $x=1$. Тогда $\left | r_{n}(1) \right |=$$\int\limits_{0}^{1}\frac{(1-\tau )^{n}}{(1+\tau )^{n+1}}d\tau$$ \leq \int\limits_{0}^{1}(1-\tau )^{n}d\tau$$ =\frac{1}{n+1}$ $\rightarrow 0.$
Если $x\in (-1,1]$, то остаточный член $r_{n}(x)$ для функции $f(x)=\ln(1+x)$ стремится к нулю при $n\rightarrow \infty.$
В итоге получаем разложение в ряд Маклорена
$$\ln(1+x)=x-\frac{x^{2}}{2}+ \ldots +(-1)^{n+1}\frac{x^{n}}{n}+ \ldots =$$ $$=\sum_{n=1}^{\infty }(-1)^{n+1}\frac{x^{n}}{n}, x\in \mathbb{R} (8)$$
Радиус сходимости $R=1.$
Степенная функция
Пусть $f(x)=(1+x)^{\alpha }$. Если $\alpha =0$, то $f(x)=1$, а если $\alpha =n$, где $n\in \mathbb{N}$, то $f(x)$-многочлен степени $n$, который можно представить в форме бинома Ньютона в форме конечной суммы:
$$f(x)=\sum\limits_{k=0}^{n}C_{n}^{k}x^{k}.$$ Покажем, что если $\alpha \neq 0$ и $\alpha \notin \mathbb{N}$, то функция $f(x)=(1+x)^{\alpha }$ представляется при каждом $x\in (-1,1)$ сходящимся к ней рядом Маклорена $$(1+x)^{\alpha }=\sum\limits_{n=0}^{\infty }C_{\alpha }^{n}x^{n} (9),$$ где $C_{\alpha }^{0}=1$, $C_{\alpha }^{n}=\frac{\alpha (\alpha -1) \ldots (\alpha -n+1))}{n!}$.
Так как $f^{(n+1)}(x)=\alpha (\alpha -1) \ldots (\alpha -n)(1+x)^{\alpha -n-1}$, то по формуле $r_{n}(x)=\frac{x^{(n+1)}}{n!}\int\limits_{0}^{1}(1-\tau )f^{(n+1)}(\tau x)d\tau$ получаем $$r_{n}(x)=A_{n}x^{n+1}\int\limits_{0}^{1}\left ( \frac{1-\tau}{1+\tau x} \right )^{n}(1+\tau x)^{\alpha -1}d\tau,$$ где $C_{n }=\frac{\alpha (\alpha -1) \ldots (\alpha -n)}{n!}.$
Выберем $m\in \mathbb{N}$ такое, чтобы выполнялось условие $\left | \alpha \right |\leq m$. Тогда для всех $n\geq m$ справедливо $\left | A_{n} \right |$$\leq \frac{m(m+1) \ldots (m+n)}{n!}$$\leq \frac{(m+n)!}{n!}=(n+1) \ldots (n+m)\leq (2n)^{m}$. Используя неравенства $\left | 1+\tau x \right |\geq 1-\tau \left | x \right |\geq 1-\tau$, $\left | 1+\tau x \right |\geq 1-\left | x \right |$, а также неравенство $\left | 1+\tau x \right |\leq 1+\left | x \right |$, получаем $0\leq \frac{1-\tau }{1+\tau x}\leq 1$.
Так как $\lim\limits_{t\rightarrow \infty }\frac{t^{m}}{a^{t}}=0$ при $\alpha > 1$, то $\lim\limits_{n\rightarrow \infty }\frac{n^{m}}{\left ( \frac{1}{\left | x \right |} \right )^{n+1}}=0$. Поэтому справедливо равенство $(1+x)^{\alpha }=\sum\limits_{n=0}^{\infty }C_{\alpha }^{n}x^{n}$. Радиус сходимости этого ряда $R=1$ при $\alpha \neq 0$ и $\alpha \notin \mathbb{N}.$
$$(1+x)^{\alpha }=$$ $$1+\alpha x+\frac{\alpha (\alpha -1)}{2!}x^{2}+ \ldots +\frac{\alpha (\alpha -1) \ldots (\alpha -n+1)}{n!}x^{n}+\ldots=$$$$1+\sum_{n=1}^{\infty }\frac{\alpha (\alpha -1) \ldots (\alpha -n+1)}{n!}x^{n}+\ldots, x\in \mathbb{R} (10)$$
- Частные случаи формулы (9):
- $\frac{1}{1+x}=1-x+x^{2}-\ldots=\sum\limits_{n=0}^{\infty }(-1)^{n}x^{n}, x\in \mathbb{R}$
- $\frac{1}{1-x}=\sum\limits_{n=0}^{\infty }x^{n}, x\in \mathbb{R}$
Спойлер
Разложить функцию в ряд Маклорена.
$$f(x)=x\cos 3x$$
$\cos 3x=1-\frac{(3x)^2}{2!}+\frac{(3x)^4}{4!}-\ldots+(-1)^{n}\frac{(3x)^{2n}}{(2n)!}+\ldots$
Раскрывая скобки, получим
$\cos 3x=1-\frac{3^{2}x^{2}}{2!}+\frac{3^{4}x^{4}}{4!}-\ldots+(-1)^{n}\frac{3^{(2n)}x^{(2n)}}{(2n)!}+ \ldots $
Умножая левую и правую часть на $x$, получим
$x\cos 3x=x(1-\frac{3^{2}x^{2}}{2!}+\frac{3^{4}x^{4}}{4!}-\ldots+(-1)^{n}\frac{3^{(2n)}x^{(2n)}}{(2n)!}+\ldots)$
Таким образом:
$f(x)=x\cos x=x-\frac{3^{2}x^{3}}{2!}+\frac{3^{4}x^{5}}{4!}-\ldots+(-1)^{n}\frac{3^{(2n)}x^{(2n+1)}}{(2n)!}$
[свернуть]
Литература
Разложение в ряд Тейлора основных элементарных функций
Лимит времени: 0
Информация
Для закрепления материала рекомендуется пройти этот тест
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 4
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
Рубрики
- Математический анализ 0%
- С ответом
- С отметкой о просмотре
ib.mazurok.com
Ряд Тейлора. Разложение функции в ряд Тейлора.
Ряд Тейлора. Разложение функции в ряд Тейлора.
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1:
При использовании рядов, называемых рядами Тейлора, смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.
Ряд Тейлора в окрестности точки a имеет виды:
1), где f(x) — функция, имеющая при х=а производные всех порядков. Rn — остаточный член в ряде Тейлора определяется выражением
2)
k-тый коэффициент (при хk) ряда определяется формулой
3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)
при a=0
члены ряда определяются по формуле
Условия применения рядов Тейлора.
1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).
2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.
Свойства рядов Тейлора.
- Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.
- Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:
Ряды Тейлора применяются при аппроксимации ( приближение — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от linearis — линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.tehtab.ru
Ряд Тейлора. Разложение функции в ряд Тейлора.
Ряд Тейлора. Разложение функции в ряд Тейлора.
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1:
При использовании рядов, называемых рядами Тейлора, смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.Ряд Тейлора в окрестности точки a имеет виды:
1), где f(x) — функция, имеющая при х=а производные всех порядков. Rn — остаточный член в ряде Тейлора определяется выражением
2)
k-тый коэффициент (при хk) ряда определяется формулой
3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)
при a=0
члены ряда определяются по формуле
Условия применения рядов Тейлора.
1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).
2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.
Свойства рядов Тейлора.
- Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.
- Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:
Ряды Тейлора применяются при аппроксимации ( приближение — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от linearis — линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.
dpva.ru
Моделирование в электроэнергетике — Разложение функции в ряд Тейлора
Разложение функции в ряд Тейлора
› Формула Тейлора для функции одной переменной
Ряд Тейлора (в англоязычной литературе Taylor series) – это способ представления сложной функции (периодической или непериодической) с помощьюбесконечной суммы простейших степенных функций.
где — степенной ряд, полученный разложением функции в окрестности точке в ряд Тейлора;
– точка, в окрестности которой производится разложение функции ;
– производная n-степени функции в окрестности точке
n – число членов ряда разложения.
Следует отметить, что в случае, если , то ряд Тейлора преобразуется в ряд Маклорена (в англоязычной литературе Maclaurin series).
Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка. Так же формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении.
› Формула Тейлора для функции двух переменных
В случае если функция является функцией от двух переменных и имеет производные вплоть до n-го порядка включительно в некоторой окрестности точки , тогда разложение функции в ряд Тейлора будет иметь следующий вид:
где — степенной ряд, полученный разложением функции в окрестности точке в ряд Тейлора;
n – число членов ряда разложения.
Представленная формула распространяется на функции от любого числа переменных.
В качестве первого примера, рассмотрим разложение тригонометрической функции в ряд Тейлора в окрестности точки .
Рассматриваемая функция дифференцируема и имеет производные вплоть до n-го порядка, которые вычисляются следующим образом: . Таким образом, функция раскладывается в следующий ряд Тейлора:
В итоге получаем следующий степенной ряд:
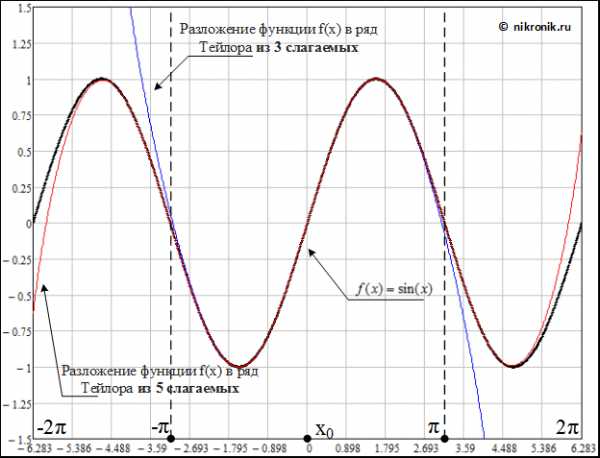
Рис.1. Зависимость изменения функция и ее представление в виде ряда Тейлора
В качестве второго примера, рассмотрим разложение тригонометрической функции в ряд Тейлора в окрестности точки .
Рассматриваемая функция дифференцируема и имеет производные вплоть до n-го порядка, которые вычисляются следующим образом: . Таким образом, функция раскладывается в следующий ряд Тейлора:
В итоге получаем следующий степенной ряд:
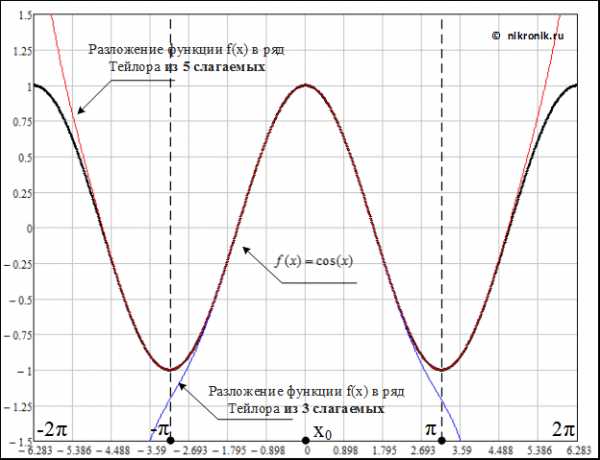
Рис.2. Зависимость изменения функция и ее представление в виде ряда Тейлора
В качестве третьего примера, рассмотрим разложение тригонометрической функции в ряд Тейлора в окрестности точки .
Рассматриваемая функция дифференцируема и имеет производные вплоть до n-го порядка, которые вычисляются следующим образом: . Таким образом, функция раскладывается в следующий ряд Тейлора:
В итоге получаем следующий степенной ряд:

Рис.3. Зависимость изменения функция и ее представление в виде ряда Тейлора
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
simenergy.ru
Разложение некоторых элементарных функций в ряд Тейлора.
Задача разложения
функции в ряд Тейлора в окрестности
точки  решается в следующем порядке:
решается в следующем порядке:
Находятся последовательно .
Записываются (1).
Находим интервал сходимости ряда (1): .
Записываем остаточный член
 в каком-то виде.
в каком-то виде.Находим те точки , для которых.
После выполнения
этих пунктов в (1) вместо  можно поставить равенство
можно поставить равенство .
.
Функция 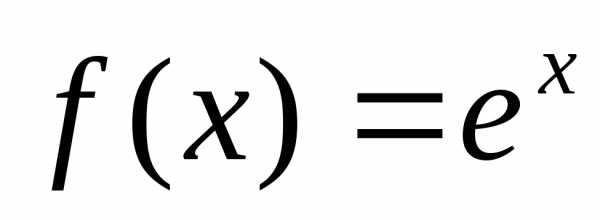 .
.
Пусть задана
функция 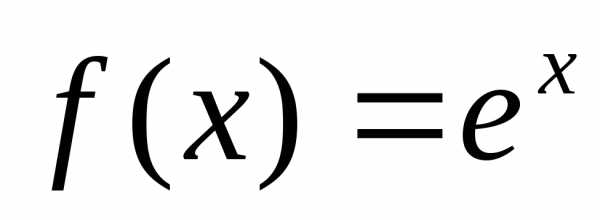 ,
она бесконечно дифференцируемая и
,
где
,
она бесконечно дифференцируемая и
,
где .
.
Найдем коэффициенты разложения , тогда
-это
ряд Маклорена для функции 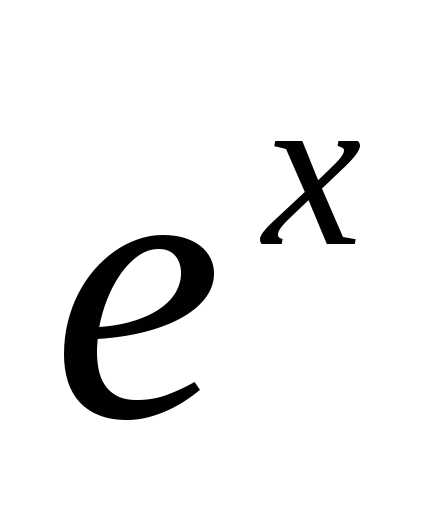 ,
который сходится к этой функции на всей
числовой прямой.
,
который сходится к этой функции на всей
числовой прямой.
Функция .
Найдем ее производные
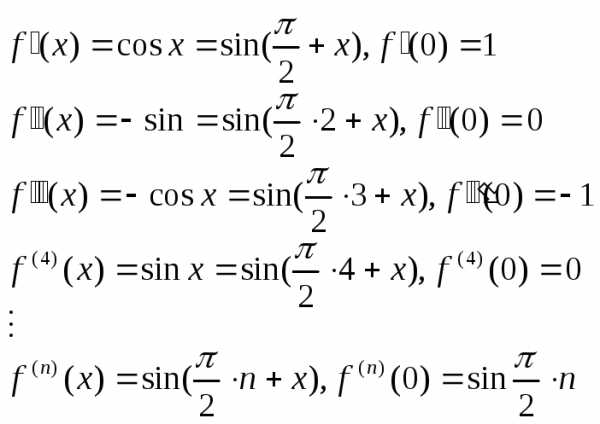
Вычислим коэффициенты в формуле Тейлора:
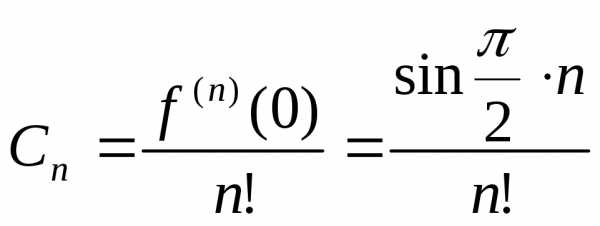 .
Пусть
.
Пусть  ,
тогда
,
тогда 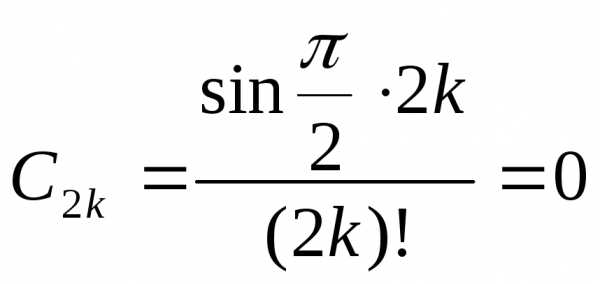 ,
если
,
то так как
,
то по теореме 2, можно утверждать, что
ряд Тейлора сходится к функции
,
если
,
то так как
,
то по теореме 2, можно утверждать, что
ряд Тейлора сходится к функции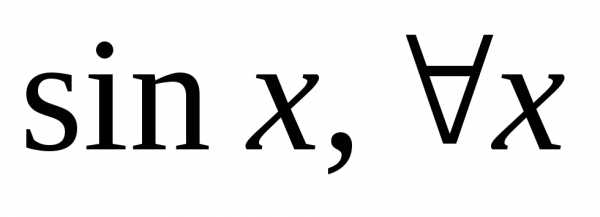 .
.
.
Функция . Можно провести аналогично разложение, а можно разложить другим способом. Мы знаем, что степенной ряд можно дифференцировать в интервале его сходимости. Тогда .
Ряд Маклорена для функции.
Так как функция  и ее производные не определены в точке
и ее производные не определены в точке ,
поэтому будем рассматривать функцию ,
которая определена
,
вместе с производными. Продифференцируем
,
поэтому будем рассматривать функцию ,
которая определена
,
вместе с производными. Продифференцируем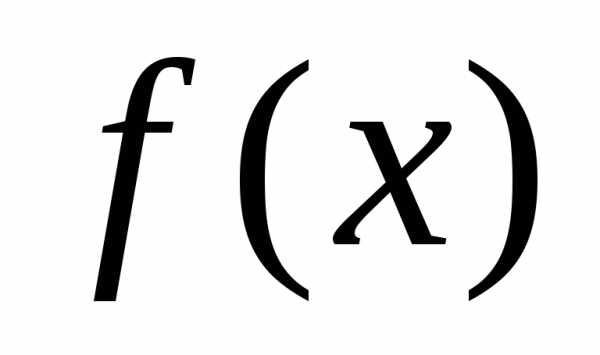 :
:
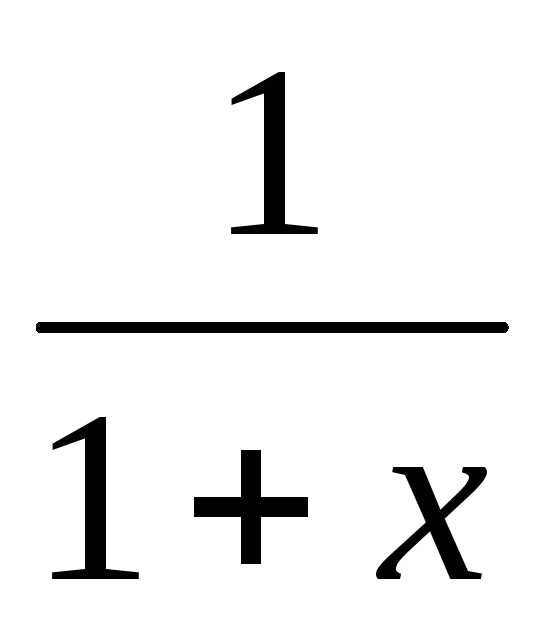 —
как сумма бесконечно убывающей
геометрической прогрессии
—
как сумма бесконечно убывающей
геометрической прогрессии 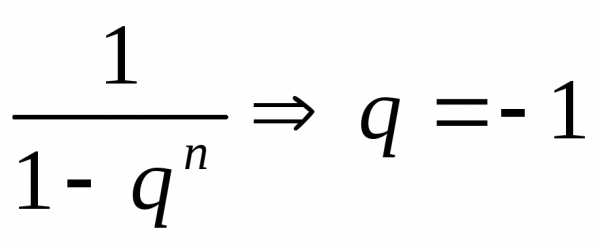 (имеет сумму при
(имеет сумму при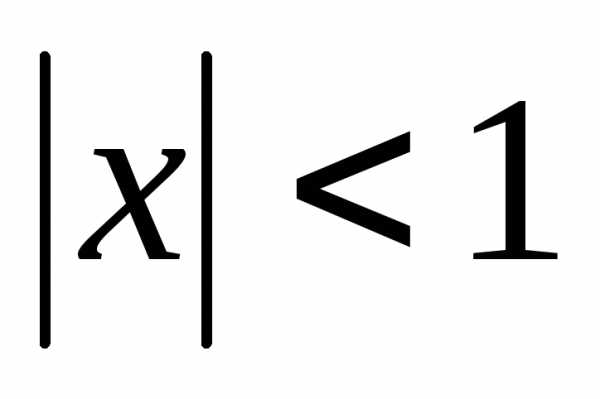 ).
).
Проинтегрируем
этот ряд почленно по любому отрезку от 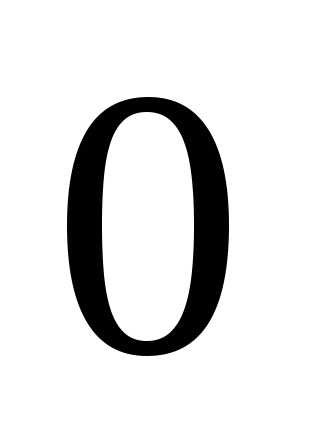 до
до ,
где
.
Получим
он сходится при
,
где
.
Получим
он сходится при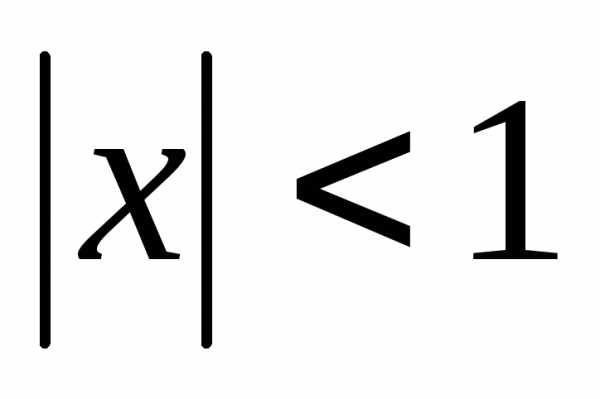 .
Проверим сходится ли ряд на границах
интервала
.
Проверим сходится ли ряд на границах
интервала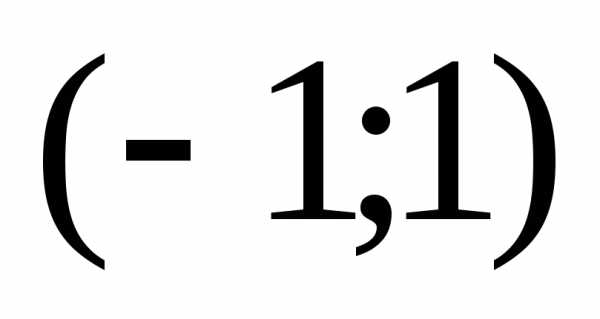 :
:
при 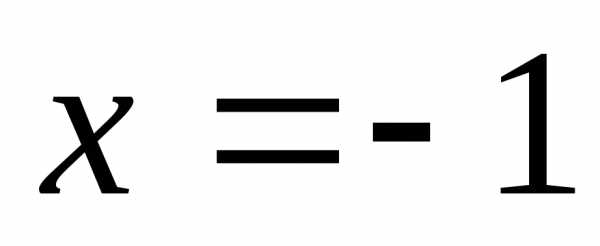 ряд вообще суммы не имеет, при
ряд вообще суммы не имеет, при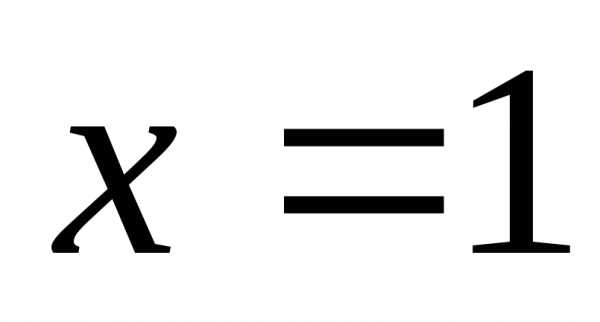 получается знакочередующийся рядпо теореме Лейбница он сходится, покажем,
что он сходится к
получается знакочередующийся рядпо теореме Лейбница он сходится, покажем,
что он сходится к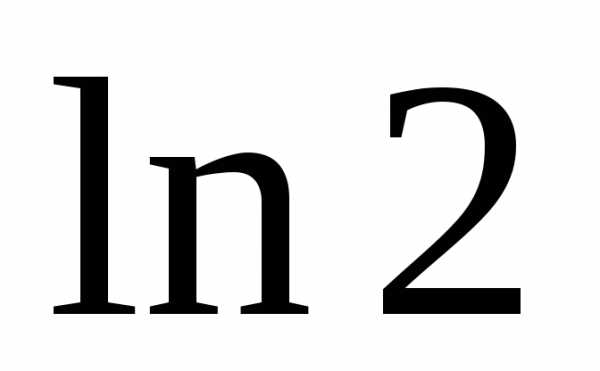 ,
то есть.
Воспользуемся теоремой (достаточным
условием разложимости в ряд Тейлора).
Для этого оценим остаточный член в
формуле Лагранжа.при
,
то есть.
Воспользуемся теоремой (достаточным
условием разложимости в ряд Тейлора).
Для этого оценим остаточный член в
формуле Лагранжа.при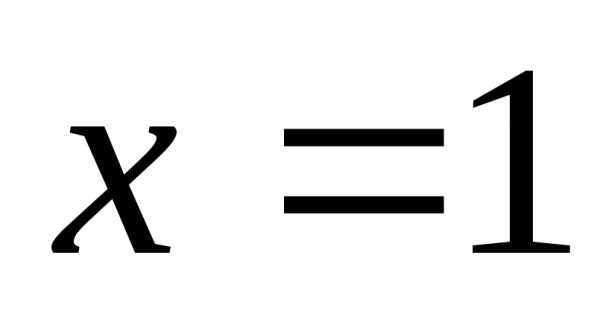
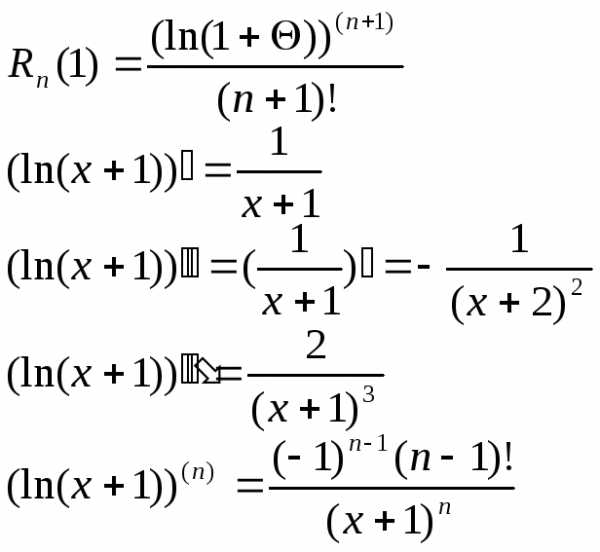 Тогда
.
Тогда
.
Таким образом, , то есть ряд сходится при.
При 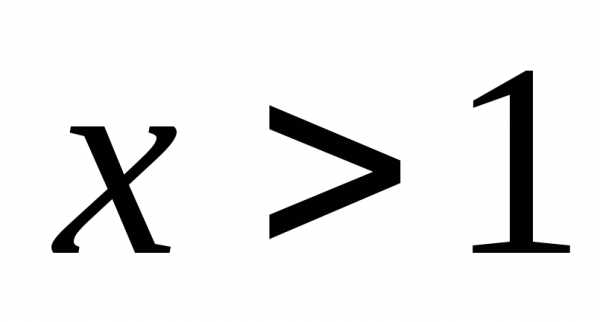 ряд расходится, так как не выполнено
необходимое условие сходимости ряда,
так как
ряд расходится, так как не выполнено
необходимое условие сходимости ряда,
так как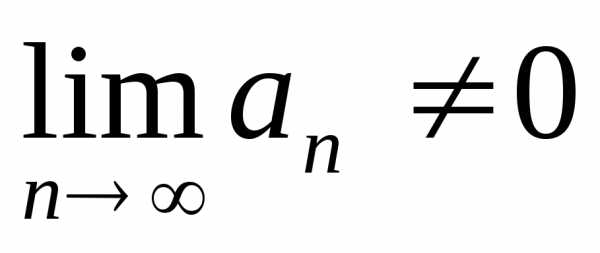 .
.
Разложение степенной функции в ряд Тейлора.
Рассмотрим функцию . (5).
Область сходимости ряда . на границе интервала надо проверять отдельно для каждого конкретного ряда
Отметим наиболее часто встречающиеся частные случаи биномиального ряда:
 , тогда
—
бесконечно убывающая геометрическая
прогрессия, сходится при
, тогда
—
бесконечно убывающая геометрическая
прогрессия, сходится при  .
. ,
тогда
,
тогда ,
тогда
,
тогда
Используя свойство степенных рядов о почленном интегрировании и дифференцировании внутри области сходимости можно получить следующие разложения:
Пример 1: сходится при 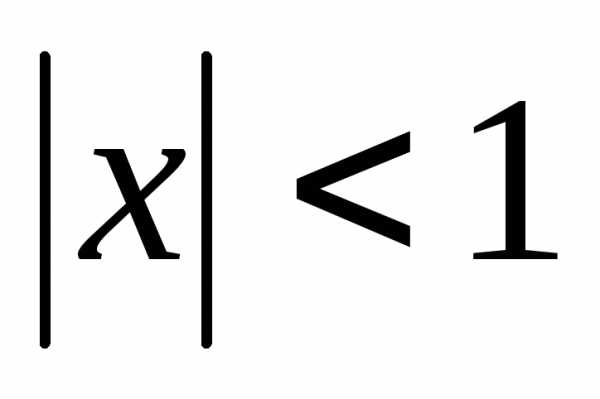 .
Проинтегрируем внутри отрезка сходимости:Пример
2:
.
Проинтегрируем внутри отрезка сходимости:Пример
2:
Сходится
при
.
Проинтегрировав по на
на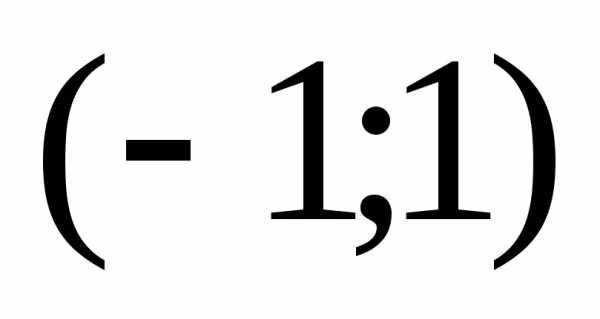 получим:
.
получим:
.
Дробно-рациональная функция.
—
многочлены. Чтобы разложить 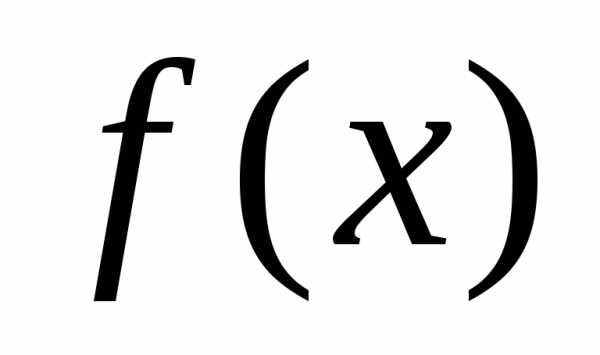 в ряд Тейлора, вначале приводим к
правильной дроби, далее полученную
дробь разбиваем на сумму более простых
методом неопределенных коэффициентов.
Эти более простые дроби раскладываем
в ряд Тейлора, используя разложение в
геометрическую прогрессию.
в ряд Тейлора, вначале приводим к
правильной дроби, далее полученную
дробь разбиваем на сумму более простых
методом неопределенных коэффициентов.
Эти более простые дроби раскладываем
в ряд Тейлора, используя разложение в
геометрическую прогрессию.
.
.
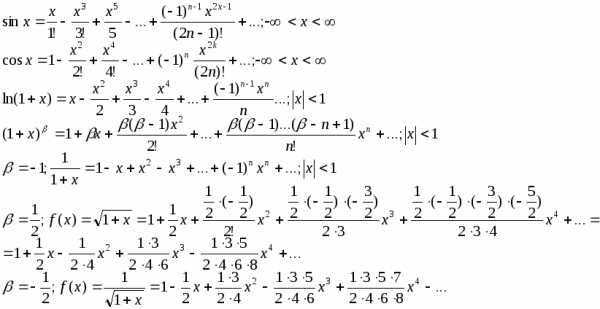
Ряд Тейлора. Разложение основных элементарных функций в степенные ряды.
Теорема: Всякая функция, бесконечно дифференцируемая
в интервале  ,
то есть,
может быть разложена в этом интервале
в сходящийся к ней степенной ряд Тейлора.
,
то есть,
может быть разложена в этом интервале
в сходящийся к ней степенной ряд Тейлора.
,
если в этом интервале выполняется
условие
,
где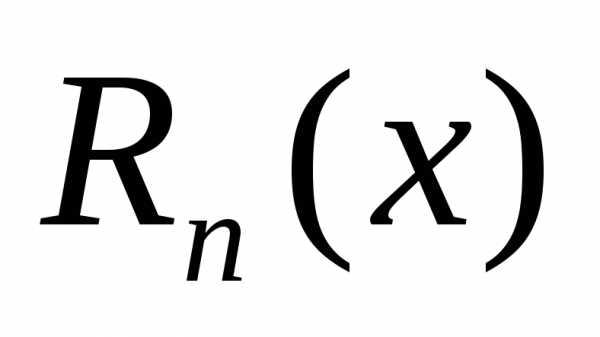 —
остаточный член формулы Тейлора,.
При
—
остаточный член формулы Тейлора,.
При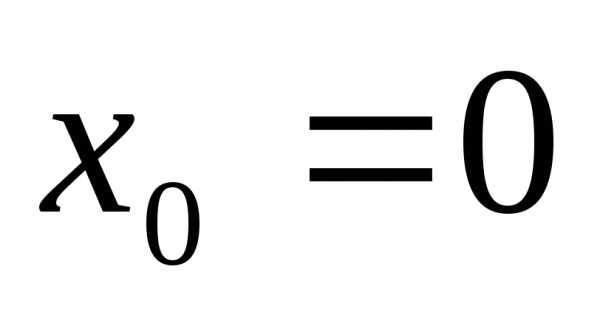 получается ряд Маклорена:.
Если в некотором интервале, содержащем
точку
получается ряд Маклорена:.
Если в некотором интервале, содержащем
точку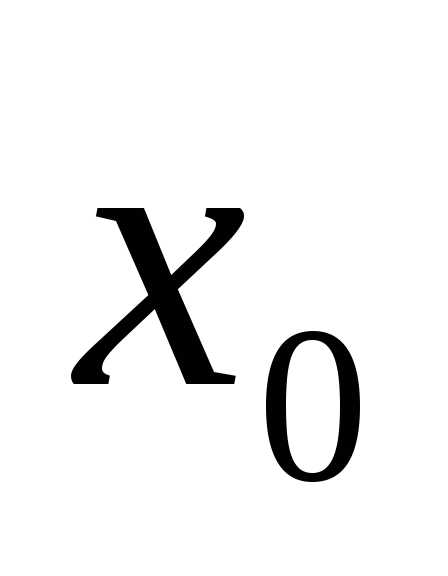 ,
при любом
,
при любом 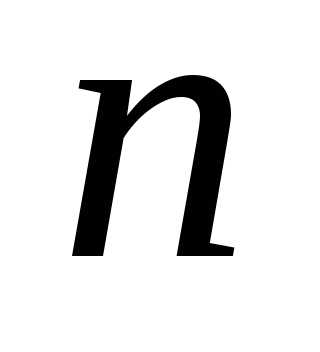 выполняется неравенство
,
где
выполняется неравенство
,
где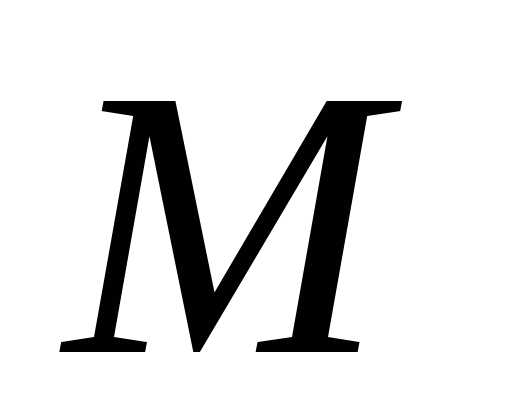 —
положительная постоянная, то
—
положительная постоянная, то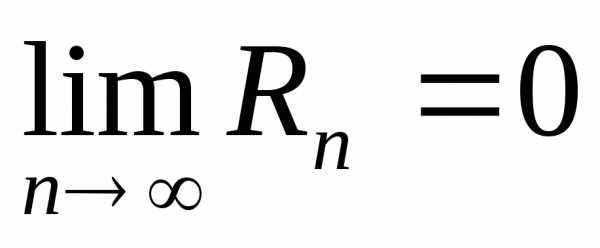 и функция
и функция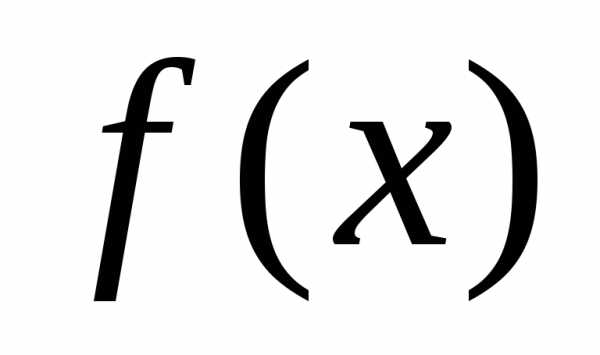 разложима в ряд Тейлора.
разложима в ряд Тейлора.
studfiles.net

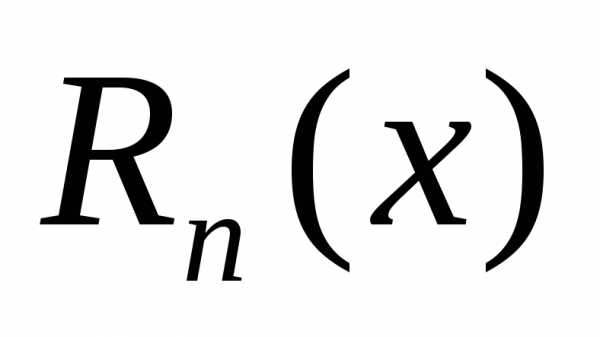 в каком-то виде.
в каком-то виде.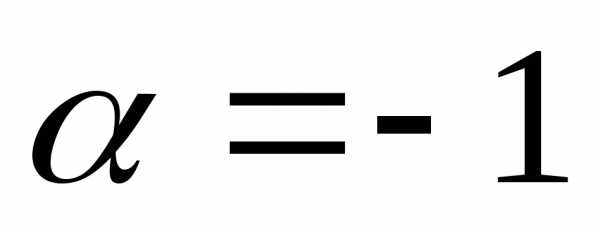 , тогда
—
бесконечно убывающая геометрическая
прогрессия, сходится при
, тогда
—
бесконечно убывающая геометрическая
прогрессия, сходится при 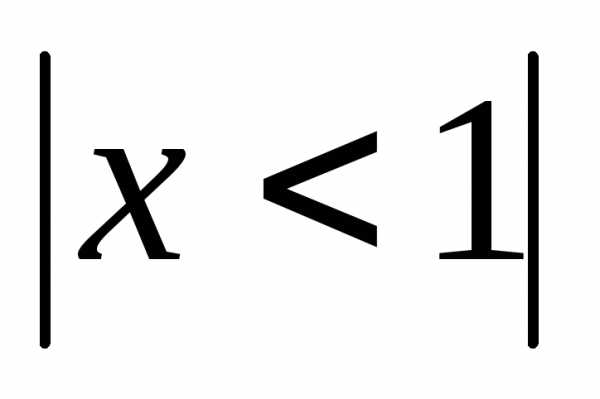 .
.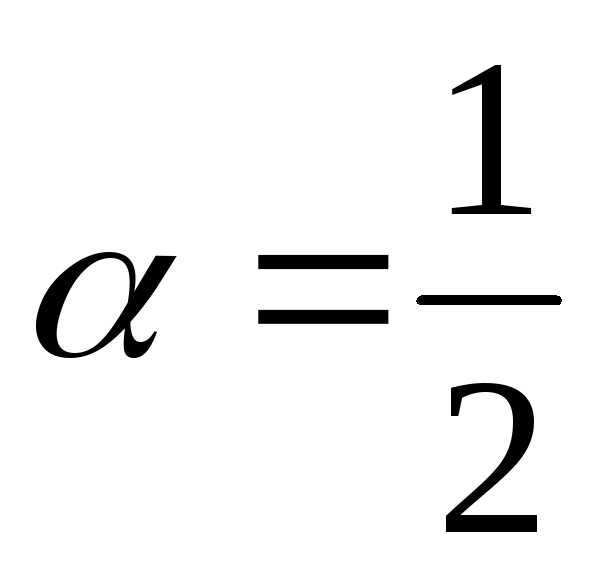 ,
тогда
,
тогда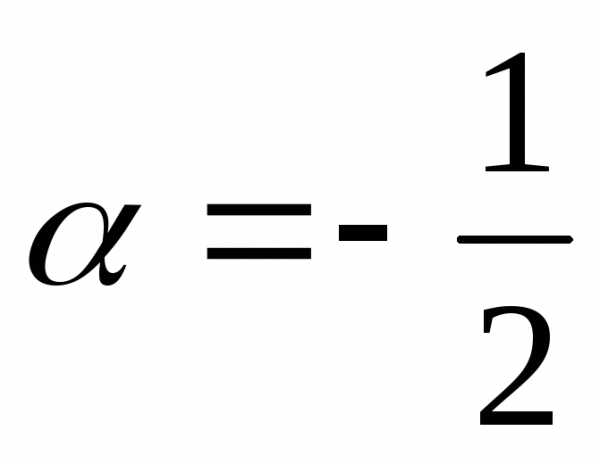 ,
тогда
,
тогда