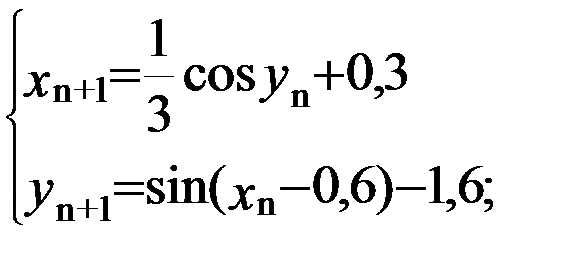Численные методы решения систем нелинейных уравнений / Habr
Введение
Многие прикладные задачи приводят к необходимости нахождения общего решения системы нелинейных уравнений. Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.
Следует отметить интересный факт о том, что любая система уравнений над действительными числами может быть представлена одним равносильным уравнением, если взять все уравнения в форме , возвести их в квадрат и сложить.
Для численного решения применяются итерационные методы последовательных приближений (простой итерации) и метод Ньютона в различных модификациях. Итерационные процессы естественным образом обобщаются на случай системы нелинейных уравнений вида:
(1)
Обозначим через вектор неизвестных и определим вектор-функцию Тогда система (1) записывается в виде уравнения:
(2)
Теперь вернёмся к всеми любимому Python и отметим его первенство среди языков программирования, которые хотят изучать [1].
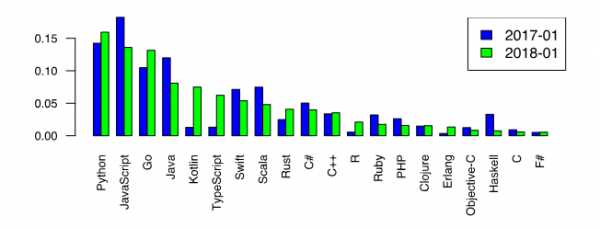
Этот факт является дополнительным стимулом рассмотрения числительных методов именно на Python. Однако, среди любителей Python бытует мнение, что специальные библиотечные функции, такие как scipy.optimize.root, spsolve_trianular, newton_krylov, являются самым лучшим выбором для решения задач численными методами.
С этим трудно не согласится хотя бы потому, что в том числе и разнообразие модулей подняло Python на вершину популярности. Однако, существуют случаи, когда даже при поверхностном рассмотрении использование прямых известных методов без применения специальных функций библиотеки SciPy тоже дают неплохие результаты. Иными словами, новое- это хорошо забытое старое.
Так, в публикации [2], на основании проведенных вычислительных экспериментов, доказано, что библиотечная функция newton_krylov, предназначенная для решения больших систем нелинейных уравнений, имеет в два раза меньшее быстродействие, чем алгоритм TSLS+WD
Целью настоящей публикации является сравнение по числу итераций, быстродействию, а главное, по результату решения модельной задачи в виде системы из ста нелинейных алгебраических уравнений при помощи библиотечной функции scipy.optimize.root и методом Ньютона, реализованного средствами библиотеки NumPy.
Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений
Библиотечная функция scipy.optimize.root выбрана в качестве базы сравнения, потому что имеет обширную библиотеку методов, пригодных для сравнительного анализа.
scipy.optimize.root(fun, x0, args=(), method=’hybr’, jac=None, tol=None,callback=None, ptions=None)
fun — Векторная функция для поиска корня.
x0 –Начальные условия поиска корней
method:
hybr -используется модификация Пауэлл гибридный метод;
lm – решает системы нелинейных уравнений методом наименьших квадратов.
Как следует из документации [3] методы
Методы решения систем нелинейных уравнений
Приведенный далее материал действительно можно прочитать в литературе, например в [4], но я уважаю своего читателя и для его удобства приведу вывод метода по возможности в сокращенном виде. Те, кто не любит формулы, этот раздел пропускают.
В методе Ньютона новое приближение для решения системы уравнений (2) определяется из решения системы линейных уравнений:
(3)
Определим матрицу Якоби:
 (4)
(4)
Запишем(3) в виде:
(5)
Многие одношаговые методы для приближенного решения (2) по аналогии с двухслойными итерационными методами для решения систем линейных алгебраических уравнений можно записать в виде:
(6)где — итерационные параметры, a — квадратная матрица n х n, имеющая обратную.
При использовании записи (6) метод Ньютона (5) соответствует выбору:
Система линейных уравнений (5) для нахождения нового приближения может решаться итерационно. В этом случае мы имеем двухступенчатый итерационный процесс с внешними и внутренними итерациями. Например, внешний итерационный процесс может осуществляться по методу Ньютона, а внутренние итерации — на основе итерационного метода Зейделя
При решении систем нелинейных уравнений можно использовать прямые аналоги стандартных итерационных методов, которые применяются для решения систем линейных уравнений. Нелинейный метод Зейделя применительно к решению (2) дает:
(7)
В этом случае каждую компоненту нового приближения из решения нелинейного уравнения, можно получить на основе метода простой итерации и метода Ньютона в различных модификациях. Тем самым снова приходим к двухступенчатому итерационному методу, в котором внешние итерации проводятся в соответствии с методом Зейделя, а внутренние — с методом Ньютона.
Основные вычислительные сложности применения метода Ньютона для приближенного решения систем нелинейных уравнений связаны с необходимостью решения линейной системы уравнений с матрицей Якоби на каждой итерации, причем от итерации к итерации эта матрица меняется. В модифицированном методе Ньютона матрица Якоби обращается только один раз:
(8)
Выбор модельной функции
Такой выбор не является простой задачей, поскольку при увеличении числа уравнений в системе в соответствии с ростом числа переменных результат решения не должен меняться, поскольку в противном случае невозможно отследить правильность решения системы уравнений при сравнении двух методов. Привожу следующее решение для модельной функции:
n=100
def f(x):
f = zeros([n])
for i in arange(0,n-1,1):
f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2
f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3
f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4
return f Функция f создаёт систему из n нелинейных уравнений, решение которой не зависит от числа уравнений и для каждой из n переменных равно единице.
Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней
from numpy import*
from scipy import optimize
import time
ti = time.clock()
n=100
def f(x):
f = zeros([n])
for i in arange(0,n-1,1):
f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2
f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3
f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4
return f
x0 =zeros([n])
sol = optimize.root(f,x0, method='krylov')
print('Solution:\n', sol.x)
print('Krylov method iteration = ',sol.nit)
print('Optimize root time', round(time.clock()-ti,3), 'seconds')Только один из методов, приведенных в документации [3] прошёл тестирование по результату решения модельной функции, это метод ‘krylov’.
Решение для n=100:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Krylov method iteration = 4219
Optimize root time 7.239 seconds:
Solution:
[1.00000018 0.99999972 0.99999985 1.00000001 0.99999992 1.00000049
0.99999998 0.99999992 0.99999991 1.00000001 1.00000013 1.00000002
0.9999997 0.99999987 1.00000005 0.99999978 1.0000002 1.00000012
1.00000023 1.00000017 0.99999979 1.00000012 1.00000026 0.99999987
1.00000014 0.99999979 0.99999988 1.00000046 1.00000064 1.00000007
1.00000049 1.00000005 1.00000032 1.00000031 1.00000028 0.99999992
1.0000003 1.0000001 0.99999971 1.00000023 1.00000039 1.0000003
1.00000034 1.00000004 0.99999993 0.99999987 0.99999969 0.99999985
0.99999981 1.00000051 1.0000004 1.00000035 0.9999998 1.00000065
1.00000061 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.0000006 1.0000006
1.0000006 1.0000006 1.0000006 1.0000006 1.00000059 1.00000056
1.00000033 1.00000034 1.0000004 1.00000046 1.00000009 1.00000024
1.00000017 1.00000014 1.00000054 1.00000006 0.99999964 0.99999968
1.00000005 1.00000049 1.0000005 1.00000028 1.00000029 1.00000027
1.00000027 0.9999998 1.00000005 0.99999974 0.99999978 0.99999988
1.00000015 1.00000007 1.00000005 0.99999973 1.00000006 0.99999995
1.00000021 1.00000031 1.00000058 1.00000023 1.00000023 1.00000044
0.99999985 0.99999948 0.99999977 0.99999991 0.99999974 0.99999978
0.99999983 1.0000002 1.00000016 1.00000008 1.00000013 1.00000007
0.99999989 0.99999959 1.00000029 1.0000003 0.99999972 1.00000003
0.99999967 0.99999977 1.00000017 1.00000005 1.00000029 1.00000034
0.99999997 0.99999989 0.99999945 0.99999985 0.99999994 0.99999972
1.00000029 1.00000016]
Krylov method iteration = 9178
Optimize root time 23.397 seconds
Вывод: С увеличением числа уравнений вдвое заметно появление ошибок в решении. При дальнейшем увеличении n решение становится не приемлемым, что возможно из-за автоматической адаптации к шагу, эта же причина резкого падения быстродействия. Но это только моё предположение.
Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона
Программа отыскания корней по модифицированному методу Ньютона
from numpy import* import time ti = time.clock() def jacobian(f, x): h = 1.0e-4 n = len(x) Jac = zeros([n,n]) f0 = f(x) for i in arange(0,n,1): tt = x[i] x[i] = tt + h f1= f(x) x[i] = tt Jac [:,i] = (f1 - f0)/h return Jac, f0 def newton(f, x, tol=1.0e-9): iterMax = 50 for i in range(iterMax): Jac, fO = jacobian(f, x) if sqrt(dot(fO, fO) / len(x)) < tol: return x, i dx = linalg.solve(Jac, fO) x = x - dx print ("Too many iterations for the Newton method") n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f x0 =zeros([n]) x, iter = newton(f, x0) print ('Solution:\n', x) print ('Newton iteration = ', iter) print('Newton method time', round(time.clock()-ti,3), 'seconds')
Решение для n=100:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Newton iteration = 13
Newton method time 0.496 seconds
Решение для n=200:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1.]
Newton iteration = 14
Newton method time 1.869 seconds
Чтобы убедиться в том, что программа действительно решает систему, перепишем модельную функцию для ухода от корня со значением 1 в виде:
n=10
def f(x):
f = zeros([n])
for i in arange(0,n-1,1):
f[i] = (3 + 2*x[i])*x[i]*sin([i]) - x[i-1] - 2*x[i+1] - 2+e**-x[i]
f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3
f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4
return fПолучим:
Solution:
[ 0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
Newton iteration = 16
Newton method time 0.046 seconds
Вывод: Программа работает и при изменении модельной функции.
Теперь вернёмся к начальной модельной функции и проверим более широкий диапазон для n, например в 2 и 500.
n=2
Solution:
[1. 1.]
Newton iteration = 6
Newton method time 0.048 seconds
n=500
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
Newton iteration = 15
Newton method time 11.754 seconds
Выводы:
Программа, написанная на Python по модифицированному методу Ньютона, при решении систем нелинейных уравнений из приведенной модельной функции обладает большей устойчивостью решения, чем при решении с помощью библиотечной функции optimize.root(f,x0, method=’krylov’) для метода Крылова. Относительно быстродействия окончательного вывода сделать нельзя из-за разного подхода к управлению шагом.
Ссылки:
- Рейтинг языков программирования 2018.
- Бондарь И.В, Фалейчик Б.В. Безматричные итерационные процессы со среднеквадратичным подавлением ошибки для больших систем нелинейных уравнений.
- scipy.optimize.root.
- Вабищевич П.Н. Численные методы: Вычислительный практикум. — М.: Книжный дом «ЛИБРОКОМ», 2010. — 320 с.
habr.com
6 Численное решение систем нелинейных уравнений » СтудИзба
Численное решение систем нелинейных уравнений
Постановка задачи
Дана система линейных уравнений
(1)
Введём обозначения: вектор — вектор аргументов:
Аналогично вектор функций
Тогда систему 1 можно переписать в виде:
Система линейных уравнений в общем виде неразрешима. Поэтому мы будем рассматривать только численные методы решения системы линейных уравнений.
Метод Ньютона
Для уравнения имеет вид:
По анологии метод Ньютона для системы линейных уравнений
где — вектор аргументов на -ом шаге итерации
— значения вектора функций (системы уравнений ) при
— обратная матрица Якоби
— матрица, Якоби-матрица, состоящая из частных производных
Вполне естественно очевидно, что формулу Ньютона можно применять в том случае, когда Якоби-матрица неособенная, невырождённая, то есть .
Пример:
Дано:
Матрица Якоби
Превоначальная оцнка
1)
2)
3)
-=-=
и так далее
Результаты итераций лучше всего сводить в таблицу
0 | 3,4 | 0,097 | 2,2 | 0,076 |
1 | 3,497 | 2,276 | ||
2 |
Прекращаем вычисления, когда — заданная точность.
Как и в любых численных методах встают следующие задачи: о сходимости метода и о выборе начального значения.
Сходимость метода Ньютона
Вопросами сходимости метода Ньютона занимались такие учёные, как Виллус, Стёпин, Островский, Канторович и другие. Мы же будем рассматривать сходимость, единственность корня и выбор начального условия по Канторовичу. При рассмотрении этих характеристик метода ипользуются понятия нормы. Поэтому прежде дадим определения :
-нормой — называется максимальная сумма модулей элементов по строкам.
-нормой — называется максимальная сумма модулей элементов по столбцам.
-нормой — нызывается квадратный корень из суммы квадратов модулей элементов матрицы
Пример:
Для оценки матриц, используемых в методе Ньютона для нелинейных систем, будем использовать -нормы, а именно
Теорема о существовании корней и сходимости процесса Ньютона
Пусть дана нелинейная система уравнений
,
где — вектор-функция определена и непрерывна вместе со своими частными производными первого и второго порядков в некоторой области . Положим, что — есть точка, лежащая в вместе со своей замкнутой -окрестностью. При этом выполняются следующие условия:
1) матрица Якоби при имеет обратную функцию
2)
3)
4) постоянные удовлетворяют неравенству
Тогда процесс Ньютона при начальном приблежении сходится к решению — есть решение такое, что
Для проверки условия даёт оценку расходимости начального и первого приблежения.
Быстрота сходимости процесса Ньютона
Если выполнимы все четыре условия теоремы 1, то для последовательных приближений , справедливо неравенство:
где — искомое решение, а
При сходимость метода — сверхбыстрая.
Единственность решения
Если выполнимы все четыре условия, в области
то содержится единственное решение системы
Выбор начального условия
Если выполнимы все четыре условия и , то процесс сходится к единственному решению в основной области при любом выборе начального условия из области
Модифицированный метод Ньютона
При использовании метода Ньютона наиболее трудоёмким является процесс вычисления обратной матрицы Якоби.
Если матрица невырождённая для некоторого приближения , и достаточно близко к (искомому решению), то можно использовать модифицированный метод Ньютона.
Метод итераций
Дана система нелинейных уравнений:
или
(1)
Допустим, что систему 1 можно привести к виду:
(2)
Введём обозначения:
, ,
Можно систему уравнений 2 переписать в виде:
Приведённое матричное уравнение и есть формула метода итераций
Необходимое и достаточное условие сходимости процесса итерации
Пусть функции и непрерывны в области , причём в области выполнимо неравенство:
где — некоторая константа.
Если последовательные приближения
,
не выходят из области , то этот процесс сходится к единственному решению системы.
Следствие:
оценка пиближённо
На практике лучше всего рассматривать матрицу с элементами
Для сходимости должно выполнятся условие
1)
2)
3)
Метод скорейшего спуска (градиентный метод)
Дана система линейных уравнений:
(1)
В матричном виде
Считаем, что действительны и непрерывно дифференцируемы в их общей области определения.
Рассмотрим функцию
(2)
Очевидно, что если мы найдём решение системы уравнений 1 , то это решение является и решением системы уравнений 2 и наоборот.
Предполагаем, что система 1 имеет лишь одно изолированное решение, представляющего собой точку строго минимум функции . Таким образом задача сводится к нахождению минимум функции в -мерном пространстве.
Берём точку — нулевое приближение. Через точку проходит поверхность уровня и . Если близка , то поверхность = будет похожа на элипсоид.
Из точки движемся по нормали к поверхности до тех пор, пока эта нормаль не коснётся другой поверхности:
И так далее.
Так как , то двигаясь таким образом, мы быстро приближаемся к точке с минимальным значением , которая соответствует некоему корню .
Градиент функции U
— набла или grad — есть вектор приложенный к точке , имеющий направление нормали. Из векторных произведений
, (3)
Как определить ? Для этого рассматривают скалярную функцию :
Уравнение 3 можно преобразовать так, чтобы не было явного выражения градиента. Введем обозначения , тогда итерационная формула градиентного метода будет иметь вид:
,
где
Вычисления производятся до тех пор, пока не станет справедливым следующее неравенство:
e,
где e — заданная точность вычисления.
Пример. Дана система нелинейных уравнений:
Найти решение системы градиентным методом с точностью e=0,01
Определим начальное приближение как:
Вектор-функция имеет вид:
Якобиан, или матрица частных производных имеет вид:
1 итерация
2 итерация
Решение системы нелинейных уравнений представлено в таблице:
K | x | ½Dx½ | y | ½Dy½ | z | ½Dz½ |
0 | 0.000 | 0,100 | 0.000 | 0,200 | 0.000 | 0,300 |
1 | 0.100 | 0,030 | -0.200 | 0,250 | 0.300 | 0,250 |
2 | 0,130 | 0,095 | 0,050 | 0,251 | 0,050 | 0,209 |
3 | 0,035 | 0,018 | -0,201 | 0,016 | 0,259 | 0,013 |
4 | 0,017 | 0,003 | -0,185 | 0,007 | 0,246 | 0,001 |
5 | 0,014 | -0,178 | 0,245 |
Таким образом, решение системы уравнений имеет вид:
Сходимость градиентного метода
Сходимость метода гарантируется при выборе начального приближения вблизи .
В любом случае метод может остановитья в точке относительного метода.
studizba.com
Решение систем нелинейных уравнений
Простейшие системы нелинейных уравнений система МС может решать с помощью символьных преобразований. ВНИМАНИЕ! Знаки = в уравнениях набираются не с клавиатуры, а вызываются с панели булевых функций Boolean. Вот несколько примеров:
,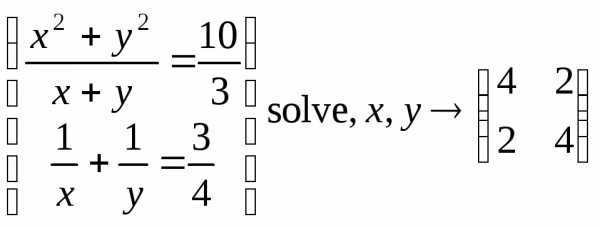 ,
,
.
Системы, которые не удается решить символьными преобразованиями, можно попытаться решить численными методами. Для этого в системе МС нужно произвести следующие действия:
Неизвестным присвоить начальные значения по возможности близкие к ожидаемому решению.
В очередном блоке записать с клавиатуры слово given, которое является директивой системы МС и открывает «увеличенный блок», где записываются уравнения системы. В слове given не имеет значения, записано оно прописными буквами или строчными.
В последующих блоках записать уравнения, используя знак =, взятый с панели Boolean. В каждом блоке записывается одно уравнение.
Записать функцию Find(x,y,z,…), где в скобках указываются неизвестные системы уравнений. Лишние шаблоны в аргументе функции можно удалить. Эта функция, записанная в отдельном блоке, завершает «увеличенный блок», посвященный решению системы. Значения этой функции (решение системы) образуют вектор. Можно какому-нибудь переменному присвоить значение этой функции. Можно просто посмотреть ответы на экране, поставив после функции знак = с клавиатуры.
Рассмотрим пример
given
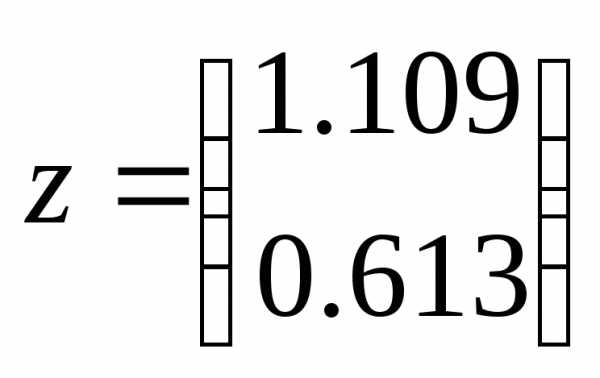
Итак, система MATHCAD выдала решение x = 1.109, y = 0.613. Произведем проверку
.
Видим, что с точностью до тысячных равенства системы выполнены. Эта точность соответствует точности, с которой выведены на экран результаты. На самом деле результат значительно лучше. Используем найденные значения z, а не их округленную запись на экране:
.
Таким образом, ошибка появляется только в пятнадцатом знаке после запятой!
Очень
многое зависит от задания начальных
значений. Если в приведенном выше примере
изменить начальные условия, задав 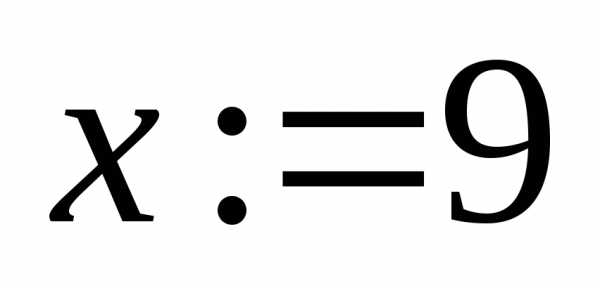 ,
то система сообщит, что решение задачи
не найдено. Неизвестные и их начальные
значения можно задавать в векторном
виде. Пример (установите начало нумерации
элементов матриц с 1):
,
то система сообщит, что решение задачи
не найдено. Неизвестные и их начальные
значения можно задавать в векторном
виде. Пример (установите начало нумерации
элементов матриц с 1):
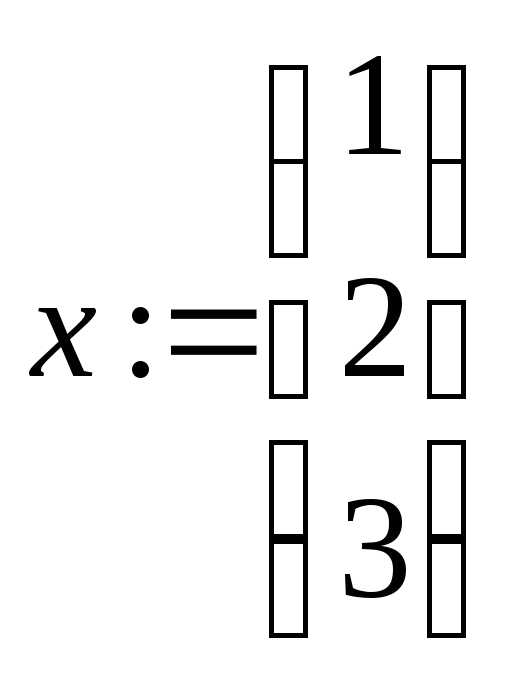
given
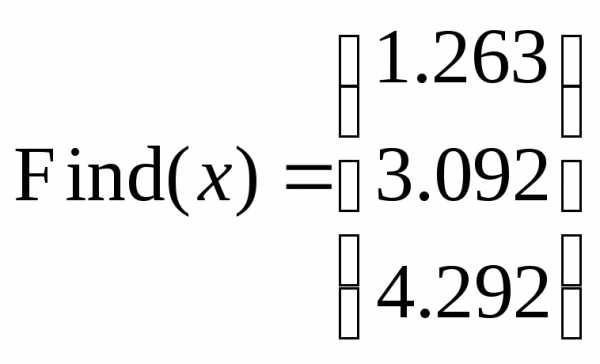 .
.
Точность решения системы уравнений с помощью функции Find регулируется двумя системными переменными TOL и CTOL, которые можно найти через меню Tools пункт Worksheet Options.
Корни многочлена
Как
мы видели на первом занятии, в системе
МС имеется возможность разложить
многочлен на множители с помощью
символьных операций. Но эта возможность
реализуется только в том случае, когда
получающиеся множители имеют целые
коэффициенты.
При этом множители не всегда получаются
линейными или квадратичными. Проверьте
это на многочленах
,,,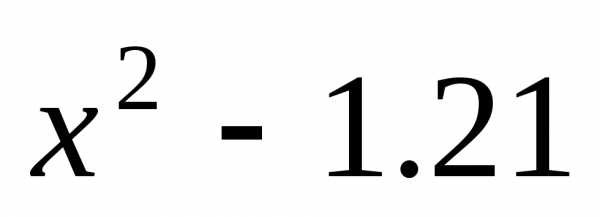 ,
,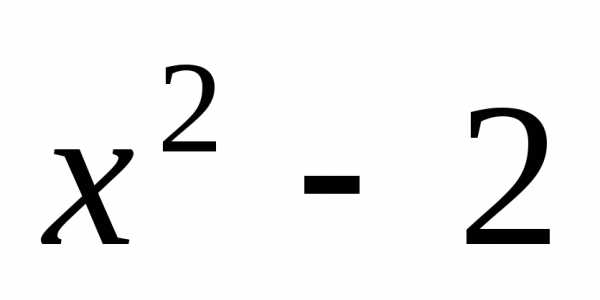 .
В других случаях для разложения на
множители приходится находить корни
многочлена. Как это можно сделать в
системе МС, описано выше. Следует, однако,
учесть, что функцияpolyroots
гарантирует хорошие результаты только
для многочленов невысокой степени.
Аналогичным недостатком обладает и
директива solve
для символьного нахождения корней.
Рассмотрим следующий пример. Пусть
.
В других случаях для разложения на
множители приходится находить корни
многочлена. Как это можно сделать в
системе МС, описано выше. Следует, однако,
учесть, что функцияpolyroots
гарантирует хорошие результаты только
для многочленов невысокой степени.
Аналогичным недостатком обладает и
директива solve
для символьного нахождения корней.
Рассмотрим следующий пример. Пусть
.
Этот многочлен имеет два кратных корня 1.5 и 1.9 кратности 2. Раскроем скобки, для чего воспользуемся директивой Collect из меню Symbolics (из-за формата страницы результат записан в двух строчках):
Попробуем найти корни с помощью символьной операции solve (на экране условие записывается в одной строке):
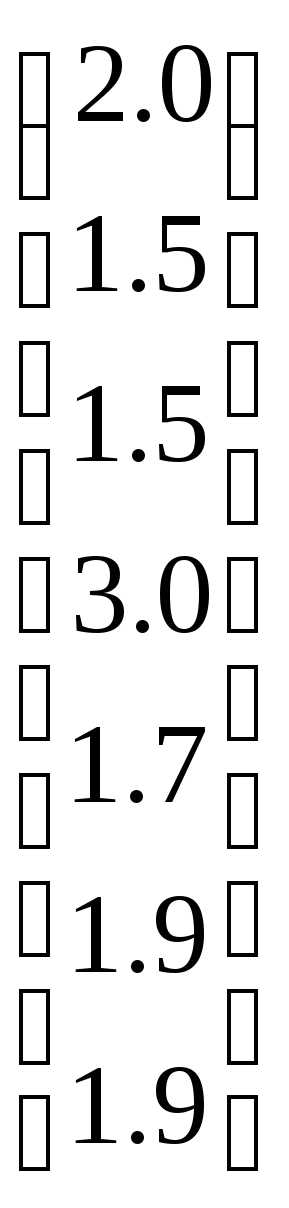
Как видим, корни найдены точно, и каждый показан столько раз, какова его кратность. Используем функцию polyroots. Для этого потребуется вектор из коэффициентов многочлена. Чтобы его компоненты не набирать вручную, воспользуемся пунктом Polynomial coefficient из меню Symbolics, выделив сначала переменную x в записи многочлена. В результате получим

Тот же результат можно получить кнопкой coeffs на панели Symbolic. Скопируем результат и выполним присвоение:
 .
Вычислим корни:
.
Вычислим корни:  .
.
В этом случае результаты значительно отличаются от точных корней. Это связано и со степенью многочлена, которая является довольно высокой, и с наличием кратных корней, которые превратились в комплексно сопряженные простые корни. Если по этим корням получить многочлен, производя округления с точностью до 5 знаков после запятой, то получим многочлен, коэффициенты которого отличаются от исходных только в четвертом знаке.
Посмотрим,
как изменение коэффициентов влияет на
корни. Для этого в многочлене p(x) уменьшим коэффициент при x на единицу последнего знака, т.е. на 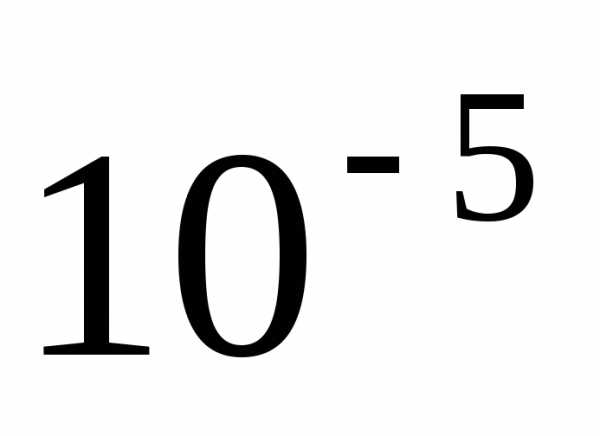 ,.
Найдем корни с помощью функцииpolyroots.
Увидим, что изменения происходят уже в
третьем знаке после десятичной точки,
причем простой вещественный корень 2
превращается в комплексный:
,.
Найдем корни с помощью функцииpolyroots.
Увидим, что изменения происходят уже в
третьем знаке после десятичной точки,
причем простой вещественный корень 2
превращается в комплексный:

 .
.
Если воспользоваться символьным нахождением корней, то получим результат, заметно отличающийся от ранее вычисленного. В частности, корень 2 исходного многочлена превращается в корень, приближенно равный 1.8 (из-за громоздких записей распечатка не приводится). Таким образом, мы убедились, что для многочлена высокой степени малое изменение коэффициентов может вызвать существенное изменение корней и к полученным результатам с помощью функции polyroots нужно относиться осторожно.
Если
подставить найденные значения корней
в многочлен, то для корней, вычисленных
символьным методом, результаты будут
иметь порядок 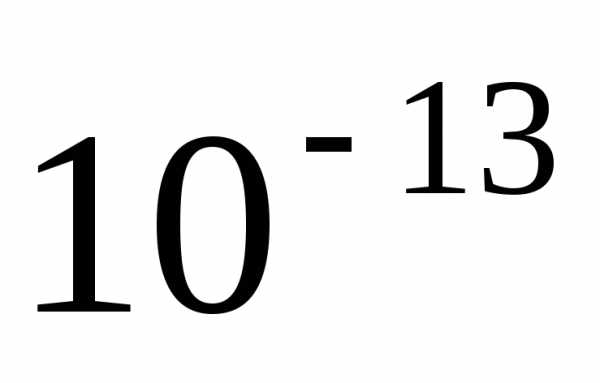 ,
а для корней, полученных с помощью
функцииpolyroots,
– порядок
,
а для корней, полученных с помощью
функцииpolyroots,
– порядок 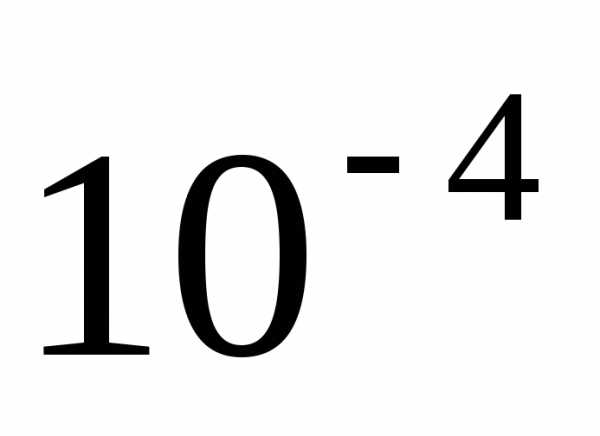 .
.
Если результат, полученный символьным способом, желательно округлить до меньшего числа цифр после десятичной точки, то нужно его выделить, а затем в меню Symbolics выбрать пункт Evaluate и в развернувшемся меню пункт Floating Point. В появившемся окне указывается общее число значащих цифр результата (до точки и после нее, нули слева не учитываются). То же можно сделать и с помощью панели Symbolic. Округлим корни предыдущего многочлена до пяти цифр после точки, используя эту панель. Из-за громоздкой записи здесь в исходных корнях приведены только 7 цифр после точки, на экране их 19.

 .
.
После того как найдены корни многочлена, мы можем представить его в виде произведения. Произведение будет содержать в вещественном случае линейные и квадратичные множители, в комплексном случае – только линейные. Произведем это разложение для рассмотренного выше многочлена. Используем корни, округленные до пяти цифр после запятой. Это округление у нас уже имеется. Чтобы не переписывать длинные наборы цифр, скопируем набор корней и создадим соответствующую векторную величину
 .
.
Найдем квадратичные множители. Для этого используем пары комплексно сопряженных корней. Если за счет вычислений комплексные корни отличаются от комплексно сопряженных на величину, лежащую за пределами заданной точности, то их нужно исправить. Исправить нужно так, чтобы они стали комплексно сопряженными. Для удобства преобразований используем кнопку стрелка с шаблоном на панели Symbolic. Сначала набираем выражение . Затем нажимаем стрелку с шаблоном. Нажимаемcollect на той же панели. Клавишей табулирования переходим на следующий шаблон. Нажимаем кнопку float. Вписываем 6 в шаблон. Переходим на следующий шаблон и удаляем его. Щелкаем мышью за пределами блока. В результате получаем
.
Аналогично получим
.
Теперь можно записать разложение многочлена на множители (из-за размера страницы мы приводим только 2 цифры после десятичной точки):
.
studfiles.net
3.Численное решение систем нелинейных уравнений.
Метод Ньютона для систем нелинейных уравнений.
Пусть дана система:

Согласно методу Ньютона последовательные приближения вычисляются по формулам:
, где
Начальные
приближения  определяются приближенно (например,
графически).
определяются приближенно (например,
графически).
Метод Ньютона эффективен только при достаточной близости начального приближения к решению системы.
4.Численные методы решения систем линейных алгебраических уравнений (слау).
Метод Гаусса с выбором главного элемента для системы линейных уравнений
Система из п линейных уравнений с п неизвестными вида:
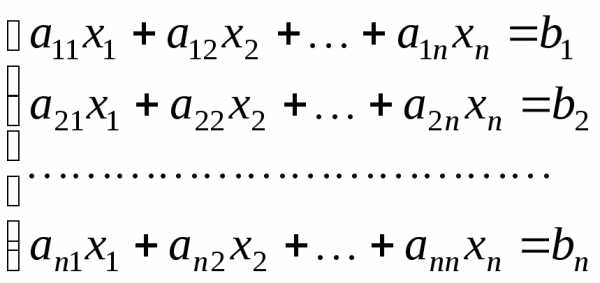 (3.1)
(3.1)
имеет
единственное решение при условии: 
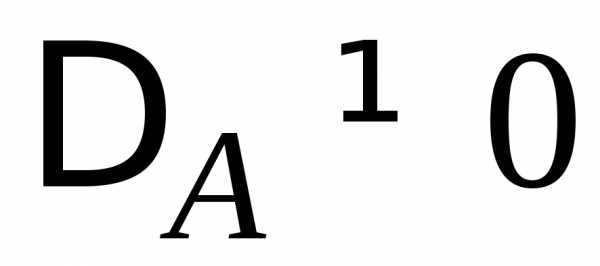 ,
где
,
где
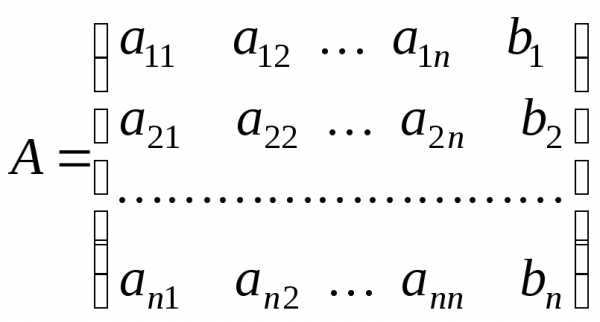
матрица коэффициентов
матрица коэффициентов  системы (3.1)
системы (3.1)
К
точным методам относится метод Гаусса
с выбором главного элемента. Среди
элементов  матрицыА выберем наибольший по модулю, называемый
главным
элементом.
Пусть им будет элемент
матрицыА выберем наибольший по модулю, называемый
главным
элементом.
Пусть им будет элемент 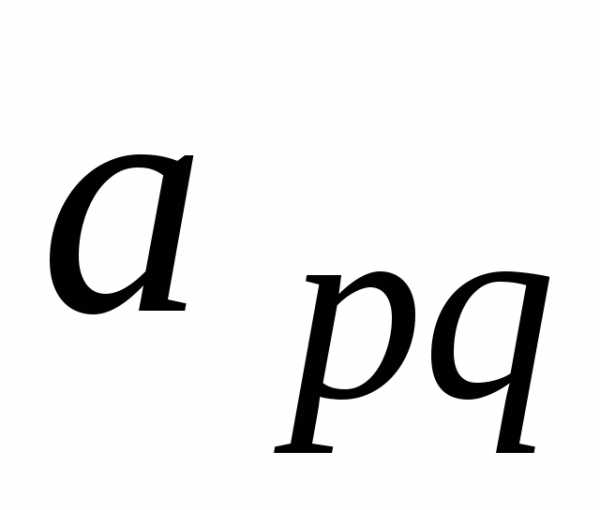 .
Строка с номеромр,
содержащая главный элемент, называется
главной строкой.
.
Строка с номеромр,
содержащая главный элемент, называется
главной строкой.
Далее
вычисляем множители:  для всех
для всех .
Затем преобразуем матрицу следующим
образом: из каждой неглавной строки
вычитаем почленно главную строку,
умноженную наmi . В результате получим матрицу, у которой
все элементы q-го
столбца, за исключением
.
Затем преобразуем матрицу следующим
образом: из каждой неглавной строки
вычитаем почленно главную строку,
умноженную наmi . В результате получим матрицу, у которой
все элементы q-го
столбца, за исключением 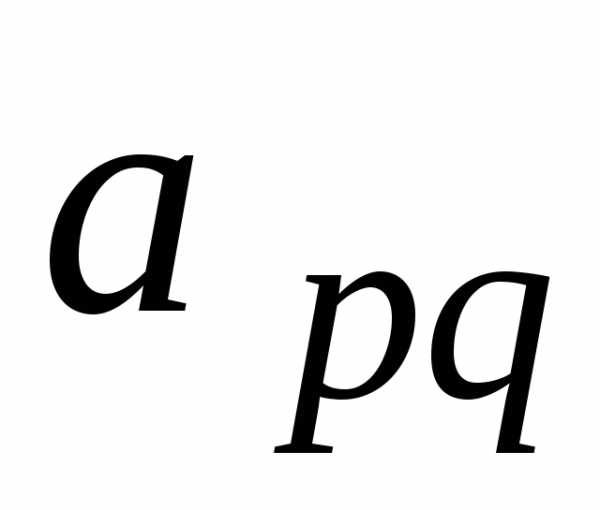 ,
равны нулю. Отбрасываем этот столбец и
главную строку и
,
равны нулю. Отбрасываем этот столбец и
главную строку и
получаем
новую матрицу  с меньшим на единицу числом строк и
столбцов. Над матрицей
с меньшим на единицу числом строк и
столбцов. Над матрицей повторяем аналогичные операции, после
чего получаем матрицуА2 и т. д. Такие преобразования продолжаем
до тех пор, пока не получим матрицу,
содержащую одну строку, которую считаем
тоже главной. Затем объединяем все
главные строки, начиная с последней.
После некоторой перестановки они
образуют треугольную матрицу, эквивалентную
исходной. На этом заканчивается этап
вычислений, называемый прямым
ходом. Решив
систему с полученной треугольной
матрицей коэффициентов, найдём
последовательно значения неизвестных
.
Этот этап вычислений называетсяобратным
ходом. Смысл
выбора главного элемента состоит в том,
чтобы сделать достаточно малым число mi и тем самым уменьшить погрешность
вычислений.
повторяем аналогичные операции, после
чего получаем матрицуА2 и т. д. Такие преобразования продолжаем
до тех пор, пока не получим матрицу,
содержащую одну строку, которую считаем
тоже главной. Затем объединяем все
главные строки, начиная с последней.
После некоторой перестановки они
образуют треугольную матрицу, эквивалентную
исходной. На этом заканчивается этап
вычислений, называемый прямым
ходом. Решив
систему с полученной треугольной
матрицей коэффициентов, найдём
последовательно значения неизвестных
.
Этот этап вычислений называетсяобратным
ходом. Смысл
выбора главного элемента состоит в том,
чтобы сделать достаточно малым число mi и тем самым уменьшить погрешность
вычислений.
Вычисление обратной матрицы для системы линейных уравнений
Пусть
дана невырожденная матрица 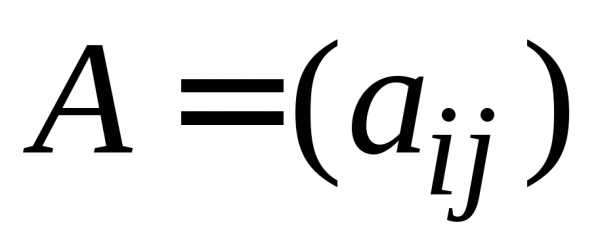 ,
где(i, j = 1, 2,…, n).
Для нахождения элементов обратной
матрицы
,
где(i, j = 1, 2,…, n).
Для нахождения элементов обратной
матрицы  ,
где (i, j = 1, 2,… n)
воспользуемся основным соотношением:
,
где (i, j = 1, 2,… n)
воспользуемся основным соотношением:
АА-1 =Е, где Е – единичная матрица.
Перемножая
матрицы А и А-1 и используя
равенство их матрице Е,
получим п систем линейных уравнений вида: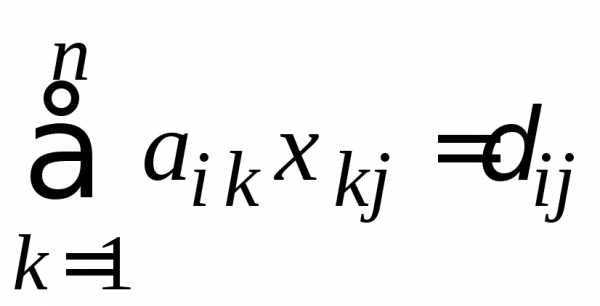 (i = 1, 2, …, n; j – фиксировано),
где
(i = 1, 2, …, n; j – фиксировано),
где 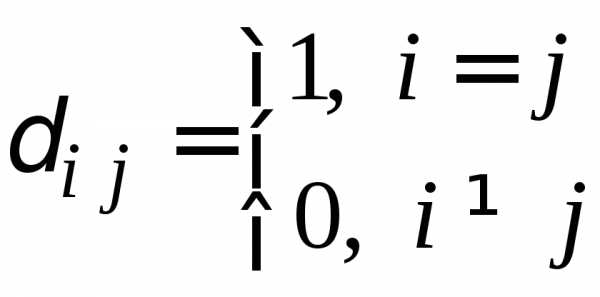 .
.
Полученные п систем линейных уравнений имеют одну и ту же матрицу А и различные столбцы свободных членов. Эти системы можно решать методом Гаусса (см. п. 3.1.1). В результате решения систем получаем единичную матрицу A.
Метод простой итерации для систем линейных уравнений
Метод простой итерации даёт возможность получить последовательность приближённых значений, сходящуюся к точному решению системы.
Преобразуем систему (3.1) к нормальному виду:
. (3.2)
Правая часть системы (3.2) определяет отображение:
, преобразующее точку -мерного
метрического пространства в точку того же пространства.
Выбрав начальную точку , можно построить итерационную последовательность точекп — мерного пространства:
При определённых условиях данная последовательность сходится.
Так, для исследования сходимости таких последовательностей используется принцип сжимающих отображений, который состоит в следующем.
Если F – сжимающее
отображение, определённое в полном
метрическом пространстве с метрикой  ,
то существует единственная неподвижная
точка
,
то существует единственная неподвижная
точка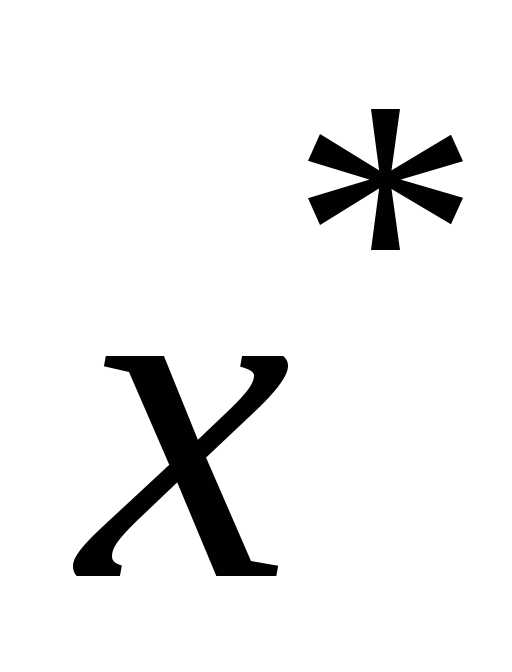 ,
такая, что
,
такая, что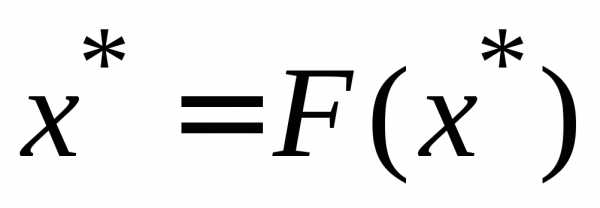 .
При этом итерационная последовательность,
.
При этом итерационная последовательность,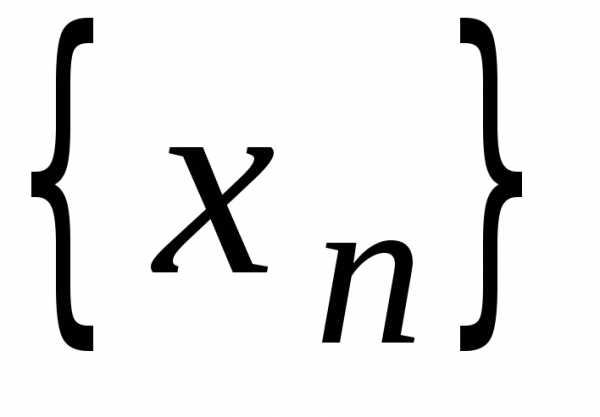 ,
полученная с помощью отображенияF с любым начальным членом х(0),
сходится к
,
полученная с помощью отображенияF с любым начальным членом х(0),
сходится к 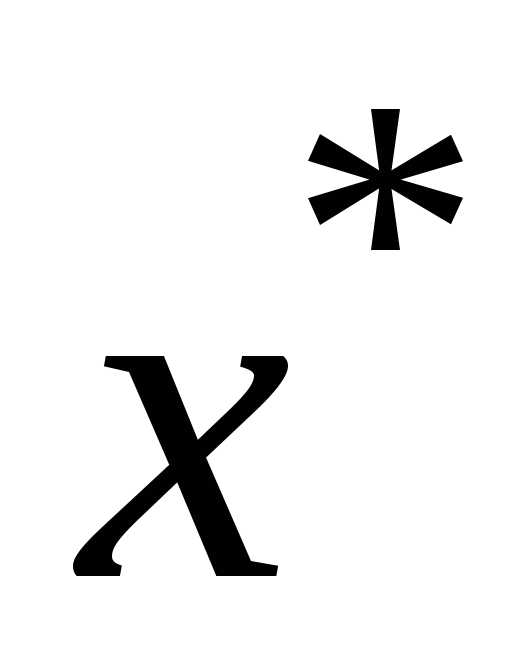 .
.
Оценка
расстояния между неподвижной точкой 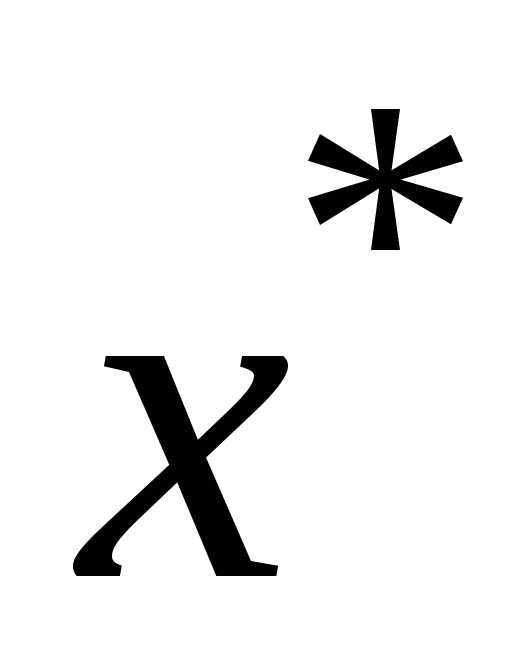 отображенияF и приближением х(к) даётся формулами:
отображенияF и приближением х(к) даётся формулами:
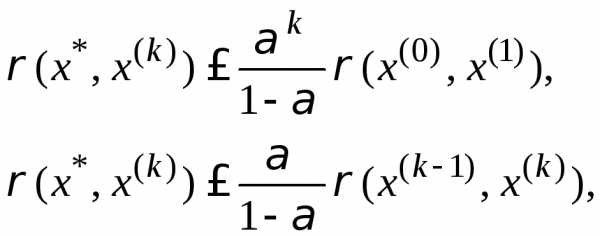 (3.3)
(3.3)
где α – множитель, определяемый достаточными условиями сжимаемости отображения F.
Значение
множителя α,
определяется выбором метрики, в которой
проверяется сходимость последовательности
значений 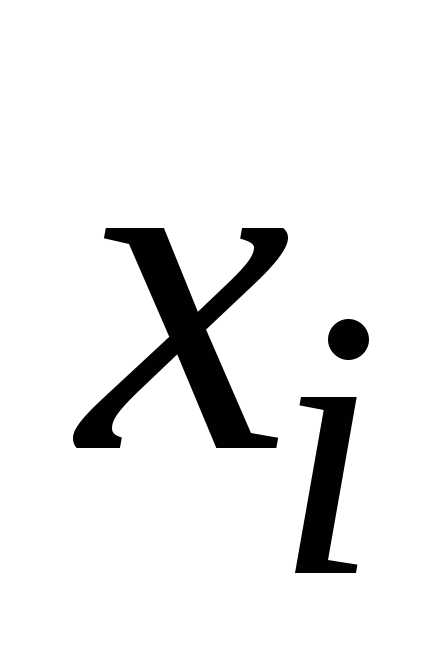 .
.
Рассмотрим
Достаточные условия сходимости
итерационной последовательности 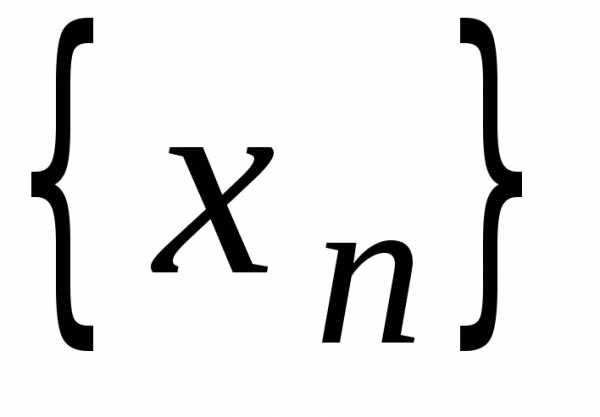 .
.
Практически, для применения метода итерации систему линейных уравнений удобно «погрузить» в одну из трёх следующих метрик:
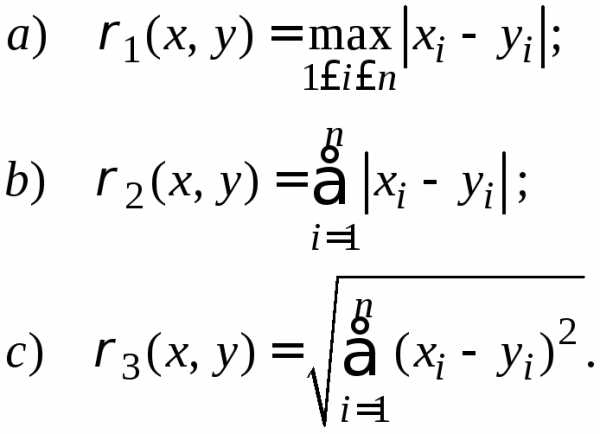 (3.4)
(3.4)
Для того, чтобы отображение F, заданное в метрическом пространстве соотношениями (3.2), было сжимающим, достаточно выполнение одного из следующих условий:
а)
в пространстве с метрикой  :
:
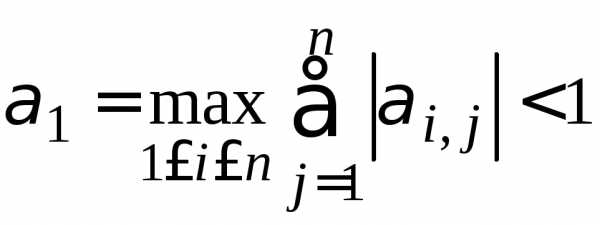 ,
т. е. максимальная из сумм модулей
коэффициентов в правой части системы
(3.2), взятых по строкам, должна быть меньше
единицы.
,
т. е. максимальная из сумм модулей
коэффициентов в правой части системы
(3.2), взятых по строкам, должна быть меньше
единицы.
б) в
пространстве с метрикой 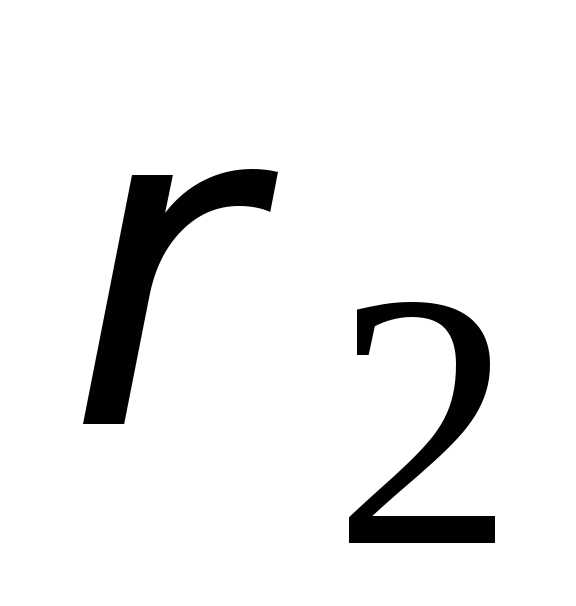 :
: ,
т. е. максимальная из сумм модулей
коэффициентов в правой части системы
(3.2), взятых по столбцам, должна быть
меньше единицы.
,
т. е. максимальная из сумм модулей
коэффициентов в правой части системы
(3.2), взятых по столбцам, должна быть
меньше единицы.
в) в
пространстве с метрикой  :
: 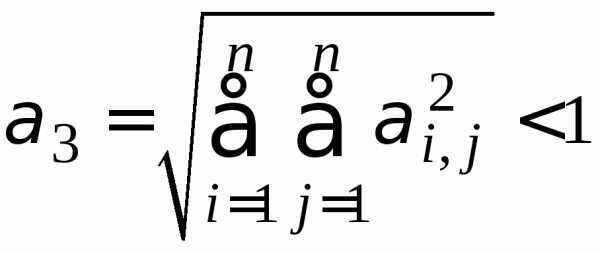 ,
т. е. сумма квадратов при неизвестных в
правой части системы (3.2) должна быть
меньше единицы
,
т. е. сумма квадратов при неизвестных в
правой части системы (3.2) должна быть
меньше единицы
Метод Зейделя для систем линейных уравнений
Метод
Зейделя является модификацией метода
простой итерации. Вычисление 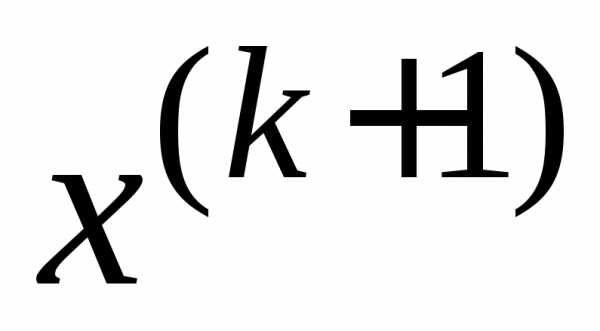 проводится по следующим формулам:
проводится по следующим формулам:
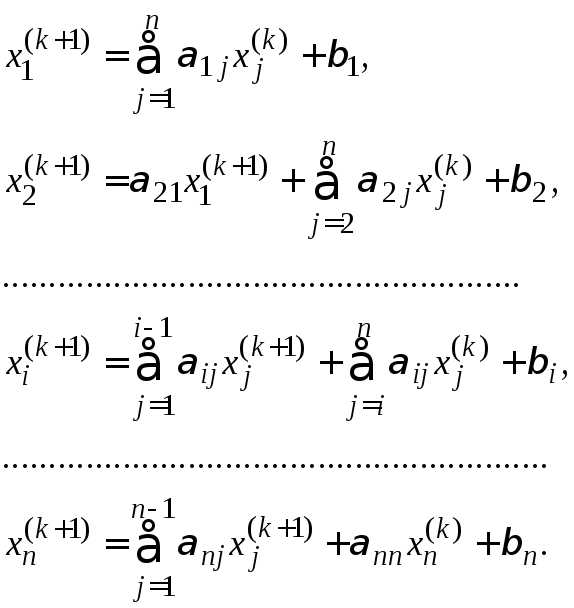
Достаточные условия сходимости итерационной последовательности приближенных решений системы и оценка погрешности проводятся по тем же формулам, что и в методе простой итерации.
studfiles.net
|
⇐ ПредыдущаяСтр 3 из 6Следующая ⇒ Задание: 1) Используя метод итераций, решить систему нелинейных уравнений с точностью до 0,001. 2) Используя метод Ньютона, решить систему нелинейных уравнений с точностью до 0,001. Задание №1Используя метод итераций, решить систему нелинейных уравнений с точностью до 0,001. Теоретическая часть. Метод итераций это способ численного решения математических задач. Его суть – нахождение алгоритма поиска по известному приближению (приближенному значению) искомой величины следующего, более точного приближения. Применяется в случае, когда последовательность приближений по указанному алгоритму сходится. Данный метод называют также методом последовательных приближений, методом повторных подстановок, методом простых итераций и т.п. Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Улучшением метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства. Обоснование Чтобы численно решить уравнение методом простой итерации, его необходимо привести к следующей форме: , где — сжимающее отображение. Для наилучшей сходимости метода в точке очередного приближения должно выполняться условие . Решение данного уравнения ищут в виде , тогда: В предположении, что точка приближения «достаточно близка» к корню , и что заданная функция непрерывна , окончательная формула для такова: С учётом этого функция определяется выражением: Эта функция в окрестности корня осуществляет сжимающее отображение[1], и алгоритм нахождения численного решения уравнения сводится к итерационной процедуре вычисления: .
Варианты заданий №1. 1) 2) №2. 1) 2) №3. 1) 2) №4. 1) 2) №5. 1) 2) №6. 1) 2) №7. 1) 2) №8. 1) 2) №9. 1) 2) №10.1) 2) №11.1) 2) №12.1) 2) №13.1) 2) №14.1) 2) №15.1) 2) №16.1) 2) №17.1) 2) №18.1) 2) №19.1) 2) №20.1) 2) №21. 1) 2) №22. 1) 2) №23. 1) 2) №24. 1) 2) №25. 1) 2) №26. 1) 2) №27. 1) 2) №28. 1) 2) №29. 1) 2) №30. 1) 2)
Образец выполнения задания
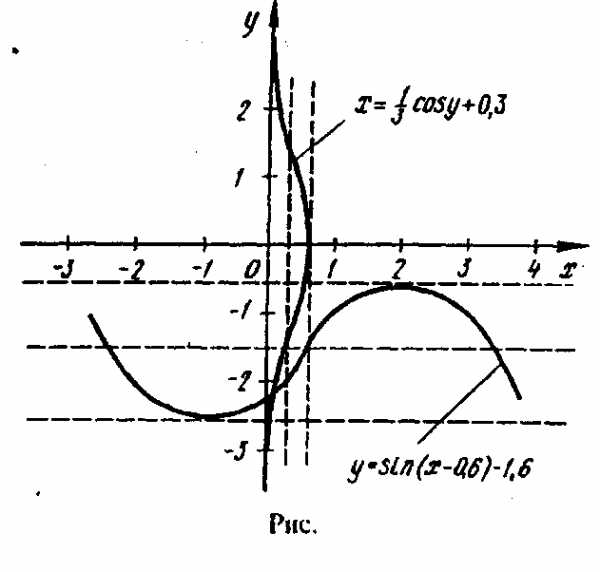
№1. 1) 2) Пример решения системы нелинейных уравнений методом итераций Перепишем данную систему в виде: Отделение корней производим графически (рис.1). Из графика видим, что система имеет одно решение, заключенное в области D:0<х<0,3;-2,2<y<-1,8. Убедимся в том, что метод итераций применим для уточнения решения системы, для чего запишем ее в следующем виде:
Так как ,то имеем в области D + = ; + = Таким образом, условия сходимости выполняются.
Рис.1
Таблица №2
За начальные приближения принимаем хо=0,15, у0 = -2. (таб.№2). Тогда ответ запишется:
Пример решения системы нелинейных уравнений методом Ньютона
Отделение корней производим графически (рис.2). Для построения графиков функций составим таблицу значений функций и , входящих в первое и второе уравнения (табл. I).
Рис.2 Значения для x можно брать исходя из следующих условий: из первого уравнения 1≤1,2х+0,4≤1, т.е. 1,16≤х≤0,5; из второго уравнения , т.е. . Таким образом, . Система имеет два решения. Уточним одно из них, принадлежащее области D: 0,4<x<0,5; 0,76<y<0,73. За начальное приближение примем Имеем:
Таблица №3
Уточнение корней проводим методом Ньютона: где ; ; ; ;
Все вычисления производим по таблице 3
Контрольные вопросы
1) Представьте на графике возможные случаи решения системы двух нелинейных уравнений. 2) Сформулируйте постановку задачи о решении системы n-линейных уравнений. 3) Приведите итерационные формулы метода простой итерации в случае системы двух нелинейных уравнений. 4) Сформулируйте теорему о локальной сходимости метода Ньютона. 5) Перечислите трудности, возникающие при использовании метода Ньютона на практике. 6) Объяснить каким образом можно модифицировать метод Ньютона. 7) Изобразите в виде блок-схем алгоритм решения систем двух нелинейных уравнений методами простой итерации и Ньютона. Лабораторная работа №3 |
cyberpedia.su
Итерационные методы решения систем нелинейных уравнений
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
СУМСКИЙ ГОСУДАСТВЕННЫЙ УНИВЕРСИТЕТ
кафедра информатики
КУРСОВАЯ РАБОТА
ПО КУРСУ:
Численные методы
на тему:
«Итерационные методы решения систем нелинейных уравнений»
Сумы, 2006
Содержание
1. Методы решения систем нелинейных уравнений. Общая информация
2. Итерационные методы решения систем нелинейных уравнений
2.1 Метод простых итераций
2.2 Преобразование Эйткена
2.3 Метод Ньютона
2.3.1 Модификации метода Ньютона
2.3.2 Квазиньютоновские методы
2.4 Другие итерационные методы решения систем нелинейных уравнений
2.4.1 Метод Пикара
2.4.2 Метод градиентного спуска
2.4.3 Метод релаксаций
3. Реализация итерационных методов программно и с помощью математического пакета Maple
3.1 Метод простых итераций
3.2 Метод градиентного спуска
3.3 Метод Ньютона
3.4 Модифицированный метод Ньютона
Выводы
Список использованной литературы
1. Методы решения нелинейных уравнений. Общая информация.
Пусть нам дана система уравнений, где
— некоторые нелинейные операторы: (1.1)Она может быть также представлена в матричном виде:
(1.1)Где
Её решением называется такое значение
, для котрогоОчень распространенной является вычислительная задача нахождения некоторых или всех решений системы (1.1) из n нелинейных алгебраических или трансцендентных уравнений с n неизвестными.
Обозначим через Х вектор-столбец (х 1, х 2,…, хn )T и запишем систему уравнений в виде формулы (1.2): F (Х ) = 0, где F = (f 1, f 2,…, fn )T .
Подобные системы уравнений могут возникать непосредственно, например, при конструировании физических систем, или опосредованно. Так, к примеру, при решении задачи минимизации некоторой функции G (х )часто необходимо определить те точки, в которых градиент этой функции равен нулю. Полагая F = grad G, получаем нелинейную систему.
В отличие от систем линейных алгебраических уравнений, для решения которых могут применяться как прямые (или точные ), так и итерационные (или приближенные ) методы, решение систем нелинейных уравнений можно получить только приближенными, итерационными методами. Они позволяют получать последовательность приближений
. Если итерационный процесс сходится, то граничное значение является решением данной системы уравнений.Для полноты представления о методах нахождения решения системы необходимо разъяснить такое понятие, как «скорость сходимости». Если для последовательности xn , сходящейся к пределу х* , верна формула
(k — положительное действительное число), то k называется скоростью сходимости данной последовательности.
2. Итерационные методы решения систем нелинейных уравнений
2.1 Метод простых итераций
Метод простых итераций (последовательных приближений) является одним из основных в вычислительной математике и применяется для решения широкого класса уравнений. Приведём описание и обоснование этого метода для систем нелинейных уравнений вида
fi (x1 ,x2 ,…xn ) = 0, i =1,2,..n ;
Приведём систему уравнений к специальному виду:
(2.1)Или в векторном виде
. (2.2)Причем переход к этой системе должен быть только при условии, что
является сжимающим отображением.Используя некоторое начальное приближение X(0) = (x1(0) ,x2(0) ,…xn(0) )
построим итерационный процесс X(k+1) = (X(k) ). Расчёты продолжаются до выполнения условия
. Тогда решением системы уравнений является неподвижная точка отображения .Проведём обоснование метода в некоторой норме
пространства .Приведём теорему о сходимости, выполнение условий которой приводит к нахождению решения системы.
Теорема (о сходимости). Пусть
1). Вектор-функция Ф(х) определена в области
;2). Для
выполняется условие3). Справедливо неравенство
Тогда в итерационном процессе:
1.
2.
,где
– решение системы уравнений;3.
,Замечание. Неравенство условия 2) есть условие Липшица для вектор -функции Ф(х) в области S с константой
(условие сжатия). Оно показывает, что Ф является оператором сжатия в области S , т. е. для уравнения (2.2) действует принцип сжатых отображений. Утверждения теоремы означают, что уравнение (2.2) имеет решение в области S , и последовательные приближения сходятся к этому решению со скоростью геометрической последовательности со знаменателем q .Доказательство . Поскольку
, то для приближения в силу предположения 3) имеем . Это значит, что . Покажем, что , k=2,3,… причём для соседних приближений выполняется неравенство (2.3)Будем рассуждать по индукции. При
утверждение справедливо, т.к. и . Допустим, что приближения принадлежат S, и неравенство (2.3) выполнено для . Поскольку , то для с учётом условия 2) теоремы имеем .По индуктивному предположению
.Следовательно,
,т.е. неравенство (2.3) справедливо для
. Покажем, что . Учитывая свойство (2.3) при , получаемИтак,
, и первое утверждение теоремы доказано.Покажем, что последовательность
является сходящейся. С этой целью проверим признак сходимости Коши (покажем, что последовательность является фундаментальной).mirznanii.com
Глава 7. Численное решение систем нелинейных уравнений
Задача нахождения некоторых или всех решений системы из n нелинейных алгебраических или трансцендентных уравнений сn неизвестными
f 1(x1,…,xn)=0 |
|
|
|
f 2(x1,…,xn)=0 | (7.1) |
………. | |
|
|
f (x ,…,x )=0
n 1 n
является одной из самых распространенной вычислительных задач. Подобные системы уравнений могут возникать непосредственно, например, при конструировании физических систем, или к таким системам сводится решение других задач. Так, к примеру, при решении задачи минимизации некоторой функции G(x1, x2,…, xn) часто необходимо определить те точки, в которых
градиент этой функции равен нулю. Полагая F = grad G, получаем нелинейную систему.
Векторная запись нелинейных систем. Введем векторные обозначения:
|
| x1 |
|
|
|
| f 1(x) |
|
| f 1(x1,…,xn) | |||
r | = |
| … |
| , | r |
| …….. |
| = |
| …………….. |
|
x |
|
| F(x)= |
|
|
|
| ||||||
|
|
|
|
|
|
| fn(x1,…,xn) | ||||||
|
| xn |
|
|
| fn(xr) |
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где f 1,.., fn — заданные, в общем случае, нелинейные вещественные функцииn переменных(x1,x2,…,xn ) и запишем систему уравнений в виде
| F(x)=0 | |
относительно векторной функции F | векторного аргумента xr. Таким | |
образом, исходная задача может быть | рассмотрена как задача о нулях | |
нелинейного отображения | F:Rn→Rn . | Фактически это та же задача, |
которую рассматривали в | предыдущей | главе, только в пространствах |
большей размерности и для ее решения применяются итерационные методы. Например, итерационный процесс, где компоненты приближений определяются из соотношений
|
| f 1(x1k +1,x2k,…,xnk )= 0 |
| ||||||||||||||
| f | 2 |
| x | k +1 | x | k | +1 |
| x | k |
| |||||
|
| 1 | , | 2 | ,…, | n)= 0 | |||||||||||
| ( |
|
|
|
|
|
| ||||||||||
……………………………… |
| ||||||||||||||||
|
|
|
|
|
| 1k+1, |
|
| 2k +1,…, |
|
| nk+1) = |
| ||||
f | n | ( | x | x | x | 0 | |||||||||||
|
|
|
|
|
|
|
|
|
|
| |||||||
является | аналогом | метода Зейделя | в | случае | системы | нелинейных | |
уравнений. | Нахождение каждого нового значения xik +1 требует в общем | ||||||
случае решения нелинейного уравнения |
|
|
|
| |||
|
|
| f i(x1k +1,xik−+11,xik +1,xik+1…,xnk )= 0 |
| |||
с одним неизвестным. |
|
|
|
|
| ||
Рассмотрим семейство итерационных методов с матричными | |||||||
параметрами | Ak. | Пусть (Ak) — | некоторая | последовательность | |||
невырожденных | вещественных матриц | n ×n. | Тогда, | очевидно, | |||
последовательность задач | k =0,1,… |
|
| ||||
|
|
| xr= xr− AkF(xr) , |
|
| ||
имеет те же решения, что и исходное уравнение (7.1), и для приближенного нахождения этих решений можно формально записать итерационный процесс
xr(k +1)= xr(k )− AkF(xr(k )) | k =0,1,…. | (7.2) |
Эта формула определяет большое семейство итерационных методов. В случае Ak ≡A получают метод простых итераций с линейной сходимостью
r(k ) | ) . | Если | A | k | = |
| ′ | r(k) | ) | −1 | |||
последовательности (x |
| F (x |
| , получим метод | |||||||||
Ньютона (7.7). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
7.1. Метод простой итерации |
|
|
|
|
|
|
|
|
|
|
| ||
Преобразуем систему уравнений к виду |
|
|
|
| |||||||||
x1=ϕ1(x1,…,xn) |
|
|
|
|
| ||||||||
|
| =ϕ2(x1,…,xn) |
|
|
|
|
| ||||||
x2 |
|
|
|
|
| ||||||||
…………………. |
|
|
|
| (7.3) | ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| n | =ϕ | n | 1 |
|
| n | ) |
|
|
|
|
|
x |
| (x ,…,x |
|
|
|
|
| ||||||
или иначе, в компактной записи, |
| x =Φ(xr) , |
|
|
|
| |||||||
|
|
|
|
|
|
| (7.4) | ||||||
где
Тогда:
ϕ1(x)
Φ(xr) =ϕ2(xr)M
ϕn(xr)
|
| ϕ1(x1,…,xn) |
|
|
| ϕ2(x1,…,xn) |
|
| = |
| . |
| M |
| |
|
| ϕn(x1,…,xn) |
|
|
|
| |
Это можно сделать, например, умножив (7.1) на некоторуюr невырожденную
матрицу −A и прибавив затем к тождествуx = x .Получится система x = xr− AF(xr)
эквивалентная исходной, где Φ(x) = xr− AF(xr) . Проблема теперь состоит лишь в подборе матричного параметраA такого, при которомΦ(x)
обладала бы нужными свойствами.
Задача о решении системы нелинейных уравнений в записи (7.4) – это задача о неподвижной точке нелинейного отображения Φ:Rn → Rn .
Запишем рекуррентное равенство r
x(k +1)=Φ(x(k )) ,
которое определяет метод простых итераций (или метод последовательных приближений). Если начать процесс построения последовательности(x(k ) ) с некоторого вектораxr(0) =(x1(0) ,…, xn(0) )T и продолжить по формуле
xik +1 =ϕi(x1k,…,xnk),i=1,…,n , | (7.5) |
то при определенных условиях эта последовательность со скоростью геометрической прогрессии будет приближаться к вектору x* — неподвижной точке отображенияΦ(x) .
Справедлива следующая теорема:
Теорема: Пусть функцияΦ(x) и замкнутое множествоM D(Φ) Rn
таковы, что
1. Φ(xr) M xr M;
2. q <1 : ||Φ(xr)−Φ(xr*) ||≤q ||xr−xr* ||.
— Φ(xr) имеет вM единственную неподвижную точкуxr*;
— последовательность (xr(k ) ) , определяемая методом простых итераций
(7.5) сходится к этой точке; — справедливы следующие оценки:
в ряд Тейлора:
J (xrk )
|| xr* −xr(k ) ||≤ |
| q | || xr(k )−xr(k −1)||≤ |
| qk |
| || xr(1) | −xr(0)|| | k . | |||||
|
|
|
|
| ||||||||||
|
| 1−q |
|
| 1−q |
|
|
| ||||||
Можно вместо (7.5) компоненты приближений xik +1определять из | ||||||||||||||
соотношений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1(k +1)=ϕ1(x1(k ),…,xn(k )) |
|
|
|
|
|
|
|
|
| |||||
| (k+1) |
|
| (k +1) | (k ) | ) |
|
|
|
|
|
|
| |
x2 | =ϕ2(x1 | ,…,xn |
|
|
|
|
|
|
| (7.6) | ||||
…………………………….. |
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (k +1) |
|
| (k +1) | ,…,xn −1 | (k+1) | ,xn | (k ) | ) |
|
| |||
xn | =ϕn(x1 |
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Этот метод также является аналогом метода Зейделя и наряду с (7.5) широко используется на практике, так как они требуют малого объема памяти и просты в реализации.
7.2. Метод Ньютона
Основная идея метода Ньютона состоит в выделении из уравнений линейных частей, которые являются главными при малых приращениях аргументов. Это позволяет свести исходную задачу к решению последовательности линейных систем.
Метод Ньютона для n уравнений применим толькоrтогда, когда могут быть вычислены все частные производные функцийfi(x) по переменным
x j . Пусть |
| обозначает матрицу Якоби и | ||||||
значение производной в точке xrk : | ∂f1(xrk ) | |||||||
|
|
|
|
|
| ∂f1(xrk ) | ||
|
|
|
|
|
| ∂x1 | ∂x2 | |
r | k | ′ | r | k |
| |||
J (x | ) = F (x | ) = …… | …… | |||||
|
| |||||||
|
|
|
|
|
| r | r | |
|
|
|
|
|
| ∂fn(xk ) | ∂fn(xk ) | |
|
|
|
|
|
| ∂x1 | ∂x2 | |
|
|
|
|
|
| |||
ее (i, j)-йэлемент есть
… | ∂f1(xrk ) | |
∂xn |
| |
… |
| |
…… |
| |
| r |
|
… | ∂fn(xk ) | |
∂xn |
| |
|
| |
Как и в одномерном случае (n = 1), метод Ньютонаr начинается с
произвольного xr , обозначенногоxr0 . РазложимF(x)
F(xr)= F(xr0 )+F′(xr0 )(xr−xr0 )+…
и, учитывая лишьr первые члены, получим линейное приближение к уравнениюF(x) =0:
| 0 | ′ |
| r0 |
|
| r |
| r0 |
|
|
|
| |
|
|
|
|
|
|
| −x )=0 |
|
| |||||
F(x) +F(x)(x |
|
| ||||||||||||
Естественно записать решение в форме |
|
|
|
|
|
|
|
|
|
| ||||
r | r0 |
| ′ | r0 |
| −1 |
|
| r0 |
|
|
| ||
|
|
|
|
|
|
|
| F(x), |
|
| ||||
x = x−F(x) |
|
|
|
| ||||||||||
сильно напоминающей | одномерную |
| формулу метода | Ньютона. Здесь | ||||||||||
F′(xr0)−1 — матрица, обратная матрице ЯкобиJ (x0 ) . |
|
| ||||||||||||
В общем случае, имея xk , можно найтиxk +1 появной формуле метода | ||||||||||||||
Ньютона: |
|
|
|
|
|
|
|
| −1 |
|
|
|
|
|
r(k +1) | r(k ) |
|
| ′ | r(k ) |
|
|
| r(k ) | ) . |
| |||
x | = x | − F(x |
| ) | F(x | (7.7) | ||||||||
Новым, по сравнению со скалярным случаем, фактором, осложняющим применение метода Ньютона к решению n — мерной системы, является
необходимость обращения матриц J (xk ) на каждой итерации.
Однако, вычисление обратной матрицы F′(x0)−1 не является необходимым.
Этого можно избежать, если формулу (7.7), требующую обращения матриц на каждой итерации, переписать в неявном виде:
′ r(k ) | r(k +1) | r(k ) | r(k ) | ) | (7.8) |
F (x | )(x | −x | )=−F(x |
Применение метода Ньютона в форме (7.8)r
прибавлением к xrk векторной поправкиr(k ) = x
решения линейной алгебраической системы
F′(xr(k ))rr(k )=−F(xr(k )), т.е. xr(k +1)= xr(k )+rr(k ).
позволяет найти xk +1 | |
(k +1) | −xr(k ) , полученной из |
| (7.9) |
| (7.10) |
.
К решению таких линейных систем (7.9) можно привлекать самые разные методы как прямые, так и итерационные в зависимости от размерности n решаемой задачи и особенностей матрицы Якоби.
Сходимость итерационного процесса (7.10) доказывается теоремой, смысл которой сводится к следующему.
Пусть xr* — решение системыF(x) =0 такое, при котором матрица ЯкобиJ (xr*) не вырождена и вторые частные производные функцииF(x)
непрерывны вблизи xr*. Тогда, еслиx0 достаточно близко кxr*, то
итерации по методу Ньютона сходятся. Более того, для er(k ) = xr* −xr(k ) отношение
e (k +1)
er(k )2
второго порядка.
Как и в одномерном случае, здесь основная проблема состоит в удачном выборе начального приближения, которое желательно было бы выбрать достаточно близко к предполагаемому решению, чтобы могла начаться быстрая сходимость.
На практике такое приближение достигается или очень большим везением (удачно выбран x0 ), или мужеством и настойчивостью исследователя (выполняется очень много итераций до того, как процесс начнет быстро сходиться).
Если матрицу Якоби |
| ′ |
|
| вычислить и обратить лишь один раз – | |||||
F (x) | ||||||||||
для начального приближения |
| x(0), | и использовать на последующих | |||||||
итерациях, то получим модифицированный метод Ньютона: |
| |||||||||
r(k+1) | r(k ) | − |
|
| r(0) | −1 | r(k ) | ) |
| |
x | = x |
| F (x | ) | F(x | (7.11) | ||||
|
|
|
|
| ′ |
|
|
|
| |
Этот метод требует значительно меньших вычислительных затрат на один итерационный шаг, но итераций при этом может потребоваться значительно больше для достижения заданной точности.
studfiles.net