Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
Пусть система линейных алгебраических уравнений задана в матричной форме , где матрицаAимеет размерностьnнаnи ее определитель отличен от нуля.
Так как , то матрицаА– обратима, то есть, существует обратная матрица. Если умножить обе части равенстванаслева, то получим формулу для нахождения матрицы-столбца неизвестных переменных. Так мы получили решение системы линейных алгебраических уравнений матричным методом.
Пример.
Решите систему линейных уравнений матричным методом.
Решение.
Перепишем систему уравнений в матричной форме:
Так как то СЛАУ можно решать матричным методом. С помощью обратной матрицы решение этой системы может быть найдено как.
Построим
обратную матрицу
с
помощью матрицы из алгебраических
дополнений элементов матрицыА(при
необходимости смотрите статьюметоды
нахождения обратной матрицы):
Осталось
вычислить
—
матрицу неизвестных переменных, умножив
обратную матрицуна
матрицу-столбец свободных членов(при
необходимости смотрите статьюоперации
над матрицами):
Ответ:
или в другой записи x1 = 4, x2 = 0, x3 = -1.
Основная проблема при нахождении решения систем линейных алгебраических уравнений матричным методом заключается в трудоемкости нахождения обратной матрицы, особенно для квадратных матриц порядка выше третьего.
Более подробное описание теории и дополнительные примеры смотрите в статье матричный метод решения систем линейных уравнений.
К началу страницы
Решение систем линейных уравнений методом Гаусса.
Пусть нам требуется найти решение системы из nлинейных уравнений с nнеизвестными переменнымиопределитель основной матрицы которой отличен от нуля.
Суть метода Гауссасостоит в последовательном исключении неизвестных переменных: сначала исключаетсяx1из всех уравнений системы, начиная со второго, далее исключаетсяx2из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменнаяxn. Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называетсяпрямым ходом метода Гаусса. После завершения прямого хода метода Гаусса из последнего уравнения находитсяxn, с помощью этого значения из предпоследнего уравнения вычисляетсяxn-1, и так далее, из первого уравнения находитсяx1. Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называетсяобратным ходом метода Гаусса
Кратко опишем алгоритм исключения неизвестных переменных.
Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменнуюx1из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на, к третьему уравнению прибавим первое, умноженное на, и так далее, кn-омууравнению прибавим первое, умноженное на. Система уравнений после таких преобразований примет видгде, а.
К такому же результату мы бы пришли, если бы выразили x1через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменнаяx1исключена из всех уравнений, начиная со второго.
Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке
Будем считать, что (в противном случае мы переставим местами вторую строку с k-ой, где). Приступаем к исключению неизвестной переменнойx2из всех уравнений, начиная с третьего.
Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на, и так далее, кn-омууравнению прибавим второе, умноженное на. Система уравнений после таких преобразований примет видгде, а. Таким образом, переменнаяx2исключена из всех уравнений, начиная с третьего.
Далее приступаем к исключению неизвестной x3, при этом действуем аналогично с отмеченной на рисунке частью системы
Так продолжаем прямой ход метода Гаусса пока система не примет вид
С этого момента начинаем обратный ход метода Гаусса: вычисляем xnиз последнего уравнения как, с помощью полученного значенияxnнаходимxn-1
Пример.
Решите систему линейных уравнений методом Гаусса.
Решение.
Исключим
неизвестную переменную x1из второго и третьего уравнения системы.
Для этого к обеим частям второго и
третьего уравнений прибавим соответствующие
части первого уравнения, умноженные наи
насоответственно:
Теперь
из третьего уравнения исключим x2,
прибавив к его левой и правой частям
левую и правую части второго уравнения,
умноженные на:
На этом прямой ход метода Гаусса закончен, начинаем обратный ход.
Из последнего уравнения полученной системы уравнений находим x3:
Из второго уравнения получаем .
Из первого уравнения находим оставшуюся неизвестную переменную и этим завершаем обратный ход метода Гаусса .
Ответ:
x1 = 4, x2 = 0, x3 = -1.
Более детальную информацию и дополнительные примеры смотрите в разделе решение элементарных систем линейных алгебраических уравнений методом Гаусса.
К началу страницы
studfiles.net
23. Решение слау методом обратной матрицы
Метод обратной матрицы (Матричный метод) решения систем линейных алгебраических уравнений с ненулевым определителем основной матрицы состоит в поиске матрицы, обратной к основной матрице, и умножению ее на матрицу свободных членов.
Обратная матрица
Пусть имеется квадратная матрица n-го порядка
Матрица А-1 называется обратной матрицей по отношению к матрице А, если А*А-1 = Е, где Е — единичная матрица n-го порядка.
Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:
Обратная матрица может существовать только для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают.
Теорема условия существования обратной матрицы
Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
Матрица А = (А1, А2,…Аn) называется невырожденной, если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.
Алгоритм нахождения обратной матрицы
Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е.
Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е.
Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е.
Записать обратную матрицу А-1, которая находится в последней таблице под матрицей Е исходной таблицы.
Пример 1
Для матрицы А найти обратную матрицу А-1
Решение: Записываем матрицу А и справа приписываем единичную матрицу Е. Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.

Проверим правильность вычислений умножением исходной матрицы А и обратной матрицы А-1.
В результате умножения матриц получилась единичная матрица. Следовательно, вычисления произведены правильно.
Ответ:
Решение матричных уравнений
Матричные уравнения могут иметь вид:
АХ = В, ХА = В, АХВ = С,
где А,В,С — задаваемые матрицы, Х- искомая матрица.
Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.
Например, чтобы найти матрицу из уравнения , необходимо умножить это уравнение на слева.
Тогда:
Следовательно, чтобы найти решение уравнения , нужно найти обратную матрицу и умножить ее на матрицу , стоящие в правой части уравнения.
Аналогично решаются другие уравнения.
Пример 2
Решить уравнение АХ = В, если
Решение: Так как обратная матрица равняется (см. пример 1)
24. Решение слау методом гаусса
Ме́тод Га́усса[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Описание метода
Пусть исходная система выглядит следующим образом
Матрица A называется основной матрицей системы, b — столбцом свободных членов.
Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных .
Тогда переменные называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число, где i > r, то рассматриваемая система несовместна.
Пусть для любых i > r.
Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом (, где — номер строки):
,
где
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
Следствия:
1: Если в совместной системе все переменные главные, то такая система является определённой.
2: Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной.
Условие совместности
Упомянутое выше условие для всехможет быть сформулировано в качестве необходимого и достаточного условия совместности:
Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны).
Теорема Кронекера-Капелли.
Система совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы.
Следствия:
Количество главных переменных равно рангу системы и не зависит от её решения.
Если ранг совместной системы равен числу переменных данной системы, то она определена.
Алгоритм
Описание
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.
На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Метод Гаусса требует порядка O(n3) действий.
Этот метод опирается на: Теорема (о приведении матриц к ступенчатому виду).
Любую матрицу путём элементарных преобразований только над строками можно привести к ступенчатому виду.
studfiles.net
Решение систем линейных уравнений методом обратной матрицы
Задача №5. Найти решение системы методом обратной матрицы:

Решение.
Здесь 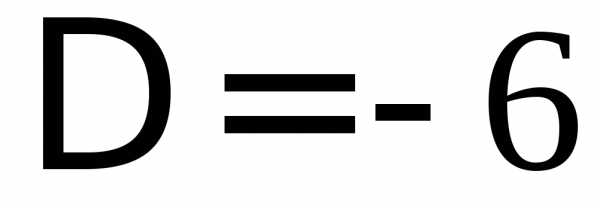 ,
так что матрица А невырожденная и искомое
решение имеет вид.
,
так что матрица А невырожденная и искомое
решение имеет вид.
.
Отсюда
Задача №6. Решить систему уравнений матричным методом:

Решение.

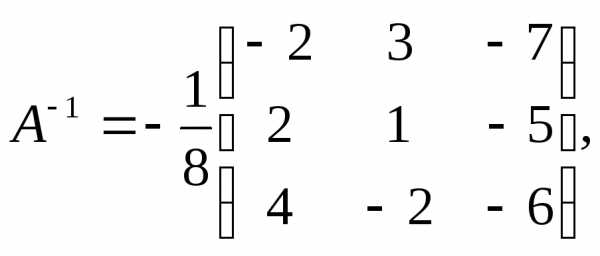
Находим:
т.е. – решение данной системы.
Задачи для самостоятельного решения:
Решить системы уравнений методом Крамера и методом обратной матрицы.
1. 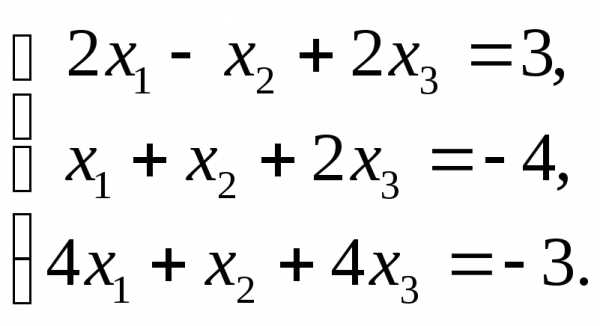 2.
2.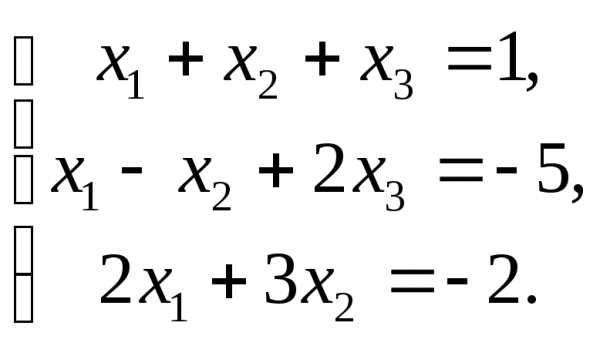
3.  4.
4.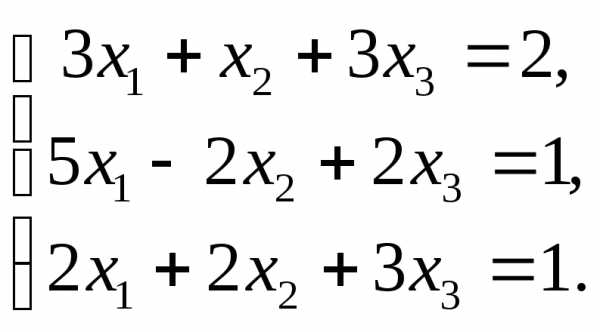
5. 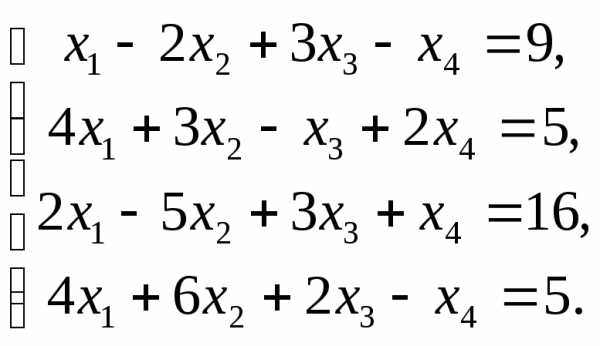 6.
6.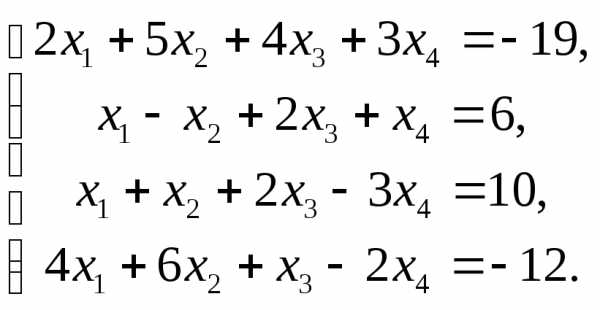
Занятие 4. Решение систем линейных уравнений методом Гаусса.
Для усвоения практического материала нужно ответить на следующие теоретические вопросы:
Понятие системы линейных алгебраических уравнений.
Понятие решения системы линейных алгебраических уравнений.
Определение совместной и несовместной системы.
Достаточное условие совместной системы.
Определение однородной и неоднородной системы.
Определение ранга матрицы.
Алгоритм решения неоднородной системы линейных уравнений методом Гаусса.
Алгоритм решения однородной системы линейных уравнений.
Типовые задачи
Задача №1. Решить систему методом Гаусса:
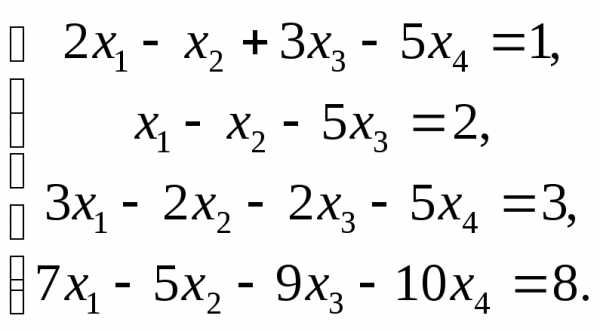
Решение.
В результате элементарных преобразований над расширенной матрицей системы
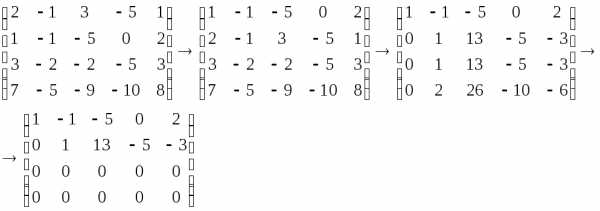
исходная система свелась к ступенчатой:
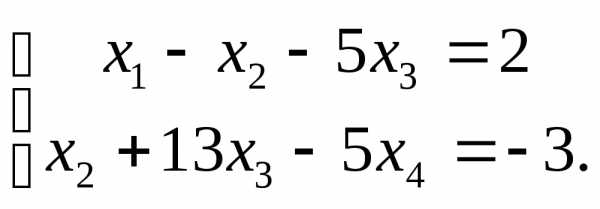
Поэтому общее решение системы:
Если положить, например, , то найдем одно из частных решений этой системы ;.
Задача №2. Решить систему методом Гаусса:
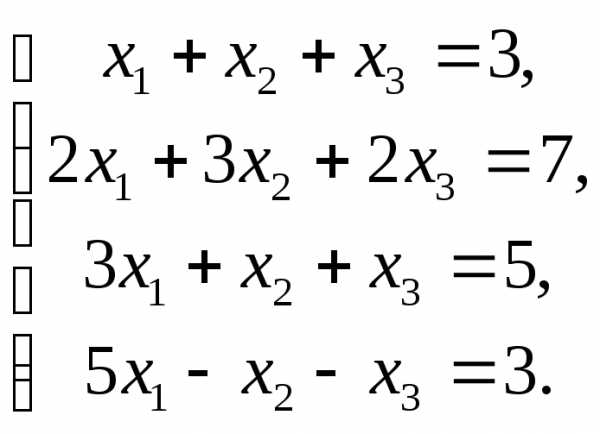
Решение.
Произведем элементарные преобразования над строками расширенной матрицы системы:
.
Полученная матрица соответствует системе
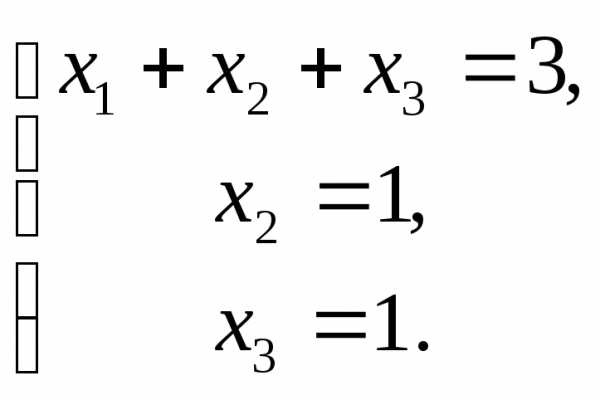
Осуществляя обратный ход, находим
Задача №3. Решить систему методом Гаусса:
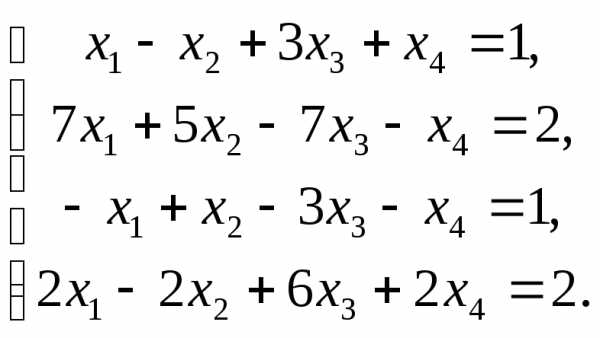
Решение:
.
Наличие противоречивой строки говорит о несовместности системы линейных уравнений.
Задача №4. Решить однородную систему линейных уравнений методом Гаусса:
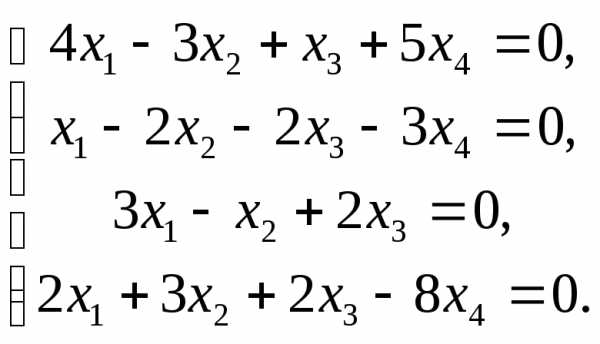
Решение.
Ранг основной матрицы системы равен рангу расширенной матрицы и равен числу неизвестных. Система имеет единственное решение, т.е. нулевое (тривиальное):
Задача №5. Решить однородную систему линейных уравнений методом Гаусса:
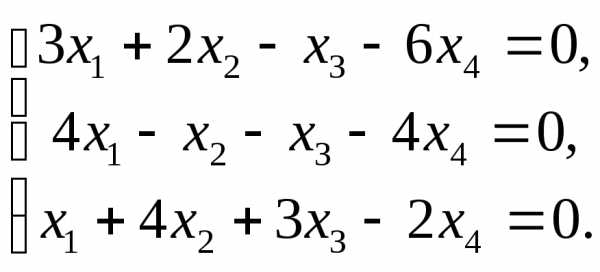
Решение.
Ранг основной матрицы системы равен рангу расширенной матрицы и меньше числа неизвестных (3<4). Система имеет бесконечно много решений. Получим систему:
Если
положить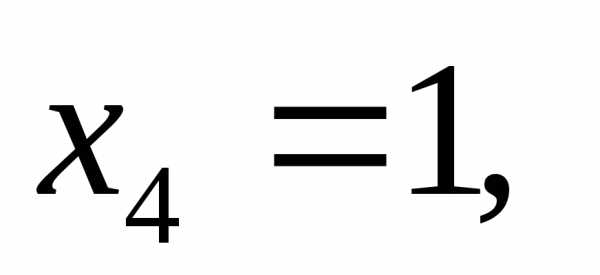 тои
получиличастное
решение исходной системы.
тои
получиличастное
решение исходной системы.
Задачи для самостоятельного решения:
I. Решить системы линейных уравнений:
1.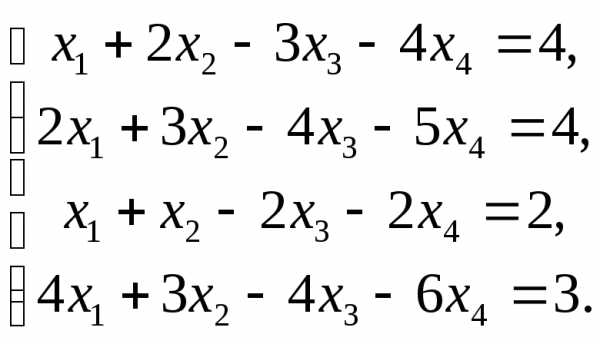
2. 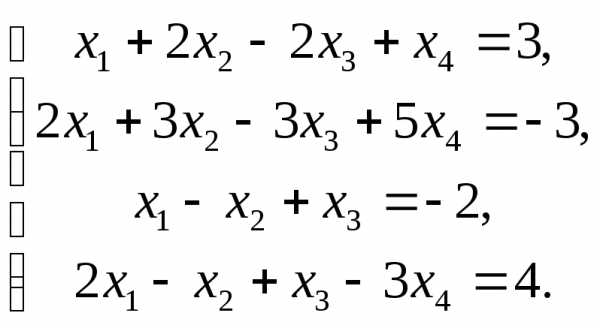
3. 
4. 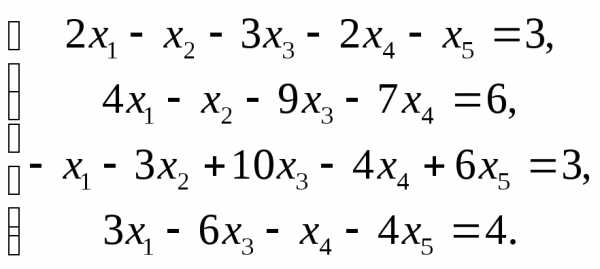
5. 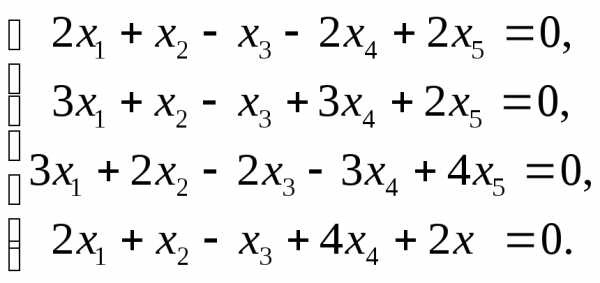
6. 
II. Найти решение системы
линейных уравнений в зависимости от
параметра :
:
1.
2. 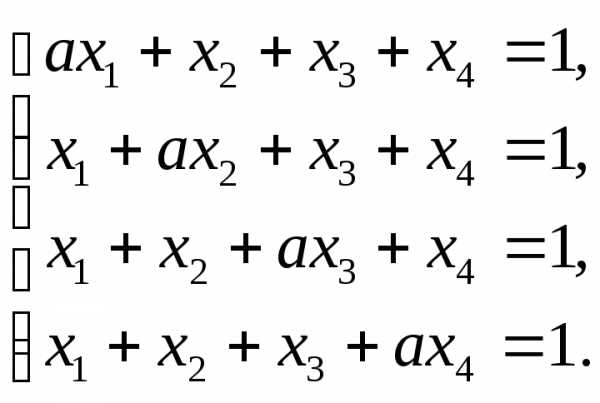
3.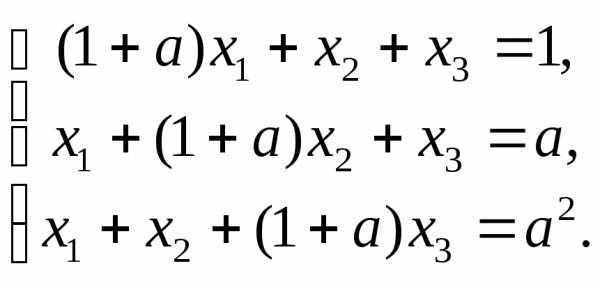
Занятие 5. Скалярное, векторное и смешанное произведения векторов..
Для усвоения практического материала нужно ответить на следующие теоретические вопросы:
Дать определение скалярного произведения векторов.
Перечислить свойства скалярного произведения векторов.
Скалярное произведение векторов в координатной форме.
Приложения скалярного произведения для нахождении.
Какое произведение векторов называется векторным?
Перечислить свойства векторного произведения.
Какие приложения имеет векторное произведение в геометрии и механике?
Записать условие коллинеарности (параллельности) векторов.
Какое произведение векторов называется смешанным?
Перечислить свойства смешанного произведения. Его геометрический смысл.
Как выражается смешанное произведение через координаты?
studfiles.net
Решение систем линейных алгебраических уравнений матричным способом (с помощью обратной матрицы)
Рассмотрим систему n-линейных алгебраических уравнений с n-неизвестными:
(1)
Составим матрицу из коэффициентов при неизвестных:
A = .
Запишем матрицу-столбец из неизвестных членов:
Х = .
Запишем матрицу-столбец из свободных членов:
B = .
Запишем систему (1) в матричной форме:
A ∙ X = B. (2)
Умножим обе части (2) на слева, тогда получим:
или
или
Пример.
Решить систему линейных алгебраических уравнений матричным способом:
Составим матрицу из коэффициентов при неизвестных:
A = .
Запишем матрицу-столбец из неизвестных членов и матрицу-столбец из свободных членов:
X = ,B = .
Найдем обратную матрицу для матрицы А:
Метод Гаусса
Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений . Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Матрица называется основной матрицей системы,b — столбцом свободных членов.
Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных , … ,.
Тогда переменные , … ,называютсяглавными переменными. Все остальные называются свободными.
Если хотя бы одно число , где, то рассматриваемая система несовместна.
Пусть для любых.
Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом (,где— номер строки):
, (2)
где ,,
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
Пример
Покажем, как методом Гаусса можно решить следующую систему:
Обнулим коэффициенты при во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную наи, соответственно:
Теперь обнулим коэффициент при в третьей строке, вычтя из неё вторую строку, умноженную на 4:
В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
из третьего;
из второго, подставив полученное ;
из первого, подставив полученные и.
Таким образом исходная система решена.
studfiles.net
Решение системы линейных уравнений методом обратной матрицы с примерами
Метод обратной матрицы не представляет ничего сложного, если знать общие принципы работы с матричными уравнениями и, конечно, уметь производить элементарные алгебраические действия.
Решение системы уравнений методом обратной матрицы. Пример.Удобнее всего постигать метод обратной матрицы на наглядном примере. Возьмем систему уравнений:
Первый шаг, который необходимо сделать для решения этой системы уравнений — найти определитель. Поэтому преобразим нашу систему уравнений в следующую матрицу:
И найдем нужный определитель:
Формула, использующаяся для решения матричных уравнений, выглядит следующим образом:
Х = А-1b.
Таким образом, для вычисления Х нам необходимо определить значение матрицы А-1 и умножить его на b. В этом нам поможет другая формула:
Ат в данном случае будет транспонированной матрицей — то есть, той же самой, исходной, но записанной не строками, а столбцами.
Не следует забывать о том, что метод обратной матрицы, как и метод Крамера, подходит только для систем, в которых определитель больше или меньше нуля. Если же определитель равен нулю, нужно использовать метод Гаусса.
Следующий шаг — составление матрицы миноров, представляющей собой такую схему:
В итоге мы получили три матрицы — миноров, алгебраических дополнений и транспонированную матрицу алгебраических дополнений. Теперь можно переходить к собственно составлению обратной матрицы. Формулу мы уже знаем. Для нашего примера это будет выглядеть так:
Работа почти закончена. Теперь осталось выполнить только умножение матрицы.
Таким образом, ответ для взятого нами примера получается следующим: х1 = 5, х2 = -1, х3 = 1.
Похожие статьи
infoogle.ru
Рекомендации по использованию excel для решения слау № 1 и 3 с помощью обратной матрицы
Полученные
матрицы (для СЛАУ
№ 1 и 2)
представляют собой матрицу коэффициентов А и
вектор свободных членов 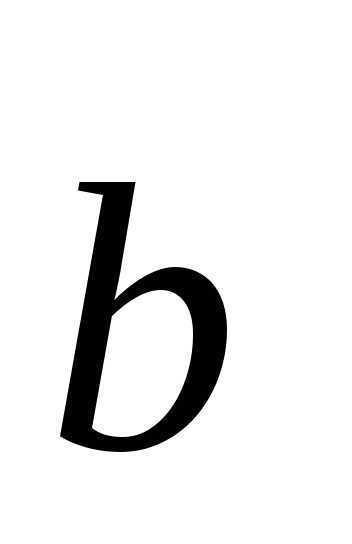 системы
уравнений, записанной
в матричной форме
системы
уравнений, записанной
в матричной форме
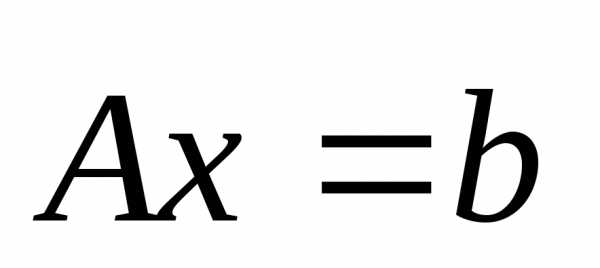 (4.2)
(4.2)
Решение СЛАУ имеет вид
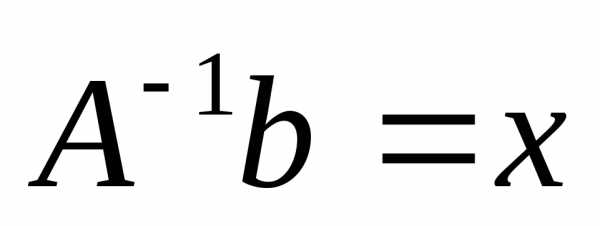 ,
,
где А-1 – обратная матрица, полученная с помощью функции МОБР.
Значения
вектора неизвестных 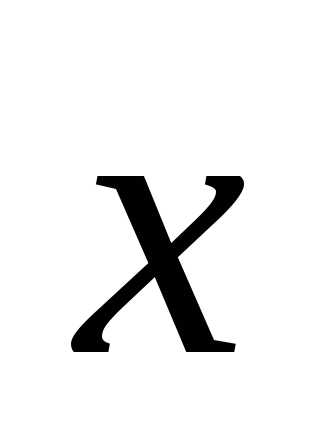 получаются
умножением обратной матрицы А-1 и
вектора
свободных членов
получаются
умножением обратной матрицы А-1 и
вектора
свободных членов 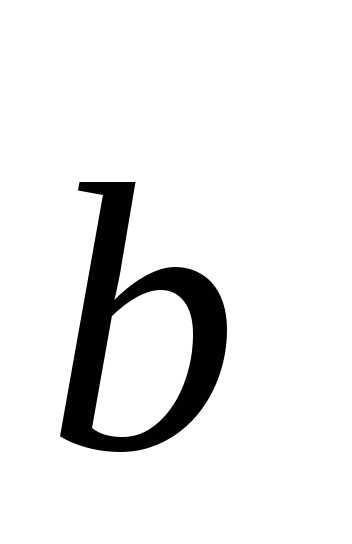 с
помощью функции МУМНОЖ.
с
помощью функции МУМНОЖ.
| A | B | C | D | E | F | G | H | I | J | K | L |
1 | СЛАУ № 1 |
|
|
|
|
|
|
| ||||
2 | N = | 40 |
|
|
|
| Метод обратной матрицы |
|
| |||
3 | Матрица коэффициентов А |
| Вектор свобод. членов, b |
| Обратная матрица А -1 |
| Вектор неиз-вест- ных |
| ||||
4 | 3 | -7 | 2 |
| 3 |
| 0,1391 | 0,1127 | 0,012 |
| x1 | 0,957 |
5 | 4 | 8 | -3 |
| 5 |
| -0,127 | -0,017 | 0,0408 |
| x2 | -0,55 |
6 | 11 | 6 | 5 |
| -2 |
| -0,153 | -0,228 | 0,1247 |
| x3 | -1,85 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
Пояснения
В ячейках строки 3 записаны заголовки объектов расчета
В ячейки диапазона А4 : С6 введены значения элементов исходной матрицы коэффициентов
В ячейки диапазона Е4 : Е6 введены значения элементов вектора свободных членов
Для получения обратной матрицы необходимо выделить диапазон ячеек, в который будет размещена обратная матрица G4 : I6. Затем выбрать функцию МОБР категории Математические функции. Следуя указаниям Мастера функций, указать диапазон обращаемой матрицы А4 : С6. Нажать комбинацию клавиш Ctrl + Shift + Enter.
Выделить диапазон L4 : L6. Затем выбрать функцию МУМНОЖ категории Математические функции. Следуя указаниям Мастера функций, указать диапазоны перемножаемых элементов: матрицы G4 : I6 и вектора Е4 : Е6. Нажать комбинацию клавиш Ctrl + Shift + Enter.
Рекомендации по использованию excel для решения слау № 2 с помощью метода прогонки
| A | B | C | D | E | F | G |
1 | N = | 40 | СЛАУ № 2 |
| Метод прогонки |
| |
2 | Трехдиагональная матрица коэффициентов А |
| Вектор свобод. членов, d |
| |||
3 | 2 | 3 | 0 | 0 |
| 8 |
|
4 | 3 | 4 | 1 | 0 |
| 14 |
|
5 | 0 | 5 | 3 | 2 |
| 27 |
|
6 | 0 | 0 | 2 | 4 |
| 22 |
|
7 |
| Прогоночные коэффициенты |
| Решение |
| ||
8 | p0 = | -0,3 | q0 = | 0,8 | x0 = | 0,76367 |
|
9 | p1 = | -0,0901 | q1 = | 0,3243 | x1 = | 0,12111 |
|
10 | p2 = | -0,1896 | q2 = | 2,4056 | x2 = | 2,25573 |
|
11 | p3 = | 0 | q3 = | 0,7907 | x3 = | 0,79071 |
|
Пояснения
В ячейках диапазона А 3: С6 записаны коэффициенты трехдиагональной матрицы коэффициентов СЛАУ № 2
В ячейках диапазона F 3: F 6 записаны элементы вектора свободных членов СЛАУ № 2
В ячейках столбцов А8 : А11, С8 : С11, Е8 : Е11 записаны обозначения прогоночных коэффициентов и неизвестных
В ячейку В8 введена формула = — B3 / A3 (см. формулу метода прогонки для прогоночного коэффициента p0 = — c0 / a0)
В ячейку D8 введена формулу = F3 / A3 (см. формулу метода прогонки для прогоночного коэффициента q0 = d0 / a0)
В ячейку B9 введена формулу = — C4 / (B4+A4*$B8) (см. формулу для прогоночных коэффициентов pi )
Эти же формулы использованы для заполнения ячеек диапазона B9 : B 11
Аналогичные действия произведены для вычисления (по соответствующим формулам) прогоночных коэффициентов qi (диапазон D 8 : D 11) и вычисления неизвестных хi (диапазон F 8 : F 11)
studfiles.net
14. Решение слау с квадратной невырожденной матрицей методом Гаусса (прямой обратный ход)
ешите систему линейных уравнений методом Гаусса.
Решение.
Исключим
неизвестную переменную x1 из
второго и третьего уравнения системы.
Для этого к обеим частям второго и
третьего уравнений прибавим соответствующие
части первого уравнения, умноженные
на и
на соответственно: 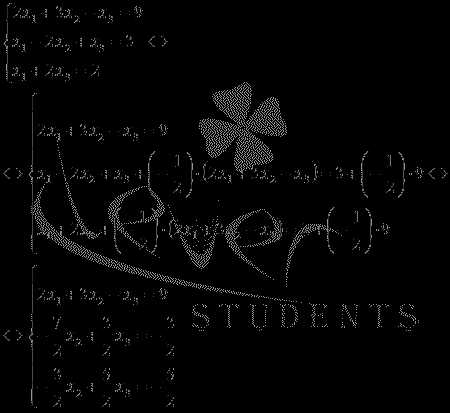
Теперь
из третьего уравнения исключим x2,
прибавив к его левой и правой частям
левую и правую части второго уравнения,
умноженные на : 
На этом прямой ход метода Гаусса закончен, начинаем обратный ход.
Из последнего уравнения полученной системы уравнений находим x3:
Из второго уравнения получаем .
Из первого уравнения находим оставшуюся неизвестную переменную и этим завершаем обратный ход метода Гаусса .
Ответ:
x1 = 4, x2 = 0, x3 = -1.
Определение
15. Решение слау с квадратной невырожденной матрицей методом Крамера.
Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений (СЛАУ) с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и оно единственно).
При решении СЛАУ методом Крамера используется вычисление определителя или детерминанты основной матрицы. Для того, чтобы систему уравнение можно было решить методом Крамера, необходимо и достаточно, чтобы определитель ее основной матрицы был отличен от нуля, тоесть матрица должна быть невырожденной.
16. Решение слау с квадратной невырожденной матрицей с помощью обратной матрицы.
Пример 1.
Найти решение системы
С помощью обратной матрицы.
Выпишем матрицу системы
Найдем присоединенную матрицу Ã. Имеем:
Следовательно,
Вычислим определитель матрицы А с помощью разложения по первой строке:
|A| = 1·(-3) + 2·(-3) + (-1)·3 = -12.
Таким образом,
Отсюда
Тем самым Х1 = 1, Х2 = 2, Х3 = 1.
17. Теорема Кронекера – Капелли .
Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных и бесконечное множество решений, если ранг меньше числа неизвестных.
Необходимость
Пусть система совместна. Тогда существуют числа x1…xn € R такие, что b= x1a1+….+xnxn. Следовательно, столбец b является линейной комбинацией столбцов a1,…an матрицы A . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что rangA=rangB.
Достаточность
Пусть rangA=rangB=r. Возьмем в матрице A какой-нибудь базисный минор. Так как rangB=r , то он же и будет базисным минором и матрицы B. Тогда, согласно теореме о базисном миноре, последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A .
Следствия
Количество главных переменных системы равно рангу системы.
Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.
studfiles.net
