Пределы. Примеры решений — matematika
Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.
Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который заложил основы математического анализа и дал строгие определения, определение предела, в частности. Надо сказать, этот самый Коши снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причем одна теорема отвратительнее другой. В этой связи мы не будем рассматривать строгое определение предела, а попытаемся сделать две вещи:
1. Понять, что такое предел.
2. Научиться решать основные типы пределов.
Прошу прощения за некоторую ненаучность объяснений, важно чтобы материал был понятен даже чайнику, что, собственно, и является задачей проекта.
Итак, что же такое предел?
А сразу пример, чего бабушку лохматить….
Любой предел состоит из трех частей:
1) Всем известного значка предела .
2) Записи под значком предела, в данном случае . Запись читается «икс стремится к единице». Чаще всего – именно ,
хотя вместо «икса» на практике встречаются и другие переменные. В
практических заданиях на месте единицы может находиться совершенно
любое число, а также бесконечность ().
3) Функции под знаком предела, в данном случае .
Сама запись читается так: «предел функции при икс стр
www.sites.google.com
Сложные пределы и методы их решения
В этой статье собраны наиболее интересные и сложные случаи пределов, решение которых требует определенных навыков и знаний. В большинстве случаев, пределы, изучаемые в
базовом курсе высшей математики, просты и решаются в одно-два действия. Однако иногда приходится сталкиваться со сложными примерами пределов, которые чтобы решить
нужно знать хитростные способы. Рассмотрим же их!
Пример 1. Решить предел
Чтобы решить данный предел, необходимы знания по теме первый замечательный предел и эквивалентные бесконечно малые функции. Ну а в начале долгого пути, нам предстоит сделать преобразования в числителе, используя свойства тригонометрических функций, и в знаменателе, используя обманный ход, но обо всем по порядку. Начнем с числителя, представим
в равнозначной записи и запишем числитель уже в новой форме:
Тот факт, что x стремится к нулю, позволяет нам считать что в будущем можно будет использовать свойства эквивалентных бесконечно малых. Поэтому, обращаем внимание на
значений. Обращаемся к таблице эквивалентных бесконечно малых величин и видим, что для счастья нам не хватает единицы. Вот здесь-то мы и используем способ (как я его
называю) «искусственного добавления» числа:
Все довольно просто, мы не нарушая баланса выражения, добавили и убавили единицу к косинусу. С учетом всех знаков , преобразуем выражение:
В результате наших действий, мы получили идеальных кандидатов на эквивалентные замены. В числителе вынесли знак минус за скобки, получив тем самым
в знаменателе подготовили выражение с логарифмом. С ними все понятно, что же делать в синусом? Все просто, используем первый замечательный предел и получаем законную
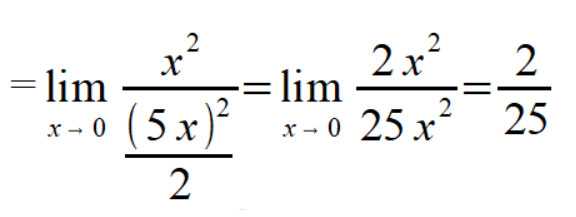
Краткие пояснения к тому, какие эквивалентные замены были произведены, а также как был использован первый предел:
— первый предел, при
Отдельной строкой хотелось бы остановиться на третьей формуле. Как известно, эквивалентная малая для логарифма выглядит следующим образом:
ln(1+x) ~x
В нашем случае, в роли х выступала вся скобка (-(1-cos(5x))).
Далее, мы повторно используем правило, но только уже для случая с косинусом:
при
В нашем случае, cos(x) — это cos(5x) и соответствующая замена была такой:
при
Ну вот и все. Предел был непростым, но интересным, и его решение, надеюсь, было вам понятным.
Правило Лопиталя: теория и примеры решений
Раскрытие неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций значительно упрощается с помощью правила Лопиталя (на самом деле двух правил и замечаний к ним).
Суть правил Лопиталя состоит в том, что в случае, когда вычисление предела отношений двух бесконечно малых или бесконечно больших функций даёт неопределённости видов 0/0 или ∞/∞, предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.
Перейдём к формулировкам правил Лопиталя.
Правило Лопиталя для случая предела двух бесконечно малых величин. Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, может быть, самой точки a, причём в этой окрестности g‘(x)≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны нулю
(),
то предел отношения этих функций равен пределу отношения их производных
().
Правило Лопиталя для случая предела двух бесконечно больших величин. Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, может быть, самой точки a, причём в этой окрестности g‘(x)≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности
(),
то предел отношения этих функций равен пределу отношения их производных
().
Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный или бесконечный).
Замечания.
1. Правила Лопиталя применимы и тогда, когда функции f(x) и g(x) не определены при x = a.
2. Если при вычисления предела отношения производных функций f(x) и g(x) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).
3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a, а к бесконечности (x → ∞).
К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.Пример 1. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x=2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем
В числителе вычисляли производную многочлена, а в знаменателе — производную сложной логарифмической функции. Перед последним знаком равенства вычисляли обычный предел, подставляя вместо икса двойку.
Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Решение. Подстановка в заданную функцию значения x=0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:
Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Решение. Подстановка в заданную функцию значения x=0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:
Пример 4. Вычислить
.
Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:
Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.
Пример 5. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Решение. Находим
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида ∞/∞.
Пример 6. Вычислить
.
Решение. Находим
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида 0/0.
Пример 7. Вычислить
.
Решение. Находим
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида — ∞/∞, а затем неопределённость вида 0/0.
Пример 8. Вычислить
.
Решение. Находим
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида ∞/∞, а затем неопределённость вида 0/0.
Применить правило Лопиталя самостоятельно, а затем посмотреть решение
Пример 11. Вычислить
.
Решение. Получаем
(здесь неопределённость вида 0∙∞ мы преобразовали к виду ∞/∞, так как
а затем применили правила Лопиталя).
Пример 12. Вычислить
.
Решение. Получаем
В этом примере использовано тригонометрическое тождество .
Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида
Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .
Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:
Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.
Пример 13. Вычислить, пользуясь правилом Лопиталя
.
Решение. Получаем
Вычисляем предел выражения в показателе степени
.
Итак,
.
Пример 14. Вычислить, пользуясь правилом Лопиталя
.
Решение. Получаем
Вычисляем предел выражения в показателе степени
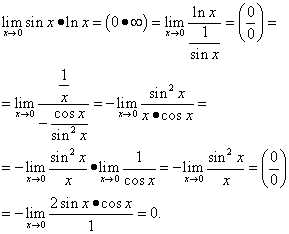 .
.
Итак,
.
Пример 15. Вычислить, пользуясь правилом Лопиталя
.
Решение. Получаем
Вычисляем предел выражения в показателе степени
Итак,
.
Это случаи, когда вычисление предела разности функций приводит к неопределённости «бесконечность минус бесконечность»: .
Вычисление такого предела по правилу Лопиталя в общем виде выглядит следующим образом:
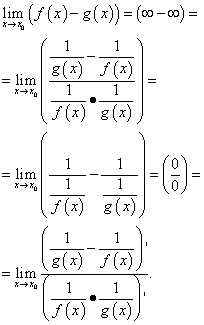
В результате таких преобразований часто получаются сложные выражения, поэтому целесообразно использовать такие преобразования разности функций, как приведение к общему знаменателю, умножение и деление на одно и то же число, использование тригонометрических тождеств и т.д.
Пример 16. Вычислить, пользуясь правилом Лопиталя
.
Решение. Пользуясь вышеперечисленными рекомендациями, получаем
Пример 17. Вычислить, пользуясь правилом Лопиталя
.
Решение. Пользуясь вышеперечисленными рекомендациями, получаем
Весь блок «Производная»
function-x.ru
11. Предел сложной функции.
Th. Пусть ф-цияfзадана на множествеX, функцияg-на множествеYиf(X)Y. Если сущ-ет конечные или бесконечные пределы.
,
то при x→x0 сущ-т предел (кон-й или беск-й) сложный функцииg[f(x)], причем
Пусть xn→x0, xnX,n=1,2,…; тогда в силу (1) имеемyn=f(xn)→y0, ynY,n=1,2,…
Поэтому в силу (2) g(yn)→z0, ноyn=f(xn) =>g[f(xn)]→z0,n=1,2,.., т.е. имеет место рав-во (3).
Зам1. Если ф-ция gнепр-на в точкеy0, т.е.,
то формулу (3) можно записать виде
Иначе говоря, предельный переход перестановочен с операцией взятия непр-ой ф-ции. В самом деле согласно Th..
Отсюда => в частности что непре-ая ф-ция от непр-й ф-ции непр-на, точнее:
След. Если ф-ция fнепр-на в точкеx0, а ф-цияgнепр-на в точкеy0=f(x0), то и их композицияg°fнепрерывна в точкеx0.
Действительно, непрерывность ф-ции fв точкеx0 означает, что
Поэтому в силу непр-ти ф-ции gв точкеy0 из формулы (5) получим
,
т.е. ф-ция g°fнепр-на в точкеx0.
Зам2. Обычно, когда говорят, что некоторая ф-ция в данной точке имеет предел, что имеют в виду, что этот предел конечный, а случай бесконечного предела оговаривают особо.
12. Первый замечательный предел.
sin0=0
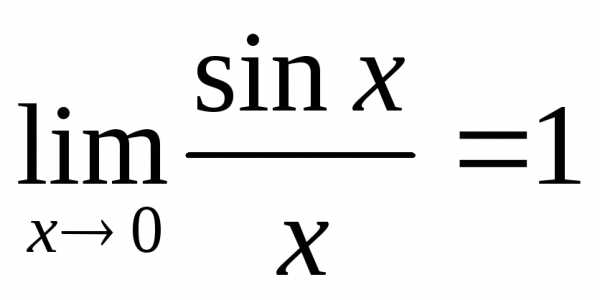
sinx~xв т.0!
Д-во:
I. 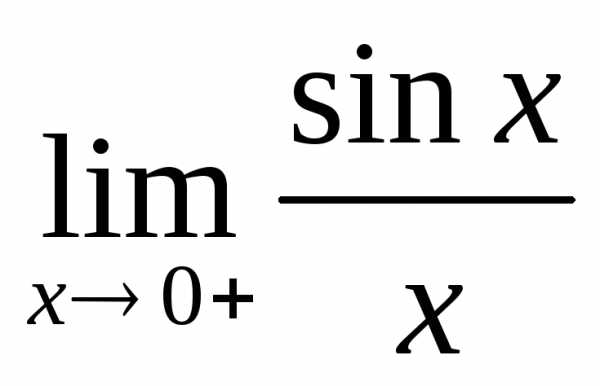 x(0,
x(0,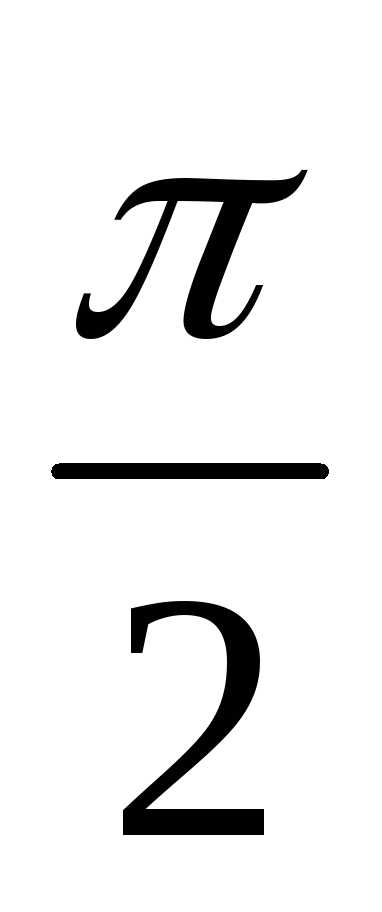 )
)
tgx=cd
S∆oda<Sсекторaoda<S∆odc
S=
sinx<x<tgx
ab<ad<cd
sinx<x<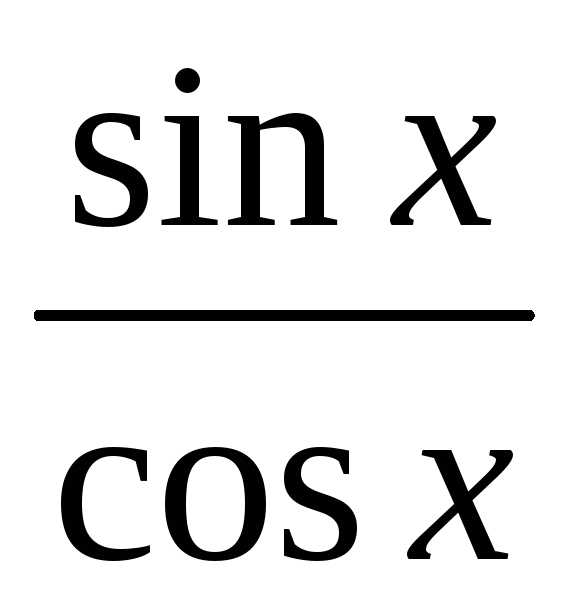
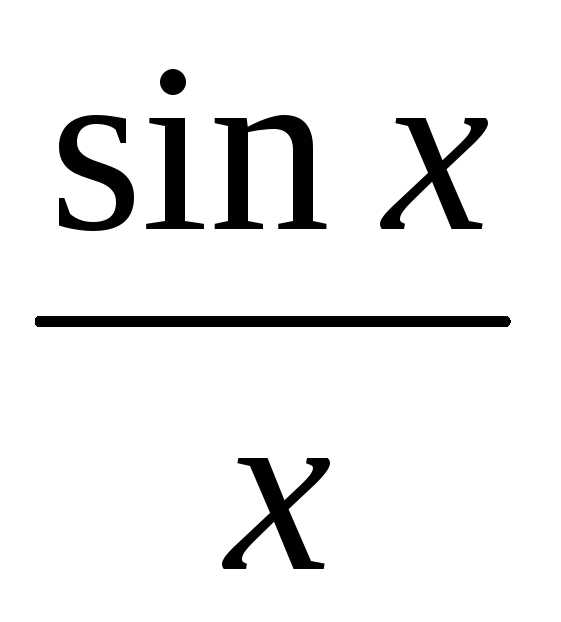 <1<
<1<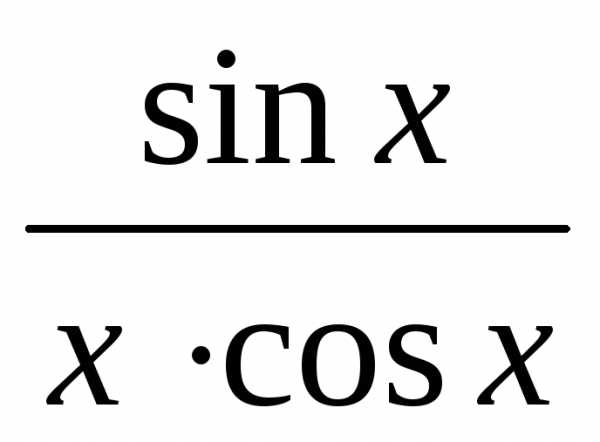
cosx<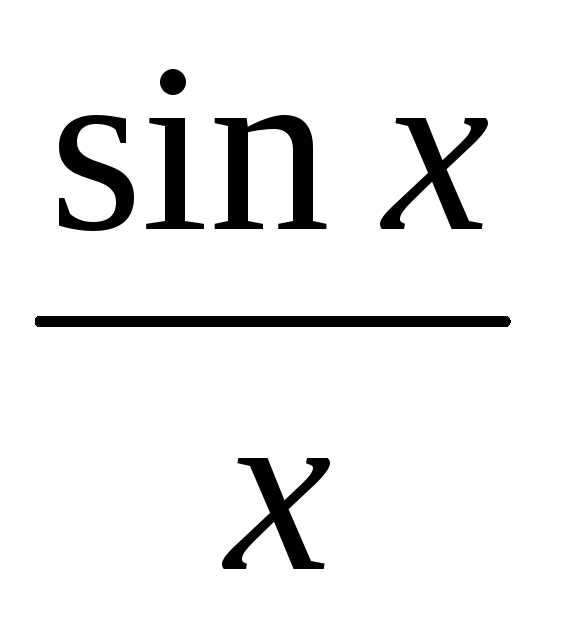 <1
<1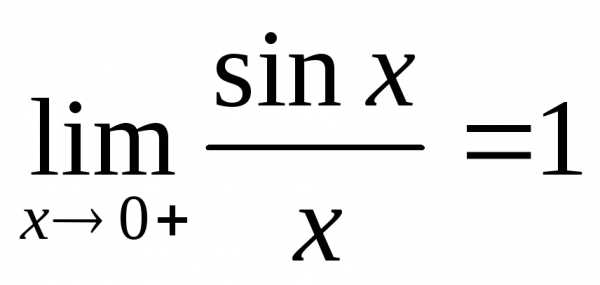
lim cosx=1
II. 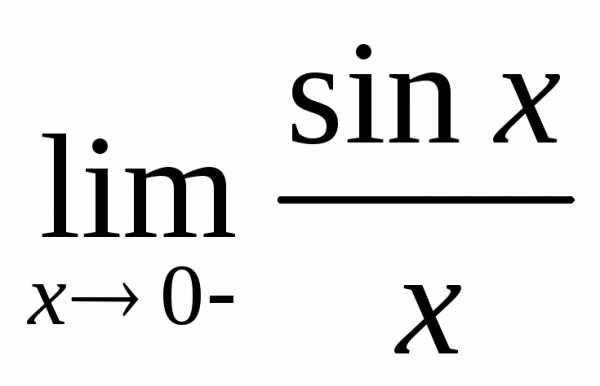 x(-
x(-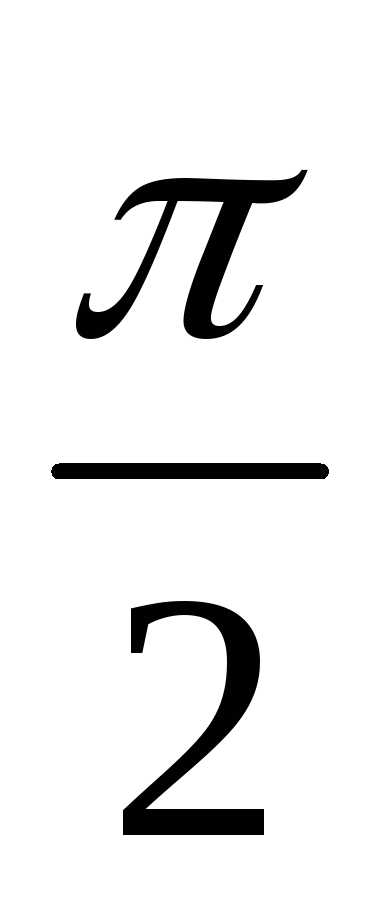 ,0)
,0)
x=-t
t(0,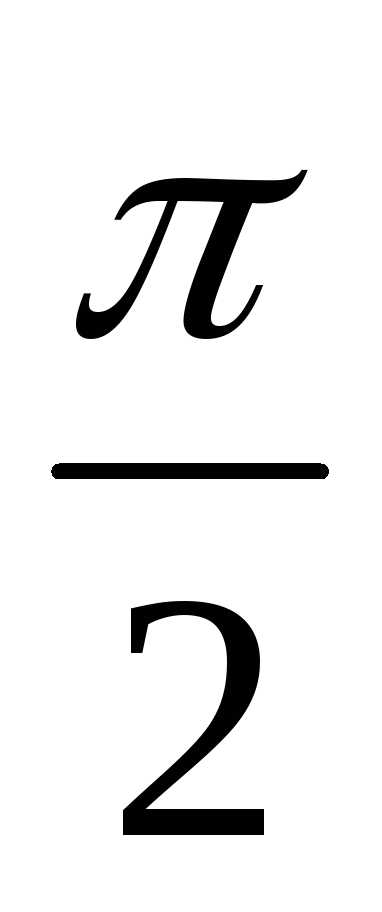 )
)
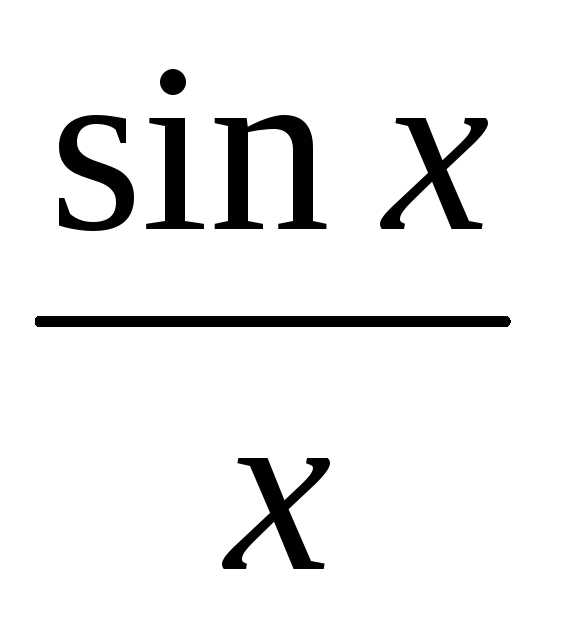 =
=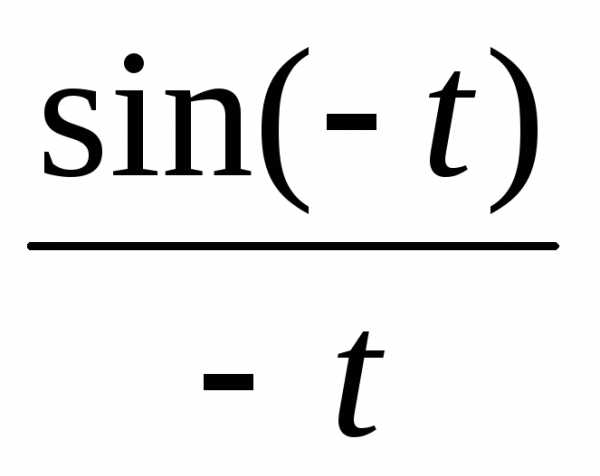 =
=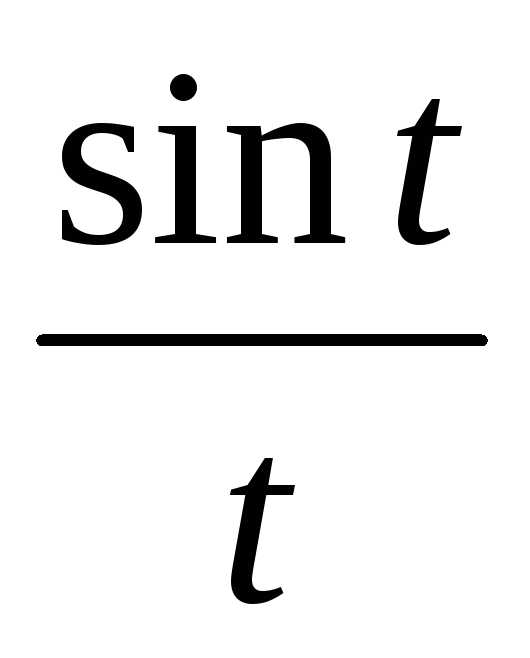
13. Второй замечательный предел.
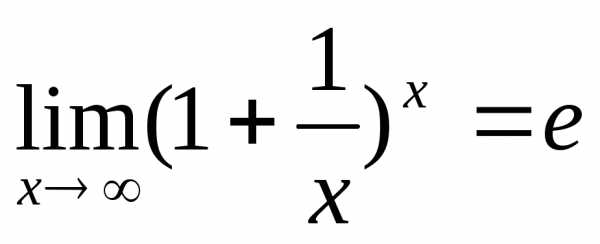
xn→∞
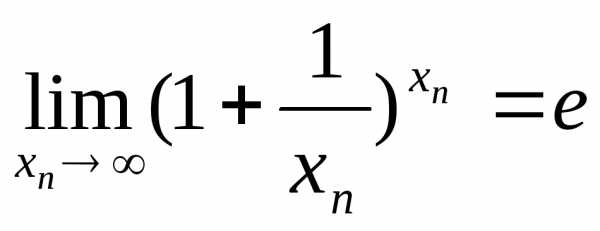
1) xn-натуральные значения
1,2,1,3,2,4,3
Для N:n>N|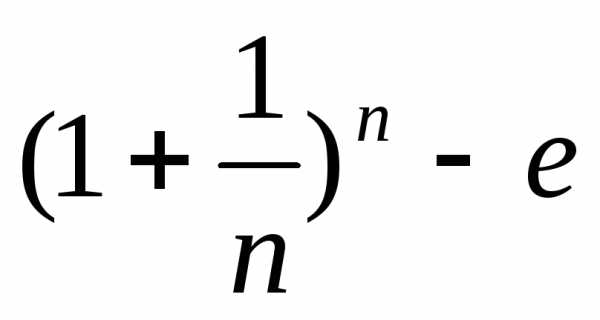 |<
|<
xn-б.б. тоKn>Kxn>N
>0
Kn>K|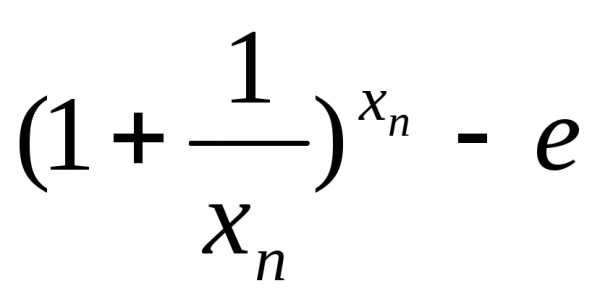 |<
|<
2) xn>0 начин. с некот.n
[xn]-целая часть
[xn]≥xn-1=> [xn]-б.б. посл.
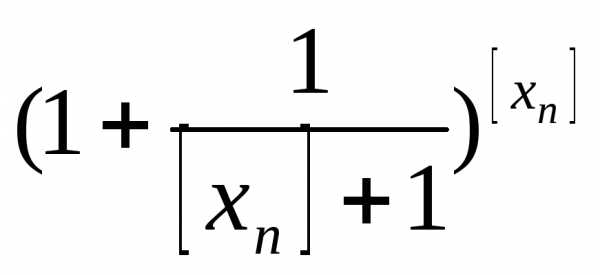 ≤
≤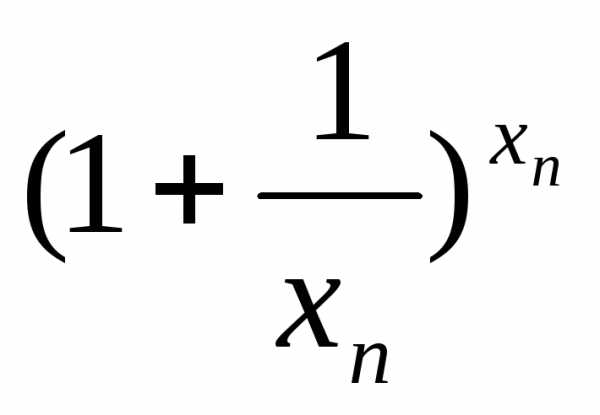 ≤
≤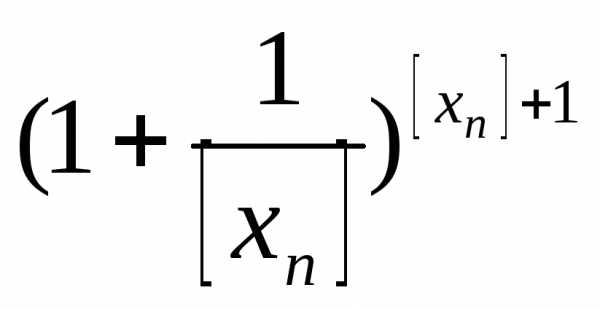
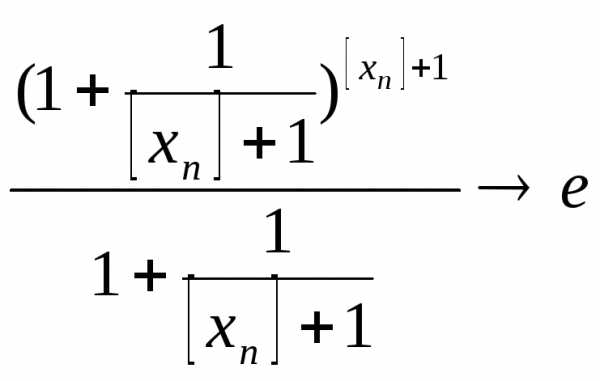
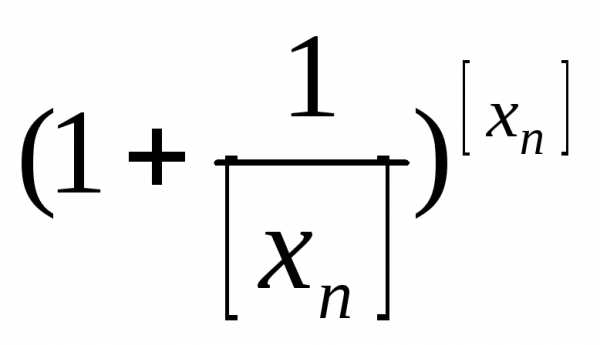 ∙
∙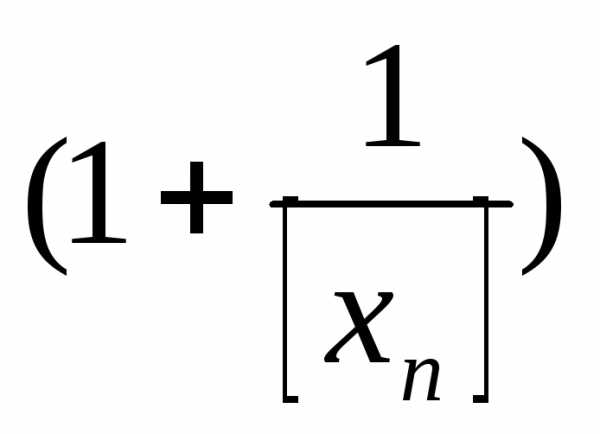
3) xn<0 начин. с некот.n
xn=-1-znzn=-1-xn
4) общая послед-ть xn-произв-е
xn+-положительныеxn—-отрицательные
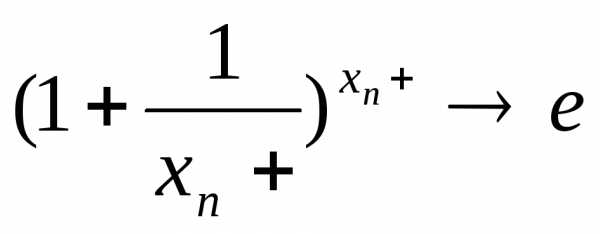
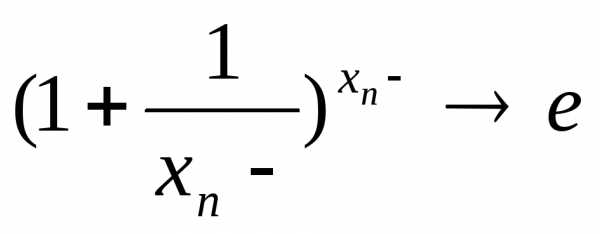
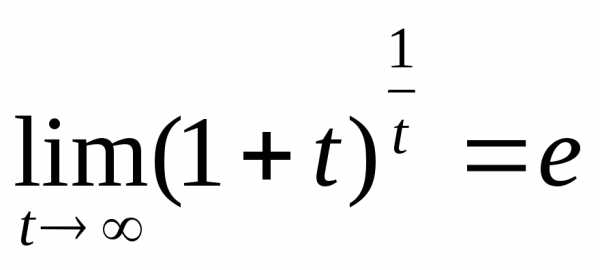
14. Сравнение бесконечно малых и бесконечно больших функций. Теоремы об эквивалентных бесконечно малых и бесконечно больших.
Две б.м. функций сравниваются между собой с помощью их отношения(сумма, разность и произведение).
Рассмотрим правило сравнения б.м. функций:
Пусть при хх0функции(х) и(х) являются б.м., т.е.Lim(х){при хх0}=0 иLim(х){при хх0}=0, тогда Правила:
1)Если Lim(х)/(х){при хх0}=0, то(х) – б.м. более высокого порядка, чем(х).
2)Если Lim(x)/(х){при хх0}=А0, то(х) и(х) – б.м. одного порядка.
3)Если Lim(х)/(х){при хх0}=1, то(х) и(х) – эквивалентные б.м.. Иногда нужно оценивать как высок порядок б.м. более высокого порядка, поэтому
4)Если Lim(х)/bn(х){при хх0}=А0, то(х) – б.м.n-го порядка относительно(х)
Замечания: Для сравнения б.м. функций, при х∞, х+\-∞, хх0+\-. Существует аналогичное правило.
1) Если
α(x)= (β(x))
в т.а
(β(x))
в т.а
то α(x)+β(x)~ β(x) в т.а
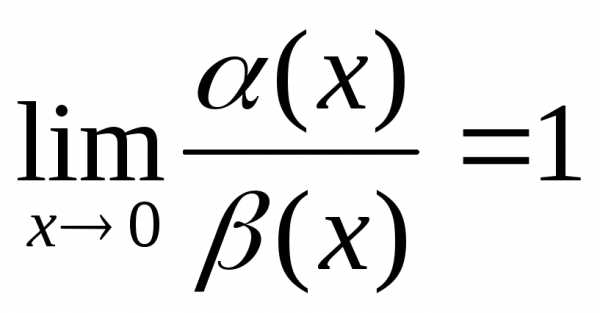 =>
они эквивалентны
=>
они эквивалентны
2) α(x),β(x) б.м. в а
α(x)∙β(x)=  (α(x))
(α(x))
3) α(x)~α1(x)
β(x)~β1(x) в т. а
M(x), N(x) б.б. в а
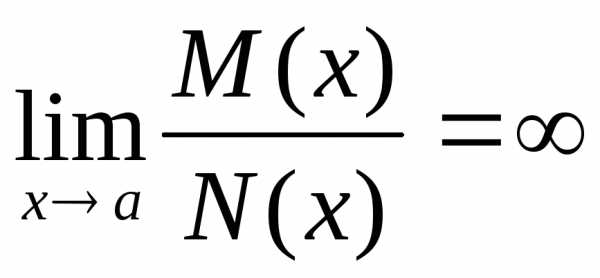
Для раскрытия неопределённостей вида [0/0] часто бывает полезным применить принцип замены б. м. эквивалентными.
1.sinx~xпри х->0
2.tgx~x
arcsin x ~ x
arctg x ~x
(1- cos x)~ x
ex-1 ~x
ax-1 ~xlna
ln(1+x)~x
logа(1+x)~ xlogаe
(1+x)к -1~kx,k>0
studfiles.net
Описание способов решения пределов — 1.doc
Описание способов решения пределов
скачать (220.5 kb.)
Доступные файлы (1):
содержание
1.doc
Реклама MarketGid:Пределы с неопределенностью вида и метод их решения
Группа следующих пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.
Пример 4
Решить предел
Сначала попробуем подставить -1 в дробь:
В данном случае получена так называемая неопределенность .
^ если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида , то для ее раскрытия нужно разложить числитель и знаменатель на множители.
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, тогда посетите страницу Математические формулы и таблицы и ознакомьтесь с методическим материалом Горячие формулы школьного курса математики. Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.
Итак, решаем наш предел
Разложим числитель и знаменатель на множители
Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:
Сначала находим дискриминант:
И квадратный корень из него: .
В случае если дискриминант большой, например 361, используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе.
! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.
Далее находим корни:
Таким образом:
Всё. Числитель на множители разложен.
Знаменатель. Знаменатель уже является простейшим множителем, и упростить его никак нельзя.
Очевидно, что можно сократить на :
Теперь и подставляем -1 в выражение, которое осталось под знаком предела:
Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:
Разложим числитель на множители.
Пример 5
Вычислить предел
Сначала «чистовой» вариант решения
Разложим числитель и знаменатель на множители.
Числитель:
Знаменатель:
,
Что важного в данном примере?
Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.
Рекомендация: ^
Более того, такие числа целесообразно выносить за значок предела. Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.
Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.
! Важно
В ходе решения фрагмент типа встречается очень часто. Сокращать такую дробь нельзя. Сначала нужно поменять знак у числителя или у знаменателя (вынести -1 за скобки).
, то есть появляется знак «минус», который при вычислении предела учитывается и терять его совсем не нужно.
Вообще, я заметил, что чаще всего в нахождении пределов данного типа приходится решать два квадратных уравнения, то есть и в числителе и в знаменателе находятся квадратные трехчлены.
^
Продолжаем рассматривать неопределенность вида
Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.
Пример 6
Найти предел
Начинаем решать.
Сначала пробуем подставить 3 в выражение под знаком предела
^ Данное действие обычно проводится мысленно или на черновике.
Получена неопределенность вида , которую нужно устранять.
Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по-возможности, избавляться. Зачем? А без них жизнь проще.
Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности используют метод умножения числителя и знаменателя на сопряженное выражение.
Вспоминаем нашу нетленную формулу разности квадратов:
И смотрим на наш предел:
Что можно сказать? у нас в числителе уже есть. Теперь для применения формулы осталось организовать (которое в и называется сопряженным выражением).
^
Обратите внимание, что под корнями при этой операции мы ничего не трогаем.
Хорошо, мы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на :
То есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.
Умножили. Теперь самое время применить вверху формулу :
Неопределенность не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:
Число, как уже отмечалось ранее, лучше вынести за значок предела.
Теперь осталось разложить числитель и знаменатель на множители, собственно, это следовало сделать раньше.
Готово.
Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:
Умножим числитель и знаменатель на сопряженное выражение.
Пример 7
Найти предел
Сначала попробуйте решить его самостоятельно.
Окончательное решение примера может выглядеть так:
Разложим числитель на множители:
Умножим числитель и знаменатель на сопряженное выражение
Чем же замечательны замечательные пределы? Замечательность данных пределов состоит в том, что они доказаны величайшими умами знаменитых математиков, и благодарным потомкам не приходиться мучаться страшными пределами с нагромождением тригонометрических функций, логарифмов, степеней. То есть при нахождении пределов мы будем пользоваться готовыми результатами, которые доказаны теоретически.
Замечательных пределов существует несколько, но на практике у студентов-заочников в 95% случаев фигурируют два замечательных предела: Первый замечательный предел, Второй замечательный предел. Следует отметить, что это исторически сложившиеся названия, и, когда, например, говорят о «первом замечательном пределе», то подразумевают под этим вполне определенную вещь, а не какой-то случайный, взятый с потолка предел.
Начнем.
^
Рассмотрим следующий предел: (вместо родной буквы «хэ» я буду использовать греческую букву «альфа», это удобнее с точки зрения подачи материала).
Согласно нашему правилу нахождения пределов (см. статью Пределы. Примеры решений) пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида , которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что:
Данный математический факт носит название ^ .
Нередко в практических заданиях функции могут быть расположены по-другому, это ничего не меняет:
– тот же самый первый замечательный предел.
! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде , то и решать его нужно в таком же виде, ничего не переставляя.
На практике в качестве параметра может выступать не только переменная , но и элементарная функция, сложная функция. ^ .
Примеры:
, , ,
Здесь , , , , и всё гуд – первый замечательный предел применим.
А вот следующая запись – ересь:
Почему? Потому-что многочлен не стремится к нулю, он стремится к пятерке.
Кстати, вопрос на засыпку, а чему равен предел ? Ответ можно найти в конце урока.
На практике не все так гладко, почти никогда студенту не предложат решить халявный предел и получить лёгкий зачет. Хммм… Пишу эти строки и пришла в голову очень важная мысль – все-таки «халявные» математические определения и формулы вроде лучше помнить наизусть, это может оказать неоценимую помощь на зачете, когда вопрос будет решаться между «двойкой» и «тройкой», и преподаватель решит задать студенту какой-нибудь простой вопрос или предложить решить простейший пример («а может он (а) все-таки знает чего?!»).
Переходим к рассмотрению практических примеров:
Пример 1
Найти предел
Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.
Сначала пробуем подставить 0 в выражение под знак предела (делаем это мысленно или на черновике):
Итак, а нас есть неопределенность вида , ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится , а в знаменателе .
В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас , значит, в знаменателе нам тоже нужно получить ».
А делается это очень просто:
То есть, знаменатель искусственно умножается в данном случае на 7 и делится на ту же семерку. Теперь запись у нас приняла знакомые очертания.
Когда задание оформляется от руки, то первый замечательный предел желательно пометить простым карандашом:
Что произошло? По сути, обведенное выражение у нас превратилось в единицу и исчезло в произведении:
Теперь только осталось избавиться от трехэтажности дроби:
Готово. Окончательный ответ:
Если не хочется использовать пометки карандашом, то решение можно оформить так:
“
Используем первый замечательный предел
“
Пример 2
Найти предел
Опять мы видим в пределе дробь и синус. Пробуем подставить в числитель и знаменатель ноль:
Действительно, у нас неопределенность и, значит, нужно попытаться организовать первый замечательный предел. На уроке Пределы. Примеры решений мы рассматривали правило, что когда у нас есть неопределенность , то нужно разложить числитель и знаменатель на множители. Здесь – то же самое, степени мы представим в виде произведения (множителей):
Далее, по уже знакомой схеме организовываем первые замечательные пределы. Под синусами у нас , значит, в числителе тоже нужно получить :
Аналогично предыдущему примеру, обводим карандашом замечательные пределы (здесь их два), и указываем, что они стремятся к единице:
Собственно, ответ готов:
В следующих примерах, я не буду заниматься художествами в Пэйнте, думаю, как правильно оформлять решение в тетради – Вам уже понятно.
Пример 3
Найти предел
Подставляем ноль в выражение под знаком передела:
Получена неопределенность , которую нужно раскрывать. Если в пределе есть тангенс, то почти всегда его превращают в синус и косинус по известной тригонометрической формуле (кстати, с котангенсом делают примерно то же самое, см. методический материал Горячие тригонометрические формулы на странице Математические формулы, таблицы и справочные материалы).
В данном случае:
Косинус нуля равен единице, и от него легко избавиться (не забываем пометить, что он стремится к единице):
Таким образом, если в пределе косинус является МНОЖИТЕЛЕМ, то его, грубо говоря, нужно превратить в единицу, которая исчезает в произведении.
Дальше по накатанной схеме, организуем первый замечательный предел:
Здесь все вышло проще, без всяких домножений и делений. Первый замечательный предел тоже превращается в единицу и исчезает в произведении:
В итоге получена бесконечность, бывает и такое.
Пример 4
Найти предел
Пробуем подставить ноль в числитель и знаменатель:
Получена неопределенность (косинус нуля, как мы помним, равен единице)
Используем тригонометрическую формулу . Возьмите на заметку! Пределы с применением этой формулы почему-то встречается очень часто.
Постоянные множители вынесем за значок предела:
Организуем первый замечательный предел:
Здесь у нас только один замечательный предел, который превращается в единицу и исчезает в произведении:
Избавимся от трехэтажности:
Предел фактически решен, указываем, что оставшийся синус стремится к нулю:
Пример 5
Найти предел
Этот пример сложнее, попробуйте разобраться самостоятельно:
Скачать файл (220.5 kb.)
gendocs.ru
