9 Класс. Информатика. ФГОС. Урок 8. Использование графов при решении задач
Вариант № 5338085
1. Задание 3 № 364
Между населёнными пунктами А, В, С, D, Е, F построены дороги, протяжённость которых приведена в таблице:
Определите длину кратчайшего пути между пунктами А и F. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 5
2) 6
3) 7
4) 4
Пояснение.
Найдём все варианты маршрутов из A в F и выберем самый короткий.
A-B-C-D-E-F: длина маршрута 18 км.
A-B-C-F: длина маршрута 9 км.
A-C-D-E-F: длина маршрута 15 км.
A-C-F: длина маршрута 6 км.
A-D-C-F: длина маршрута 7 км.
A-D-E-F: длина маршрута 10 км.
A-E-D-C-F: длина маршрута 8 км.
A-E-F: длина маршрута 7 км.
Кратчайший маршрут имеет длину 6 км.
Правильный ответ указан под номером 2.
Ответ: 2
2. Задание 3 № 303
Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 13
2) 12
3) 11
4) 10
Пояснение.
Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из пункта A можно попасть в пункты B, C.
Из пункта B можно попасть в пункты C, E.
Из пункта C можно попасть в пункт D.
Из пункта D можно попасть в пункт E.
A—B—C—D—E: длина маршрута 18 км.
A—B—E: длина маршрута 12 км.
A—C—D—E: длина маршрута 13 км.
А—С—В—Е: длина маршрута 11 км.
Правильный ответ указан под номером 3.
Ответ: 3
3. Задание 3 № 4908
В таблице приведена стоимость перевозок между пятью железнодорожными станциями, обозначенными буквами A, B, C, D и E. Укажите схему, соответствующую таблице.
A
B
C
D
E
A
1
4
1
B
1
3
C
4
2
D
3
E
1
2
1)
2)
3)
4)
Пояснение.
Из таблицы видно, что только из пункта D есть всего одна дорога, которая идёт в пункт B, а из дорога из пункта A в пункт E равняется 1. Следовательно, подходит только вариант 2.
Правильный ответ указан под номером 2.
Ответ: 2
4. Задание 3 № 942
Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в км) приведена в таблице.
Определите длину кратчайшего пути между пунктами A и C. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 7
2) 8
3) 9
4) 12
Пояснение.
Найдём все варианты маршрутов из A в С и выберем самый короткий.
A—B—C: длина маршрута 9 км.
A—C: длина маршрута 9 км.
A—D—C: длина маршрута 8 км.
A—D—E—C: длина маршрута 7 км.
Правильный ответ указан под номером 1.
Ответ: 1
5. Задание 3 № 624
Учитель Иван Петрович живёт на станции Антоновка, а работает на станции Дружба. Чтобы успеть с утра на уроки, он должен ехать по самой короткой дороге. Проанализируйте таблицу и укажите длину кратчайшего пути от станции Антоновка до станции Дружба:
1) 6
2) 2
3) 8
4) 4
Пояснение.
Найдём все варианты маршрутов из Антоновки в Дружбу и выберем самый короткий.
Из пункта Антоновка(А) можно попасть в пункты Васильки(В), Ежевичная(Е).
Из пункта B можно попасть в пункт Дружба(Д).
Из пункта Сельская(С) можно попасть в пункты Д, Е.
Из пункта Д можно попасть в пункт Е.
А—В—Д: длина маршрута 6 км.
А—Е—Д: длина маршрута 8 км.
А—Е—С—Д: длина маршрута 4 км.
Правильный ответ указан под номером 4.
Ответ: 4
6. Задание 11 № 1062
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Пояснение.
Начнем считать количество путей с конца маршрута — с города К. Пусть NX — количество различных путей из города А в город X, N — общее число путей.
В К можно приехать из Д, В, Г или Е, поэтому N = NК = NД + NВ + NГ + NЕ(*).
Аналогично:
NД = NБ + NВ = 1 + 3 = 4;
NВ = NБ + NА + NГ = 1 + 1 + 1 = 3;
NГ = NА = 1;
NЕ = NГ= 1;
NБ = NА = 1;
NА = 1.
Подставим в формулу (*): N = 4 + 3 + 1 + 1 = 9.
Ответ: 9.
Ответ: 9
7. Задание 11 № 271
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Пояснение.
Начнем считать количество путей с конца маршрута — с города К. Пусть NX — количество различных путей из города А в город X, N — общее число путей.
В К можно приехать из Е, В, Г или Ж, поэтому N = NК = NЕ + NВ + NГ + NЖ (*).
Аналогично:
NЕ = NБ = 1;
NВ = N
NГ = NВ + NА + NД = 2 + 1 + 1 = 4;
NЖ = NГ + NД = 4 + 1 = 5;
NБ = NА = 1;
NД = NА = 1.
Подставим в формулу (*): N = 1 + 2 + 4 + 5 = 12.
Ответ: 12
8. Задание 11 № 572
На рисунке изображена схема соединений, связывающих пункты А, В, С, D, Е, F, G, Н. По каждому соединению можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт Н?
Пояснение.
Начнем считать количество путей с конца маршрута — с города H. Пусть NX — количество различных путей из города H в город X, N — общее число путей.
В H можно приехать из G, E или D, поэтому N = NH = NG + NE + ND (*).
Аналогично:
NG = NF = 0;
NE = NF + NC + ND = 0 + 0 + 2 = 2;
ND = NB + NA = 1 + 1 = 2;
NF = NC = 0;
NC = 0;
NB = NА + NC = 1.
Подставим в формулу (*): N = 2 + 2 = 4.
Ответ: 4
9. Задание 11 № 632
На рисунке изображена схема соединений, связывающих пункты А, В, С, D, Е, F, G, H. По каждому соединению можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт H?
Пояснение.
Начнем считать количество путей с конца маршрута — с города H. Пусть NX — количество различных путей из города H в город X, N — общее число путей.
В H можно приехать из F или G, поэтому N = NH = NF + NG (*).
Аналогично:
NF = NE + ND = 2 + 2 = 4;
NG = ND = 2;
NE = NB + NA = 1 + 1 = 2;
ND = NA + NC = 1 + 1 = 2;
NB = NA = 1;
NA = NC = 1;
Подставим в формулу (*): N = 4 + 2 = 6.
Ответ: 6
10. Задание 11 № 4798
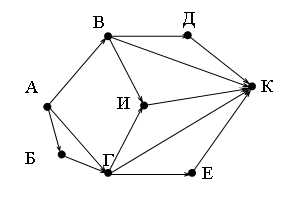
На рисунке − схема дорог, связывающих города А, Б, В, Г, Д, Е, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Пояснение.
Начнем считать количество путей с конца маршрута — с города К. Пусть NX — количество различных путей из города А в город X, N — общее число путей.
N = NК = NД + NВ + NИ + NГ + NЕ(*).
Аналогично:
NД = NВ = NБ = 1;
NГ = NА + NБ = 2;
NИ = NВ + NГ = 1 + 2 = 3;
NЕ = NГ = 2;
Подставим в формулу (*): N = 1 + 1 + 3 + 2 + 2 = 9.
Ответ: 9.
Ответ: 9
infourok.ru
Задание №15. Графы. Поиск количества путей
Автор — Лада Борисовна Есакова.
Подсчет путей в ориентированном графе. ЗАДАЧА № 15.
В этой задаче требуется подсчитать количество путей, ведущих из одной вершины графа в другую. Обычно задачу решают преобразованием графа в дерево. Однако, при сложной структуре графа такое решение становится очень трудоемким. Велика вероятность ошибки.
Рассмотрим простой и эффективный способ решения.
В этой задаче мы имеем дело с ориентированным графом (графом, у которого ребра имеют направление). Т.е. ребра имеют вид стрелок. Две вершины, соединенные напрямую стрелкой, называются смежными. Вершина, из которой выходит стрелка, называется предком, а вершина, в которую входит стрелка – потомком.
Несложно понять, что количество путей, которыми можно попасть в некоторую вершину, равно сумме количеств путей предков этой вершины.
Пример:
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
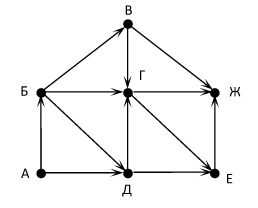
Решение:
Каждой вершине, начиная с начальной (A), поставим в соответствие индекс, равный количеству путей, которыми можно попасть в эту вершину. Для вершины A (начало пути) индекс всегда равен 1 (в начало пути можно попасть единственным образом – никуда не двигаясь). Теперь сформулируем правило: индекс вершины равен сумме индексов его предков. Исходя из этого индекс Б равен 1 (предок у Б один – вершина A).
У вершины Д предками являются А и Б, значит индекс вершины Д равен 1+1=2.
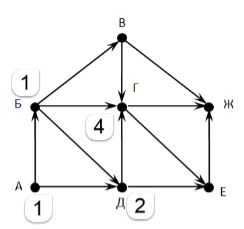
Очевидно, что мы можем посчитать индекс только тех вершин, индексы предков которых уже посчитаны. Например, мы не можем посчитать индекс Г, пока не посчитан индекс В. Двигаясь последовательно, мы рассчитаем индексы всех вершин.
Индекс вершины Ж и будет ответом задачи.
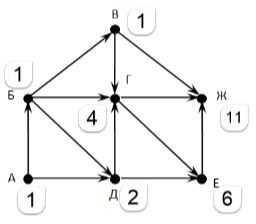
Ответ: 11
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
| 1. |
Таблица
Сложность: лёгкое |
1 |
| 2. |
Дороги
Сложность: лёгкое |
1 |
| 3. |
Одноклассники
Сложность: лёгкое |
2 |
| 4. |
Количество вершин графа
Сложность: среднее |
2 |
| 5. |
Граф
Сложность: среднее |
2 |
| 6. |
Составление задачи
Сложность: среднее |
3 |
| 7. |
Трёхзначные числа
Сложность: сложное |
2 |
| 8. |
Слово
Сложность: сложное |
3 |
| 9. |
Кратчайший путь
Сложность: сложное |
3 |
www.yaklass.ru
Информационные модели на графах. Использование графов при решении задач
Вопросы занятия:
· граф;
· дерево;
· иерархия.
На прошлых уроках мы с вами узнали об информационных моделях, которые в сжатой форме помогают представлять информацию и решать задачи.
Давайте вспомним:
Сделать табличную информацию более наглядной и легко доступной помогают графики и диаграммы.
График – это линия, применяемая для наглядного изображения зависимости одной какой-либо величины от другой.
Диаграмма – это чертёж, показывающий соотношение нескольких величин. В зависимости от цели можно использовать разные типы диаграмм. Например, круговые или столбчатые.
Следующий вид графических средств представления информации – схемы.
Схема – это информационная модель, в которой с помощью особых приемов и географических обозначений выделяется один или несколько признаков рассматриваемого объекта.
Есть ещё один вид графических средств – это графы.
Сегодня на уроке мы узнаем:
Какие информационные модели называются графами, для чего применяются графы, и как с помощью графов решать задачи.
Граф — это группа объектов со связями между ними.
Объекты представляются как вершины графа, а связи — это линии соединяющие вершины.
Например, все шестиклассники пользуются мобильными телефонами и многие общаются друг с другом через SMS.
В данном примере вершины графа – это отдельные ребята, а связи – это процесс «пишут друг другу SMS».
Вершины графа можно изображать по-разному. Это может быть овал либо круг, точка или прямоугольник.
Разберёмся более подробно со связями, то есть с линиями, соединяющими вершины графа.
Дуга
Если линия, соединяющая вершины графа направленная, то есть со стрелкой, то она называется дугой.
То есть дугой называется направленная линия, соединяющая вершины графа.
Ребро
Если линия ненаправленная, то есть, нет стрелки, то эта линия называется ребром.
Ребро – это ненаправленная линия, которая соединяет вершины графа.
Петля
Если линия выходит из некоторой вершины и входит в неё же, то эта линия называется петлёй.
Петля – это линия, которая выходит из некоторой вершины и входит в нее же
Вернёмся к примеру, с шестиклассниками. Здесь система – это ученики шестого класса в какой-то школе. Мы, объекты этой системы (т.е. отдельных ребят) изобразили вершинами, и соединили вершины ненаправленными линиями (рёбрами). Ребра в данном случае являются двухсторонними отношениями, потому что ребята пишут SMS-ки друг другу.
Мы получили информационную модель рассматриваемой системы в форме графа.
Рассмотрим виды графов.
Если вершины графа соединены рёбрами, то такой граф называется неориентированным.
Рассмотрим пример: Таня написала SMS Никите, Никита ответил Тане, Таня написала Маше, Маша ответила Тане, Никита написал Маше. Здесь ребята отвечали друг другу на смски.
Данное отношение называется цепью графа.
Цепь графа – это путь по вершинам и рёбрам графа, который включает любое ребро не меньше одного раза.
Если в цепи начальная и конечная вершины совпадают, то такая цепь называется циклом.
Например, Таня написала SMS Никите, Никита – Маше, Маша – Платону, а Платон написал Тане.
Здесь цикл – это цепь Таня – Никита – Маша – Платон – Таня.
Далее, рассмотрим следующий вид графа.
Если вершины графа соединены дугами (стрелками), то такой граф называется ориентированным.
В нашем примере цепь будет выглядеть следующим образом: Таня написала SMS Никите, Никита – Маше, Маша – Платону. То есть СМС-ки были без ответа.
Рассмотрим следующий пример:
Город Москва основан в 1147 году, город Санкт-Петербург основан в1703 году. Расстояние от Москвы до Санкт-Петербурга 713 км. Год основания города Тверь 1135 год, расстояние от Москвы до Твери 175 км. Ярославль основан в 1010 год, расстояние от Москвы до Ярославля 272 км. Город Смоленск основан в 863 году, а расстояние от Москвы до Смоленска 400 км.
Мы получили взвешенный граф.
Взвешенным называется граф, который характеризуется дополнительной информацией – весом вершины или весом ребра (дуги).
Рассмотрим следующий вид графа с циклами, то есть граф, в цепи которого начальная и конечная вершины совпадают.
Помните сказку о царе Солтане? Давайте построим граф по отрывкам из сказки.
К морю лишь подходит он,
Вот и слышит будто стон…
Бьётся лебедь средь зыбей,
Коршун носится над ней;
Но как раз стрела запела,
В шею коршуна задела —
Коршун в море кровь пролил,
Лук царевич опустил;
Смотрит: коршун в море тонет
И не птичьим криком стонет,
Лебедь около плывёт,
Злого коршуна клюёт,
И царевичу потом
Молвит русским языком…
Вот открыл царевич очи;
Отрясая грёзы ночи
И дивясь, перед собой
Видит город он большой,
Мать и сын идут ко граду.
Лишь ступили за ограду,
Пышный двор встречает их;
Все их громко величают
И царевича венчают
Княжий шапкой, и главой
Возглашают над собой…
И так далее.
Мы получили граф с циклами, который называется сетью. Если раньше мы рассматривали примеры, в которых связи были одинаковые (ребята писали смски), то в данном примере связи различны. Поэтому мы их подписывали.
Следующий вид графа, называется дерево.
Дерево – это граф с иерархической системой, где Иерархия – это структура распределения частей целого от высшего к низшему. А Иерархическая система – это система, части которой находятся в определённых отношениях. К отношениям иерархической системы относятся «является разновидностью», «входит в состав» и другие «отношения подчинённости».
Рассмотрим иерархическую систему фирмы, которая, например, занимается реализацией техники. Здесь будет такая система подчинённости: генеральный директор — самый главный человек и владелец фирмы, ему подчиняются директора магазинов, которые руководят работой администраторов, ну а тем, в свою очередь, подчиняются продавцы.
Рассмотрим систему, связанную системой подчинённости «входят в состав». Она имеет иерархическую структуру. Например, изобразим следующий граф иерархической системы:
Периодическая система элементов в неё состав входят металлы и неметаллы. В свою очередь металлы делятся на 2 группы – группа 1 и группа 2, неметаллы делятся также на 2 группы – группа 5 и группа 6 и так далее. В отличие от остальных графов дерево не содержит циклов и петель, так как между любыми двумя его вершинами существует только один путь.
Так же у графа «Дерево» выделяется главная вершина, которая называется корень дерева. У любой вершины дерева могут быть потомки. А вершины, у которых нет потомков, называются листьями.
Следующий вид древовидного графа с отношением «является разновидностью» применяется для представления классификации объектов.
Например, разновидностями отряда «Насекомые» являются: Прямокрылые к ним относятся кузнечики, сверчки. Полужёсткокрылые – к ним относятся клопы, Чешуекрылые к ним относятся бабочки и Стрекозы.
Некоторые виды задач удобно решать с помощью графов.
Давайте решим одну из задач.
В коробке три шарика: жёлтый, зелёный и красный. Шестиклассница Таня со своими двумя друзьями Машей и Никитой вынимают их из коробки по одному. Сколько комбинаций выбора при этом возможно? Нужно выписать все варианты выбора.
Решение данной задачи удобно представить в виде дерева. Возьмём за корневую вершину произвольную току О., Таня может взять из коробки один из трёх шариков. Обозначим их буквами Ж, З и К. На схеме это соответствует трём ветвям, исходящим из точки О. Первый уровень в нашей задаче – это выбор Тани.
Теперь мы будем строить второй уровень графа. Второй уровень – это выбор Никиты.
Если Таня взяла жёлтый шарик, то Никита может взять зелёный или красный. Если же Таня взяла зелёный шарик, то Никита может взять жёлтый или красный. Аналогично, если Таня взяла красный шарик, то Никита может взять жёлтый или зелёный.
Осталось построить третий уровень, который отображает выбор Маши. Маша в каждом случае может взять оставшийся шарик. То есть если Таня взяла жёлтый шарик, а Никита зелёный, то Таня возьмёт красный шарик. Следующий вариант: если Таня взяла жёлтый шарик, а Никита Красный, Маша возьмёт зелёный шарик. И так далее мы достраиваем оставшиеся ветви.
Выпишем все пути от вершин первого уровня к вершине третьего. Каждый из выписанных путей определяет один из вариантов вытягивания шестиклассниками шариков из коробки. Так как других путей нет, то искомое число вариантов – 6.
Если при решении задачи не нужно указывать все возможные варианты, а нужно просто указать их число, то дерево можно и не строить. Тогда рассуждаем так: Таня может взять один из трёх шариков, Никита может взять один из двух оставшихся шариков, а Маша – один оставшийся. Получаем: 3, умножить на 2, умножить на 1 получаем ответ – 6 вариантов.
Итак, сегодня на уроке мы узнали:
Граф является наглядным средством представления информации состава и структуры системы.
Дерево – это граф с иерархической системой. Отличительная особенность дерева – это то, что между любыми двумя вершинами существует единственный путь.
Иерархия – это структура распределения частей целого от высшего к низшему.
Иерархическая система – это система, части которой находятся в отношениях подчинённости «является разновидностью», «входит в состав» и других.
Перейдём к практической части урока.
Сегодня на уроке мы научимся:
пользоваться инструментом Надпись
добавлять (вписывать) текст в автофигуру
строить схемы.
1-e задание. Солнечная система.
1. Открыть текстовый документ «Солнечная система.docx».
2. На картинке по информации из таблицы указать положение планет.
3. Сохранить документ под именем «Солнечная система надписи».
Приступим.
Открываем в своей рабочей папке документ Солнечная система.docx. Здесь мы видим схему солнечной системы, по информации из таблицы, нам нужно указать положение планет.
Для этого:
Смотрим внимательно на схему и таблицу.
Ближе всего к солнцу находится Меркурий. Обозначим на схеме Меркурий.
Выбираем вкладку Вставка, затем в группе Текст выберем инструмент Надпись, и нажимаем Нарисовать надпись, при этом указатель мыши примет форму «плюса».
Чтобы вставить надпись стандартного размера просто щёлкните в документе.
Если размер надписи нужно изменить поднесите мышку к любому из маркеров в прямоугольнике и растяните до нужного размера.
Перетащим надпись на нужное место.
Если надпись окружена рамкой, уберём рамку. Нажимаем Формат – Контуры фигуры – Нет контура.
Аналогично подпишем остальные планеты солнечной системы.
Сохраним результат работы в своей рабочей папке под именем Солнечная система надписи.
2-e задание. Поездка в автобусе.
1. Открыть текстовый документ «Поездка в автобусе.docx».
2. Дорисовать схему отношений при поездке в автобусе и подписать их названия с помощью глаголов.
3. Сохранить документ под именем «Поездка в автобусе граф».
Открываем файл Поездка в автобусе.docx в своей рабочей папке. Здесь мы видим незаконченную схему отношений при поездке в автобусе, дорисуем её и подпишем отношения с помощью глаголов. Для этого:
Смотрим на схему. Водитель ведёт автобус.
Выбираем вкладку Вставка, в группе Иллюстрации нажимает на Фигуры. Здесь нам нужна стрелка. Соединяем вершины графа Водитель – Автобус стрелкой и, также как в первом задании, добавляем надпись.
Аналогично достраиваем всю схему.
Сохраним результат работы в своей рабочей папке под именем Поездка в автобусе граф.
Третье задание называется Арифметические выражения.
1. Открыть текстовый документ «Арифметические выражения.docx».
2. По данному образцу построить дерево для арифметического выражения.
3. Сохранить документ под именем «Выражение дерево».
Открываем файл Арифметические выражения.docx в своей рабочей папке. Здесь мы видим образец дерева для арифметического выражения. С помощью вкладки Вставка – Автофигуры построим дерево для нашего арифметического выражения.
Листьями данного дерева являются числа, а остальные вершины – это арифметические операции. Листья связаны с вершинами рёбрами.
Сохраним свою работу в своей рабочей папке под именем Выражение дерево.
Таким образом, сегодня на уроке мы научились:
• пользоваться инструментом Надпись;
• добавлять (вписывать) текст в автофигуру;
• строить разнообразные схемы.
videouroki.net
МЕТОДИЧЕСКАЯ РАЗРАБОТКА УРОКА по информатике «Решение задач перестановки с использованием графа» (5 класс)
Самсонова Людмила Николаевна
МЕТОДИЧЕСКАЯ РАЗРАБОТКА УРОКА
Решение задач перестановки с использованием графа
Урок информатики
Тип урока: Комбинированный урок.
Оборудование:
ПК, мультимедийный проектор, интерактивная доска SmartBoard, колонки, программа Notebook, ПК учеников для выполнения практической работы, модель задачи “Переставь коней”, разнообразный раздаточный материал.
ПО:
-ПМК Роботландия
— Урок — Smart “Использование графов”.
Информация о предметной направленности разработки
Предмет
Информатика и ИКТ
Класс
5
УМК (программа)
Авторская программа (Программа создана на основе программы Л.Л.Босовой и предполагает использования УМК Л.Л.Босовой и программно-методического комплекса «Роботландия» (Ю.А.Первин, А.А. Дуванов и др.)
Раздел учебной программы, тема
Решение задач перестановки с использованием графа, урок 4 в теме: «Координаты клетки. Задача о перестановке коней. Графы. Решение задач перестановки с использованием графа».
Необходимые предварительные знания и умения: Предложенный урок, является частью комплекта сценариев занятий по теме: «Координаты клетки. Графы. Решение задач перестановки с помощью графа».
В комплекте представлены сценарии 5 уроков, презентации к урокам, разнообразный раздаточный материал.
ЗУНЫ уч-ся:
Основные понятия:
Координата
Координатная сетка
Граф, принципы построения графа
Принципы решения задачи “Переставь коней” в среде Конюх.
Цели урока:
1. Образовательная:
Перенос знаний полученных на предыдущих уроках на новый, творческий уровень и приобретение первых навыков решения задач с использованием изученного материала.
2. Дидактическая:
В результате деятельности учащиеся должны знать: как строить граф для задач на перестановку и как составлять алгоритм перестановки с помощью графа.
3. Развивающая:
Развивать УУД уч-ся через стремление к активной, познавательной деятельности, умение работать самостоятельно, в паре, и в группе, а так же пытаться разрешать возникшие проблемные ситуации на любом этапе деятельности, таким образом, развивая навыки критического мышления.
4. Воспитательная:
Формировать познавательные интересы учащихся, воспитывать трудолюбие, работу в коллективе, культуру умственного труда.
Ожидаемые результаты: Учащиеся должны научиться использовать метод графов при решении задач перестановки, закрепить понятия координаты, граф.
Формы контроля и оценки результатов урока:
тренировочные упражнения (индивидуальные, в паре, в группе)
самостоятельные работы (3 варианта, по уровню сложности)
проверочный тест (3 варианта, по уровню сложности)
обучающая программа для определения координат, написанная с помощью языка программирования Delphi
Учет специфики новых стандартов: В процессе работы ученики получают возможность для формирования всех видов универсальных учебных действий:
личностных (отношение к себе, к другим, к определенным видам деятельности т. е. установление учащимися связи между целью учебной деятельности и ее мотивом и оценивания усваиваемого содержания)
регулятивных (управление своей деятельностью, контроль и коррекция, инициативность и самостоятельность)
познавательных (самостоятельное выделение и формулирование познавательной цели, поиск вариантов решения задачи и выбор наиболее эффективных способов решения задач в зависимости от конкретных условий, т.е. перенос знаний в новые условия, рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности)
коммуникативных (обеспечивают умение полно и точно выражать свои мысли, аргументировать точку зрения, вступать в диалог, эффективно работать в паре, в группе)
Технологическая карта урока для формирования УУД учащихся: https://docs.google.com/spreadsheet/ccc?key=0AmyZNGCeqjh5dEpmN21HQ3lZQjN1RUpnNUJMRFdJX0E&usp=sharing
Рефлексия учебной деятельности: рефлексия учебной деятельности на этапе подведения итогов урока.
Виды:
Ретроспективная рефлексия — анализ уже выполненной деятельности
Проспективная рефлексия — включает в себя размышления о предстоящей деятельности.
Ребята помогают Незнайке продолжить начатые фразы.
Урок в сети Интернет:
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
№
стр
Этап урока, слайды
Действия учителя Формы организации работы учителя
Действия учеников
Формы организации работы
детей
Используемые
функции
программного
обеспечения
1.
Организационный этап урока
Формирование положительного настроя для
учащихся:
Сегодня на уроке мы снова отправимся в путешествие…
Наш маршрут — страна Роботландия.
По дороге мы поможем Незнайке, заглянем в гости к Конюху и должны будем найти дорогу домой. Чтобы не потеряться в новой стране, пусть у каждого будут свои координаты, т.е. адрес, по которому Вас можно найти. Согласны? Прикрепите, пожалуйста, свои координаты. Наше путешествие начинается… ”
Учащиеся прикрепляют бейджи с координатами А1, А2…(по месту посадки) и настраиваются на работу
Использованы встроенные объекты — картинки
, которые приглашают ребят в путешествие.
Также
использована
Гиперссылка со слов «об авторе» на Google — сайт учителя.
Мотивационно-ориентировочный этап
2.
Актуализация знаний:
Учитель:
«Ребята! У нас первая остановка! Необходимо ответить на вопросы, чтобы двигаться дальше».
Учитель предлагает ответить на вопросы теста, актуализирует знания учащихся. Организует совместную работу по поиску правильного ответа. Работает с тестом на Smart- доске.
Учащиеся предлагают ответы и выбирают правильный вариант ответа, при необходимости корректируют, и анализирует ответы.
Использован режим работы с встроенным интерактивным объектом — тест, который используется для выявления ЗУНОв, и актуализации темы урока.
3.
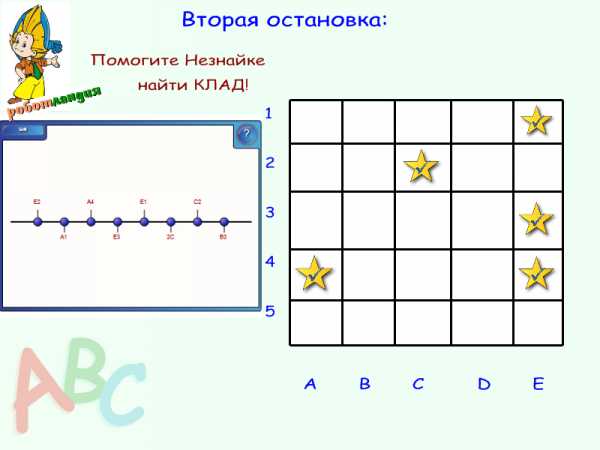
Смотрите, Незнайка, он чем-то озадачен.
Незнайка просит помощи. Задание: Помогите Незнайке найти клад.
Назовите правильно записанные координаты, которые соответствуют месту расположения кладов-звездочек?
Учитель работает у Smart- доски, последовательно открывая объекты flash
Ученики работают с табличками, (верно, не верно), которые заготовлены заранее.
Варианты работы:
— индивидуально
— в парах
— в группах
(в зависимости от целей и уровня об учености уч-ся)
Средствами программы разработан тест для проверки знаний учащихся. Тест выполнен с использованием flash-объекта timeline.
4.
Ребята, перед нами новая проблема. Помогите Незнайке прочитать текст телеграммы. Чтобы работу выполнить быстрее, разделимся на пары. Каждая парта — это пара. Каждой паре необходимо составить свою часть телеграммы.
Учитель раздаёт каждой паре бланк задания.
По итогам работы, просит каждую пару подойти к доске и написать свою часть телеграммы.
Учащиеся выполняют задание на бланках, заполняют свою часть телеграммы.
По итогам работы, каждая пара работает на Smart- доске, записывая свою часть телеграммы. Пример бланка:
Используется вставка объекта – таблица. В каждой ячейке отведено поле для написания текста. Используются инструменты – перо, текст, ластик.
5.
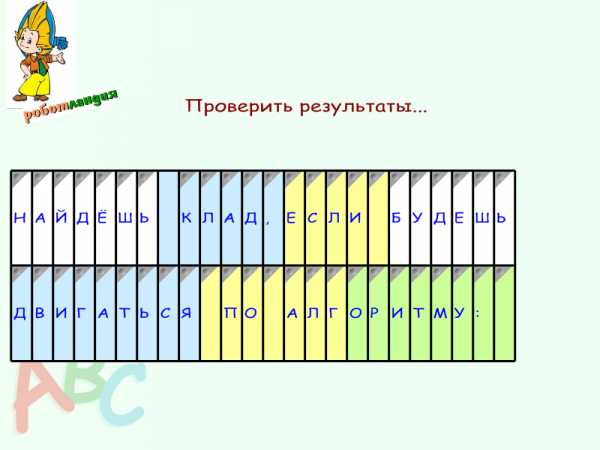
По итогам работы, учитель предлагает проверить и сравнить свои результаты, с оригиналом телеграммы.
Приглашает одного ученика к доске.
Один из учеников открывает затенение ячеек таблицы, ребята сравнивают свои варианты с оригиналом, при необходимости обсуждают и корректируют свою работу
Используется вставка объекта – таблица. В каждой ячейке располагаются буквы общей телеграммы, использован эффект затенения ячеек.
6.
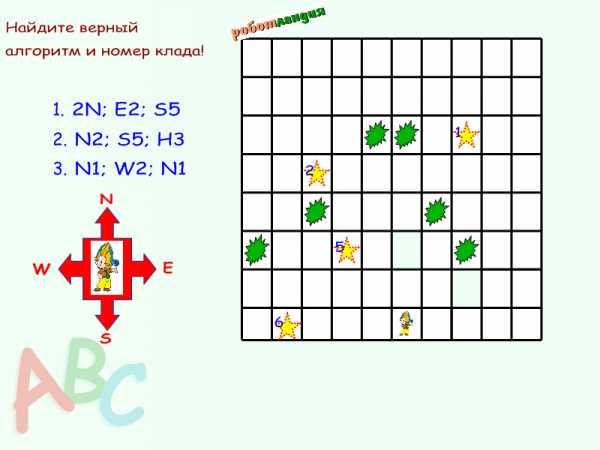
Учитель организует диалог: Где же алгоритм? Опять препятствие!
Посмотрите здесь 3 алгоритма. Какой из них верный?
Сможем ли мы двигаться по 1-ому алгоритму?
2N, E2, S5?
Учитель: Почему?
Аналогичная работа со всеми алгоритмами.
Учитель: Какой клад выберет Незнайка, двигаясь по этому алгоритму?
Учитель: Прошу каждого найти № клада и поднять табличку с верным ответом. Покажите путь, по которому двигался Незнайка
При наличии времени, возможно, написание и обсуждение других вариантов алгоритма передвижения.
Учащиеся отвечают на вопросы учителя, анализируя предложенные алгоритмы.
Делают вывод о том, какой выбрать алгоритм и почему. Выбираем алгоритм №3.
Один из учащихся приглашается к Smart- доске, чтобы продемонстрировать путь, по которому двигается Незнайка.
Использован встроенный объект-таблица, на котором располагается движущийся объект-картинка.
7.
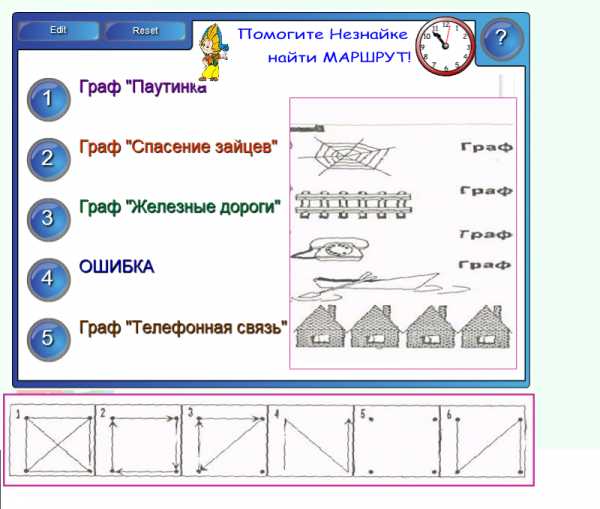
Учитель: Отправляемся дальше! Координаты, новая остановка. У нас новое препятствие…
Учитель: Какой путь выбрать, по какой дороге идти дальше?
Подсказка: маршрут указан в графе “Железные дороги”. Попробуем найти его по описанию.
Учитель читает описание графов (картинки есть на экране), а у уч-ся раздаточный материал.
Один из учащихся приглашается к Smart- доске, чтобы найти и продемонстрировать граф по описанию.
Группа проверяет результат на доске и при необходимости ведется корректировка.
Использован режим работы с встроенным интерактивным объектом – тест на соответствие (номер описания и номер графа), анимация для объекта – картинки (описание графа)
8.

Учитель: Маршрут по железной дороге у нас не совсем обычный. Мы сможем перемещаться, только используя «ход конем». Давайте отработаем это правило перемещения. Прошу по очереди подходить к доске и перемещать коня, в те клетки, куда это возможно. Начальная позиция – постоянная! Запомним ее! Использует выделитель или маркер для фиксации начальной клетки.
Ученики по очереди подходят к доске и предлагают свои пути перемещения коня, используя правило «ход конём».
Ребята проверяют предложенные варианты, при необходимости обсуждают и корректируют.
Один из учеников открывает итоговый результат в таблице.
Использован режим работы с встроенным интерактивным объектом flash – таблица. В ней расположен перемещаемый объект – картинка, текст в ячейках, цвет ячеек с функцией Random.
9.
Физкультминутка — игра:

Звучит музыка. На экране появляются координаты, учитель читает действия, имитирует их выполнение.
Помахали ручкой клетки (C2, C1, B2, A4) и.т.д.
Закивали им соседки
Встали- с места номера
Топнуть ножкой всем пора!
Ученики в роли координат, выполняют физкультурную разминку.
Игра направлена не только на отдых и смену деятельности младших школьников, но и на закрепление понятий координаты и их обозначение.
Использована вставка объектов WordArt и анимация по щелчку мышки, для появления следующего объекта.
Используется встроенный звук, через гиперссылку «Музыка» для эмоционального настроя учащихся
10.

Продолжает звучать музыка. На экране появляются координаты, учитель читает действия, имитирует их выполнение.
Эти клетки повернулись
Их соседки потянулись
Взялись за руки друзья
Граф построен без труда.
(используемый стих – авторский)
Ученики в роли координат, выполняют физкультурную разминку.
Использована вставка объектов WordArt и анимация по щелчку мышки, для появления следующего объекта.
Используется встроенный звук, через гиперссылку «Музыка» для эмоционального настроя учащихся
11.

Учитель: Ну, вот мы и добрались до Роботландии! Смотрите, кто нас встречает!
Заканчивают разминку, настраиваются на работу, поддерживают высказывания учителя.
Использована вставка объектов в форме скриншота и анимация по щелчку мышки.
Операционно-исполнительский этап
12.

Учитель задает проблемный вопрос: «Ребята вспомните, пожалуйста, чем мы занимались на прошлом уроке и попробуйте догадаться, какова тема нашего сегодняшнего урока»?
Может быть, граф нам поможет решить задачу перестановки намного быстрей и наиболее эффективно? Давайте построим граф!
Ученики предлагают варианты ответов, рассуждают, самостоятельно формулируют тему урока, примерно так:
«На прошлом уроке мы переставляли коней в среде «Конюх».
Сегодня мы будем решать задачу перестановки с использованием графа».
Во время обсуждения используется затенение экрана, после того как дети сформулировали тему урока, учитель закрывает затенение и на экране появляется тема урока и модель задачи.
13.
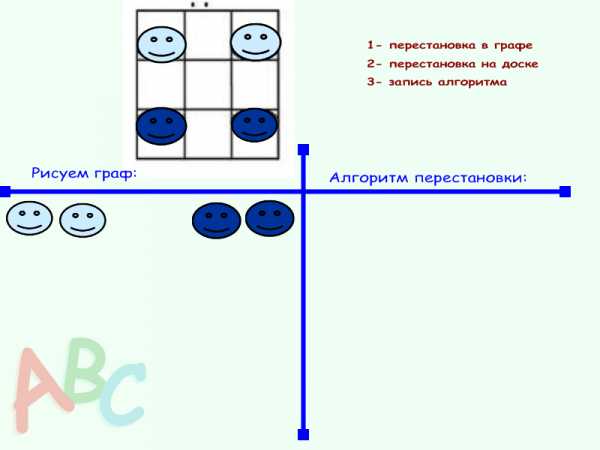
Учитель работает с доской, задавая вопросы ученикам: Обозначим клетки цифрами 1, 2, 3…и.т.д. Что это будет в графе?
Найдем все возможные пути перемещения, из 1-ой клетки мы можем попасть в какие клетки? и.т.д. Учитель: Рисуем граф. Я на доске, вы в тетради . Упростим изображение:
1-6-7-2-9-4-3-8
Модель графа готова.
Ребята, как надо двигаться, чтобы выполнить перестановку? Принимает ответы, выбираю наиболее разумные решения, приглашаю к доске помочь 3-х учащихся. Объясняю, что надо делать:
Первый учащийся – выполняет алгоритм на графе
Второй учащийся – дублирует действия на шахматной доске
Третьей учащийся – записывает алгоритм перестановки
Всех остальных просит записать алгоритм перестановки в тетрадь.
Организует работу детей со смарт-доской, задает направляющие вопросы, при необходимости
Учащиеся: Отвечают на вопросы и работают в своих тетрадях.
1в: Вершины
2в.: в 6-ую и в 8-ую
и.т.д.
Построение графа в своих тетрадях, Далее, записывают алгоритм перестановки.
Три ученика работают со Smart- доской: работа с моделью задачи, перестановка в графе, запись алгоритма.
На Слайде представлена модель задачи в виде рисунка, на котором располагаются перемещаемые объекты (фишки) для перестановки.
Учитель построил граф, используя инструменты рисования.
На граф размещаются перемещаемые объекты (фишки) для перестановки.
Отведено поле для
написание алгоритма. Инструменты – перья, ластик. Идет запись алгоритма.
14.

Учитель предлагает переместится за компьютеры и выполнить алгоритм перестановки в среде “Конюх”. Напоминает, о переносе алгоритма в новые условия обозначения координат. Далее,
координирует
Учащиеся выполняют задания за компьютерами в среде “Конюх”.
Варианты работы:
— индивидуально
— в парах
— в группах
(в зависимости от кол-ва ПК и от уровня об учености)
Средствами программы на слайде размещена ссылка на модель задачи в сети Интернет, представлен скриншот программы, с которой индивидуально работают дети.
При необходимости, можно использовать гиперссылку для демонстрации программы на Smart-доске.
15.
Пробуют за столами выполнить перестановку в графе. Варианты самостоятельной работы, по уровню сложности. Один из вариантов представлен на доске.
Работают:
В зависимости от успеха и
времени затраченного при
работе за ПК.
— самостоят.-в паре
-в группе
Учитель координирует. По итогам, приглашает группы для демонстрации алгоритма на Smart –доске.
Подводит к выводу, о разнообразии вариантов перестановки и вводит понятие – эффективного алгоритма.
Совместная работа над заданием, по мере завершения практической работы за ПК.
Демонстрация вариантов перестановки (решения без повторений!)
Поиск вариантов решения задачи и выбор наиболее эффективных способов решения задач в зависимости от конкретных условий. Таким образом, развитие регулятивных УУД.
Средствами программы построен граф, на котором размещены движущиеся объекты-вершины.
Рефлексивно-оценочный этап
15.
Учитель предлагает выполнить Тест «Проверь себя» для контроля знаний (3 варианта, по уровню сложности).
Далее, учитель открывает общий тест (собраны все вопросы для 3-х вариантов) на Smart –доске и организует проверку.
Учащиеся выполняют тест на листочках. Результаты сдают. Проверка теста:
Предлагают ответы на соответствие, при необходимости корректируют, и анализирует ответы.
Таким образом используется самоанализ, корректировка знаний.
.
Использован режим работы с встроенным интерактивным объектом flash – Тест «Проверь себя» для контроля знаний. Используются перемещаемые объекты для отображения соответствий.
16.

Подводит итоги, организует обсуждение — рефлексия, планы на след. занятие
Делятся впечатлениями, говорят о том, что происходило, чему научилось, чем отличается занятие от других, что еще предстоит сделать.
На экране расположены объекты: текст, рисунок, бланк д/з.
Использована возможность перемещать объекта, для привлечения внимания учеников.
Какие возможности программы Notebook использованы?
1. Запись урока, всех ответов учеников при помощи программы Notebook
2. Фигуры, заливка фигур. Пипетка. группировка
3. Коллекция рисунков
4. Коллекция LAT (анимированные страницы, объекты)
5. Вложенный звук
6. Вставка флеш — объектов
7. Гиперссылки на Интернет — страницы
8. Анимация появления.
9. Инструмент перо.
10. Инструмент рисования. Перо. Линии – для создания графической модели (граф)
11. Клонирование
12. Захват экрана – для создания рисунков. закладок.
13. Таблица – для работы с терминами
14. Назначение групп – иерархия страниц
Литература
Рекомендуемые ученикам учебные материалы к занятию
1. Учебник Л.Л.Босовой «Информатика 5 класс»
2. Программно-методического комплекс «Роботландия» (Ю.А.Первин, А.А. Дуванов и др.)
Список литературы, используемой для разработки занятия
Интернет- ресурсы:
Оценка деятельности участников конкурса для дистанционного тура будет проводиться по следующим критериям:
демонстрация ресурсов коллекции программного обеспечения SMART Notebook и интерактивной коллекции LAT;
использование инструментов программного обеспечения SMART Notebook;
системность содержания методической разработки урока;
умение презентовать разработанный материал в ПО SMART Notebook;
владение современными методическими приемами обучения учащихся.
По каждому критерию экспертной комиссией будет выставлена оценка по пятибалльной шкале с последующим подсчетом среднего балла.
infourok.ru
Конспект урока по информатике «Информационные модели на графах. Использование графов при решении задач.»
Конспект урока информатики в 6 классе
МБОУ СОШ № 35, учитель Маршала Ирина Алексеевна
ТЕМА: Информационные модели на графах. Использование графов при решении задач.
Цель: формирование навыков и умений структурирования и визуализации информации с помощью графов для решения учебных и жизненных задач, воспитание ответственного и избирательного отношения к информации.
Задачи
Предметные:
сформировать навыки и умения представлять состав и структуру системы с помощью графа;
использовать граф для решения предметных и жизненных задач;
закрепить умения определять целесообразные источники для поиска необходимой информации с помощью ИКТ.
Метапредметные:
владеть общепредметными понятиями «объект», «система», «модель», «схема» и др.;
структурировать и визуализировать информацию.
преобразовать объекты из чувственной формы в модель;
уметь устанавливать причинно-следственные связи, строить логическое рассуждение и делать выводы;
корректировать свои действия в соответствии с изменяющейся ситуацией; оценивать правильность выполнения учебной задачи;
Личностные:
овладеть первичными навыками анализа и критичной оценки получаемой информации;
проявить способность увязать учебное содержание с собственным жизненным опытом;
выработать способность к общению и сотрудничеству со сверстниками и взрослыми в процессе образовательной деятельности;
понимать ценности здорового образа жизни за счет знания основных гигиенических, эргономических и технических условий безопасной эксплуатации средств ИКТ
ЦОР: презентация.
Основные понятия: граф, вершина, дуга, ребро, петля, цепь, цикл, иерархия, дерево.
Планируемые результаты
Предметные результаты: формирование представления о графе как о наглядном средстве представления состава и структуры системы.
Личностные результаты: волевая саморегуляция как способность к мобилизации сил и преодолению препятствия, наличие мотивации к творчеству.
Формирование УУД
Личностные: планировать свое действие в соответствии с поставленной задачей и условиями её реализации;
Предметные: знаково-символические действия, включая моделирование.
Ход урока
1.Оргмомент: приветствие, настрой на работу. Сообщаем, что работаем сегодня по группам. (1мин)
2. Проверка домашнего задания. Активизация знаний.(3-4мин)
Раздаются карточки (кейс) со схемами. (Схема Курская дуга; Метрополитен; Золотое кольцо России, карта города Курска)
Учитель: ребята, посмотрите внимательно на карточки. Что вы на них видите? Опишите, опираясь на вопросы под рисунком.(1 мин. на подготовку ответа)
Вопросы на карточках: 1) как называется этот графический объект?
2) дайте определение; 3) для чего применяют такой способ отображения объекта?
4) дает ли данное изображение полное представление об объекте?
Ответы 2-х обучающихся.
3. Введение нового материала
На доске слайд 2.(2 мин) Изображение школы, дома, библиотеки, кафе, цирка, соединенных между собой. Всем известна сказка колобок и её главный герой. Сегодня колобка будет много неизвестного и ждут испытания. В новое место попал Колобок. Можно ли эту схему изобразить по другому?
Учащиеся: предлагают варианты изображения. Даем подсказку, что можно ввести условные обозначения. (Думают группы 1 мин) Предложения на доске на новом слайде. Если изображение напоминает граф, то учитель сообщает:
Учитель: ребята сейчас вы сами изобразили главного героя сегодняшнего урока и графически отразили нашу тему. Это граф! Тема нашего урока — Информационные модели на графах. Использование графов при решении задач.
Учитель: ребята, а какие цели мы можем перед собой поставить при изучении нового материала? (предполагаемые ответы учащихся: узнать, что такое граф, какие графыбывают? Где и для чего используются? Научиться создавать графы, решать с его помощью задачи) (3мин)
слайд 4. Даем определение графа.(2-3мин)
Граф-совокупность конечного числа точек, называемых вершинами графа, и попарно соединяющих некоторые из этих вершин линий, называемых ребрами или дугами графа.
( запись в тетради)
слайд 5 Марина пригласила друзей в гости. Друзья пили чай и разговаривали. Как вы считаете, какая модель графа подходит под описание ситуации? Почему вы так решили?
Ответы уч-ся: Неориентированный, т.к. не указано кто с кем конкретно разговаривал.
Учитель: верно. И так, если в задании указываются отношения между объектами, то граф будет ориентированным, если нет, то неориентированным (запись в тетради) (3-5 мин)
слайд 6. Учитель: Посмотрите, пожалуйста, а чем этот граф отличается от тех, что были ранее? ( Ответы учащихся: написана информация на ребрах или дугах) (1 мин)
Учитель: верно! Такой граф называется взвешенный (имеет вес, утяжелен информацией)
Учитель: Как в сказке колобок путешествовал главный герой? От кого и к кому? Ответы учащихся (от бабушки к лисе). Правильно и показать это можно так. (слайд 7. )Такой граф называется Цепь .
Учитель: а вот если бы колобка не съела лиса, и он вернулся назад к бабушке, то был бы Цикл. Слайд 8.
Первичная отработка нового материала.
Слайд 9. Найдите граф, согласно описанному заданию (с пояснением 1-2 мин)
Слайд 10. Учитель: Посмотрите, наш колобок! Какой забывчивый. Укатился от бабушки и вдруг вернулся. Такое поведение объекта можно изобразить петлей.(1 мин)
НА 20 минуте ФИЗКУЛЬТМИНУТКА для тела (покачались деревья)- 2мин
Учитель: что- то странное на экране. Зачем нам эти изображения? (слайд11)
Слайд 12. (1-2 мин) Теперь понятно — это новые понятия темы. Сеть- граф с циклом
И Дерево- это граф, в котором нет циклов (учащиеся пишут в тетради.)
Где же мы могли встречаться с такими графами? (предположительные ответы учащихся)
Учитель: да — генеалогическое древо. Демонстрация слайда 13
ОПРЕДЕЛЕНИЯ: Корень-главная вершина. Листья- вершины, не имеющие порожденных вершин.
Каждая вершина — имеет только одного предка. Любая вершина дерева может порождать несколько потомков.
Учитель: (слайд 14) Деревья на уроках ИЗО вы научились рисовать, а наше информационное дерево как будет выглядеть, если у нас такая задача: Петя, Коля и Маша приготовили рефераты по информатике и физике по темам: Интернет, Компьютерные вирусы, Оптические явления. А Аня нашла и сохранила картинки Закат и Зима. Вся информация хранится на диске С. Изобразите данную информацию схематически. (задание лежит в кейсах) Соберите схему из отдельных деталей (работает группа) (проверка слайд 15)
Слайд 16 (3мин) А вот еще одну известную сказку я попрошу вас записать дома в виде сети, не простой, а семантической (показ слайда 14) записывают определение.
ОПРЕДЕЛЕНИЕ: Семантическая сеть-сеть, на которой отражены объекты (понятия) и связи(отношения) между ними.
Закрепление нового материала(5 мин): выполнение задания из тетради на печатной основе……..№ 151. В таблице приведена стоимость проезда между соседними железнодорожными станциями. Числа, стоящие на пересечении строк и столбцов таблицы, означают стоимость проезда между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними.
А
B
C
D
E
A
X
1
4
1
B
1
X
3
C
4
X
2
D
3
X
E
1
2
X

Учитель: наша работа со схемами разного вида продолжается. Сейчас вы пройдете к компьютерам с учебниками и выполните задание 2 работы № 14. Для этого вы используете Заготовки и постараетесь достроить сеть. Необходимые объекты найдете во вкладке Вставка. ( 10 мин)
автобус
пассажир
водитель
остановка
билет
контролер
На 35 минуте ФИЗКУЛЬТМИНУТКА для глаз (1 мин) Возьмите в руки карандаш или ручку. Поднимите перед собой на уровне глаз. Смотрите на острие карандаша и рисуйте в воздухе им восьмерку, квадрат, круг. Приблизьте, удалите карандаш. Закройте глаза.(1,2,3) Откройте глаза.
Учитель: давайте подведем предварительный итог. Что мы смогли узнать и запомнить.(2мин) (Слайд 18) Опишите графические объекты на слайде. Предложены 1) семантическая цепь — сказка Курочка ряба,2) Граф, имеющий ребра и дуги;3) взвешенный граф; 4) дерево
Рефлексия (1-2 мин)
Учитель: Наше занятие подошло к концу. Интересной для вас оказалась тема занятия? Что вас удивило? Что было трудно? Какие проявления в поведении участников группы способствовали работе, а какие мешали? Оцените свое впечатление о проделанной работе, заполнив листы самооценки.
1. Листок самооценки: (лежат в кейсах)
1. Материал занятия был мне полезен
2. Материал занятия был мне интересен
3. При работе в группе мне не нашлось интересной работы
4. Занятие прошло очень быстро
5. Об этом занятии я расскажу родителям много интересного
Самым активным, участвующим, стремящимся познать, раздаются наклейки- оценки деятельности.
Учитель: Домашнее задание: параграф 13 п 2-3 РТ № 52
План урока:
Организационный момент
Проверка выполнения домашнего задания
Актуализация знаний
Знакомство учащихся с темой и планом занятия
Изучение нового материала, работа с учебником
Организация проектной деятельности и разработка проектов (работа в группах)
Защита проектов (закрепление материала)
Инструктаж учителя по выполнению домашнего задания
Рефлексия учебной деятельности
Технологическая карта занятия
Осуществляемые действия:



infourok.ru
Модели на графах. Решение задач. 9 класс

Решить задачу:
Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Венера; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?
Использование моделей на графах при решении задач
абстрактный математический объект, представляющий собой множество вершин графа и набор рёбер , то есть соединений между парами вершин.
Граф —
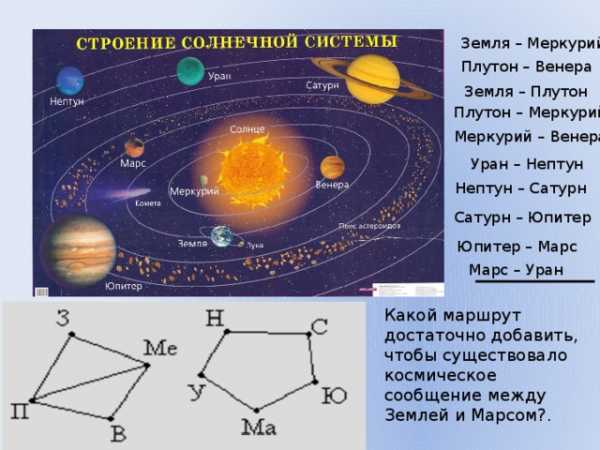
Земля – Меркурий
Плутон – Венера
Земля – Плутон
Плутон – Меркурий
Меркурий – Венера
Уран – Нептун
Нептун – Сатурн
Сатурн – Юпитер
Юпитер – Марс
Марс – Уран
Какой маршрут достаточно добавить, чтобы существовало космическое сообщение между Землей и Марсом?.
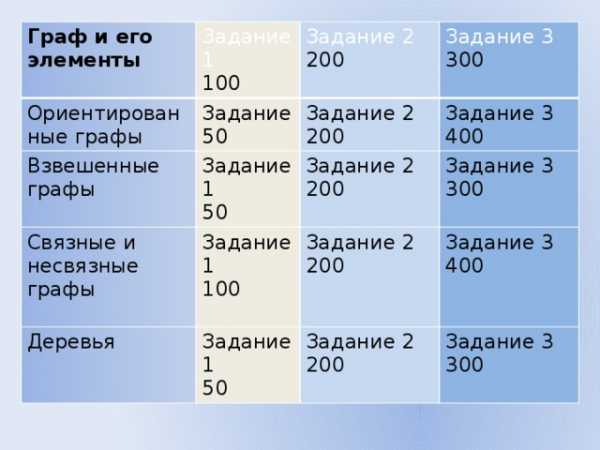
Граф и его элементы
Ориентированные графы
Задание 1
Задание 50
Взвешенные графы
100
Задание 2
Задание 1
Задание 3
200
Задание 2
Связные и несвязные графы
50
Деревья
300
Задание 2
Задание 3
200
Задание 1
400
200
Задание 3
100
Задание 1
Задание 2
50
300
Задание 3
200
Задание 2
400
200
Задание 3
300

Ориентированные графы
Задание № 1:
Какой граф называется ориентированным?
Как называются ребра в ориентированном графе?
начало

Ориентированные графы
Задание № 2
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З?
начало

Ориентированные графы
Задание 3
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, не проходящих через город Е ?
начало

Взвешенные графы
Задание № 1
Какой граф называется взвешенным?
Что может обозначать вес?
начало
Взвешенные графы
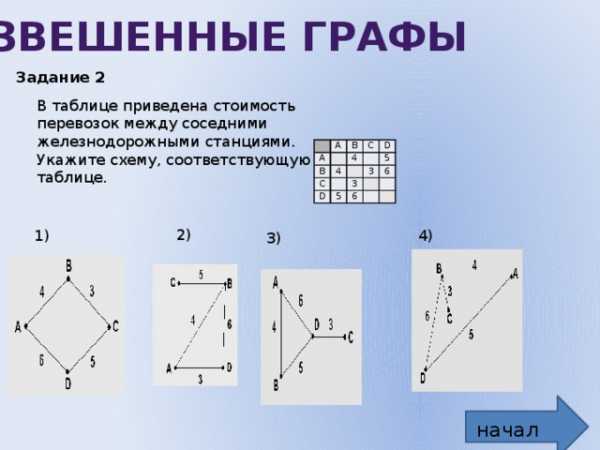
Задание 2
В таблице приведена стоимость перевозок между соседними железнодорожными станциями. Укажите схему, соответствующую таблице.
A
A
B
B
4
C
4
C
D
D
3
5
5
3
6
6
2)
1)
4)
3)
начало

Взвешенные графы
Задание 3
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
A
A
B
B
C
C
4
4
D
D
E
6
6
E
F
3
F
3
6
6
4
4
2
2
5
5
начало
Связные и несвязные графы
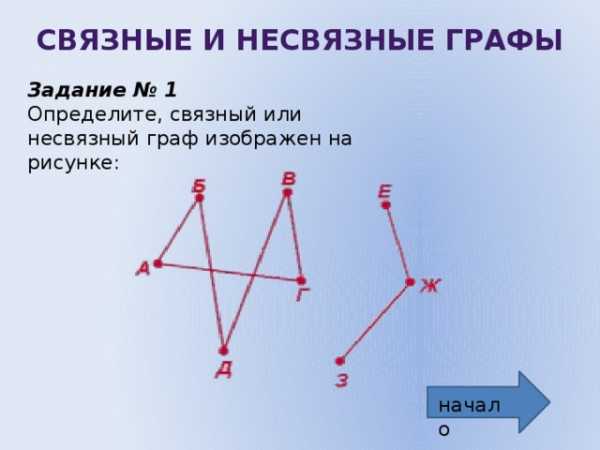
Задание № 1
Определите, связный или несвязный граф изображен на рисунке:
начало

Связные и несвязные графы
Задание № 2
Нарисуйте граф , в котором 5 вершин и 3 компоненты связности. Сколько существует разных графов, удовлетворяющих условию задачи?
начало

Связные и несвязные графы
Задание № 3
- В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией в том и только в том случае, если двузначное число, образованное названиями городов, делится на 3. Можно ли долететь по воздуху из города 1 в город 9 ?
начало
Деревья
Задание №1 . Ч то называется деревом?
начало

Деревья
Задание №2 . Для отправки поздравления есть конверты трех видов, на которые клеится одна из двух марок и в которые вкладывается одна из четырех открыток. Сколько существует способов сделать поздравления по почте?
начало

Деревья
Задание №2.
Сколькими способами можно рассадить в ряд на три стула трех учеников? Выписать все возможные случаи.
начало

Деревья
Задание 3. Квартет.
« Проказница мартышка, осел, козел да косолапый мишка затеяли сыграть в квартет». Мартышка расположилась напротив медведя, а слева и справа от нее – осел и козел. «Ударили в смычки, дерут, а толку нет». Тогда осел и козел поменялись местам. «Расселись, начали квартет. Он все-таки на лад нейдет». Таким образом, они перепробовали все возможные вариант. Медведь всегда оставался на одном месте. Сколько всего было вариантов расположения незадачливых музыкантов?
начало
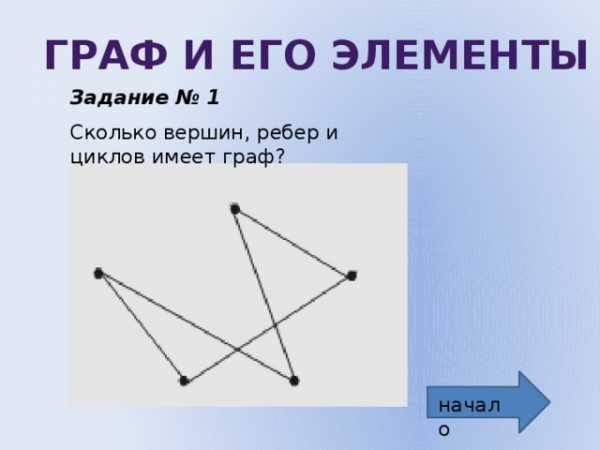
Граф и его элементы
Задание № 1
Сколько вершин, ребер и циклов имеет граф?
начало

Граф и его элементы
Задание №2
Изобразите с помощью графа договорные отношения между предприятиями А, Б, В, Г, Д, Е, если к рассматриваемому моменту:
предприятие А установило договорные отношения со всеми другими предприятиями;
Б установило с Г и Д;
В установило со всеми предприятиями, кроме предприятия Е.
Сколько вершин и сколько ребер имеет полученный граф?
начало

Граф и его элементы
Задание №3
Среди семи стран установлены экономические отношения, причем каждая страна имеет экономические договоры с каждой другой страной. Изобразите в виде графа результат установленных экономических отношений. Сколько ребер имеет полученный граф?
начало
multiurok.ru
