задачи с двумя переменными, задача с двумя неизвестнами, axmara.narod.ru о математике.
Мой племянник опять не может решить задачу!
Давайте вместе попробуем решить несколько задач с двумя неизвестными!
Уясните для себя самое главное! Не бойтесь математику! Полюбите её! И вы будете щелкать эти задачи как семечки! Ведь математика – это самая главная наука!
И неважно, что эта задача не похожа на вашу, если вы не научитесь решать их самостоятельно, то любое изменение условия задачи, будет всегда для вас проблемой!
Условие задачи с двумя неизвестными :
Миша сказал, что одна лента в 2 раза длиннее, чем вторая.
А Оля сказала, что одна лента длиннее другой на 3см.
Решение задачи с двумя неизвестными:
Правильное решение задачи с двумя переменными зависит от правильности составления уравнений!
Большую ленту выразим через – х.
Маленькую выразим через – у.
Слова Миши можно записать как х = 2у.
Слова Оли можно записать как х – у = 3.
У нас получилось 2 уравнения с двумя неизвестными.
Заменим во втором уравнении х на 2у, ведь х = 2у.
И получим 2у – у = 3, у = 3.
Подставим у = 3, в первое уравнение х = 2*х=6.
Ответ к задаче с двумя неизвестными:
Первая лента равна 6см, а вторая 3см.
Написать что-нибудь…
задачи с двумя переменными , решить задачу два велосипедиста . задачи с двумя неизвестными , задача два автомобиля выехали одновременно , задача два пешехода вышли одновременно , задача две трубы , axmara.narod.ruГрафическое решение задач с двумя неизвестными, заданных линейными неравенствами ограничений.
Для представления задачи линейного программирования в геометрической форме для каждого i-го ограничения в n-мерном пространстве задается полуплоскость (или гиперплоскость) решений. В результате пересечения всех полуплоскостей, определяемых ограничениями, образуется выпуклый многогранник допустимых решений.
Целевую функцию в n-мерном пространстве геометрически можно интерпретировать как семейство параллельных полуплоскостей, положение каждой из которых определяется значением параметра F.
Задача состоит в том, чтобы найти такую точку многогранника решений, в которой целевая функция принимает максимальное или минимальное значение.
На рис. 1 показано геометрическое представление некоторой задачи линейного программирования в двумерном пространстве с четырьмя ограничениями и целевой функцией вида . Выпуклым многогранником допустимых решений является многогранник ABCDE. Координаты любой его точки удовлетворяют как систему ограничений, так и условие неотрицательности переменных, поскольку он находится в первой координатной полуплоскости.
В том случае, если в системе ограничений будет не две, а три переменных, то каждое ограничение геометрически будет определяться гиперполуплоскостью трехмерного пространства. Если же в системе ограничений количество переменных больше, чем три (х1, х2,… хn), то каждое ограничение определяет гиперполуплоскость n-мерного пространства.
Заметим что, если область допустимых решений неограниченна, то минимум или максимум линейной функции может и не достигаться.

Рис. 1. Геометрическая форма представления задачи линейного программирования
Графический метод решения задач линейного программирования базируется на ее геометрической интерпретации и применяется, как правило, при количестве переменных n = 2 и в отдельных случаях при n = 3 (трехмерное пространство) . Ограниченное использование графического метода обусловлено сложностью построения многогранника решений в трехмерном пространстве (для задач с тремя переменными), а графическое изображение задачи с количеством переменных больше трех вообще невозможно. Однако графический метод позволяет выработать у студентов наглядные представления о линейном программирование и подтвердить справедливость некоторых его теорем. В дальнейшем мы будем рассматривать и решать задачи линейного программирования графическим методом только в двумерном пространстве.
Согласно геометрической интерпретацией задачи линейного программирования каждое i-е ограничение-неравенство определяет полуплоскость с граничной прямой (і = 1, 2, …, т). Если графически изобразить общую часть, или пересечение всех указанных полуплоскостей, то мы получим множество точек, координаты которых удовлетворяют одновременно все ограничения задачи, это множество точек называют многогранником допустимых решений. Условие неотрицательности переменных означает, что область допустимых решений задачи принадлежит первому квадранту системы координат двумерного пространства. Целевая функция геометрически интерпретируется как семья параллельных прямых .
Проиллюстрируем решение задачи линейного программирования графическим методом на примере системы ограничений с двумя переменными.
Пример. Решить графически следующую задачу линейного программирования: найти максимум и минимум целевой функции при ограничениях
Решение: Сначала нам необходимо получить область допустимых решений. Неравенство определяет полуплоскость с граничной прямой . Строим эту прямую (рис. 3.2 , прямая (1)) и определяем полуплоскость допустимых решений. С этой целью в неравенство подставляем координаты какой-то характерной точки, например . Убеждаемся, что эта точка принадлежит выбранной полуплоскости и иллюстрируем этот факт соответствующими направленными стрелками. Аналогичным образом строим полуплоскости для остальных неравенств из системы ограничений задачи. В результате пересечения этих полуплоскостей получаем область допустимых решений – многогранник ОABCD.
Вектор нормали (иногда его называют также как радиус-вектор) задает направление роста значений целевой функции F. Целевая функция определяет семейство параллельных прямых
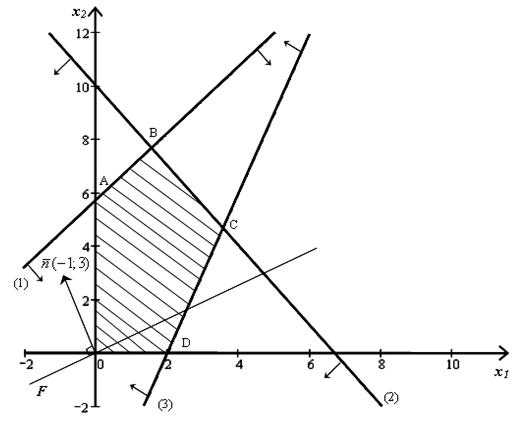
Рис. 2. Графическое представление задачи
Допустимыми базисными решениями данной задачи являются угловые точки многогранника ОABCD, а одна (в отдельных случаях – две) из этих точек придает максимального значения целевой функции. В этом примере максимального значения целевая функция достигнет в точке B, т.е. в вершине многогранника области допустимых решений, которая является наиболее отдаленной от начала координат, если двигаться в направлении вектора .
Координаты точки B находим, решив систему из уравнений прямых № 1 и № 2, на пересечении которых эта точка находится:
Имеем систему двух линейных уравнений с двумя неизвестными, которую можно решить методами Крамера, Гаусса и некоторыми другими.
По методу Крамера решениями этой системы будут значения:
; .
Таким образом оптимальным планом задачи линейного программирования, который обеспечивает максимум целевой функции является точка B (1,54 ; 7,68).
Значение целевой функции в этой точке: .
Минимального значения целевая функция достигает в точке D. Если мы движемся в направлении противоположном вектору нормали , то данная точка является последней вершиной многогранника ОABCD через которую проходит линия уровня F. Прямая (3) пересекает ось 0х1 при х1 = 2 , следовательно координаты точки D (2 , 0) .
Оптимальным планом задачи линейного программирования, который обеспечивает минимум целевой функции является точка D ( 2 , 0) .
Значение целевой функции в этой точке: .
Рекомендуемые страницы:
lektsia.com
Уравнения с четырьмя и более неизвестными
68. Уравнения с четырьмя и более неизвестными. Теперь ясны следующие соображения: одно уравнение с четырьмя неизвестными имеет бесконечно много решений, причем можно давать произвольные значения трем неизвестным, два уравнения с 4 неизвестными имеют бесконечно много решений, причем произвольные значения можно давать двум неизвестным, три уравнения с 4 неизвестными имеют бесконечно много решений, причем произвольные значения можно давать одному неизвестному, четыре уравнения с 4 неизвестными имеют лишь одно решение (конечно, если ни одно из этих уравнений не есть следствие остальных и не противоречит остальным).
Такие соображения можно продолжить и дальше. Например, 5 уравнений с 8-ю неизвестными имеют бесконечно много решений, причем произвольные значения можно давать трем неизвестным и т. п.
Решать системы уравнений с большим числом неизвестных приходится редко. Следует при этом решении пользоваться по возможности всеми особенностями уравнений, чтобы упростить решение.
Рассмотрим 2 примера. Пример 1:
x + y + 2z – t = 9
x + y – 2z + t = 7
x – y + z + 2t = –9
x – y – z – 2t = 5
Сложив 1-е и 2-е уравнения по частям, мы получим очень простое уравнение только с двумя неизвестными, а именно
2x + 2y = 16 или x + y = 8.
Сложив по частям 3-е и 4-е уравнения, получим:
2x – 2y = –4 или x – y = –2.
Теперь легко решить 2 полученных уравнения (x + y = 8 и x – y = –2), и тогда найдем x = 3 и y = 5.
Подставляя эти значения в 1-е и в 3-е уравнения, получим:
3 + 5 + 2z – t = 9 или 2z – t = 1
3 – 5 + z + 2t = –9 или z + 2t = –7
Подстановка этих значений во 2-е и 4-е уравнения приведет к таким же точно уравнениям.
Теперь остается решить 2 уравнения с 2 неизвестными:

maths-public.ru
Решение задач с помощью систем уравнений
Вопросы занятия:
· показать основные этапы решения задач с помощью систем.
Материал урока
На предыдущих уроках мы с вами говорили о системах линейных уравнений с двумя неизвестными и научились решать такие системы тремя способами. А именно, графическим способом, способом подстановки и способом сложения. На практике обычно используют способ подстановки и способ сложения, так как графический способ чаще всего позволяет найти решения лишь приближенно.
На этом уроке мы научимся с помощью систем уравнений решать задачи.
Давайте, рассмотрим задачу.
В корзине лежат бананы и яблоки. Известно, что бананов на 5 больше, чем яблок. Сколько бананов и сколько яблок в корзине, если всего в ней 17 фруктов?
Пусть х – количество бананов в корзине, а игрек – количество яблок.
Так как по условию задачи бананов на 5 больше, чем яблок, то можем составить уравнение:
Также из условия задачи известно, что всего в корзине 17 фруктов, а тогда можем записать следующее уравнение:
Объединим уравнения в систему, так как эти условия должны выполняться одновременно.
Теперь, чтобы ответить на вопрос задачи, нам надо решить эту систему.
Таким образом, чтобы решить задачу с помощью системы уравнений, надо:
1. выделить две неизвестные величины и обозначить их буквами;
2. используя условие задачи, составить систему уравнений;
3. решить систему уравнений удобным способом;
4. истолковать результат в соответствии с условием задачи.
Решим следующую задачу.
Пример.
И решим ещё одну задачу.
Пример.
videouroki.net
Решение задач с помощью систем линейных уравнений. 7-й класс
Разделы: Математика
Аннотация: Урок объяснения нового материала. На уроке рассматриваются три разных способа решения одной задачи. Тем самым школьники приучаются анализировать условие задачи и выбирать более простой способ решения. Первый опыт применения уравнений для решения текстовых задач у учащихся уже имеется. Различные способы решения систем линейных уравнений уже изучены. И одна из целей урока — показать использование системы уравнений как математической модели реальной ситуации. Использование на уроке технических средств позволяет сделать урок ярким, насыщенным, полным и дает возможность мгновенно осуществить проверку решаемых на уроке заданий. Это очень важно, так как экономится время, а учащиеся, работающие самостоятельно, получают возможность проверить себя и вернуться назад, чтобы устранить свои ошибки. Тем самым осуществляется самоконтроль, внутренняя обратная связь — важнейший фактор самоуправления процесса обучения.<Приложение1>
Цели
- Показать использование системы линейных уравнений как математической модели реальной ситуации
- Применение знаний по теме «Системы линейных уравнений» для решения текстовых задач.
- Учить анализировать условие задачи и выбирать более простой способ решения.
Ход урока
Устная работа:
Решите задачу, составив числовое выражение:
Купили 7 тетрадей по 2р. и 2 ручки по 4р. Сколько денег заплатили?
Турист ехал 2ч на поезде со скоростью 60км/ч и 3ч шел пешком со скоростью 5км/ч. Какое расстояние он преодолел?
Решите задачу, составив буквенное выражение:
Купили 10 тетрадей по Х р и 3 ручки по У р. Сколько заплатили за всю покупку?
Турист ехал 3ч на автобусе со скоростью Х км/ч и 2ч шел пешком со скоростью 4км/ч
Перейдите от словесной модели к математической:
Числа В и С равны
Число А на 18 больше числа В
Число Х в 6 раз меньше числа У
Разность Р и Н на 17 больше их частного
Создайте реальную ситуацию по модели:
a=2b
a+7=b
a-b=3
3a=b
I Этап. Объяснение нового материала.
Задача На турбазе имеются палатки и домики. Всего их 25. В каждом домике размещается по 4 человека, в каждой палатке — по 2 человека. Сколько палаток и сколько домиков на турбазе, если на ней отдыхает всего 70 человек?
Решим задачу арифметически.
25*2=50(чел) разместилось бы, если селить по 2
70-50=20(чел) не расселили
20:2=10(домиков), т.к. подселяют еще по 2
25-10=15(палаток)
Ответ: 10 домиков, 15 палаток.
Решим эту задачу с помощью уравнения.
(Вспомним этапы математического моделирования)
II этап. Составление математической модели.
Пусть на турбазе Х палаток, тогда домиков 25-Х. Т. к. в каждой палатке по 2 человека, то 2Х чел живут в палатках. Т. к. в каждом домике по 4 человека, то 4(25-Х) чел. живут в домиках. Зная, что всего на турбазе 70 чел, составим уравнение:
2Х+4(25-Х)=70
III этап. Работа с моделью.
2Х+100-4Х=70
-2Х= — 30
Х=15
IV. этап. Ответ на вопрос задачи: 15 палаток и 10 домиков.
Самый трудный этап в решении задач - составление математической модели. Ученик всегда затрудняется, что удобнее обозначить за Х. Всегда возникает желание обозначить за Х то, о чем спрашивается в задаче. Но в данной задаче два вопроса. Две искомые величины. Можно ли решить эту задачу, введя два неизвестных? Попробуем.
Пусть Х — палаток, а У — домиков. Т. к их всего 25, то Х+У=25. 2Х чел живут в палатках, а 4У чел — в домиках. 2Х+4У=70 Получили два уравнения и оба с двумя незвестными.
Как же их решить? Составить систему двух уравнений с двумя неизвестными и решить ее.
Х+У=25
2Х+4У=70
Вспоминаем способы решения систем линейных уравнений.
Решив систему, получаем тот же ответ: 10 домиков, 15 палаток.
Делаем вывод: Система линейных уравнений тоже может быть использована как математическая модель реальной ситуации. Чтобы решить задачу с помощью системы надо ввести два неизвестных и составить два уравнения с ними. Способ решения системы надо выбирать тот, который представляется более уместным, или тот, который больше нравиться. Этапы математического моделирования те же, что и при решении задач с помощью уравнения.
Закрепление изученного материала.
Решите с помощью системы уравнений:
1. У причала находилось 6 лодок, часть из которых была двухместными, а часть - трехместными. Всего в эти лодки может поместиться 14 человек. Сколько двухместных и сколько трехместных лодок было у причала?
2. В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?
Подведение итогов урока.
Домашнее задание: параграф 14 , №14.7, 14.14.
26.02.2011
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Решение систем уравнений с двумя неизвестными как математические модели реальных ситуаций 9 класс
Долхонова В.В. МБОУ «Еланцынская СОШ»
Урок по алгебре
Класс: 9
Тема: «Решение систем уравнений как математические модели реальных ситуаций»
Цели урока:
Обучающие:
Продолжать работу по формированию навыков решения задач с помощью систем уравнений второй степени.
Закрепить знания решения систем уравнений второй степени аналитическим способом (способ подстановки)в ходе решения задач.
решать задания, которые наиболее часто встречаются на «ГИА».
Развивающие:
использование для достижения поставленной задачи уже полученные знания;
умение обосновывать свои рассуждения;
Воспитательные:
выработка желания и потребности обобщать полученные факты;
воспитание настойчивости и терпения при выполнении заданий.
Побуждать учеников к самоконтролю, воспитывать интерес к математике.
Оборудование: проектор, ПК
Прогнозируемый результат:
Знать способы и методы решения систем уравнений второй степени.
Уметь правильно отбирать способы решения систем уравнений второй степени для решения задач с помощью систем уравнений.
Эпиграф:
1.Китайская мудрость: « Я слышу – я забываю, я вижу – запоминаю,
я делаю – я усваиваю».
2. «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их!»
Д. Пойа
План урока:
Организационный момент.
Математический диктант.
Объяснение материала
Закрепление материала
Подведение итога урока.
Домашняя работа
Ход занятия
Организационный момент
Проверка подготовленности учащихся к занятию.
Приветствие учителя и учащихся.
3. Постановка целей и задач занятия.
Прочитайте высказывание математика Д. Пойа. Какой совет дает ученый нам? Мудрость высказывания математика Д.Пойа объедините с предыдущей темой и сформулируйте тему урока.
Сегодня мы познакомимся с задачами, решение которых сводится к
системам уравнений. Запишем тему урока. Назовите цель урока.
Мотивация (самоопределение) к учебной деятельности.
— Работать сегодня мы будем коллективно, в парах и индивидуально.
Вспомните правила работы в парах. (Прислушиваться к мнению соседа, работать дружно, помогать друг другу). В конце урока каждый из вас оценит свою работу и работу партнёра.
2.Математический диктант
Перед вами лежат задания математического диктанта, выполните его.
1вариант.
Составьте уравнение с двумя переменными, если:
Сумма двух натуральных чисел равна 16.
Периметр прямоугольника равен 12 см.
Одна сторона прямоугольника на 8 см больше другой.
Произведение двух натуральных чисел равно 28.
Диагональ прямоугольника равна 5 см.
2 вариант
Составьте уравнение с двумя переменными, если:
Разность двух натуральных чисел равна 14.
Площадь прямоугольника равна 26 см².
Катет прямоугольного треугольника на 5 см больше другого.
Сумма квадратов двух натуральных чисел равна 30.
Гипотенуза прямоугольного треугольника равна 8 см.
На экране проецируются ответы и критерии оценивания.
Ребятам в парах предлагается проверить и оценить работу друг друга.
Объяснение материала
При решении задач с помощью системы уравнений придерживаемся следующего алгоритма: (слайд)
I. Составление математической модели:
Внимательно изучить условие задачи:
Какой процесс описывается в задаче?
Какими величинами характеризуется этот процесс?
Как связаны между собой эти величины?
Значения, каких величин требуется найти?
Обозначить буквами искомые величины;
Выразить искомые величины через данные;
Составить уравнения и из них соответствующую систему;
II. Работа с математической моделью:
Найти решение системы;
III. Ответ на вопрос задачи:
Проверить, какие из решений системы удовлетворяют условиям задачи.
Алгоритм решения задачи дать каждому ученику.
Задача 1. Прямоугольный газон обнесен изгородью, длина которого 40 м. Площадь газона 96 . Найдите длины сторон газона.
I этап:
Составим выражения по данным задачи, пусть a и b –длины сторон, тогда 2(a+b)=40 будет периметр газона, площадь газона выразим как . По данным выражениям составим систему уравнений и найдем решения данной системы.
II этап:
III этап: обе пары чисел удовлетворяют условию задачи.
Ответ: 12 м и 8м
После решения задачи необходимо ещё раз объяснить ход решения и поинтересоваться у учащихся, понятно ли им данное решение. Так же необходимо заметить, что в некоторых случаях целесообразно создавать геометрические модели для лучшего восприятия условия задачи. Чаще всего такие модели составляются к задачам на движение, которые нам еще предстоит решать.
Закрепление материала
Выполнение заданий на карточках:
Задача 2. Гипотенуза прямоугольного треугольника равна 13 см. Один из катетов на 7 см больше другого. Найдите катеты прямоугольного треугольника.
I этап:
Пусть катеты равны x и y, составляем 1 уравнение. По теореме Пифагора составляем 2 уравнение. Методом подстановки:
II этап:
III этап : По смыслу задачи пара чисел -5 и -12 не могут быть решением системы
Ответ: 12 см и 5 см.
Взаимопроверка решения задачи в парах. После этого решение проецируется на экран.
Задача 3. Произведение двух положительных чисел равно 96. Одно из них на 4 больше другого. Найдите эти числа.
I этап:
Пусть 1 число – x, 2 число – у.
x>0 и y>0
II этап:
III этап: По смыслу задачи исключаем числа – 8 и — 12
Ответ: 12 и 8.
Также взаимопроверка в парах.
Теперь решим задачу №7.2 коллективно.
Расстояние между двумя пунктами по реке составляет 14 км. Лодка проходит этот путь по течению за 2 часа, против течения – за 2 часа 48 минут. Найдите скорость лодки в стоячей воде и скорость течения реки.
Решение:
I этап:
Вспомним уравнение прямолинейного равномерного движения:
S – расстояние,
V – скорость,
T – время.
Переведем 2 часа 48 минут в часы, это составит
Пусть x км/ч – скорость лодки в стоячей воде, y км/ч – скорость течения реки. Вспоминаем движение по течению и против течения реки. Составим математическую модель.
Составим таблицу:.
S, км
V, км/ч
T, ч
По течению
14
Против течения
14
II этап:
Решим полученную систему.
III этап:
Ответ: 6 км/ч; 1 км/ч.
Подведение итогов занятия
1.Обсуждение успешности достижения целей занятия.
2.Оценивание работы учащихся
Разъяснение дом. задания — №№ 7.6 и 7.12
infourok.ru
Решение задач составлением систем линейных уравнений с двумя неизвестными
Розробка уроку з алгебри для 7 класу з теми: «Розв’язування задач за допомогою систем лінійних рівнянь з двома невідомими» з застосуванням елементів здоров’єзберігаючих технологій, мета уроку – формування навичок розв’язування задач за допомогою систем рівнянь, розвиток критичного мислення, ділової активності та зацікавленості учнів у збереженні свого здоров’я.
Разработка урока алгебры для 7-го класса по теме:
«Решение задач составлением систем линейных уравнений»
Тема урока. Решение задач составлением систем линейных уравнений с двумя неизвестными.
Задачи урока. Ознакомить учащихся с решением задач составлением систем линейных уравнений с двумя неизвестными; формировать навыки решения задач составлением систем уравнений; развивать критическое мышление; активизировать деятельность учащихся; развивать интерес к своему организму и способам сохранения здоровья, пропагандировать здоровый образ жизни.
Оборудование. Компьютер, проектор, плакаты с формулами.
Тип урока. Урок усвоения новых знаний.
Эпиграф к уроку. «Здоровье – не все,
но и все без здоровья – ничто»
Сократ
Ход урока.
Организационный момент.
Разминка:
1) Упражнение «Белая ворона» (что лишнее?) Текст на экране:
а) «Система, график, переменная, решение, общение »;
б) «Показатель, многочлен, степень, гребень »;
в) « Равенство, уравнение, предложение, тождество».
г) «Число, значение, лечение, формула, задача»
«Собери формулы». Установите соответствие между выражениями. (Учащиеся объединены в три группы)
По команде учителя ученики из каждой группы по одному подходят к соответствующей доске и составляют формулу (какая команда быстрее…).
На трех досках в две колонки записаны на цветных листах выражения:
(а + в)2 | а3 + в3 |
(а + в)(а2 – а в + в2) | (а – в)2 |
(а + в)3 | (а — в)(а2 + а в + в2) |
а3— 3а2в + 3ав2 — в3 | (а — в) (а + в) |
а2 – 2ав +в2 | (а — в)3 |
а3 — в3 | а2 + 2ав + в2. |
а2 — в2 | а3 +3а2в + 3ав2 +в3 |
3) Найдите пары тождественно равных выражений: (на экране цветные прямоугольники с выражениями — таблица)
1) а2 + 10а + 25 | 5) (1 – а)2 | 9) 49 а2 |
2) (а + 7) (7– а) | 6) (а 3)( 3а) | 10) (а 3) (а+3) |
3) а2 2а + 1 | 7) (5 + а)2 | 11) 8 – а3 |
4) а2 9 | 8) (2–а)(4+2а+а2 ) | 12) а2 6а + 9 |
На уроках применяю элементы хромотерапии.
С этой целью на уроке использую карточки, таблицы, изображение фигур на компьютере определенных цветов (в зависимости от этапа урока), что влияет на физическое и психическое состояние:
синий цвет снимает головную боль, (расслабляющий) красный – повышает работоспособность, (стимулирующий) желтый – улучшает настроение, (укрепляющий) зеленый цвет используют для коррекции зрения (тонизирующий)
Следующее упражнение учащиеся выполняют стоя. (Режим динамических поз на уроке – по необходимости ученик и самостоятельно может, не мешая, изменит позу…)
4) Является ли пара чисел: (3; -2), (8; 6), (3,5; 1,5), (7; -2)
решением системы двух уравнений
х + у = 5;
х – у = 2? (условие на цветном экране)
(если «да» учащиеся поднимают руки и тянутся вверх на носочках, если «нет» — опускают руки вниз, расслабляются)
5) Ученик, который заботится о своем здоровье, должен правильно питаться.
На экране красочная таблица: «Разговор о правильном питании» и условие следующей задачи:
В день можно съедать не более 1/10кг сладостей и сахара, дневная норма потребления хлеба составляет 1/5кг, масла (сливочного и растительного) – 1/8кг. Сколько граммов сладостей, хлеба, масла может съедать в день ученик? (каждая группа отвечает на один вопрос).
II. Актуализация опорных знаний (этап вызова) 1) Какие способы решения систем двух линейных уравнений вам известны?
2) Решить задачу: В поясничном, крестцовом и копчиковом отделах позвоночника позвонков поровну. В грудном отделе их на семь больше, чем в поясничном, а шейном отделе – на пять меньше, чем в грудном. Сколько позвонков в каждом отделе позвоночника, если всего их 34?
«Минутка здоровья» Напомнить учащимся о правильной осанке: “Что такое осанка? Осанка – это привычная поза спокойно стоящего или сидящего человека. Плохая, неправильная осанка приносит вред здоровью: нарушает работу внутренних органов. А как некрасиво выглядит человек, у которого плохая осанка. Правильная осанка не только делает фигуру стройной, но и придает человеку уверенность в себе, бодрость, жизнерадостность”. Поэтому необходимо вырабатывать правильную осанку: опустить плечи, соединить лопатки, поднять подбородок, втянуть живот, и следить за своей осанкой в течение урока. (На экране цветные плакаты с изображением позы стоящего и сидящего человека).
НЕПРАВИЛЬНО ПРАВИЛЬНО
А теперь вернемся к задаче. Учащиеся предлагают решить задачу с помощью составления уравнения, так как легко все неизвестные выразить через одну переменную, решают коллективно с записью на доске.
III. Мотивация учебной деятельности.
Продолжим разговор о правильном питании. Рассмотрим следующую задачу: Одно из чисел, соответствующее суточной потребности витамина В1, на 0,3 больше другого, соответствующего суточной потребности – В2. 60º/0
большего числа на 0,03 больше, чем 700/0 меньшего числа. Найдите эти числа
и узнайте, какова суточная потребность организма в витаминах В1 и В2 в миллиграммах.
Дефицит витамина В1 может привести к нарушению обмена углеводов, и как следствие к болезням. Витамин В2 отвечает за состояние зрения. На экране условие задачи, цветная таблица о витаминах и продуктах, в которых они содержатся.
Прочитаем еще раз условие задачи и подумаем, как ее решить. Очевидно, что довольно трудно решить задачу уравнением, выражая неизвестные, через одну переменную, так как же решить эту задачу рациональным способом? Это вы сможете сделать, изучив новую тему.
IV. Сообщение темы и задач урока.
V. Изучение нового материала. (Этап осмысления)
1. Работа с учебником. Прочитать п. 29 стр. 249, выделить главное. Ответьте на вопросы (предварительно, обсудив в группах, прием — «вертушка» учащиеся могут переходить из одной группы в другую):
Приведите пример линейного уравнения с двумя переменными.
Что такое решение уравнения с двумя переменными?
Сколько решений может иметь система двух линейных уравнений с двумя переменными?
Сколько решений может иметь система двух уравнений первой степени с двумя переменными?
Составьте несколько разных моделей задачи: найдите два числа, если
их сумма равна 5, а разность равна 3.
2. Решение упражнений № 1158, 1159 (устно).
3. Решение задачи (образец записи решения) № 1185(коллективно).
VI. Физкультминутка (в зависимости от номера урока по расписанию)
VII. Закрепление новых знаний и умений.
1. № 1178 (комментированное решение, образец записи решения задачи)
2. Вернемся теперь к задаче о витаминах и решим ее с помощью составления системы уравнений с записью на доске и в тетрадях.
3. Работа в группах. Каждая группа получает задание – решить задачу.
Для 1-й группы: Дефицит железа сказывается на росте и устойчивости к инфекциям. От железа зависит содержание гемоглобина – переносчика кислорода ко всем органам. Медь также синтезирует гемоглобин и определяет антиоксидантный потенциал сыворотки крови.
Задача. Сумма двух чисел равна 11. 600/0 большего числа на 2,7 больше, чем 700/0 меньшего числа. Найдите эти числа и узнайте, какова суточная потребность организма в железе и меди в миллиграммах.
Для 2-й группы:
Таблица: «Курение – одна из вреднейших привычек»
Задача. Сумма двух чисел равна 18. Если большее из этих чисел
умножить на два, а меньшее умножить на четыре, то их сумма будет равна 48. Найдите эти числа. Меньшее число покажет вам, сколько минут жизни
забирает одна сигарета.
Для 3-й группы:
Задача. Сумма двух чисел равна 82. Если первое число увеличить в 4,5 раза, а ко второму прибавить 28, то их сумма будет равна 180. Найдите эти числа, и вы узнаете, сколько лет полноценной жизни забирает табак у курильщиков и сколько лет в среднем живут курящие мужчины.
(Представитель каждой группы знакомит весь класс с условием и записывает решение задачи на доске)
VIII. Этап рефлексии.
Поставьте в тетрадях буквы, соответствующие вашему восприятию материала урока.
На светло- синем экране:
А) все понятно, интересно;
Б) все понятно, но не интересно;
В) не все понятно;
Г) почти ничего не понятно;
Д) ничего не понятно;
Ж) кроме, математических знаний получил полезную информацию;
З) ничего полезного.
IX. Подведение итогов. Мотивация выставления оценок.
X. Комментированное домашнее задание: п. 29(читать, ответить на вопросы к пункту)
I и II уровень №1164, 1165, 1174;
III уровень №1184, 1187, 1189;
IV уровень 1191, 1195, (творческое задания, по данным на карточках составить задачу).
Карточка № 1. (Для первой группы) На карточке плакат: «Никотин — яд!» — убедите в этом своих близких, если они курят.
«Никотин – один из самых опасных ядов растительного происхождения. Птицы (воробьи, голуби) погибают, если к их клюву всего, лишь поднести стеклянную палочку, смоченную никотином. Кролик погибает от 1/4 капли никотина, собака – от 1/2 капли. Для человека смертельная доза никотина составляет от 50 до 100 мг, или 2-3 капли. Именно такая доза поступает ежедневно в кровь после выкуривания 20-25 сигарет (в одной сигарете содержится примерно 6-8 мг никотина, из которых 3-4 мг попадает в кровь). Курильщик не погибает потому, что доза вводится постепенно, не в один прием. К тому же, часть никотина нейтрализует формальдегид – другой яд, содержащийся в табаке. В течение 30 лет такой курильщик выкуривает примерно 20000 сигарет, или 160кг табака, поглощая в среднем 800г никотина».
Карточка №2.(Для второй группы) На карточке плакат: «Никотин яд!» «Сломай сигарету, пока сигарета не сломала тебя!»
«Врачи также выяснили, что рост числа курящих параллельно увеличивает количество опасных болезней. Начиная с начала 1960 годов, стали публиковать в газетах и журналах результаты научных исследований. И люди ужаснулись! Оказывается, если человек курит в день от 1 до 9 сигарет, то сокращает свою жизнь (в среднем) на 4, 6 года по сравнению с некурящими. Если курит от 10 до 19 сигарет, то на 5, 5 года; если выкуренных 20 до 39 сигарет – более 7 лет».
Карточка № 3.(Для третьей группы) На карточке плакат: «Если человек курит…» — статистические данные о болезнях курильщиков.
«Длительно и много курящие в 13 раз чаще заболевают стенокардией, в 12 — инфарктом миокарда, в 10 раз — язвой желудка и в 30 раз от тяжелейшего заболевания легких».
gigabaza.ru
