Графическое решение систем неравенств
Здесь мы рассмотрим графические решения нескольких систем неравенств. Умение решать такие задачи очень помогает впоследствии, при освоении задач с параметрами.
Задача 1. Найти площадь фигуры, задаваемой на плоскости множеством решений системы неравенств:
Перепишем иначе:
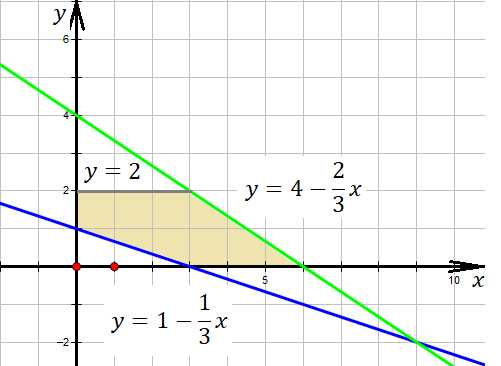
Рисунок 1
Нас интересует только правая полуплоскость (), область, лежащая выше оси (), но ниже прямой () – проведена серым цветом.
Теперь построим графики первых двух функций. Возьмем в решения область ниже зеленой прямой , но выше синей .
Определим площадь полученной фигуры (залита бежевым) по формуле Пика:
Ответ: 7,5
Задача 2. Найти площадь фигуры, задаваемой на плоскости множеством решений системы неравенств:
Перепишем иначе:
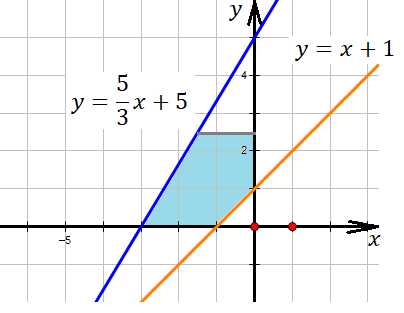
Рисунок 2
Нас интересует только левая полуплоскость (), область, лежащая выше оси (), но ниже прямой () – проведена серым цветом.
Теперь построим графики первых двух функций. Возьмем в решения область выше рыжей прямой , но ниже синей .
Определим площадь данной фигуры путем разбиения ее на простейшие геометрические фигуры: две трапеции. У левой трапеции основания 0,5 и 2, высота 2,5, площадь ее равна
У правой основания 2,5 и 1,5 (она на боку лежит), а высота равна 1. Ее площадь
Общая площадь фигуры равна 5, 125.
Ответ: 5, 125.
Задача 3. Изобразить на плоскости множество решений системы неравенств. Найти площадь замкнутой части получившейся фигуры:
Вместо исходной системы можем записать совокупность из двух:
и
Первая система имеет решения, но область решений не замкнута.
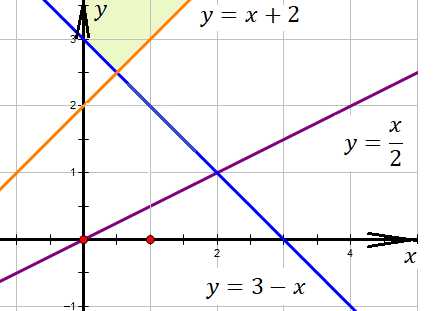
Рисунок 3
Вторая дает нам искомую замкнутую область:
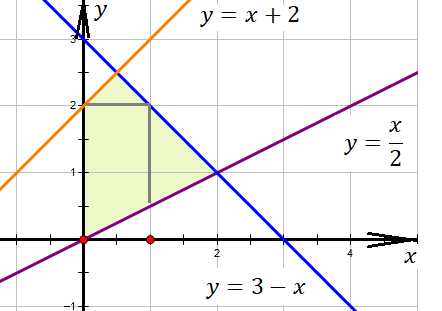
Рисунок 4
Определим площадь данной фигуры путем разбиения ее на простейшие геометрические фигуры: два треугольника и трапецию. У трапеции основания 1,5 и 2, высота 1, площадь ее равна
У верхнего малого треугольника основание 1, а высота равна 0,5. Его площадь
У правого треугольника основание 1,5, высота – 1, его площадь
Общая площадь фигуры равна 2, 75.
Ответ: 2,75.
Задача 4. Изобразить на плоскости множество решений системы неравенств. При каком значении площадь получившейся фигуры ?
Первое двойное неравенство задает две окружности и область между ними. Две прямые вырезают сектор, показанный на рисунке фиолетовым цветом. Для рисунка был выбран радиус , на самом деле он может быть любым – собственно, его и нужно определить.
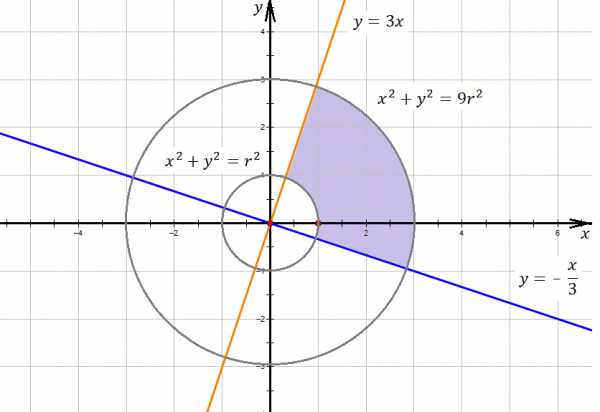
Рисунок 5
Так как прямые перпендикулярны (это понятно по их коэффициентам наклона, их произведение – (-1)), то необходимо определить четверть площади кольца.
По условию, эта площадь равна :
Ответ: .
Задача 5. Изобразить на плоскости множество решений системы неравенств. При каком значении площадь получившейся фигуры ?
Снова имеем окружность, центр ее лежит на прямой , поэтому она вписана в первый координатный угол (квадрант). Причем по условию, нас интересует внешняя часть этой окружности.

Рисунок 6
Из этой внешней части мы возьмем в решения область над осью (), а по оси нас интересует полоса от 0 до центра окружности.
Нас интересует маленький, закрашенный зеленым, уголок. Его площадь можно найти как разность площади треугольника и сектора круга. Этот сектор – часть круга. Поэтому
По условию, эта площадь равна .
Определим :
Ответ: .
easy-physic.ru
калькулятор системы неравенств онлайн
Вы искали калькулятор системы неравенств онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и решить графически систему неравенств онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «калькулятор системы неравенств онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как калькулятор системы неравенств онлайн,решить графически систему неравенств онлайн,решить систему неравенств графически онлайн,решить систему неравенств онлайн графически. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и калькулятор системы неравенств онлайн. Просто введите задачу в окошко и нажмите «решить» здесь или введите в окно ввода ниже свой запрос (например, решить систему неравенств графически онлайн).
Где можно решить любую задачу по математике, а так же калькулятор системы неравенств онлайн Онлайн?
Решить задачу калькулятор системы неравенств онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на этой странице.
www.pocketteacher.ru
Решение систем неравенств графическим способом при помощи программы GeoGebra
Просмотр содержимого документа
«Решение систем неравенств графическим способом при помощи программы GeoGebra»
Решение систем неравенств графическим способом при помощи программы GeoGebra
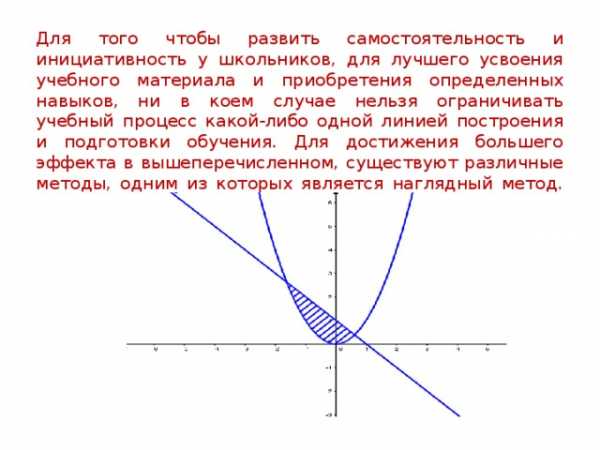
Для того чтобы развить самостоятельность и инициативность у школьников, для лучшего усвоения учебного материала и приобретения определенных навыков, ни в коем случае нельзя ограничивать учебный процесс какой-либо одной линией построения и подготовки обучения. Для достижения большего эффекта в вышеперечисленном, существуют различные методы, одним из которых является наглядный метод.
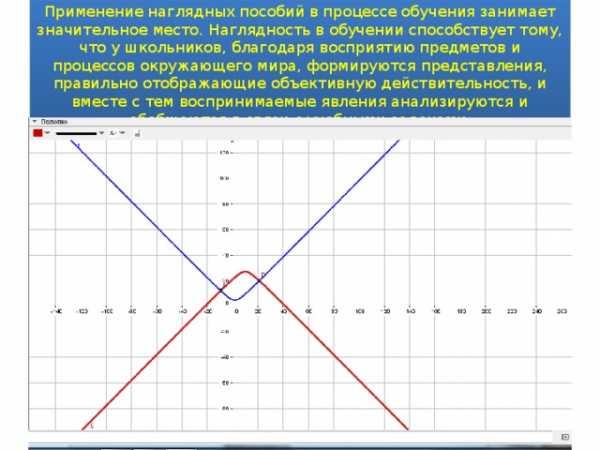
Применение наглядных пособий в процессе обучения занимает значительное место. Наглядность в обучении способствует тому, что у школьников, благодаря восприятию предметов и процессов окружающего мира, формируются представления, правильно отображающие объективную действительность, и вместе с тем воспринимаемые явления анализируются и обобщаются в связи с учебными задачами.

Решение задач является важнейшим видом учебной деятельности, в процессе которой учащимися усваивается математическая теория и развиваются логическое мышление и творческие способности. Развитие творческих способностей учащихся при обучении математики осуществляется более эффективно при вовлечении в их деятельность различных компьютерных программ и математических пакетов. Одним из таких математических пакетов является — GEOGEBRA.
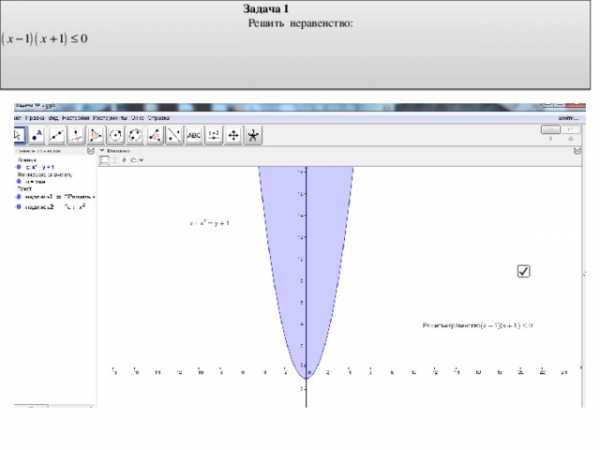
Задача 1
Решить неравенство:
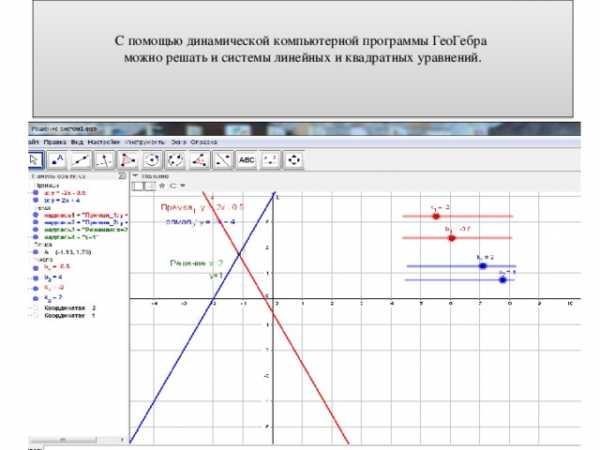
С помощью динамической компьютерной программы ГеоГебра можно решать и системы линейных и квадратных уравнений.

Методика работы с динамической компьютерной программы ГеоГебра. Алгоритм выполнения. 1. Открываем ГеоГебру двойным нажатием левой клавишей, появляется окно
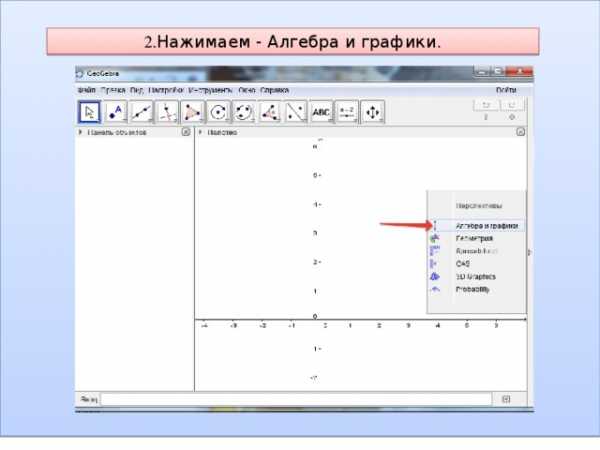
2. Нажимаем — Алгебра и графики.
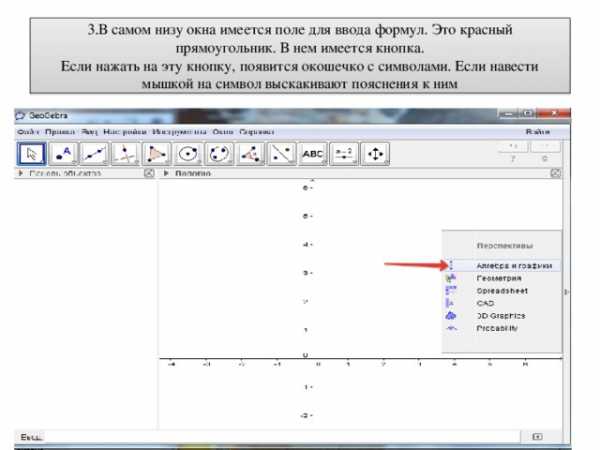
3.В самом низу окна имеется поле для ввода формул. Это красный прямоугольник. В нем имеется кнопка. Если нажать на эту кнопку, появится окошечко с символами. Если навести мышкой на символ выскакивают пояснения к ним
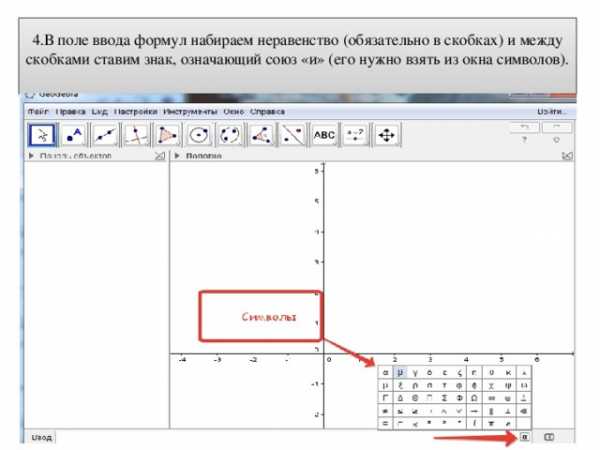
4.В поле ввода формул набираем неравенство (обязательно в скобках) и между скобками ставим знак, означающий союз «и» (его нужно взять из окна символов).
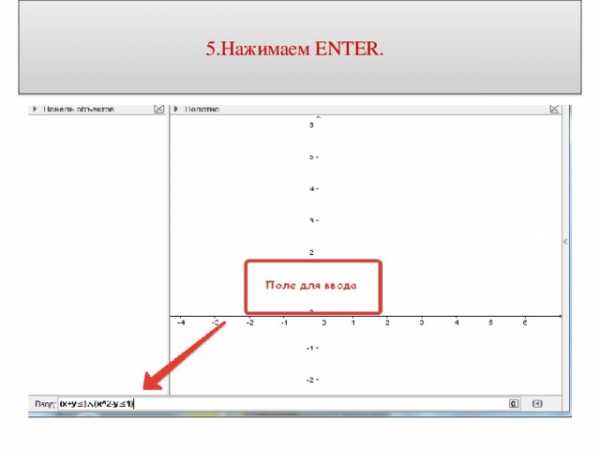
5.Нажимаем ENTER.
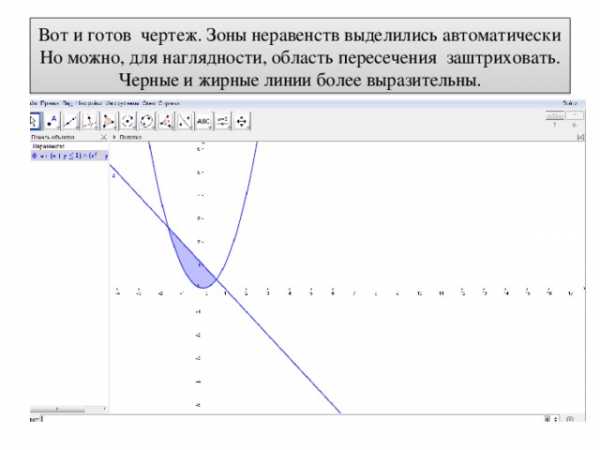
Вот и готов чертеж. Зоны неравенств выделились автоматически Но можно, для наглядности, область пересечения заштриховать. Черные и жирные линии более выразительны.
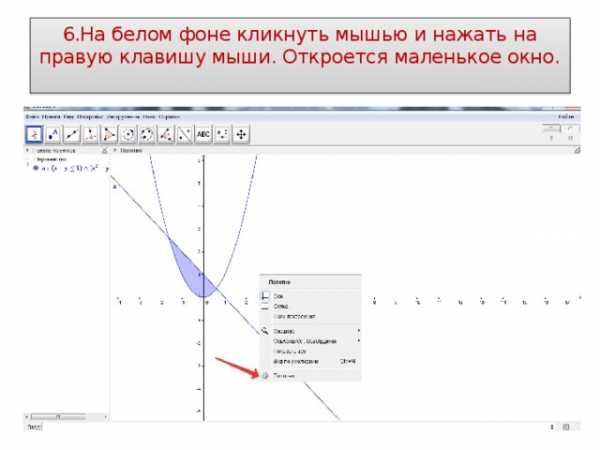
6.На белом фоне кликнуть мышью и нажать на правую клавишу мыши. Откроется маленькое окно.

7.Нажимаем Полотно. В открывшемся окне ставим галочку против Полужирный и нажав против Стиль линии, выбираем нужный вид осей координат.

8.Теперь щелкаем мышкой внутри закрашенной области и жмем правую клавишу мыши.
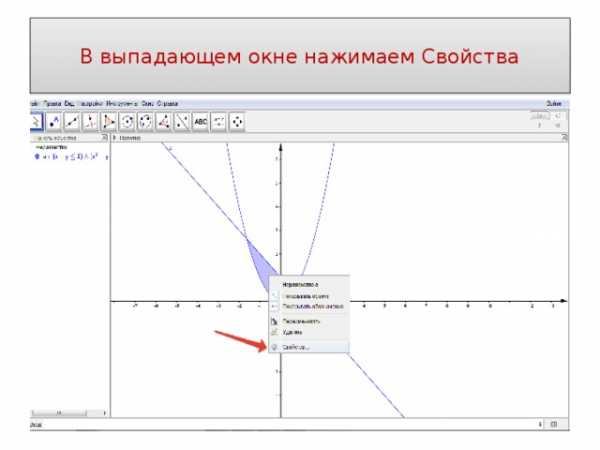
В выпадающем окне нажимаем Свойства
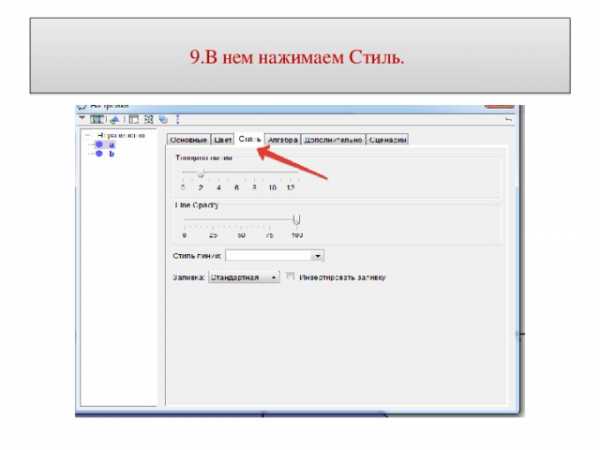
9.В нем нажимаем Стиль.
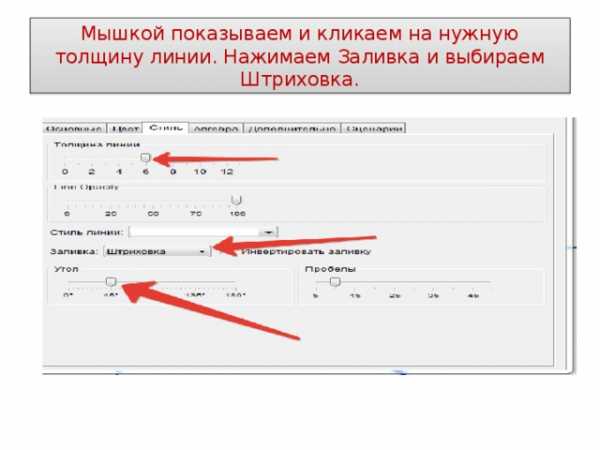
Мышкой показываем и кликаем на нужную толщину линии. Нажимаем Заливка и выбираем Штриховка.


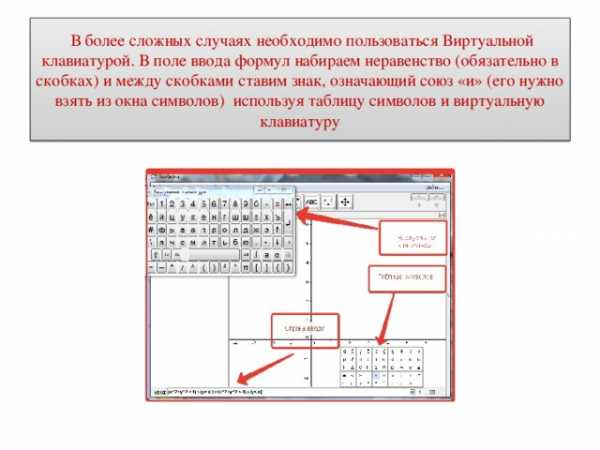
В более сложных случаях необходимо пользоваться Виртуальной клавиатурой. В поле ввода формул набираем неравенство (обязательно в скобках) и между скобками ставим знак, означающий союз «и» (его нужно взять из окна символов) используя таблицу символов и виртуальную клавиатуру

Заключение.
В моей работе созданы компьютерные материалы по темам: «Неравенства с одной переменной второй степени » и «Уравнения и неравенства с двумя переменными» с использованием компьютерной программы GEO GEBRA.
Используя эти материалы можно улучшить качество проведения уроков.
Спасибо за внимание!
multiurok.ru
