5. Системы линейных уравнений
Раздел 5. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Системы линейных уравнений
Основные понятия
Системой линейных алгебраических уравнений, содержащей т уравнений и п неизвестных, называется система вида
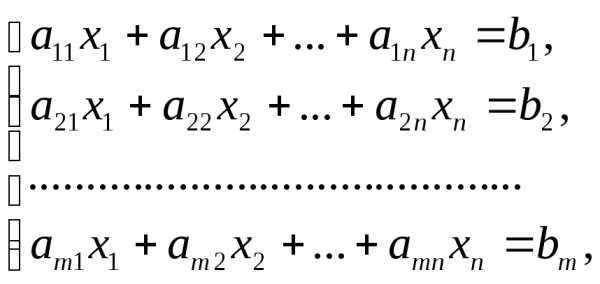
где числа аij, i=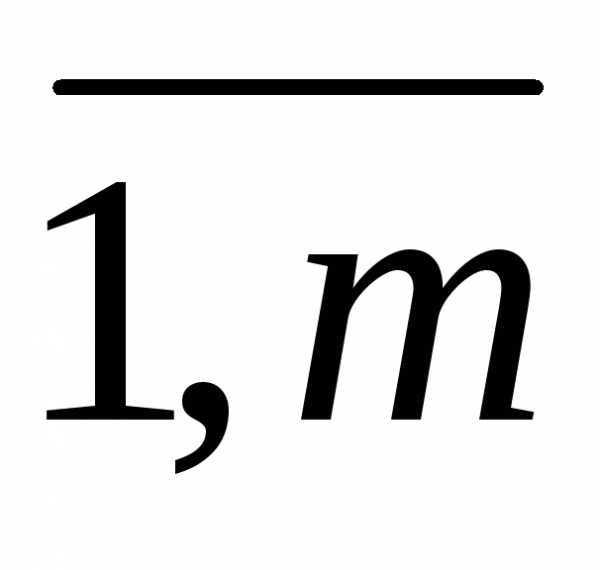 ,j=
,j=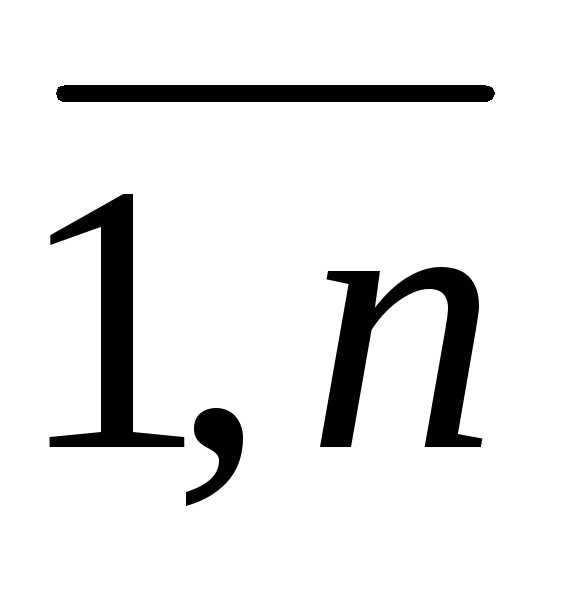 называются коэффициентами системы, числа bi – свободными членами. Подлежат нахождению числа
называются коэффициентами системы, числа bi – свободными членами. Подлежат нахождению числа
Такую систему удобно записывать в компактной матричной форме .
Здесь А – матрица коэффициентов системы, называемая основной матрицей:
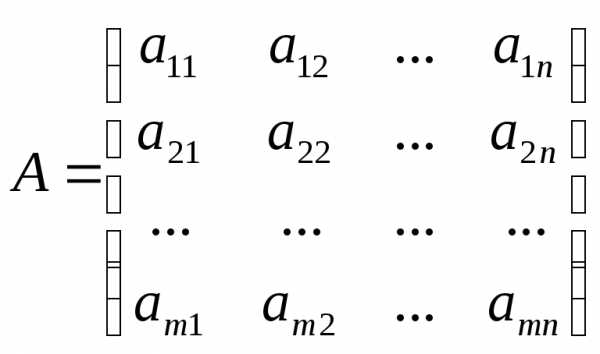 ,
,
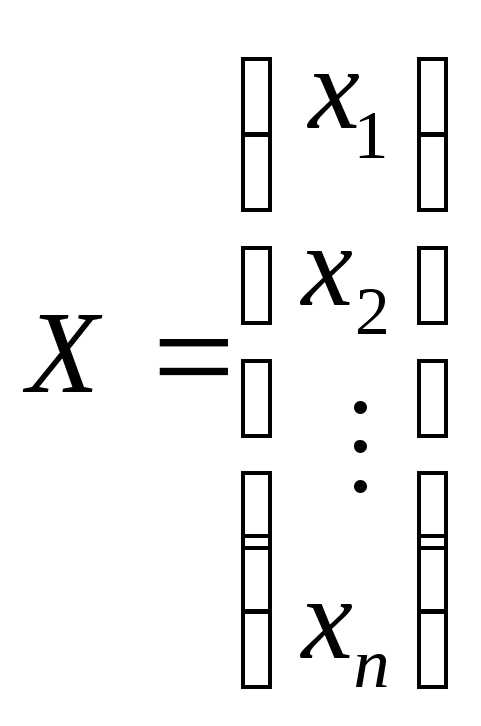 –вектор-столбец
из неизвестных хj,
–вектор-столбец
из неизвестных хj, 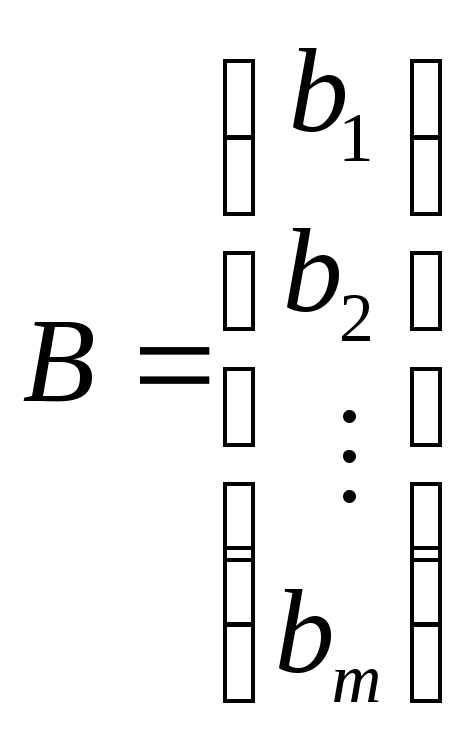 – вектор-столбец из свободных членовbi.
– вектор-столбец из свободных членовbi.
Расширенной матрицей системы называется матрица  системы, дополненная столбцом свободных
членов
системы, дополненная столбцом свободных
членов
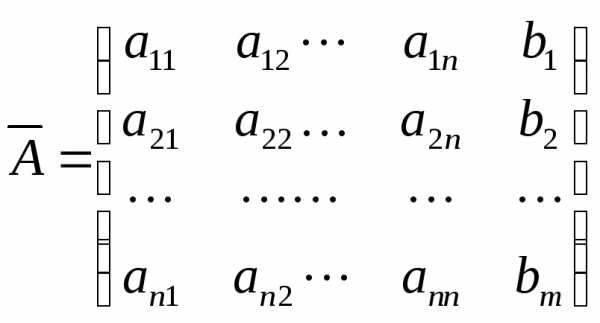
Решением системы
называется п значений неизвестных х1=с1,
х2=с2,
…, хп=сп, при подстановке которых все уравнения
системы обращаются в верные равенства.
Всякое решение системы можно записать
в виде матрицы-столбца 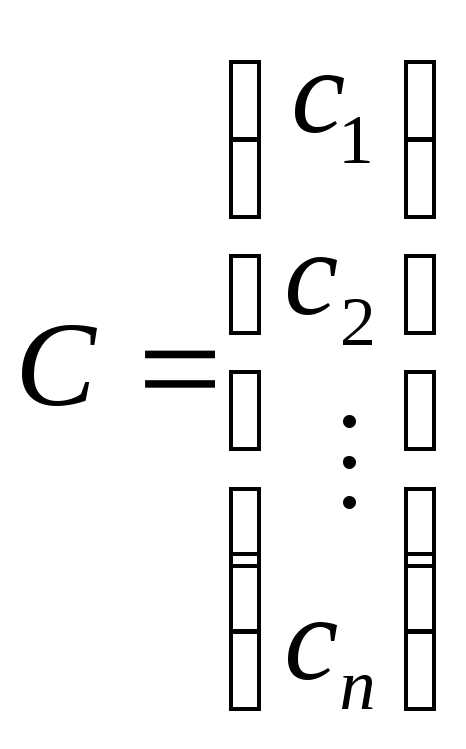 .
.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется
Решить систему – это значит выяснить, совместна она или не совместна. Если система совместна, то найти ее общее решение.
Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.
Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.
Система линейных уравнений называется однородной, если все свободные члены равны нулю:
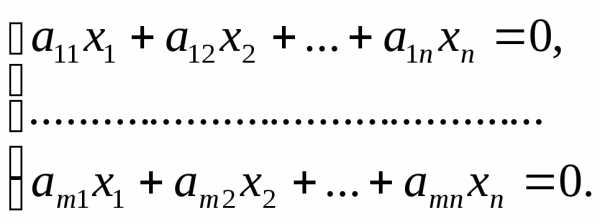
Однородная система всегда совместна, так как х1=х2=…=х п=0 является решением системы. Это решение называется нулевым или тривиальным.
Решение систем линейных уравнений
Пусть дана произвольная система т линейных уравнений с п неизвестными
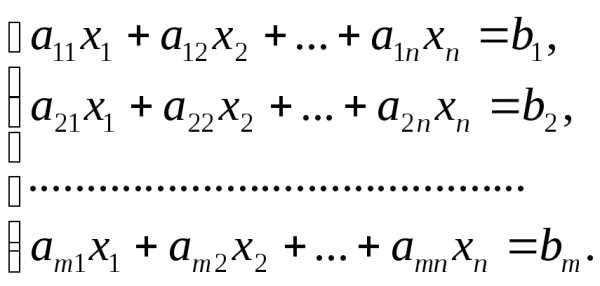
Теорема 1 (Кронекера-Капелли). Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы равен рангу основной матрицы.
Теорема 2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
Теорема 3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесконечное множество решений.
П р и м е р. Исследовать
на совместность систему 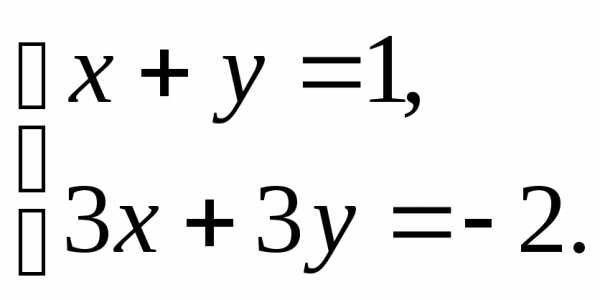
Решение. 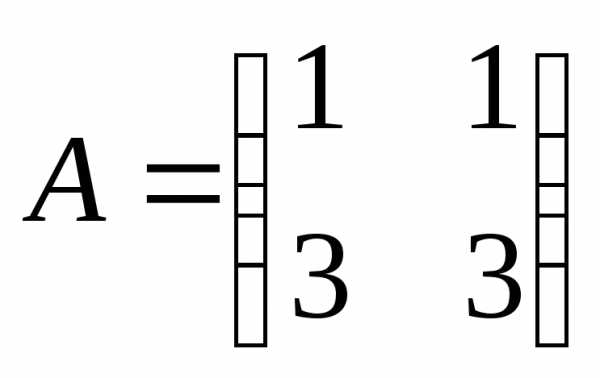 ,r(A)=1;
,r(A)=1; 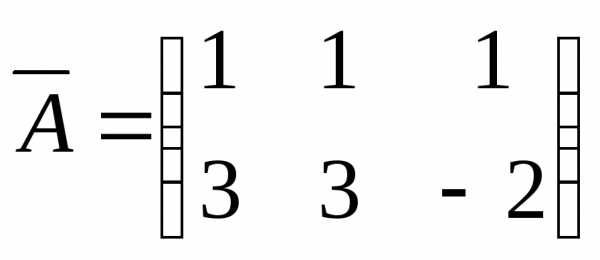 , r(
, r( )=2,
)=2, 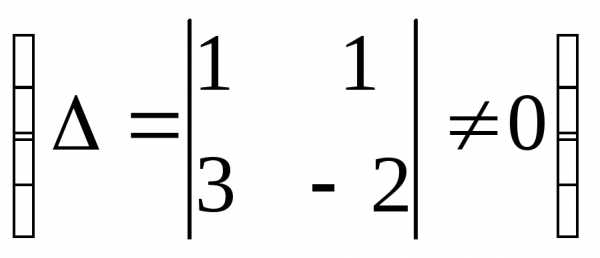 .
.
Таким образом, r(A) r( ),
следовательно, система несовместна.
),
следовательно, система несовместна.
Решение невырожденных систем линейных уравнений. Формулы Крамера
Пусть дана система п линейных уравнений с п неизвестными
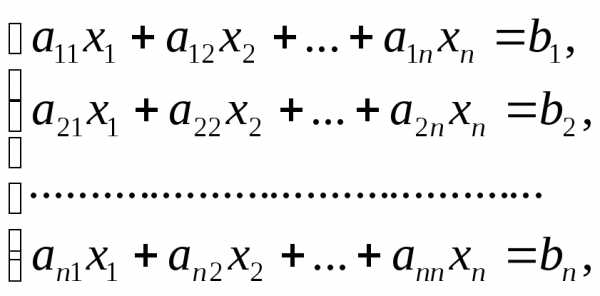
или в матричной форме А∙Х=В.
Основная матрица А такой системы – квадратная. Определитель этой матрицы называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной.
Найдем решение данной системы уравнений в случае ∆0. умножив обе части уравнения А∙Х=В слева на матрицу А1, получим А1∙ А∙Х= А1∙В. Поскольку А1∙ А=Е и Е∙Х=Х, то Х= А1∙ В. Данный способ решения системы называют матричным.
Из матричного
способа вытекают формулы
Крамера 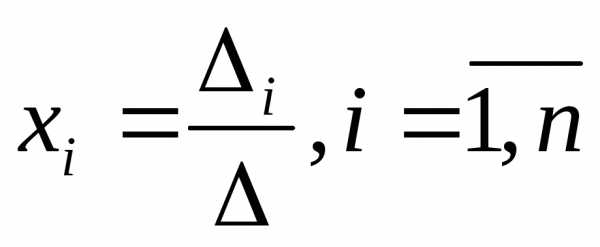 ,
где ∆ – определитель основной матрицы
системы, а ∆i – определитель, полученный из определителя
∆ путем замены
,
где ∆ – определитель основной матрицы
системы, а ∆i – определитель, полученный из определителя
∆ путем замены
П р и м е р. Решить
систему 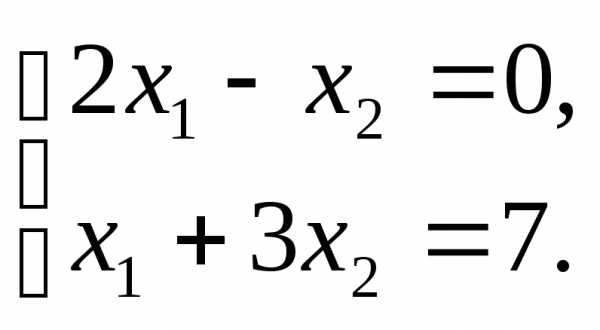
Решение. 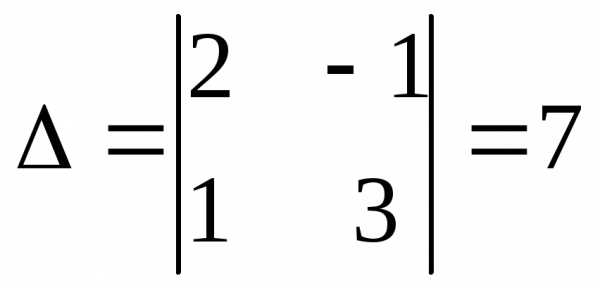 ,
70,
,
70, 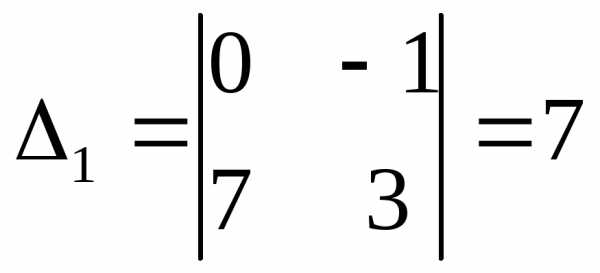 ,
,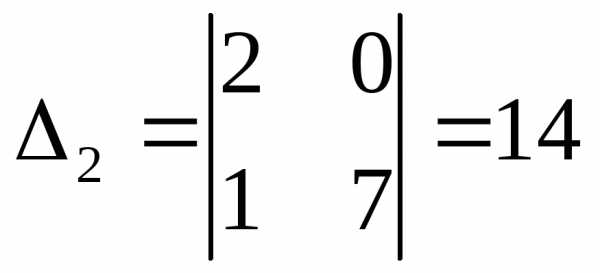 .
Значит,х1=
.
Значит,х1=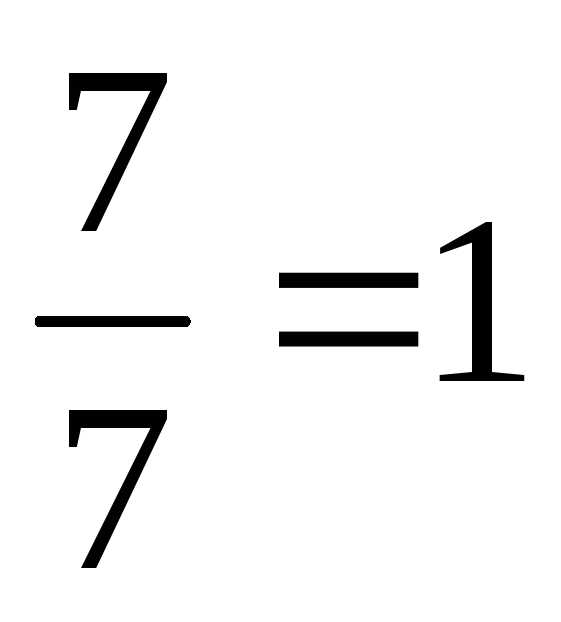 ,
х2=
,
х2=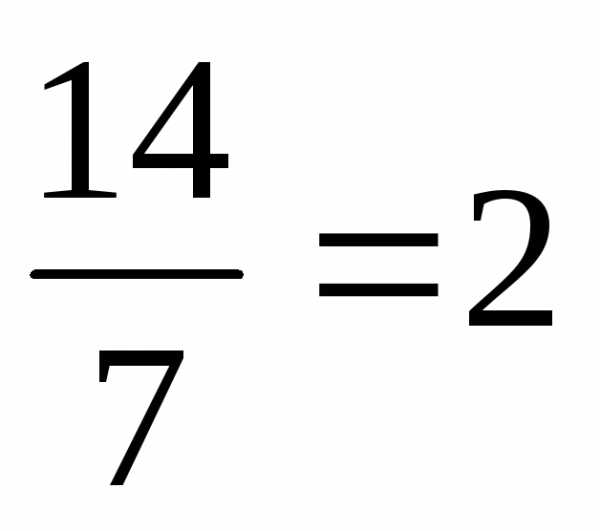 .
.
Решение систем линейных уравнений методом Гаусса
Метод Гаусса состоит в последовательном исключении неизвестных.
Пусть дана система уравнений
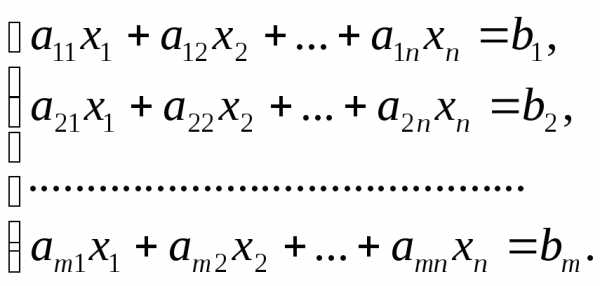
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.
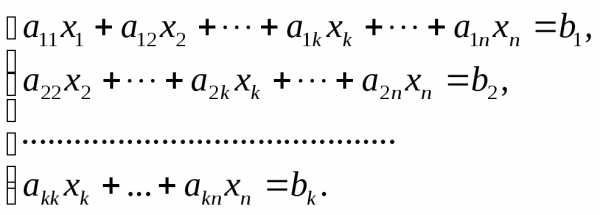
где k ≤ п, аii
0, i=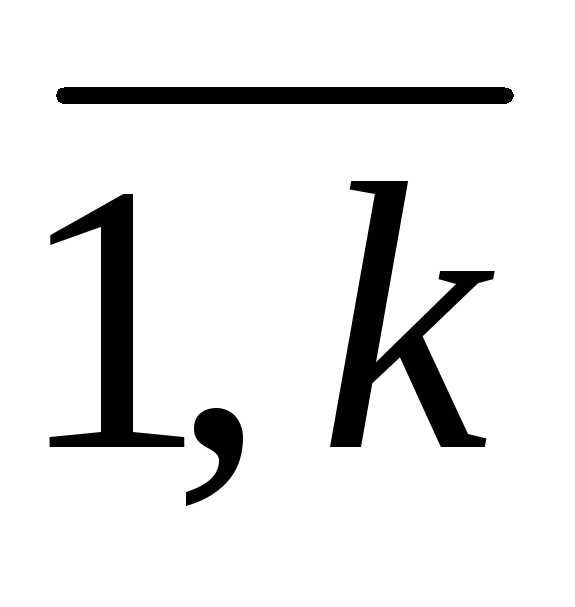 . Коэффициенты аii называются главными элементами системы.
. Коэффициенты аii называются главными элементами системы.
На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.
Замечания:
На практике удобнее работать с расширенной матрицей системы, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент а11 был равен 1(уравнения переставить местами, либо разделить на а111).
П р и м е р. Решить
систему методом Гаусса 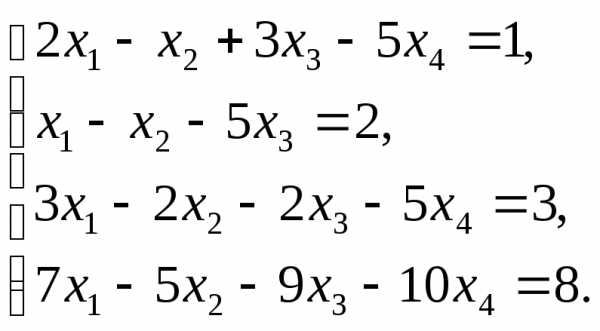
Решение. В результате элементарных преобразований над расширенной матрицей системы
 ~
~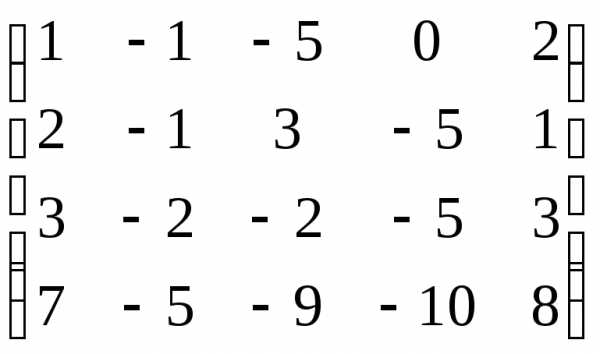 ~
~ ~
~ ~
исходная система
свелась к ступенчатой: 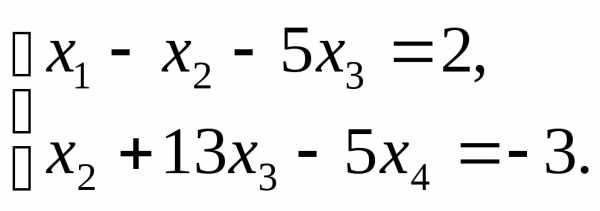
Поэтому общее решение системы: x2=5x4 13x3 3; x1=5x4 8x3 1.
Если положить, например, х3=х4
Систем однородных линейных уравнений
Пусть дана система линейных однородных уравнений
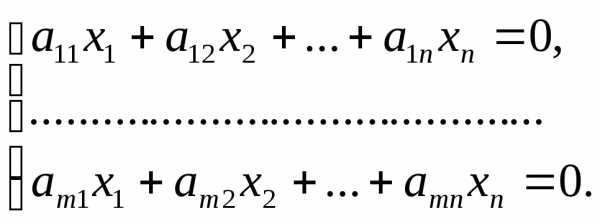
Очевидно, что однородная система всегда совместна, она имеет нулевое (тривиальное) решение.
Теорема 4. Для того, чтобы система однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы ранг ее основной матрицы был меньше числа неизвестных, т.е. r<n.
Теорема 5. Для того, чтобы однородная система п линейных уравнений с п неизвестными имела ненулевое решение, необходимо и достаточно, чтобы определитель ее основной матрицы был равен нулю, т.е. ∆=0.
Если система имеет ненулевые решения, то ∆=0.
П р и м е р. Решить
систему 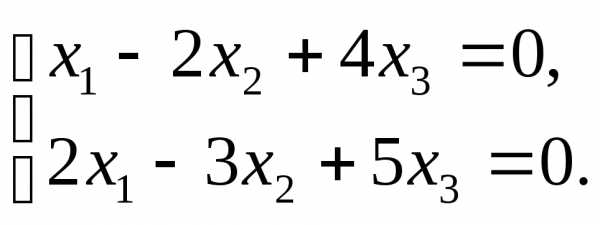
Решение. 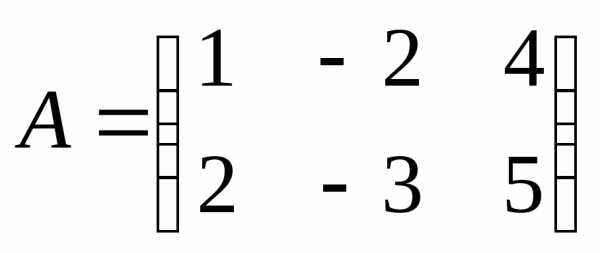 ,r(A)=2
,r(A)=2 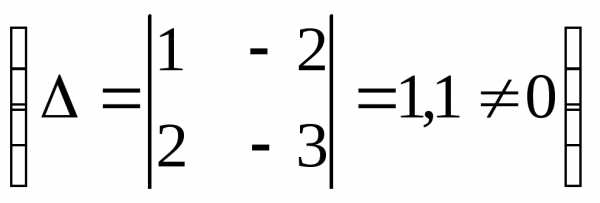 , п=3. Так как r<n, то система
имеет бесконечное множество решений.
, п=3. Так как r<n, то система
имеет бесконечное множество решений.
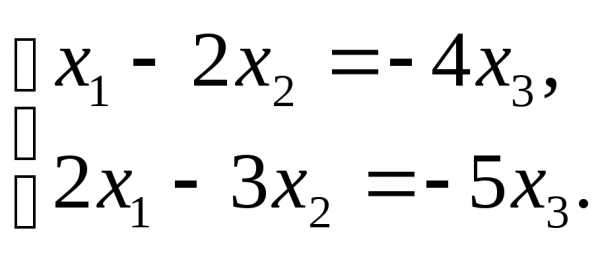
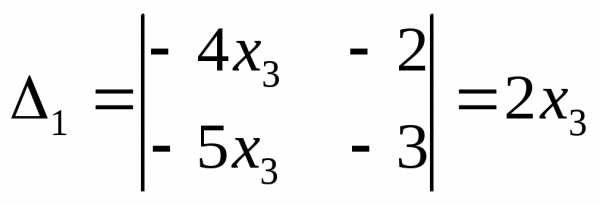 ,
, 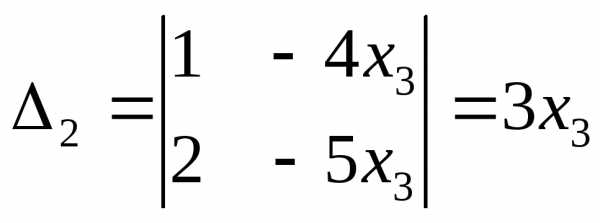 .
Стало быть,х1=
.
Стало быть,х1=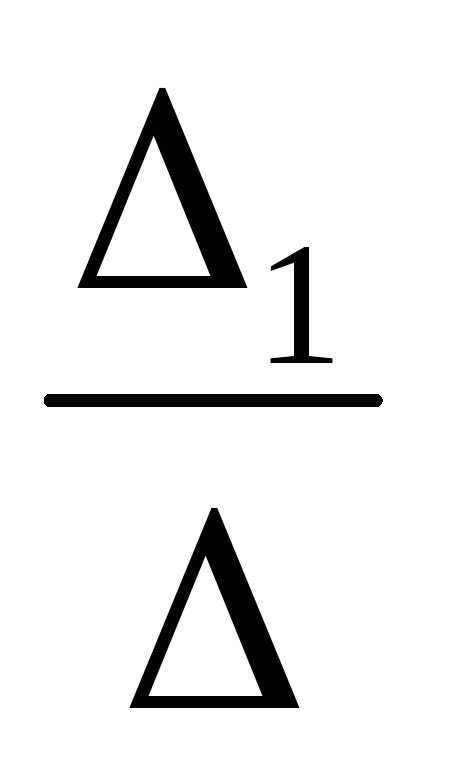 =2х3,
х2=
=2х3,
х2=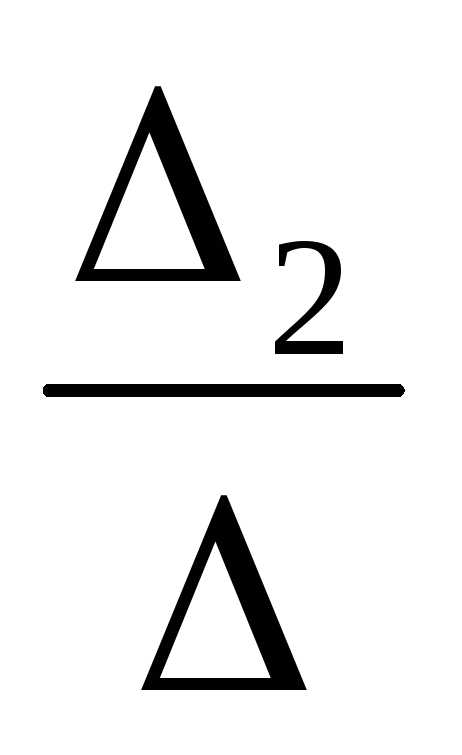 =3х3 – общее решение.
=3х3 – общее решение.
Положив х3=0, получим одно частное решение: х1=0, х2=0, х3=0. Положив х3=1, получим второе частное решение: х1=2, х2=3, х3=1 и т.д.
Вопросы для контроля
Что такое система линейных алгебраических уравнений?
Поясните следующие понятия: коэффициент, свободный член, основная и расширенная матрицы.
Какими бывают системы линейных уравнений? Сформулируйте теорему Кронкера-Капелли (о совместности системы линейных уравнений).
Перечислите и поясните методы решения систем линейных уравнений.
5
studfiles.net
Система линейных уравнений называется определенной если, при решении
Высшая математика » Системы линейных алгебраических уравнений » Основные термины. Матричная форма записи.
Система линейных алгебраических уравнений. Основные термины. Матричная форма записи.
Содержание темы:
- Определение системы линейных алгебраических уравнений. Решение системы. Классификация систем.
- Матричная форма записи систем линейных алгебраических уравнений.
Определение системы линейных алгебраических уравнений. Решение системы. Классификация систем.
Под системой линейных алгебраических уравнений (СЛАУ) подразумевают систему
\begin{equation} \left \{ \begin{aligned} & a_{11}x_1+a_{12}x_2+a_{13}x_3+\ldots+a_{1n}x_n=b_1;\\ & a_{21}x_1+a_{22}x_2+a_{23}x_3+\ldots+a_{2n}x_n=b_2;\\ & \ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots \\ & a_{m1}x_1+a_{m2}x_2+a_{m3}x_3+\ldots+a_{mn}x_n=b_m. \end{aligned} \right. \end{equation}
содержащую $m$ уравнений и $n$ неизвестных ($x_1,x_2,\ldots,x_n$). Прилагательное «линейных» означает, что все неизвестные (их еще называют переменными) входят только в первой степени.
Параметры $a_{ij}$ ($i=\overline{1,m}$, $j=\overline{1,n}$) называют коэффициентами, а $b_i$ ($i=\overline{1,m}$) – свободными членами СЛАУ. Иногда, чтобы подчеркнуть количество уравнений и неизвестных, говорят так «$m\times n$ система линейных уравнений», – тем самым указывая, что СЛАУ содержит $m$ уравнений и $n$ неизвестных.
Если все свободные члены $b_i=0$ ($i=\overline{1,m}$), то СЛАУ называют однородной. Если среди свободных членов есть хотя бы один, отличный от нуля, СЛАУ называют неоднородной.
Решением СЛАУ (1) называют всякую упорядоченную совокупность чисел ($\alpha_1, \alpha_2,\ldots,\alpha_n$), если элементы этой совокупности, подставленные в заданном порядке вместо неизвестных $x_1,x_2,\ldots,x_n$, обращают каждое уравнение СЛАУ в тождество.
Любая однородная СЛАУ имеет хотя бы одно решение: нулевое (в иной терминологии – тривиальное), т.е. $x_1=x_2=\ldots=x_n=0$.
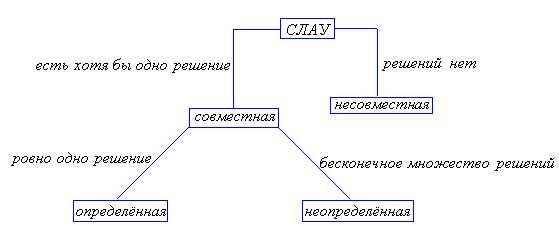
Если СЛАУ (1) имеет хотя бы одно решение, ее называют совместной, если же решений нет – несовместной. Если совместная СЛАУ имеет ровно одно решение, её именуют определённой, если бесконечное множество решений – неопределённой.
Пример №1
Рассмотрим СЛАУ
\begin{equation} \left \{ \begin{aligned} & 3x_1-4x_2+x_3+7x_4-x_5=11;\\ & 2x_1+10x_4-3x_5=-65;\\ & 3x_2+19x_3+8x_4-6x_5=0. \\ \end {aligned} \right. \end{equation}
Имеем систему линейных алгебраических уравнений, содержащую $3$ уравнения и $5$ неизвестных: $x_1,x_2,x_3,x_4,x_5$. Можно, сказать, что задана система $3\times 5$ линейных уравнений.
Коэффициентами системы (2) есть числа, стоящие перед неизвестными. Например, в первом уравнении эти числа таковы: $3,-4,1,7,-1$. Свободные члены системы представлены числами $11,-65,0$. Так как среди свободных членов есть хотя бы один, не равный нулю, то СЛАУ (2) является неоднородной.
Упорядоченная совокупность $(4;-11;5;-7;1)$ является решением данной СЛАУ. В этом несложно убедиться, если подставить $x_1=4; x_2=-11; x_3=5; x_4=-7; x_5=1$ в уравнения заданной системы:
\begin{aligned} & 3x_1-4x_2+x_3+7x_4-x_5=3\cdot4-4\cdot(-11)+5+7\cdot(-7)-1=11;\\ & 2x_1+10x_4-3x_5=2\cdot 4+10\cdot (-7)-3\cdot 1=-65;\\ & 3x_2+19x_3+8x_4-6x_5=3\cdot (-11)+19\cdot 5+8\cdot (-7)-6\cdot 1=0. \\ \end{aligned}
Естественно, возникает вопрос том, является ли проверенное решение единственным. Вопрос о количестве решений СЛАУ будет затронут в соответствующей теме.
Пример №2
Рассмотрим СЛАУ
\begin{equation} \left \{ \begin{aligned} & 4x_1+2x_2-x_3=0;\\ & 10x_1-x_2=0;\\ & 5x_2+4x_3=0; \\ & 3x_1-x_3=0;\\ & 14x_1+25x_2+5x_3=0. \end{aligned} \right. \end{equation}
Система (3) является СЛАУ, содержащей $5$ уравнений и $3$ неизвестных: $x_1,x_2,x_3$. Так как все свободные члены данной системы равны нулю, то СЛАУ (3) является однородной. Несложно проверить, что совокупность $(0;0;0)$ является решением данной СЛАУ. Подставляя $x_1=0, x_2=0,x_3=0$, например, в первое уравнение системы (3), получим верное равенство: $4x_1+2x_2-x_3=4\cdot 0+2\cdot 0-0=0$. Подстановка в иные уравнения делается аналогично.
Матричная форма записи систем линейных алгебраических уравнений.
С каждой СЛАУ можно связать несколько матриц; более того – саму СЛАУ можно записать в виде матричного уравнения. Для СЛАУ (1) рассмотрим такие матрицы:
Матрица $A$ называется матрицей системы. Элементы данной матрицы представляют собой коэффициенты заданной СЛАУ.
Матрица $\widetilde{A}$ называется расширенной матрицей системы. Её получают добавлением к матрице системы столбца, содержащего свободные члены $b_1,b_2,…,b_m$. Обычно этот столбец отделяют вертикальной чертой, – для наглядности.
Матрица-столбец $B$ называется матрицей свободных членов, а матрица-столбец $X$ – матрицей неизвестных.
Используя введённые выше обозначения, СЛАУ (1) можно записать в форме матричного уравнения: $A\cdot X=B$.
Примечание
Матрицы, связанные с системой, можно записать различными способами: всё зависит от порядка следования переменных и уравнений рассматриваемой СЛАУ. Но в любом случае порядок следования неизвестных в каждом уравнении заданной СЛАУ должен быть одинаков (см. пример №4).
Пример №3
Записать СЛАУ $ \left \{ \begin{aligned} & 2x_1+3x_2-5x_3+x_4=-5;\\ & 4x_1-x_3=0;\\ & 14x_2+8x_3+x_4=-11. \end{aligned} \right. $ в матричной форме и указать расширенную матрицу системы.
Решение
Имеем четыре неизвестных, которые в каждом уравнении следуют в таком порядке: $x_1,x_2,x_3,x_4$. Матрица неизвестных будет такой: $\left( \begin{array} {c} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array} \right)$.
Свободные члены данной системы выражены числами $-5,0,-11$, посему матрица свободных членов имеет вид: $B=\left( \begin{array} {c} -5 \\ 0 \\ -11 \end{array} \right)$.
Перейдем к составлению матрицы системы. В первую строку данной матрицы будут занесены коэффициенты первого уравнения: $2,3,-5,1$.
Во вторую строку запишем коэффициенты второго уравнения: $4,0,-1,0$. При этом следует учесть, что коэффициенты системы при переменных $x_2$ и $x_4$ во втором уравнении равны нулю (ибо эти переменные во втором уравнении отсутствуют).
В третью строку матрицы системы запишем коэффициенты третьего уравнения: $0,14,8,1$. Учитываем при этом равенство нулю коэффициента при переменной $x_1$(эта переменная отсутствует в третьем уравнении). Матрица системы будет иметь вид:
$$ A=\left( \begin{array} {cccc} 2 & 3 & -5 & 1\\ 4 & 0 & -1 & 0 \\ 0 & 14 & 8 & 1 \end{array} \right) $$
Чтобы была нагляднее взаимосвязь между матрицей системы и самой системой, я запишу рядом заданную СЛАУ и ее матрицу системы:
В матричной форме заданная СЛАУ будет иметь вид $A\cdot X=B$. В развернутой записи:
$$ \left( \begin{array} {cccc} 2 & 3 & -5 & 1\\ 4 & 0 & -1 & 0 \\ 0 & 14 & 8 & 1 \end{array} \right) \cdot \left( \begin{array} {c} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array} \right) = \left( \begin{array} {c} -5 \\ 0 \\ -11 \end{array} \right) $$
Запишем расширенную матрицу системы. Для этого к матрице системы $ A=\left( \begin{array} {cccc} 2 & 3 & -5 & 1\\ 4 & 0 & -1 & 0 \\ 0 & 14 & 8 & 1 \end{array} \right) $ допишем столбец свободных членов (т.е. $-5,0,-11$). Получим: $\widetilde{A}=\left( \begin{array} {cccc|c} 2 & 3 & -5 & 1 & -5 \\ 4 & 0 & -1 & 0 & 0\\ 0 & 14 & 8 & 1 & -11 \end{array} \right) $.
Пример №4
Записать СЛАУ $ \left \{\begin{aligned} & 3y+4a=17;\\ & 2a+4y+7c=10;\\ & 8c+5y-9a=25; \\ & 5a-c=-4. \end{aligned}\right.$ в матричной форме и указать расширенную матрицу системы.
Решение
Как видите, порядок следования неизвестных в уравнениях данной СЛАУ различен. Например, во втором уравнении порядок таков: $a,y,c$, однако в третьем уравнении: $c,y,a$. Перед тем, как записывать СЛАУ в матричной форме, порядок следования переменных во всех уравнениях нужно сделать одинаковым.
Упорядочить переменные в уравнениях заданной СЛАУ можно разными способами (количество способов расставить три переменные составит $3!=6$). Я разберу два способа упорядочивания неизвестных.
Способ №1
Введём такой порядок: $c,y,a$. Перепишем систему, расставляя неизвестные в необходимом порядке: $\left \{\begin{aligned} & 3y+4a=17;\\ & 7c+4y+2a=10;\\ & 8c+5y-9a=25; \\ & -c+5a=-4. \end{aligned}\right.$
Для наглядности я запишу СЛАУ в таком виде: $\left \{\begin{aligned} & 0\cdot c+3\cdot y+4\cdot a=17;\\ & 7\cdot c+4\cdot y+2\cdot a=10;\\ & 8\cdot c+5\cdot y-9\cdot a=25; \\ & -1\cdot c+0\cdot y+5\cdot a=-4. \end{aligned}\right.$
Матрица системы имеет вид: $ A=\left( \begin{array} {ccc} 0 & 3 & 4 \\ 7 & 4 & 2\\ 8 & 5 & -9 \\ -1 & 0 & 5 \end{array} \right) $. Матрица свободных членов: $B=\left( \begin{array} {c} 17 \\ 10 \\ 25 \\ -4 \end{array} \right)$. При записи матрицы неизвестных помним о порядке следования неизвестных: $X=\left( \begin{array} {c} c \\ y \\ a \end{array} \right)$. Итак, матричная форма записи заданной СЛАУ такова: $A\cdot X=B$. В развёрнутом виде:
$$ \left( \begin{array} {ccc} 0 & 3 & 4 \\ 7 & 4 & 2\\ 8 & 5 & -9 \\ -1 & 0 & 5 \end{array} \right) \cdot \left( \begin{array} {c} c \\ y \\ a \end{array} \right) = \left( \begin{array} {c} 17 \\ 10 \\ 25 \\ -4 \end{array} \right) $$
Расширенная матрица системы такова: $\left( \begin{array} {ccc|c} 0 & 3 & 4 & 17 \\ 7 & 4 & 2 & 10\\ 8 & 5 & -9 & 25 \\ -1 & 0 & 5 & -4 \end{array} \right) $.
Способ №2
Введём такой порядок: $a,c,y$. Перепишем систему, расставляя неизвестные в необходимом порядке: $\left \{ \begin{aligned} & 4a+3y=17;\\ & 2a+7c+4y=10;\\ & -9a+8c+5y=25; \\ & 5a-c=-4. \end{aligned}\right.$
Для наглядности я запишу СЛАУ в таком виде: $\left \{ \begin{aligned} & 4\cdot a+0\cdot c+3\cdot y=17;\\ & 2\cdot a+7\cdot c+4\cdot y=10;\\ & -9\cdot a+8\cdot c+5\cdot y=25; \\ & 5\cdot c-1\cdot c+0\cdot y=-4. \end{aligned}\right.$
Матрица системы имеет вид: $ A=\left( \begin{array} {ccc} 4 & 0 & 3 \\ 2 & 7 & 4\\ -9 & 8 & 5 \\ 5 & -1 & 0 \end{array} \right)$. Матрица свободных членов: $B=\left( \begin{array} {c} 17 \\ 10 \\ 25 \\ -4 \end{array} \right)$. При записи матрицы неизвестных помним о порядке следования неизвестных: $X=\left( \begin{array} {c} a \\ c \\ y \end{array} \right)$. Итак, матричная форма записи заданной СЛАУ такова: $A\cdot X=B$. В развёрнутом виде:
$$ \left( \begin{array} {ccc} 4 & 0 & 3 \\ 2 & 7 & 4\\ -9 & 8 & 5 \\ 5 & -1 & 0 \end{array} \right) \cdot \left( \begin{array} {c} a \\ c \\ y \end{array} \right) = \left( \begin{array} {c} 17 \\ 10 \\ 25 \\ -4 \end{array} \right) $$
Расширенная матрица системы такова: $\left( \begin{array} {ccc|c} 4 & 0 & 3 & 17 \\ 2 & 7 & 4 & 10\\ -9 & 8 & 5 & 25 \\ 5 & -1 & 0 & -4 \end{array} \right) $.
Как видите, изменение порядка следования неизвестных равносильно перестановке столбцов матрицы системы. Но каким бы этот порядок расположения неизвестных ни был, он должен совпадать во всех уравнениях заданной СЛАУ.
laservirta.ru
5. Системы линейных уравнений. Основные понятия
Системой 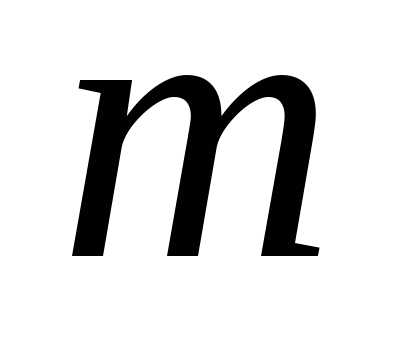 линейных уравненийс
линейных уравненийс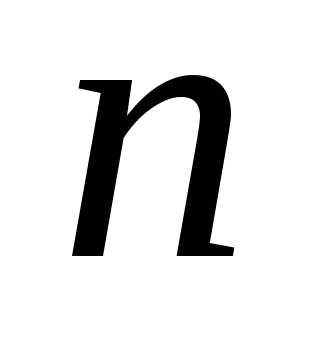 неизвестными
неизвестными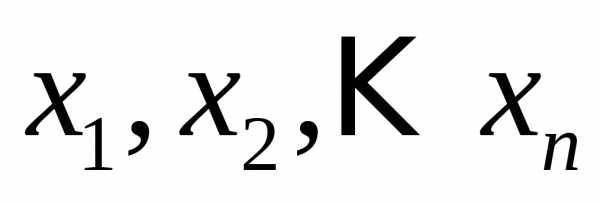 (линейной системой)
называется система вида
(линейной системой)
называется система вида
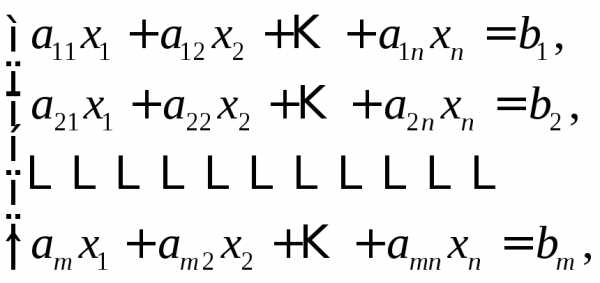 (7)
(7)
где 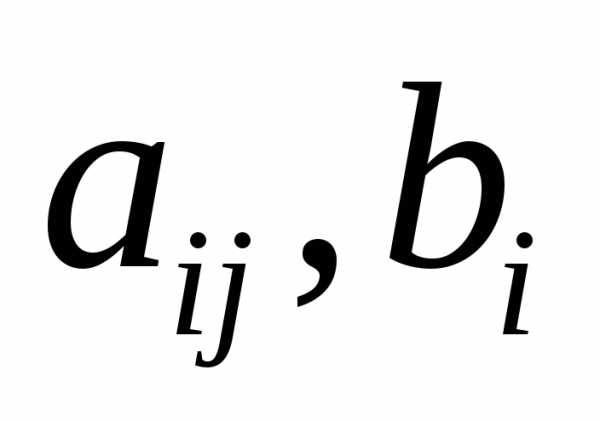 − заданные числа. Числаназываютсякоэффициентамисистемы, а числа
− заданные числа. Числаназываютсякоэффициентамисистемы, а числа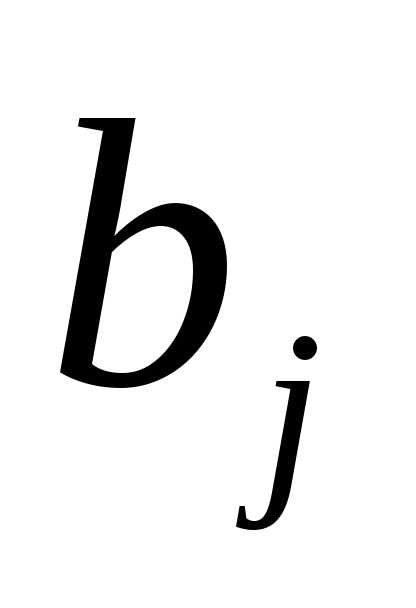 —свободными
членами.
—свободными
членами.
Линейная система называется однородной, если все свободные члены равны нулю, т.е.
 (8)
(8)
В противном случае линейная система называется неоднородной.
Решениемсистемы (7) называется упорядоченная
совокупность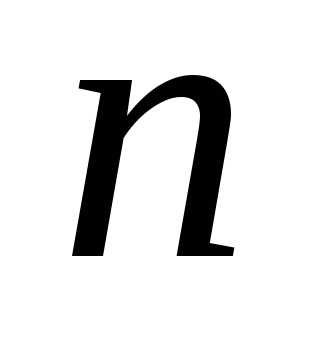 чисел:
чисел:
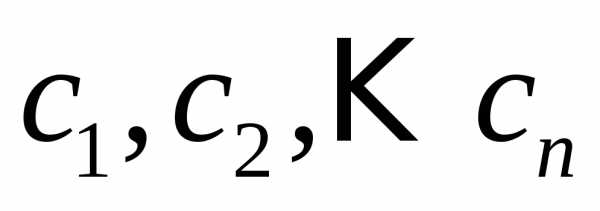 ,
(9)
,
(9)
при подстановке которых вместо 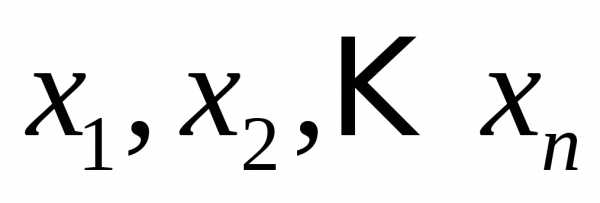 каждое уравнение системы обращается
в тождество.
каждое уравнение системы обращается
в тождество.
Система, имеющая хотя бы одно решение, называется совместной, а система, не имеющая ни одного решения, —несовместной. Совместная система называетсяопределенной, если она имеет единственное решение, инеопределенной, если она имеет более одного решения.
Однородная система (8) всегда совместна, так как она имеет очевидное решение: . Нулевое решение однородной системы называетсятривиальным.
Две системы называются равносильными илиэквивалентными, если любое решение одной из них является также решением и другой, и обратно, т.е. они имеют одно и то же множество решений. В частности, любые две несовместные системы являются эквивалентными.
Линейную систему можно записать в матричной форме. Введем матрицы
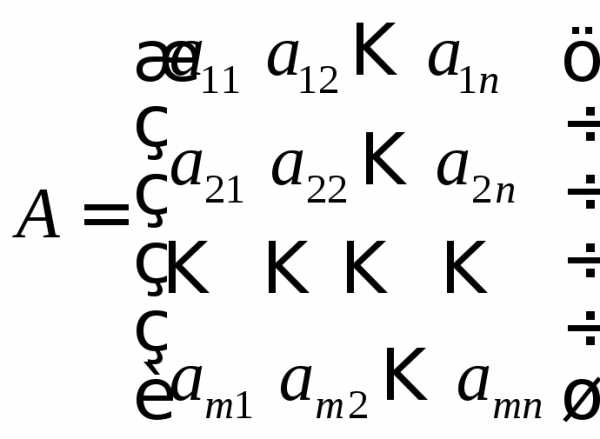 – матрица коэффициентов при неизвестных,
– матрица коэффициентов при неизвестных,
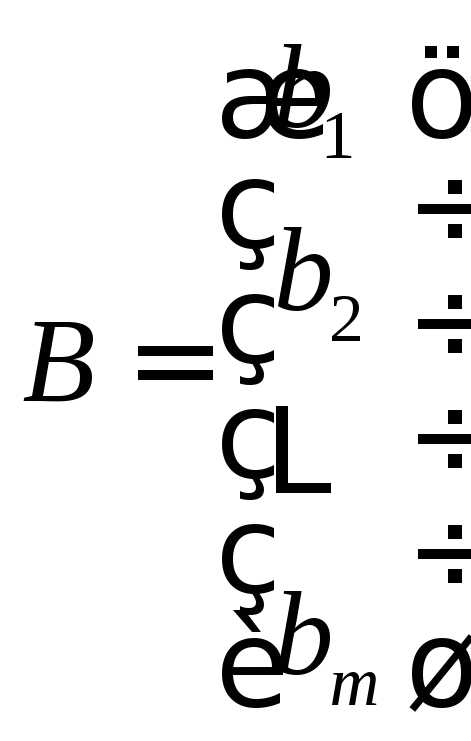 — матрица-столбец свободных членов,
— матрица-столбец свободных членов,
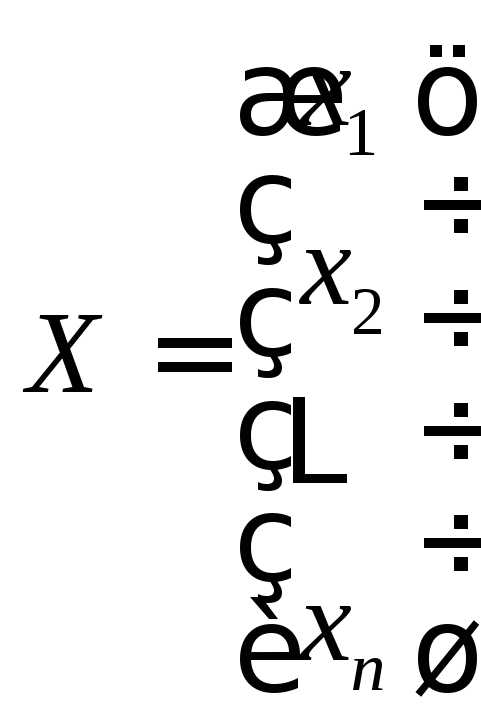 — матрица-столбец неизвестных.
— матрица-столбец неизвестных.
Тогда систему (7) можно записать в виде матричного уравнения
,
а решение (9) в виде матрицы-столбца 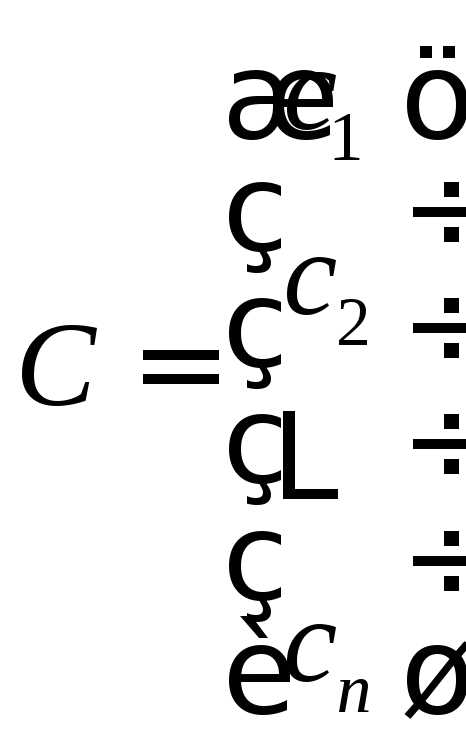 .
.
Матрица коэффициентов
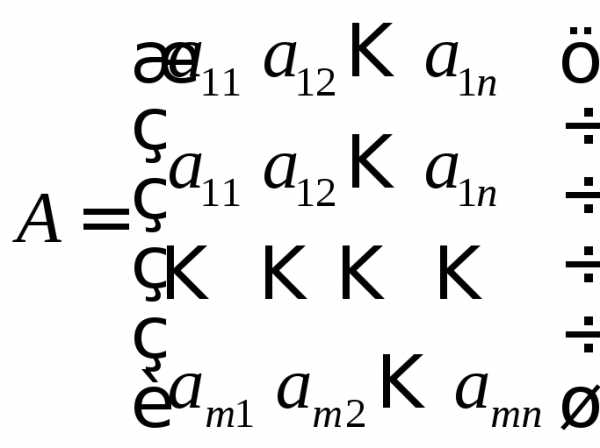
называется основнойматрицей системы. Матрица, составленная из коэффициентов и свободных членов,

называется расширеннойматрицей системы.
Выражение «решить систему» означает: выяснить, совместна или несовместна система, а в случае совместности – найти все ее решения.
6. Решение линейных систем по формулам Крамера
Теорема Крамера.
Пусть дана система, в которой число уравнений совпадает с числом неизвестных
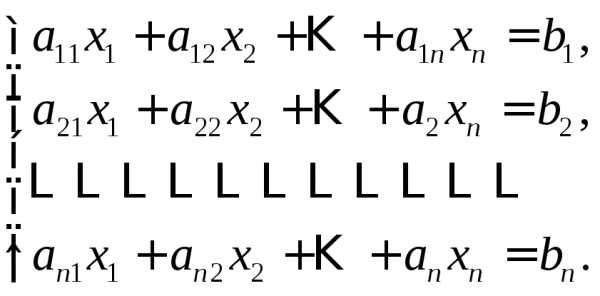 (10)
(10)
Если определитель основной матрицы системы
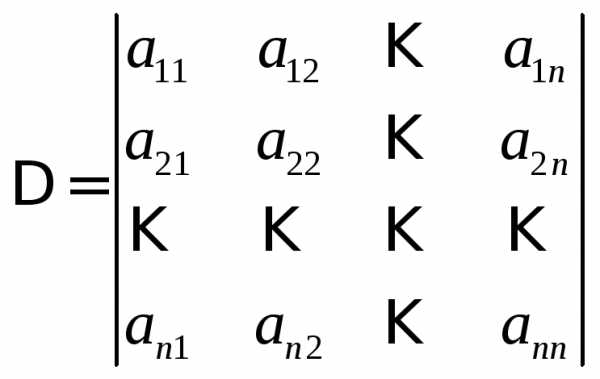 ,
(11)
,
(11)
не равен нулю, то система имеет
единственное решение и 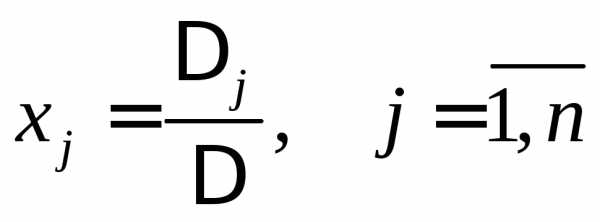 ,
где
,
где
Определители , получены из определителя (11) заменой соответствующего столбца на столбец свободных членов.
►Пример 8. По формулам Крамера найти
решение системы уравнений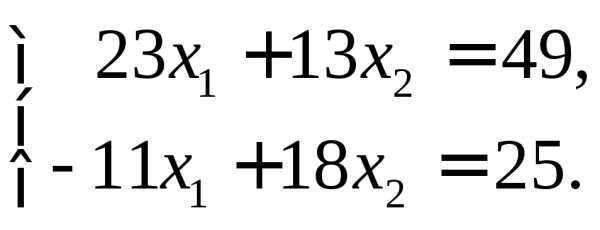
Решение.
Вычислим определители и найдем решение
Ответ: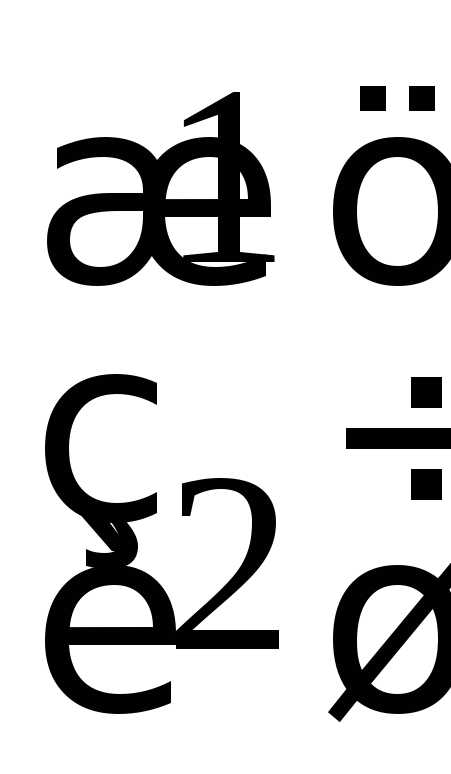 .◄
.◄
Упражнения.
Решить системы по формулам Крамера:
1) 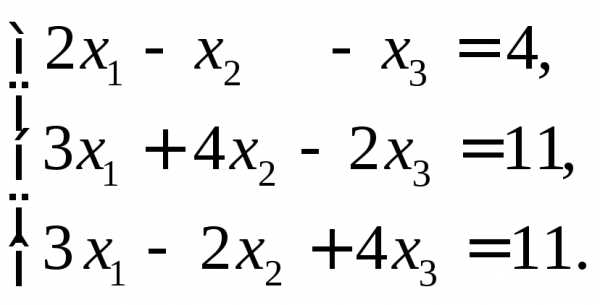 2)
2)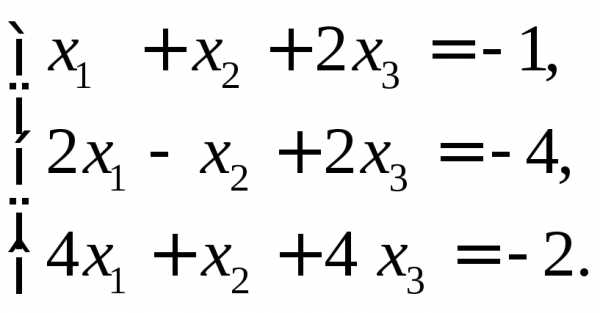 3)
3)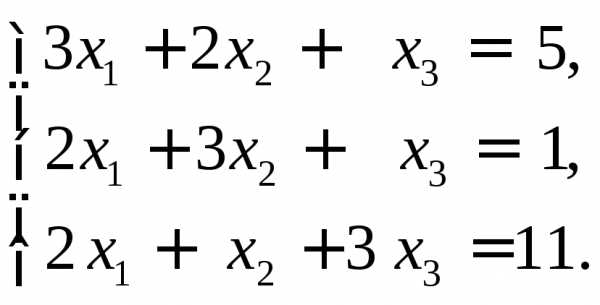
Ответы: 1)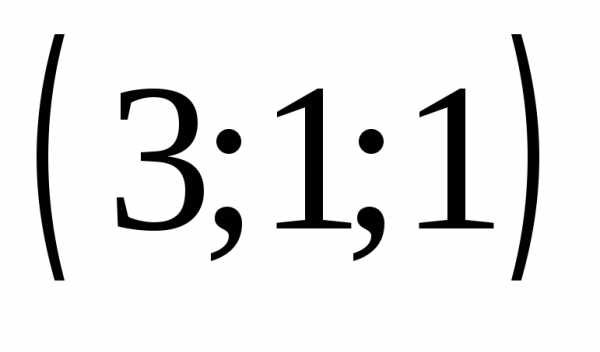 ,
2)
,
2)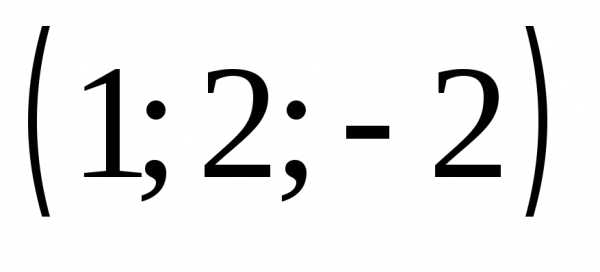 ,
3)
,
3)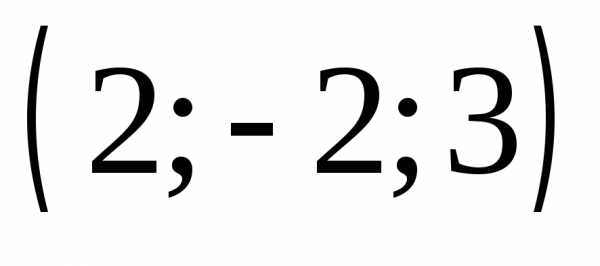 .
.
7. Решение систем с помощью обратной матрицы
Система из 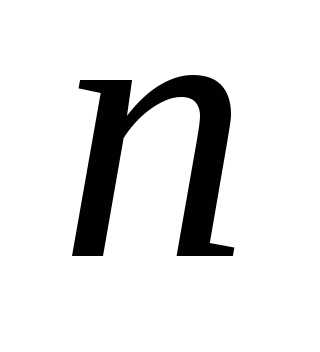 уравнений с
уравнений с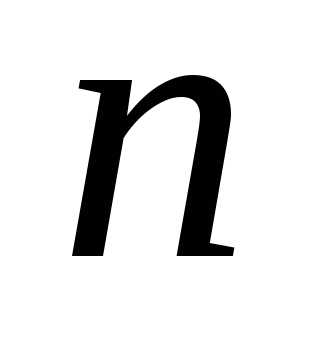 неизвестными (10) в матричной форме
имеет вид (5)
неизвестными (10) в матричной форме
имеет вид (5)
,
где 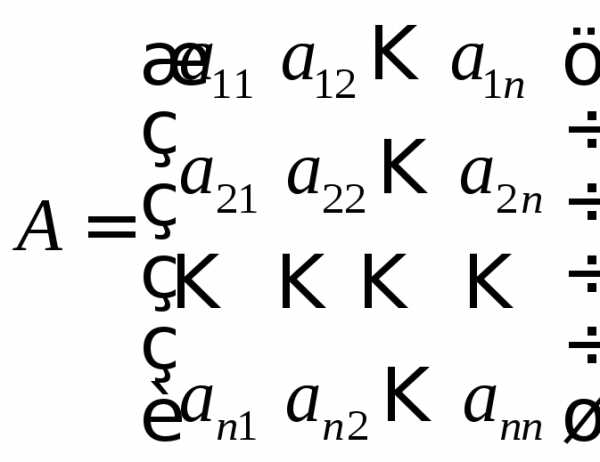 ,
,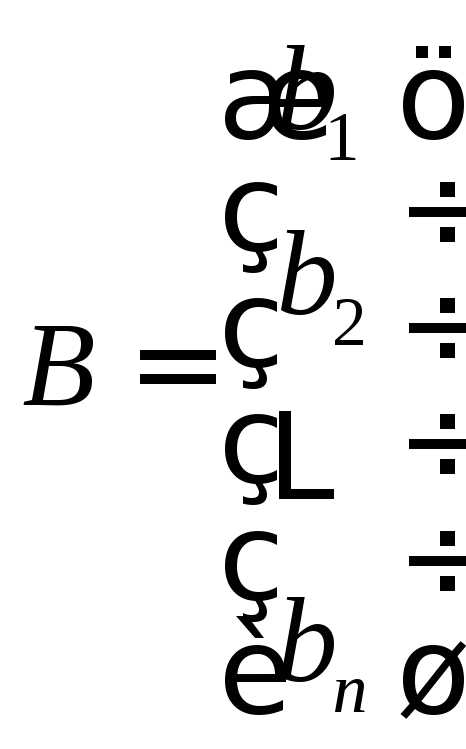 ,
,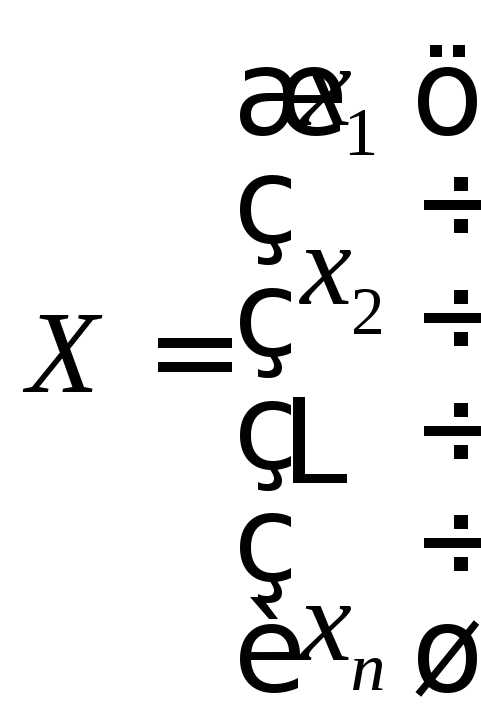 .
.
Если матрица  невырожденная, то система имеет
единственное решение, которое вычисляется
по формуле.
невырожденная, то система имеет
единственное решение, которое вычисляется
по формуле.
►Пример 9. С помощью обратной матрицы найти решение системы
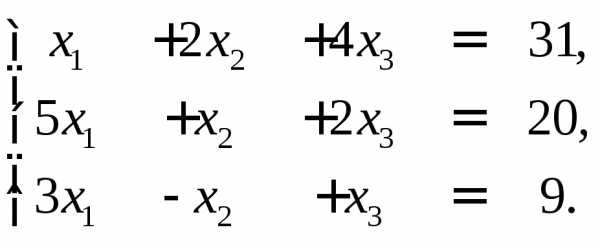
Решение.
Проведем необходимые вычисления:
.
Ответ: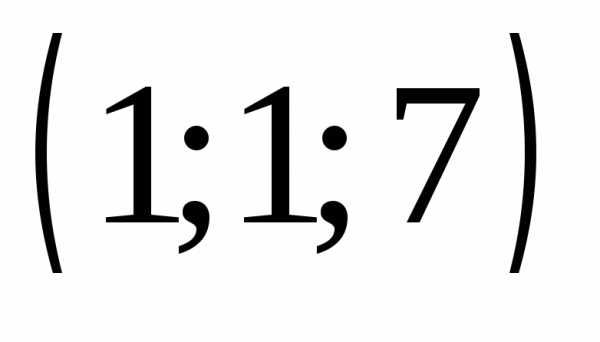 .
◄
.
◄
Упражнения.
Найти решение систем с помощью обратной матрицы:
а) 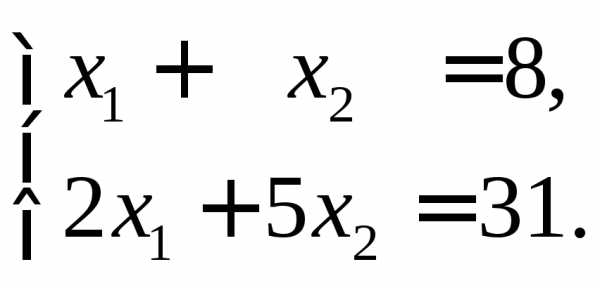 б)
б)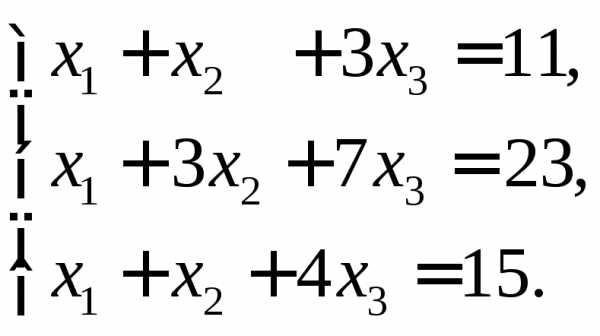 в)
в)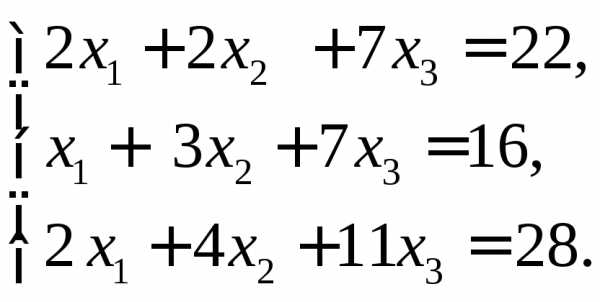
г) 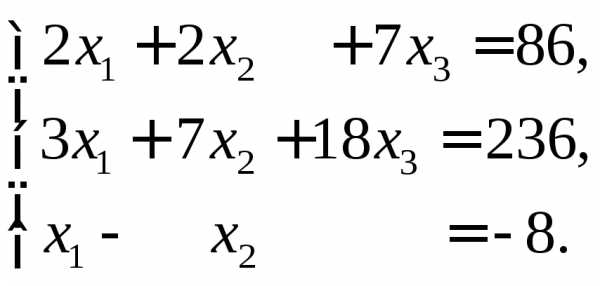 Ответы:а)
Ответы:а)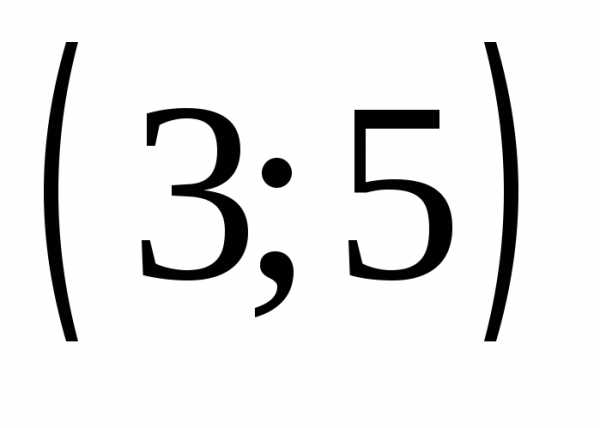 ;
б)
;
б)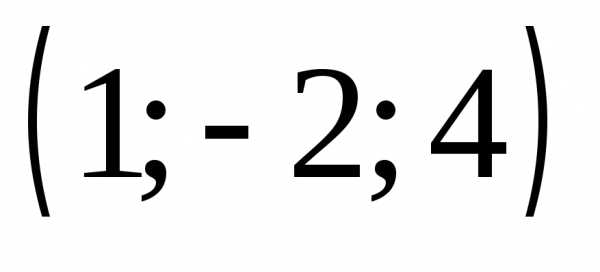 ;
в)
;
в)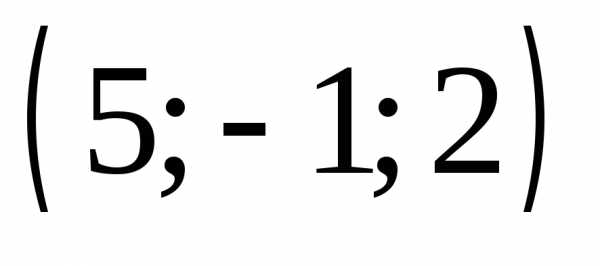 г)
г)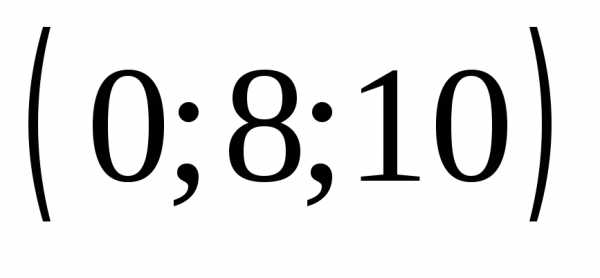 .
.
studfiles.net
Система линейных алгебраических уравнений — это… Что такое Система линейных алгебраических уравнений?
Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида
| (1) |
Здесь — количество уравнений, а — количество неизвестных. x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными[1]. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[2].
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
| c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2). |
Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.
Матричная форма
Система линейных уравнений может быть представлена в матричной форме как:
или:
- .
Здесь — это матрица системы, — столбец неизвестных, а — столбец свободных членов. Если к матрице приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.
Эквивалентные системы линейных уравнений
Системы линейных уравнений называются эквивалентными, если множество их решений совпадает, то есть любое решение одной системы одновременно является решением другой, и наоборот.
Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений даёт систему, эквивалентную исходной.
Система линейных алгебраических уравнений
эквивалентна системе
- ,
где — невырожденная матрица.
В частности, если сама матрица — невырожденная, и для неё существует обратная матрица , то решение системы уравнений можно формально записать в виде
- .
Методы решения
Прямые (или точные) методы позволяют найти решение за определённое количество шагов. Итерационные методы основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.
Прямые методы
Итерационные методы
Итерационные методы устанавливают процедуру уточнения определённого начального приближения к решению. При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций. Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений. Суть этих методов состоит в том, чтобы найти неподвижную точку матричного уравнения
- ,
эквивалентного начальной системе линейных алгебраических уравнений. При итерации в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:
- .
Среди итерационных методов можно отметить самые популярные:
См. также
Примечания
- ↑ В рамках данной статьи коэффициенты системы, свободные члены и неизвестные считаются действительными числами, хотя они могут быть комплексными или даже сложными математическими объектами с условием, что для них определены операции умножения и сложения.
- ↑ Ильин В. А., Позняк Э. Г. Линейная алгебра: Учебник для вузов. — 6-е изд., стер. — М.: ФИЗМАТЛИТ, 2004. — 280 с.
- ↑ Вержбицкий В. М. Основы численных методов. — М.: Высшая школа, 2009. — С. 80—84. — 840 с. — ISBN 9785060061239
Ссылки
dic.academic.ru
Формулы, связывающие координаты векторов в старом и новом базисах
Запишите систему линейных алгебраических уравнений в общем виде
Что называется решением СЛАУ?
Решением системы уравнений называется набор из n чисел,
X1=α1
X2=α2
.
.
.
Xn=αn
При подстановке которой в систему каждое уравнение обращается в тождество.
Какая система называется совместной (несовместной)?
Система уравнений называется совместной, если она имеет хотя бы одно решение.
Система называется несовместной , если она не имеет решений.
Какая система называется определенной (неопределенной)?
Совместная система называется определенной, если она имеет единственное решение.
Совместная система называется неопределенной, если она имеет больше одного решения.
Матричная форма записи системы уравнений
AX=B
Ранг системы векторов
Ранг системы векторов называется максимальное число линейно независимых векторов.
Ранг матрицы и способы его нахождения
Ранг матрицы — наивысший из порядков миноров этой матрицы, определитель которых отличен от нуля.
Первый метод –- метод окантовки — заключается в следующем:
Если все миноры 1-го порядка, т.е. элементы матрицы равны нулю, то r=0 .
Если хоть один из миноров 1-го порядка не равен нулю, а все миноры 2-го порядка равны нулю то r=1.
Если минор 2-го порядка отличен от нуля то исследуем миноры 3-го порядка. Таким образом находят минор k-го порядка и проверяют, не равны ли нулю миноры k+1-го порядка.
Если все миноры k+1-го порядка равны нулю, то ранг матрицы равен числу k. Такие миноры k+1-го порядка, как правило, находят путем «окантовки» минора k-го порядка.
Второй метод определения ранга матрицы заключается в применении элементарных преобразований матрицы при возведении ее к диагональному виду. Ранг такой матрицы равно числу отличных от нуля диагональных элементов.
Общее решение неоднородной системы линейных уравнений, его свойства.
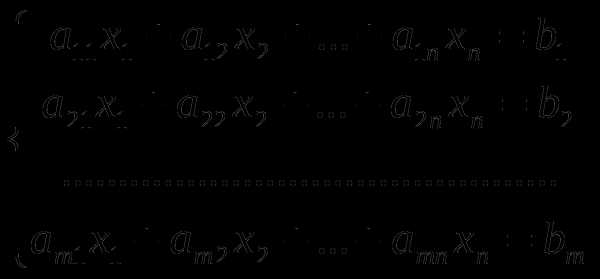
Свойство 1.Сумма любого решения системы линейных уравнений и любого решения соответствующей однородной системы является решением системы линейных уравнений.
Свойство 2. Разность любых двух решений неоднородной системы линейных уравнений является решением соответствующей однородной системы.
Метод Гаусса решения СЛАУ
Последовательность:
1)составляется расширенная матрица системы уравнения
2)с помощью элементарных преобразований матрица приводится к ступенчатому виду
3)определяется ранг расширенной матрицы системы и ранг матрицы системы и устанавливается пакт совместимости или несовместимости системы
4)в случае совместимости записывается эквивалентная система уравнения
5)находится решение системы. Главные переменные выражаются через свободные
Теорема Кронекера-Капелли
Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
Для того чтобы линейная система являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу её основной матрицы.
Когда система не имеет решения, когда имеет единственное решение, имеет множество решений?
Если число уравнений системы равно числу неизвестных переменных и определитель ее основной матрицы не равен нулю,значит Такие системы уравнений имеют единственное решение, причем в случае однородной системы все неизвестные переменные равны нулю.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.
pdnr.ru
Общие понятия системы линейных уравнений.
Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом:
,
где aij – коэффициенты, а bi – постоянные.
Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.
Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.
Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.
Определение. Для системы линейных уравнений матрица
А = называется матрицей системы, а матрица
А*= называется расширенной матрицей системы
Определение. Если b1, b2, …,bm = 0, то система называется однородной. Замечание. Однородная система всегда совместна, т.к. всегда имеет нулевое решение.
Элементарные преобразования систем.
1. Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю.
2. Перестановка уравнений местами.
3. Удаление из системы уравнений, являющихся тождествами для всех х.
Формулы Крамера.
Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений.
Теорема. Система из n уравнений с n неизвестными
в случае, если определитель матрицы системы не равен нулю, то система имеет единственное решение и это решение находится по формулам: xi = где D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Di =
Пример. Найти решение системы уравнений:
D = = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
D1 = = (28 – 48) – (42 – 32) = -20 – 10 = -30.
x1 =
D2 = = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
x2 =
D3 = = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
x3 =
Замечание 1. Если система однородна, т.е. bi = 0, то при D¹0 система имеет единственное нулевое решение x1 = x2 = … = xn = 0.
Замечание 2. При D = 0 система имеет бесконечное множество решений.
Метод обратной матрицы.
Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.
Пусть дана система уравнений: Составим матрицы:
A = — матрица коэффициентов при переменных или матрица системы;
B = — матрица –столбец свободных членов;
X = — матрица – столбец неизвестных.
Тогда систему уравнений можно записать:A×X = B. Домножим слева обе части равенства на A-1: A-1×A×X = A-1×B, т.к. А-1×А = Е, то Е×Х = А-1×В, то справедлива следующая формула:
Х = А-1×В
Таким образом, для применения данного метода необходимо находить обратную матрицу.
Пример. Решить систему уравнений:
Х = , B = , A =
Найдем обратную матрицу А-1.
D = det A = 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30≠0 ⇒ обратная матрица существует.
M11 = ; M21 = ; M31 = ;
M12 = M22 = M32 =
M13 = M23 = M33 =
A-1 = ;
Cделаем проверку:
A×A-1 = =E.
Находим матрицу Х.
Х = = А-1В = × = .
Получили решения системы: x =1; y = 2; z = 3.
4.Метод Гаусса.
Пусть дана система m линейных уравнений с n неизвестными:
Полагая, что в системе коэффициент a11 отличен от нуля (если это не так, то следует на первое место поставить уравнение с отличным от нуля коэффициентом при x1). Преобразуем систему следующим образом: первое уравнение оставляем без изменения, а из всех остальных уравнений исключаем неизвестную x1 с помощью эквивалентных преобразований описанным выше способом.
В полученной системе
,
считая, что (что всегда можно получить, переставив уравнения или слагаемые внутри уравнений), оставляем без изменений первые два уравнения системы, а из остальных уравнений, используя второе уравнения, с помощью элементарных преобразований исключаем неизвестную x2. Во вновь полученной системе
при условии оставляем без изменений первые три уравнения, а из всех остальных с помощью третьего уравнения элементарными преобразованиями исключаем неизвестную x3.
Этот процесс продолжается до тех пор, пока не реализуется один из трех возможных случаев:
1) если в результате приходим к системе, одно из уравнений которой имеет нулевые коэффициенты при всех неизвестных и отличный от нуля свободный член, то исходная система несовместна;
2) если в результате преобразований получаем систему с матрицей коэффициентов треугольного вида, то система совместна и является определенной;
3) если получается ступенчатая система коэффициентов (и при этом не выполняется условие пункта 1), то система совместна и неопределенна.
Рассмотрим квадратную систему: (1)
У этой системы коэффициент a11 отличен от нуля. Если бы это условие не выполнялось, то чтобы его получить, нужно было бы переставить местами уравнения, поставив первым то уравнение, у которого коэффициент при x1 не равен нулю.
Проведем следующие преобразования системы:
1) поскольку a11¹0, первое уравнение оставим без изменений;
2) вместо второго уравнения запишем уравнение, получающееся, если из второго уравнения вычесть первое, умноженное на 4;
3) вместо третьего уравнения запишем разность третьего и первого, умноженного на 3;
4) вместо четвертого уравнения запишем разность четвертого и первого, умноженного на 5.
Полученная новая система эквивалентна исходной и имеет во всех уравнениях, кроме первого, нулевые коэффициенты при x1 (это и являлось целью преобразований 1 – 4): (2)
Для приведенного преобразования и для всех дальнейших преобразований не следует целиком переписывать всю систему, как это только что сделано. Исходную систему можно представить в виде матрицы
. (3)
Матрица (3) называется расширенной матрицей для исходной системы уравнений. Если из расширенной матрицы удалить столбец свободных членов, то получится матрица коэффициентов системы, которую иногда называют просто матрицей системы.
Системе (2) соответствует расширенная матрица
.
Преобразуем эту матрицу следующим образом:
1) первые две строки оставим без изменения, поскольку элемент a22 не равен нулю;
2) вместо третьей строки запишем разность между второй строкой и удвоенной третьей;
3) четвертую строку заменим разностью между удвоенной второй строкой и умноженной на 5 четвертой.
В результате получится матрица, соответствующая системе, у которой неизвестная x1 исключена из всех уравнений, кроме первого, а неизвестная x2 — из всех уравнений кроме первого и второго:
.
Теперь исключим неизвестную x3 из четвертого уравнения. Для этого последнюю матрицу преобразуем так:
1) первые три строки оставим без изменения, так как a33 ¹ 0;
2) четвертую строку заменим разностью между третьей, умноженной на 39, и четвертой: .
Полученная матрица соответствует системе
. (4)
Из последнего уравнения этой системы получаем x4 = 2. Подставив это значение в третье уравнение, получим x3 = 3. Теперь из второго уравнения следует, что x2 = 1, а из первого — x1 = –1. Очевидно, что полученное решение единственно (так как единственным образом определяется значение x4, затем x3 и т. д.).
Определение: Назовем квадратную матрицу, у которой на главной диагонали стоят числа, отличные от нуля, а под главной диагональю – нули, треугольной матрицей.
Матрица коэффициентов системы (4) – треугольная матрица.
Замечание: Если с помощью элементарных преобразований матрицу коэффициентов квадратной системы можно привести к треугольной матрице, то система совместна и определенна.
Рассмотрим другой пример: . (5)
Проведем следующие преобразования расширенной матрицы системы:
1) первую строку оставим без изменения;
2) вместо второй строки запишем разность между второй строкой и удвоенной первой;
3) вместо третьей строки запишем разность между третьей строкой и утроенной первой;
4) четвертую строку заменим разностью между четвертой и первой;
5) пятую строку заменим разностью пятой строки и удвоенной первой.
В результате преобразований получим матрицу
.
Оставив без изменения первые две строки этой матрицы, приведем ее элементарными преобразованиями к следующему виду:
.
Если теперь, следуя методу Гаусса, который также называют и методом последовательного исключения неизвестных, с помощью третьей строки привести к нулю коэффициенты при x3 в четвертой и пятой строках, то после деления всех элементов второй строки на 5 и деления всех элементов третьей строки на 2 получим матрицу
.
Каждая из двух последних строк этой матрицы соответствует уравнению 0x1+0x2+0x3+0x4+0x5 = 0. Это уравнение удовлетворяется любым набором чисел x1, x2, ¼, x5, и его следует удалить из системы. Таким образом, система с только что полученной расширенной матрицей эквивалентна системе с расширенной матрицей вида
. (6)
Последняя строка этой матрицы соответствует уравнению
x3 – 2x4 + 3x5 = –4. Если неизвестным x4 и x5 придать произвольные значения: x4 = С1; x5 = С2, то из последнего уравнения системы, соответствующей матрице (6), получим x3 = –4 + 2С1 – 3С2. Подставив выражения x3, x4, и x5 во второе уравнение той же системы, получим x2 = –3 + 2С1 – 2С2. Теперь из первого уравнения можно получить x1 = 4 – С1+ С2. Окончательно решение системы представляется в виде .
Рассмотрим прямоугольную матрицу A, у которой число столбцов m больше, чем число строк n. Такую матрицу A назовем ступенчатой.
Очевидно, что матрица (6) — ступенчатая матрица.
Если при применении эквивалентных преобразований к системе уравнений хотя бы одно уравнение приводится к виду
0x1 + 0x2 + ¼0xn = bj (bj ¹ 0),
то система несовместна или противоречива, так как ни один набор чисел x1, x2, ¼, xn не удовлетворяет этому уравнению.
Если при преобразовании расширенной матрицы системы матрица коэффициентов приводится к ступенчатому виду и при этом система не получается противоречивой, то система совместна и является неопределенной, то есть имеет бесконечно много решений.
В последней системе можно получить все решения, придавая конкретные числовые значения параметрам С1 и С2.
Определение: Те переменные, коэффициенты при которых стоят на главной диагонали ступенчатой матрицы (это значит, что эти коэффициенты отличны от нуля), называются основными. В рассмотренном выше примере это неизвестные x1, x2, x3. Остальные переменные называются неосновными. В рассмотренном выше примере это переменные x4, и x5. Неосновным переменным можно придавать любые значения или выражать их через параметры, как это сделано в последнем примере.
Основные переменные единственным образом выражаются через неосновные переменные.
Определение: Если неосновным переменным приданы конкретные числовые значения и через них выражены основные переменные, то полученное решение называется частным решением.
Определение: Если неосновные переменные выражены через параметры, то получается решение, которое называется общим решением.
Определение: Если всем неосновным переменным приданы нулевые значения, то полученное решение называется базисным.
Замечание: Одну и ту же систему иногда можно привести к разным наборам основных переменных. Так, например, можно поменять местами 3-й и 4-й столбцы в матрице (6). Тогда основными будут переменные x1, x2, x4, а неосновными – x3 и x5.
Определение: Если получены два различных набора основных переменных при различных способах нахождения решения одной и той же системы, то эти наборы обязательно содержат одно и то же число переменных, называемое рангом системы.
Рассмотрим еще одну систему, имеющую бесконечно много решений: .
Проведем преобразование расширенной матрицы системы по методу Гаусса:
.
Как видно, мы не получили ступенчатой матрицы, однако последнюю матрицу можно преобразовать, поменяв местами третий и четвертый столбцы: .
Эта матрица уже является ступенчатой. У соответствующей ей системы две неосновные переменные – x3, x5 и три основные – x1, x2, x4. Решение исходной системы представляется в следующем виде:
.
Приведем пример системы, не имеющей решения:
.
Преобразуем матрицу системы по методу Гаусса:
.
Последняя строка последней матрицы соответствует не имеющему решения уравнению 0x1 + 0x2 + 0x3 = 1. Следовательно, исходная система несовместна.
Лекция № 3.
Тема: Векторы. Скалярное, векторное и смешанное произведение векторов
План:
1. Понятие вектора. Коллинарность, ортогональность и компланарность векторов.
2. Линейная операция над векторами.
3. Скалярное произведение векторов и его применение
4. Векторное произведение векторов и его применение
5. Смешанное произведение векторов и его применение
1. Понятие вектора.Коллинарность, ортогональность и компланарность векторов.
Определение: Вектором называется направленный отрезок с начальной точкой А и конечной точкой В.Обозначение: , ,
Определение: Длиной или модулем вектора вектора называется число, равное длине отрезка АВ, изображающего вектор.
Определение: Вектор называется нулевым, если начало и конец вектора совпадают.
Определение: Вектор единичной длины называется единичным. Определение: Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых ( || ).
Замечание:
1.Коллинеарные векторы могут быть направлены одинаково или противоположно.
2. Нулевой вектор считается коллинеарным любому вектору.
Определение: Два вектора называются равными, если они коллинеарные,
одинаково направлены и имеют одинаковые длины ( = )
Определение: Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях
2. Линейные операции над векторами:
Произведением вектора на число λ называется вектор , имеющий длину , направление которого совпадает с направлением вектора , если λ>0, и противоположно ему, если λ<0
Противоположным вектором – называется произведение вектора на число (-1), т. е. – =(-1)
Суммой двух векторов и называется вектор , начало которого совпадает с началом вектора , а конец – с концом вектора , при условии, что начало вектора совпадает с концом вектора (правило треугольников)
Сумму двух векторов можно построить также по правилу параллелограмма, где вектор представляет собой диагональ параллелограмма
Аналогично определяется сумма нескольких векторов.
Например, суммой четырех вектор является вектор , начало которого совпадает с началом вектора , а конец – с концом вектора (правило многоугольника)
Вектор , определяемый таким образом, представляет собой диагональ параллелепипеда, построенного на векторах , не лежащих в одной плоскости или в параллельных плоскостях (правило параллелепипеда)
Разностью двух векторов называется сумма вектора и вектора , противоположного (можно вычитать векторы по правилу , т. е. вычитание векторов заменить сложением вектора с вектором, противоположным вектору )
Замечание: в параллелограмме, построенном на векторах , одна направленная диагональ является суммой этих векторов, а другая – разностью.
Определение: Координатами вектора называются координаты его конечной точки.
На плоскости Oxy координатами вектора являются числа x и y ( (x, y)), а в пространстве Oxyz – три числа x, y, z ( (x, y, z))В соответствии с приведенными выше операциями над векторами, имеем:
пусть даны векторы (x1, y1) и (x2, y2),тогда
1. = (x1 +x2, y1+y2)
2. = (x1 — x2, y1— y2)
3.
4.
Аналогично, для вектора в пространстве (x1, y1, z1) и (x2, y2, z2)
1. = (x1 +x2, y1+y2, z1+z2)
2. = (x1 — x2, y1— y2, z1 — z2)
3.
4.
Рекомендуемые страницы:
lektsia.com
4 Система линейных уравнений
Лекция 4
ТЕМА: Система линейных уравнений (СЛУ)
Определение 4.1
Системой линейных уравнений (СЛУ) называют систему уравнений первого порядка:
(4.1),
где .
Матрица коэффициентов при неизвестных
называется основной матрицей системы.
Матрица
называется расширенной матрицей системы.
Определение 4.2
1). Множество всех значений , подстановка которых в систему уравнений (4.1) каждое уравнение обращает в тождество, называется решением данной системы.
2). Если все свободные члены системы равны нулю, то есть , то система называется однородной.
Определение 4.3
Система линейных уравнений, имеющая хотя бы одно решение называется совместной, если решение только одно, то система называется определенной, если решений множество, то система называется неопределенной. Если решений нет, то система несовместная.
Определение 4.4
Две системы называются равносильными, если каждое решение первой системы является решением второй и наоборот.
Над системами можно производить следующие линейные преобразования:
менять уравнения местами
умножать обе части уравнения на любое не равное нулю число
прибавлять к обеим частям одного из уравнений системы соответствующие части другого уравнения, умноженное на любое действительное число.
Система n линейных уравнений с n неизвестными
(4.2)
1). Матричный способ решения системы (4.2)
Назовем (4.3)
матричным уравнением системы (4.2)
или (4.4),
где
Каждую часть равенства (4.4) умножим слева на обратную матрицу :
(4.5)- решение системы (4.2).
Запишем (5) в развернутом виде:
Таким образом, из , из определения равенства матриц (2.1) следует:
(4.6)
Пример 4.1
Решить систему матричным способом:
Далее вычисляются алгебраические дополнения и составляется матрица .
.
, тогда
.
2). Решение системы (4.2) по формулам Крамера
Определение 4.5
Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы (4.2):
.
— побочные определители системы (4.2), которые составляются следующим образом: при составлении в определителе-й столбец заменяется на свободные члены, например:
.
Возвращаясь к формулам (4.6), нетрудно заметить, что суммы, стоящие в числителях есть ни что иное, как побочные определители, разложенные по столбцу свободных членов и тогда формулы (4.6) примут вид:
(4.7) — формулы Крамера.
Пример 4.1.1
Решим систему линейных уравнений из примера 4.1 с помощью формул Крамера:
,
Теорема Кронекера-Капелли 4.1
Система линейных уравнений (4.1) совместна тогда и только тогда, когда (4.8).
Следствия
1). Система линейных уравнений (4.1) имеет единственное решение, если , где-число неизвестных в системе.
2). Если , то система линейных уравнений (4.1) имеет бесконечное множество решений (т.е. система неопределенная).
Пример4.2
Как видно, , поскольку ранги не равны, то по теореме 6 данная СЛУ решений не имеет (несовместна).
5
studfiles.net
