Свойства функции тангенса
Перед изучением функции тангенса и её свойств, вспомним понятие самого тангенса. Определение тангенса можно ввести двумя способами: с помощью прямоугольного треугольника и с помощью понятий синуса и косинуса.
Определение 1
Тангенсом острого угла называется отношение длины противолежащего катета к прилежащему катету прямоугольного треугольника (рис 1):
\[cos\alpha =\frac{a}{b}\]Рисунок 1. Прямоугольный треугольник.
Определение 2
Тангенсом угла называется отношение значения синуса этого угла к значению косинуса этого угла.
Введем таблицу некоторых значений тангенса (таблица 1).
Рисунок 2. Значения тангенса.
Геометрический смысл
Рассмотрим тригонометрическую единичную окружность и прямую $x=1$. Ордината точки $B$ на прямой $x=1$ является тангенсом угла $\alpha $ (рис. 2).
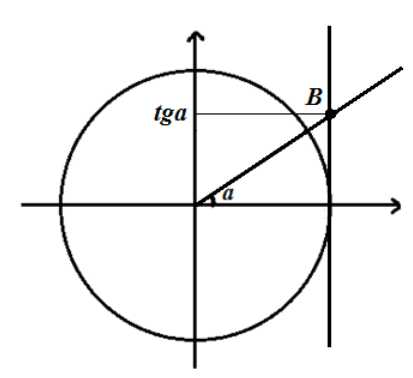
Рисунок 3. Значение тангенса с помощью единичной окружности.
Поэтому, когда точка $B$ опишет вертикальную прямую $x=1$ её ордината примет все значения множества действительных чисел, откуда $tg\alpha $ — вся числовая прямая. Поэтому прямая $x=1$ называется линией тангенсов.
Свойства функции $f(x)=tgx$
Рассмотрим теперь свойства функции $f\left(x\right)=tgx$.
- По определению 2, получим, что область определения$x\in {\mathbb R}{\rm ,}{\rm \ }x\ne \frac{\pi }{2}+\pi n,\ n\in Z$.
- Из геометрического смысла следует, что область значения — все числа.
- $f\left(-x\right)={tg \left(-x\right)\ }=-tgx=-f(x)$, следовательно, функция$f\left(x\right)=tgx$ нечетна.
- $f\left(x+\pi \right)={tg \left(x+\pi \right)\ }=tgx=f(x)$, следовательно, функция$f\left(x\right)=tgx$ периодическая с минимальным периодом $\pi $.
- Пересечение с осями координат:
При $x=0$, $f\left(0\right)=tg0=0$.
При $y=0$, $x=\pi n,n\in Z$.
- Функция выше оси $Ox$ при $x\in (\pi n,\frac{\pi }{2}+\pi n),n\in Z$.
- Функция ниже оси $Ox$ при $x\in (-\frac{\pi }{2}+\pi n,\frac{\pi }{2}+\pi n),n\in Z$.
- $f’\left(x\right)={\left(tgx\right)}’=\frac{1}{{cos}^2x}$.
Функция $f\left(x\right)=tgx$ возрастает, при $x\in \left(-\frac{\pi }{2}+\pi n,\frac{\pi }{2}+\pi n\right)$.
Функция имеет точку разрыва второго рода при $x=\frac{\pi }{2}+\pi n,\ n\in Z$.
${\mathop{lim}_{x\to \frac{\pi }{2}+\pi n-0} tgx\ }=-\infty $, ${\mathop{lim}_{x\to \frac{\pi }{2}+\pi n+0} tgx\ }=+\infty $,
График функции $y=tgx$
Графиком функции $y=tgx$ является тангенсоида (рис. 3).
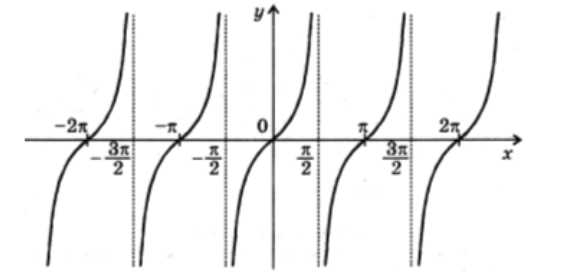
Рисунок 4. Тангенсоида.
Задача на построение тангенсоиды
Пример 1
Построить график функции $y=tg(x-2\pi )$.
Так как $tgx$ периодическая с минимальным периодом $\pi $, то получим, что $y=tg\left(x-2\pi \right)=tg\left(x-\pi \right)=tgx$. Получаем график:
Рисунок 5.
spravochnick.ru
| Развернуть структуру обучения | Свернуть структуру обучения |
|
Тригонометрический круг тангенса. Тригонометричне коло тангенса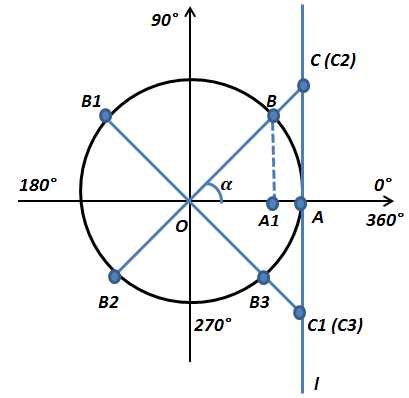
Значения функции тангенса угла (tg α)
Смотрите также: Теорема косинусов. Пример решения задачи | Описание курса | Тригонометрические соотношения в прямоугольном треугольнике |
profmeter.com.ua
Свойства синуса, косинуса, тангенса и котангенса
Глава 1. Тригонометрические функции
Тема 1. Тригонометрические формулы
Тема 2. Тригонометрические функции и их графики.
Тема 3. Решение тригонометрических уравнений.
Содержание обучения
Синус, косинус, тангенс и котангенс числового аргумента. Соотношения между тригонометрическими функциями одного аргумента. Формулы приведения.
Тригонометрические функции: синус, косинус, тангенс и котангенс; область определения и множество значений тригонометрических функций. Их свойства: возрастание и убывание, экстремумы, сохранение знака, периодичность, ограниченность. Графики синуса, косинуса. Простейшие тригонометрические уравнения.
Основная цель – ввести понятия синуса, косинуса, тангенса и котангенса числового аргумента; сформировать умения находить значения тригонометрических выражений на основе определений, с помощью калькулятора или таблиц, и выполнять несложные преобразования тригонометрических выражений; сформировать умения студентов строить графики синуса, косинуса, тангенса и котангенса, связывать свойства синуса и косинуса с их графиками; познакомить студентов со способами решения тригонометрических уравнений, формировать умение решать простейшие тригонометрические уравнения.
Тема 1. Тригонометрические формулы.
Цель: Ввести понятия синуса, косинуса, тангенса и котангенса произвольного угла, понятие радианной меры угла; познакомить со свойствами перечисленных тригонометрических функций, с основными формулами тригонометрии.
Оборудование: модель единичной окружности, справочная литература.
План
Тригонометрия и геометрия.
Радианная мера угла.
Синус, косинус, тангенс и котангенс числового аргумента.
Свойства синуса, косинуса, тангенса и котангенса.
Формулы приведения.
Основные тригонометрические формулы.
Свойства синуса, косинуса, тангенса и котангенса.
При нахождении значений чисел 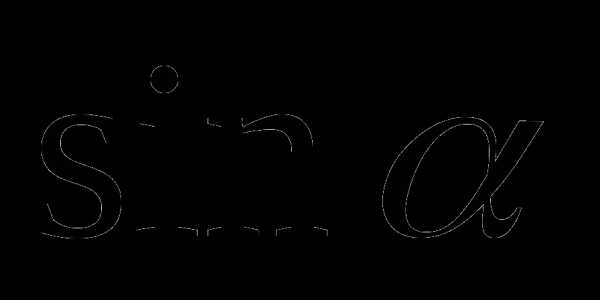 ,
, 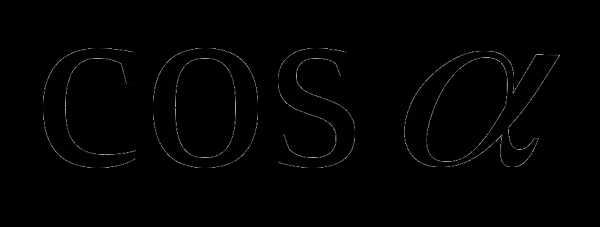 ,
, 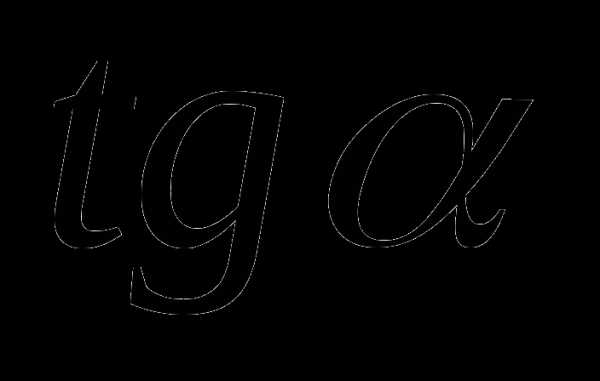 и
и 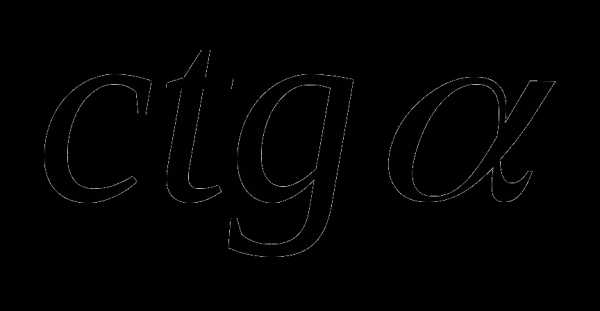 любого угла иногда удобно использовать следующие свойства:
любого угла иногда удобно использовать следующие свойства:
Знаки чисел
 ,
,  ,
,  и
и  .
.
Пусть при повороте на угол  точка
точка 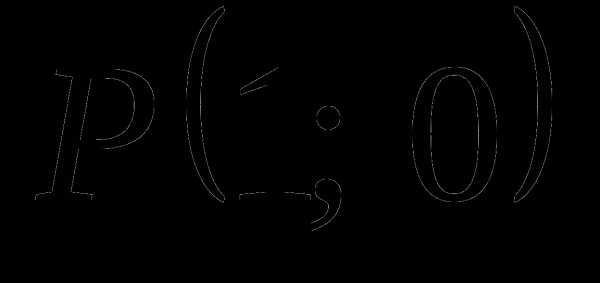 переходит в точку
переходит в точку 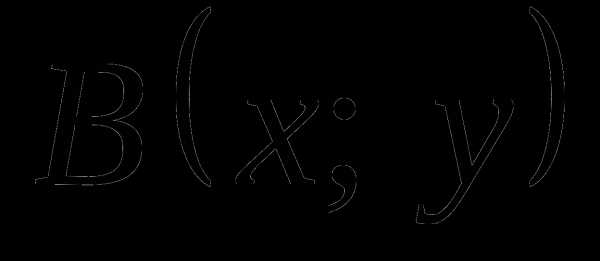 .
.
а) 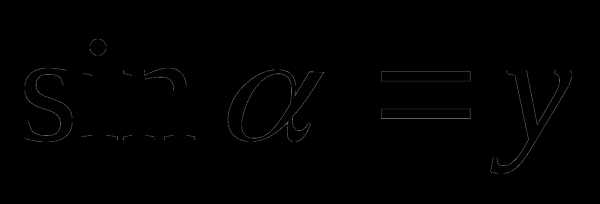 .
. 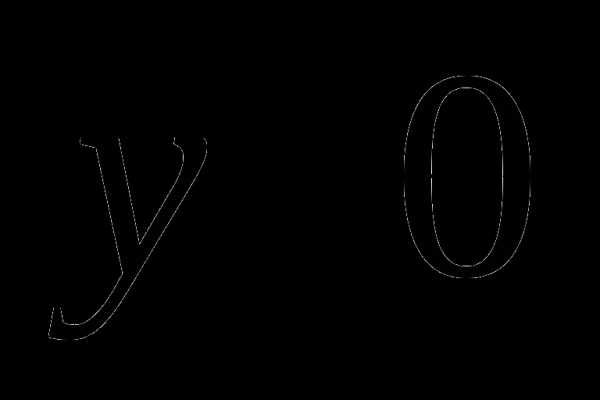 в I и II четвертях,
в I и II четвертях, 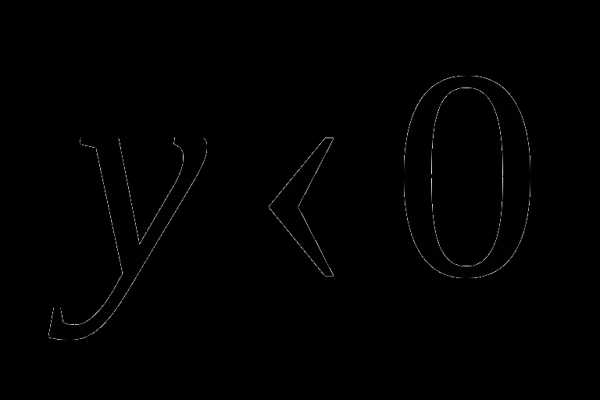 в III и IV четвертях. Значит
в III и IV четвертях. Значит
 , если точка
, если точка  окажется в I или II четвертях
окажется в I или II четвертях
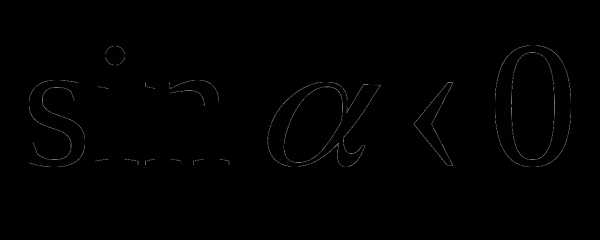 , если точка
, если точка  окажется в III или IV четвертях (рис. 5а)
окажется в III или IV четвертях (рис. 5а)
б) . 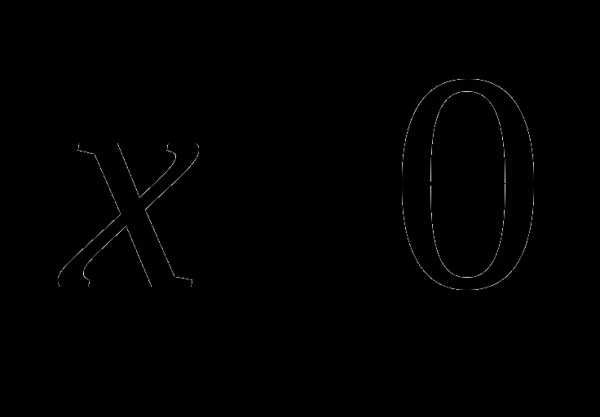 в I и IV четвертях,
в I и IV четвертях, 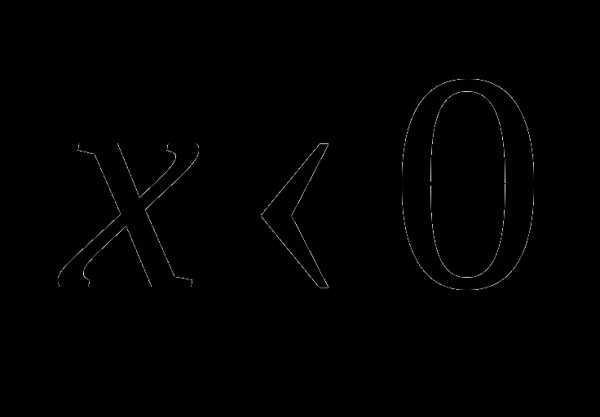 во II и III четвертях. Значит
во II и III четвертях. Значит
 , если точка
, если точка  окажется в I или IV четвертях
окажется в I или IV четвертях
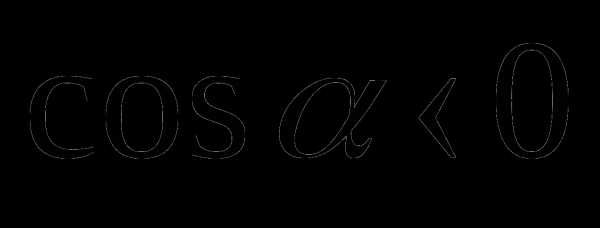 , если точка
, если точка  окажется во II или III четвертях (рис. 5б)
окажется во II или III четвертях (рис. 5б)
в) 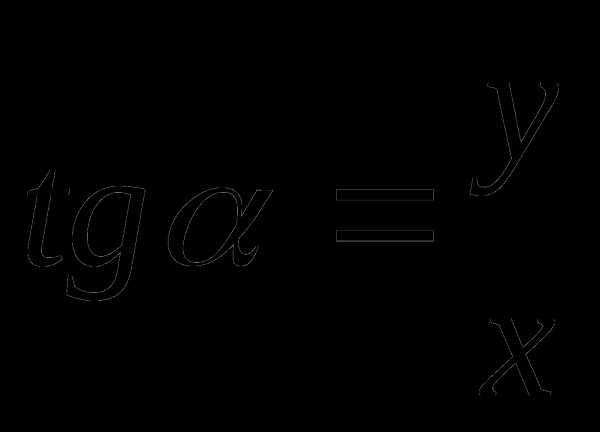 ,
, 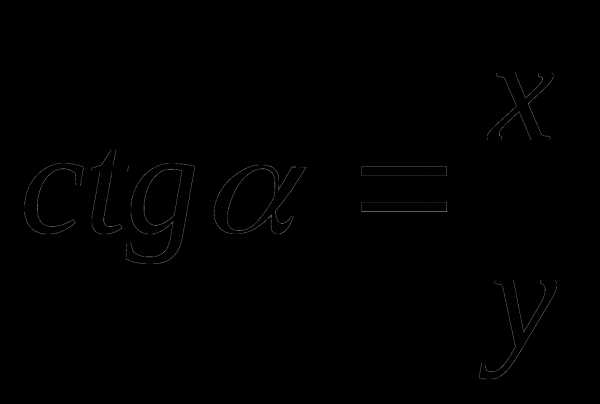 .
.  и
и  имеют одинаковые знаки в I и III четвертях и разные во II и IV четвертях. Значит
имеют одинаковые знаки в I и III четвертях и разные во II и IV четвертях. Значит
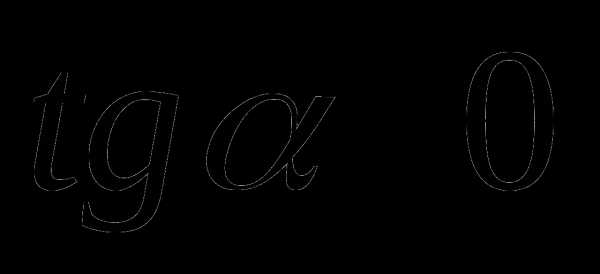 и
и 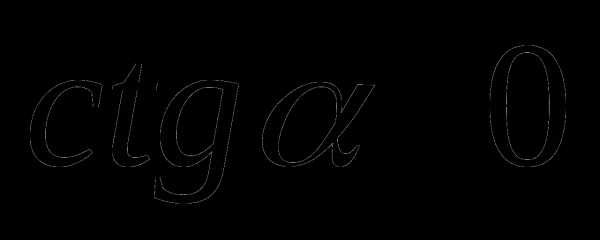 , если точка
, если точка  расположена в I или III четвертях
расположена в I или III четвертях
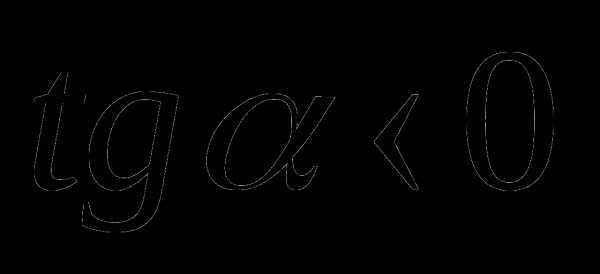 и
и 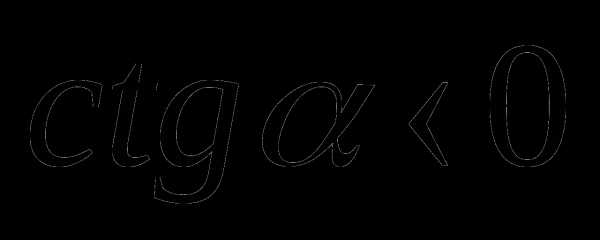 , если точка
, если точка  расположена во II или IV четвертях (рис. 5б)
расположена во II или IV четвертях (рис. 5б)
Рис. 5а
знаки синуса
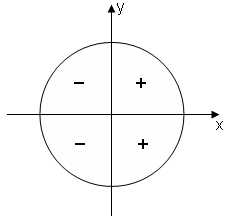
Рис. 5б
знаки косинуса
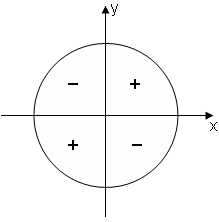
Рис. 5в
знаки тангенса и котангенса
Пример.
Определите знаки синуса, косинуса, тангенса углов:
а)  ; б)
; б) 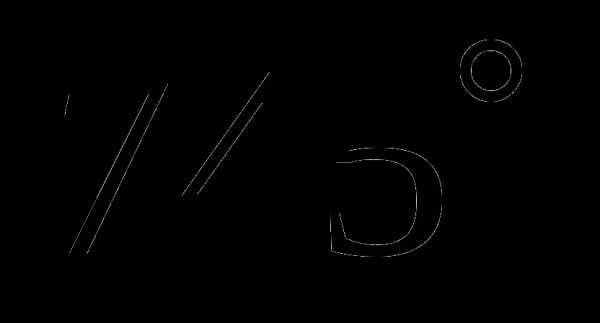 ; в)
; в) 
Решение:
а) Углу  соответствует точка единичной окружности, расположенная во II четверти. Поэтому
соответствует точка единичной окружности, расположенная во II четверти. Поэтому 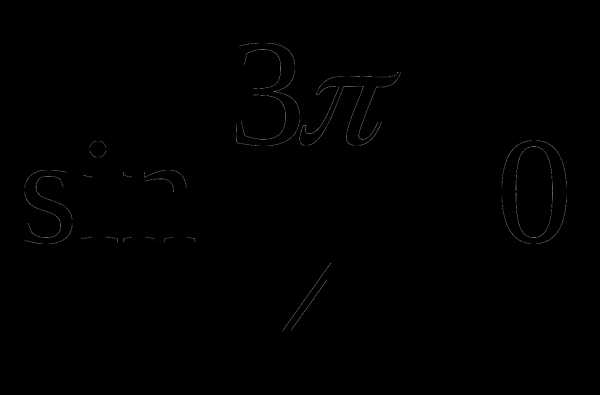 ,
,  ,
, 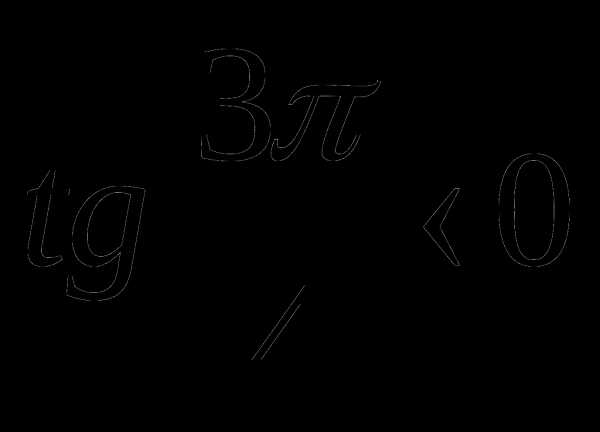 .
.
б) Так как , то повороту точки  на угол
на угол 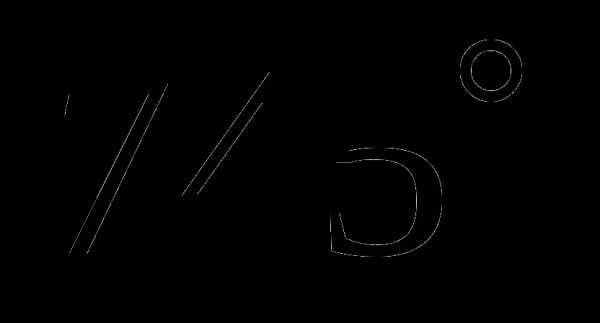 соответствует точка, расположенная в I четверти, Поэтому , , .
соответствует точка, расположенная в I четверти, Поэтому , , .
в) Так как 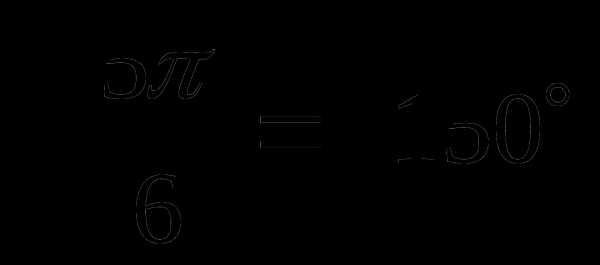 , то при повороте точки
, то при повороте точки  на угол
на угол 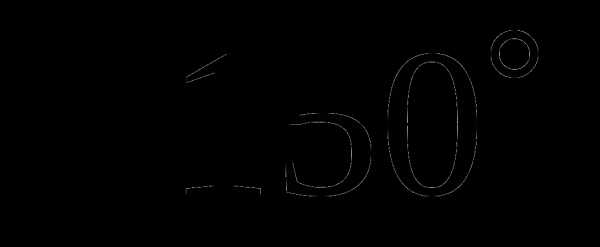 получается точка III четверти. Поэтому
получается точка III четверти. Поэтому  ,
,  ,
,  .
.
Задание 1. Выполните самостоятельно!
Определите знак выражения:
- Решение:
а) Повороту точки на угол соответствует точка единичной окружности, расположенная в III четверти, поэтому .
б) Повороту точки на угол соответствует точка единичной окружности, расположенная в IV четверти, поэтому .
в) Повороту точки на угол соответствует точка единичной окружности, расположенная в I четверти, поэтому .
Ответ: ; ; .
Синус, косинус, тангенс и котангенс углов
 и
и  .
.
Пусть точки
 и
и  единичной окружности получены поворотом точки
единичной окружности получены поворотом точки  на углы
на углы  и
и  (рис.6).
(рис.6).Рис. 6
 — равнобедренный ()
— равнобедренный ()луч
 — биссектриса
— биссектриса  , тогда отрезок
, тогда отрезок  — медиана и высота
— медиана и высота  . Тогда точки
. Тогда точки  и
и  симметричны относительно оси абсцисс. Если координаты точки
симметричны относительно оси абсцисс. Если координаты точки  , тогда координаты точки
, тогда координаты точки  , отсюда
, отсюда
Полученные формулы позволяют сводить вычисления значений синуса, косинуса, тангенса и котангенса отрицательных углов к вычислению их значений для положительных углов. Например,
Задание 2. Решить самостоятельно:
Вычислите .
Решение:
Ответ: .
Периодичность синуса и косинуса.
Если угол поворота
 равен
равен  , то при повороте на каждый из углов
, то при повороте на каждый из углов  ,
,  ,
,  ,
,  ,
,  ,
,  и т.д. точка придет из
и т.д. точка придет из  в
в  . Абсцисса и ордината точки
. Абсцисса и ордината точки  — это косинус и синус не только числа (угла)
— это косинус и синус не только числа (угла)  , но и чисел (углов)
, но и чисел (углов)  ,
,  ,
,  ,
,  ,
,  ,
,  и т.д.
и т.д.Значит, для любого числа
 выполняются равенства
выполняются равенства,
 ,
,,
 .
.Понятно, что аналогичные преобразования верны для
 и
и  .
.Из сказанного можно сделать вывод: при изменении угла на целое число оборотов значения синуса, косинуса, тангенса и котангенса не изменяются.
Пример.
Вычислить:
1)
 2)
2) 
Решение:
1)
2)
Задание 3. Вычислить самостоятельно
Вычислить:
- Решение:
а) .
б)
.
в) с.
Домашнее задание:
Упражнение 5.
Определите знак чисел:
Упражнение 6Найдите значение выражения:
Упражнение 7
Вычислите:
infourok.ru
тангенсоида — это… Что такое тангенсоида?
ТАНГЕНСОИДА — плоская кривая график функции y=tg x. См. Тригонометрические функции … Большой Энциклопедический словарь
ТАНГЕНСОИДА — ТАНГЕНСОИДА, тангенсоиды, жен. (от слова тангенс и греч. eidos вид) (мат.). Кривая линия, изображающая изменения тангенса в зависимости от изменения угла. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
тангенсоида — сущ., кол во синонимов: 1 • линия (182) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Тангенсоида — плоская кривая, изображающая изменение тангенса в зависимости от изменения его аргумента (угла). Т. состоит (см. рис.) из бесконечного числа отдельных конгруэнтных кривых, получаемых одна из другой сдвигом по оси Ох: на величину, кратную… … Большая советская энциклопедия
ТАНГЕНСОИДА — (от тангенс и греч. eidos вид) график ф ции у = tgx; плоская кривая, изображающая изменение тангенса в зависимости от изменения его аргумента (угла). Т. состоит (см. рис.) из бесконечного числа отд. конгруэнтных кривых, получаемых одна из другой… … Большой энциклопедический политехнический словарь
тангенсоида — плоская кривая график функции у = tgx. См. Тригонометрические функции. * * * ТАНГЕНСОИДА ТАНГЕНСОИДА, плоская кривая график функции y=tg x. См. Тригонометрические функции (см. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ) … Энциклопедический словарь
тангенсоида — тангенсоида, тангенсоиды, тангенсоиды, тангенсоид, тангенсоиде, тангенсоидам, тангенсоиду, тангенсоиды, тангенсоидой, тангенсоидою, тангенсоидами, тангенсоиде, тангенсоидах (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов
ТАНГЕНСОИДА — график функции y=tg x(рис. a). Т. периодич. кривая с периодом и асимптотами При изменении хот до умонотонно растет от до таким образом, Т. состоит из бесконечного числа отдельных конгруэнтных кривых, получаемых одна из другой сдвигом по оси Ох на … Математическая энциклопедия
ТАНГЕНСОИДА — плоская кривая график функции y = tgx. См. Тригонометрические функции … Естествознание. Энциклопедический словарь
тангенсоида — тангенс оида, ы … Русский орфографический словарь
dic.academic.ru

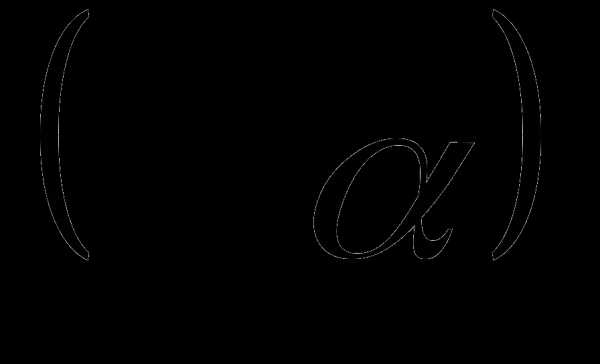 .
. единичной окружности получены поворотом точки
единичной окружности получены поворотом точки 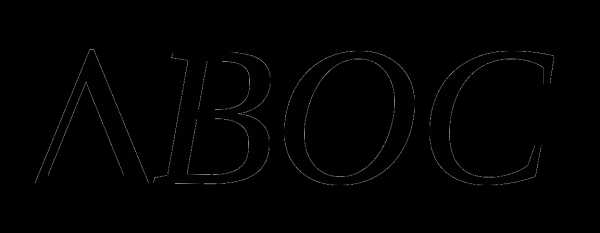 — равнобедренный ()
— равнобедренный ()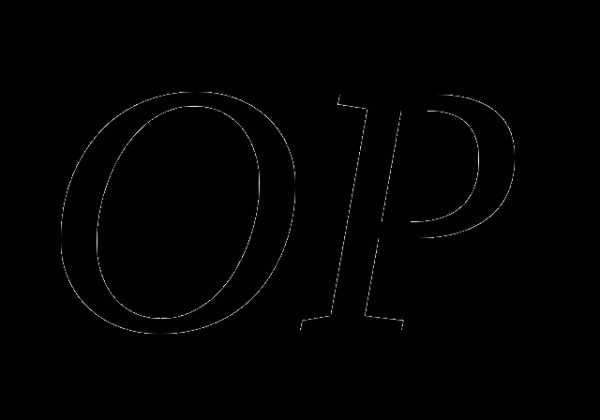 — биссектриса
— биссектриса 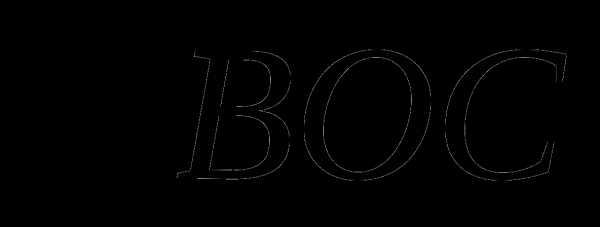 , тогда отрезок
, тогда отрезок  — медиана и высота
— медиана и высота  , отсюда
, отсюда равен
равен  ,
,  ,
,  ,
,  ,
,  ,
,  и т.д. точка придет из
и т.д. точка придет из  в
в  ,
, 2)
2) 