Несобственные интегралы
Сегодня я подготовил для вас подробную статью о несобственных интегралах.
Определенные интегралы , для которых отрезок [a; b] конечен, а функция f(x) – непрерывна на этом отрезке, называют собственными.
С целью обобщения понятия интеграла рассмотрим:
1) определенные интегралы от непрерывных функций, но с бесконечными пределами интегрирования;
2) определенные интегралы с конечными пределами интегрирования, но от функций, имеющих бесконечный разрыв на промежутке интегрирования. Такие определенные интегралы называют несобственными.
1. Интегралы с бесконечными пределами.
Пусть функция f(x) определена на промежутке [a; +∞) и пусть f(x) интегрирована на любом отрезке [a; b] (b> a– произвольные действительные числа).
Определение 1.1. Предел интеграла при b→+∞ называется несобственными интегралом функции f(x) от а до +∞ и обозначается символом:
Если предел (1.1) есть конечное число, то несобственный интеграл называют сходящимся. Если предел (1.1) не существует или равен бесконечности, то несобственный интеграл называют расходящимся.
Пример 1.1. Исследовать на сходимость интеграл
Решение. Вычислим определенный интеграл
Имеем
Следовательно, заданный интеграл сходится и он равен
Из рассмотренного следует, что вопрос о сходимости (расходимости) несобственных интегралов решается с помощью первоначальной функции для подынтегральной функции. Это обстоятельство сильно сужает круг практического использования понятия несобственного интеграла. В отдельных случаях вопрос о сходимости (расхождении) несобственного интеграла можно решить, не находя первообразной для подынтегральной функции. При этом пользуются так называемыми признаками сходимости несобственных интегралов. Простейшим признаком сходимости является признак сравнения.
Теорема 1.1. Пусть для всех x ≥ a функции f(x) и g(x) определены и выполняются неравенства 0 ≤ f(x) ≤ g(x). Тогда:
Для функции f(x), непрерывной на бесконечном промежутке -∞ < x ≤ b, определяется несобственный интеграл
Для функции f(x), непрерывной на всей числовой оси, несобственный интеграл определяется равенством:
где с – произвольное действительное число.
2. Интегралы от неограниченных функций.
Пусть функция f(x) такая, что для произвольного малого ɛ>0 она определена, ограничена и интегрирована на отрезке [a+ɛ; b] и неограниченна на (a; b].
Определение 1.2. Предел определенного интеграла при ɛ→0 называется несобственным интегралом функции f(x) на отрезке [a; b] и обозначается символом
Аналогично для функции f(x), определенной, непрерывной и интегрированной на отрезке [a; b- ɛ] и неограниченной на [a; b) обозначается несобственный интеграл:
Если пределы (1.4), (1.5) есть конечные числа, то несобственные интегралы называются сходящимися, а если эти пределы не существуют, то несобственные интегралы называются расходящимися.
В конце отметим, что для функции f(x), которая имеет на промежутке (a; b) точку с, в окрестности которой f(x) неограниченная, но является ограниченной и интегрированной на каждом из отрезков [a; c- ɛ] и [ñ + ɛ; b], интеграл определяется равенством.
Аналогично обозначается несобственный интеграл на отрезке [a; b] от функции, которая непрерывна на нем всюду, кроме конечного числа точек, и неограниченной вблизи этих точек.
Пример 1.2.Исследовать сходимость интегралов. Для сходящихся интегралов найти их значение:
Решение.
а) функция
ограничена и непрерывна, а потому и интегрируемая. Предельное значение
существует; таким образом,
ограничена и непрерывна, но
расходится.
Пример 1.3. Исследовать сходимость интегралов. Для сходящихся интегралов найти их значение
Решение.
если α > 0, интеграл сходится; если α ≤ 0, то интеграл расходится;
если α > 1; если 0 < α ≤ 1, интеграл расходится как и при α = 1:
так и при 0 < α < 1:
Пример 1.4. Найти несобственный интеграл
Решение. Функция непрерывна при 0 ≤ x < 2 и имеет бесконечный разрыв в точке x=2, поэтому имеем
Поэтому данный интеграл сходится и равен 2√2.
Пример 1.5. Исследовать сходимость интегралы. Для сходящихся интегралов найти их значение:
Решение.
то есть, несобственный интеграл расходится
то есть, несобственный интеграл I2 сходится и равен .
Пример 1.5. Исследовать на сходимость интегралы:
Решение.
Если у Вас есть ко мне вопросы, или нужна помощь, консультация по решению несобственных интегралов, записывайтесь на мои занятия. Буду рад Вам помочь.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Сходимость интегралов, формулы и примеры
Теорема (Признак сравнения). Пусть на промежутке функции и непрерывны, а в правом конце указанного промежутка, то есть в точке , терпят разрыв второго рода. Пусть для указанных функций справедливо следующее неравенство: . Тогда из сходимости интеграла следует сходимость интеграла , а из расходимости интеграла следует расходимость интеграла .3.3 Признаки сходимости несобственных интегралов
Рассмотрим достаточные признаки сходимости несобственных интегралов (признаки сравнения), позволяющие выяснить вопрос о сходимости несобственного интеграла без знания первообразной его подынтегральной функции.
Признак
сравнения 1 (без доказательства). Пусть
на промежутке 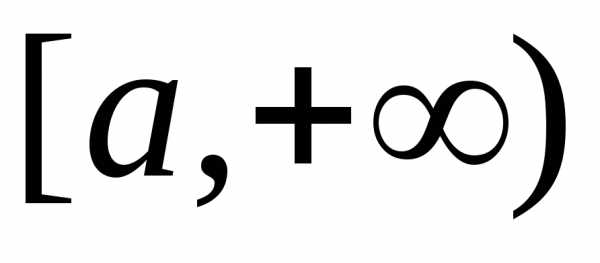 функции
функции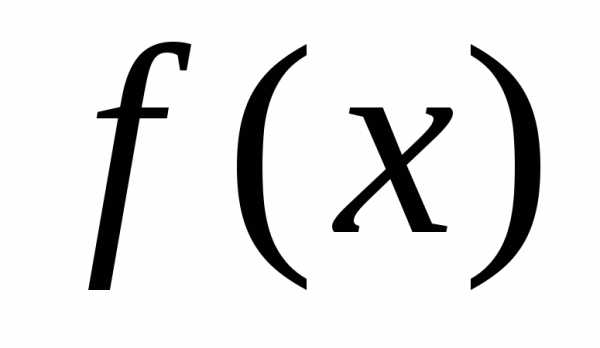 и
и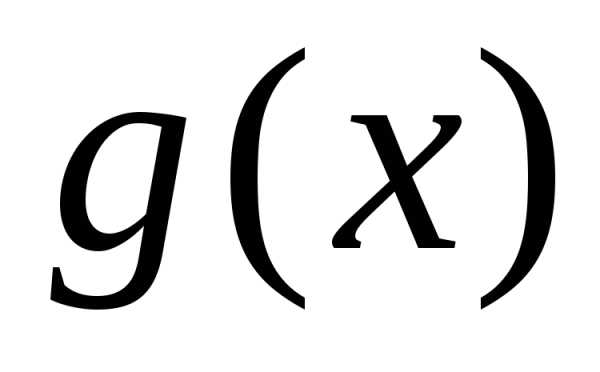 непрерывны и удовлетворяют неравенствам.
Тогда:
непрерывны и удовлетворяют неравенствам.
Тогда:
1) если интеграл  сходится, то сходится и интеграл
сходится, то сходится и интеграл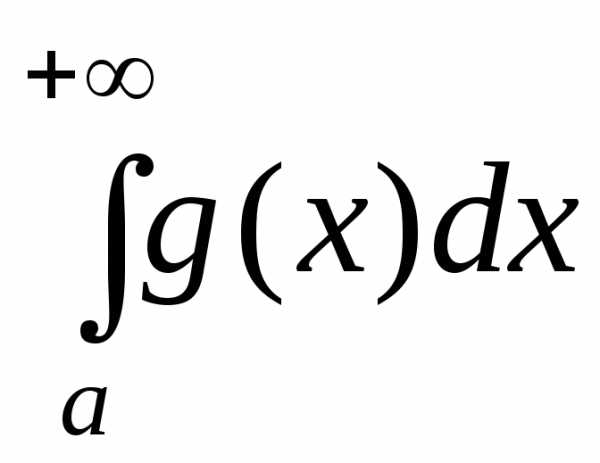 ;
;
2) если интеграл 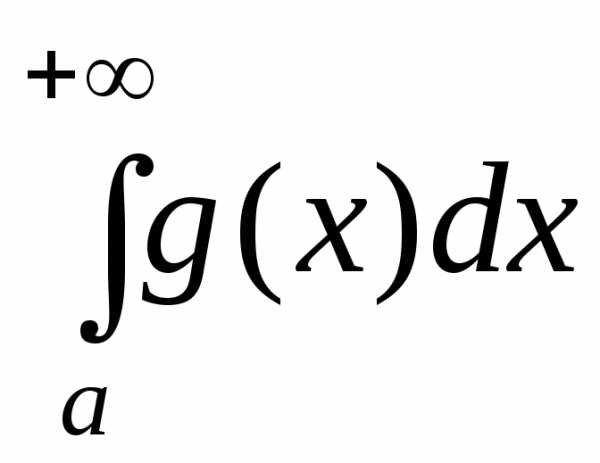 расходится, то расходится и интеграл
расходится, то расходится и интеграл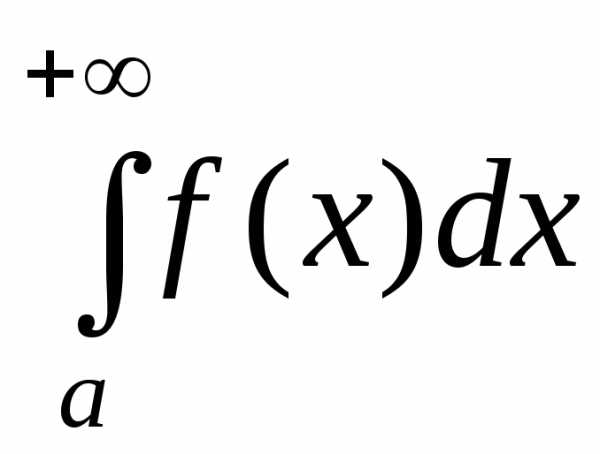 .
.
Признак
сравнения 2 (без доказательства). Пусть
на промежутке 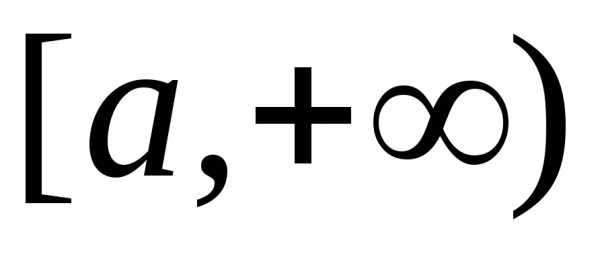 функции
функции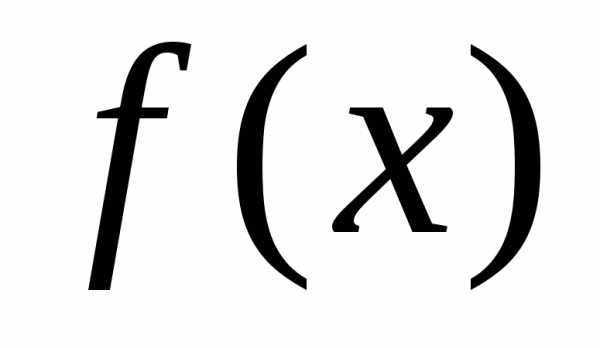 и
и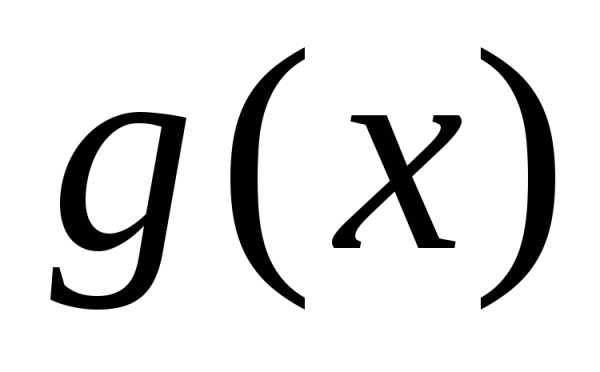 непрерывны и удовлетворяют неравенствам.
Тогда, если существует конечный и
отличный от нуля предел
непрерывны и удовлетворяют неравенствам.
Тогда, если существует конечный и
отличный от нуля предел
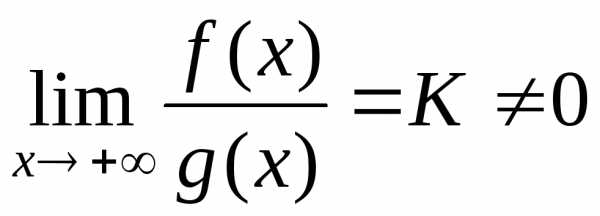
то несобственные
интегралы 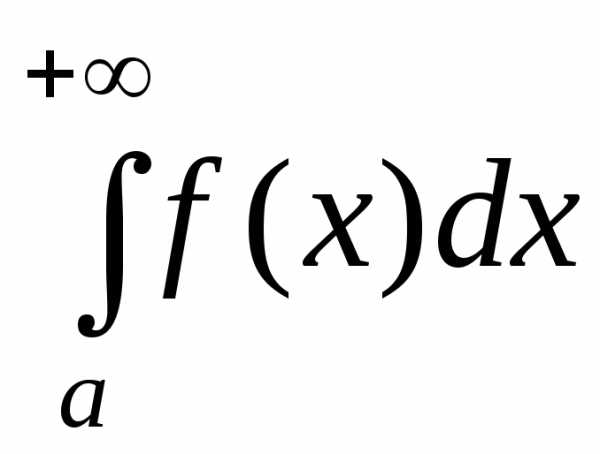 и
и оба сходятся или оба расходятся.
оба сходятся или оба расходятся.
Замечание 1. Аналогичные признаки сравнения справедливы и для других видов несобственного интеграла первого рода, а также для несобственных интегралов второго рода.
Замечание 2. При применении признаков сравнения требуется знать несобственные интегралы, относительно которых заранее известно, сходятся они или расходятся. В качестве таких «эталонных» интегралов на практике часто используются следующие несобственные интегралы:
1) несобственный интеграл первого рода
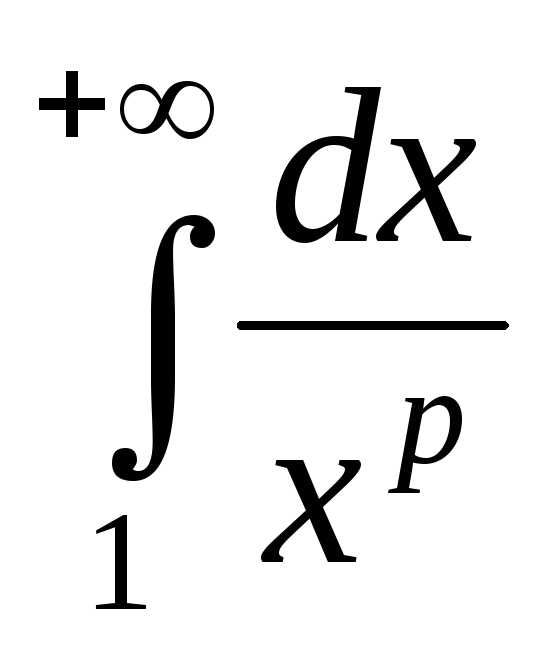 ,
,
который сходится
при 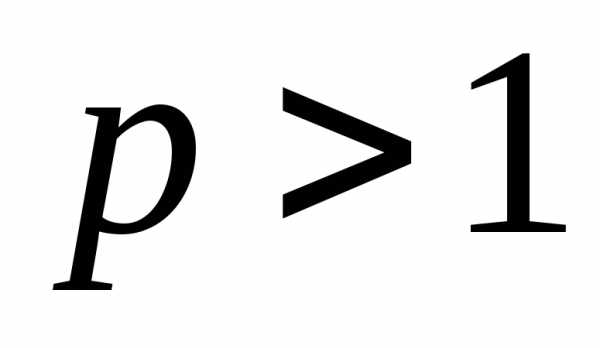
 ;
;2) несобственный интеграл второго рода
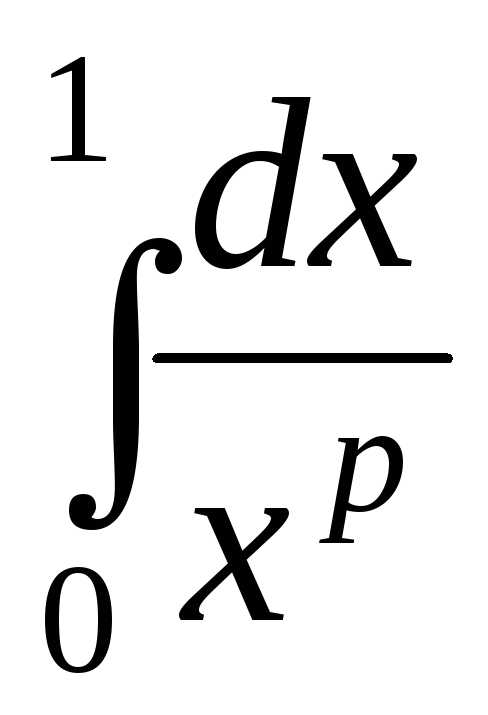 ,
,
который сходится
при 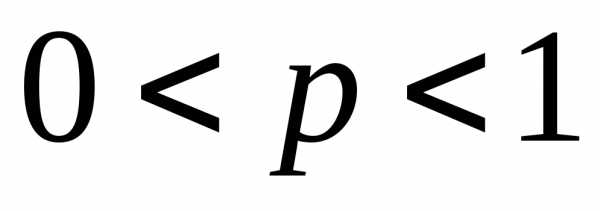 и расходится при
и расходится при .
.
Пример. Исследуем на сходимость несобственный интеграл первого рода
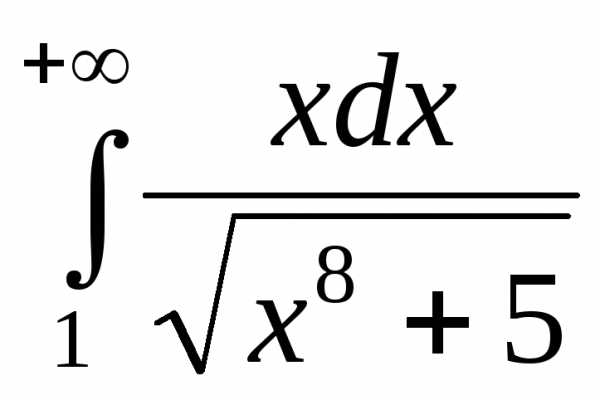 .
.
Так как на промежутке 
 ,
,
а интеграл  сходится,
то по признаку сравнения 1 исходный
интеграл также сходится.
сходится,
то по признаку сравнения 1 исходный
интеграл также сходится.
3.4 Абсолютная и условная сходимости
Определение. Несобственный интеграл называется абсолютно сходящимся, если сходится несобственный интеграл от абсолютной величины подынтегральной функции.
Несобственный интеграл называется условно сходящимся, если он сходится, а несобственный интеграл от абсолютной величины подынтегральной функции расходится.
Теорема 3.1 (без доказательства). Абсолютно сходящийся интеграл сходится.
Используя понятие абсолютной сходимости и данную теорему, можно исследовать сходимость несобственных интегралов от знакопеременных функций, применяя признаки сравнения.
Пример. Исследуем на сходимость несобственный интеграл первого рода
от знакопеременной функции
 .
.
Так как на промежутке 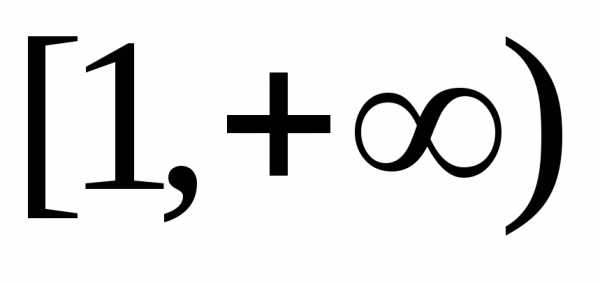
,
и интеграл 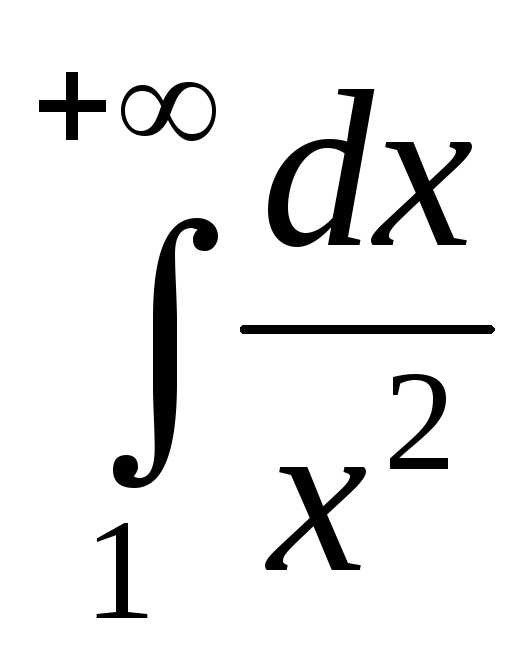 сходится,
то по признаку сравнения 1 исходный
интеграл также сходится (абсолютно).
сходится,
то по признаку сравнения 1 исходный
интеграл также сходится (абсолютно).
4 Обыкновенные дифференциальные уравнения
4.1 Общие понятия
Определение. Дифференциальным уравнением называется уравнение, содержащее производные или дифференциалы неизвестной функции.
Если неизвестная функция зависит только от одного аргумента, то дифференциальное уравнение называется обыкновенным.
Если же неизвестная функция зависит от двух или большего числа независимых переменных, то дифференциальное уравнение называется уравнением в частных производных.
Определение. Порядком n дифференциального уравнения называется порядок наивысшей производной или наивысшего дифференциала, входящих в уравнение.
В данном разделе
будем изучать только обыкновенные
дифференциальные уравнения, как правило,
относительно неизвестной функции 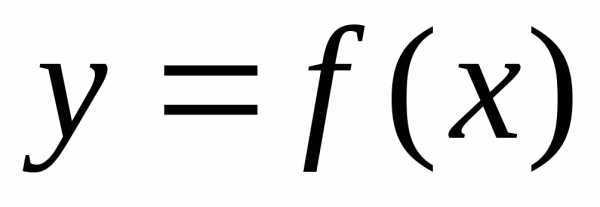 аргументаx.
аргументаx.
Примеры
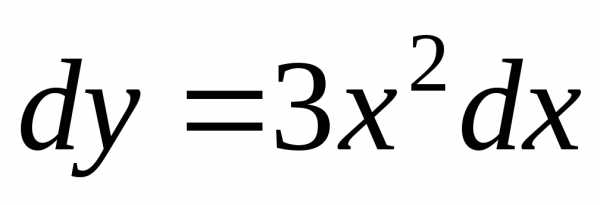 ,
, 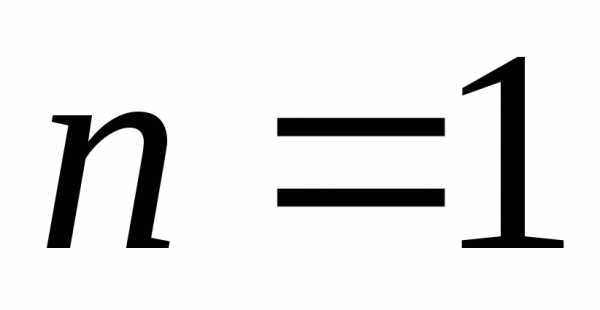 , уравнение 1-го порядка;
, уравнение 1-го порядка;
,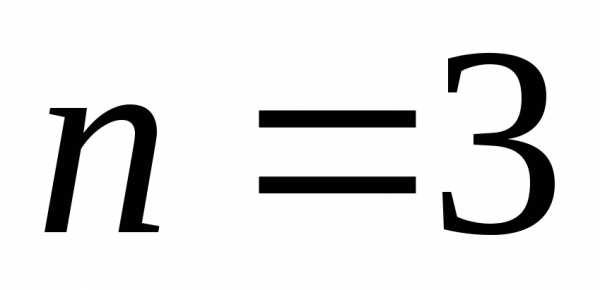 , уравнение 3-го порядка;
, уравнение 3-го порядка;
,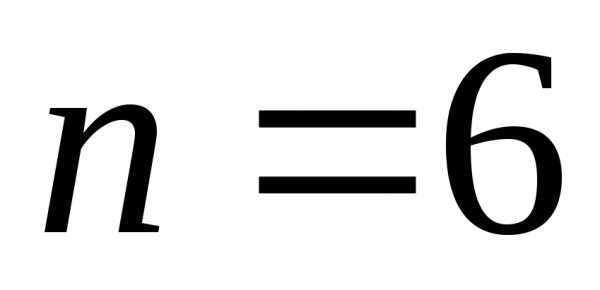 , уравнение 6-го порядка.
, уравнение 6-го порядка.
Определение. Решением дифференциального
уравнения называется функция  ,
которая при подстановке в дифференциальное
уравнение обращает его в верное равенство
(тождество).
,
которая при подстановке в дифференциальное
уравнение обращает его в верное равенство
(тождество).
Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения, а действие интегрирования функций называется квадратурой.
При этом под
квадратурой 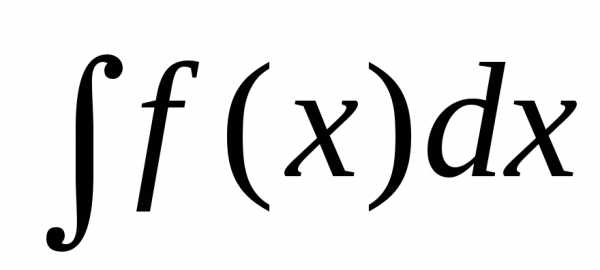 всегда будем понимать какую-либоодну первообразную.
всегда будем понимать какую-либоодну первообразную.
Однако не всегда
решение дифференциального уравнения
может быть получено в виде явно заданной
функции 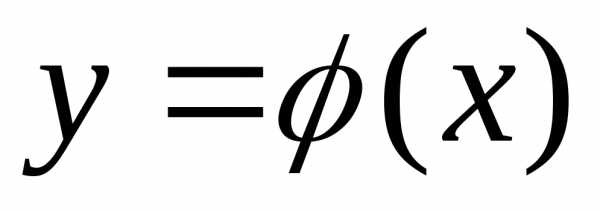 .
.
Пример
;
;
.
Обозначим
.
Определение.
Уравнение
,которое
определяет решение 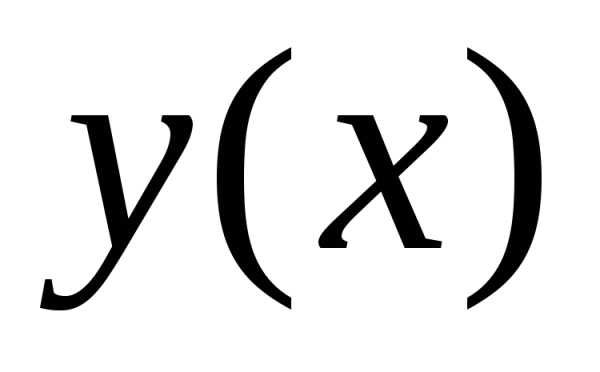 дифференциального уравнения как неявную
функциюx,
называется интегралом рассматриваемого
дифференциального уравнения.
дифференциального уравнения как неявную
функциюx,
называется интегралом рассматриваемого
дифференциального уравнения.
studfiles.net
Определение определенного интеграла. Основные свойства определенного интеграла. Приложения определенного интеграла, страница 7
7. Несобственные интегралы
Рассмотрим так называемые несобственные интегралы, т.е. определенный интеграл от непрерывной функции, но с бесконечным промежутком интегрирования (несобственный интеграл I рода), или определенный интеграл с конечным промежутком интегрирования, но от функции, имеющей на нем бесконечный разрыв (несобственный интеграл II рода).
Рассмотрим, как вычисляются несобственные интегралы I рода. Здесь возможны три варианта:
1) Пусть функция непрерывна на промежутке , тогда
0 а х Рисунок 19 | . Если этот предел существует, то говорят, что интеграл сходится; если же предел не существует или бесконечен, то говорят, что интеграл расходится. |
2) Если функция непрерывна на промежутке , тогда
в 0 х Рисунок 20 | . Сходимость и расходимость такого интеграла определяется аналогично. |
Несобственный интеграл с двумя бесконечными пределами интегрирования определяется формулой
,
где с – произвольное число.
у
0 с х Рисунок 21 | Интеграл, стоящий в левой части равенства, сходится лишь тогда, когда сходятся оба интеграла, стоящие в правой части равенства. |
Вычислить несобственные интегралы или установить их расходимость :
1. данный интеграл сходится.
2. т. к. при не существует, данный интеграл расходится.
следовательно, данный интеграл сходится.
В некоторых задачах нет необходимости вычислять интеграл, достаточно лишь знать, сходится он или нет.
Сформулируем признак сходимости:
Интеграл : 1) сходится, если и ;
2) расходится, если и , где М, m — постоянные.
Пример. Установить, сходится или расходится интеграл , используя признак сходимости.
Решение. Так как , то , т.е. подынтегральная функция удовлетворяет условию (1) при , данный интеграл сходится.
Теперь рассмотрим, как вычисляются несобственные интегралы II рода.
Если функция терпит бесконечный разрыв в точках , или , или , то интеграл называется несобственным интегралом II рода.
Таким образом, при вычислении таких интегралов также возможны три варианта:
Если хотя бы один из пределов не существует или равен бесконечности, несобственный интеграл II рода расходится. В противном случае – сходится.
Вычислить несобственные интегралы или установить их расходимость:
1.
,
следовательно, данный интеграл сходится.
2.
так как этот предел не существует, следовательно, данный интеграл расходится.
3.
следовательно, данный интеграл расходится .
Задания для самостоятельной работы
Вычислить несобственные интегралы или установить их расходимость:
Ответы:
1. | . |
2. | 1. |
3. . | Расходится. |
4. . | 6. |
5. . | 1. |
6. . | . |
vunivere.ru
2. Несобственные интегралы
Несобственный интеграл
Определенный интеграл как предел интегральной суммы
может существовать (т.е. иметь определенное конечное значение) лишь при выполнении условий
отрезок интегрирования [a; b] конечный;
подынтегральная функция непрерывная (или хотя бы кусочно-непрерывная) и, следовательно, ограниченная на этом отрезке.
Если хотя бы одно из этих условий нарушено, то определение теряет смысл. Действительно, в случае бесконечного отрезка, например [a; ) его нельзя разбить на п частей конечной длины , которая к тому же с увеличением количества отрезков стремилась бы к нулю. В случае же неограниченной в некоторой точкес[a; b] нарушается требование произвольного выбора точки на частичных отрезках – нельзя выбрать=с, поскольку значение функции в этой точке не определено. Однако и для этих случаев можно обобщить понятие определенного интеграла, введя еще один предельный переход. Интегралы по бесконечным промежуткам и от разрывных (неограниченных) функций называют несобственными.
Определение.
Пусть функция определена на промежутке [a; ) и интегрируема на любом конечном отрезке [a; b], т.е. существует для любого b > a. Предел вида называютнесобственным интегралом первого рода (или несобственным интегралом по бесконечному промежутку) и обозначают .
Таким образом, по определению, =.
Если предел справа существует и конечен, то несобственный интеграл называютсходящимся. Если этот предел бесконечен, или не существует вообще, то говорят, что несобственный интеграл расходится.
Аналогично можно ввести понятие несобственного интеграла от функции по промежутку (–; b]:
=.
А несобственный интеграл от функции по промежутку (–; +) определяется как сумма введенных выше интегралов:
=+,
где а – произвольная точка. Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно из слагаемых.
С геометрической точки зрения, интеграл,, определяет численное значение площади бесконечной криволинейной трапеции, ограниченной сверху графиком функции, слева – прямой, снизу – осью ОХ. Сходимость интеграла означает существование конечной площади такой трапеции и равенство ее пределу площади криволинейной трапеции с подвижной правой стенкой.
На случай интеграла с бесконечным пределом можно обобщить и формулу Ньютона-Лейбница:
= =F(+) – F(a),
где F(+) = . Если этот предел существует, то интеграл сходится, в противном случае – расходится.
Мы рассмотрели обобщение понятия определенного интеграла на случай бесконечного промежутка.
Рассмотрим теперь обобщение для случая неограниченной функции.
Определение
Пусть функция определена на промежутке [a; b), неограниченна в некоторой окрестности точки b, и непрерывна на любом отрезке , где>0 (и, следовательно, интегрируема на этом отрезке, т.е. существует). Предел виданазываетсянесобственным интегралом второго рода (или несобственным интегралом от неограниченной функции) и обозначается .
Таким образом, несобственный интеграл от неограниченной в точке b функции есть по определению
=.
Если предел справа существует и конечен, то интеграл называется сходящимся. Если конечного предела не существует, то несобственный интеграл называется расходящимся.
Аналогично можно определить несобственный интеграл от функции имеющей бесконечный разрыв в точкеа:
=.
Если функция имеет бесконечный разрыв во внутренней точкес, то несобственный интеграл определяется следующим образом
=+ = +.
Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно слагаемое.
С геометрической точки зрения, несобственный интеграл от неограниченной функции также характеризует площадь неограниченной криволинейной трапеции:
Поскольку несобственный интеграл выводится путем предельного перехода из определенного интеграла, то все свойства определенного интеграла могут быть перенесены (с соответствующими уточнениями) на несобственные интеграла первого и второго рода.
Во многих задачах, приводящих к несобственным интегралам, не обязательно знать, чему равен этот интеграл, достаточно лишь убедиться в его сходимости или расходимости. Для этого используют признаки сходимости. Признаки сходимости несобственных интегралов:
1) Признак сравнения.
Пусть для всех х. Тогда, еслисходится, то сходится и, причем. Еслирасходится, то расходится и.
2) Если сходится , то сходится и(последний интеграл в этом случае называетсяабсолютно сходящимся).
Признаки сходимости и расходимости несобственных интегралов от неограниченных функций аналогичны сформулированным выше.
Примеры решения задач.
Пример 1.
Вычислить несобственный интеграл или установить его расходимость:
а) ; б); в)
г) ; д).
Решение.
а) По определению имеем:
,
Следовательно, данный интеграл сходится и равен .
б) Аналогично
.
Следовательно, данный интеграл сходится и равен .
в) По определению =+, причем,а – произвольное число. Положим в нашем случае , тогда получим:
.
Данный интеграл сходится.
г)
Значит, данный интеграл расходится.
д) Рассмотрим. Чтобы найти первообразную подынтегральной функции, необходимо применить метод интегрирования по частям. Тогда получим:
Поскольку ни , нине существуют, то не существует и
.
Следовательно, данный интеграл расходится.
Пример 2.
Исследовать сходимость интеграла в зависимости от п.
Решение.
При имеем:
.
Если , тои. Следовательно, интеграл расходится.
Если , то, а, тогда
,
=,
Следовательно, интеграл сходится.
Если , то
,
следовательно, интеграл расходится.
Таким образом,
Пример 3.
Вычислить несобственный интеграл или установить его расходимость:
а) ; б); в) .
Решение.
а) Интегралявляется несобственным интегралом второго рода, поскольку подынтегральная функцияне ограничена в точке. Тогда, по определению,
.
Интеграл сходится и равен .
б) Рассмотрим. Здесь также подынтегральная функция не ограничена в точке. Поэтому, данный интеграл – несобственный второго рода и по определению,
.
Следовательно, интеграл расходится.
в) Рассмотрим. Подынтегральная функциятерпит бесконечный разрыв в двух точках:и, первая из которых принадлежит промежутку интегрирования. Следовательно, данный интеграл – несобственный второго рода. Тогда, по определению
==
.
Следовательно, интеграл сходится и равен .
studfiles.net
Примеры исследования несобственных интегралов на сходимость
Примеры исследования несобственных интегралов на сходимость
Пример 1 Исследовать на сходимость . Вычислим интеграл по определению: .
Таким образом, данный интеграл сходится при a>1 и расходится при a£1.
Пример 2 Исследовать на сходимость . Вычислим интеграл по определению: .
Таким образом, данный интеграл сходится при a<1 и расходится при a³1.
Пример 3 Исследовать на сходимость .
Подынтегральная функция может быть бесконечно большой ( если m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два
.
Сходимость первого интеграла I1 исследуем с помощью эквивалентной функции: ( т. к. n>0), а интеграл сходится при m>-1 (пример 2). Аналогично, для интеграла I2 :
, а интеграл сходится при m+n<-1 (пример2). Следовательно, исходный интеграл сходится при выполнении одновременно двух условий m>-1 и m+n<-1, и будет расходится при нарушении хотя бы одного из них.
Пример 4 Исследовать на сходимость .
Подынтегральная функция может быть бесконечно большой ( если m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два:
.
Так как arctgx »x при x®0, то интеграл I1 эквивалентен интегралу , который сходится при m+1>-1 т. е. при m>-2 (пример1).
Для подынтегральная функции в несобственном интеграле первого рода I2 подберем эквивалентную:
т. к. arctgx » p/2 при x® ¥. Следовательно, по второму признаку сравнения интеграл I2 будет сходится при m+n<-1, и расходится в противном случае.
Объединяя условия сходимости интегралов I1 и I2 получим условия сходимости исходного интеграла: m>-2 и m+n<-1 одновременно.
Замечание. В примерах 2-4 использовался 2 признак сравнения, который обеспечивает необходимые и достаточные условия сходимости, что позволяет, установив сходимость при некотором условии на значения параметров, не доказывать расходимость интеграла при нарушении полученных условий сходимости.
Пример 5 Исследовать на сходимость .
Данный интеграл содержит особую точку 0, в которой подынтегральная функция может обращается в бесконечность при p<0, поэтому снова разобьем исходный интеграл на два:
.
Интеграл I1 является несобственным интегралом второго рода, и подынтегральная функция эквивалентна при x®0 функции xp (e-x ®1 при x®0), т. е. I1 сходится при p>-1 (пример 1).
Интеграл I2 является несобственным интегралом первого рода. Подобрать функцию, эквивалентную подынтегральной функции, такую, чтобы она не содержала показательной функции, не удается. Поэтому использовать признак сравнения 2, как в предыдущих примерах, нельзя. Применим первый признак сравнения, для чего используем следующий известный факт:
При a>0 и любом p. Из этого, и того, что функция xpe-ax непрерывна, следует, что эта функция ограничена, т. е. существует такая константа M>0, что xpe-ax < M. Возьмем, например, a=1/2, и оценим интеграл I2 сверху:
,
Т. е. интеграл I2 сходится при любом p.
Таким образом, исходный интеграл сходится при p>-1.
Пример 6 Исследовать на сходимость .
Проведем замену переменной: t = lnx, и получим
.
Разбиение интеграла на два произведено аналогично примеру 5. Интеграл I1 полностью эквивалентен интегралу I1 из примера 5 и, следовательно, сходится при q<1.
Рассмотрим интеграл I2 . При условии 1-p<0 этот интеграл полностью эквивалентен интегралу I2 в примере 5 (доказательство сходимости аналогично, а условие 1-p<0 нужно для выполнения и a=(1-p)/2. ).
Итак, I2 сходится при p>1. Однако, на этом исследование сходимости этого интеграла не закончено, так как использованный признак сходимости дает только достаточные условия сходимости. Поэтому нужно исследование сходимости при 1-p£0.
Рассмотрим случай p=1. Тогда интеграл I2 эквивалентен , который сходится при q>1 (заметим, что в этом случае интеграл I1 расходится) и расходится в противном случае.
При p<1 оценим интеграл I2 и покажем его расходимость. Для этого вспомним, что При 1-p>0, и, следовательно, начиная с некоторого А>1 выполнено T—QE(1-P)T ³ M=const>0. Тогда для интеграла I2 справедлива оценка
,
Где интеграл в правой части расходится, что и доказывает расходимость интеграла I2 .
Суммируя полученные результаты, получаем что исходный интеграл сходится при q<1 и p>1, в противном случае интеграл расходится.
Пример 6 Исследовать на абсолютную и условную сходимость .
Разобьем исходный интеграл на два:
.
Сходимость. Интеграл I1 эквивалентен , т. е. сходится при p<2 (пример 1) , причем абсолютно, так как подынтегральная функция положительна на отрезке интегрирования.
Интеграл I2 сходится про признаку Дирихле-Абеля при p>0 т. к. первообразная sin(x) ограничена, а функция 1/xp монотонно стремится к нулю при x стремящемся к бесконечности.
Покажем, что при p£0 интеграл расходится. Воспользуемся для этого критерием Коши, а точнее его отрицанием
.
Возьмем в качестве R1и R2 следующие величины: R1=2pk и R2=2pk+p/2, тогда
, при p>0.
Таким образом, интеграл сходится при 0<p<1.
Абсолютная сходимость Абсолютная сходимость интеграла I1 уже установлена, рассмотрим абсолютную сходимость I2 . Оценим интеграл сверху:
, т. е. интеграл сходится при p>1.
Для доказательства расходимости при p£1 оценим интеграл снизу
.
Разобьем последний интеграл от разности функций на разность интегралов
.
Если оба интеграла сходятся, то и интеграл от разности сходится, если один из интегралов расходится, а другой сходится — то интеграл от разности расходится. В случае расходимости обоих интегралов сходимость интеграла от разности подлежит дальнейшему исследованию. Нас интересует второй из описанных случаев.
расходится (пример 1) при p<1. сходится по признаку Дирихле-Абеля при 1>p>0 (см. Сходимость), следовательно интеграл оценивается снизу расходящимся интегралом, т. е. расходится.
Случай p³1 нас не интересует, т. к. при этих значениях параметра интеграл расходится.
Таким образом, исходный интеграл сходится абсолютно при 0<p<1, сходится условно при 1£p<2.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
§1. Несобственные интегралы 1-го рода
– 68–
Тема НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
В
теме «Определенный интеграл» было
рассмотрено понятие определенного
интеграла 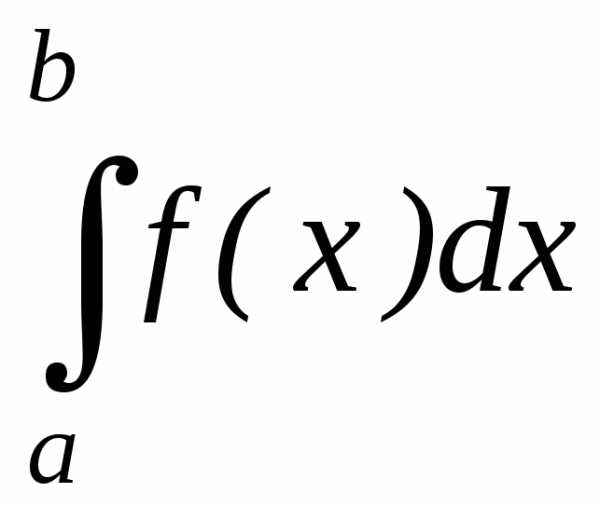 для случая конечного промежутка
для случая конечного промежутка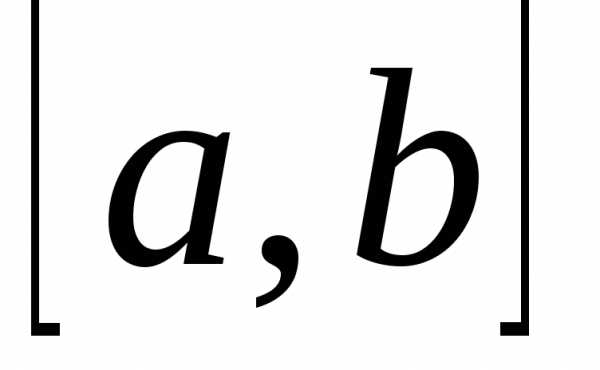 и ограниченной функции
и ограниченной функции (см. теорему 1 из §3). Теперь займемся
обобщением этого понятия для случаев
бесконечного промежутка и неограниченной
функции. Необходимость такого обобщения
показывают, например, такие ситуации.
(см. теорему 1 из §3). Теперь займемся
обобщением этого понятия для случаев
бесконечного промежутка и неограниченной
функции. Необходимость такого обобщения
показывают, например, такие ситуации.
1. Если, используя формулу для длины дуги, попытаться вычислить длину четверти окружности ,, то придем к интегралу от неограниченной функции:
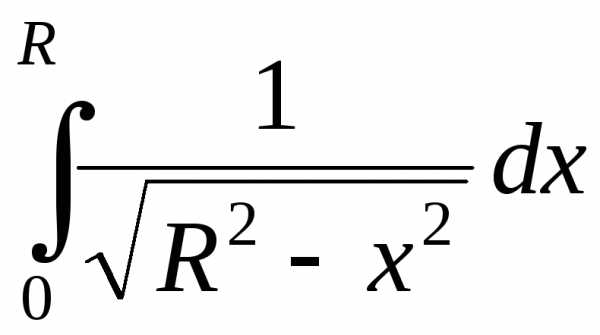 ,
где
,
где 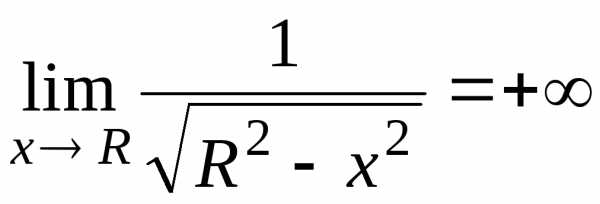 .
.
2.
Пусть тело массой 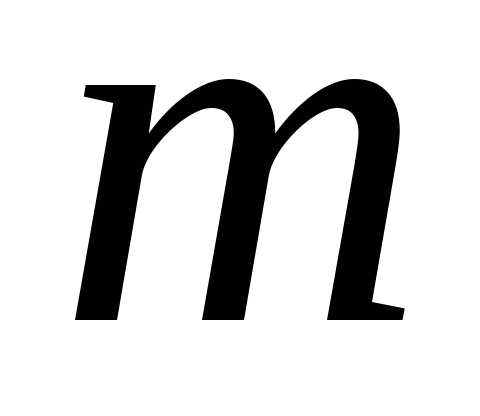 движется
по инерции в среде с силой сопротивления
,
где
движется
по инерции в среде с силой сопротивления
,
где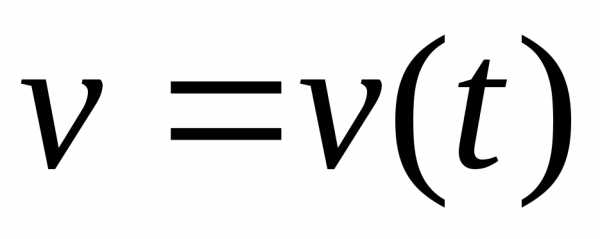 — скорость тела. Используя второй закон
Ньютона (
— скорость тела. Используя второй закон
Ньютона (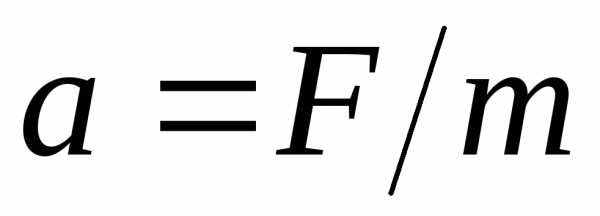 ,
где
,
где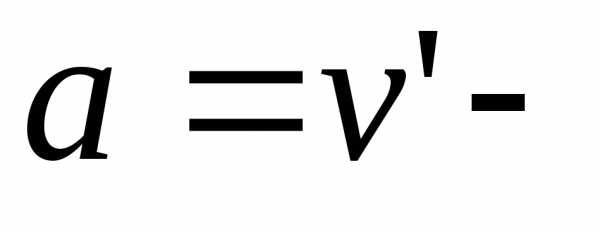 ускорение),
получим уравнение:,
где
ускорение),
получим уравнение:,
где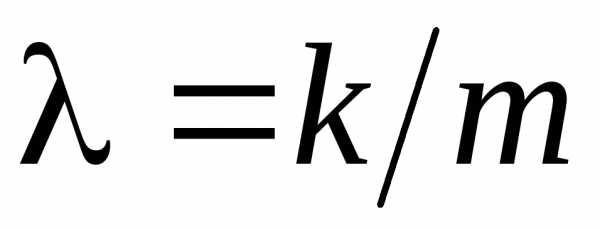 .
Нетрудно показать, что решением этого
(дифференциального!) уравнения является
функцияЕсли
нам потребуется вычислить путь, пройденный
телом до полной остановки, т.е. до момента,
когда
.
Нетрудно показать, что решением этого
(дифференциального!) уравнения является
функцияЕсли
нам потребуется вычислить путь, пройденный
телом до полной остановки, т.е. до момента,
когда  ,
то придем к интегралу по бесконечному
промежутку:
,
то придем к интегралу по бесконечному
промежутку:
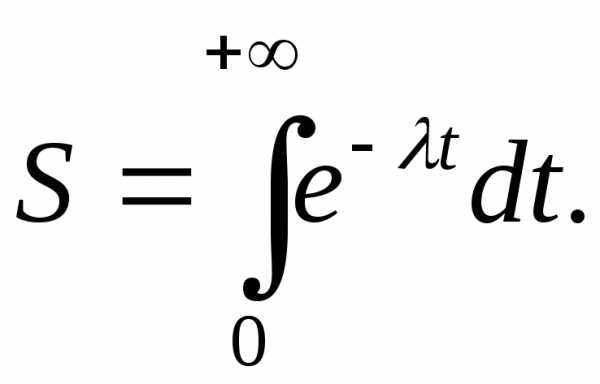
I Определение
Пусть
функция 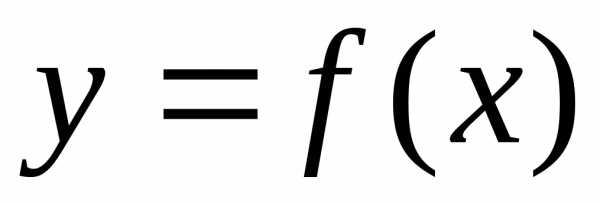 определена и непрерывна на промежутке
определена и непрерывна на промежутке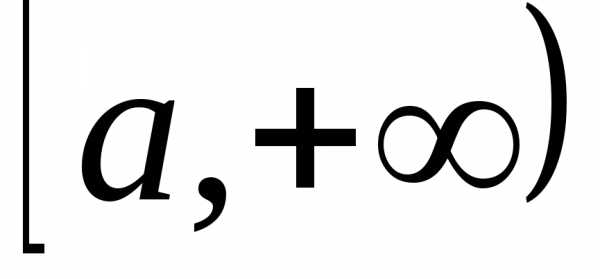 .
Тогда для любого
.
Тогда для любого она интегрируема на промежутке
она интегрируема на промежутке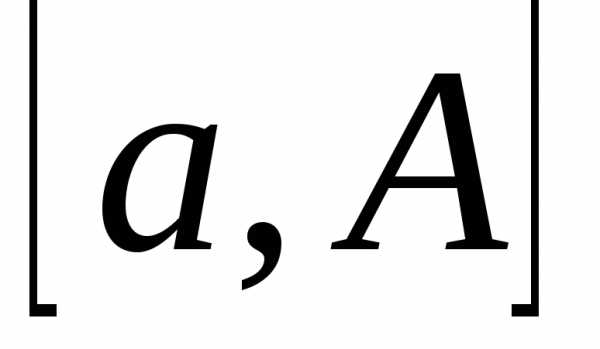 ,
то есть существует интеграл
,
то есть существует интеграл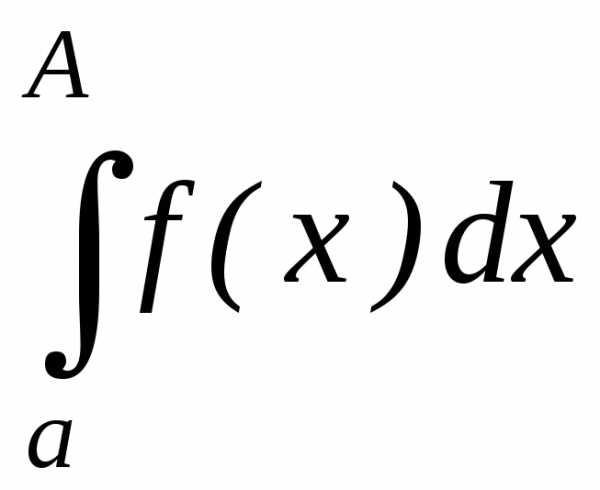 .
.
Определение
1.
Конечный или бесконечный предел этого
интеграла при
называют несобственным интегралом 1-го
рода от функции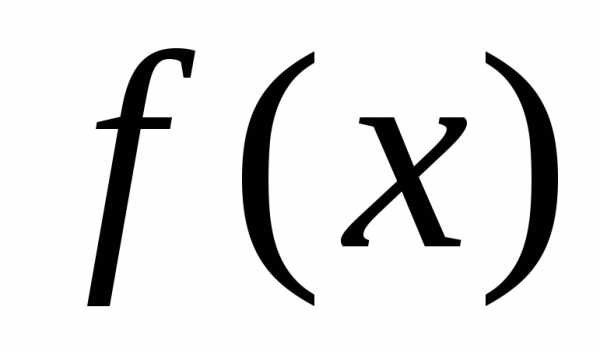 по промежутку
по промежутку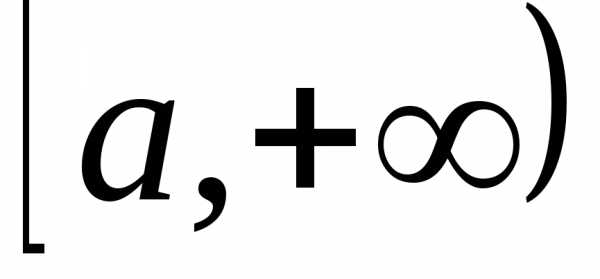 и обозначают символом
и обозначают символом .
При этом, если указанный предел конечен,
то несобственный интеграл называют
сходящимся, в противном случае (или не существует ) – расходящимся.
.
При этом, если указанный предел конечен,
то несобственный интеграл называют
сходящимся, в противном случае (или не существует ) – расходящимся.
Итак, по определению
(1) |
Примеры
1..
2..
3.– не существует.
Несобственный интеграл из примера 1 сходится, в примерах 2 и 3 интегралы расходятся.
II Формула Ньютона – Лейбница для несобственного интеграла первого рода
Пусть 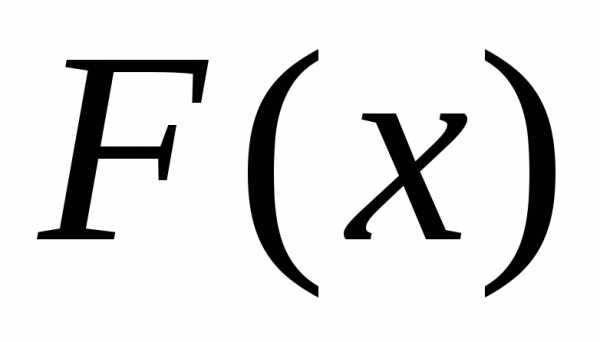 — некоторая первообразная для функции
— некоторая первообразная для функции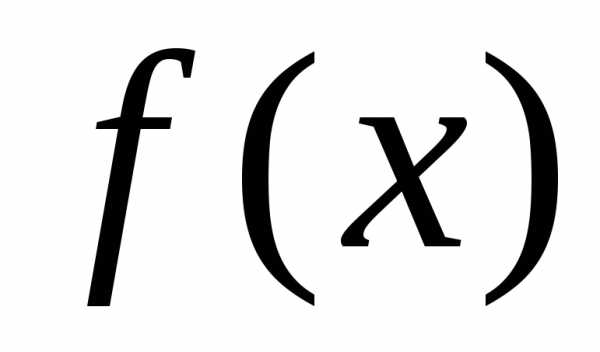 (сущест-вует на
(сущест-вует на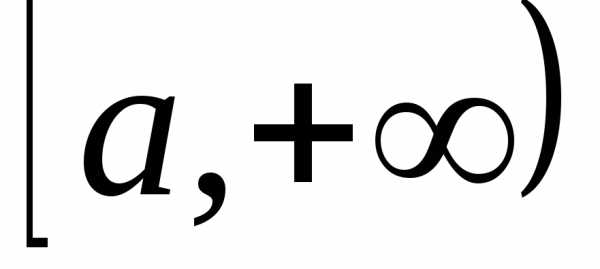 ,
т.к.
,
т.к.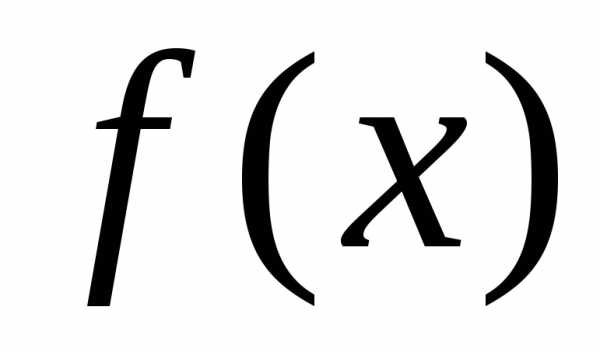 — непрерывна). Тогда
— непрерывна). Тогда
Отсюда
ясно, что сходимость несобственного
интеграла (1) равносильна существованию
конечного предела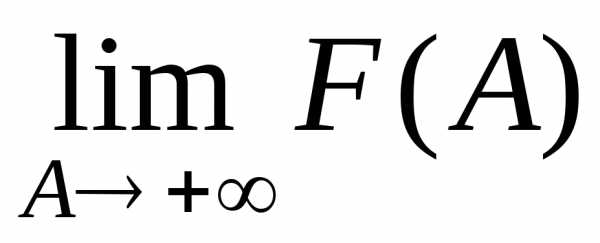 .
Если этот предел обозначить
.
Если этот предел обозначить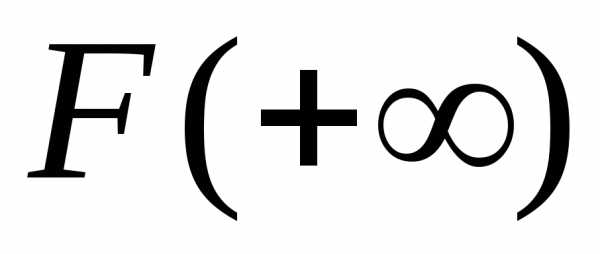 ,
то можно написать для интеграла (1)
формулу Ньютона-Лейбница:
,
то можно написать для интеграла (1)
формулу Ньютона-Лейбница:
, где .
Примеры.
4. .
5. .
6.
Более сложный пример: 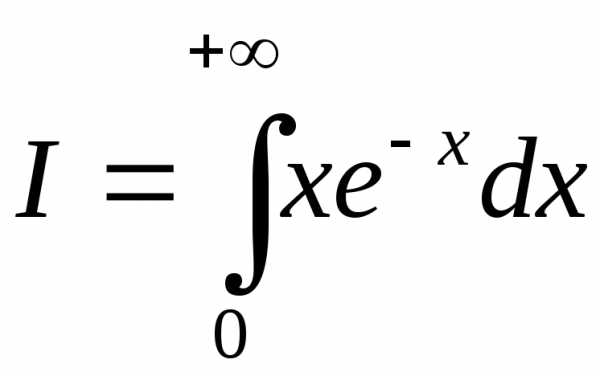 .
Сначала найдем первообразную:
.
Сначала найдем первообразную:
Теперь
можем найти интеграл 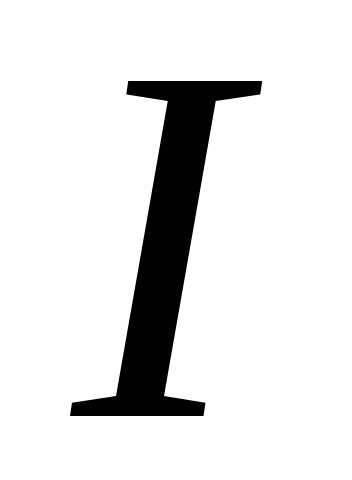 , учитывая,
что
, учитывая,
что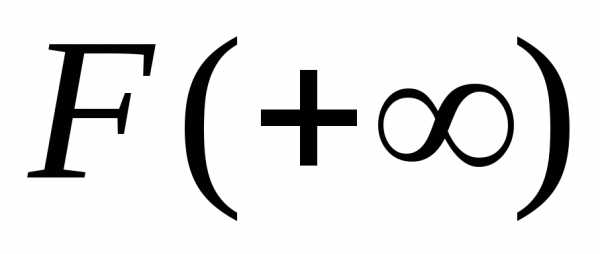
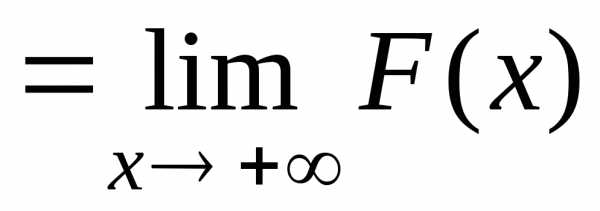 :
:
.
III Свойства
Приведем ряд свойств несобственного интеграла (1), которые вытекают из общих свойств пределов и определенного интеграла:
интегралы
 и
и
 сходятся или расходятся одновременно;
сходятся или расходятся одновременно;если
 ,
то интегралы
,
то интегралы и
и сходятся или рас-ходятся одновременно;
сходятся или рас-ходятся одновременно;если интеграл
 сходится, то
сходится, то .
.
IV Другие определения
Определение
2.
Если 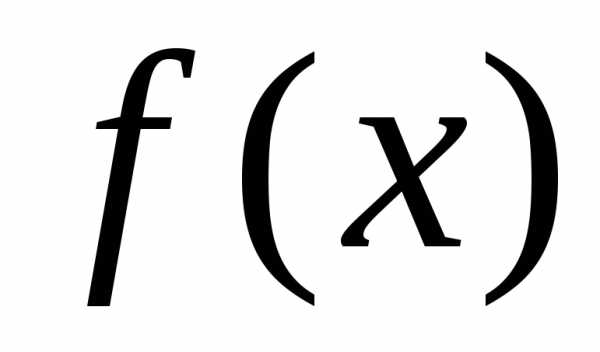 непрерывна
на
непрерывна
на  ,
то
,
то
.
Определение
3.
Если 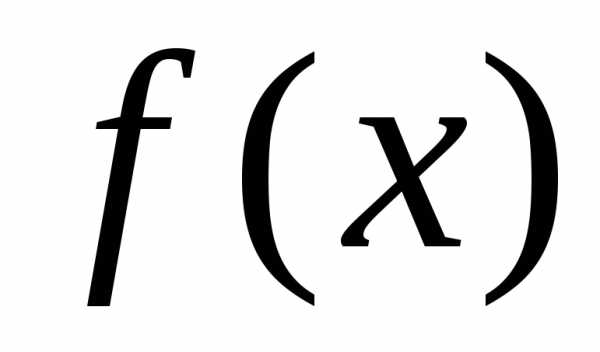 непрерывна
на
непрерывна
на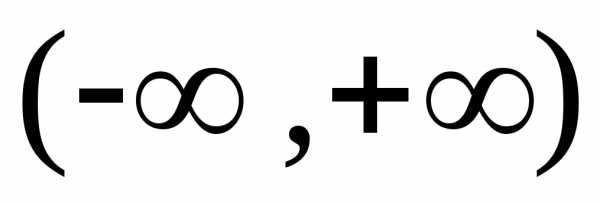 ,
то принимают по определению
,
то принимают по определению
( –
произвольное),
–
произвольное),
причем несобственный интеграл в левой части сходится, если только оба ин-теграла в правой части сходятся.
Для этих интегралов, как и для интеграла (1) можно написать соответствующие формулы Ньютона – Лейбница.
Пример 7.
§2. Признаки сходимости несобственного интеграла 1-го рода
Чаще всего несобственный интеграл вычислить по определению не-возможно, поэтому используют приближенное равенство
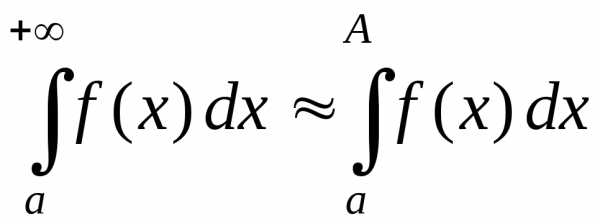 (для
больших
(для
больших  ).
).
Однако, это соотношение имеет смысл лишь для сходящихся интегралов. Необходимо иметь методы выяснения поведения интеграла минуя определение.
I Интегралы от положительных функций
Пусть 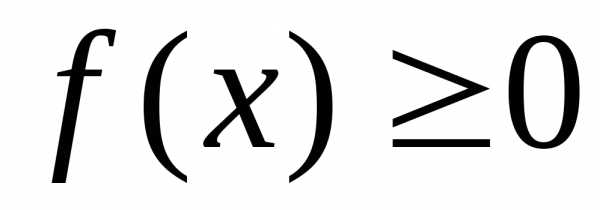 на
на  . Тогда определенный интеграл
. Тогда определенный интеграл 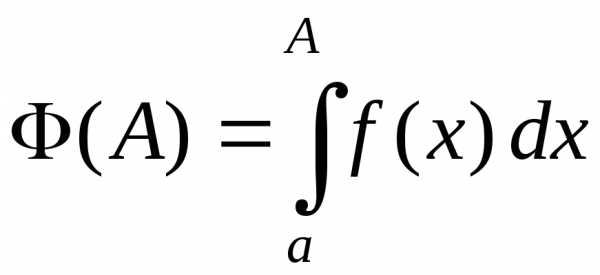 как функция верхнего предела есть
функция возрастаю-щая (это следует из
общих свойств определенного интеграла).
как функция верхнего предела есть
функция возрастаю-щая (это следует из
общих свойств определенного интеграла).
Теорема
1.
Несобственный интеграл 1го рода от неотрицательной функ-ции сходится
тогда и только тогда, когда функция  остается
ограниченной при увеличении
остается
ограниченной при увеличении .
.
Эта теорема – следствие общих свойств монотонных функций. Практического смысла теорема почти не имеет, но позволяет получить т.н. признаки сходимости.
Теорема
2 (1-й признак сравнения). Пусть функции  и
и непре-рывны на
непре-рывны на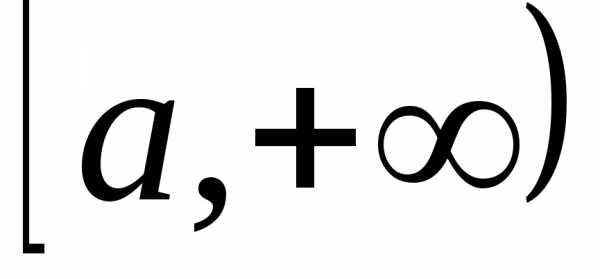 и удовлетворяют неравенству.
Тогда:
и удовлетворяют неравенству.
Тогда:
1)
если интеграл
сходится, то и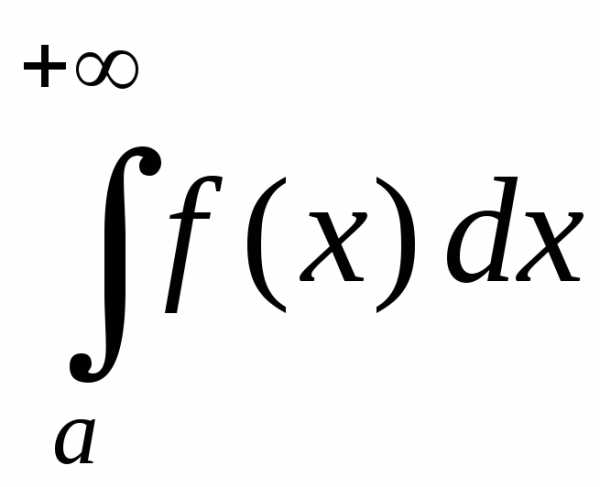 сходится;
сходится;
2)
если интеграл 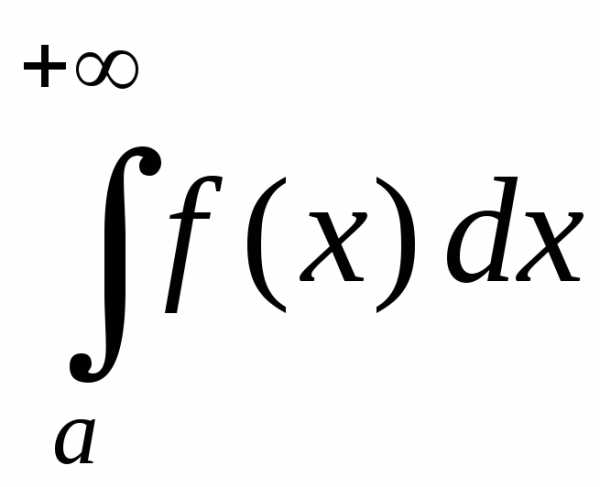 расходится, то и
расходится, то и расходится.
расходится.
Доказательство.
Обозначим:  и
и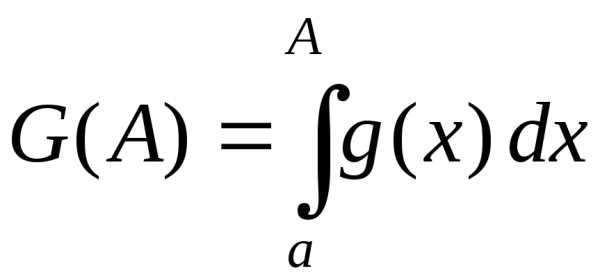 .
Так как,
то.
Пусть интеграл
.
Так как,
то.
Пусть интеграл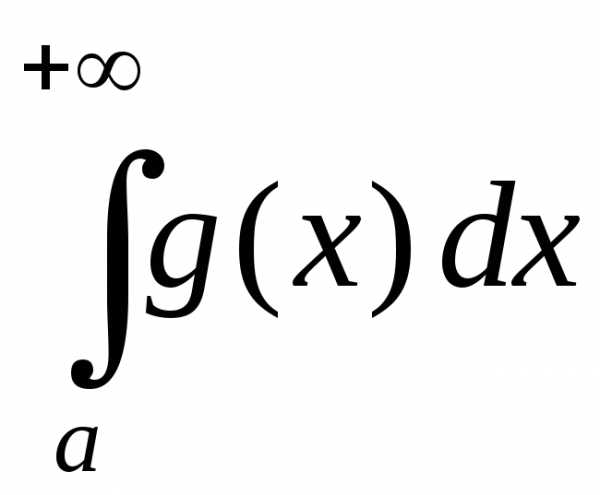 сходится, тогда (в силу теоремы 1) функция
сходится, тогда (в силу теоремы 1) функция ‒ ограничена. Но тогда и
‒ ограничена. Но тогда и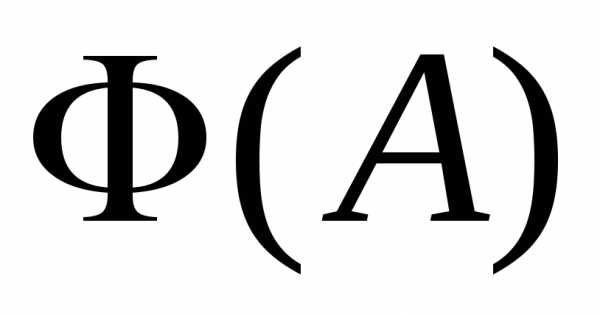 ограничена,
а значит, интеграл
ограничена,
а значит, интеграл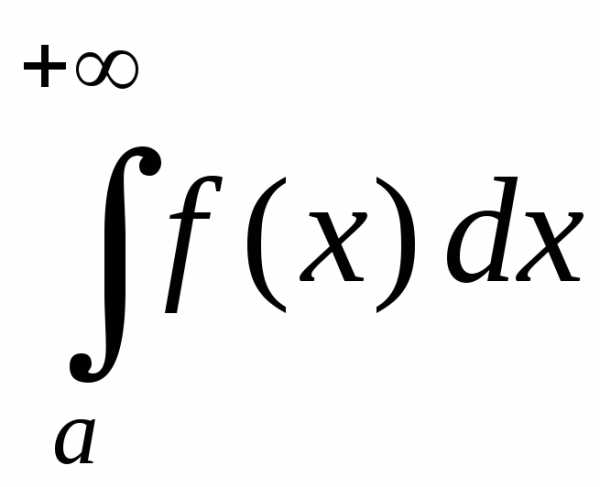 тоже сходится. Аналогично доказывается
и вторая часть теоремы.
тоже сходится. Аналогично доказывается
и вторая часть теоремы.
Этот
признак не применим в случае расходимости
интеграла от 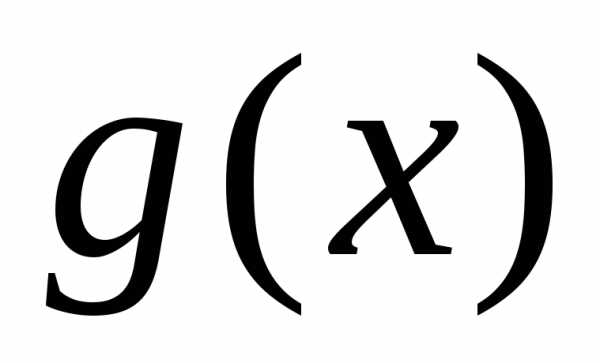 или сходимости интеграла от
или сходимости интеграла от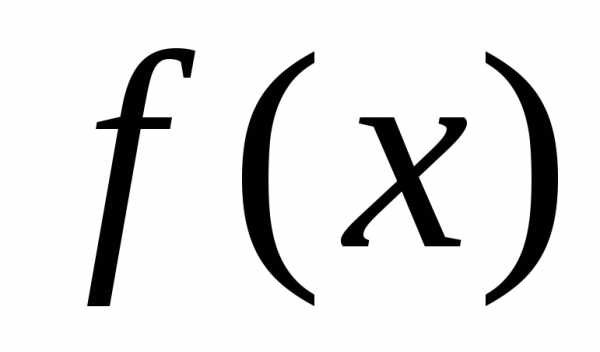 .
Этот недостаток отсутствует у 2-го
признака сравнения.
.
Этот недостаток отсутствует у 2-го
признака сравнения.
Теорема
3 (2-й признак сравнения). Пусть функции 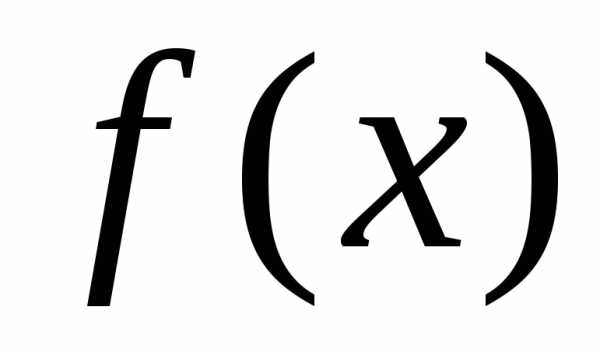 и
и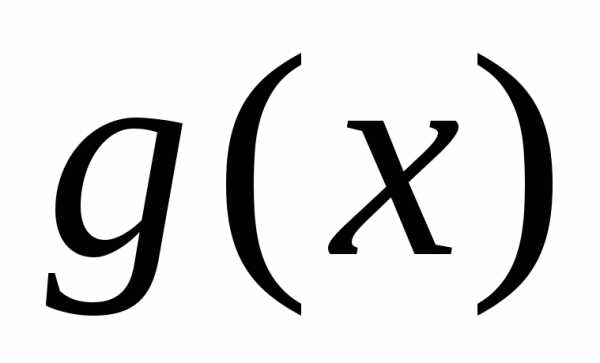 непрерывны и неотрицательны на
непрерывны и неотрицательны на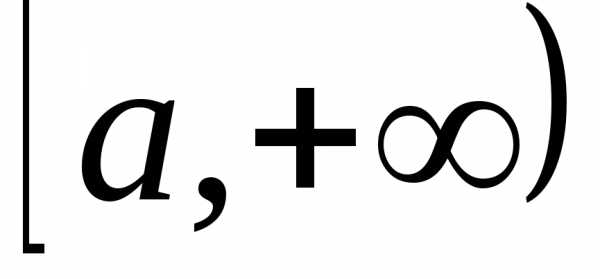 .
Тогда, еслипри,
то несобственные интегралы
.
Тогда, еслипри,
то несобственные интегралы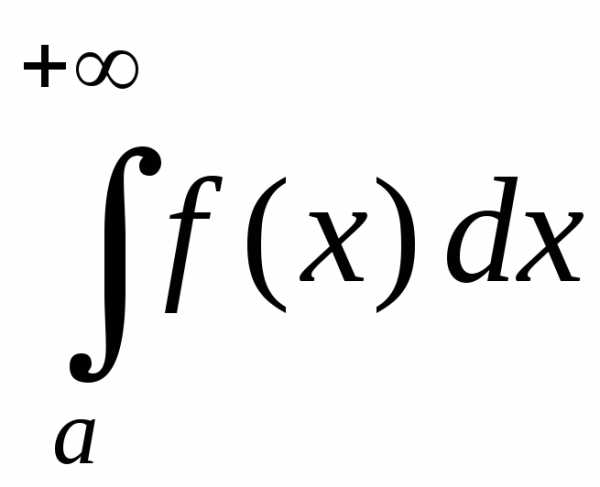 и
и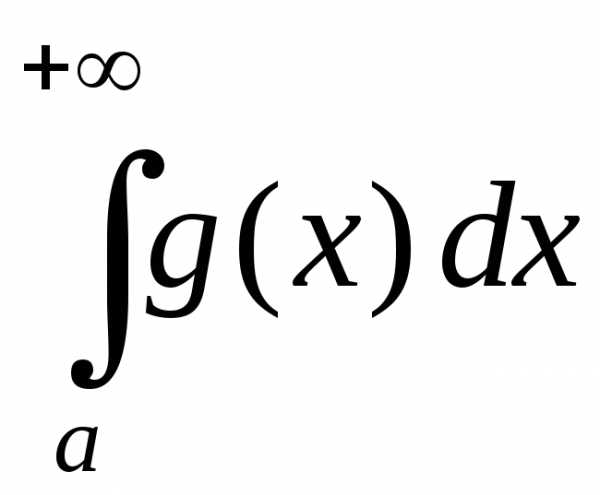 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство. Из условия теоремы получим такую цепочку равно-сильных утверждений:
, ,
.
Пусть,
например, 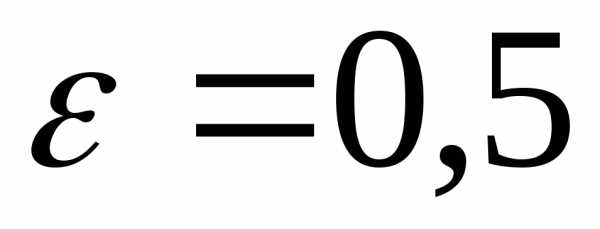 .
Тогда:
.
Тогда:
.
Применим теорему 2 и свойство 1) из §1 и получим утверждение теоремы 3.
В
качестве эталонной функции, с которой
сравнивают данную, высту-пает степенная
функция 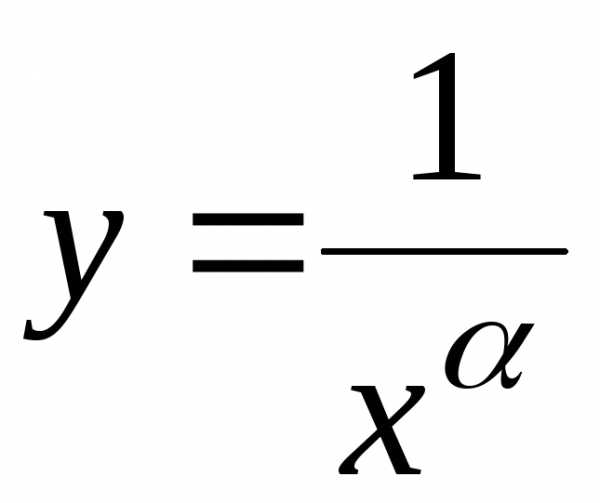 ,.
Предлагаем студентам самим доказать,
что интеграл
,.
Предлагаем студентам самим доказать,
что интеграл

сходится
при  и расходится при
и расходится при .
.
Примеры.
1.  .
.
Рассмотрим
подынтегральную функцию на промежутке 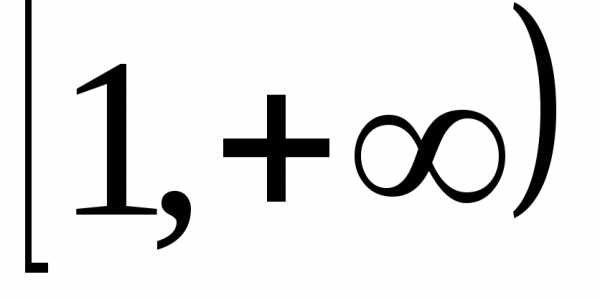 :
:
, .
Интеграл  сходится, ибо.
По 2-му признаку сравнения сходится и
интеграл
сходится, ибо.
По 2-му признаку сравнения сходится и
интеграл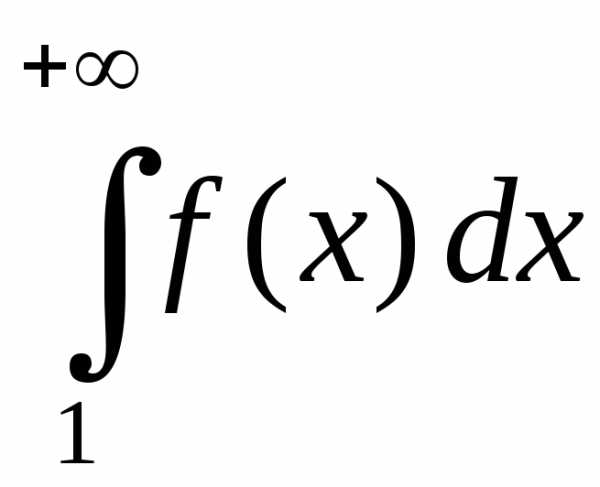 ,
а в силу свойства 2) из §1 сходится и
исход-ный интеграл.
,
а в силу свойства 2) из §1 сходится и
исход-ный интеграл.
2.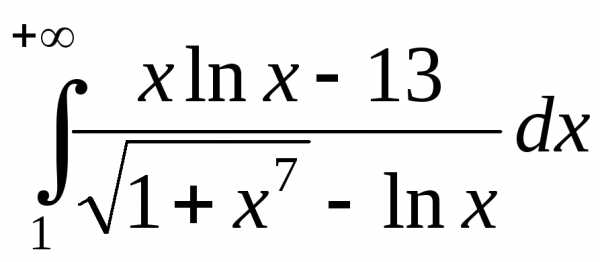 .
.
Так
как
,
тоcуществует  такое, что при
такое, что при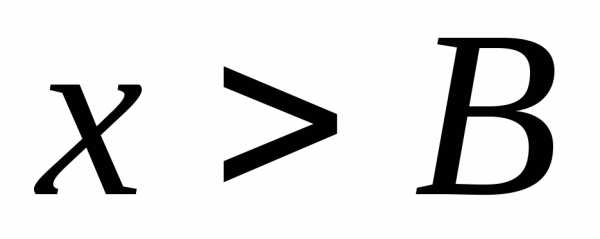
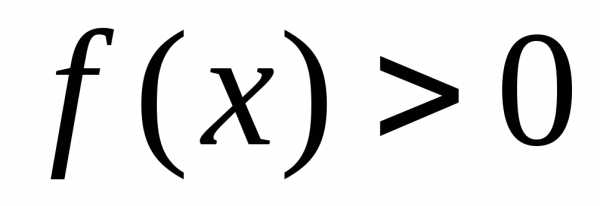 .
Для таких значений переменной:
.
Для таких значений переменной:
.
Известно, что логарифмическая функция растет медленнее степенной, т.е.
 ,
,
а значит, начиная с некоторого значения переменной, эта дробь меньше 1. Поэтому
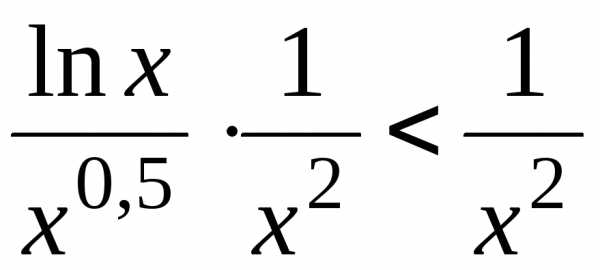 .
.
Интеграл 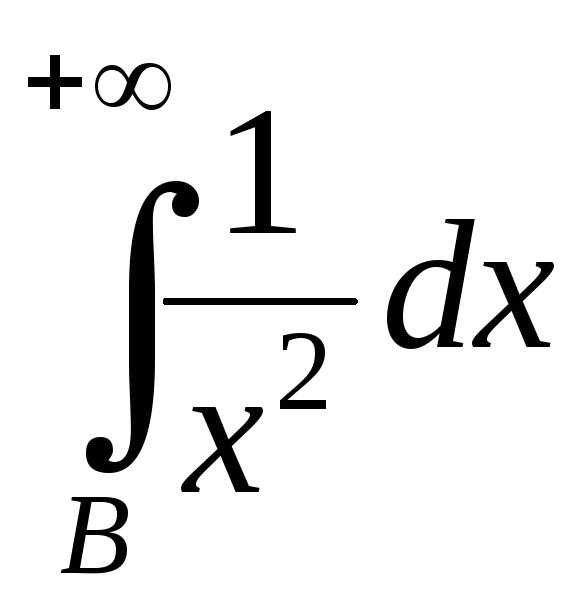 сходится как эталонный. В силу 1-го
признака сравнения сходится и
сходится как эталонный. В силу 1-го
признака сравнения сходится и .
Применяя 2-й признак, получим, что и
интеграл
.
Применяя 2-й признак, получим, что и
интеграл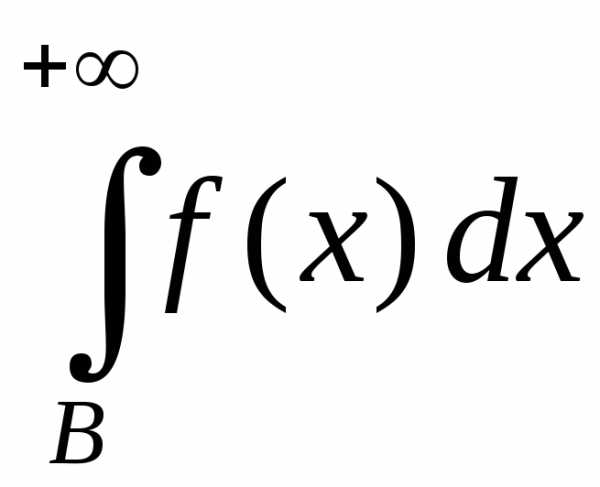 сходится. И снова свойство 2) из §1
доказывает сходимость исходного
интеграла.
сходится. И снова свойство 2) из §1
доказывает сходимость исходного
интеграла.
studfiles.net

 у
у у
у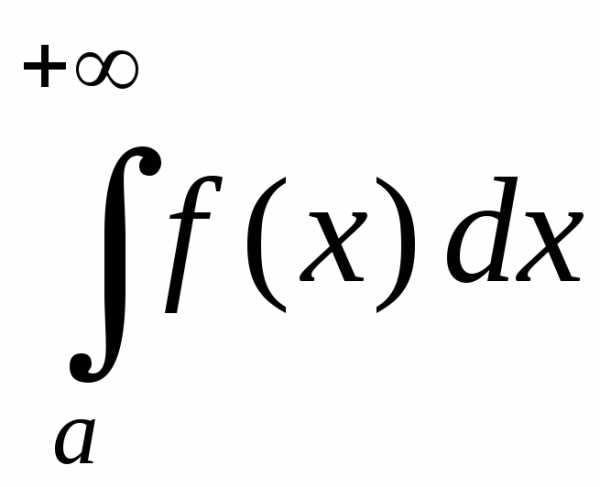 и
и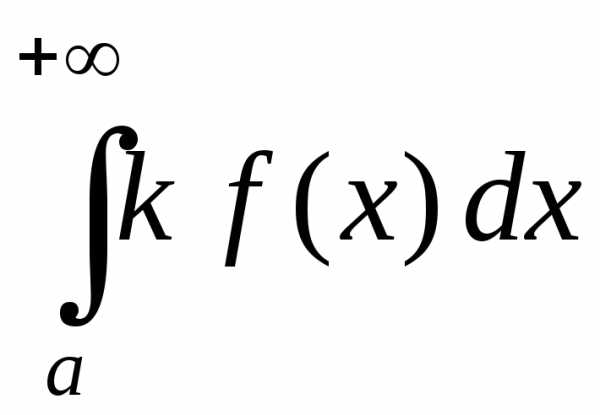
 сходятся или расходятся одновременно;
сходятся или расходятся одновременно;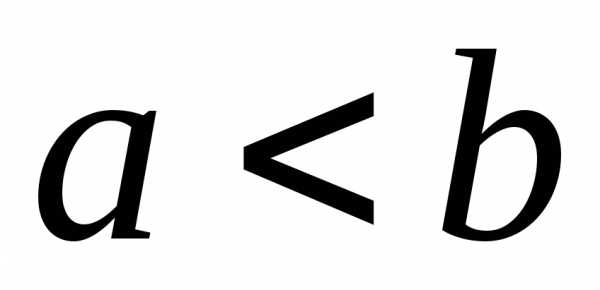 ,
то интегралы
,
то интегралы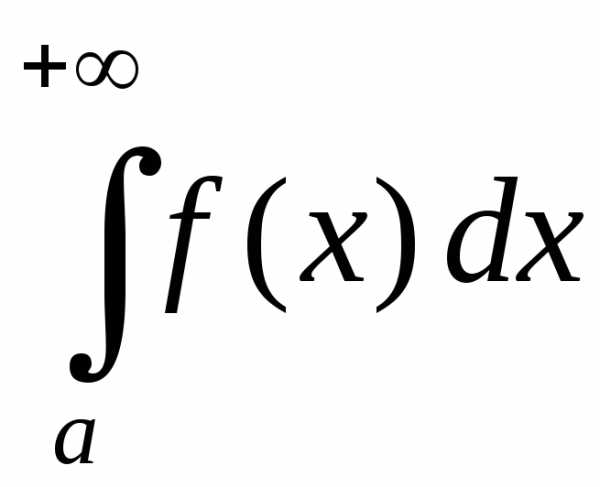 и
и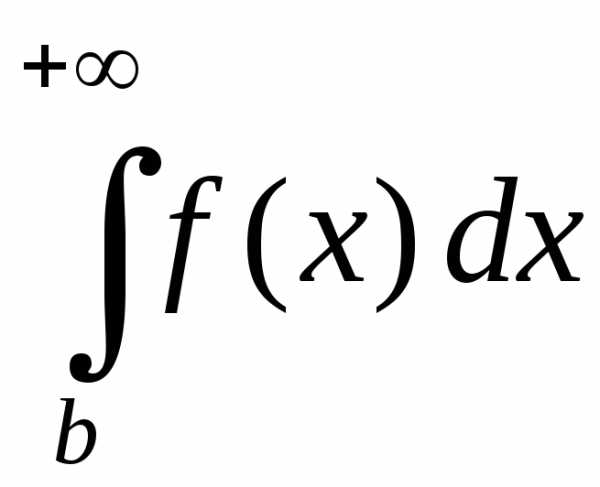 сходятся или рас-ходятся одновременно;
сходятся или рас-ходятся одновременно; сходится, то
сходится, то .
.