| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Предел функции, суммы ряда. Ограниченность функции, замечательные пределы, односторонние и бесконечные пределы, необходимые и достаточные условия существования предела функции в точке. Правила вычисления. / / Виды и правила раскрытия неопределенностей при вычислении пределов
| |||||||||||||||||||||
dpva.ru
Основные правила вычисления пределов, связанные с арифметическими операциями
Если функции y = f(x)иy = (x)имеют конечные пределы прих а, то:
, предел суммы равен сумме пределов.
, предел произведения равен произведению пределов.
 ,
предел частного равен отношению
пределов, если
,
предел частного равен отношению
пределов, если .
.
 ,
предел постоянной величины равен самой
постоянной.
,
предел постоянной величины равен самой
постоянной. − постоянную величину можно выносить за знак предела.
Первый и второй замечательные пределы и следствия из них.
Таблица эквивалентных БМ величин
ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ: | |
ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ: | , где …(натуральное число) |
Второй замечательный предел на практике можно использовать и в такой форме ( а, в – соnst)
Следствия из замечательных пределов – это соотношения эквивалентности между некоторыми БМ величинами.
ТАБЛИЦА ЭКВИВАЛЕНТНЫХ БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИН
Пусть  ,
т.е. является бесконечно малой величиной.
,
т.е. является бесконечно малой величиной.
Следствия из первого замечательного предела. | Следствия из второго замечательного предела. |
sin x ~ x tg x ~ x arcsin x ~ x arctg x ~ x 1 — cos x ~ x2 / 2 | |
Техника вычисления пределов
При вычислении пределов функций используется правило предельного перехода под знаком непрерывной функции,которое формулируется так:
.
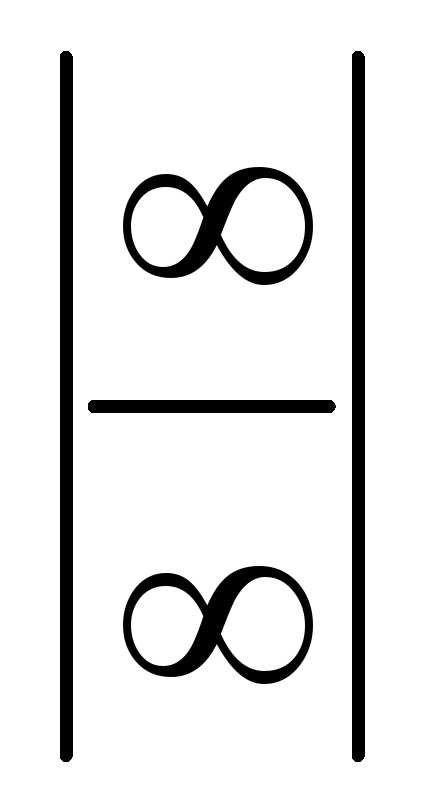
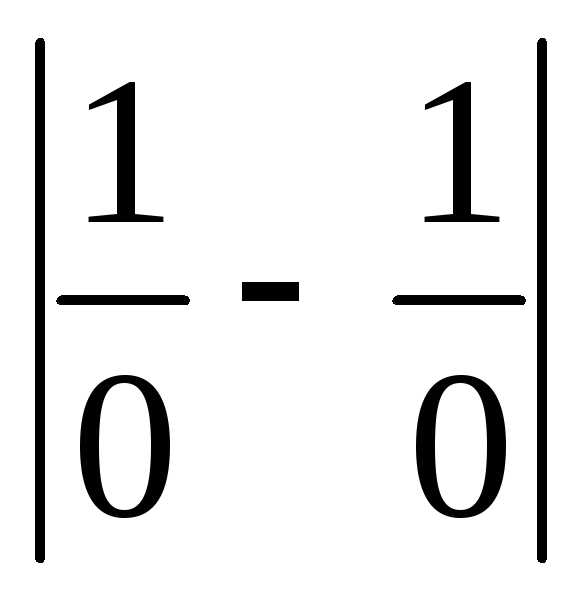
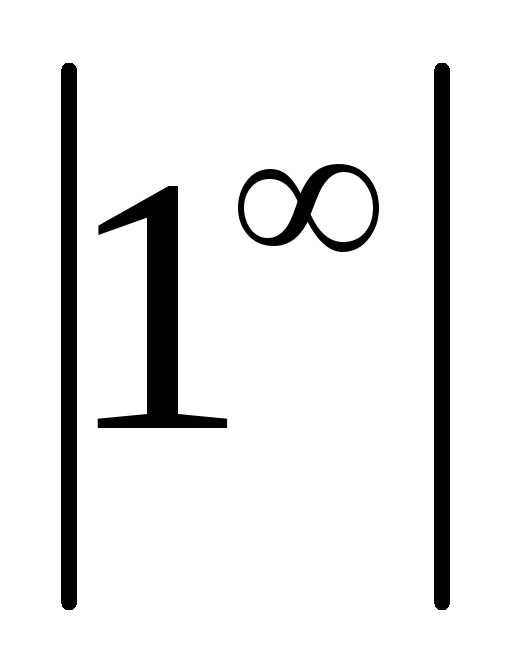
Оно справедливо для всех элементарных функций, так как они непрерывны в своих областях определения. Из правила следует, что при вычислении пределов, прежде всего, необходимо аргумент функции заменить его предельным значением и выяснить, имеется ли неопределенноесоотношениие. Кнеопределеннымотносятся соотношения вида:
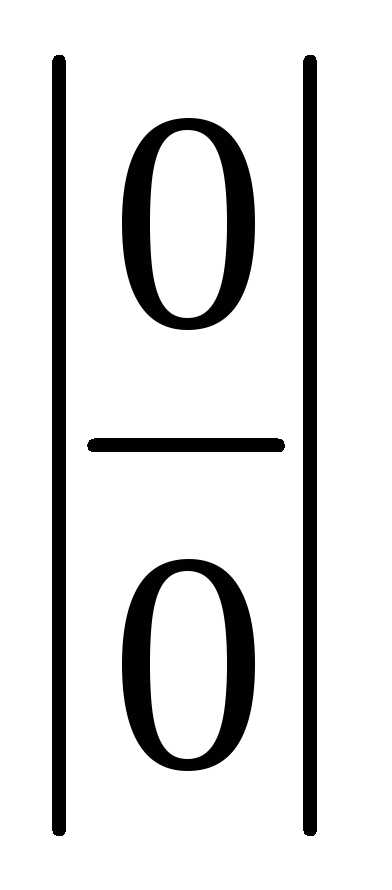 ,
, 
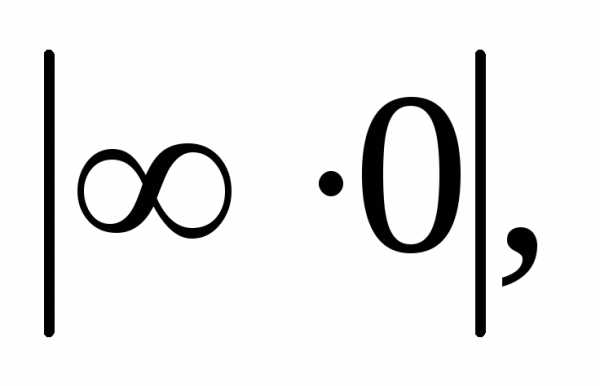
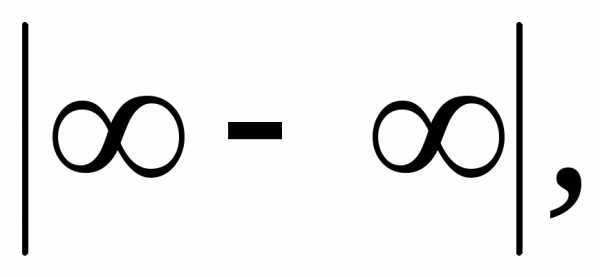
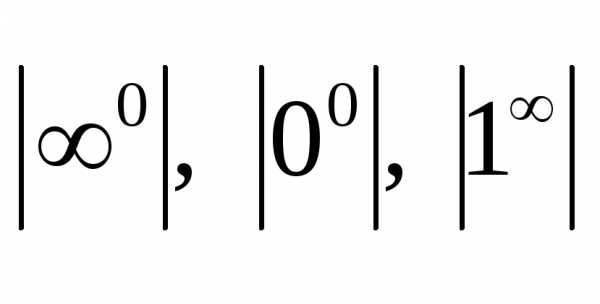 .
.Если такое выражение существует, необходимо выполнить тождественные преобразования, в результате которых устраняется неопределенность, а затем вычисляется предел.
Логическая схема техники вычисления пределов
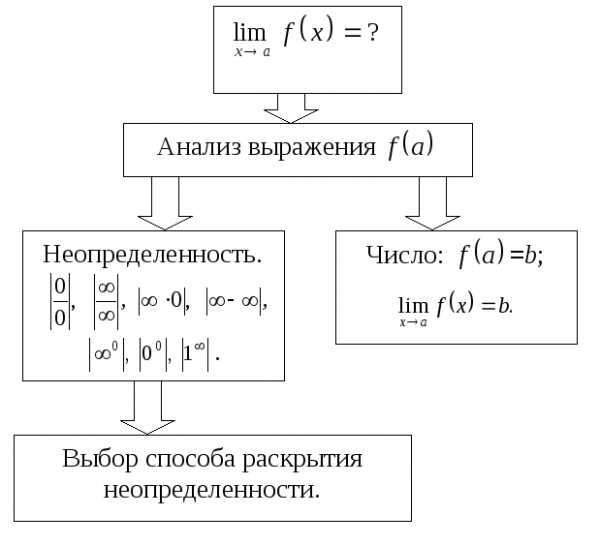
Основные этапы поиска способа раскрытия неопределенности представлены в алгоритме на следующей странице, а конкретные примеры вычисления пределов функции приведены в разделе «Примеры выполнения обязательных заданий по теме 4».
Общий алгоритм вычисления предела функции
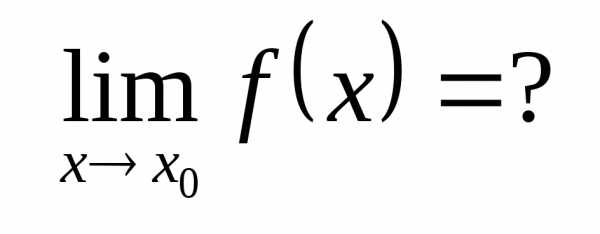 .
.
| Подставить | |||||
| |||||
Проанализировать
полученное неопределенное соотношение: | |||||
| |||||
| Если это отношение многочленов, то выделяется главная часть: | ||||
| | алгебраические преобразования выделение в числителе и знаменателе множителя, стремящегося к нулю. | | Если это отношение многочленов, то определяются корни числителя и знаменателя дроби и многочлены раскладываются на множители. | |
| Если предел содержит квадратные (кубические) корни, то следует умножить и разделить дробь на соответствующий сопряженный множитель. | ||||
использование эквивалентных бесконечно малых величин. | | Отношение степенных функций. | |||
| Это неопределенное выражение приводится к виду: | ||||
| | Если 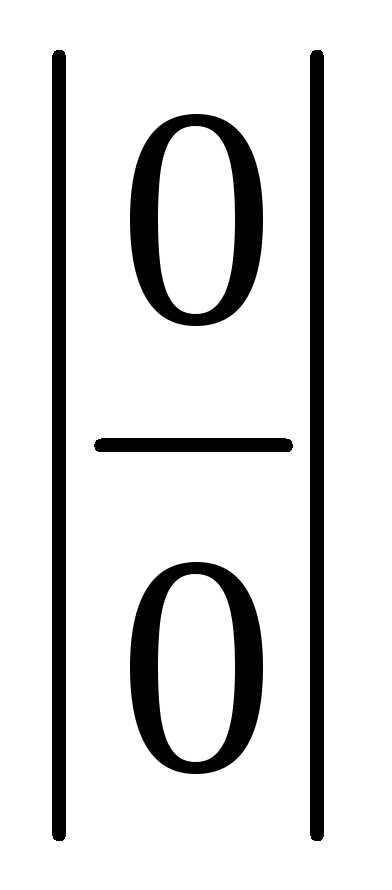 . . | |||
Преобразование иррациональности . | |||||
| Приведение
предела к виду второго замечательного
предела, т.е.
,
где Затем используют известные формулы или . | ||||
studfiles.net
Пределы — Все для студента
Пределы — Все для студентаУчебно-методические материалы
Студенческие работы
Теги, соответствующие этому тематическому разделу
Файлы, которые ищут в этом разделе
Доверенные пользователи и модераторы раздела
Активные пользователи раздела
این کتاب ترجمه کتابی از یک نویسنده روسی با نام الکساندر الکساندرویچ کیریلوف است This book is the translation of a book from Alexandre Aleksandrovich Kirillov, a Russian mathematician.
- №1
- 3,78 МБ
- добавлен
- изменен
Тамбов: Изд-во ТГТУ, 2015. — 25 с. Limit of function х→∞ Limit of function х→а Unilateral limits. Infinitesimal functions and there properties Infinitely large functions and their properties Basic theorems about function limits Remarkable limits Tasks for training References
- №2
- 515,31 КБ
- добавлен
- изменен
Л.А. Альсевич, С.Г. Красовский, А.Ф. Наумович, Н.Ф. Наумович. — Минск: БГУ, 2011. — 58 с. Пособие содержит основные теоретические сведения о последовательностях и их свойствах и предлагает основные приемы нахождения пределов последовательностей. Изложение материала иллюстрируется подробно разобранн
www.twirpx.com

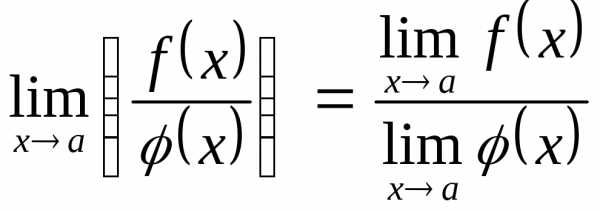 ,
предел частного равен отношению
пределов, если
,
предел частного равен отношению
пределов, если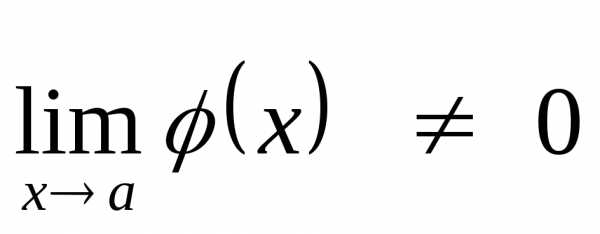 .
.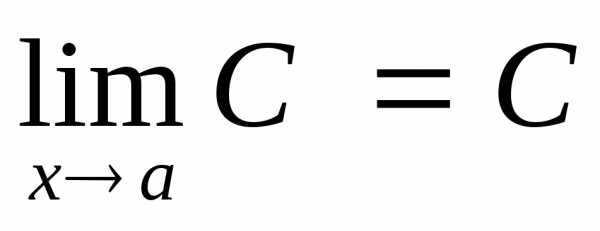 ,
предел постоянной величины равен самой
постоянной.
,
предел постоянной величины равен самой
постоянной.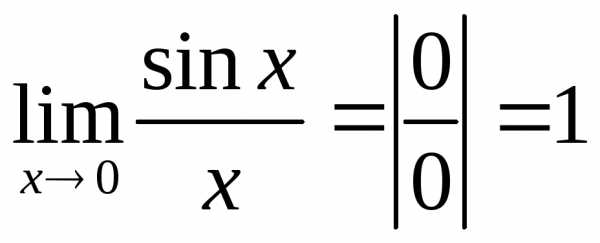 .
.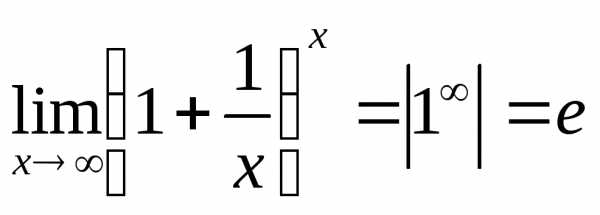 ,
,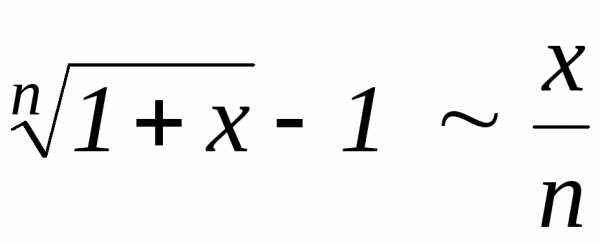
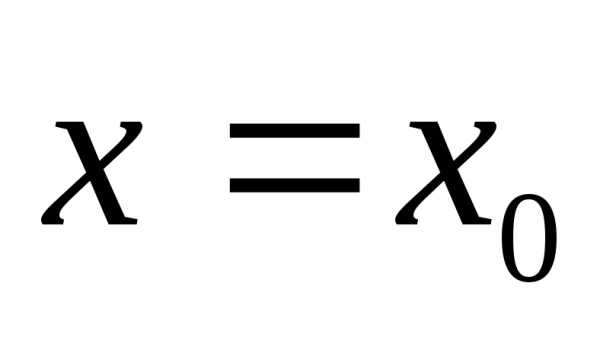 (в том числе и
(в том числе и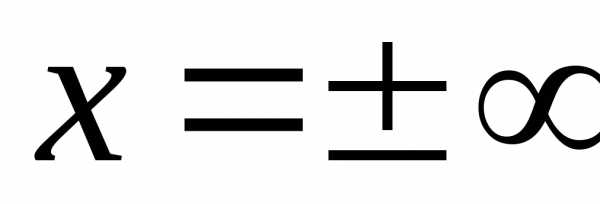 )
в
)
в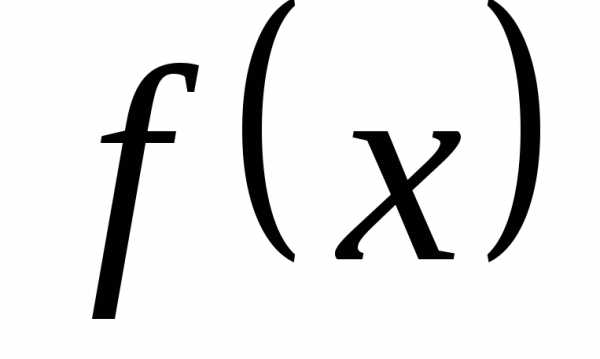 .
.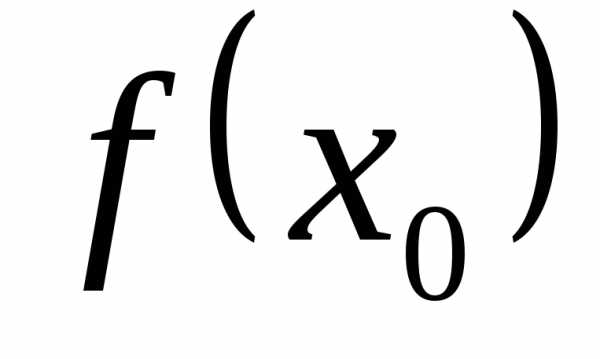 .
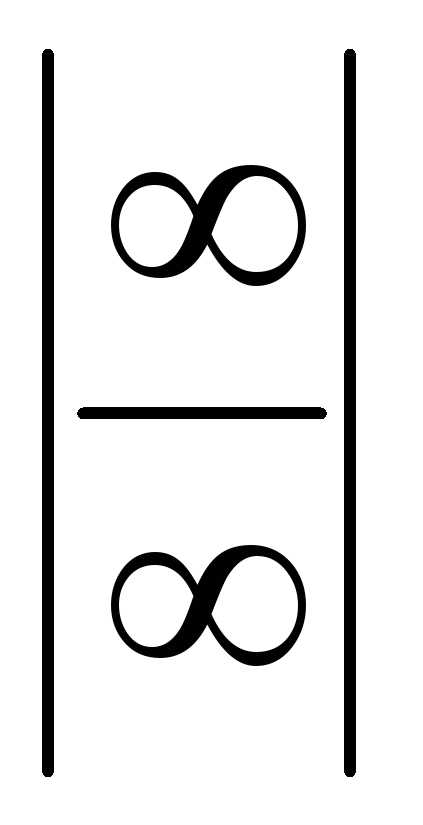
.
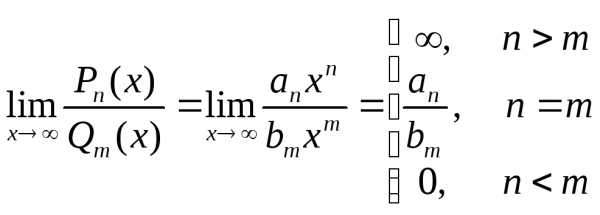
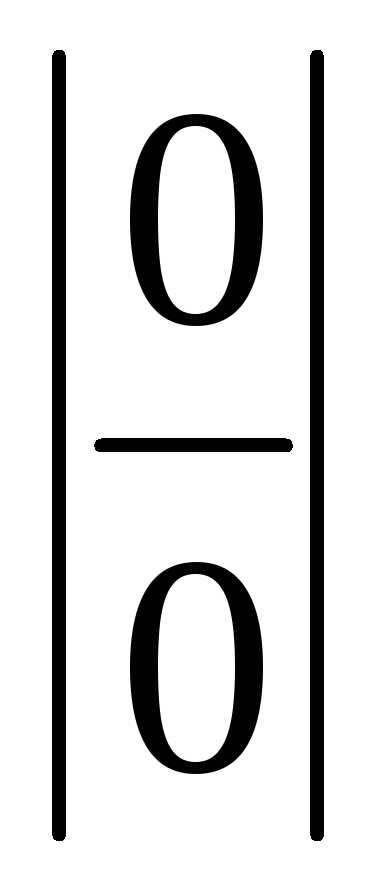
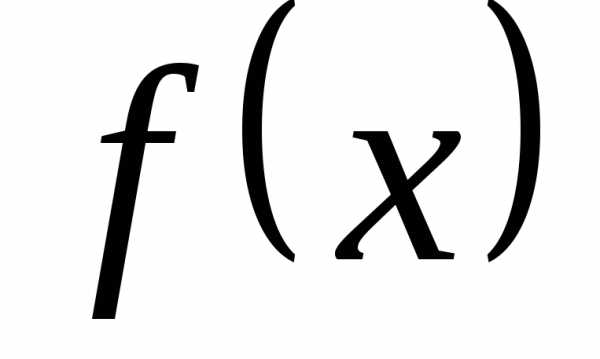 :
: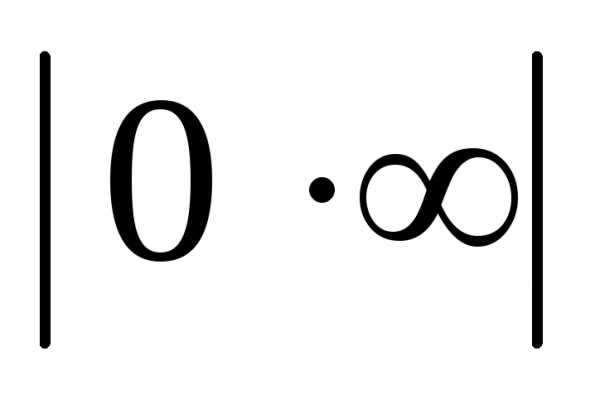
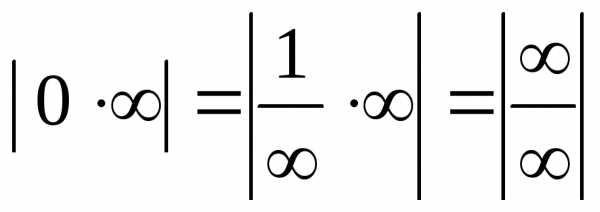 или
или 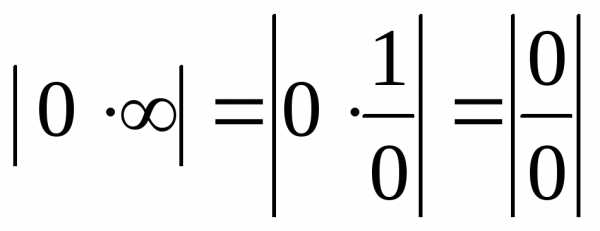 .
.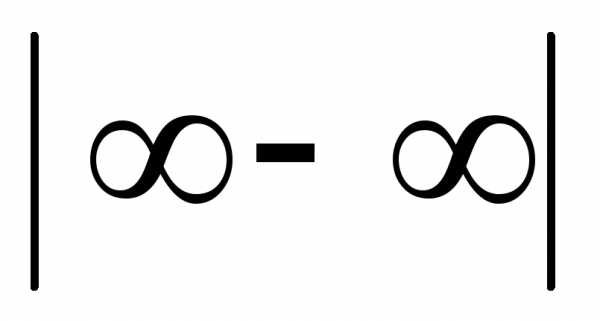
 — бесконечно малая величина.
— бесконечно малая величина.