Точка пересечения высот треугольника свойства – Свойства высот треугольника | Формулы с примерами

Ортоцентр треугольника: полезные факты.

Ортоцентр треугольника: полезные факты

В этой статье доказываются некоторые факты, касающиеся точки пересечения высот треугольника (ортоцентра треугольника), которые могут быть весьма полезны при решении задач.

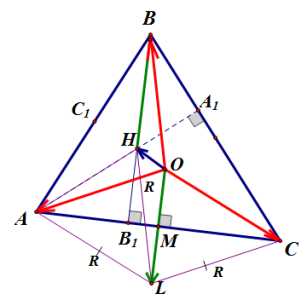
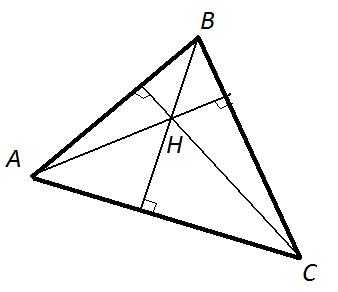
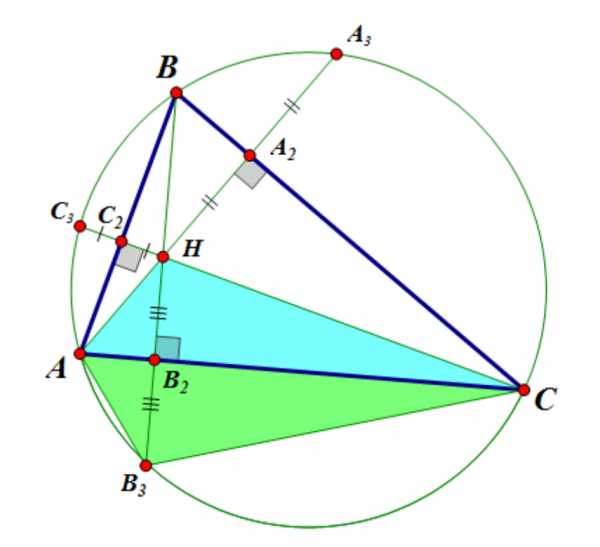
Пусть — точка пересечения высот треугольника ,  — центр описанной окружности.

Тогда:

1) радиусы окружностей, описанных около треугольников , , и равны;

2) расстояние от вершины до точки  вдвое больше расстояния от центра описанной окружности до стороны ;

3) расстояние между серединами отрезков и равно радиусу описанной окружности треугольника ;

4) ;

5)  точки, симметричные точке  относительно прямой  и относительно середины стороны , лежат на описанной окружности треугольника .

Доказательство.

1) Радиусы окружностей, описанных около треугольников , , и равны.

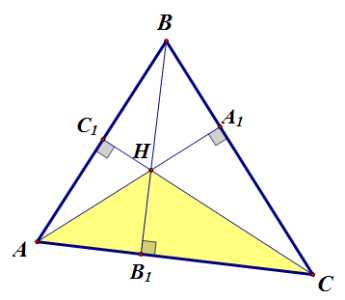
Радиус окружности, описанной около треугольника можно найти по формуле:

   

, где — произвольная сторона треугольника, а — величина противолежащего угла.

Для треугольника   радиус описанной окружности

Рассмотрим четырехугольник : по свойству вертикальных углов. 

Тогда для треугольника  радиус описанной окружности , то есть равен радиусу описанной окружности треугольника .

 

2) Расстояние от вершины до точки  вдвое больше расстояния от центра описанной окружности до стороны .

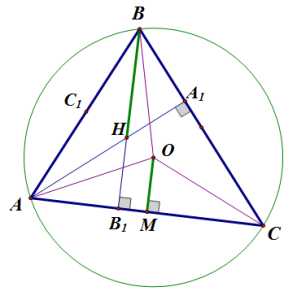
Докажем, что , где — центр описанной окружности, а — основание серединного перпендикуляра, опущенного из точки  на сторону . (Вспомним, что центр описанной окружности лежит в точке пересечения серединных перпендикуляров.)

Пусть точка   симметрична точке  относительно отрезка .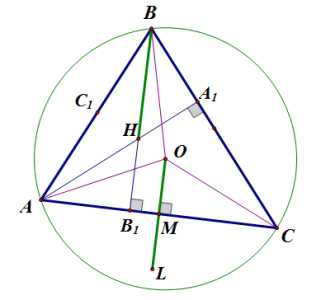

Рассмотрим треугольник .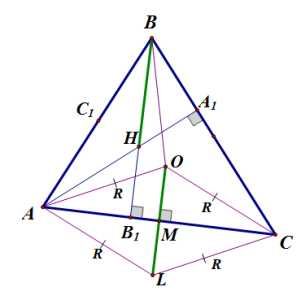 

Из соображений симметрии , следовательно, .

Так как расстояние от точки до точек и равно радиусу окружности, описанной около треугольника , и мы только что доказали, что радиус окружности, описанной около треугольника также равен , следовательно, точка  — центр окружности, описанной около треугольника , и .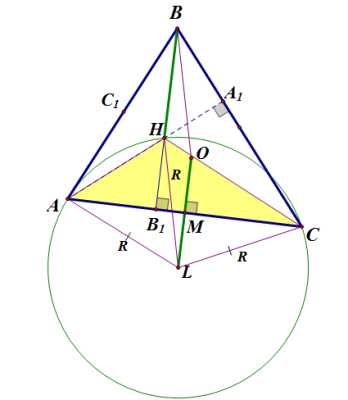 

Проведем окружность с центром в точке , описанную около треугольника :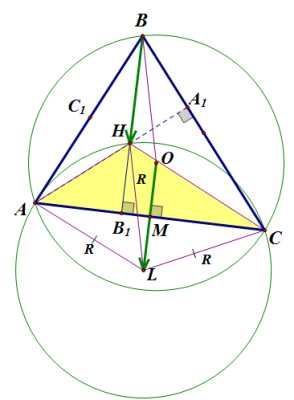

Мы видим, что при параллельном переносе на вектор  окружность с центром в точке  переходит в окружность c центром в точке , и точка   переходит в точку , следовательно, . Но так как , получили, что .

Что и требовалось доказать.

3) Расстояние между серединами отрезков и равно радиусу описанной окружности треугольника .

Рассмотрим четырехугольник .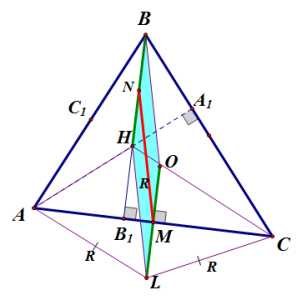

 

 

Мы доказали, что . Кроме того, по доказанному выше, . Следовательно, этот четырехугольник  — параллелограмм. Точка — середина отрезка , является также серединой отрезка . Следовательно, отрезок, соединяющий точку  с точкой — серединой отрезка , параллелен отрезкам  и и равен им:

.

Что и требовалось доказать.

4)

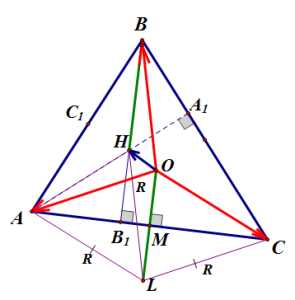
Используем доказанные выше факты.

Четырехугольник   — ромб, следовательно, по правилу параллелограмма для сложения векторов получаем :

Далее, четырехугольник   -параллелограмм, следовательно,  .

Утверждение доказано.

5)  Точки, симметричные точке  относительно прямой  и относительно середины стороны , лежат на описанной окружности треугольника .

Пусть точка  симметрична точке  относительно прямой :

 

 

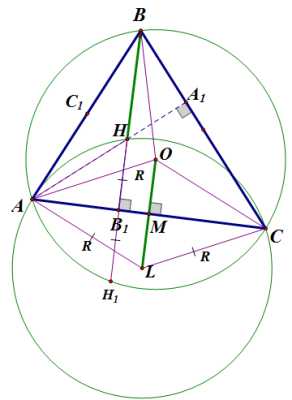
Точка симметрична точке относительно прямой . Следовательно, окружность с центром в точке  симметрична окуржности с центром в точке . Точка лежит на окружности с центром в точке  (см. п. 2), следовательно, симметричная ей относительно прямой точка  симметричной окружности с центром в точке , то есть описанной около треугольника .

Пусть точка  симметрична точке  относительно относительно середины стороны :

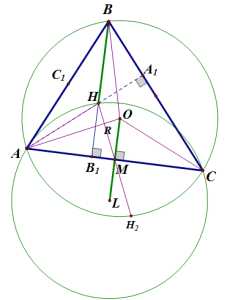
Треугольники равны по двум сторонам и углу между ними, следовательно, , и точка  лежит на окружности, описанной около треугольника  

.

Утверждение доказано.

И. В. Фельдман, репетитор по математике.

 

 

ege-ok.ru

Теорема о пересечении высот треугольника. Видеоурок. Геометрия 8 Класс

Тема: Окружность

Урок: Теорема о пересечении высот треугольника

Для данного урока нам полезно знать свойства серединного перпендикуляра к отрезку и свойство трех серединных перпендикуляров треугольника.

Задан треугольник .  – серединный перпендикуляр к ВС, – серединный перпендикуляр к АС, – серединный перпендикуляр к АВ (см. Рис. 1).

Точка О равноудалена от вершин треугольника,

Рис. 1

Переходим к рассмотрению центральной теоремы данного урока.

Три высоты треугольника пересекаются в одной точке, эта точка носит название ортоцентра (см. Рис. 2).

Задан треугольник , , , .

Доказать, что

Рис. 2

Доказательство:

Проведем через вершины треугольника прямые, параллельные их противоположным сторонам:

через вершину А – прямую ,

через вершину В – прямую ,

через вершину С – прямую .

Получили новый треугольник , рассмотрим его свойства (см. Рис. 3).

, значит,  . Аналогично . Отсюда четырехугольник  является параллелограммом.

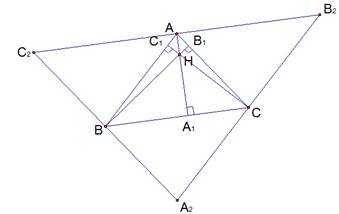
Рис. 3

Противоположные стороны параллелограмма попарно равны, отсюда , .

Аналогично ,  по построению. Четырехугольник  – параллелограмм. Отсюда , .

, , отсюда . Таким образом, точка А – середина отрезка , а значит, высота АА₁ в маленьком треугольнике – это серединный перпендикуляр в большом треугольнике.

Аналогичные действия можно выполнить для вершин В и С. Получим, что В – середина отрезка , ВВ₁ – серединный перпендикуляр к стороне большого треугольника; С – середина , СС

1 – серединный перпендикуляр к стороне большого треугольника.

Мы знаем, что серединные перпендикуляры в большом треугольнике АА₁, ВВ₁, СС₁ пересекутся в одной точке – в точке Н. Также мы знаем, что эти серединные перпендикуляры являются высотами маленького треугольника, таким образом, высоты треугольника пересекаются в одной точке Н, что и требовалось доказать.

В треугольнике все медианы и биссектрисы принадлежат треугольнику, чего нельзя сказать о высотах. В остроугольном треугольнике каждая высота принадлежит треугольнику.

Задача

Треугольник  остроугольный, АА₁ – высота (см. Рис. 4). Доказать, что основание высоты А₁ – это внутренняя точка отрезка ВС.

Дано: треугольник , , , ,

Доказать, что А₁ – это внутренняя точка отрезка ВС

Рис. 4

Доказательство:

Докажем от противного: пусть АА₂ – это высота, и точка А

2 не является точкой отрезка ВС (см. Рис. 5).

Тогда угол  – внешний угол для треугольника . Внешний угол равен сумме внутренних углов треугольника, несмежных с ним, то есть углов  и , то есть сумме прямого угла и какого-то острого угла, а данная сумма будет больше , то есть угол  будет тупой, что противоречит условию.

Рис. 5

Таким образом, основание высоты треугольника является внутренней точкой отрезка ВС.

Сделаем вывод: аналогичное доказательство можно выполнить для двух других высот остроугольного треугольника , отсюда все три высоты остроугольного треугольника лежат внутри треугольника, точка их пересечения – ортоцентр – находится внутри треугольника.

Рассмотрим тупоугольный треугольник и докажем, что его ортоцентр находится вне треугольника (см. Рис. 6).

Задан треугольник ,  тупой. АА₁ – высота треугольника. Докажем, что точка В₁ – основание высоты ВВ₁ – не принадлежит отрезку АС.

От противного: пусть точка В₁ принадлежит отрезку АС. Тогда треугольник  не существует, т.к. сумма тупого угла  и прямого угла  больше . Таким образом, основание высоты ВВ₁ расположено на продолжении отрезка АС.

Рис. 6

Аналогично можно выполнить доказательство для высоты СС₁, получим, что ее основание также лежит на продолжении отрезка АВ. Таким образом, точка пересечения данного треугольника лежит вне треугольника.

Итак, мы рассмотрели теорему о пересечении высот треугольника, на следующем уроке мы рассмотрим окружность, вписанную в треугольник.

 

Список литературы

1. Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
3. Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Home-edu.ru (Источник).
2. Mat.1september.ru (Источник).

 

Домашнее задание

1. Задание 1 – Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия, 7-9, № 685, ст. 180.
2. Задание 2 – доказать, что шесть углов остроугольного треугольника, образованных при пересечении высот треугольника, попарно равны углам треугольника.
3. Задание 3 – докажите, что если две замечательные точки треугольника совпадают, то треугольник равносторонний. Рассмотрите все возможные случаи.

interneturok.ru

Теорема о пересечении высот треугольника

Сегодня на уроке мы продолжим изучение темы замечательные точки треугольника и познакомимся с теоремой о пересечении высот треугольника.

На прошлых уроках мы доказали, что биссектрисы треугольника пересекаются в одной точке и серединные перпендикуляры к сторонам треугольника также пересекаются в одной точке. До этого мы также доказали, что медианы треугольника пересекаются в одной точке. Оказывается, таким же свойством обладают и высоты треугольника.

Теорема. Высоты треугольника (или их продолжения) пересекаются в одной точке.

Доказательство.

Рассмотрим .

Значит, четырехугольник  параллелограмм.

Значит, четырехугольник  параллелограмм.

Точка  является серединой отрезка  серединный перпендикуляр .

Точка  является серединой отрезка  серединный перпендикуляр .

Точка  является серединой отрезка  серединный перпендикуляр .

Значит, высоты  пересекаются в одной точке, в точке .

Что и требовалось доказать.

В любом треугольнике медианы и биссектрисы принадлежат самому треугольнику. Чего нельзя сказать о высотах треугольника. Три высоты треугольника всегда пересекаются в одной точке. Точку их пересечения называют ортоцентром треугольника. В остроугольном и прямоугольном треугольниках высоты принадлежат треугольнику. Их точка пересечения – ортоцентр – в остроугольном треугольнике находится внутри треугольника, в прямоугольном треугольнике находится в прямом угле. А вот в тупоугольном треугольнике точка пересечения высот – ортоцентр – находится вне треугольника.

Рассмотрим тупоугольный . У него  – тупой,  – высота. Докажем, что точка  – основание высоты  – не принадлежит отрезку .

Доказательство.

Пусть точка .

.

Что не может быть.

Точка пересечения тупоугольного треугольника лежит вне треугольника.

 

 

Итак, с каждым треугольником связаны четыре точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам треугольника и точка пересечения высот (или их продолжений). Эти четыре точки называются замечательными точками треугольника.

Из истории замечательных точек треугольника. В четвертой книге «Начал» Евклид решает задачу: «Вписать круг в данный треугольник». Из решения вытекает, что три биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанного круга.

Из решения другой задачи Евклида вытекает, что перпендикуляры, восстановленные к сторонам треугольника в их серединах, тоже пересекаются в одной точке – центре описанного круга. В «Началах» не говорится о том, что и три высоты треугольника пересекаются в одной точке, называемой ортоцентром.

Четвертой особенной точкой треугольника является точка пересечения медиан. Архимед доказал, что она является центром тяжести (барицентром) треугольника. На вышеназванные четыре точки было обращено особое внимание, и начиная с XVIII века они были названы «замечательными» или «особенными» точками треугольника.

Исследование свойств треугольника, связанных с этими и другими точками, послужило началом для создания новой ветви элементарной математики – «геометрии треугольника» или «новой геометрии треугольника», одним из родоначальников которой стал Леонард Эйлер.

Повторим главное:

На этом уроке мы узнали, что высоты треугольника (или их продолжения) пересекаются в одной точке. Эту точку называют ортоцентром и она является замечательной точкой треугольника.

videouroki.net

Про медиану и биссектрису в треугольнике в рамках школьной математике имеется много различных теорем, но вот про некоторые свойств высот умалчивается. Факт про незнание школьниками свойств высот, как мне кажется, активно используется при организации различных математических олимпиад и конкурсов. Т.е. такими задачами отсекаются сразу школьники, которые не занимаются математикой дополнительно.

Про высоты в треугольнике известно, что они проводятся перпендикулярно к сторонам, что точка пересечения срединных перпендикуляров является центром описанной окружности. Ну еще, что в равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой. По моему, я перечислил все факты, что знают школьники о высотах.

Важной точкой является ортоцентр – точка пересечения высот. Известны следующие свойства ортоцентра:

• Если точка H является ортоцентром треугольника ABC, то любая вершина является ортоцентром треугольника, составленного из остальных вершин, т.е. А – ортоцентр треугольника BCH и т.д. Точки A, B, C, H при этом называют ортоцентрической системой.
• Радиусы окружностей, проходящих через любые три точки ортоцентрической системы, равны.
• Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.

Пусть O является центром описанной около треугольника ABC окружности, тогда дополнительно верны следующие утверждения:

• .
• . Здесь R – радиус описанной окружности.
• Расстояние от вершины треугольника до ортоцентра вдвое больше расстояния от центра описанной окружности до противоположной стороны.

Здесь приведены наиболее используемые факты, связанные с перпендикулярами. Я настоятельно рекомендую запомнить эти свойства. А еще полезней будет провести доказательство этих утверждений, т.к. поняв доказательство, можно легко запомнить свойства.

Связанные статьи

mathi.ru

Свойства биссектрисы, медианы и высоты треугольника

В этой статье вы найдете свойства биссектрисы и медианы треугольника, которые могут быть полезны при решении задач.

Биссектрисы.

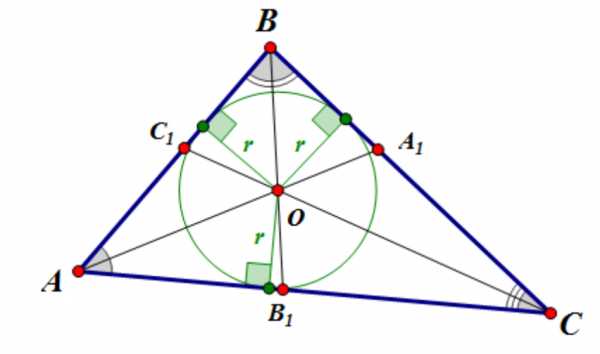
1. Точка пересечения биссектрис треугольника является центром вписанной в треугольник окружности.

Доказательство.

показать

Действительно, точки, лежащие на биссектрисе угла равноудалены от сторон угла. Следовательно, точка пересечения биссектрис равноудалена от всех сторон треугольника, то есть является центром вписанной окружности.

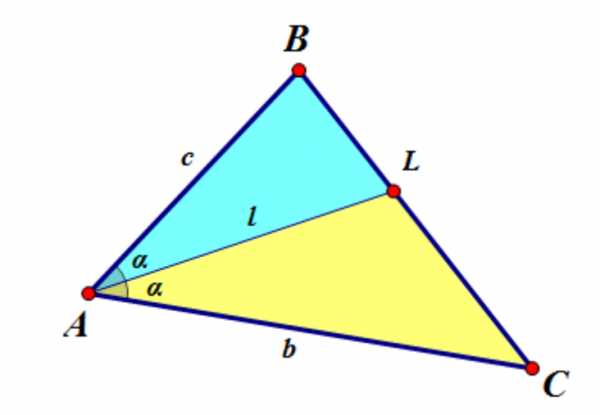
2. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам:

 

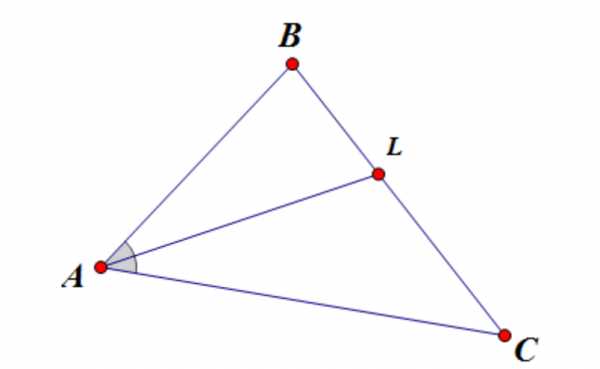
 Доказательство.

показать

3. Длина биссектрисы вычисляется по таким формулам:

(1)

Докажем вторую формулу.

показать

Введем обозначения:

Приравняем выражения для площади треугольника :

Отсюда:

4. Пусть О-центр вписанной окружности, -биссектриса угла   треугольника :

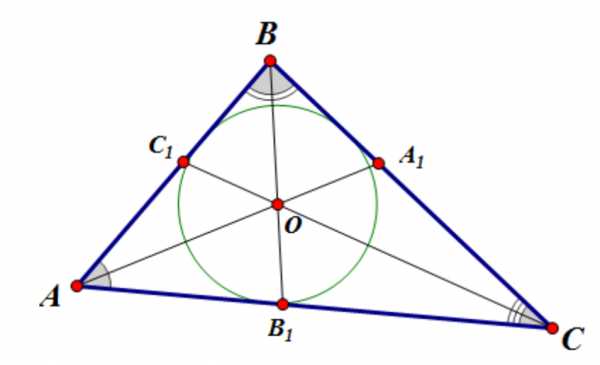
Тогда выполняется соотношение:

Доказательство:

показать

 

Биссектрису треугольника в некоторых задачах удобно продолжить до пересечения с описанной окружностью.

Лемма о трилистнике.

Дан треугольник . Точка — точка пересечения биссектрисы угла с описанной около треугольника окружностью. Пусть — центр вписанной в треугольник окружности. Тогда

   

Доказательство.

показать

Докажем формулу (1) из п. 3:

 

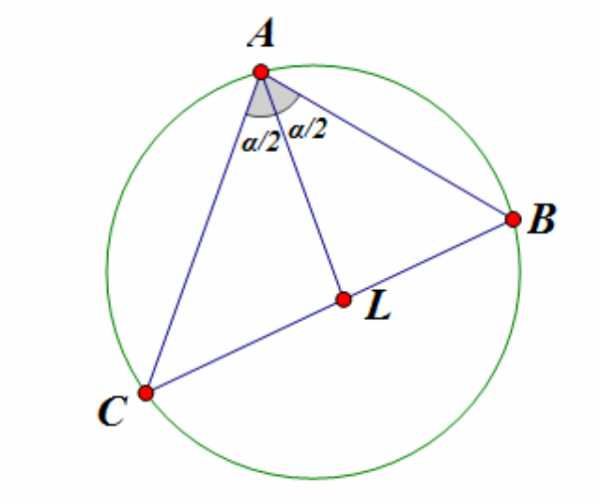
Доказательство:

показать

Продолжим биссектрису до пересечения с описанной окружностью. Рассмотрим треугольники и  . Отметим равные углы:

 

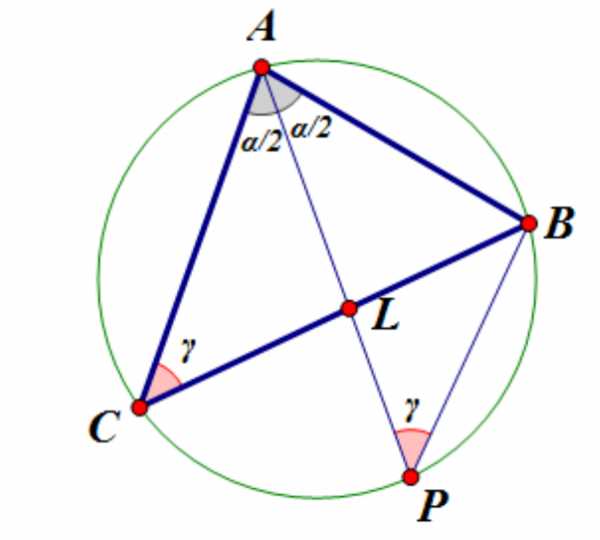
Треугольник  подобен треугольнику по двум углам. Отсюда:

   

   

(2)

   

(3)

По свойству отрезков пересекающихся хорд

   

   

(4)

Подставим (3) в (2) и воспользуемся (4):

   

   

   

Отсюда

   

   

Выразим длины отрезков, на которые биссектриса делит сторону треугольника через длины сторон треугольника. Введем обозначения:

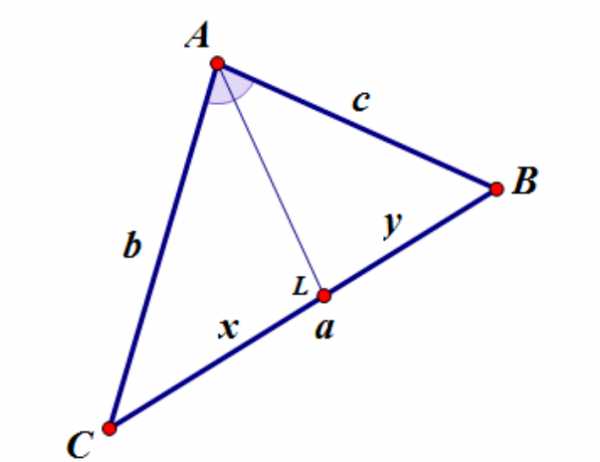
Получим систему:

   

Отсюда

   

   

   

   

 

Медианы.

1. Медианы треугольника делятся точкой пересечения в отношении 2:1, считая от вершины:

 

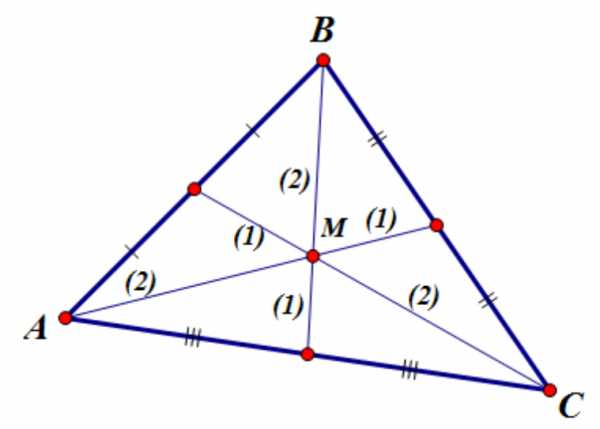
2. Пусть — точка внутри треугольника такая, что выполняется соотношение: , то — точка пересечения медиан треугольника .

Доказательство.

показать

3. Медианы треугольника, пересекаясь, разбивают его на 6 равновеликих треугольника.

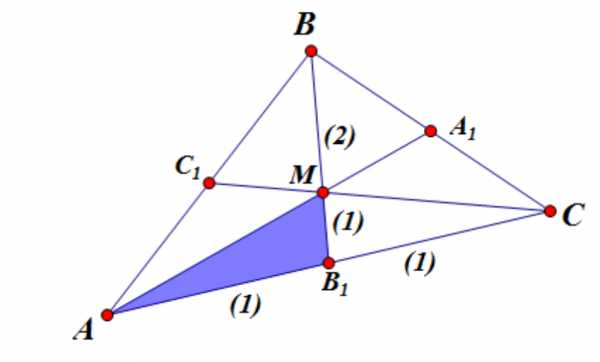
Доказательство.

показать

Докажем, что

так как ,

так как ,

Следовательно,

[\spoiler]

 

 

Высоты.

1. Прямые, содержащие высоты треугольника пересекаются в одной точке. В случае остроугольного треугольника в одной точке пересекаются сами высоты.

 

 

 

 

 

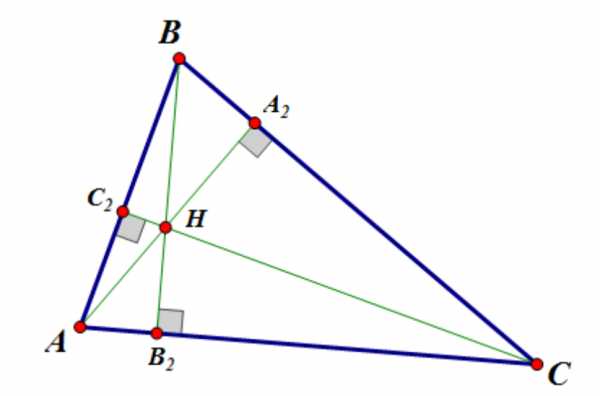
2. Точка пересечения высот треугольника обладает следующим свойством: сумма квадрата расстояния от вершины треугольника и квадрата противолежащей стороны одинаковая для любой вершины:

Доказательство.

[spoiler]

Докажем первую часть равенства:

Перепишем его в виде:

(1)

По теореме Пифагора: (из треугольников  и )

  (из треугольника )

(из треугольника )

Подставим эти выражения в (1), получим:

Раскроем скобки, получим:

.

Получили тождество. Вторая часть равенства доказывается аналогично.

3. Если описать вокруг треугольника окружность и продлить высоты треугольника до пересечения с этой окружностью,

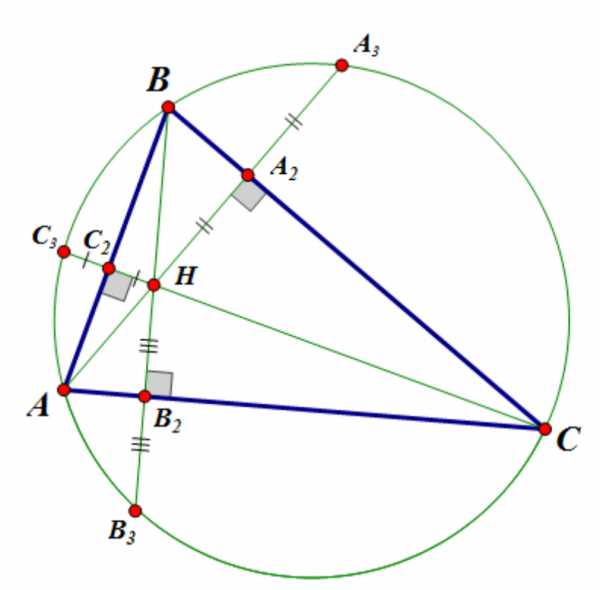
то для любой высоты треугольника расстояние от основания высоты до точки пересечения продолжения высоты с окружностью равно расстоянию от основания высоты до точки пересечения высот:

Или так: Точки, симметричные точке пересечения высот треугольника относительно сторон треугольника, лежат на описанной около треугольника окружности.

Доказательство.

показать

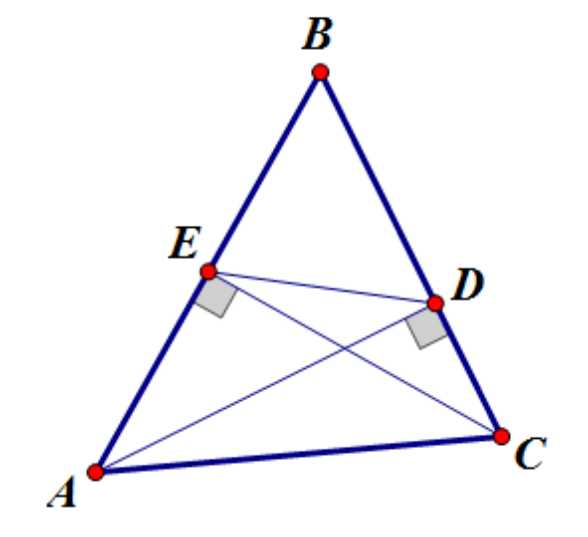
Докажем, что .

Для этого рассмотрим треугольники   и ,  и докажем, что :

Воспользуемся признаком равенства треугольников по стороне и двум прилежащим углам. — общая сторона. Докажем равенство двух углов.

Докажем, что ∠∠

Пусть ∠,  тогда из треугольника получим, что

∠. Следовательно, из треугольника получим, что

∠, и

∠

Но ∠ и ∠ опираются на одну дугу  , следовательно, ∠∠∠

Аналогично получаем, что ∠∠

4. В треугольнике точки   и — основания высот, проведенных из вершин   и . Доказать, что треугольник подобен треугольнику и коэффициент подобия равен .

Доказательство:

показать

Теорема Чевы

Пусть в треугольнике 

Отрезки пересекаются в одной точке в том и только том случае, если

   

(1)

 

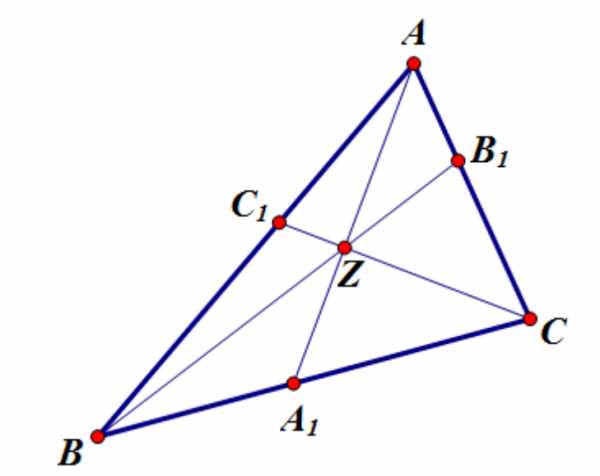
Доказательство.

показать

Докажем, что если отрезки пересекаются в одной точке, то соотношение (1) выполняется.

Легко проверить, что если , то выполняется

Применим это свойство пропорции:

   

   

Аналогично:

   

   

Тогда

   

(2)

Теорему Чевы можно записать в таком виде:

Если отрезки пересекаются в одной точке, то  выполняется соотношение:

   

Чтобы доказать теорему Чевы в форме синусов, достаточно во вторую часть равенства (2) вместо площадей треугольников подставить для площади каждого треугольника формулу .

 

Из лекций Агаханова Назара Хангельдыевича и Владимира Викторовича Трушкова,  КПК МФТИ.

ege-ok.ru

8 класс. Геометрия. Окружность. Теорема о пересечении высот треугольника. — Теорема о пересечении высот треугольника.

Комментарии преподавателя

Тео­ре­ма о пе­ре­се­че­нии высот тре­уголь­ни­ка

Для дан­но­го урока нам по­лез­но знать свой­ства се­ре­дин­но­го пер­пен­ди­ку­ля­ра к от­рез­ку и свой­ство трех се­ре­дин­ных пер­пен­ди­ку­ля­ров тре­уголь­ни­ка.

Задан тре­уголь­ник .  – се­ре­дин­ный пер­пен­ди­ку­ляр к ВС, – се­ре­дин­ный пер­пен­ди­ку­ляр к АС, – се­ре­дин­ный пер­пен­ди­ку­ляр к АВ (см. Рис. 1).

Точка О рав­но­уда­ле­на от вер­шин тре­уголь­ни­ка, 

Рис. 1

Пе­ре­хо­дим к рас­смот­ре­нию цен­траль­ной тео­ре­мы дан­но­го урока.

Три вы­со­ты тре­уголь­ни­ка пе­ре­се­ка­ют­ся в одной точке, эта точка носит на­зва­ние ор­то­цен­тра (см. Рис. 2).

Задан тре­уголь­ник , , , .

До­ка­зать, что 

Рис. 2

До­ка­за­тель­ство:

Про­ве­дем через вер­ши­ны тре­уголь­ни­ка пря­мые, па­рал­лель­ные их про­ти­во­по­лож­ным сто­ро­нам:

через вер­ши­ну А – пря­мую ,

через вер­ши­ну В – пря­мую ,

через вер­ши­ну С – пря­мую .

По­лу­чи­ли новый тре­уголь­ник , рас­смот­рим его свой­ства (см. Рис. 3).

, зна­чит,  . Ана­ло­гич­но . От­сю­да че­ты­рех­уголь­ник  яв­ля­ет­ся па­рал­ле­ло­грам­мом.

Рис. 3

Про­ти­во­по­лож­ные сто­ро­ны па­рал­ле­ло­грам­ма по­пар­но равны, от­сю­да , .

Ана­ло­гич­но ,  по по­стро­е­нию. Че­ты­рех­уголь­ник  – па­рал­ле­ло­грамм. От­сю­да , .

, , от­сю­да . Таким об­ра­зом, точка А – се­ре­ди­на от­рез­ка , а зна­чит, вы­со­та АА1 в ма­лень­ком тре­уголь­ни­ке – это се­ре­дин­ный пер­пен­ди­ку­ляр в боль­шом тре­уголь­ни­ке.

Ана­ло­гич­ные дей­ствия можно вы­пол­нить для вер­шин В и С. По­лу­чим, что В – се­ре­ди­на от­рез­ка , ВВ1 – се­ре­дин­ный пер­пен­ди­ку­ляр к сто­роне боль­шо­го тре­уголь­ни­ка; С – се­ре­ди­на , СС1 – се­ре­дин­ный пер­пен­ди­ку­ляр к сто­роне боль­шо­го тре­уголь­ни­ка.

Мы знаем, что се­ре­дин­ные пер­пен­ди­ку­ля­ры в боль­шом тре­уголь­ни­ке АА1, ВВ1, СС1 пе­ре­се­кут­ся в одной точке – в точке Н. Также мы знаем, что эти се­ре­дин­ные пер­пен­ди­ку­ля­ры яв­ля­ют­ся вы­со­та­ми ма­лень­ко­го тре­уголь­ни­ка, таким об­ра­зом, вы­со­ты тре­уголь­ни­ка пе­ре­се­ка­ют­ся в одной точке Н, что и тре­бо­ва­лось до­ка­зать.

В тре­уголь­ни­ке все ме­ди­а­ны и бис­сек­три­сы при­над­ле­жат тре­уголь­ни­ку, чего нель­зя ска­зать о вы­со­тах. В ост­ро­уголь­ном тре­уголь­ни­ке каж­дая вы­со­та при­над­ле­жит тре­уголь­ни­ку.

За­да­ча

Тре­уголь­ник  ост­ро­уголь­ный, АА1 – вы­со­та (см. Рис. 4). До­ка­зать, что ос­но­ва­ние вы­со­ты А1 – это внут­рен­няя точка от­рез­ка ВС.

Дано: тре­уголь­ник , , , , 

До­ка­зать, что А1 – это внут­рен­няя точка от­рез­ка ВС

Рис. 4

До­ка­за­тель­ство:

До­ка­жем от про­тив­но­го: пусть АА2 – это вы­со­та, и точка А2 не яв­ля­ет­ся точ­кой от­рез­ка ВС (см. Рис. 5).

Тогда угол  – внеш­ний угол для тре­уголь­ни­ка . Внеш­ний угол равен сумме внут­рен­них углов тре­уголь­ни­ка, несмеж­ных с ним, то есть углов  и , то есть сумме пря­мо­го угла и ка­ко­го-то остро­го угла, а дан­ная сумма будет боль­ше , то есть угол 

www.kursoteka.ru

Высота треугольника — Википедия

Материал из Википедии — свободной энциклопедии

Высота в треугольниках различного типа

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону). В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника у тупоугольного треугольника.

Свойства точки пересечения трех высот треугольника (ортоцентра)

Высоты треугольника

• Все три высоты треугольника пересекаются в одной точке, называемой ортоцентром. Это утверждение легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E{\displaystyle A,\ B,\ C,\ E}, не обязательно даже лежащих в одной плоскости:

EA→⋅BC→+EB→⋅CA→+EC→⋅AB→=0{\displaystyle {\overrightarrow {EA}}\cdot {\overrightarrow {BC}}+{\overrightarrow {EB}}\cdot {\overrightarrow {CA}}+{\overrightarrow {EC}}\cdot {\overrightarrow {AB}}=0}

(Для доказательства тождества следует воспользоваться формулами

AB→=EB→−EA→,BC→=EC→−EB→,CA→=EA→−EC→{\displaystyle {\overrightarrow {AB}}={\overrightarrow {EB}}-{\overrightarrow {EA}},\,{\overrightarrow {BC}}={\overrightarrow {EC}}-{\overrightarrow {EB}},\,{\overrightarrow {CA}}={\overrightarrow {EA}}-{\overrightarrow {EC}}}

В качестве точки E следует взять пересечение двух высот треугольника.)

• Ортоцентр изогонально сопряжен центру описанной окружности.
• Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
• Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
• Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
• Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника.
• Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.
• Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
• Если О — центр описанной окружности ΔABC, то OH→=OA→+OB→+OC→{\displaystyle {\overrightarrow {OH}}={\overrightarrow {OA}}+{\overrightarrow {OB}}+{\overrightarrow {OC}}} ,
  • |OH|=9R2−(a2+b2+c2){\displaystyle |OH|={\sqrt {9R^{2}-(a^{2}+b^{2}+c^{2})}}} , где R{\displaystyle R} — радиус описанной окружности; a,b,c{\displaystyle a,b,c} — длины сторон треугольника.
• Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
• Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью всегда делится окружностью Эйлера пополам. Ортоцентр есть центр гомотетии этих двух окружностей.
• Теорема Гамильтона. Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник.
• Следствия теоремы Гамильтона:
  • Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника Гамильтона, имеющих равные радиусы описанных окружностей.
  • Радиусы описанных окружностей трёх треугольников Гамильтона равны радиусу окружности, описанной около исходного остроугольного треугольника.
• В остроугольном треугольнике ортоцентр лежит внутри треугольника; в тупоугольном — вне треугольника; в прямоугольном — в вершине прямого угла.

Свойства высот равнобедренного треугольника

• Если в треугольнике две высоты равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья высота одновременно является медианой и биссектрисой того угла, из которого она выходит.
• Верно и обратное: в равнобедренном треугольнике две высоты равны, а третья высота одновременно является медианой и биссектрисой.
• У равностороннего треугольника все три высоты равны.

Видео по теме

Свойства оснований высот треугольника

• Основания высот образуют так называемый ортотреугольник, обладающий собственными свойствами.
• Описанная около ортотреугольника окружность — окружность Эйлера. На этой окружности также лежат три середины сторон треугольника и три середины трёх отрезков, соединяющих ортоцентр с вершинами треугольника.
• Другая формулировка последнего свойства:
  • Теорема Эйлера для окружности девяти точек. Основания трёх высот произвольного треугольника, середины трёх его сторон (основания его внутренних медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (на окружности девяти точек).
• Теорема. В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному.
• Теорема. В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащие на двух сторонах, антипараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины третьей упомянутой стороны всегда можно провести окружность.

Другие свойства высот треугольника

Свойства минимальной из высот треугольника

Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:

• Минимальная ортогональная проекция треугольника на прямые, лежащие в плоскости треугольника, имеет длину, равную наименьшей из его высот.
• Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
• При непрерывном движении двух точек по периметру треугольника друг навстречу другу, максимальное расстояние между ними за время движения от первой встречи до второй, не может быть меньше длины наименьшей из высот треугольника.
• Минимальная высота в треугольнике всегда проходит внутри этого треугольника.

Основные соотношения

• ha=b⋅sin⁡γ=c⋅sin⁡β,{\displaystyle h_{a}=b{\cdot }\sin \gamma =c{\cdot }\sin \beta ,}
• ha=2⋅Sa,{\displaystyle h_{a}={\frac {2{\cdot }S}{a}},} где S{\displaystyle S} — площадь треугольника, a{\displaystyle a} — длина стороны треугольника, на которую опущена высота.
• ha2=12(b2+c2−12(a2+(b2−c2)2a2)){\displaystyle h_{a}^{2}={\frac {1}{2}}(b^{2}+c^{2}-{\frac {1}{2}}(a^{2}+{\frac {(b^{2}-c^{2})^{2}}{a^{2}}}))}
• ha=b⋅c2⋅R,{\displaystyle h_{a}={\frac {b{\cdot }c}{2{\cdot }R}},} где b⋅c{\displaystyle b{\cdot }c} — произведение боковых сторон, R−{\displaystyle R-} радиус описанной окружности
• ha:hb:hc=1a:1b:1c=(b⋅c):(a⋅c):(a⋅b).{\displaystyle h_{a}:h_{b}:h_{c}={\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}=(b{\cdot }c):(a{\cdot }c):(a{\cdot }b).}
• 1ha+1hb+1hc=1r{\displaystyle {\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}={\frac {1}{r}}}, где r{\displaystyle r} — радиус вписанной окружности.
• S=1(1ha+1hb+1hc)⋅(1ha+1hb−1hc)⋅(1ha+1hc−1hb)⋅(1hb+1hc−1ha){\displaystyle S={\frac {1}{\sqrt {({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{b}}}){\cdot }({\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{a}}})}}}}, где S{\displaystyle S} — площадь треугольника.
• a=2ha⋅(1ha+1hb+1hc)⋅(1ha+1hb−1hc)⋅(1ha+1hc−1hb)⋅(1hb+1hc−1ha){\displaystyle a={\frac {2}{h_{a}{\cdot }{\sqrt {({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{b}}}){\cdot }({\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{a}}})}}}}}, a{\displaystyle a} — сторона треугольника к которой опускается высота ha{\displaystyle h_{a}}.
• Высота равнобедренного треугольника, опущенная на основание:

  hc=12⋅4a2−c2,{\displaystyle h_{c}={\frac {1}{2}}{\cdot }{\sqrt {4a^{2}-c^{2}}},}

где c{\displaystyle c} — основание, a{\displaystyle a} — боковая сторона.

• h=32⋅a{\displaystyle h={\tfrac {\sqrt {3}}{2}}{\cdot }a} — высота в равностороннем треугольнике со стороной a{\displaystyle a}.

Теорема о высоте прямоугольного треугольника

Если высота в прямоугольном треугольнике ABC{\displaystyle ABC} длиной h{\displaystyle h}, проведённая из вершины прямого угла, делит гипотенузу длиной c{\displaystyle c} на отрезки m{\displaystyle m} и n{\displaystyle n}, соответствующие катетам b{\displaystyle b} и a{\displaystyle a}, то верны следующие равенства:

• h3=n⋅m{\displaystyle h^{2}=n{\cdot }m}
• a2=c⋅n{\displaystyle a^{2}=c{\cdot }n}; b2=c⋅m{\displaystyle b^{2}=c{\cdot }m}
• h⋅c=a⋅b{\displaystyle h{\cdot }c=a{\cdot }b}

Теорема о проекциях

См. с. 51, ф. (1.11-4)^[2]. Теорема о проекциях: c=acos⁡β+bcos⁡α; a=bcos⁡γ+ccos⁡β; b=ccos⁡α+acos⁡γ{\displaystyle c=a\cos \beta +b\cos \alpha ;\ a=b\cos \gamma +c\cos \beta ;\ b=c\cos \alpha +a\cos \gamma }. Из теоремы о проекциях следует то, что высота, опущенная, например, из вершины C{\displaystyle C}, делит противоположную ей сторону c{\displaystyle c} на две части acos⁡β{\displaystyle a\cos \beta } и bcos⁡α{\displaystyle b\cos \alpha }, считая от вершины A{\displaystyle A} к B{\displaystyle B}.

Высота похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И сторону хвостом.^[3]

Вариации по теме. Высоты в четырехугольнике

Теорема^[4]. Пусть ABCD{\displaystyle ABCD} – вписанный четырёхугольник, A1{\displaystyle A_{1}} – основание перпендикуляра (высоты), опущенного из вершины A{\displaystyle A} на диагональ BD{\displaystyle BD}; аналогично определяются точки B1,C1,D1{\displaystyle B_{1},C_{1},D_{1}}. Тогда точки A1,B1,C1,D1{\displaystyle A_{1},B_{1},C_{1},D_{1}} лежат на одной окружности.

Примечания

1. ↑ Зетель С.И. Новая геометрия треугольника. Пособие для учителей. 2-е издание.. — М.: Учпедгиз, 1962. — С. 137-138, п. 126, теорема, следствия.
2. ↑ Корн Г.А., Корн Т.М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974. — 832 с.
3. ↑ Сафронова Вера Николаевна,. Урок геометрии в 7-м классе по теме: «Медиана, биссектриса, высота» (рус.). Открытый урок. Издательский дом «Первое сентября». Проверено 19 июля 2017.
4. ↑ Вокруг задачи Архимеда. Упр. 7, рис. 11, следствие, c. 5.

Ссылки

wiki2.red

No related posts.