Тест по «Теории вероятности и математической статистике» — тест
Тест — Экстернат. Теория вероятностей и математическая статистика
Вопрос: 1 — й
Бросают игральный кубик. Найдите вероятность выпадения грани с 1 или 3 очками:
Ответ: 1/3
Вопрос: 2 — й
Бросают игральный кубик. Найдите вероятность выпадения грани с 6 очками:
Ответ: 1/6
Вопрос: 3 — й
Бросают игральный кубик. Найдите вероятность выпадения грани с нечѐтным числом очков:
Ответ: 1/2
Вопрос: 4 — й
Бросают игральный кубик. Найдите вероятность выпадения грани с чѐтным числом очков:
Ответ: 1/2
Вопрос: 5 — й
В задачах на расчѐт вероятности того, что в n независимых испытаниях событие A появится от a до b раз, используется при большом числе испытаний и вероятности p, отличной от 0 и 1:
Ответ: интегральная теорема Муавра-Лапласа
Вопрос: 6 — й
В задачах на расчѐт вероятности того, что в n независимых испытаниях событие A появится ровно m раз, используется при большом числе испытаний и малой вероятности p:
Ответ: формула Пуассона
Вопрос: 7 — й
В задачах на расчѐт вероятности того, что в n независимых испытаниях событие А появится ровно m раз, используется при большом числе испытаний и вероятности p, отличной от 0 и 1:
Ответ: локальная теорема Муавра-Лапласа
Вопрос: 8 — й
В каких пределах заключена вероятность появления случайного события?
Ответ: любое число от 0 до 1
Вопрос: 9 — й
В каких пределах изменяется множественный коэффициент детерминации?
Ответ: от 0 до 1
Вопрос: 10 — й
В каких пределах изменяется множественный коэффициент корреляции?
Ответ: от 0 до 1
Вопрос: 11 — й
В каких пределах изменяется парный коэффициент корреляции?
Ответ: от -1 до 1
Вопрос: 12 — й
В каких пределах изменяется частный коэффициент корреляции?
Ответ: от -1 до 1
Вопрос: 13 — й
В какое из этих понятий комбинаторики входят все элементы изучаемого множества?
Ответ: число перестановок
Вопрос: 14 — й
В каком критерии используется G-распределение?
Ответ: Кохрана
Вопрос: 15 — й
В каком критерии используется нормальное распределение?
Ответ: при проверке гипотезы о значении вероятности события
Вопрос: 16 — й
В каком критерии используется распределение Пирсона?
Ответ: Бартлетта
Вопрос: 17 — й
В каком критерии используется распределение Стьюдента?
Ответ: при проверке гипотезы о равенстве генеральных средних
Вопрос: 18 — й
В каком критерии используется распределение Фишера-Снедекора?
Ответ: при проверке гипотезы о равенстве генеральных дисперсий
Вопрос: 19 — й
В коробке 12 стандартных и 3 бракованных детали. Вынимают 1 деталь. Найти вероятность того, что эта деталь — стандартная.
Ответ: 12/15
Вопрос: 20 — й
В коробке 12 стандартных и 3 бракованных детали. Вынимают 1 деталь. Найти вероятность того, что эта деталь – бракованная.
Ответ: 3/15
Вопрос: 21 — й
В коробке 4 стандартных и 2 бракованных детали. Подряд вынимают две детали, при этом не возвращают их обратно в коробку. Найти вероятность того, что обе вынутые детали – бракованные.
Ответ: 2/30
Вопрос: 22 — й
В коробке 4 стандартных и 2 бракованных детали. Последовательно по одной вынимают две детали, при этом каждый раз возвращают их обратно в коробку. Найти вероятность того, что обе вынутые детали – бракованные.
Ответ: 4/36
Вопрос: 23 — й
В связке 10 похожих ключей от сейфов. Определите вероятность, с которой первыми наугад выбранными ключами можно открыть сейф с двумя последовательно открывающимися замками.
Ответ: 1/90
Вопрос: 24 — й
В теории статистического оценивания оценки бывают:
Ответ: точечные и интервальные
Вопрос: 25 — й
В урне 2 белых и 3 черных шара. Вынимают шар. Найти вероятность того, что этот шар — белый
Ответ: 2/5
Вопрос: 26 — й
В урне 2 белых и 3 черных шара. Подряд вынимают два шара, при этом каждый раз шары возвращают обратно в корзину. Найти вероятность того, что оба вынутых шара — белые.
Ответ: 4/25
Вопрос: 27 — й
В урне 2 белых и 3 черных шара. Подряд вынимают два шара, при этом шары не возвращают обратно в корзину. Найти вероятность того, что оба вынутых шара — белые.
Ответ: 2/20
Вопрос: 28 — й
В урне 5 белых и 3 черных шара. Вынимают шар. Найти вероятность того, что этот шар — белый
Ответ: 5/8
Вопрос: 29 — й
Выборка репрезентативна. Это означает, что:
Ответ: она правильно отражает пропорции генеральной совокупности
Вопрос: 30 — й
Выборочной совокупностью (выборкой) называют множество результатов, отобранных из генеральной совокупности:
Ответ: случайно
Вопрос: 31 — й
Гиперболическое относительно аргумента уравнение регрессии имеет вид:
Ответ:
Вопрос: 32 — й
Границы двусторонней критической области при заданном уровне значимости α находят из соотношения:
Ответ:
Вопрос: 33 — й
Границы левосторонней критической области при заданном уровне значимости α находят из соотношения:
Ответ:
Вопрос: 34 — й
Границы правосторонней критической области при заданном уровне значимости α находят из соотношения:
Ответ:
Вопрос: 35 — й
Два события называют несовместными (несовместимыми), если:
Ответ: их совместное наступление в результате испытания невозможно
Вопрос: 36 — й
Два события называют совместными (совместимыми), если:
Ответ: они могут произойти одновременно в результате испытания
Вопрос: 37 — й
Для проверки какой гипотезы используется статистика
Ответ:
Вопрос: 38 — й
Если в трѐхмерной совокупности XYZ оказалось, что парный коэффициент между X и Y по модулю больше частного, и коэффициенты не имеют разных знаков, то это значит:
Ответ: переменная Z усиливает связь между X и Y
Вопрос: 39 — й
Если в трѐхмерной совокупности XYZ оказалось, что парный коэффициент между X и Y по модулю меньше частного, и коэффициенты не имеют разных знаков, то это значит:
Ответ:переменная Z ослабляет связь между X и Y
Вопрос: 40 — й
Если вероятность наступления одного события зависит от того, произошло ли другое событие, то они называются:
Ответ: зависимыми
Вопрос: 41 — й
Если вероятность наступления одного события не зависит от того, произошло ли другое событие, то они называются:
Ответ: независимыми
Вопрос: 42 — й
Если все значения случайной величины увеличить в какое-то число раз, то как изменится еѐ дисперсия?
Ответ: увеличится в это число раз, возведѐнное в квадрат
Вопрос: 43 — й
Если все значения случайной величины увеличить в какое-то число раз, то как изменится еѐ математическое ожидание?
Ответ: увеличится в это число раз
Вопрос: 44 — й
Если все значения случайной величины увеличить на какое-то число, то как изменится еѐ дисперсия?
Ответ: не изменится
Вопрос: 45 — й
Если все значения случайной величины увеличить на какое-то число, то как изменится еѐ математическое ожидание?
Ответ: увеличится на это число
Вопрос: 46 — й
Если все значения случайной величины уменьшить в какое-то число раз, то как изменится еѐ дисперсия?
Ответ: уменьшится в это число раз, возведѐнное в квадрат
Вопрос: 47 — й
Если все значения случайной величины уменьшить в какое-то число раз, то как изменится еѐ математическое ожидание?
Ответ: уменьшится в это число раз
Вопрос: 48 — й
Если все значения случайной величины уменьшить на какое-то число, то как изменится еѐ дисперсия?
Ответ: не изменится
Вопрос: 49 — й
Если все значения случайной величины уменьшить на какое-то число, то как изменится еѐ математическое ожидание?
Ответ: уменьшится на это число
Вопрос: 50 — й
Если два события могут
Ответ: совместными
Вопрос: 51 — й
Если два события не могут произойти одновременно, то они называются:
Ответ: несовместными
Вопрос: 52 — й
Если математическое ожидание оценки при любом объѐме выборки равно самому оцениваемому параметру, то точечная оценка называется:
Ответ: несмещенной
Вопрос: 53 — й
Если нулевую гипотезу в результате проверки критерия отвергают, какова вероятность при этом совершить ошибку?
Ответ: Ошибка 1-го рода α
Вопрос: 54 — й
Если случайная величина распределена по нормальному закону, то еѐ средняя арифметическая распределена:
Ответ: по нормальному закону
Вопрос: 55 — й
Если событие может произойти, а может не произойти в результате испытания, то оно называется:
Ответ: случайным
Вопрос: 56 — й
Если событие не происходит ни при каком испытании, то оно называется:
Ответ: невозможным
Вопрос: 57 — й
Если событие обязательно
Ответ: достоверным
Вопрос: 58 — й
Если точечная оценка параметра при увеличении объѐма выборки сходится по вероятности к самому оцениваемому параметру, то точечная оценка называется:
Ответ: состоятельной
Вопрос: 59 — й
Значимость уравнения
Ответ: Фишера-Снедекора
Вопрос: 60 — й
Из колоды 36 карт наудачу вытягивается одна. Какова вероятность, что это будет бубновая дама?
Ответ: 1/36
Вопрос: 61 — й
Из колоды 36 карт наудачу вытягивается одна. Какова вероятность, что это будет дама?
Ответ: 1/9
Вопрос: 62 — й
Из колоды 36 карт наудачу вытягивается одна. Какова вероятность, что это будет карта бубновой масти?
Ответ: 1/4
Вопрос: 63 — й
Из колоды 52 карт наудачу вытягивается одна. Какова вероятность, что это будет валет пик?
Ответ: 1/52
Вопрос: 64 — й
Из колоды 52 карт наудачу вытягивается одна. Какова вероятность, что это будет валет?
Ответ: 1/13
Вопрос: 65 — й
Из колоды 52 карт наудачу вытягивается одна. Какова вероятность, что это будет карта пиковой масти?
Ответ: 1/4
Вопрос: 66 — й
Из колоды 52 карт наудачу вытягивается одна. Какова вероятность, что это будет карта червовой масти?
Ответ: 1/4
Вопрос: 67 — й
Из колоды 52 карт наудачу вытягивается одна. Какова вероятность, что это будет король пик?
Ответ: 1/52
Вопрос: 68 — й
Из колоды 52 карт наудачу вытягивается одна. Какова вероятность, что это будет король?
Ответ: 1/13
Вопрос: 69 — й
Известен доход по 4 из 5 фирм X1=10, X2=15, X3=18, X4=12. Известно также, что средний доход по 5 фирмам равен 15. Доход пятой фирмы равен:
Ответ: 20
Вопрос: 70 — й
Известен доход по 4 из 5 фирм X1=14, X2=21, X3=16, X4=18. Известно также, что средний доход по 5 фирмам равен 16. Доход пятой фирмы равен:
Ответ: 11
Вопрос: 71 — й
Известен доход по 4 из 5 фирм X1=16, X2=13, X3=10, X4=20. Известно также, что средний доход по 5 фирмам равен 15. Доход пятой фирмы равен:
Ответ: 16
Вопрос: 72 — й
Известен доход по 4 из 5 фирм X1=3, X2=5, X3=4, X4=6. Известно также, что средний доход по 5 фирмам равен 4. Доход пятой фирмы равен:
Ответ: 2
Вопрос: 73 — й
Известен доход по 4 из 5 фирм X1=4, X2=8, X3=9, X4=6. Известно также, что средний доход по 5 фирмам равен 7. Доход пятой фирмы равен:
Ответ: 8
Вопрос: 74 — й
Интеграл в бесконечных
Ответ: 1
Вопрос: 75 — й
К какому типу относится случайная величина – расстояние от центра мишени до точки попадания пули стрелка?
Ответ: непрерывная
Вопрос: 76 — й
К какому типу относится случайная величина – рост человека?
Ответ: непрерывная
Вопрос: 77 — й
К какому типу относится случайная величина – число очков, выпавших на игральном кубике?
Ответ: дискретная
Вопрос: 78 — й
К какому типу относится случайная величина – число студентов, пришедших на лекцию?
Ответ: дискретная
Вопрос: 79 — й
Как называются два события, непоявление одного из которых влечѐт появление другого?
Ответ: противоположные
Вопрос: 80 — й
Как называются два события, сумма которых есть событие достоверное, а произведение — событие невозможное?
Ответ: противоположные
Вопрос: 81 — й
Как отношение числа случаев, благоприятствующих событию A, к числу всех возможных случаев вычисляется…
Ответ: вероятность
Вопрос: 82 — й
Как по-другому называют функцию
плотности вероятности любой
непрерывной случайной
Ответ: дифференциальная функция
Вопрос: 83 — й
Как по-другому называют функцию
распределения любой
Ответ: интегральная функция
Вопрос: 84 — й
Какая критическая область
Ответ: правосторонняя
Вопрос: 85 — й
Какая критическая область
Ответ: правосторонняя
Вопрос: 86 — й
Какая критическая область
Ответ: правосторонняя
Вопрос: 87 — й
Какая статистика используется при проверке гипотезы о значении генеральной дисперсии H0: σ2 = σ2 0 :
Ответ:
Вопрос: 88 — й
Какая статистика используется при проверке гипотезы о значении генеральной средней H0: μ=μ0 при известной генеральной дисперсии:
Ответ:
Вопрос: 89 — й
Какая статистика используется при проверке гипотезы о значении генеральной средней H0: μ=μ0 при неизвестной генеральной дисперсии:
Ответ:
Вопрос: 90 — й
yaneuch.ru
Тесты по курсу ТВиМС — Стр 2
б) Гипотеза H0 верна, но ее отвергают согласно критерию
в) Гипотеза H0 неверна и ее отвергают согласно критерию
г) Гипотеза H0 неверна, но ее принимают согласно критерию
Тест 3.11. Что называют мощностью критерия:
а) вероятность не допустить ошибку второго рода
б) вероятность не допустить ошибку первого рода
в) вероятность не допустить ошибку первого или второго рода
г) нет правильного ответа
Тест 3.12. Что называют мощностью критерия:
а) Гипотеза H0 верна и ее принимают согласно критерию
б) Гипотеза H0 верна, но ее отвергают согласно критерию
в) Гипотеза H0 неверна и ее отвергают согласно критерию
г) Гипотеза H0 неверна, но ее принимают согласно критерию
Тест 3.13. Когда при проверке гипотезы H0: µ=µ0 при H1:µ=µ1 следует выбирать правостороннюю критическую область:
а) µ1<µ0 б) µ1>µ0 в) µ1≠µ0 г) µ1=µ0
Тест 3.14. Когда при проверке гипотезы H0: µ=µ0 при H1:µ=µ1 следует выбирать левостороннюю критическую область:
а) µ1<µ0 б) µ1>µ0 в) µ1≠µ0 г) µ1=µ0
Тест 3.15. Когда при проверке гипотезы H0: µ=µ0 при H1:µ=µ1 следует выбирать двустороннюю критическую область:
а) µ1<µ0 б) µ1>µ0 в) µ1≠µ0 г) µ1=µ0
Тест 3.16. Когда при проверке гипотезы H0: σ2=σ02 при H1: σ2=σ12 следует выбирать двустороннюю критическую область:
а) σ1<σ0 б) σ1>σ0 в) σ1≠σ0 г) σ1=σ0
Тест 3.17. Когда при проверке гипотезы H0: σ2=σ02 при H1: σ2=σ12 следует выбирать левостороннюю критическую область:
а) σ1<σ0 б) σ1>σ0 в) σ1≠σ0 г) σ1=σ0
Тест 3.18. Когда при проверке H0: σ2=σ02 при H1: σ2=σ12 следует выбирать правостороннюю критическую область:
а) σ1<σ0 б) σ1>σ0 в) σ1≠σ0 г) σ1=σ0
Тест 3.19. Какая статистика используется при проверке гипотезы о значении генеральной дисперсии H0: σ2=σ02:
а) 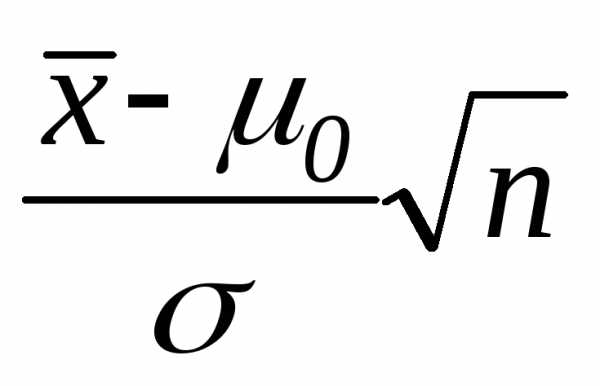 б)
б) 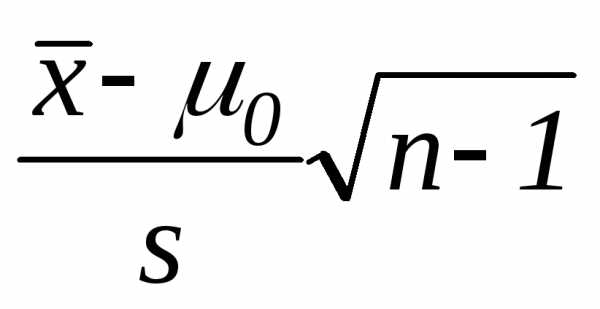 в)
в) 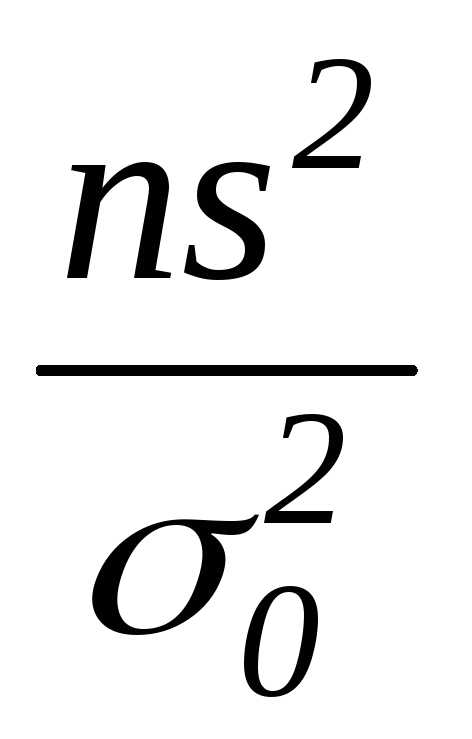 г)
г) 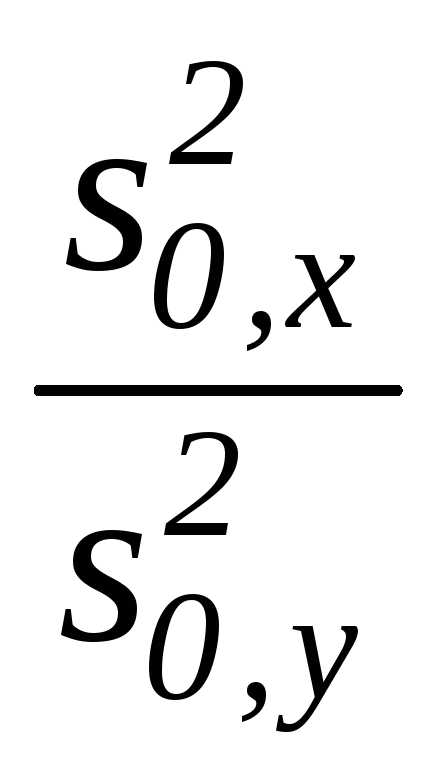
Тест 3.20. Какая статистика используется при проверке гипотезы о значении генеральной средней H0: µ=µ0 при известной генеральной дисперсии:
а) 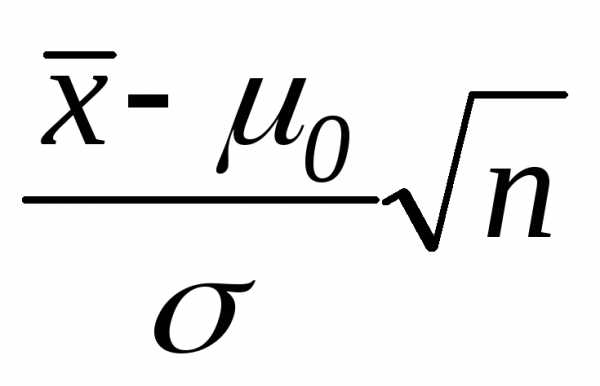 б)
б) 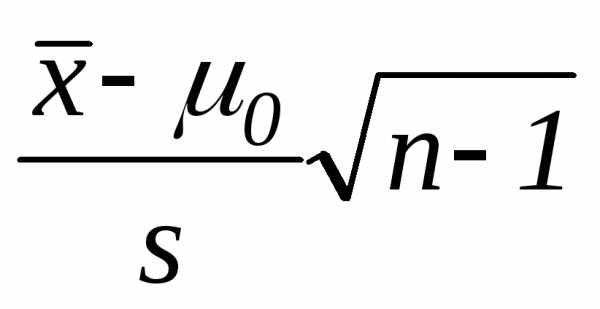 в)
в) 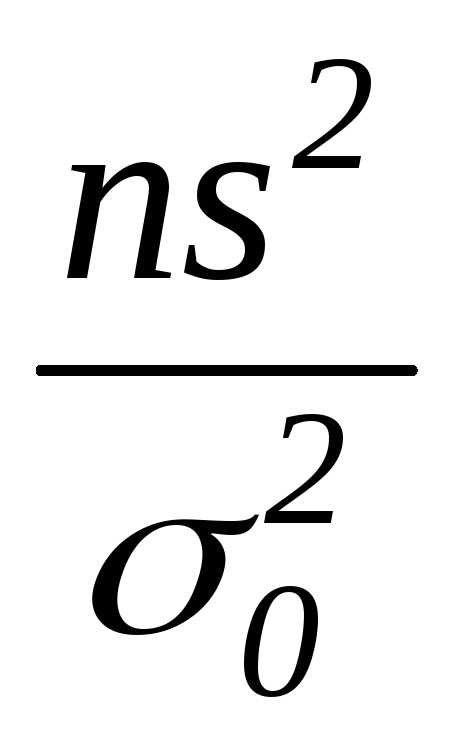 г)
г) 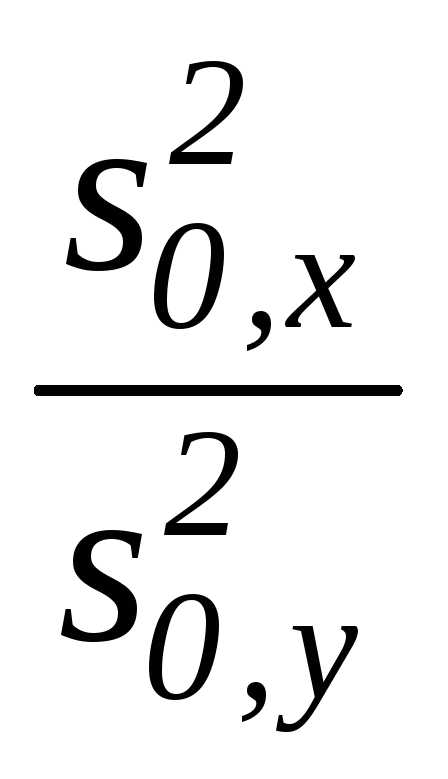
Тест 3.21. Какая статистика используется при проверке гипотезы о значении генеральной средней H0: µ=µ0 при неизвестной генеральной дисперсии:
а) 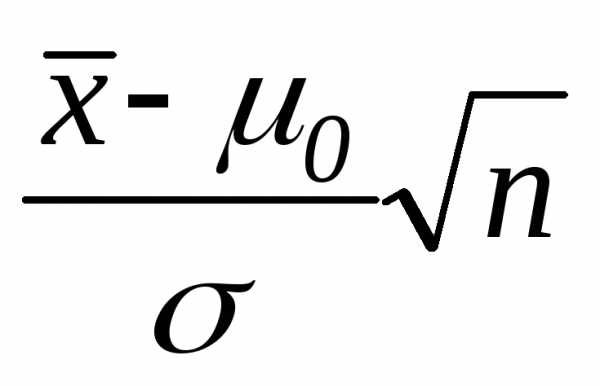 б)
б) 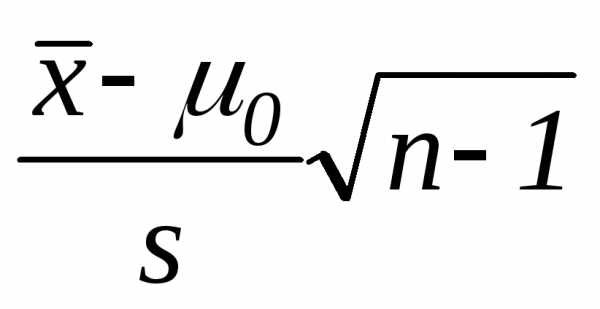 в)
в) 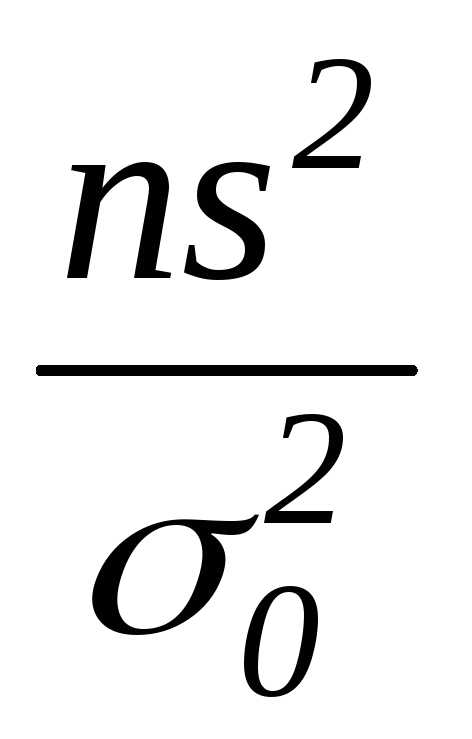 г)
г) 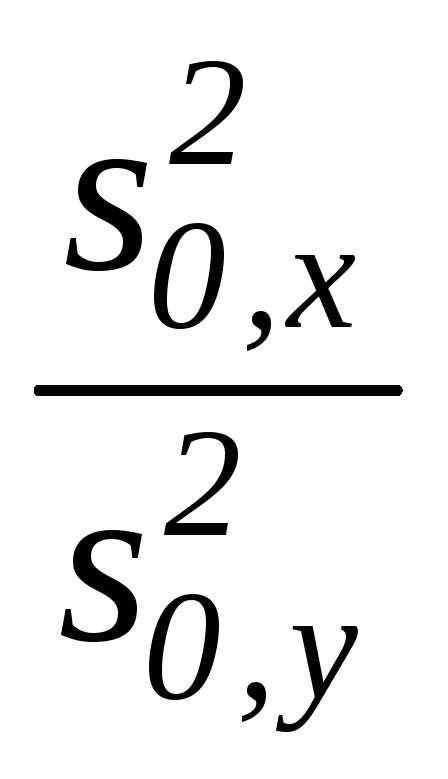
Тест 3.22. В каком критерии используется распределение Стьюдента?
а) при проверке гипотезы о равенстве генеральных средних
б) при проверке гипотезы о значении вероятности события
Тест 3.23. В каком критерии используется распределение Фишера-Снедекора?
а) при проверке гипотезы о равенстве генеральных средних
б) при проверке гипотезы о значении вероятности события
в) при проверке гипотезы о равенстве генеральных дисперсий
г) при проверке гипотезы о значении генеральной дисперсии
Тест 3.24. В каком критерии используется нормальное распределение?
а) при проверке гипотезы о равенстве вероятностей
б) при проверке гипотезы о значении вероятности события
в) при проверке гипотезы о равенстве генеральных дисперсий
г) при проверке гипотезы о значении генеральной дисперсии
Тест 3.25. В каком критерии используется распределение Пирсона?
а) при проверке гипотезы о равенстве генеральных средних
б) при проверке гипотезы о значении вероятности события
Тест 3.26. Когда при проверке гипотезы H0: р=р0 при H1: р=р1 следует выбирать правостороннюю критическую область:
а) р1<р0 б) р1>р0 в) р1≠р0 г) р1=р0
Тест 3.27. Когда при проверке гипотезы H0: р=р0 при H1: р=р1 следует выбирать левостороннюю критическую область:
а) р1<р0 б) р1>р0 в) р1≠р0 г) р1=р0
Тест 3.28. Когда при проверке гипотезы H0: р=р0 при H1: р=р1 следует выбирать двустороннюю критическую область:
а) р1<р0 б) р1>р0 в) р1≠р0 г) р1=р0
Тест 3.29. Какая критическая область используется при проверке гипотезы о равенстве генеральных дисперсий двух нормальных совокупностей H0: σx2=σy2 при H1: σx2≠σy2?
а) двусторонняя
б) левосторонняя
в) правосторонняя
Тест 3.30. Какая статистика используется при проверке гипотезы о равенстве генеральных дисперсий двух нормальных совокупностей H0: σx2=σy2
а) 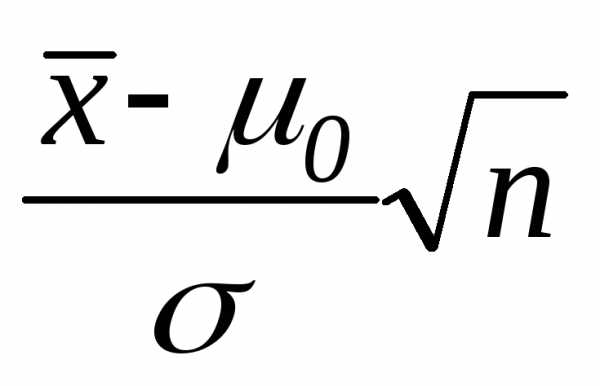 б)
б) 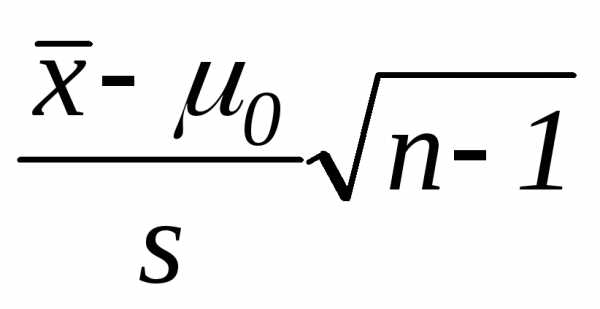 в)
в) 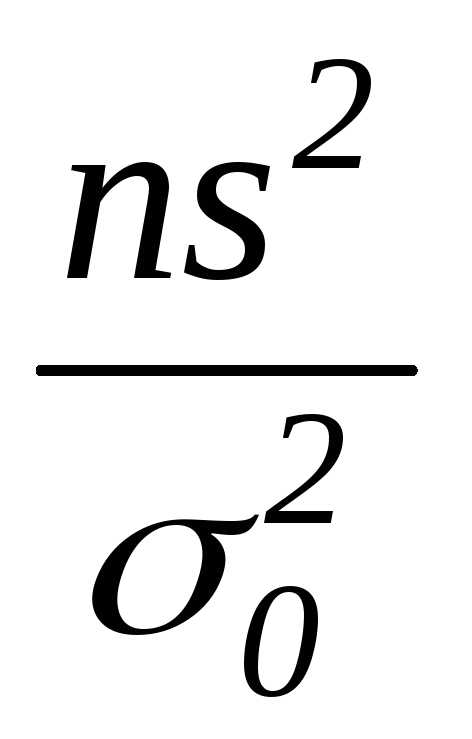 г)
г) 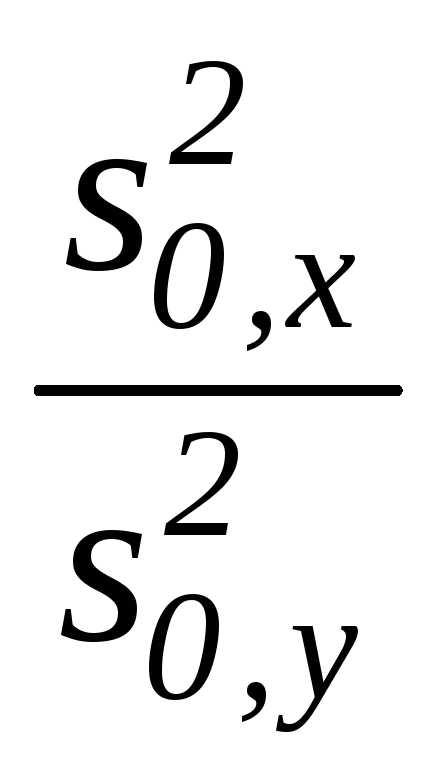
Тест
3.31. Для проверки какой гипотезы используется
статистика 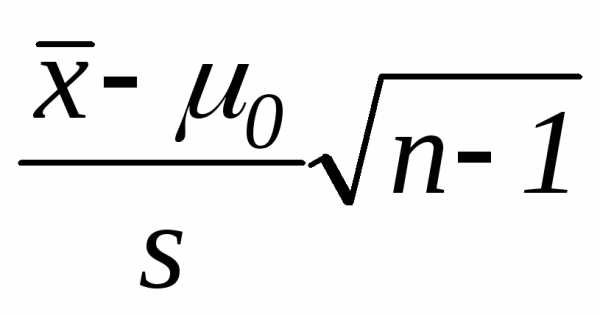
а) H0:р1=р2 б) H0:µ1=µ2 в) H0:σ12=σ22 г) нет правильного ответа
Тест 3.32. При проверке гипотезы о значении генеральной средней гипотеза H0 отвергается, если:
а) наблюдаемое значение по модулю больше критического
б) наблюдаемое значение по модулю больше или равно критическому
в) наблюдаемое значение меньше критического
г) наблюдаемое значение не равно критическому
Тест 3.33. При проверке гипотезы о значении вероятности события гипотеза H0 отвергается, если:
а) наблюдаемое значение по модулю больше критического
б) наблюдаемое значение по модулю больше или равно критическому
в) наблюдаемое значение меньше критического
г) наблюдаемое значение не равно критическому
Тест 3.34. При проверке гипотезы о равенстве генеральных средних двух нормальных совокупностей гипотеза H0 не отвергается, если:
а) наблюдаемое значение по модулю больше критического
б) наблюдаемое значение по модулю больше или равно критическому
в) наблюдаемое значение меньше критического
г) наблюдаемое значение не равно критическому
Тест 3.35. При проверке гипотезы о значении генеральной средней при неизвестной генеральной дисперсии используется:
а) распределение Пирсона б) распределение Фишера-Снедекора
в) распределение Стьюдента г) нормальное распределение
Тест 3.36. При проверке гипотезы о значении генеральной средней при известной дисперсии используется:
а) распределение Пирсона б) распределение Фишера-Снедекора
в) распределение Стьюдента г) нормальное распределение
Тест 3.37. При проверке гипотезы о равенстве генеральных средних двух нормальных совокупностей с неизвестными генеральными дисперсиями используется:
а) распределение Пирсона б) распределение Фишера-Снедекора
в) распределение Стьюдента г) нормальное распределение
Тест 3.38. При проверке гипотезы о равенстве генеральных средних двух нормальных совокупностей с известными генеральными дисперсиями используется:
а) распределение Пирсона б) распределение Фишера-Снедекора
в) распределение Стьюдента г) нормальное распределение
Тест 3.46. По какому принципу выбирается критическая область?
а) вероятность попадания в нее должна быть минимальной, если верна гипотеза H0 и максимальной в противном случае
б) вероятность попадания в нее должна быть минимальной, если верна гипотеза H1 и максимальной в противном случае
в) вероятность попадания в нее должна быть равна 0
г) вероятность попадания в нее должна быть максимальной, если верна гипотеза H0 и минимальной в противном случае
Тест 3.47. Границы правосторонней критической области при заданном уровне значимости α находят из соотношения:
а) P(S>Sкр)=α
б) P(S<Sкр)=α
в) P(S>Sкр.пр)=α/2; P(S<Sкр.лев)=α/2
г) нет правильного ответа
Тест 3.48. Границы левосторонней критической области при заданном уровне значимости α находят из соотношения:
а) P(S>Sкр)=α
б) P(S<Sкр)=α
в) P(S>Sкр.пр)=α/2; P(S<Sкр.лев)=α/2
г) нет правильного ответа
Тест 3.49. Границы двусторонней критической области при заданном уровне значимости α находят из соотношения:
а) P(S>Sкр)=α
б) P(S<Sкр)=α
в) P(S>Sкр.пр)=α/2; P(S<Sкр.лев)=α/2
г) нет правильного ответа
studfiles.net
Критерии согласия
При анализе вариационных рядов распределения большое значение имеет, насколько эмпирическое распределение признака соответствует нормальному. Для этого частоты фактического распределения нужно сравнить с теоретическими, которые характерны для нормального распределения. Значит, нужно по фактическим данным вычислить теоретические частоты кривой нормального распределения, являющиеся функцией нормированных отклонений.
Иначе говоря, эмпирическую кривую распределения нужно выровнять кривой нормального распределения.
Объективная характеристика соответствия теоретических и эмпирических частот может быть получена при помощи специальных статистических показателей, которые называют критериями согласия.
Критерием согласия называют критерий, который позволяет установить, является ли расхождение эмпирического и теоретического распределений случайным или значимым, т. е. согласуются ли данные наблюдений с выдвинутой статистической гипотезой или не согласуются. Распределение генеральной совокупности, которое она имеет в силу выдвинутой гипотезы, называют теоретическим.
Возникает необходимость установить критерий (правило), которое позволяло бы судить, является ли расхождение между эмпирическим и теоретическим распределениями случайным или значимым. Если расхождение окажется случайным, то считают, что данные наблюдений (выборки) согласуются с выдвинутой гипотезой о законе распределения генеральной совокупности и, следовательно, гипотезу принимают; если же расхождение окажется значимым, то данные наблюдений не согласуются с гипотезой и ее отвергают.
Обычно эмпирические и теоретические частоты различаются в силу того, что:
- расхождение случайно и связано с ограниченным количеством наблюдений;
- расхождение неслучайно и объясняется тем, что статистическая гипотеза о том, что генеральная совокупность распределена нормально — ошибочна.
Таким образом, критерии согласия позволяют отвергнуть или подтвердить правильность выдвинутой при выравнивании ряда гипотезы о характере распределения в эмпирическом ряду.
Эмпирические частоты получают в результате наблюдения. Теоретические частоты рассчитывают по формулам.
Для закона нормального распределения их можно найти следующим образом:
- Σƒi—сумма накопленных (кумулятивных) эмпирических частот
- h — разность между двумя соседними вариантами
- σ — выборочное среднеквадратическое отклонение
- t–нормированное (стандартизированное) отклонение
- φ(t)–функция плотности вероятности нормального распределения (находят по таблице значений локальной функции Лапласа для соответствующего значения t)
Имеется несколько критериев согласия, наиболее распространенными из которых являются: критерий хи-квадрат (Пирсона), критерий Колмогорова, критерий Романовского.
Критерий согласия Пирсона χ2 – один из основных, который можно представить как сумму отношений квадратов расхождений между теоретическими (fТ) и эмпирическими (f) частотами к теоретическим частотам:
- k–число групп, на которые разбито эмпирическое распределение,
- fi–наблюдаемая частота признака в i-й группе,
- fT–теоретическая частота.
Для распределения χ2 составлены таблицы, где указано критическое значение критерия согласия χ2 для выбранного уровня значимости α и степеней свободы df (или ν).
Уровень значимости α – вероятность ошибочного отклонения выдвинутой гипотезы, т.е. вероятность того, что будет отвергнута правильная гипотеза. Р — статистическая достоверность принятия верной гипотезы. В статистике чаще всего пользуются тремя уровнями значимости:
α=0,10, тогда Р=0,90 (в 10 случаях из 100)
α=0,05, тогда Р=0,95 ( в 5 случаях из 100)
α=0,01, тогда Р=0,99 (в 1 случае из 100) может быть отвергнута правильная гипотеза
Число степеней свободы df определяется как число групп в ряду распределения минус число связей: df = k –z. Под числом связей понимается число показателей эмпирического ряда, использованных при вычислении теоретических частот, т.е. показателей, связывающих эмпирические и теоретические частоты. Например, при выравнивании по кривой нормального распределения имеется три связи. Поэтому при выравнивании по кривой нормального распределения число степеней свободы определяется как df =k–3. Для оценки существенности, расчетное значение сравнивается с табличным χ2табл
При полном совпадении теоретического и эмпирического распределений χ2=0, в противном случае χ2>0. Если χ2расч> χ2табл, то при заданном уровне значимости и числе степеней свободы гипотезу о несущественности (случайности) расхождений отклоняем. В случае, если χ2расч< χ2табл то гипотезу принимаем и с вероятностью Р=(1-α) можно утверждать, что расхождение между теоретическими и эмпирическими частотами случайно. Следовательно, есть основания утверждать, что эмпирическое распределение подчиняется нормальному распределению. Критерий согласия Пирсона используется, если объем совокупности достаточно велик (N>50), при этом, частота каждой группы должна быть не менее 5.
Критерий согласия Колмогорова основан на определении максимального расхождения между накопленными эмпирическими и теоретическими частотами:
где D и d – соответственно, максимальная разность между накопленными частотами и накопленными частостями эмпирического и теоретического распределений.
По таблице распределения статистики Колмогорова определяют вероятность, которая может изменяться от 0 до 1. При Р(λ)=1- происходит полное совпадение частот, Р(λ)=0 – полное расхождение. Если величина вероятности Р значительна по отношению к найденной величине λ, то можно предположить, что расхождения между теоретическим и эмпирическим распределениями несущественны, т. е. носят случайный характер.
Основное условие использования критерия Колмогорова – достаточно большое число наблюдений.
Критерий согласия Колмогорова
Рассмотрим как критерий Колмогорова (λ) применяется при проверке гипотезы о нормальном распределении генеральной совокупности. Выравнивание фактического распределения по кривой нормального распределения состоит из нескольких этапов:
- Сравнивают фактические и теоретические частоты.
- По фактическим данным определяют теоретические частоты кривой нормального распределения, которая является функцией нормированного отклонения.
- Проверяют на сколько распределение признака соответствует нормальному.
Для IV колонки таблицы:
В MS Excel нормированное отклонение (t) рассчитывается с помощью функции НОРМАЛИЗАЦИЯ. Необходимо выделить диапазон свободных ячеек по количеству вариант (строк электронной таблицы). Не снимая выделения, вызвать функцию НОРМАЛИЗАЦИЯ. В появившемся диалоговом окне указать следующие ячейки, в которых размещены, соответственно, наблюдаемые значения (Xi), средняя (X) и среднеквадратическое отклонение Ϭ. Операцию обязательно завершить одновременным нажатием клавиш Ctrl+Shift+Enter
Для V колонки таблицы:
Функцию плотности вероятности нормального распределения φ(t) находим по таблице значений локальной функции Лапласа для соответствующего значения нормированного отклонения (t)
Для VI колонки таблицы:
Критерий согласия Колмогорова (λ) определяется путем деления модуля max разности между эмпирическими и теоретическими кумулятивными частотами на корень квадратный из числа наблюдений:
По специальной таблице вероятности для критерия согласия λ определяем, что значению λ=0,59 соответствует вероятность 0,88 (λ<P) критерий статистически не значим. Это значит, что с вероятностью 0,88 можно судить, что отклонения фактических (эмпирических) частот от теоретических являются случайными. Следовательно, нулевая гипотеза принимается и есть основания утверждать, что эмпирическое распределение подчиняется нормальному распределению.
Распределение эмпирических и теоретических частот, плотности вероятности теоретического распределения
Применяя критерии согласия для проверки соответствия наблюдаемого (эмпирического) распределения теоретическому, следует различать проверку простых и сложных гипотез.
Одновыборочный критерий нормальности Колмогорова-Смирнова основан на максимуме разности между кумулятивным эмпирическим распределением выборки и предполагаемым (теоретическим) кумулятивным распределением. Если D статистика Колмогорова-Смирнова значима, то гипотеза о том, что соответствующее распределение нормально, должна быть отвергнута.
Смотри также по теме:
helpstat.ru
G — критерий знаков | univer-nn.ru
Предназначен для установления общего направления сдвига изучаемого признака (сдвигом называют разность между вторым и первым измерениями). Критерий знаков позволяет установить, в какую сторону в выборке в целом произошли изменения (произошло увеличение значений, уменьшение или значения не изменились).
Суть метода: Если попарно сравниваемые значения двух выборок существенно не отличаются друг от друга, то число «+» и «-» будет примерно одинаковым. Если заметно преобладают «+» или «-», это указывает на положительное или отрицательное действие фактора.
Критерий знаков может быть применим не только к количественным признакам, но и к качественным, имеющим не менее трех градаций.
Чтобы обработать экспериментальные данные с помощью критерия знаков, в таблицу выписывают результаты первого и второго измерений. Первое измерение проводится до действия фактора на изучаемую величину, второе измерение – после воздействия фактора. В столбце, обозначенном «сдвиг», указывается величина и направление сдвига (в случае количественного признака) или только направление (в случае качественного признака).
Примеры таблиц для количественного и качественного признаков:
| № измерения | Х («до») | Y («после») | сдвиг | № измерения | Х («до») | Y ( «после») | сдвиг | ||
| 1 2 3 … n | 16 18 12 … 16 | 15 19 12 … 18 | -1 +1 0 … +2 | 1 2 3 … n | +++ ++ +++ … ++ | + ++ ++ … +++ | — 0 — … + |
После заполнения таблицы подсчитывается общее число положительных и отрицательных сдвигов и вводятся следующие понятия:
- типичный сдвиг – сдвиг, чаще встречающийся в выборке;
- нетипичный сдвиг – сдвиг, реже встречающийся в выборке; количество нетипичных сдвигов является наблюдаемым значением критерия (Gн).
По таблице критических точек находим значение Gкр(α;n’) , где n’ — объем выборки за вычетом нулевых сдвигов.
Осуществляем выбор гипотезы, учитывая, что критерий знаков является левосторонним.
Если Gн < Gк, то гипотеза Н0 отвергается, принимается гипотеза Н1; нетипичных сдвигов мало и преобладание типичного сдвига является неслучайным, оно обусловлено влиянием фактора.
Если Gн > Gк, то нет оснований отвергать гипотезу Н0; нетипичных сдвигов много, преобладание типичного сдвига является случайным.
Ограничения критерия:
- выборки должны быть зависимыми и иметь одинаковый объем;
- объем каждой выборки должен быть не менее 5 и не более 300;
- критерий неприменим, когда величины типичного и нетипичного сдвигов равны.
univer-nn.ru
Критерии согласия распределений
В некоторых случаях исследователь не знает заранее, по какому именно закону распределены наблюдаемые значение исследуемого признака. Но у него могут быть достаточно веские причины предполагать, что распределение подчинено тому или иному закону, например, нормальному или равномерному. В этом случае выдвигаются основная и альтернативная статистические гипотезы следующего вида:
H0: распределение наблюдаемого признака подчинено закону распределения A,
H1: распределение наблюдаемого признака отличается от A;
где в качестве A может выступать тот или иной закон распределения: нормальный, равномерный, показательный и т. д.
Проверка гипотезы о предполагаемом законе распределения проводится при помощи так называемых критериев согласия. Имеется несколько критериев согласия. Наиболее универсальным из них является -критерий Пирсона, так как он применим к любому виду распределения.
-Критерий Пирсона
Обычно эмпирические и теоретические частоты различаются. Случайно ли расхождение частот? Критерий Пирсона дает ответ на этот вопрос, правда, как и любой статистический критерий, он не доказывает справедливость гипотезы в строго математическом смысле, а лишь устанавливает на определенном уровне значимости ее согласие или несогласие с данными наблюдений.
Итак, пусть по выборке объема получено статистическое распределение значений признака, где— наблюдаемые значения признака,— соответствующие им частоты:
Суть критерия Пирсона состоит в вычислении критерия по следующей формуле:
где — это число разрядов наблюдаемых значений, а— теоретические частоты соответствующих значений.
Понятно, что чем меньше разности , тем ближе эмпирическое распределение к эмпирическому, поэтому, чем меньше значение критерия, тем с большей достоверностью можно утверждать, что эмпирическое и теоретическое распределение подчинены одному закону.
Алгоритм критерия Пирсона
Алгоритм критерия Пирсона несложен и состоит в выполнении следующих действий:
Сначала по данным выборки получают статистическое распределение наблюдаемого признака.
Затем — вычисляют теоретические частоты признака, какими они должны были бы быть, если бы признак был действительно распределен в соответствии с данным законом.
По данной выше формуле вычисляют эмпирическое значение критерия
По таблице критических значений критерия Пирсона определяют на необходимом уровне значимостии при заданном числе степеней свободы. Число степеней свободы вычисляется по формуле, где— число разрядов наблюдаемых значений,— число параметров предполагаемого распределения, в случае нормального или равномерного распределения.
В случае, если , основную гипотезу принимают, в этом случае на заданном уровне значимости можно утверждать, что статистическое распределение изучаемого параметра подчинено данному закону распределения. Если же имеет место обратное неравенство, принимают альтернативную гипотезу: статистическое распределение отличается от данного.
Итак, единственным нетривиальным действием в этом алгоритме является определение теоретических частот. Они, разумеется, зависят от закона распределения, поэтому — для различных законов определяются по-разному.
studfiles.net
Гамма распределение
Символом обозначают гамма-распределение или Г-распределение.
Это распределение с двумя параметрами : ,
Распределение сосредоточено на положительной полуоси.
Плотность распределения имеет вид:
(1)
где — положительные параметры, — параметр формы, — параметр масштаба.
есть гамма-функция Эйлера, по определению равная:
.
Напомним свойства гамма-функции:
Иными словами, гамма-функция есть обобщение факториала.
Кроме этого, полезно знать: ,
При гамма-распределение превращается в обычное экспоненциальное распределение, которое широко используется при анализе телекоммуникационных данных.
Характеристическая функция Г-распределения имеет вид:
(2)
Если случайная величина имеет гамма-распределение, что символически обозначается как , то ее моменты вычисляются по формуле:
(3)
При целых t>0 это может быть получено прямым дифференцированием характеристической функции, см. формулу (2).
В частности, полагая , находим
(4)
Из формул (2), (3) видно, что параметр играет роль масштаба гамма-распределения
, если .
В силу этого многие свойства Г-распределения достаточно изучать при каком-либо одном значении параметра , например = 1 или = 1/2.
Распределение играет важную роль в математической статистике и называется распределением хи-квадрат (или ).
Связанные определения:
Гамма-распределение
В начало
Содержание портала
statistica.ru
Тест 3 23 в каком критерии используется распределение стьюдента? стр. 9
а) при проверке гипотезы о равенстве генеральных средних
б) при проверке гипотезы о равенстве генеральных дисперсий
в) Бартлетта
г) Кохрана
Тест 3.23. В каком критерии используется распределение Стьюдента?
а) при проверке гипотезы о равенстве генеральных средних
б) при проверке гипотезы о значении вероятности события
в) Бартлетта
г) Кохрана
Тест 3.24. В каком критерии используется распределение Фишера-Снедекора?
а) при проверке гипотезы о равенстве генеральных средних
б) при проверке гипотезы о значении вероятности события
в) при проверке гипотезы о равенстве генеральных дисперсий
г) при проверке гипотезы о значении генеральной дисперсии
Тест 3.25. В каком критерии используется нормальное распределение?
а) при проверке гипотезы о равенстве вероятностей
б) при проверке гипотезы о значении вероятности события
в) при проверке гипотезы о равенстве генеральных дисперсий
г) при проверке гипотезы о значении генеральной дисперсии
Тест 3.26. В каком критерии используется распределение Пирсона?
а) при проверке гипотезы о равенстве генеральных средних
б) при проверке гипотезы о значении вероятности события
в) Бартлетта
г) Кохрана
Тест 3.27. Какая критическая область используется при проверке гипотезы о равенстве вероятностей в случае биномиального распределения
а) двусторонняя
б) левосторонняя
в) правосторонняя
Тест 3.28. Какая критическая область используется при проверке гипотезы о равенстве генеральных дисперсий нескольких нормальных совокупностей
а) двусторонняя
б) левосторонняя
в) правосторонняя
Тест 3.29. Какая критическая область используется при проверке гипотезы о равенстве генеральных дисперсий двух нормальных совокупностей
а) двусторонняя
б) левосторонняя
в) правосторонняя
Тест 3.30. Какая статистика используется при проверке гипотезы о равенстве генеральных дисперсий двух нормальных совокупностей
а)
б)
в)
г)
Тест 3.31. Для проверки какой гипотезы используется статистика
а)
б)
в)
г)
Тест 3.32. При проверке гипотезы о значении генеральной средней гипотеза H0 отвергается, если:
а) наблюдаемое значение по модулю больше критического
б) наблюдаемое значение по модулю больше или равно критическому
в) наблюдаемое значение меньше критического
г) наблюдаемое значение не равно критическому
Тест 3.33. При проверке гипотезы о значении вероятности события гипотеза H0 отвергается, если:
а) наблюдаемое значение по модулю больше критического
б) наблюдаемое значение по модулю больше или равно критическому
в) наблюдаемое значение меньше критического
г) наблюдаемое значение не равно критическому
Тест 3.34. При проверке гипотезы о равенстве генеральных средних двух нормальных совокупностей гипотеза H0 не отвергается, если:
а) наблюдаемое значение по модулю меньше или равно критического
б) наблюдаемое значение по модулю больше или равно критическому
в) наблюдаемое значение меньше критического
г) наблюдаемое значение не равно критическому
Тест 3.35. При проверке гипотезы о значении генеральной средней при неизвестной генеральной дисперсии используется:
а) распределение Пирсона
б) F-распределение Фишера-Снедекора
в) распределение Стьюдента
г) нормальный закон распределения
Тест 3.36. При проверке гипотезы о значении генеральной средней при известной дисперсии используется:
а) распределение Пирсона
б) F-распределение Фишера-Снедекора
в) распределение Стьюдента
г) нормальный закон распределения
Тест 3.37. При проверке гипотезы о равенстве генеральных средних двух нормальных совокупностей с неизвестными генеральными дисперсиями используется:
а) распределение Пирсона
б) F-распределение Фишера-Снедекора
в) распределение Стьюдента
г) нормальный закон распределения
Тест 3.38. При проверке гипотезы о равенстве генеральных средних двух нормальных совокупностей с известными генеральными дисперсиями используется:
а) распределение Пирсона
б) F-распределение Фишера-Снедекора
в) распределение Стьюдента
г) нормальный закон распределения
Тест 3.39. При проверке гипотезы о равенстве генеральных дисперсий нескольких нормальных совокупностей в случае разных объёмов выборки используется:
а) распределение Стьюдента
б) F-распределение Фишера-Снедекора
в) критерий Бартлетта
г) критерий Кохрана
Тест 3.40. При проверке гипотезы о равенстве генеральных дисперсий нескольких нормальных совокупностей в случае равных объёмов выборки используется:
а) распределение Пирсона
б) F-распределение Фишера-Снедекора
в) критерий Бартлетта
г) критерий Кохрана
Тест 3.41. Критерий Бартлетта и критерий Кохрана применяются:
а) при проверке гипотезы о значении генеральной средней
б) при проверке гипотезы о равенстве генеральных средних
в) при проверке гипотезы о равенстве генеральных дисперсий
г) при проверке гипотезы о значении генеральной дисперсии
Тест 3.42. При проверке гипотезы о равенстве генеральных дисперсий двух нормальных совокупностей используется:
а) распределение Пирсона
б) F-распределение Фишера-Снедекора
в) распределение Стьюдента
г) критерий Бартлетта
Тест 3.43. Критерий Бартлетта и критерий Кохрана применяются в случае:
а) сравнения 2 генеральных дисперсий
б) сравнения значений генеральных средних
в) сравнения более 2 генеральных дисперсий
г) сравнения значений вероятностей
Тест 3.44. При использовании критерия Кохрана рассматриваются выборки:
а) равного объема
б) разного объема
в) любого объема
г) объемом 30
Тест 3.45. При использовании критерия Бартлетта рассматриваются выборки:
а) равного объема
б) разного объема
в) любого объема
г) объемом 30
Тест 3.46. По какому принципу выбирается критическая область?
а) вероятность попадания в нее должна быть минимальной, если верна гипотеза H0и максимальной в противном случае
б) вероятность попадания в нее должна быть минимальной, если верна гипотеза H1и максимальной в противном случае
в) вероятность попадания в нее должна быть равна 0
г) вероятность попадания в нее должна быть максимальной, если верна гипотеза H0и минимальной в противном случае
Тест 3.47. Границы правосторонней критической области при заданном уровне значимости находят из соотношения:
а)
б)
в)
г) нет правильного ответа
Тест 3.48. Границы левосторонней критической области при заданном уровне значимости находят из соотношения:
а)
б)
в)
г) нет правильного ответа
Тест 3.49. Границы двусторонней критической области при заданном уровне значимости находят из соотношения:
а)
б)
в)
г) нет правильного ответа
Тест 3.50. При проверке гипотезы о равенстве вероятностей в случае биномиального распределения используется:
а) распределение Пирсона
б) F-распределение Фишера-Снедекора
в) распределение Стьюдента
г) нормальный закон распределения
Тест 3.51. При проверке гипотезы об однородности ряда вероятностей в случае полиномиального распределения используется:
а) распределение Пирсона
б) F-распределение Фишера-Снедекора
в) распределение Стьюдента
г) нормальный закон распределения
Тест 3.52. Какие выборочные характеристики используются при расчёте статистики FН при проверке гипотезы о равенстве генеральных дисперсий:
а) исправленные выборочные дисперсии
б) выборочные дисперсии
в) средние арифметические
г) частости
Тест 3.53. При проверке гипотезы о виде неизвестного закона распределения используется:
а) критерий согласия Пирсона
б) F-распределение Фишера-Снедекора
в) критерий Бартлетта
г) критерий Кохрана
uchebana5.ru
