Величины вектора – определение, обозначение, примеры :: SYL.ru

Вообразите себе ось вращения в виде полюса, проведенного сквозь центр колеса. Он проходит с обеих сторон. В зависимости от расположения наблюдателя, обороты осуществляются по часовой стрелке или против нее. Подобное влияние перспективы негативно сказывается на попытках определить угол поворота.

Однако есть стандарт для измерения, который согласовывает эти типы величин. Речь идет о правиле правой руки.

На (а) видно, что диск совершает обороты в обратном направлении часовой стрелки, если смотреть на все сверху. На (b) – правило правой руки. Чтобы найти направление угловых скорости (ω) и момента (L), сожмите пальцы правой руки. Большой палец укажет на нужное направление, а пальцы – направление вращения

Правило правой руки срабатывает каждый раз, когда вы ищите направленность угловых скорости или момента. Вернемся к вращающему диску. Представьте, что правая рука хватает полюс, где четыре пальца идут в сторону вращения, а большой палец укажет на ось (перпендикулярна другим пальцам). Так вы отыщите угловые скорость (ω) и момент (L) и не попадетесь на обман перспективы.

v-kosmose.com

Векторная величина в физике. Примеры векторных величин

Физика и математика не обходятся без понятия «векторная величина». Ее необходимо знать и узнавать, а также уметь с нею оперировать. Этому обязательно стоит научиться, чтобы не путаться и не допускать глупых ошибок.

Как отличить скалярную величину от векторной?

Первая всегда имеет только одну характеристику. Это ее числовое значение. Большинство скалярных величин могут принимать как положительные, так и отрицательные значения. Их примерами может служить электрический заряд, работа или температура. Но есть такие скаляры, которые не могут быть отрицательными, например, длина и масса.

Векторная величина, кроме числовой величины, которая всегда берется по модулю, характеризуется еще и направлением. Поэтому она может быть изображена графически, то есть в виде стрелки, длина которой равна модулю величины, направленной в определенную сторону.

При письме каждая векторная величина обозначается знаком стрелки на буквой. Если идет речь о числовом значении, то стрелка не пишется или ее берут по модулю.

Какие действия чаще всего выполняются с векторами?

Сначала — сравнение. Они могут быть равными или нет. В первом случае их модули одинаковые. Но это не единственное условие. У них должны быть еще одинаковые или противоположные направления. В первом случае их следует называть равными векторами. Во втором они оказываются противоположными. Если не выполняется хотя бы одно из указанных условий, то векторы не равны.

Потом идет сложение. Его можно сделать по двум правилам: треугольника или параллелограмма. Первое предписывает откладывать сначала один вектор, потом от его конца второй. Результатом сложения будет тот, который нужно провести от начала первого к концу второго.

Правило параллелограмма можно использовать, когда нужно сложить векторные величины в физике. В отличие от первого правила, здесь их следует откладывать от одной точки. Потом достроить их до параллелограмма. Результатом действия следует считать диагональ параллелограмма, проведенную из той же точки.

Если векторная величина вычитается из другой, то они снова откладываются из одной точки. Только результатом будет вектор, который совпадает с тем, что отложен от конца второго к концу первого.

Какие векторы изучают в физике?

Их так же много, как скаляров. Можно просто запомнить то, какие векторные величины в физике существуют. Или знать признаки, по которым их можно вычислить. Тем, кто предпочитает первый вариант, пригодится такая таблица. В ней приведены основные векторные физические величины.

Теперь немного подробнее о некоторых из этих величин.

Первая величина — скорость

С нее стоит начать приводить примеры векторных величин. Это обусловлено тем, что ее изучают в числе первых.

Скорость определяется как характеристика движения тела в пространстве. Ею задается числовое значение и направление. Поэтому скорость является векторной величиной. К тому же ее принято разделять на виды. Первый является линейной скоростью. Ее вводят при рассмотрении прямолинейного равномерного движения. При этом она оказывается равной отношению пути, пройденного телом, ко времени движения.

Эту же формулу допустимо использовать при неравномерном движении. Только тогда она будет являться средней. Причем интервал времени, который необходимо выбирать, обязательно должен быть как можно меньше. При стремлении промежутка времени к нулю значение скорости уже является мгновенным.

Если рассматривается произвольное движение, то здесь всегда скорость — векторная величина. Ведь ее приходится раскладывать на составляющие, направленные вдоль каждого вектора, направляющего координатные прямые. К тому же определяется он как производная радиус-вектора, взятая по времени.

Вторая величина — сила

Она определяет меру интенсивности воздействия, которое оказывается на тело со стороны других тел или полей. Поскольку сила — векторная величина, то она обязательно имеет свое значение по модулю и направление. Так как она действует на тело, то важным является еще и точка, к которой приложена сила. Чтобы получить наглядное представление о векторах сил, можно обратиться к следующей таблице.

Также еще векторной величиной является равнодействующая сила. Она определяется как сумма всех действующих на тело механических сил. Для ее определения необходимо выполнить сложение по принципу правила треугольника. Только откладывать векторы нужно по очереди от конца предыдущего. Результатом окажется тот, который соединяет начало первого с концом последнего.

Третья величина — перемещение

Во время движения тело описывает некоторую линию. Она называется траекторией. Эта линия может быть совершенно разной. Важнее оказывается не ее внешний вид, а точки начала и конца движения. Они соединяются отрезком, который называется перемещением. Это тоже векторная величина. Причем оно всегда направлено от начала перемещения к точке, где движение было прекращено. Обозначать его принято латинской буквой r.

Здесь может появиться такой вопрос: «Путь — векторная величина?». В общем случае это утверждение не является верным. Путь равен длине траектории и не имеет определенного направления. Исключением считается ситуация, когда рассматривается прямолинейное движение в одном направлении. Тогда модуль вектора перемещения совпадает по значению с путем, и направление у них оказывается одинаковым. Поэтому при рассмотрении движения вдоль прямой без изменения направления перемещения путь можно включить в примеры векторных величин.

Четвертая величина — ускорение

Оно является характеристикой быстроты изменения скорости. Причем ускорение может иметь как положительное, так и отрицательное значение. При прямолинейном движении оно направлено в сторону большей скорости. Если перемещение происходит по криволинейной траектории, то вектор его ускорения раскладывается на две составляющие, одна из которых направлена к центру кривизны по радиусу.

Выделяют среднее и мгновенное значение ускорения. Первое следует рассчитывать как отношение изменения скорости за некоторый промежуток времени к этому времени. При стремлении рассматриваемого интервала времени к нулю говорят о мгновенном ускорении.

Пятая величина — импульс

По-другому его еще называют количеством движения. Импульс векторной величиной является из-за того, что напрямую связан со скоростью и силой, приложенной к телу. Обе они имеют направление и задают его импульсу.

По определению последний равен произведению массы тела на скорость. Используя понятие импульса тела, можно по-другому записать известный закон Ньютона. Получается, что изменение импульса равно произведению силы на промежуток времени.

В физике важную роль имеет закон сохранения импульса, который утверждает, что в замкнутой системе тел ее суммарный импульс является постоянным.

Мы очень кратко перечислили, какие величины (векторные) изучаются в курсе физики.

Задача о неупругом ударе

Условие. На рельсах стоит неподвижная платформа. К ней приближается вагон со скоростью 4 м/с. Массы платформы и вагона — 10 и 40 тонн соответственно. Вагон ударяется о платформу, происходит автосцеп. Необходимо вычислить скорость системы «вагон-платформа» после удара.

Решение. Сначала требуется ввести обозначения: скорость вагона до удара — v1, вагона с платформой после сцепки — v, масса вагона m1, платформы — m2. По условию задачи необходимо узнать значение скорости v.

Правила решения подобных заданий требуют схематичного изображения системы до и после взаимодействия. Ось OX разумно направить вдоль рельсов в ту сторону, куда движется вагон.

В данных условиях систему вагонов можно считать замкнутой. Это определяется тем, что внешними силами можно пренебречь. Сила тяжести и реакция опоры уравновешены, а трение о рельсы не учитывается.

Согласно закону сохранения импульса, их векторная сумма до взаимодействия вагона и платформы равна общему для сцепки после удара. Сначала платформа не двигалась, поэтому ее импульс был равен нулю. Перемещался только вагон, его импульс — произведение m1 и v1.

Так как удар был неупругий, то есть вагон сцепился с платформой, и дальше он стали катиться вместе в ту же сторону, то импульс системы не изменил направления. Но его значение стало другим. А именно произведением суммы массы вагона с платформой и искомой скорости.

Можно записать такое равенство: m1 * v1 = (m1 + m2) * v. Оно будет верно для проекции векторов импульсов на выбранную ось. Из него легко вывести равенство, которое потребуется для вычисления искомой скорости: v = m1 * v1 / (m1 + m2).

По правилам следует перевести значения для массы из тонн в килограммы. Поэтому при подстановке их в формулу следует сначала умножить известные величины на тысячу. Простые расчеты дают число 0,75 м/с.

Ответ. Скорость вагона с платформой равна 0,75 м/с.

Задача с разделением тела на части

Условие. Скорость летящей гранаты 20 м/с. Она разрывается на два осколка. Масса первого 1,8 кг. Он продолжает двигаться в направлении, в котором летела граната, со скоростью 50 м/с. Второй осколок имеет массу 1,2 кг. Какова его скорость?

Решение. Пусть массы осколков обозначены буквами m1 и m2. Их скорости соответственно будут v1 и v2. Начальная скорость гранаты — v. В задаче нужно вычислить значение v2.

Для того чтобы больший осколок продолжал двигаться в том же направлении, что и вся граната, второй должен полететь в обратную сторону. Если выбрать за направление оси то, которое было у начального импульса, то после разрыва большой осколок летит по оси, а маленький — против оси.

В этой задаче разрешено пользоваться законом сохранения импульса из-за того, что разрыв гранаты происходит мгновенно. Поэтому, несмотря на то что на гранату и ее части действует сила тяжести, она не успевает подействовать и изменить направление вектора импульса с его значением по модулю.

Сумма векторных величин импульса после разрыва гранаты равна тому, который был до него. Если записать закон сохранения импульса тела в проекции на ось OX, то он будет выглядеть так: (m1 + m2) * v = m1 * v1 — m2 * v2. Из него просто выразить искомую скорость. Она определится по формуле: v2 = ((m1 + m2) * v — m1 * v1) / m2. После подстановки числовых значений и расчетов получается 25 м/с.

Ответ. Скорость маленького осколка равна 25 м/с.

Задача про выстрел под углом

Условие. На платформе массой M установлено орудие. Из него производится выстрел снарядом массой m. Он вылетает под углом α к горизонту со скоростью v (данной относительно земли). Требуется узнать значение скорости платформы после выстрела.

Решение. В этой задаче можно использовать закон сохранения импульса в проекции на ось OX. Но только в том случае, когда проекции внешних равнодействующих сил равна нулю.

За направление оси OX нужно выбрать ту сторону, куда полетит снаряд, и параллельно горизонтальной линии. В этом случае проекции сил тяжести и реакции опоры на OX будут равны нулю.

Задача будет решена в общем виде, так как нет конкретных данных для известных величин. Ответом в ней является формула.

Импульс системы до выстрела был равен нулю, поскольку платформа и снаряд были неподвижны. Пусть искомая скорость платформы будет обозначена латинской буквой u. Тогда ее импульс после выстрела определится как произведение массы на проекцию скорости. Так как платформа откатится назад (против направления оси OX), то значение импульса будет со знаком минус.

Импульс снаряда — произведение его массы на проекцию скорости на ось OX. Из-за того, что скорость направлена под углом к горизонту, ее проекция равна скорости, умноженной на косинус угла. В буквенном равенстве это будет выглядеть так: 0 = — Mu + mv * cos α. Из нее путем несложных преобразований получается формула-ответ: u = (mv * cos α) / M.

Ответ. Скорость платформы определяется по формуле u = (mv * cos α) / M.

Задача о переправе через реку

Условие. Ширина реки по всей ее длине одинакова и равна l, ее берега параллельны. Известна скорость течения воды в реке v1 и собственная скорость катера v2. 1). При переправе нос катера направлен строго к противоположному берегу. На какое расстояние s его снесет вниз по течению? 2). Под каким углом α нужно направить нос катера, чтобы он достиг противоположного берега строго перпендикулярно к точке отправления? Сколько времени t потребуется на такую переправу?

Решение. 1). Полная скорость катера является векторной суммой двух величин. Первая из них течение реки, которое направлено вдоль берегов. Вторая — собственная скорость катера, перпендикулярная берегам. На чертеже получается два подобных треугольника. Первый образован шириной реки и расстоянием, на которое сносит катер. Второй — векторами скоростей.

Из них следует такая запись: s / l = v1 / v2. После преобразования получается формула для искомой величины: s = l * (v1 / v2).

2). В этом варианте задачи вектор полной скорости перпендикулярен берегам. Он равен векторной сумме v1 и v2. Синус угла, на который должен отклоняться вектор собственной скорости, равен отношению модулей v1 и v2. Для расчета времени движения потребуется разделить ширину реки на сосчитанную полную скорость. Значение последней вычисляется по теореме Пифагора.

v = √(v22 – v12), тогда t = l / (√(v22 – v12)).

Ответ. 1). s = l * (v1 / v2), 2). sin α = v1 / v2, t = l / (√(v22 – v12)).

teora-holding.ru

Величина вектора — Энциклопедия по машиностроению XXL

ПОСТОЯННОГО множителя, то величину вектора результирующего момента можно подсчитать, не вводя этого множителя.  [c.295]

Один и тот же стержень, закрепленный верхним концом (рис. 96), нагружается на свободном конце статически эквивалентными нагрузками, равнодействующие которых выражаются величиной вектора Р. Нагрузки приложены различными способами а — в виде сосредоточенной осевой силы б — в виде двух сил в — в виде распределенной нагрузки. Исследования показывают, что во всех случаях в поперечном сечении, удаленном на расстояние, превышающее в 1,5—2 раза его поперечные размеры, напряжения практически одинаковы. В сечениях же, расположенных близко от места приложения сил, величина напряжений и характер их распределения различны.  [c.87]

Воспользуемся теперь тем, что вектор кинетического момента остается неизменным не только по направлению, но и по величине. Величина вектора кинетического момента равна  [c.84]

МОЖНО перемещать любой вектор системы вдоль линии его действия. Чтобы показать это, рассмотрим, например, множество из трех векторов (рис. П. 11, а), предположив, что это множество составляет систему скользящих векторов. Выберем произвольную точку О на линии действия какого-либо из векторов системы, например первого, и приложим в этой точке векторный нуль, составленный из векторов / и равных по величине вектору / и действующих вдоль той же прямой (рис. П. 11, б).  [c.347]

Итак, мы установили, что вращательное действие пары сил на тело зависит от числового значения ее момента, но оно зависит еще и от положения плоскости действия пары. Поэтому момент пары можно рассматривать как векторную величину. Вектор момента пары перпендикулярен плоскости пары, причем если пара стремится повернуть плоскость против хода часовой стрелки, то вектор момента направлен к нам (рис. 1.31, а), если же пара поворачивает плоскость по часовой стрелке (рис. 1.31, б), то вектор момента пары направлен от нас. Если же на плоскость действия пары смотрят два человека с разных сторон, то оба они построят один и тот же вектор момента. Расположим плоскость П действия пары вертикально и допустим, что один из нас смотрит на эту плоскость справа (рис. 1.32, а), а второй — слева (рис. 1.32,6). Легко убедиться, что мы оба видим один и тот же вектор момента.  [c.29]

Вектор направлен iio мгновенной оси и характеризует скорость изменения вектора со только по величине. Вектор характеризует скорость изменения только по направлению. Если обозначить через (Oj угловую скорость вращения вектора со, то  [c.244]

Величина вектора i определяется равенством  [c.244]

Так как ш и (о взаимно перпендикулярны, то величина вектора равна  [c.489]

В зависимости от свойств изображаемой им величины вектор может быть свободным, т. е. приложенным в любой точке пространства, скользящим, т. е. приложенным в любой точке некоторой прямой, называемой основанием или линией действия вектора, и неподвижным, т. е. приложенным в некоторой фиксированной точке (подробнее об этом см. в конце параграфа, п. 13).  [c.19]

Вектор может быть геометрически изображен прямолинейным отрезком АВ (рис. 1). длина которого в известном масштабе соответствует численному значению вектора, а направление совпадает с направлением вектора. Численную величину вектора называют еще  [c.19]

По существу, алгебраические величины v v. w представляют собой проекции векторов v и w на ось х, т. г. v = v . и w = Wx- Однако здесь и всюду далее проекцию любого вектора и, коллинеарного оси /, на эту ось мы будем (как и модуль) обозначать символом и(иг = и) и называть, в отличие от модуля, численной или алгебраической величиной вектора и. Так как численная величина вектора может отличаться от его модуля только знаком, то это совпадение обозначений обычно несущественно. В случаях же, когда могут возникнуть недоразумения, модуль вектора будет обозначаться символом ) и .  [c.56]

Поскольку угловая скорость — векторная величина, вектором должно быть и угловое ускорение. Но при вращении тела вокруг неподвижной оси мы обычно рассматриваем угловую скорость как  [c.167]

Поскольку угловая скорость — векторная величина, вектором должно быть и угловое ускорение. Но при вращении тела вокруг неподвижной оси обычно рассматривают угловую скорость как скаляр и потому здесь нас могут интересовать только величина и знак углового ускорения.  [c.57]

Момент пары, подобно моменту силы относительно точки,— векторная величина. Вектор момента пары перпендикулярен плоскости пары. Но у всякой плоскости имеется две стороны. Условились вектор момента восставлять с той стороны, с которой пара представляется поворачивающей свое плечо против хода часовой стрелки (рис. 83, а). Таким образом, вектор момента пары сил характеризует не только величину воздействия пары на тело, но и плоскость пары, а также и направление, в котором силы пары стремятся повернуть тело.  [c.149]

Решая его графически (рис. 14, б), находят величины векторов ид и VBA-  [c.29]

Модуль, определение, нахождение, направление, величина, вектор, момент. .. равнодействующей.  [c.72]

Направление и величина вектора равнодействующей определяется равенством (с). Таким образом, направление линии действия равнодействующей можно предполагать известным. Обозначим на плоскости ii положение мгновенного центра ускорений О (рис. 49). Допустим, что К — точка пересечения линии действия равнодействующей и прямой ОС,  [c.409]

Примечание. Единицы абсолютного значения векторов элементарных трансляций обратной решетки — это не единицы длины. Если длина векторов а, Ь, с измеряется в сантиметрах, то величина векторов а, Ь, с измеряется в сантиметрах в минус первой степени (см ).  [c.67]

При изучении переменного прямолинейного движения точки под термином ускорение мы понимали только изменение скорости по величине. Однако в криволинейном движении меняется и направление скорости, так как криволинейное движение иначе не может возникнуть. Скорость является векторной величиной вектор скорости, обозначаемый V (в отличие от его модуля у), направлен по касательной к той же точке траектории, в которой в данный момент времени находится движущаяся точка .  [c.118]

Из вида этого равенства очевидно, что интеграл в его правой части определяет величину вектора Бюргерса протекающего в единицу времени через контур L, т. е. уносимого дислокациями, пересекающими линию L. Поэтому естественно назвать тензором плотности потока дислокаций.  [c.167]

Рассматривая величину вектора момента mo F), определяемую по формуле (1), и принимая во внимание его направление, приходим к заключению, что вектор момента mo F) представляет собой векторное произведение  [c.38]

Величина вектора скорости определяется равенством что совпадает с (11).  [c.165]

Вектор ускорения а в направлен от точки С к точке В параллельно направлению ВС, а вектор ускорения асо направлен от точки С к точке D параллельно направлению D. Таким образом, нормальные ускорения асв и асо известны по величине и направлению. Векторы асв и асо известны только по направлению. Первый направлен перпендикулярно к направлению ВС, второй — перпендикулярно к направлению D. Таким образом, в уравие. НИИ (4.31) неизвестными остаются только величины векторов уско. реиий асв и a D, которые могут быть определены следующим графическим построением.  [c.84]

Если вокруг дислокации L (рис. 12) обвести контур AB D, то участок контура ВС будет состоять из шести отрезков, а участок AD из пяти. Разница B —AD = b, где Ь означает величину вектора Бюргерса. Если контуром обвести несколько дислокаций (зоны искажений кристаллической решетки, которые перекрываются или сливаются), то величина его соответствует  [c.32]

Далее заметим, что оптимальный проект Si и его среднеквадратичные кривизны У1 неизвестны, но фиксированы. С другой стороны, проект Sj подчиняется лишь проектному ограничению, которое задает значение РЬ и, следовательно, определяет величину вектора Я, если выбрано его направление. Кроме того, в окрестности оптимального проекта s,-имеются проекты s,-, дающие веса конструкций, произвольно близкие к минимальному весу. Соответствующие векторы X произвольно близки к границе полупространства, определяемой неравенством (21). Если скалярное произведение Яиц будет неотрицательным для всех допустимых векторов Я, то вектор jx будет направлен вдоль внутренней нормали этого полупространства в начале координат таким образом, (19) является необходимым условием оптимальности. Это доказательство принадлежит Чжу и Прагеру [17].  [c.100]

Уравнение движения фазы у можно легко получить в явном виде, подставляя в (.5, 3. 7) вместо величины вектор вместо потока тензор напряя еяий р 1 — а вместо источника векторную величину Р . В результате находим  [c.195]

Простейшей векторной величиной, или вектором, является направленный отрезок, который вполне определяется заданием его длины (численной величины вектора), измеренной в некотором масштабе, и его направления в пространстве. Такие физические величины, как скорость, ускорение или сила, представляют собой величины векторные задание этих величин получает смысл только тогда, когда, кроме их численных значений, указывается и их направление. Термин вектор происходит от латинского слова vehere, что означает влечь , тянуть .  [c.19]

Вращение тела вокруг неподвижной оси характеризуется осью, угловой скоростью и направлением вращения. Эти характеристики движения можно отобразить одним вектором — вектором угловой скорости со, если вектор угловой скорости откладывать в масштабе на оси вращения от какой-либо ее точки и направлять так, что если смотреть с конца вектора на его начало, то вращение тела должно происходить против движения часовой стрелки. Тогда прямая, на которой расположен вектор Со, является осью вращс ния. Величина вектора со равна величине угловой скорости, а стрелка на векторе со показывает направление вращения (рис. 115).  [c.124]

Так как движение тела, имеющего одну неподвижную точку, в каждый момент времени можно считать вращением вокруг мгновенной осп, то в качестве величин, характеризующих это движение, можно ввести Х гиовеииую угловую скорость и мгновенное угловое ускорение враще-JH H твердого тела вокруг неподвижной точки. Очевидно, вводимая угловая скорость является векторной величиной, направленной в каждый момент времени по соответствующей мгновенной оси, и при использовании правой системы координат вектор угловой скорости w направлен по мгновенной оси так, что с направления этого вектора видно вращение тела вокруг мгновенной оси, проис.ходящим против движения часовой стрелки. Величину вектора угловой скорости можно вырази гь через элементарный угол поворота Аф вокруг мгновенной оси за время ДЕ  [c.168]

Абсолютная величина вектора к меняется вдоль луча просто по закону 1г = а/с (с ы = onst). Для определения же изменения  [c.366]

Покаяеем, что эти формулы выражают условие физичности, или, как иногда говорят, объективности, вектора а в том смысле, что при переходе от одной системы координат к другой, неподвижной по отношению к ней системе величина вектора а нс меняется (например, скорость самолета по от1Ю1иеи11ю к Земле не зависит от того, в какой неподвижно связанной с Землей системе координат мы рассматриваем скорость самолета). Для этого заметим, что сум.ча квадратов проекций вектора на оси координат не меняется при переходе от одних осей координат к другим и, таким образом квадрат длины вектора, т. е. квадрат абсолютного значения вектора, является инвариантом по отношению к изменению системы координат.  [c.115]

mash-xxl.info

Векторная и скалярная величина — чем они отличаются?

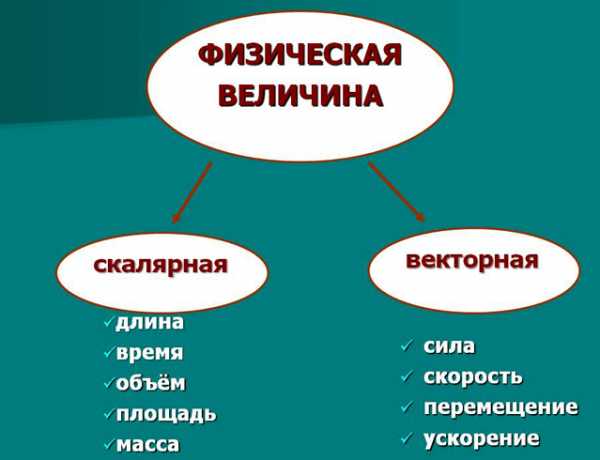
В физике существует несколько категорий величин: векторные и скалярные.

Что такое векторная величина?

Векторная величина имеет две основные характеристики: направление и модуль. Два вектора будут одинаковыми, если их значение по модулю и направление совпадают. Для обозначения векторной величины чаще всего используют буквы, над которыми отображается стрелочка. В качестве примера векторной величины можно привести силу, скорость или ускорение.

Для того, чтобы понять сущность векторной величины, следует рассмотреть ее с геометрической точки зрения. Вектор представляет собой отрезок, имеющий направление. Длина такого отрезка соотносится со значением его модуля. Физическим примером векторной величины является смещение материальной точки, перемещающейся в пространстве. Такие параметры, как ускорение этой точки, скорость и действующие на нее силы, электромагнитного поля тоже будут отображаться векторными величинами.

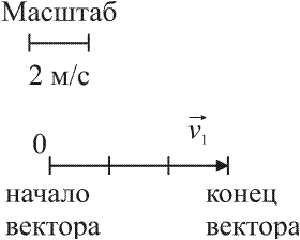
Если рассматривать векторную величину независимо от направления, то такой отрезок можно измерить. Но, полученный результат будет отображать только лишь частичные характеристики величины. Для ее полного измерения следует дополнить величину другими параметрами направленного отрезка.

В векторной алгебре существует понятие нулевого вектора. Под этим понятием подразумевается точка. Что касается направления нулевого вектора, то оно считается неопределенным. Для обозначения нулевого вектора используется арифметический нуль, набранный полужирным шрифтом.

Если проанализировать все вышесказанное, то можно сделать вывод, что все направленные отрезки определяют вектора. Два отрезка будут определять один вектор только в том случае, если они являются равными. При сравнении векторов действует тоже правило, что и при сравнении скалярных величин. Равенство означает полное совпадение по всем параметрам.

Что такое скалярная величина?

В отличие от вектора, скалярная величина обладает только лишь одним параметром – это ее численное значение. Стоит отметить, что анализируемая величина может иметь как положительное численное значение, так и отрицательное.

В качестве примера можно привести массу, напряжение, частоту или температуру. С такими величинами можно выполнять различные арифметические действия: сложение, деление, вычитание, умножение. Для скалярной величины такая характеристика, как направление, не свойственна.

Скалярная величина измеряется числовым значением, поэтому ее можно отображать на координатной оси. Например, очень часто строят ось пройденного пути, температуры или времени.

Основные отличия между скалярными и векторными величинами

Из описаний, приведенных выше, видно, что главное отличие векторных величин от скалярных заключается в их характеристиках. У векторной величины есть направление и модуль, а у скалярной только численное значение. Безусловно, векторную величину, как и скалярную, можно измерить, но такая характеристика не будет полной, так как отсутствует направление.

Для того, чтобы более четко представить отличие скалярной величины от векторной, следует привести пример. Для этого возьмем такую область знаний, как климатология. Если сказать, что ветер дует со скоростью 8 метров в секунду, то будет введена скалярная величина. Но, если сказать, что северный ветер дует со скоростью 8 метров в секунду, то речь пойдет о векторном значении.

Векторы играют огромную роль в современной математике, а также во многих сферах механики и физики. Большинство физических величин может быть представлено в виде векторов. Это позволяет обобщить и существенно упростить используемые формулы и результаты. Часто векторные значения и векторы отождествляются друг с другом. Например, в физике можно услышать, что скорость или сила является вектором.

Некоторые формулы векторной алгебры используются в таких областях науки, как:

1. Сопромат.
2. Кинематика.
3. Облучение и электрическое освещение.
4. Прикладная механика.
5. Гидравлика.
6. Электрические машины.
7. Теоретическая механика.
8. Физика.

Четкое осознание разницы между векторной и скалярной величиной позволит специалистам решать сложные задачи и более подробно характеризовать используемые данные.

vchemraznica.ru

Физические величины как векторы — Справочник химика 21

    Между тем во всех монографиях и учебниках при употреблении криволинейных координат в уравнения вставляют так называемые физические компоненты векторов и тензоров, получаемые из проекций векторов как отрезков на касательные к линиям координатных сеток в данной точке пространства. Соответствующие таким определениям величины, конечно, не являются компонентами векторов и тензоров, и уравнения, в сущности, не имеют тензорного характера. Наши уравнения и входящие в них величины не обладают таким недостатком и поэтому нам кажутся более предпочтительными. Однако для сравнения их и входящих в них величин с обычными, полезно привести формулы, дающие связь между теми и другими величинами, ограничиваясь компонентами скоростей, чего вполне достаточно для всех сравнений. Компоненты скоростей, употребляемые обычно, будем отмечать буквой V с индексами внизу  [c.54]

    Покажем, что знание нормированной волновой функции ip позволяет вычислить средние значения координаты, импульса и других физических величин в этом состоянии. Если учесть, что плотность вероятности определенных значений радиуса-вектора выражается через функцию состояния ip  [c.24]

    В заключение этого параграфа укажем вид выражения, определяющего среднее значение физической величины Р в произвольном состоянии, которое описывается вектором состояния в представлении оператора с дискретным спектром. Пусть, например, состоянию а соответствует волновая функция ( а) в Е-представлении. Оператор Р в этом же представлении определяется матрицей ( т Еп), поэтому среднее значение Р в состоянии а будет [c.138]

    Как уже отмечалось, физическая причина, приводящая к переходу части механической энергии потока в теплоту, состоит в совершении потоком работы против сил вязкого трения. Для практических расчетов удобно рассматривать два разных вида потерь потери на трение в длинных трубопроводах и потери при прохождении потоком таких участков, на которых происходит изменение вектора средней скорости потока — это потери на так называемых местных сопротивлениях. Примеры местных сопротивлений многочисленны 1) внезапное расширение и сужение потока, например при прохождении потоком нормальной диафрагмы (см. рис. 1.19) при изменении величины вектора скорости потока возникают зоны с интенсивным вихревым движением вязкой жидкости, где и происходит собственно превращение части механической энергии потока в теплоту 2) при резком повороте потока также возникают зоны вихревого движения (рис. 1.21, а) 3) при прохождении задвижки, частично перекрывающей трубопровод, также возникают зоны интенсивных завихрений (рис. 1.21,6) 4) при прохождении потоком открытого вентиля (рис. 1.21, в) сложным образом изменяются и величина, и направление вектора скорости и также образуются вихревые зоны (на рис. 1.21, в не показаны). [c.69]

    Таким образом, любая физическая величина, характеризующая свойства идеального кристалла, может быть разложена в ряд Фурье (6), где вектор я пробегает все узлы обратной решетки  [c.19]

    Если (В не зависит от координат, то любая физическая величина остается неизменной. Другая система с той же симметрией — одноосный магнетик с легкой плоскостью намагничения. Здесь параметром порядка служит двухкомпонентный вектор магнитного момента т, лежащий в плоскости легкого намагничения. [c.153]

    В отличие от скалярных величин векторы характеризуются своей величиной и направлением. Векторы, выражающие одинаковые физические величины, можно складывать, изображая их в виде стрелок и рисуя стрелки таким образом, чтобы начало одной из них исходило из конца другой. Тогда суммарный вектор будет изображаться стрелкой, соединяющей начало первого вектора и конец последнего. Часто бывает целесообразно выразить вектор в аналитической форме через его компоненты. В нашей книге векторы обозначаются жирным шрифтом, например Н. [c.429]

    Элементарные физические величины могут быть или скалярами, или векторами. Скалярные величины, обозначаемые курсивом, характеризуются только численными значениями. Для полного определения векторов, обозначаемых шрифтом, необходимо знать как численные значения [величину вектора), так и их направления. [c.754]

    Часто одна векторная физическая величина в некоторой точке анизотропной среды бывает связана с другой векторной величиной. Так, например, электрическое поле Е (полярный вектор) вызывает в диэлектрике смещение или электрическую индукцию О (также полярный вектор). В этом случае О — линейная векторная функция величины Е, т. е. каждая компонента величины О представляет собой линейную функцию множества компонент величины Е  [c.27]

    Принципиально здесь разницы нет. Просто по осям координат в механике (или электротехнике) откладывались соответствующие физические величины, описывающие движение в пространстве, которое нас окружает в обычном его представлении, в то время как в рассматриваемом случае вектор описывает движение в абстрактном, воображаемом пространстве — пространстве вероятностей. Если компонентов у вектора всего три (пространство трехмерно), то его можно легко представить графически. Ну а если их больше Тогда, конечно, графически представить его ие удается, хотя это никого не смущает, ведь в математике часто приходится иметь дело с абстрактными образами. К таким относится и многомерное пространство, щироко применяемое сейчас в самых различных науках. [c.40]

    Физические величины как векторы [c.43]

    Многие физические величины являются функциями координат, или, как иногда говорят, функциями точки. Пусть речь идет о волновой функции элементарной частицы, зависящей от координаты г (см. гл. 3 второй части книги). Несомненно, под г следует понимать вектор, проведенный из точки, выбранной нами в ка

www.chem21.info