Площадь ромба — формула, пример расчет
Ромб – это параллелограмм, у которого все стороны равны.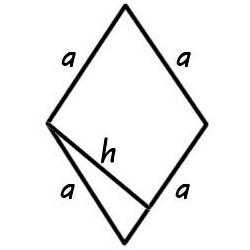
Ромб с прямыми углами называется квадратом и считается частным случаем ромба. Найти площадь ромба можно различными способами, используя все его элементы – стороны, диагонали, высоту. Классической формулой площади ромба считается расчет значения через высоту.
Пример расчета площади ромба по этой формуле очень прост. Необходимо только подставить данные и высчитать площадь.
Площадь ромба через диагонали
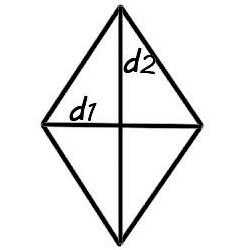
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
Формула площади ромба через диагонали представляет собой произведение его диагоналей, разделенное на 2.
d1=5 см и d2=4. Найдем площадь.
Формула площади ромба через стороны подразумевает и применение других элементов. Если в ромб вписана окружность, то площадь фигуры можно просчитать по сторонам и ее радиусу:
Пример расчета площади ромба через стороны также весьма прост. Требуется только просчитать радиус вписанной окружности. Его можно вывести из теоремы Пифагора и по формуле площади прямоугольного треугольника.
Площади ромба через сторону и угол
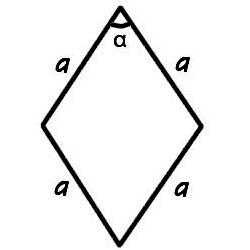
Формула площади ромба через сторону и угол используется очень часто.
Рассмотрим пример расчета площади ромба через сторону и угол.
Задача: Дан ромб, диагонали которого равны d1=4 см,d2=6 см. Острый угол равен α = 30°. Найдите площадь фигуры через сторону и угол.Для начала найдем сторону ромба. Используем для этого теорему Пифагора. Мы знаем, что в точке пересечения диагонали делятся пополам и образуют прямой угол. Следовательно:
Подставим значения:
Теперь мы знаем сторону и угол. Найдем площадь:
2mb.ru
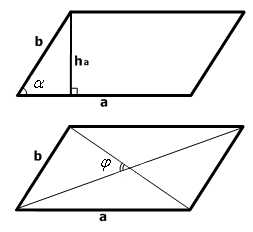
2.3 Площадь параллелограмма
Вывод формулы площади параллелограмма сводится к построению прямоугольника, равного данному параллелограмму по площади. Примем одну сторону параллелограмма за основание, а перпендикуляр, проведенный из любой точки противолежащей стороны на прямую, содержащую основание будем называть высотой параллелограмма. Тогда площадь параллелограмма будет равна произведению его основания на высоту. [4, c. 254]
Теорема. Площадь параллелограмма равна произведению его основания на высоту.
Доказательство. Рассмотрим параллелограмм с площадью. Примем сторонуза основание и проведем высотыи(рисунок 2.3.1). Требуется доказать, что.
Рисунок 2.3.1
Докажем сначала, что площадь прямоугольника также равна. Трапециясоставлена из параллелограммаи треугольника. С другой стороны, она составлена из прямоугольника НВСК и треугольника. Но прямоугольные треугольникии равны по гипотенузе и острому углу (их гипотенузыиравны как противоположные стороны параллелограмма, а углы 1 и 2 равны как соответственные углы при пересечении параллельных прямыхисекущей), поэтому их площади равны. Следовательно, площади параллелограммаи прямоугольникатакже равны, то есть площадь прямоугольникаравна. По теореме о площади прямоугольника, но так как, то.
Теорема доказана.
Пример 2.3.1.
В ромб со стороной и острым углом вписана окружность. Определить площадь четырёхугольника, вершинами которого являются точки касания окружности со сторонами ромба.[5, c. 150]
Решение:
Радиус
вписанной в ромб
окружности (рисунок 2.3.2),
поскольку
Четырёхугольникявляется прямоугольником, так как его
углы опираются на диаметр окружности.
Его площадь,
где(катет, лежащий против угла),.
Рисунок 2.3.2
Итак,
Ответ:
Пример 2.3.2.
Дан ромб , диагонали которого равны 3 см и 4 см. Из вершины тупого угла проведены высотыиВычислить площадь четырёхугольника
Решение:
Площадь ромба (рисунок 2.3.3).

Рисунок 2.3.3
Далее, из находим(см) и, следовательно,(см). Тогда изполучим:
Итак,
Ответ:
Пример 2.3.3.
Площадь четырёхугольника равна Найти площадь параллелограмма, стороны которого равны и параллельны диагоналям четырёхугольника.
Решение:
Так как и(рисунок 2.3.4), то– параллелограмм и, значит,.
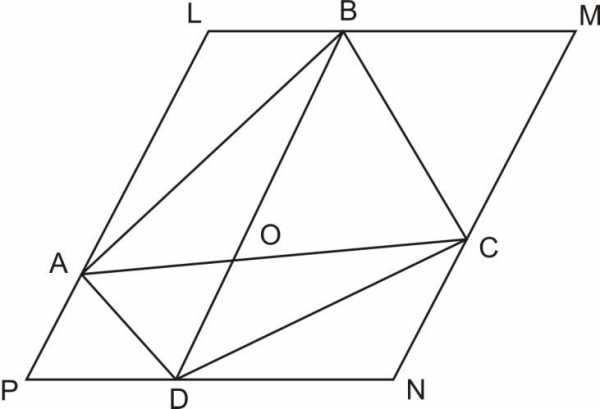
Рисунок 2.3.4
Аналогично получаем откуда следует, что.
Ответ: .
2.4 Площадь треугольника
Существует несколько формул для вычисления площади треугольника. Рассмотрим те, что изучаются в школе.
Первая формула вытекает из формулы площади параллелограмма и предлагается учащимся в виде теоремы. [4, c. 254]
Теорема. Площадь треугольника равна половине произведения его основания на высоту
.Доказательство. Пусть – площадь треугольника. Примем сторонуза основание треугольника и проведем высоту. Докажем что:
Рисунок 2.4.1
Достроим треугольник до параллелограмматак, как показано на рисунке. Треугольникииравны по трем сторонам (– их общая сторона,икак противоположные стороны параллелограма), поэтому их площади равны. Следовательно, площадь S треугольника АВС равна половине площади параллелограмма, т.е.
Теорема доказана.
Важно обратить внимание учащихся на два следствия, вытекающих из данной теоремы. А именно:
площадь прямоугольного треугольника равна половине произведения его катетов.
если высоты двух треугольников равны, то их площади относятся как основания.
Эти два следствия играют важную роль в решении разного рода задач. С опорой на данную доказывается еще одна теорема, имеющая широкое применение при решении задач.
Теорема. Если угол одного треугольника равен углу другого треугольника, то их площади относятся как произведения сторон, заключающих равные углы.
Доказательство. Пусть и– площади треугольникови, у которых углыиравны.
Рисунок 2.4.2
Докажем, что: .
Наложим треугольник . на треугольниктак, чтобы вершинасовместилась с вершиной, а стороныиналожились соответственно на лучии.
Рисунок 2.4.3
Треугольники иимеют общую высоту, поэтому,. Треугольникиитакже имеют общую высоту –, поэтому,. Перемножая полученные равенства, получим.
Теорема доказана.
Вторая формула.
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними. Существует несколько способов доказательства этой формулы, и я воспользуюсь одним из них.Доказательство. Из геометрии известна теорема о том, что площадь треугольника равна половине произведения основания на высоту, опущенную на это основание:
.
В случае остроугольного треугольника . В случае тупого угла. Ho, а поэтому. Итак, в обоих случаях. Подставив вместов геометрической формуле площади треугольника, получим тригонометрическую формулу площади треугольника:
Теорема доказана.
Третья формула для площади треугольника – формула Герона , названа так в честь древнегреческого ученого Герона Александрийского, жившего в первом веке нашей эры. Эта формула позволяет находить площадь треугольника, зная его стороны. Она удобна тем, что позволяет не делать никаких дополнительных построений и не измерять углов. Ее вывод основывается на второй из рассмотренных нами формул площади треугольника и теореме косинусов: и .
Далее мы должны из второй формулы (теоремы косинусов) выразить через сначала, а затем ии подставить в формулу для площади.
Прежде чем перейти к реализации этого плана, заметим, что
Точно так же имеем:
Теперь выразим косинус через и:
Так как любой угол в треугольнике больше и меньше, то. Значит,.
Теперь отдельно преобразуем каждый из сомножителей в подкоренном выражении. Имеем:
Значит,
Подставляя это выражение в формулу для площади, получаем:
Тема «Площадь треугольника» имеет большое значение в школьном курсе математики. Треугольник – простейшая из геометрических фигур. Он является «структурным элементом» школьной геометрии. Подавляющее большинство геометрических задач сводятся к решению треугольников. Не исключение и задача о нахождении площади правильного и произвольного n-угольника.[6,c.238]Пример 2.4.1.
Чему равна площадь равнобедренного треугольника, если его основание , а боковая сторона?
Решение:
–равнобедренный,
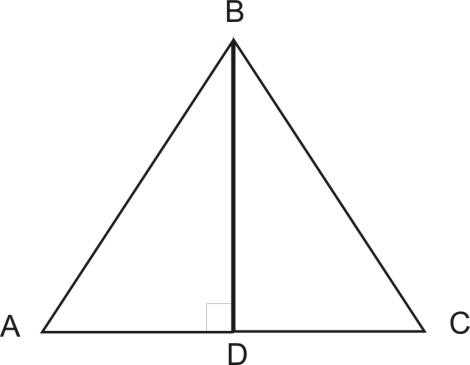
Рисунок 2.4.4
Проведём по свойству равнобедренного треугольника – медиана и высота. Тогда
В по теореме Пифагора:
Находим площадь треугольника:
Ответ:
Пример 2.4.2.
В прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезки длиной 4 и 5 см. Определить площадь треугольника.[7, c. 78]
Решение:
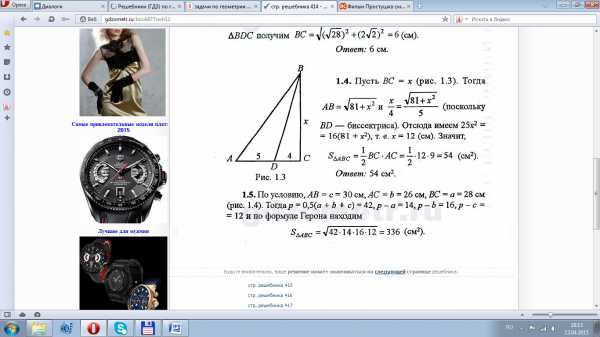
Пусть (рисунок 2.4.5). Тогдаи(посколькуBD – биссектриса). Отсюда имеем , то есть. Значит,
Рисунок 2.4.5
Ответ:
Пример 2.4.3.
Найти площадь равнобедренного треугольника, если его основание равно , а длина высоты, проведённой к основанию, равна длине отрезка, соединяющего середины основания и боковой стороны.
Решение:
По условию, – средняя линия (рисунок 2.4.6). Так какВимеем:
или
,
откудаСледовательно,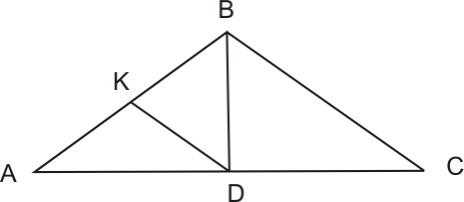
Рисунок 2.4.6
Ответ:
studfiles.net
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Планиметрия
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
S = ab,
которая позволяет найти площадь прямоугольникапрямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник | S = ab | a и b – смежные стороны | |
Посмотреть вывод формулы | d – диагональ, | ||
S = 2R2 sin φ Получается из верхней формулы подстановкой d=2R | R – радиус описанной окружности, | ||
| Параллелограмм | S = a ha Посмотреть вывод формулы | a – сторона, | |
S = absin φ Посмотреть вывод формулы | a и b – смежные стороны, | ||
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | ||
| Квадрат | S = a2 | a – сторона квадрата | |
| S = 4r2 | r – радиус вписанной окружности | ||
Посмотреть вывод формулы | d – диагональ квадрата | ||
S = 2R2 Получается из верхней формулы подстановкой d = 2R | R – радиус описанной окружности | ||
| Ромб | S = a ha Посмотреть вывод формулы | a – сторона, | |
S = a2 sin φ Посмотреть вывод формулы | a – сторона, | ||
Посмотреть вывод формулы | d1, d2 – диагонали | ||
S = 2ar Посмотреть вывод формулы | a – сторона, | ||
Посмотреть вывод формулы | r – радиус вписанной окружности, | ||
| Трапеция | Посмотреть вывод формулы | a и b – основания, | |
| S = m h | m – средняя линия, | ||
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | ||
Посмотреть вывод формулы | a и b – основания, | ||
| Дельтоид | S = ab sin φ | a и b – неравные стороны, | |
a и b – неравные стороны, | |||
S = (a + b) r Посмотреть вывод формулы | a и b – неравные стороны, | ||
Посмотреть вывод формулы | d1, d2 – диагонали | ||
| Произвольный выпуклый четырёхугольник | Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | |
| Вписанный четырёхугольник | , Посмотреть вывод формулы Брахмагупты | a, b, c, d – длины сторон четырёхугольника, Формулу называют «Формула Брахмагупты» |
| Прямоугольник | |
S = ab где | |
где Посмотреть вывод формулы | |
S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R | |
| Параллелограмм | |
S = a ha где Посмотреть вывод формулы | |
S = absin φ где Посмотреть вывод формулы | |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы | |
| Квадрат | |
| S = a2 где | |
| S = 4r2 где | |
где Посмотреть вывод формулы | |
S = 2R2 где Получается из верхней формулы подстановкой d = 2R | |
| Ромб | |
S = a ha где Посмотреть вывод формулы | |
S = a2 sin φ где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
S = 2ar где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Трапеция | |
где Посмотреть вывод формулы | |
S = m h где | |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Дельтоид | |
S = ab sin φ где | |
где | |
S = (a + b) r где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Произвольный выпуклый четырёхугольник | |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы | |
| Вписанный четырёхугольник | |
, где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты | |
| Прямоугольник |
S = ab где |
где Посмотреть вывод формулы |
S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R |
| Параллелограмм |
S = a ha где Посмотреть вывод формулы |
S = absin φ где Посмотреть вывод формулы |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Квадрат |
S = a2 где |
S = 4r2 где |
где Посмотреть вывод формулы |
S = 2R2 где Получается из верхней формулы подстановкой d = 2R |
| Ромб |
S = a ha где Посмотреть вывод формулы |
S = a2 sin φ где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
S = 2ar где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Трапеция |
где Посмотреть вывод формулы |
S = m h где |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Дельтоид |
S = ab sin φ где |
где |
S = (a + b) r где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Произвольный выпуклый четырёхугольник |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Вписанный четырёхугольник |
где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты |
Вывод формул для площадей четырехугольников
Утверждение 1. Площадь выпуклого четырёхугольника можно найти по формуле
где d1 и d2 – диагонали четырёхугольника, а φ – любой из четырёх углов между ними (рис. 1).
Рис. 1
Доказательство. В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2. Площадь параллелограммапараллелограмма можно найти по формуле
S = a ha ,
где a – сторона параллелограмма, а ha – высотавысотавысота, опущенная на эту сторону (рис. 2).
Рис. 2
Доказательство. Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
SABCD = SAEFD = a ha ,
что и требовалось доказать.
Утверждение 3.Площадь параллелограмма параллелограмма можно найти по формуле
S = ab sin φ,
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
Рис. 3
Доказательство. Поскольку
ha = b sin φ,
то, в силу утверждения 2, справедлива формула
S = a ha = ab sin φ,
что и требовалось доказать.
Утверждение 4. Площадь ромбаромба можно найти по формуле
,
где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
Рис. 4
Доказательство. Поскольку каждая из диагоналей ромба является биссектрисой угла, а каждая точка биссектрисы угла равноудалена от сторон угла, то точка пересечения диагоналей ромба равноудалена от всех сторон ромба и является центром вписанной в ромб окружности. Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
что и требовалось доказать.
Утверждение 5. Площадь трапеции можно найти по формуле
,
где a и b – основания трапеции, а h – высотавысотавысота (рис.5).
Рис. 5
Доказательство. Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD. Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF. Поэтому
что и требовалось доказать.
Утверждение 6. Площадь трапеции трапеции можно найти по формуле
,где a и b – основания, а c и d – боковые стороны трапеции,
(рис.6).
Рис. 6
Доказательство. Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

Следовательно,
где
,что и требовалось доказать.
Утверждение 7. Площадь дельтоида, дельтоида, можно найти по формуле:
S = (a + b) r,
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Рис. 7
Доказательство. Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы углов A и C пересекаются в некоторой точке O, лежащей на диагонали BD. Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то

что и требовалось доказать.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Площадь ромба | Треугольники
Площадь ромба можно найти по формулам для нахождения площади параллелограмма. С учётом свойств ромба, некоторые из этих формул меняют свой вид.
I. Площадь ромба по стороне и высоте
Площадь ромба равна произведению стороны ромба и его высоты.
Формула для нахождения площади ромба по стороне и высоте не отличается от соответствующей формулы площади параллелограмма:
Например, площадь ромба ABCD равна
Так как все стороны ромба равны и все его высоты равны, для нахождения площади можно брать любую сторону и любую высоту.
II. Площадь ромба по стороне и углу
Площадь ромба равна произведению квадрата его стороны на синус угла.
Формула для нахождения площади ромба через сторону и угол:
Например,площадь ромба ABCD равна
Так как ∠D=180-∠A, sin∠D=sin(180-∠A)=sin∠A, то для нахождения площади можно брать синус любого угла.
III. Площадь ромба через его диагонали
Площадь ромба равна половине произведения его диагоналей.
Формула для нахождения площади ромба по его диагоналям
по сравнению с соответствующей формулой площади параллелограмма упрощается (так как диагонали ромба взаимно перпендикулярны, а синус прямого угла равен единице).
Например, площадь ромба ABCD равна
IV. Площадь ромба через радиус вписанной окружности
Площадь ромба равна произведению его полупериметра на радиус вписанной окружности.
Формула для нахождения площади ромба через радиус вписанной окружности
аналогов среди формул для нахождения площади параллелограмма не имеет (поскольку из всех параллелограммов окружность можно вписать только в ромб и квадрат).
Например, площадь ромба ABCD равна
Так как полупериметр ромба равен p=2a, формулу можно записать в виде
www.treugolniki.ru
параллелограмма, трапеции, ромба, прямоугольника, квадрата.
Тестирование онлайн
Площадь четырехугольников
Площадь четырехугольника
Теорема. Площадь произвольного выпуклого четырехугольника равна половине произведения длин его диагоналей на синус угла между ними.
Площадь параллелограмма
Теорема. Площадь параллелограмма равна произведению его основания на высоту.
Площадь трапеции
Теорема. Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Площадь ромба
Площадь ромба равна половине произведения длин его диагоналей.
Площадь прямоугольника
Теорема.Площадь прямоугольника равна произведению длин его сторон.
Площадь квадрата
Площадь квадрата равна квадрату длины его стороны.
fizmat.by
Вывод формулы площади параллелограмма
Построим параллелограмм ABCD. Проведем в нем диагонали и обозначим точку их пересечения точкой О.
Рассмотрим треугольники AOD и СОВ. Эти треугольники равны между собой, а значит и площади их также равны.
Найдем сумму площадей этих двух треугольников:
Рассмотрим треугольники AOB и СОD. Эти треугольники равны между собой, а значит и площади их также равны.
Найдем сумму площадей этих двух треугольников:
Площадь параллелограмма можно найти как сумму площадей рассмотренных четырех треугольников:
Вынесем общие множители за скобки:
Сумма отрезков OD и ОВ дает диагональ параллелограмма BD, поэтому формулу перепишем в виде:
Известно, что у параллелограмма диагонали при их пересечении делятся пополам. Получаем, что отрезок АО равен половине диагонали АС. Таким образом, получим:
Итак, получена формула площади параллелограмма через его диагонали и угол между ними:
ru.solverbook.com
Урок по математике на тему «Площадь параллелограмма»
План урока
Площадь параллелограммаШкола: №55
Дата:14.03.2017г
Имя преподавателя: Абдрахманова Ш.А.
КЛАСС: 8
Число
присутствующих:
отсутствующих:
Цель обучения, способствующие данному уроку
Учащиеся будут:
– выводить и применять формулы площади параллелограмма, ромба
Цели обучения
Учащиеся будут:
– выводить формулы площадей четырёхугольников и применять их;
– выводить формулы площади треугольника и применять их;
Языковые задачи
Учащиеся будут:
– формулировать словесно формулы площадей фигур;
– формулировать вопросы для проверки понимания формул;
– комментировать вывод формул площадей фигур;
Предметная лексика и терминология
величина, единицы измерения;
длина, ширина, площадь;
периметр, полупериметр;
простая фигура, плоская фигура;
равновеликие, равносоставленные, равныефигуры
Серия полезных фраз для диалога/письма
площади параллелограмма/ромба/ ….
чтобы применить формулу …, необходимо …;
если уменьшить сторону квадрата в k раз …, то площадь …;
разделите …на равновеликие …;
Предыдущие изучения
Площадь прямоугольника
План
Планируемое время
Запланированная деятельность
Ресурсы
Начало
13 мин
Деление на группы. П
Предложу каждой группе игру «Тарсия» для повторения пройденного материала.
1.Какая фигура получилось? (параллелограмм)
2.Что имеет каждая плоская фигура? (Площадь)
Тема сегоднешнего урока: «Площадь параллелограмма»
Середина
30 мин
Запишите формулы площадей фигур в таблице которых вы знаете.
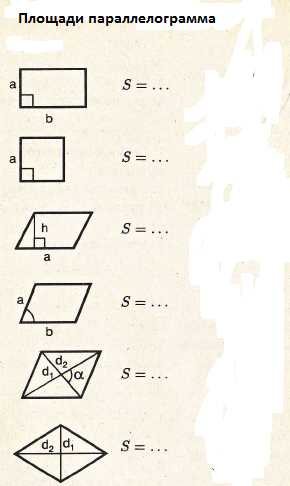
Площадь параллелограмма
Практическая работа
(Приложение1
Раздам картонную модель для составления произвольного параллелограмма и прямоугольника. Попрошу составить параллелограмм, а затем из параллелограмма прямоугольник.
Обозначить основания буквой a, высоту буквой h.
Обсудить и ответить
1) Являются ли параллелограмм и прямоугольник равновеликими? Почему?
2) Изменилась ли длина основания? Обозначьте ее a.
3) Чем является ширина прямоугольника для параллелограмма? (высотой параллелограмма) Обозначьте ее h.
4) Найдите площадь прямоугольника.
5) Сделайте вывод о площади параллелограмма. Запишите полученную формулу.
Вывешиваю все формулы площади параллелограмма на доску.



Каждая группа выводит их.
Используем формулы при решение задач.
№252( ответ:11,7), №253
Подводя учащихся к решению задачи, задать учащимся вопросы:
– Что требуется найти в задаче?
–Что нужно знать, чтобы найти площадь?
– Какую сторону можно выбрать за основание?
(7,5 или 4,8) ( двое из разных групп работают на доске )
Площадь ромба.
Практическая работа
(Приложение 2)
Раздам картонную модель треугольника, попрошу сложить ромб. и сложить из ромба прямоугольник или прямоугольный треугольник.
Сделайте вывод о площади ромба. Запишите полученную формулу.
При решении задач на применение формулы площади ромба, решаем:
№257
Дополнительное задание
Найдите площади параллелограмма:
2 мин
Рефлексия
Закончите предложения.
На этом уроке я узнал…
Я научился….
Я умею…
Дом.зад. П.19 1.
Дом. Зад для учащихся:
1) Верно ли, что равносоставленные фигуры всегда равновелики?
2) Верно ли, что равновеликие фигуры всегда равносоставленные?
3) Верно ли, что любые два равновеликих многоугольника всегда равносоставлены?
Дополнительная информация
Дифференцирование – как вы планируете оказать поддержку? Как вы планируете работать с более способными учениками?
Оценка – как вы планируете проверять учащихся?
Перекрестные ссылки.
Проверка гигиены труда и техники безопасности
ICT ссылки
Значения
Групповые занятия планируются таким образом, чтобы более слабые ученики работали в группе, в которой они смогут учиться во время бесед и наблюдения за более способными учениками.
Класс должен быть уверен, что все будут участвовать в групповых обсуждениях, чтобы более слабые не зависели от сильных.
Образовательная оценка на основании наблюдения за активности учащихся при проведении обсуждений и других мероприятий.
Значения:
Учащиеся должны быть изобретательными, критичными и поддерживать друг друга при работе в группе;
У них будет возможность проводить диалоги, в частности при групповой активности, для развития навыков общения.
Как участники групповых опросов, они поймут необходимость быть ответственными учениками, слушая других, делясь идеями, участвуя в обсуждениях.
Отражение
Был ли урок /Цели обучения реалистичным? Что учащиеся узнали сегодня? Какова была атмосфера при изучении? Хорошо ли сработал запланированная дифференциация? Уложился ли я по времени? Какие изменения я внес в план и почему?
В поле ниже опишите ваш урок. Ответьте на наиболее подходящие вопросы в столбце слева о вашем уроке.
Подведение итогов
Каких два момента прошли действительно хорошо (рассматривая и обучение, и изучение)?
Каких два момента улучшили урок (рассматривая и обучение, и изучение)?
Что я узнал из этого урока о классе или отдельных учащихся, о чем расскажу на следующем уроке?
Приложение 1
Практическая работа.Площадь параллелограмма
Из данных фигур составьте параллелограмм и обозначьте основания буквой a, высоту буквой h.
Составить из параллелограмма прямоугольник.
Обсудить и ответить:
1)Являются ли параллелограмм и прямоугольник равновеликими? Почему?
2) Изменилась ли длина основания? Обозначьте ее a.
3) Чем является ширина прямоугольника для параллелограмма? Обозначьте ее h
4) Найдите площадь прямоугольника. =
5) Сделайте вывод о площади параллелограмма.
6) Запишите полученную формулу. =
Практическая работаПлощадь ромба.
Практическая работа.
1.Из модели треугольника, попрошу сложить ромб
2.Сложить из ромба прямоугольник
3.Сделайте вывод о площади ромба.
4.Запишите полученную формулу.
Рефлексия:
Закончите предложения.
На этом уроке я узнал…
Я научился….
Я умею…
Дом.зад. П.19 1.
Дом. Зад для учащихся:
1) Верно ли, что равносоставленные фигуры всегда равновелики?
2) Верно ли, что равновеликие фигуры всегда равносоставленные?
3) Верно ли, что любые два равновеликих многоугольника всегда равносоставлены?

infourok.ru
