Постройте график функции y = –x^2 + 4
Задание.
Постройте график функции y = —x^2 + 4.
Ответ
Перед выполнением построения графика функции ее необходимо проанализировать.
Сначала определим, что за функция дана в условии.
Функция содержит квадрат переменной х, следовательно, функция — квадратная. Это значит, что ее графиком будет парабола.
При построении параболы обращают внимание на знак перед квадратом х. Если перед квадратом х не стоит знак или стоит знак «плюс», то ветви такой параболы направлены вверх, а если знак «минус» — ветви ее направлены вниз. Итак, поскольку перед квадратом х стоит минус, то ветви будут направлены вниз.
При построении параболы необходимо определить точку, в которой будет находиться ее вершина. Для определения абсциссы координаты вершины существует специальная формула. Воспользуемся ею:
Подставим найденную абсциссу в уравнение функции и найдем ее ординату:
Итак, вершиной параболы будет точка (0; 4).
Далее нужно найти точки, которые принадлежат графику параболы. Сделать это легко. Берем несколько произвольных значений переменной х и вычисляем для них значение переменной у. Полученные пары чисел будут координатами искомых точек.
х = 2: —точка с координатами (2; 0).
х = —1: —точка с координатами (—1; 3).
х = —2: —точка с координатами (—2; 0).
Нанесем найденные точки на координатную плоскость и начертим график функции y = —x^2 + 4.
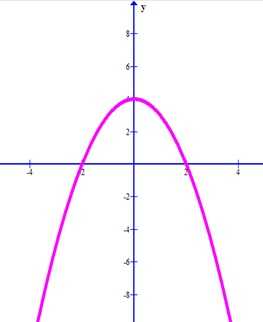
ru.solverbook.com
Постройте график функции y = x^2-4
Задание.
Постройте график функции y = x^2 — 4.
Ответ
Поскольку функция содержит квадрат переменной х, то она квадратная. Следовательно, ее графиком будет парабола.
О параболе известно, что у нее есть вершина, что ветви ее могут быть направлены вверх или вниз, и что она может быть симметрична оси Оу.
Начнем с симметричности относительно оси Оу.
Если функция симметрична, то она называется четной. Свойство четности можно проверить, подставив вместо переменной х противоположное ей значение, то есть —х. Если в результате получим уравнение функции без изменений, то функция является четной, а значит симметричной относительно оси Оу.
Итак, проверим функцию на четность:
— функция четная.
Далее определим куда направлены ветви параболы. Для этого достаточно посмотреть на знак перед квадратом переменной х. в нашем случае перед ним стоит условно знак «плюс», а это значит, что ветви параболы будут направлены вверх.
Для определения координаты точки вершины параболы будем использовать готовую формулу, которая дает возможность найти значение первой координаты точки вершины параболы:
Чтобы получить значение второй координаты вершины подставим найденное значение х в уравнение функции:
Таким образом, вершиной параболы является точка (0; —4).
Теперь нужно вычислить еще какое-то количество точек, которые будут принадлежать параболе, для ее построения.
Возьмем четыре произвольных значения переменной х и посчитаем для них значение функции у:
х = 1: —точка (1; —3).
х = 2: —точка (2; 0).
х = —1: —точка (—1; —3).
х = —2: —точка (—2; 0).
Проведем через вершину и полученные точки кривую и получим график функции y = x^2 — 4.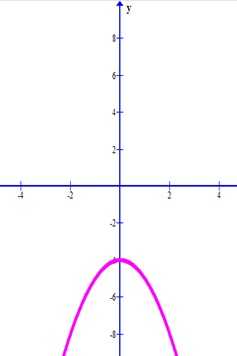
ru.solverbook.com
Постройте график функции y = x^2 – |4x + 3|
Задание.
Постройте график функции y = x^2 — |4x + 3|
Решение.
В данном уравнении сразу бросается в глаза знак модуля, который запутывает все решение. На самом же деле строить подобные графики абсолютно несложно, в чем сейчас и убедитесь.
Модуль, под знаком которого содержится переменная х, указывает на то, что она может принимать и положительные, и отрицательные значения. Такая ситуация приведет к тому, что график будет содержать две параболы.
Рассмотрим вариант, когда переменная х принимает положительные значения. Раскроем для такого значения модуль и получим:
Теперь рассмотрим вариант, при котором переменная х будет принимать отрицательные значения. Тогда:
Получили два разных уравнения параболы для отрицательных и положительных значений переменной х.
Найдем координаты вершины первой из парабол:
Вершиной первой параболы будет точка (2; —7).
Найдем координаты вершины второй из парабол:
Вершиной второй параболы будет точка (—2; —7).
Первая парабола будет пересекаться с осями координат в следующих точках:
С осью Оу при х = 0:
С осью Ох при у = 0:
— не подходит, так как х должен быть положительный
Значит, точка пересечения первой параболы с осями координат — (0; —3) и (4,65; 0).
Вторая парабола будет пересекаться с осями координат в следующих точках:
С осью Оу при х = 0:
С осью Ох при у = 0:
— не подходит, так как х должен быть отрицательный
Значит, точки пересечения второй параболы с осями координат — (0; —3) и (—4,65; 0).
Нанесем все точки графика на координатную плоскость и соединим.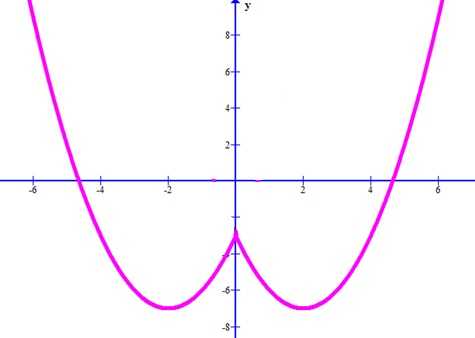
ru.solverbook.com
