Интегрированный урок (физика + геометрия) по теме «Прямоугольный треугольник в геометрии и физике»
Эпиграф:
Все науки настолько связаны между собой, что легче изучать их все сразу, нежели какую-либо одну из них в отдельности от всех. (Рене Декарт)
Цели урока:
- Образовательная: расширить представления учащихся о прямоугольном треугольнике и его свойствах, научить применять данные свойства при решении задач по геометрии и физике; проверить теоретические знания учащихся по этим темам и практические навыки решения задач.
- Развивающая: развивать у учащихся познавательный интерес к учебным дисциплинам, умение применять свои знания на практике. Выявить глубокие связи между физикой и математикой.
- Воспитательная: воспитывать внимание,
аккуратность, расширять кругозор учеников.
Оборудование: мультимедийный проектор, карточки для самостоятельной работы по геометрии и физике.
Задачи учителей: показать практическое применение теоретических знаний по геометрии при решении задач по физике.
I. Вызов интереса
Задача индийского математика XII века Бхаскары.
На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута всего широка.
Верхушка склонилась у края реки,
Осталось три фута всего от ствола.
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?
Учитель математики. Историческая справка.
Первое представление о прямоугольном
треугольнике греки получили, рассматривая
верёвку, косо идущую от вершины шеста.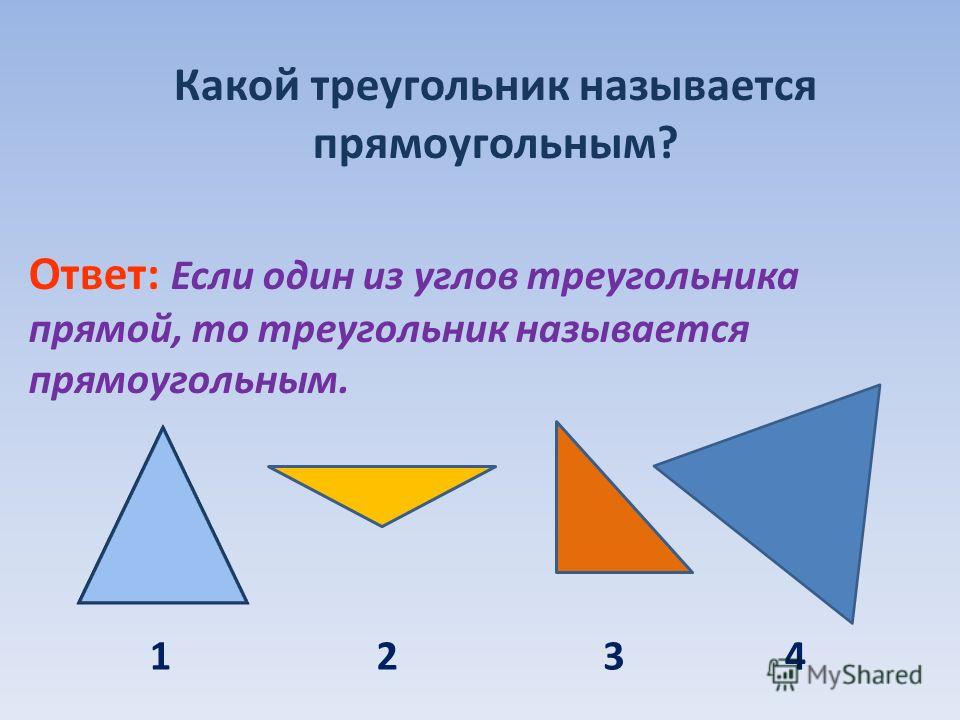
Таким образом, можно было определить расстояние до недоступных предметов, например, высоту дерева.
Прямоугольный треугольник занимает почетное место в вавилонской геометрии, упоминание о нем встречается в папирусе Ахмеса.
Термин гипотенуза происходит от греческого hypoteinsa, означающего тянущаяся под чем-либо, стягивающая. Слово берет начало от образа древнегреческих арф, на которых струны натягивались на концы двух взаимно перпендикулярных подставок.
Термин катет происходит от греческого слова “катетос”, которое означало отвес,
перпендикуляр. Евклид употреблял выражения: “стороны, заключающие прямой угол” – для катетов; “сторона, стягивающая прямой угол” – для гипотенузы.
Небесные светила так же являются недоступными
для точного измерения, а человеку всегда
хотелось знать о том, каково расстояние между
планетами.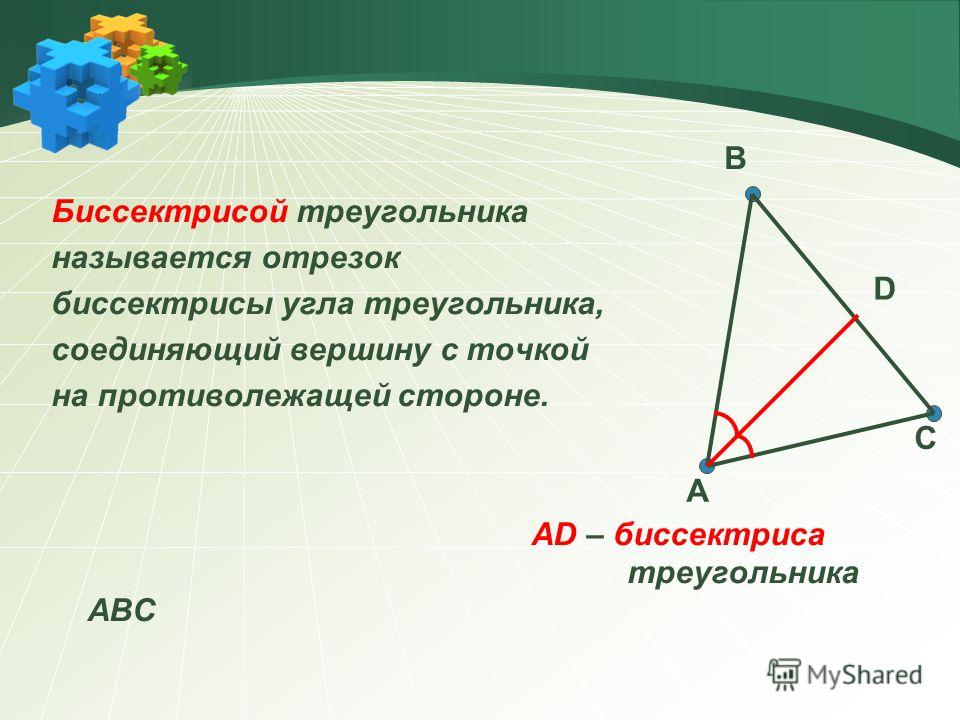
Как быть? На этот вопрос готова
ответить математика.
Учитель физики.
Параллакс (греч. “смена, чередование”) — изменение видимого положения объекта относительно удалённого фона в зависимости от положения наблюдателя. На сегодняшний день параллаксы всех планет и ближайших звезд измерены.
Параллакс определяют из двух точек земной поверхности, находящихся на одном географическом меридиане и имеющих известные географические широты.
Отрезок АС, длина которого тщательно измерена, называется базисом.
Угол АВС, под которым из недоступного места виден базис, называется параллаксом и обозначается – р.
При определении расстояний до тел солнечной системы в качестве базиса используют радиус Земли, т.е. АC = Rз = 6378 км.
r = АС : sin p = R : sin p = R : р = R х 206265″ : р (км)
При определении расстояний до ближайших звезд
за базис принимают большую полуось земной
орбиты, т.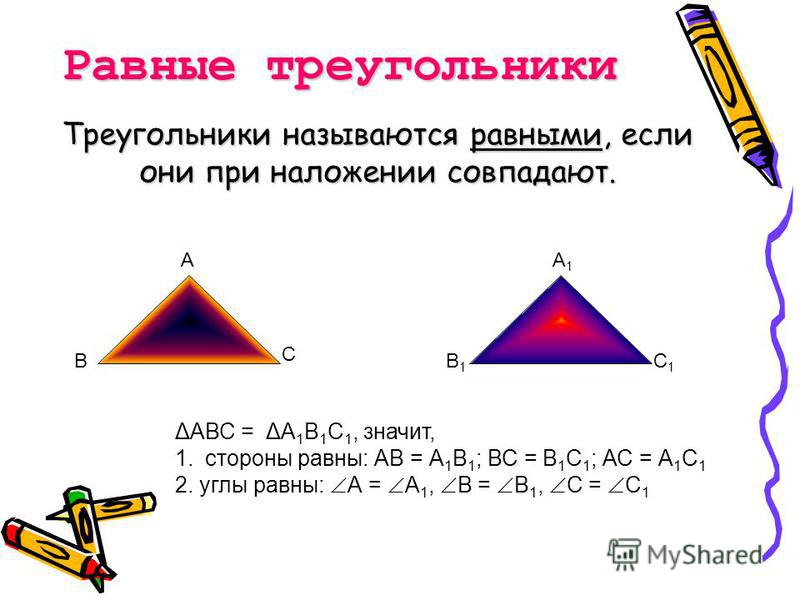
е. АС = 150 000 000 км = 1 а.е.
(1 астрономическая единица)
Параллакс – угол, под которым со звезды была бы видна большая полуось земной орбиты, развернутая перпендикулярно направлению на звезду.
Чем меньше параллакс, тем дальше находится звезда.
r = АС : sin р = 1 : sin р = 1 : р = 206265″ : р (а.е.)
II. Повторение ранее изученного материала
Учитель математики. Каждый человек, заботящийся о своем здоровье, начинает день с зарядки. Вот и мы для начала проведем интеллектуальную разминку.
Я предлагаю вам в течение 4 минут вспомнить и записать все самое важное о прямоугольном треугольнике, что вы изучали на уроках геометрии.
Через заданное время учащиеся вместе с
учителем обсуждают записанное. Если каких-либо
данных не хватает, учитель обращает на это
внимание. В итоге учащимся раздается
подготовленная учителем таблица с основными
данными о прямоугольном треугольнике.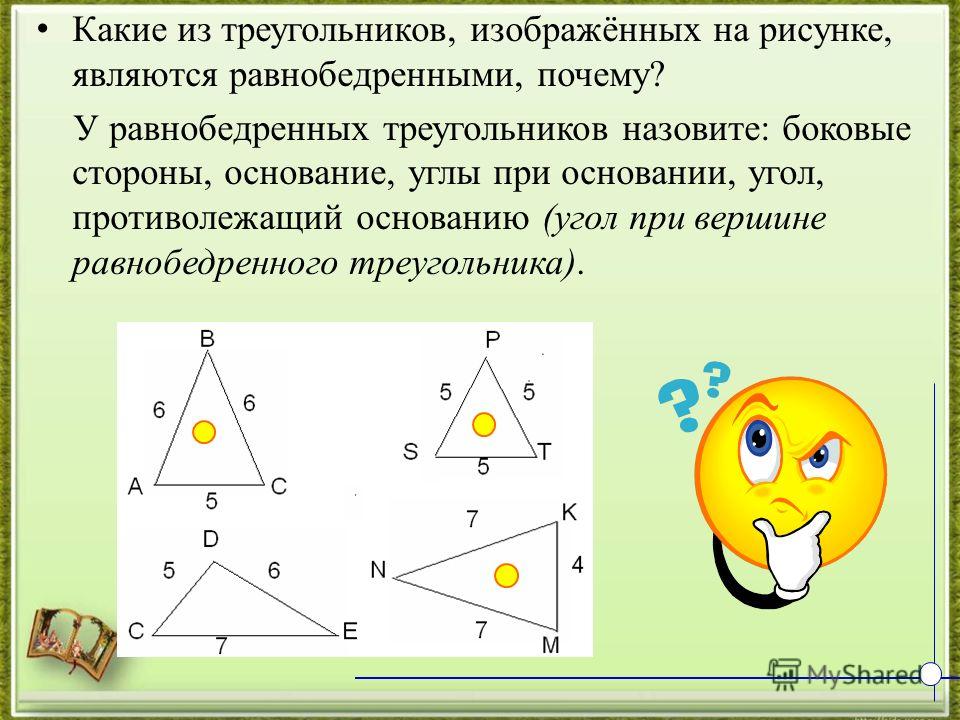
III. Решение физических задач
1. С каким ускорением скользит брусок по наклонной плоскости высотой 60 см и длиной 1 м, если коэффициент трения равен 0,2?
2. Заряды по 0,1 мкКл расположены на расстоянии 6 см друг от друга. Найти напряженность поля в точке, удаленной на 5 см от каждого из зарядов.
3. На каком расстоянии от собирающей линзы с фокусным расстоянием 60 см следует поместить предмет, чтобы получить действительное изображение, увеличенное в 2 раза?
IV. Физкультминутка
V. Тестирование
Учащимся предлагаются два теста: часть учащихся садится за компьютеры и выполняет тест по физике. Оставшиеся учащиеся выполняют тест по математике за партами. Все задания в тестах взяты из реальных ЕГЭ.
Тест по математике
1. Гипотенуза прямоугольного треугольника
равна 30 . А радиус вписанной окружности этого
треугольника равен 6.
Найдите периметр этого
треугольника.
2. В треугольнике АВС угол С равен 90
3. В треугольнике АВС угол С равен 90o, гипотенуза равна 8, катет равен 5. Найдите проекцию данного катета на гипотенузу.
4. В треугольнике АВС угол С равен 90o, гипотенуза равен 20, соsВ= 0.8 . Найдите АС.
5. В прямоугольном треугольнике АВС с углом А равным 36° проведены медиана СМ и биссектриса CD. Найдите угол DCМ (в градусах)
Тест по физике
1. Найти проекцию вектора силы тяжести на ось ОХ.
2. Лодка должна попасть на противоположный берег по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки u, а скорость лодки относительно воды v. Чему равна скорость лодки относительно берега?
3. На каком расстоянии нужно поместить предмет
перед собирающей линзой, чтобы получить
действительное изображение на расстоянии 60 см от
линзы? Высота изображения должна быть в 3 раза
больше высоты предмета.
4. На рисунке дан ход лучей, полученный при прохождении света через плоскопараллельную пластинку. Чему равен показатель преломления вещества пластинки?
5. Туристы прошли 300 м на восток и, оказавшись перед болотом, повернули на север, пройдя 400 м. Чему равна длина перемещения и пройденный ими путь?
Ответы на тесты
| Математика | Физика |
| 72 | mgsina |
| -0,8 | — u2 |
| 20 см | |
| 12 | 1,5 |
| 9 | 500 м и 700 м |
V.
Подведение итогов
Лист самоконтроля
| Ф.И. | Блиц-опрос | Задача 1 | Задача 2 | Задача 3 | Тест | Итоговая оценка |
Произвольный треугольник. Определение медианы, высоты
Рис. 1. Треугольник (общий случай)
Треугольник — замкнутая геометрическая фигура, состоящая из трёх отрезков (в общем случае, разных).
В физике эти отрезки классически называются буквами латинского алфавита (
и т.д.), в отличие от обозначений в геометрии.
Итак, треугольник, у которого все стороны имеют разную длину и ни один из углов не равен
, называется произвольным (рис. 1).
В случае, если у треугольника равны две стороны, данный треугольник называется равнобедренным
В случае, если у треугольника все стороны одинаковы, он называется равносторонним.
В случае, если у треугольника один и углов прямой (
), он называется прямоугольным.
Для произвольного треугольника вводят ряд отрезков, характеризующих треугольник и обладающих собственными свойствами:
- Биссектриса
- Высота
- Медиана
Для разных типов треугольников поиск длин параметров треугольника может происходить по-разному.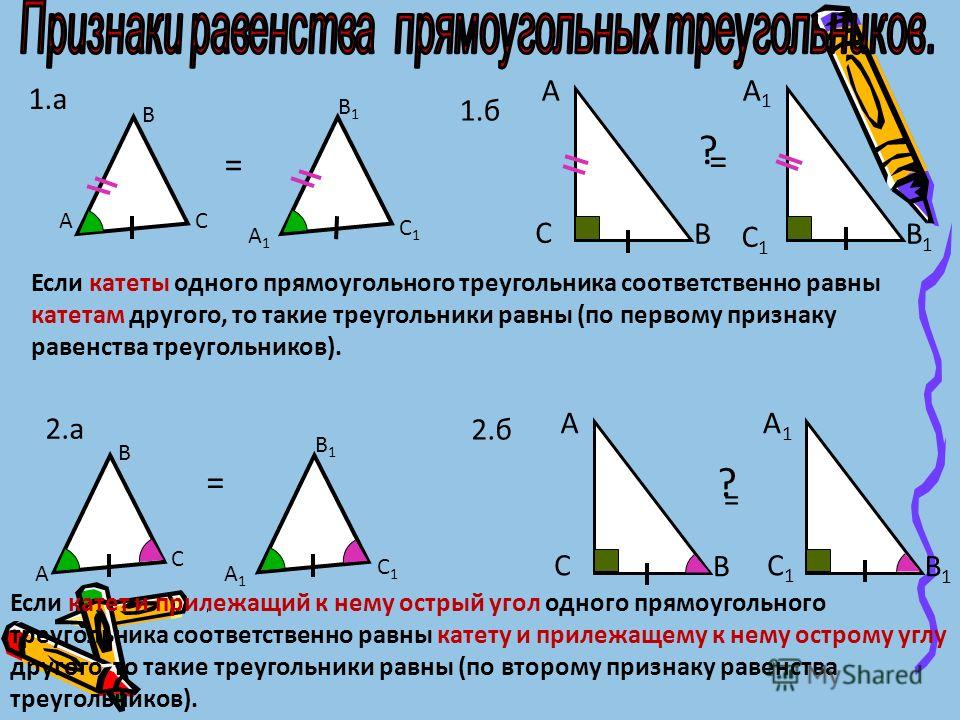
Для физических задач использование конкретной формулы диктуется конкретными данными задачи.
Рис. 2. Треугольник (биссектриса)
Биссектриса угла — геометрическое место точек, равноудалённых от сторон этого угла. Т.е. биссектриса — это линия, которая делит угол треугольника пополам (рис. 2). Известно, что биссектриса внутреннего угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
Для нахождения биссектрисы угла через различные данные можно пользоваться следующими соотношениями:
- через две стороны и угол:
(1)
- через три стороны:
(2)
Медиана треугольника — отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Все медианы треугольника пересекаются в одной точке: данная точка делит медианы в соотношении 2 к 1, считая от вершины (рис.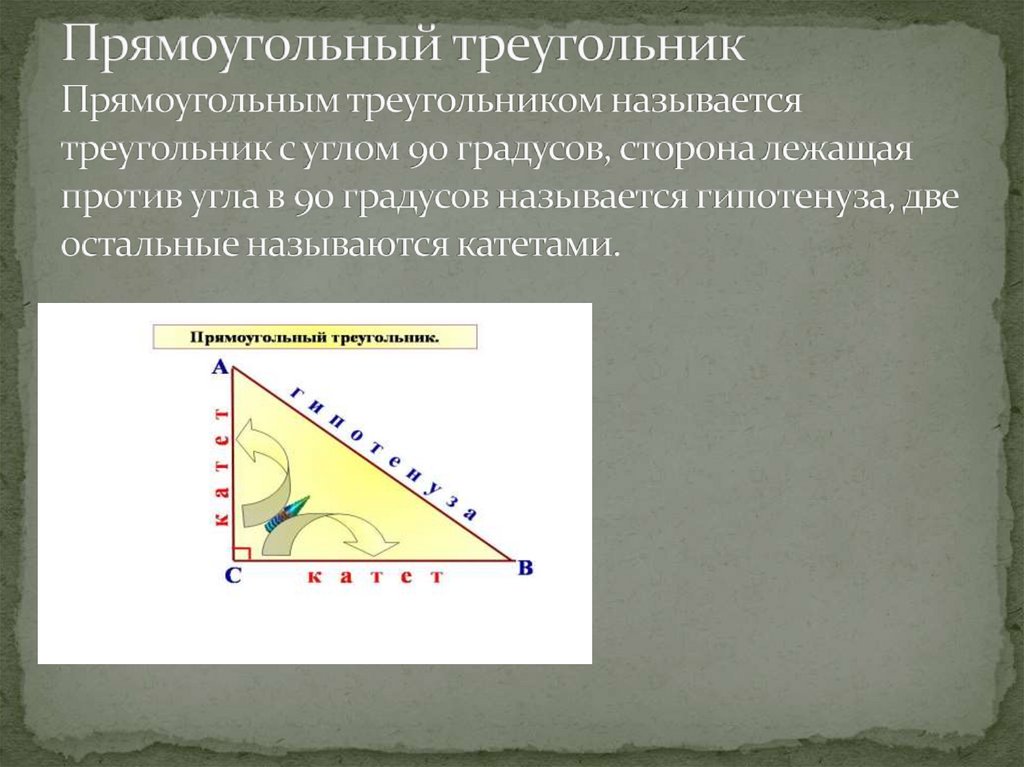
3).
Рис. 3. Треугольник (медиана)
Для нахождения медианы треугольника через различные данные можно пользоваться следующими соотношениями:
- через три стороны:
(3)
- через две стороны и угол между ними:
(4)
Рис. 4. Треугольник (высота)
Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону или на её продолжение (рис. 4).
Для нахождения высоты треугольника через различные данные можно пользоваться следующими соотношениями:
- через сторону и угол:
(5)
- через сторону и площадь треугольника ()
(6)
Важно: то, какую формулу выбрать для решения конкретной задачи, зависит от того, что легче найти, исходя из дано.
Понравилось это:
Нравится Загрузка…
Треугольники – равнобедренные, равнобедренные и разносторонние
c2ZWPA3kduw
Треугольник имеет три стороны и три угла | ||
Три угла всегда дают в сумме 180° |
Равносторонний, равнобедренный и разносторонний
Существует три специальных названия треугольников, которые говорят, сколько сторон (или углов) равны.
Могут быть 3 , 2 или нет равные стороны/углы:
Равносторонний треугольник Три равных стороны | |
Равнобедренный треугольник Две равные стороны | |
Разносторонний треугольник № равносторонние |
Как запомнить? В алфавитном порядке идут 3, 2, нет:
- Равносторонний : «равный» -боковой (боковой означает сторону), поэтому у них все равные стороны
- Равнобедренный : означает «равные ноги», и у нас две ноги , верно? тоже я SOS целе имеет два равных «S ides», соединенных стороной « O dd».
- Scalene : означает «нечетный» или «нечетный», поэтому нет равных сторон.
Какой угол?
Треугольники также могут иметь имена, которые говорят вам, какой тип угла находится внутри :
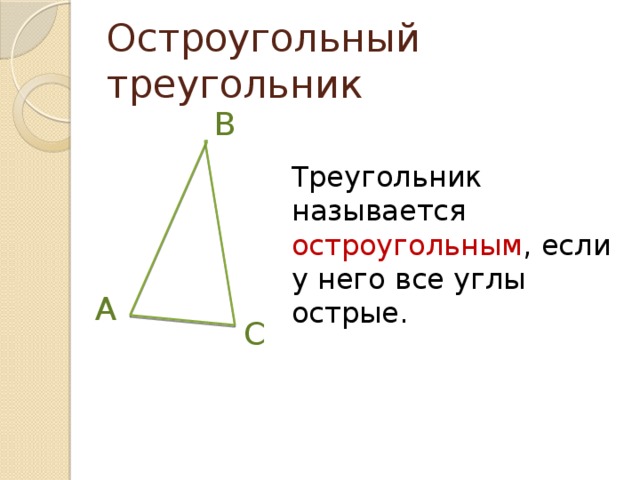
Остроугольный треугольникВсе углы меньше 90° | |
Прямоугольный треугольникИмеет прямой угол (90°) | |
Тупоугольный треугольникИмеет угол более 90° |
Объединение имен
Иногда у треугольника может быть два имени, например:Прямоугольный равнобедренный треугольникИмеет прямой угол (90°), а также два равных угла Угадайте, какие углы равны? |
Поиграй с этим.
..Попробуйте перетащить точки и сделать разные треугольники:
геометрия/изображения/triangle.js?mode=тип
Вы также можете поиграть с интерактивным треугольником.
Уголки
Сумма трех внутренних углов всегда составляет 180°
геометрия/изображения/triangle.js?mode=angles
Периметр
Периметр — это расстояние вокруг края треугольника: просто сложите три стороны:
геометрия/изображения/triangle.js?mode=perim
Район
Площадь равна половине основания, умноженному на высоты.
- «b» расстояние по базе
- «h» — высота (измеряется под прямым углом к основанию)
Площадь = ½ × b × h
Формула работает для всех треугольников.
Примечание: формулу проще записать так: bh/2
Пример: Какова площадь этого треугольника?
(Примечание: 12 — это высота , а не длина левой стороны)
Высота = h = 12 h = ½ × 20 × 12 = 120
Основание может быть любой стороной, только убедитесь, что «высота» измеряется под прямым углом к »основанию» :
геометрия/изображения/triangle.
js?mode=область
(Примечание. Вы также можете рассчитать площадь по длинам всех трех сторон, используя формулу Герона.)
Почему Зона «Половина бх»?
Представьте, что вы «раздвоили» треугольник (перевернули его вокруг одного из верхних ребер), чтобы получилась квадратная форма (параллелограмм), которую можно изменить на простой прямоугольник:
ТОГДА вся площадь равна bh , то есть для обоих треугольников, поэтому только один равен ½ × bh .
6702, 6708,720, 3134, 5032,627,723, 3132, 3133, 7502
▲ ▼ ◭ ⨻ ⨻ Символы треугольника
| Символ треугольника | Имя треугольника | Десятичный | HEX | ▲ | 9000Black AP-Pointting-Pointting-Pointting-Pointting-Pointting-Pointting-Pointting-Pointting-Pointting-Pointting-Pointtytting-Pontting-Pontting-Pontting-Pontting-Pontting-Pontting-Pointting-Ponttytting-Pointtytting-Pointtytting-Pontting | ▲ |
|---|---|---|---|
| △ | Белый треугольник вершиной вверх | △ | △ |
| ▴ | Черный маленький треугольник, направленный вверх | ▴ | ▴ |
| ▵ | Маленький треугольник белого цвета, направленный вверх | ▵ | ▵ |
| ▶ | Черный треугольник, указывающий вправо | ▶ | ▶ |
| ▷ | Белый треугольник, указывающий вправо | ▷ | ▷ |
| ▸ | Черный маленький треугольник, указывающий вправо | ▸ | ▸ |
| ▹ | Маленький треугольник, направленный вправо, белый | ▹ | ▹ |
| ▼ | Черный треугольник с вершиной вниз | ▼ | ▼ |
| ▽ | Белый треугольник с вершиной вниз | ▽ | ▽ |
| ▾ | Черный маленький треугольник, направленный вниз | ▾ | ▾ |
| ▿ | Маленький треугольник, направленный вниз, белый | ▿ | ▿ |
| ◀ | Черный треугольник, указывающий влево | ◀ | ◀ |
| ◁ | Белый треугольник, указывающий влево | ◁ | ◁ |
| ◂ | Черный маленький треугольник, направленный влево | ◂ | ◂ |
| ◃ | Белый маленький треугольник, направленный влево | ◃ | ◃ |
| ◢ | Черный нижний правый треугольник | ◢ | ◢ |
| ◣ | Черный нижний левый треугольник | ◣ | ◣ |
| ◤ | Черный левый верхний треугольник | ◤ | ◤ |
| ◥ | Черный верхний правый треугольник | ◥ | ◥ |
| Символ треугольника | Имя треугольника | Десятиц | Hex |
|---|---|---|---|
| ◬ | White Uppointing Triangle с Dot | 99908;◬ | |
| ◭ | Треугольник вершиной вверх с левой половиной черного цвета | ◭ | ◭ |
| ◮ | Треугольник вершиной вверх с правой половиной черного цвета | ◮ | ◮ |
| ◸ | Верхний левый треугольник | ◸ | ◸ |
| ◹ | Верхний правый треугольник | ◹ | ◹ |
| ◺ | Нижний левый треугольник | ◺ | ◺ |
| ◿ | Нижний правый треугольник | ◿ | ◿ |
| ⛛ | Большой белый треугольник с вершиной вниз | ⛛ | ⛛ |
| ⟁ | Белый треугольник, содержащий маленький белый треугольник | ⟁ | ⟁ |
| ⧊ | Треугольник с точкой над | ⧊ | ⧊ |
| ⧋ | Треугольник с подкладкой | ⧋ | ⧋ |
| ⧌ | S В треугольнике | ⧌ | ⧌ |
| ⧍ | Треугольник с засечками внизу | ⧍ | ⧍ |
| ⧎ | Правый треугольник Над левым треугольником | ⧎ | ⧎ |
| ⧏ | Левый треугольник рядом с вертикальной полосой | ⧏ | ⧏ |
| ⧐ | Вертикальная черта рядом с прямоугольным треугольником | ⧐ | ⧐ |
| ⧨ | Треугольник с вершиной вниз и левой половиной черного цвета | ⧨ | ⧨ |
| ⧩ | Черный треугольник с вершиной вниз и правой половиной | ⧩ | ⧩ |
| ⨞ | Оператор большого левого треугольника | ⨞ | ⨞ |
| ⨨ | Знак плюс с черным треугольником | ⨨ | ⨨ |
| Символ треугольника | Имя треугольника | Десятичный | Шестнадцатеричный |
|---|---|---|---|
| ⨹ | Плюс Войти Треугольник | ⨹ | ⨹ |
| ⨺ | Знак минус Треугольник | ⨺ | ⨺ |
| ⨻ | Знак умножения Треугольник | ⨻ | ⨻ |
Скопируйте и вставьте символ треугольника или используйте десятичное, шестнадцатеричное число Unicode или объект html на веб-сайтах социальных сетей, в своем блоге или в документе.